2. 中国科学院大学, 北京 100049;
3. 德国亥姆霍兹环境研究中心(UFZ), 莱比锡 04318, 德国
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Helmholtz Centre for Environmental Research-UFZ, Leipzig 04318, Germany
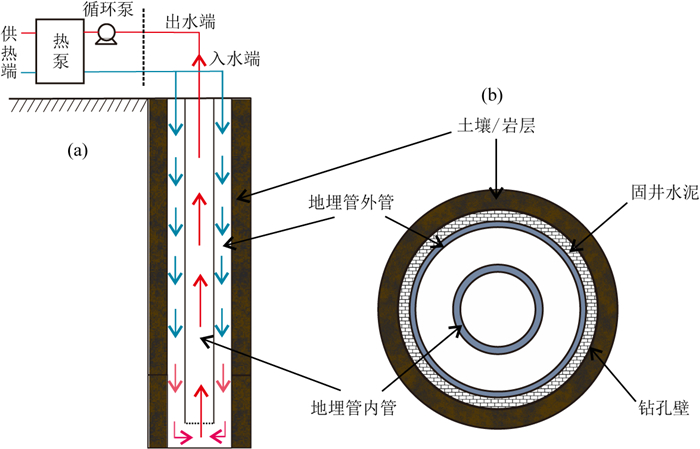
随着人类对可再生能源需求的增加,地热能的规模化开发利用势在必行.根据地热能的埋深,通常将其分为浅层(0~200 m)、中深层(200~3000 m)和超深层(大于3000 m);相应的采热技术分别为地源热泵技术、回灌式水热开采技术和以人工造储为特征的干热岩开采技术.近年来,国内地热供暖主要采用的前两类技术.然而,受地埋管占地面积大、易形成冷/热堆积等因素限制,地源热泵系统在密度高的城区建筑,或者地温较低的寒区地带,应用受到限制.中深层水热型地热能的开发,由于其本身的资源特征而推广受限:一方面热储条件地区差别大,另一方面回灌在诸多热田都较为困难(Kong et al., 2014).利用压裂技术开采超深层地热(干热岩)的技术,则因其高额成本等因素,目前在我国还处于科学研究和探索阶段.在此背景下,改进中深层地热的采热技术,实现“取热不取水”,成为国内地热界探索的新方向.其实,该项技术并非国内首创.国外20年来走过了十分相似的技术发展历程.Rybach和Hopkirk (1995)最早提出了利用深井换热技术(Deep borehole heat exchanger)开采中深层水热型地热能为建筑供暖的思想.如图 1所示,在一口钻井内,安装一同轴套管,为降低热阻,提高换热效率,往往在套管的外壁和周边地层之间灌入水泥砂浆,以保证套管和围岩之间的接触和传热,该技术也被称为套管换热技术.为实现供暖目的,在外套管中注入冷水,冷水下降过程中被周边的岩石(土)加热升温,当水流到套管底部之后,通过内管再次向上运移.热水回到地面后,将其热量经热泵机组抬升,用于建筑供暖, 冷却之后的循环水再次进入地下换热循环,将周边岩石(土)中的热量带到地表.
|
图 1 深井换热系统 (a)套管轴向截面;(b)套管横截面. Fig. 1 Schematic disgram of coaxial deep borehole heat exchanger system (a) Vertical profile; (b) Horizontal cross-section. |
经过20余年的发展,多个西方发达国家均已将深井换热技术应用于建筑供暖之中,并取得了大量实践经验.表 1列举了国外文献中所报道的一些应用实例.这些工程的开发初衷多是为寻找水热型地热资源,但在钻到预定深度之后发现是干孔,于是转变技术路线,由传统的水热型地热资源开采技术转为深井换热技术.在这些应用实例中,最高的延米换热功率是美国夏威夷的项目,达到约189 W·m-1.需要指出的是,表中所列的370 kW的功率只是短期运行的峰值数据,而非长期稳定换热负荷,并且夏威夷地热资源条件好,其他地区难以简单类比.依照作者和国外同行的交流,目前运行期较长的实际案例,延米换热功率多在100 W以下.相比之下,常规的水热型开采,给定同样的热背景,延米换热功率多在1000 W以上,显然远高于深井换热技术的换热功率.因此,国外诸多深层换热井在运行一段时间以后都最终关闭.比如德国亚琛大学的实验井,2009年开始运行,于两年之后(2011年)关闭.
|
|
表 1 国外深井换热技术应用一览 Table 1 Overview of DBHE application cases from the literature |
考虑到我国水热型地热资源受到地域限制,且受到深层地下水开发权的制约,加上在中深层地热开采中钻出干孔的情况很常见,深井换热技术仍有其利用价值.要实现有效应用,关键是要在设计阶段对该系统的可持续换热量进行定量计算,进而对热储加以适当改造.近期国内地热市场对该技术的呼声较高,多家企业在生产型项目中正开展关于这项技术的应用实践.个别企业在宣传材料中表示,他们的换热井可以获得每延米400 W,乃至600 W的稳定换热量,这样的宣传和上文中国外同行的经验存在着显著的不同.本文将基于深井换热的理论框架,介绍国外最为前沿的用于评估深井换热量的解析法和数值法.参照我国北方的地热资源条件,分别模拟短期(4个月)、短期间断式和长期(30年)背景下一系列的开采场景.通过对计算结果的分析,对该项技术的可持续换热量进行定量评估,为相关企事业单位的决策与设计提供参考.
2 换热量计算方法为确保计算的准确性,本文分别采用解析法和数值法来求解换热量,其基本的求解思路是借助于给定换热功率,获得地温和井内的进出水温度,一旦进水温度低于0 ℃,即认为达到最大换热功率.考虑到深井换热技术与浅层地热利用技术的相似性,本文对换热井中的内管、外套管、固井水泥和周边岩石(土)这4个区域分别建立传热方程,然后利用解析和数值方法进行求解.由于在深井换热情景中,地温随深度显著变化(即存在地温梯度),在采用数值法进行计算时,特别考虑了地温梯度的影响.
2.1 解析法Li和Lai(2015)分类总结了一些已有的解析解算法,其中Ingersoll等(1954)、Deerman和Kavanaugh(1990)通过将土壤视为无限大的介质,概化钻孔周围的热转移过程,使用Laplace变换方法对埋管和U型地埋管换热器进行建模分析,一般将这种方法称为无限长圆柱面源模型.在实际工程中,深井钻孔的半径相比于其长度来说十分微小,在此种情况下,可将钻孔等效为一无体积的无限长直线(Ingersoll et al., 1954),这种方法通常称为无限长线源模型.无限长线源模型简单实用,在换热器的数值模拟中得到了广泛的使用.为了解决一些更为复杂的问题,诸如考虑地表温度影响、地下水的流动、地下水结冰相变及由于垂直地埋管的运行导致的水分转移等问题,众多学者对线源模型进行了大量改进.值得注意的是,在所有改进的线源解析解模型中,都存在时间尺度的局限性,其计算从一个小时内到几十年的多地埋管换热过程仍无法实现,并且在线源模型计算中,将瞬态的钻孔内部进出水平均温度作为地埋管中液体温度进行计算,无法实现地埋管内部瞬态热转移量的计算.
对于深井换热系统而言,井口至井底的温差较大,在不同深度,内外套管内的流体温度不同,与周边岩石(土)的换热量也有显著不同.针对这一特点,Beier(2014)、Beier等(2014)提出了一套可以同时模拟换热器内部管道和周边土壤温度瞬态变化的解析解方法.其技术思路为,将温度、钻孔半径、深度和时间4个变量转换为无量纲数;然后分别构建下行管道、上行管道、固井水泥和周边土壤四个分区上的传热控制方程.上下行管道中的温度,主要受对流传热控制;固井水泥和土壤中的温度,则主要受热传导控制.将这些偏微分方程组联立之后,利用数值拉普拉斯变换法求得解析解.通过和沙箱实验获得的实测数据(Beier et al., 2011)进行比较,该解析解可以很好地同时预测换热管的进出水温度和换热管周边的岩石(土)温度,其准确性已经得到了验证.有关该解析解的具体求解过程详见附录.
将解析解应用于深井换热量的计算,需符合3个假设条件:
(1) 假设地埋管周围的岩石(土)初始温度为一均匀分布的定值.
(2) 假定换热功率不随时间发生变化.
(3) 假定无水平方向上的地下水流.
2.2 数值法为模拟深井内套管周边的换热过程,将土壤和井内套管分别作为两个相互耦合的连续介质.令Ts为土壤温度,其受热传导与热对流的双重影响.令ρf、ρs和cf、cs分别代表流体f和岩石(土)s的密度和比热容.给定地下水的Darcy流速为v, 地埋管周边土壤中的热传导和热对流过程受控制方程控制,公式为
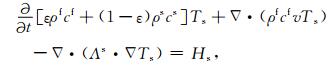
|
(1) |
其中,Λs是水动力作用下的热量扩散系数;Hs指热量生成或者消耗的源汇项;考虑土壤和套管之间存在热交换,上述控制方程的边界条件为
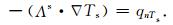
|
(2) |
令Ωk指代套管中的不同部分,对上下行水管,有k=i1, o1,管道中的热传递主要受管道中循环水r按照流速u运动时的热对流控制.深井换热器中的上,下行管路,或是管路周边的水泥部分,其控制方程为

|
(3) |
对应于k=i1, o1,式(3)在边界Γk上的边界条件为

|
(4) |
其中,循环水的水动力热扩散系数Λr定义为
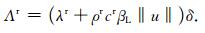
|
(5) |
管道周边的水泥区域(k=g1, g2, …)透水性差,忽略其热对流过程,则有:

|
(6) |
对应于k=g1时,式(6)在边界Γk上的边界条件为
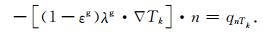
|
(7) |
针对图 1所示深井结构,利用公式(3)、公式(6)和公式(1)分别描述上下行管路、固井水泥区域以及岩石(土)中的传热过程.将以上公式联立,采用有限元方法进行空间离散,以进口端的温度作为边界条件,便可求解得到换热管中的温度Ti1、To1,水泥区域温度Tg以及岩石(土)中温度Ts随空间和时间的变化过程.其中,采用双连续介质法进行空间离散.对深井换热器中的管道和水泥,采用一维线段单元进行空间差分,形成一个连续体.而对岩石(土)区域,采用三维棱柱单元,形成第二个连续体.将上述两个连续体离散后的控制方程组装在一个线性方程组中,通过Picard迭代求得收敛数值解.双连续介质有限元法的具体细节,本文不再赘述,可参考Diersch等(2011)、Shao等(2016)的论述.
与传统上使用的有限元数值求解方法相比,双连续介质空间有限元法有明显的优势.它在对深井换热器内部物理过程进行数值模拟的同时,采用一维单元对管道区域进行了简化.这样使得有限元网格不再需要在深井套管内部进行大量加密来体现管道的几何结构,有效降低了数值计算的强度.与此同时,由于在控制方程中能够指定循环水的流速并且能够模拟管道中循环水温度的动态响应,使得数值模型不再像解析解那样受限于定功率边界条件,而是可以实现热泵启动-停止过程的模拟.鉴于双连续介质空间有限元法的优势,商业软件FEFLOW和开源科学模拟软件OpenGeoSys(Hein et al., 2016; Zheng et al., 2016; Kong et al., 2017)都采用了该方法来模拟地源热泵系统中地埋管和周边土壤的换热问题.本文利用OpenGeoSys中的双连续介质法地埋管模块,构建数值模型(见3.1—3.3节),探讨不同开采情景下地下岩石(土)中的温度演变规律,以估算深井换热技术的换热功率.
3 模型设定为准确评估深井换热技术的稳定换热功率,并探讨地温对深井换热的响应,本文分别构建一个覆盖单一采暖周期(4个月)的短期场景,和一个多年运行(30年)的长期情景,利用解析法及数值法对其进行计算.在短期场景中,再分别讨论持续换热(每天24小时持续运行)和间断换热情景下的换热功率与相应的地温变化特征.模型参数设置参考我国北方典型地热田特征(刁乃仁和方肇洪, 2006; 汪集暘, 2015; Kong et al., 2017),见表 2.
|
|
表 2 模型的参数设置 Table 2 Configuration of parameters used in the model |
模型情景设定如下:供暖期为每年11月15日至次年的3月15日,以一个月30天计,总供暖时间为2880小时;同轴换热管长2000 m,地表常年平均气温15 ℃,地温梯度为0.03 ℃/m.解析解计算过程中需将地温假定为均匀分布,在模型中设定为45 ℃.进水水流通过外管向下流动,经岩石(土)加热后的水流从内管返回(如图 1所示).上下行流量均为11.6 L/s.同轴管的内外管径,岩石(土)的比热容和热传导率等模型参数详见表 2.给定每延米换热功率分别为50、100、200、300、400 W·m-1,分别采用解析法和基于OpenGeoSys的数值模型计算换热管内部水流和周边土壤的温度变化(参见表 3).计算过程中,为满足给定的换热量边界条件,换热井进水端的温度由出水端的水温和给定的流量确定.
|
|
表 3 设定的计算情景及其属性列表 Table 3 Simulation scenarios and their attributes |
实际工程中,在某些供暖区域,仅需要间断采热.比如办公楼的供暖,系统仅需白天办公期间运行,其他时间则可关闭.这样能提高换热井的换热功率及可持续性开采周期,为评估其实际效果,本文也对间断采热情景进行了模拟.如果在一天24小时中,换热井以200 W换热功率连续运行12小时,其余12小时关闭,它在一天中的总换热量和连续24小时以100 W功率运行是相同的.因此,我们设定了每天12小时每延米200 W取热(3-A),8小时每延米300 W(3-B),和6小时每延米400 W(3-C)三个间断换热场景,与3.1节中24小时每延米100 W取热进行对比(见表 3).
3.3 长期换热情景在我国北方,供暖设备的设计使用寿命一般不短于30年.对于深井换热系统来说,它的稳定最大取热量不但要保证在4个月内的供暖期间提供温度足够高的热水,以维持热泵系统连续运行,还要实现在每年8个月的热恢复期中,岩石(土)的温度能恢复到接近初始地温的水平.为实现这一目标,本文设计了每年120天连续采热,245天自然恢复的长期采热情景,延米换热功率分别给定100 W(4-A)和150 W(4-B)进行探讨.
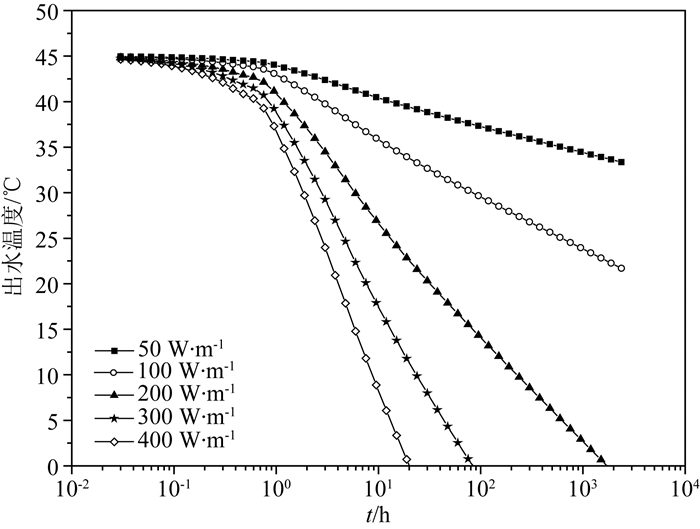
4 结果分析与讨论 4.1 短期持续采热情景的计算结果图 2展示了通过Beier解析法计算获得的换热井出水温度在一个采暖季中随时间的变化.可以看到,在不同的采热负荷下,出水端的降温幅度显著不同.当每延米换热功率为200 W时,系统在运行约12天后,出水端温度为8 ℃左右,但入水端温度已经接近0 ℃,会造成热泵系统的强制关闭.而当换热井以50和100 W·m-1连续运行4个月之后,出水温度分别约为33和21 ℃.这一水温通过热泵系统抬升后,基本可以满足供暖的需要.因此,合理地设计换热井的换热功率对整个系统的运行十分重要.同时,将解析解与表 1进行对比可以发现,国际上深井换热技术应用的延米换热功率都不超过200 W,与计算结果一致.
|
图 2 短期持续采热情景中不同热负荷下出水端温度随时间的变化 Fig. 2 DBHE outflow temperature varying with time in short-term continuous scenarios |
图 3比较了Beier解析法和OGS数值法计算得到的延米换热功率为100 W的条件下,换热井中下行外套管和上行内套管中的垂向水温分布.可以看到,在初始较短的运行时间下,解析解和数值解有略微不同.其原因是,在数值解中,对换热管所占据的空间用一维单元进行了简化,没有考虑管道和固井水泥自身尺寸造成的热传输差异.随着运行时间的延长,土壤传热逐渐占据主导地位,解析解与数值解的吻合度越来越高.图 3亦反映出,在开采的第一个月内,套管内出水温度下降较为迅速,而后逐渐变缓.
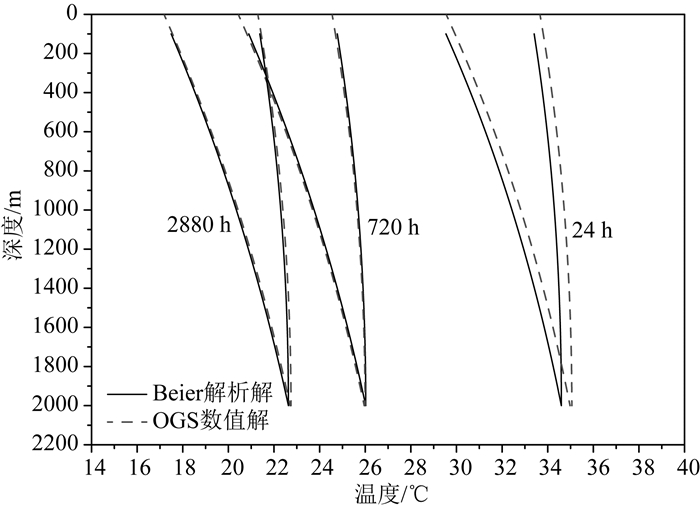
|
图 3 延米换热功率100 W条件下换热井中循环水不同时刻温度的垂向分布 Fig. 3 Vertical distribution of circulating water temperature with specific heat extraction rate of 100 W·m-1 |
在垂直方向上,进水管中的水温随着深度增加而增大,出水温度则随着深度减小而逐渐降低.造成出水温度深浅不一的原因为出水管内水温高,进水管内水温低,二者发生热交换.以运行24小时后的温度分布为例,100 m处与2000 m处进水管内的温差为5.058 ℃,出水管内温差为1.191 ℃.进出水管间的热交换对整体系统效率而言是一种损失,损失量的大小主要受进出水管之间热阻大小的控制.因此,在深井换热的工程设计上,需采用隔热性较好的套管材料,以提高系统的运行效率.
图 4为换热功率提升到200 W·m-1时,换热井管路中的水温分布.Beier解析法和OpenGeoSys数值法的结果均表明,在连续运行720小时(1个月)之后,换热井的进水温度将低于0 ℃,此时热泵系统已经不能正常工作.图 5详细对比了数值法与解析法获得的连续采热120天过程中出水端温度的动态变化过程,可以发现,在短期采热场景中,数值解与解析解吻合良好,结合图 3的结果,确认了两种方法的可靠性与一致性.

|
图 5 短期持续换热情景中100 W·m-1热功率条件下解析解与数值解进出水端温度随时间变化的过程对比 Fig. 5 Comparison of numerical and analytical results of DBHE outflow temperature over time in the short-term continuous scenario, with specific heat extraction rate of 100 W·m-1 |
考虑到实际的野外条件下,地温随深度增加逐渐变大,而解析法并不能考虑地温的垂向变化.在数值法中,则可以加入地温梯度这一参数.本文采用OpenGeoSys数值模拟平台,对比分析了地温垂向线性增加与地温均匀分布下换热井的出水温度,结果如图 5所示.可以发现,在加入地温梯度这一参数后,连续采热120天中,进出水温度都略微高于均匀地温分布.其原因为,地温随深度增加,套管内的循环水在深部地层吸收更多热量,而在浅部,内外套管之间热交换量基本不会发生太多变化.因此在长期开采情景下,地温的垂直变化对评估换热量有较为显著的影响.
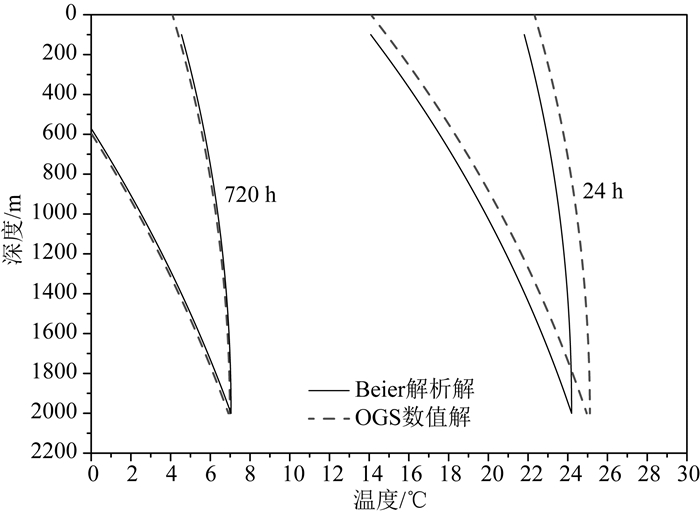
|
图 4 延米换热功率200 W工况下不同时刻循环水的垂向温度分布 Fig. 4 Vertical distribution of circulating water temperature with specific heat extraction rate of 200 W·m-1 |
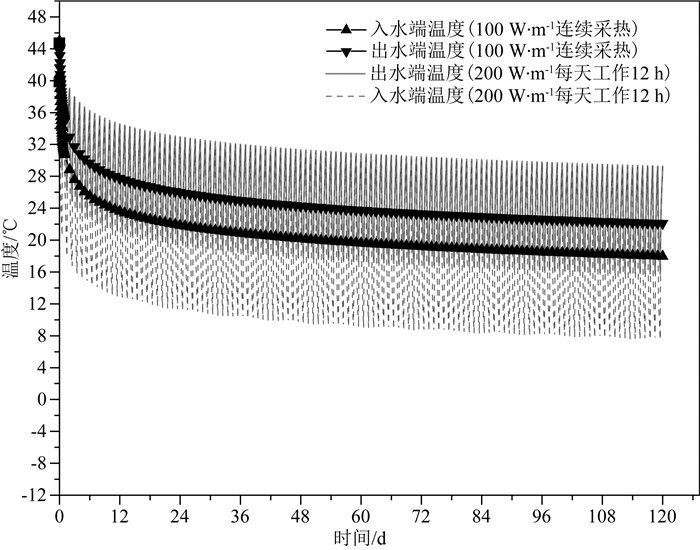
在每天运行12小时的间断采热场景下,出水端温度下降幅度远小于连续采热工况(见图 6).在运行后期,每天的出水端温度摆动幅度维持在15 ℃左右.显然,间断采热的运行工况有助于热恢复.将之与延米换热功率100 W、连续24小时运行的工况进行对比可以发现,两种工况的出水端平均温度下降趋势非常接近.说明在此种工况下,可实现稳定的200 W·m-1换热功率的持续开采.
|
图 6 延米换热功率为200 W且12小时间断运行短期情景出入水端温度 Fig. 6 DBHE outflow temperature in a 12-hour 200 W·m-1 intermittent scenario |
在每天运行8小时和6小时的间断采热工况下,数值模拟得到的进出水温度如图 7和图 8所示,可以看出,随着延米换热功率的提高,每天热恢复的时间相应提高,但每天出水端的最低温度仍低于100 W·m-1连续采热工况.此外,在换热功率为300 W·m-1和400 W·m-1工况的运行后期,较高的换热量使得进水端温度低于0 ℃,在实际工程中,这将造成机组自动关闭.因此,无法在整个采暖季中实现300 W·m-1和400 W·m-1换热功率的可持续开采.

|
图 7 延米换热功率为300 W且8小时间断运行的短期情景出入水端温度 Fig. 7 DBHE outflow temperature in a 8-hour 300 W·m-1 intermittent scenario |

|
图 8 延米换热功率为400W且6小时间断运行的短期情景出入水端温度 Fig. 8 DBHE outflow temperature in a 6-hour 400 W·m-1 intermittent scenario |
综上,间断采热可以提高换热井在短时内的延米换热功率,但它并未实质性地提高换热井在长期运行中所获得的总热量.即针对某一特定深井,在管径、岩土热传导率等参数不变的条件下,无论采用何种间断运行模式,换热井在一个采暖季中能够提取的总热量不会发生大的改变.并且,在总换热量一定的条件下,延米换热功率越高,进出水端温度的摆动幅度越大.
4.3 长期运行情景的结果在短期情景分析的基础上,针对30年的长期运行情景,进行了一系列不同换热功率工况下的模拟,以获得最大换热功率.图 9和图 10分别展示了延米换热功率为100 W和150 W工况下的模拟结果.延米换热功率为100 W时(图 9),在系统运行的前10年,采暖季开始时,出水端水温有所下降,但下降幅度随时间的推移逐年递减.系统运行15年后,出水端水温共下降2.13 ℃,之后温度下降的幅度渐趋于零.这意味着在每个采暖周期中,从岩土中提取的热量能够在8个月的恢复期内得到补充,即热开采和热恢复过程实现了平衡.该工况下,进水端的最低温度约为16 ℃.因此,延米换热功率为100 W的换热井可以实现长期稳定开采.然而,将延米换热功率设定为150 W时,开采10年后的最低进水温度为0.95 ℃(图 10),系统已经无法持续运行.因此,对于本文给定的换热系统,其长期可持续换热功率应该在100 W·m-1左右,且不会超过150 W·m-1.

|
图 9 延米换热功率为100 W且连续运行30年的长期情景出入水端温度 Fig. 9 Inflow and outflow temperature in the 30-year scenario with specific heat extraction rate of 100 W·m-1 |

|
图 10 延米换热功率为150 W且连续运行30年的长期情景出入水端温度 Fig. 10 Inflow and outflow temperature in the 30-year scenario with specific heat extraction rate of 150 W·m-1 |
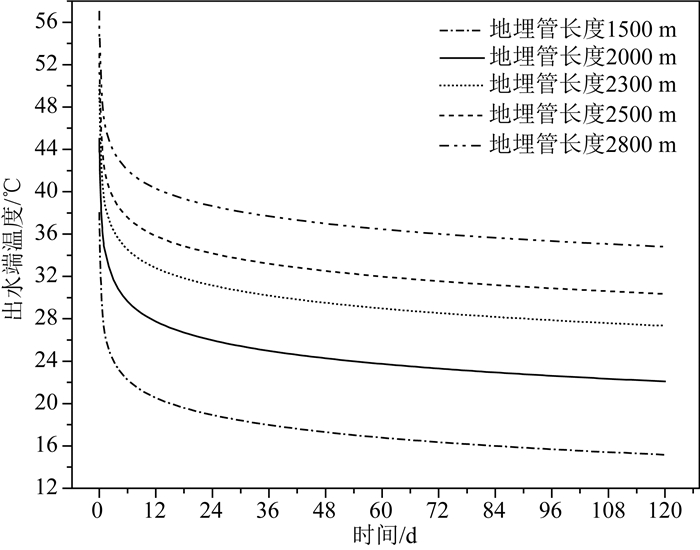
为确定模型中各参数对换热功率的影响,本文基于短期连续采热情景,对模型中主要参数(井深和岩石(土)导热系数)进行了敏感度分析(具体场景见表 3).如图 11所示,给定延米换热功率为100 W,当井深分别为2800 m、2500 m、2300 m、2000 m和1500 m时,系统最终出水端温度分别下降22.18 ℃、22.64 ℃、22.65 ℃、22.91 ℃和22.82 ℃.即当延米换热功率保持一定时,出水端温度下降幅度基本不随井深发生变化.也就是说,延米换热功率与井深基本无关.
|
图 11 延米换热功率为100 W工况下不同深度换热井的出水端温度 Fig. 11 Outflow temperature of different length of DBHE in the short-term simplified scenario with specific heat extraction rate of 100 W·m-1 |
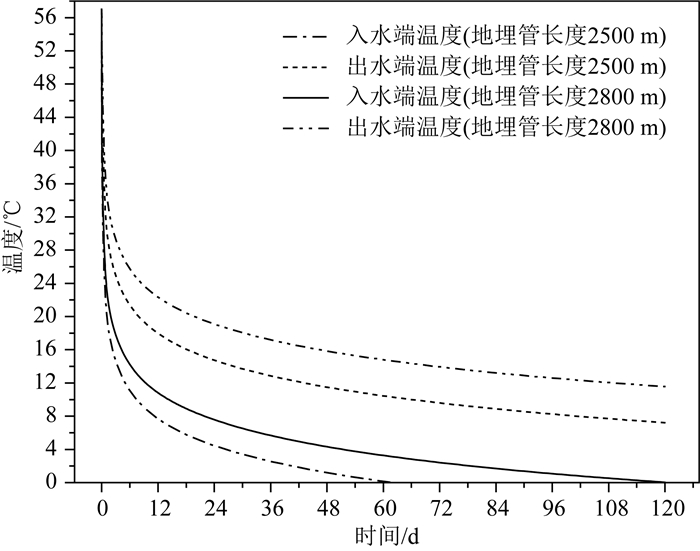
将延米换热功率提高至200 W,2500 m和2800 m深的换热井出水端降温幅度分别为45.78 ℃和45.44 ℃,与入水端的温差分别为10.29 ℃和11.52 ℃(图 12).在此温差下,2500 m深的换热井运行不到60天,入水端温度便会低于0 ℃.即使是2800 m深的换热井,在运行120天后,入水端温度也已接近0 ℃.若换热井入水端,也就是热泵出水端的温度过低,受热泵系统限制,系统将无法正常工作.然而,在实际工程中,如果发现入水端温度过低,可以通过调低循环水的流量来抬升温度,因为当换热井的采热总量保持不变时,进出水之间的温差大小与流量成负相关关系.
|
图 12 延米换热功率为200 W工况下不同深度换热井的出入水端温度 Fig. 12 Inflow and outflow temperature of different lengths of DBHE in the short-term simplified scenario with specific heat extraction rate of 200 W·m-1 |
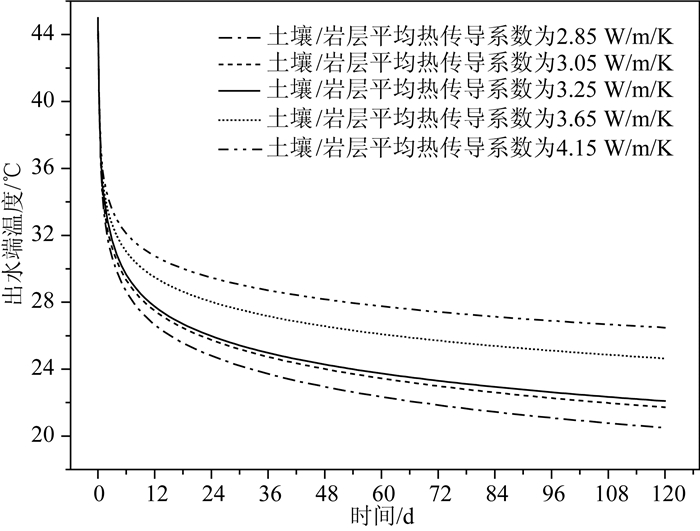
图 13表明,热传导系数的大小对出水端温度影响显著.热传导系数越大,出水端温度下降越少,当导热系数从3.65 W·mK-1减小到3.05 W·mK-1时,在短期情景中,换热井最终出水端温度相差2.93 ℃.因此,准确获得换热井周围岩石(土)的热传导系数,对评价深井换热技术的换热功率十分关键.
|
图 13 延米换热功率为100 W工况下不同热传导系数系统的出水端温度 Fig. 13 Outflow temperature of different thermal conductivities of soil/rock in the short-term simplified scenario with specific heat extraction rate of 100 W·m-1 |
本文分析了深井换热技术的基本原理与特点,将其抽象为数学模型,分别采用Beier解析法和双重连续介质数值法(OpenGeoSys平台)估算了其换热量.两种方法获得的结果高度吻合,表明:无论是1个采暖季(4个月)的短期情景还是30年长期场景,若每天连续采热,延米换热功率接近150 W时,出水端温度迅速下降,换热井无法实现可持续供热,达不到要求的设计换热负荷.若间断采热,系统可以在短期内获得较高的换热功率,但是进出水端的水温波动幅度会显著增加.
深井换热技术的设计采热负荷应采取延米换热功率结合初始出水温度来衡量.以延米换热功率取100 W为例,短期情景下出水端温度下降幅度约为22 ℃左右.通过敏感性分析发现,给定延米换热功率,井深与出水端温度的降低幅度无关.相对而言,岩石(土)热传导系数对换热井的热恢复能力影响较大.其数值越大,对应出水端温度下降越缓慢.
综合以上分析,可以发现深井换热技术应用的主要瓶颈在于其换热量有限,造成利用成本较高.但是,在特定情况下它仍有较大的利用价值,尤其是针对国内干孔率较高和热水开采受矿权限制的情况.未来,可以通过复杂钻井或者改造热储等手段提高换热量,或者说通过降低钻井和热储改造的成本,实现中深层,甚至超深层地热能的规模化开发.需要明确的是,深井换热技术,其核心在于热传导换热.因此,增加换热面积,即水与岩石的接触面积,是提高其换热量最为主要的途径.在此框架下,可供探索的技术,包括:
(1) U型井.即在岩层内打对井,同时打水平井连通对井,形成U型井,但其换热成本仍需结合钻井成本进行综合评估.
(2) 丛井.即在岩层内打一个主井的情况下,在主井末端打多个斜井.同上,其换热量有待于结合钻井成本进行综合评估.
(3) 压裂.地热能开采的压裂技术并不等同于目前较为成熟的页岩气开采压裂技术,其一方面要求更高的压裂面积,另一方面要求在长期采热过程中裂缝不闭合.未来可以考虑将压裂与酸化改造相结合,以维持高裂隙率.
(4) 爆破.井下爆破是压裂的替代手段,对其的要求同压裂技术,但其成本低于压裂.
附录在求解析解的过程中,模型的控制方程需从参数及变量的无量纲角度加以修正,其中无量纲温度TD为

|
(A1) |
其中,T为土壤中任意一点的温度,Ts为初始地温,Q为给定的延米换热功率,λs为土壤热传导系数.此外,定义无量纲半径rD为土壤中任意一点离地埋管中心线的距离r和离地埋管外套管外壁reo的比值,公式为
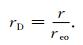
|
(A2) |
无量纲深度zD为深度z和地埋管长度L的比值,公式为
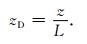
|
(A3) |
无量纲时间tD为时间t,土壤热传导率λs,土壤比热容cs,和地埋管外套管壁距离reo之间的比值,公式为
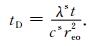
|
(A4) |
经参数无量纲化之后,同轴换热管内管在单位长度上满足能量守恒方程为

|
(A5) |
其中,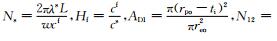
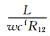

|
(A6) |
其中,hpi与hpo分别为内管内外热对流系数.
同理,内外管中部环部区域在单位长度上能量守恒方程为

|
(A7) |
其中,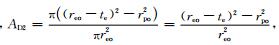
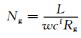
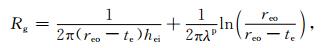
|
(A8) |
其中,hei为外管内热对流系数.
忽略轴向热传导,固井水泥的能量守恒方程为
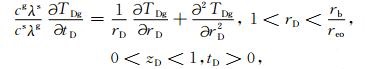
|
(A9) |
对于换热管周围土壤/岩层的能量守恒方程表示为
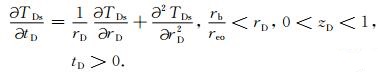
|
(A10) |
此外,进水温度T1和出水温度T2在z=0时,无量纲条件下满足边界条件为
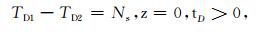
|
(A11) |
在换热管最底部即zD=1时,则满足边界条件为
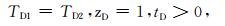
|
(A-12) |
而在固井水泥与换热管外管交界面处即rD=1时,满足边界条件为
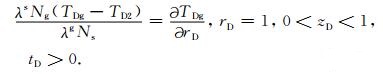
|
(A13) |
在固井水泥与土壤/岩层交界面处即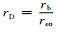
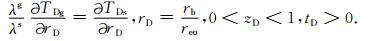
|
(A14) |
同时,固井水泥与土壤/岩层在界面温度保持相等,即当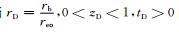
在循环水开始进行热量抽采时刻即tD=0时,固井水泥及外围土壤/岩层温度均是未受扰动的初始均一地温(无地温梯度),在这种情况下,无量纲温度则要求必须满足边界条件为

|
(A15) |
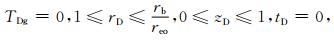
|
(A16) |

|
(A17) |
通过能量守恒方程(A5)、(A7)、(A9)及(A10)可以组成换热管完全换热模型,通过Laplace变化及边界条件(A11)、(A12)、(A13)、(A14)和初始条件(A15)、(A16)、(A17)即可求得在Laplace域内的解析解表达式.经过Stehfest数值Laplace逆变换方法,求得真实时间域内无量纲温度表达式,而后经过量纲的恢复,即可得到具有实际物理意义的温度场解析解表达式.受篇幅所限,具体的计算过程在此不做展开.为计算本文中的深部地埋管换热问题,作者基于Beier等人提出的上述解析解法编写了Matlab程序,可以从本文附带的电子文档中找到.进一步的推导细节,读者也可以参考Beier等(2014)的原始文献.
Beier R A.
2014. Transient heat transfer in a U-tube borehole heat exchanger. Applied Thermal Engineering, 62(1): 256-266.
DOI:10.1016/j.applthermaleng.2013.09.014 |
|
Beier R A, Acuña J, Mogensen P, et al.
2014. Transient heat transfer in a coaxial borehole heat exchanger. Geothermics, 51: 470-482.
DOI:10.1016/j.geothermics.2014.02.006 |
|
Beier R A, Smith M D, Spitler J D.
2011. Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis. Geothermics, 40(1): 79-85.
DOI:10.1016/j.geothermics.2010.12.007 |
|
Deerman J D, Kavanaugh S P.
1990. Simulation of vertical U-tube ground-coupled heat pump systems using the cylindrical heat source solution. ASHRAE Trans, 97: 287-295.
|
|
Diao N R, Fang Z H. 2006.
Ground-Coupled Heat Pump Technology. Beijing: Higher Education Press.
|
|
Diersch H J G, Bauer D, Heidemann W, et al.
2011. Finite element modeling ofborehole heat exchanger systems, Part 1. Fundamentals. Computers & Geosciences, 37(8): 1122-1135.
|
|
Dijkshoorn L, Speer S, Pechnig R.
2013. Measurements and design calculations for a deep coaxial borehole heat exchanger in Aachen, Germany. International Journal of Geophysics: Article ID 916541.
|
|
Hein P, Kolditz O, Görke U J, et al.
2016. A numerical study on the sustainability and efficiency of borehole heat exchanger coupled ground source heat pump systems. Applied Thermal Engineering, 100: 421-433.
DOI:10.1016/j.applthermaleng.2016.02.039 |
|
Ingersoll L R, Zobel O J, Ingersoll A C. 1954.
Heat Conduction with Engineering, Geological, and Other Applications. Madison: University of Wisconsin Press.
|
|
Kohl T, Brenni R, Eugster W.
2002. System performance of a deep borehole heat exchanger. Geothermics, 31(6): 687-708.
DOI:10.1016/S0375-6505(02)00031-7 |
|
Kohl T, Salton M, Rybach L. 2000. Data analysis of the deep borehole heat exchanger plant weissbad (Switzerland).//Proc. World Geothermal Congress. Kyushu-Tohoku, Japan, 3459-3464.
|
|
Kong Y L, Pang Z H, Shao H B, et al.
2014. Recent studies on hydrothermal systems in China:a review. Geothermal Energy, 2: 19.
DOI:10.1186/s40517-014-0019-8 |
|
Kong Y L, Pang Z H, Shao H B, et al.
2017. Optimization of well-doublet placement in geothermal reservoirs using numerical simulation and economic analysis. Environ. Earth Sci., 76: 118.
DOI:10.1007/s12665-017-6404-4 |
|
Li M, Lai A C K.
2015. Review of analytical models for heat transfer by vertical ground heat exchangers (GHEs):A perspective of time and space scales. Applied Energy, 151: 178-191.
DOI:10.1016/j.apenergy.2015.04.070 |
|
Morita K, Bollmeier W S, Mizogami H.
1992. An experiment to prove the concept of the downhole coaxial heat exchanger (DCHE) in Hawaii. GRC Transactions, 16: 9-16.
|
|
Rybach L, Hopkirk R J. 1995. Shallow and deep borehole heat exchangers-Achievements and prospects.//Proc. World Geothermal Congress. International Geothermal Association. Florence, Italy, 2133-2138.
|
|
Schneider D, Strothöffer T, Broßmann E.
1996. Die 2800 m von prenzlau oder die tiefsteerdwärmesonde der welt. Geothermische Energie, 16: 10-12.
|
|
Shao H B, Hein P, Sachse A, et al. 2016.
Geoenergy Modeling Ⅱ-Shallow Geothermal Systems. Switzerland: Springer International Publishing.
|
|
Wang J Y. 2015.
Geothermics and its Applications. Beijing: Science Press.
|
|
Zheng T Y, Shao H B, Schelenz S, et al.
2016. Efficiency and economic analysis of utilizing latent heat from groundwater freezing in the context of borehole heat exchanger coupled ground source heat pump systems. Applied Thermal Engineering, 105: 314-326.
DOI:10.1016/j.applthermaleng.2016.05.158 |
|
刁乃仁, 方肇洪. 2006.
地埋管地源热泵技术. 北京: 高等教育出版社.
|
|
汪集暘. 2015.
地热学及其应用. 北京: 科学出版社.
|
|
 2017, Vol. 60
2017, Vol. 60


