2. 有色金属成矿预测与地质环境监测教育部重点实验室(中南大学), 长沙 410083;
3. 有色资源与地质灾害探查湖南省重点实验室, 长沙 410083
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring (Central South University), Changsha 410083, China;
3. Key Laboratory of Non-ferrous Resources and Geological Hazard Detection, Changsha 410083, China
大地电磁法是一种利用天然交变电磁场源,来探测地球内部电性结构的地球物理方法(Nabighian, 1987),被广泛应用于矿产资源勘查、深部地质构造探测和地球动力学研究(Xu et al., 2016; Newman et al., 2008; Unsworth, 2003; Tang et al., 2013).
作为数据解释的基础,大地电磁正演一直是国内外学者的研究热点.大地电磁正演方法主要有:有限差分法、有限单元法、有限体积法和积分方程法.有限差分法具有实现较易的优点(谭捍东等, 2003; 李焱等, 2012),但是不适合模拟复杂异常体,且需要对整个区域进行网格离散.有限单元法能够模拟复杂模型(Mitsuhata and Uchida, 2004; Liu et al., 2008; Ansari and Farquharson, 2014; Ren et al., 2014; 殷长春等, 2017),但是需要对全空间进行网格剖分,未知数个数较多.有限体积法适合处理高对比度问题(Du et al., 2016),但是,与有限差分法和有限单元相同,需要对全空间进行网格离散,未知数个数较多.相比之下,积分方程法有如下的优点:1)只需要对异常体进行单元剖分,未知数少;2)积分方程结果具有半解析解的精度,常常被用于测试新开发的算法的精度;3)由于研究目标体为异常体,基于积分方程的反演算法具有非常高的反演效率和精度(Kruglyakov et al., 2016).因此,开发高精度的三维大地电磁积分方程正演算法仍然具有一定的研究价值.
目前,积分方程法主要用于可控源电磁法的正演计算(Zhdanov et al., 2006; Gao and Torres-Verdín, 2006; 陈桂波等, 2009, 2011, 2013),只有为数不多的研究人员从事了大地电磁问题的积分方程求解,主要集中在基于规则六面体单元的并矢Green函数计算、密实矩阵的快速迭代解法和积分方程近似解法.Hohmann在1975年基于六面体单元使用积分方程法解决了三维电磁正演问题,打开了三维解释的大门,之后积分方程法被广泛应用到三维电磁数值模拟中(Hohmann, 1975).继承着Hohmann教授的工作,Ting采用结构化网格计算了三维大地电磁法的积分方程数值解(Ting and Hohmann, 1981).Wannamaker给出了背景为层状水平地层的积分方法解(Wannamaker et al., 1984).1991年,Wannamaker对积分方程法在地球物理电磁感应的可能应用进行了综合评述(Wannamaker, 1991).张辉等2005年使用高斯求积和连分式展开计算电磁并矢Green函数积分(张辉等, 2005).鲁来玉等研究了电阻率随位置线性变化的三维大地电磁模拟(鲁来玉等, 2003).Xiong,Mackie等人着重讨论了积分密实矩阵的快速迭代求法(Xiong, 1992; Mackie et al., 1993).Zhadanov,Abubakar,Kruglyakov等人深入研究了采用扩展Born近似、广义扩展Born近似、准线性近似等方法来求解积分方程(Kruglyakov et al., 2016; Zhdanov et al., 2000; Abubakar and Habashy, 2005),从而大大加快了积分方程的计算速度,但是降低了求解的精度,难以处理电导率高对比度问题.上述研究都是基于规则的六面体单元进行网格剖分,随之计算机技术的不断发展和网格剖分技术的推进,结构化网格在模拟地下复杂异常体带来的离散误差的不足日益突出.更为重要的是,上述大部分研究通常采用等效体积法进行并矢Green函数中存在奇异性的积分,进一步降低了积分方程的计算精度.
本文采用一套新的三维大地电磁积分方程求解策略.采用四面体单元离散地下异常体,减少网格离散带来的误差,提高积分方程法处理地下复杂异常体大地电磁正演问题的能力.采用一种无奇异性的解析表达式计算并矢Green函数奇异值积分,解决并矢Green函数强奇异性问题,提高已有积分方程法的计算精度.最后,基于国际标准测试模型3D-1,将本文计算结果与面向目标的自适应有限单元法、T-Ω有限单元法、E-φ有限单元法和已有积分方程法(COMMEMI)五种结果进行对比,验证本文方法的精度.对不同电导率对比度模型进行模拟,将结果与面向目标自适应有限单元法进行比较,进一步验证本文方法的精度,同时说明本文方法能够处理高对比度问题.以棱柱体模型为例,验证本文方法的收敛性,并说明本文方法适合处理地下复杂模型.
2 积分方程理论 2.1 正演理论对于大地电磁正演问题,忽略位移电流,电磁场可以由如下形式的Maxwell方程组表示(时间因子为eiωt)(Nabighian, 1987):
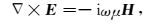
|
(1) |
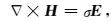
|
(2) |
其中,E为电场强度,单位为V·m-1;H为磁场强度,单位为A·m-1;μ为磁导率,单位为H·m-1;σ为电导率,单位为S·m-1;ω=2πf为角频率,f为频率,单位为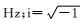
将电磁场(E、H)分为背景场(EP、HP)和二次场(ES、HS),背景场可以表示为
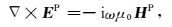
|
(3) |

|
(4) |
其中,μ0为均匀半空间的介电常数,σ1为背景模型的电导率.通过式(1)—(3),式(3)—(4),并整理得
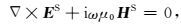
|
(5) |
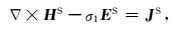
|
(6) |
其中,JS=(σ2-σ1)E,为散射电流,只存在于异常体中,σ2为任意形状的异常体的电导率.
二次场可以表示为(Ting and Hohmann, 1981)
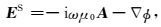
|
(7) |
其中,A和φ分别为矢量位和标量位,可以表示为
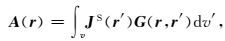
|
(8) |

|
(9) |
其中,G为标量格林函数,可以表示为

|
(10) |
其中,R=|r-r′|,表示点r=(x, y, z)到点r′=(x′, y′, z′)的距离.对于均匀半空间中存在异常体,需要加上额外项来考虑空气中的电流项.由式(7)-式(9)可知,二次场由电流和电荷产生,电荷出现在散射电流JS不连续界面.加入入射场和二次场,可以得到方程:
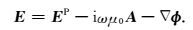
|
(11) |
式(11)可以写为
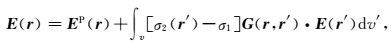
|
(12) |
其中,G为并矢Green函数.需要指出的是,背景模型为均匀半空间时,G为均匀半空间并矢Green函数(Ting and Hohmann, 1981),背景模型为层状介质时,G为层状介质并矢Green函数(Wannamaker et al., 1984).
为了进行数值求解,采用非结构化网格(Tetgen(Si, 2015))将异常体离散成N个四面体单元,假设每个单元内部的电导率和电场为一常数,那么式(12)可以写成

|
(13) |
其中,Γ为并矢Green函数的体积分,需要指出的是,Γ在r=r′时存在奇异性,需要特殊处理.那么,每个四面体单元m中点处的电场可以表示为
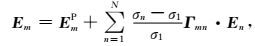
|
(14) |
重新排序,得

|
(15) |
其中,
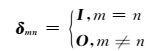
|
(16) |
其中,I为单位张量,O为零张量.将式(15)写成矩阵的形式,有

|
(17) |
通过式(17),可以计算得到异常体内的电场值,单元矩阵可以表示为

|
(18) |
计算Lmn时,需要计算并矢Green函数的体积分.当r=r′,G(r, r′)和∇∇′G(r, r′)存在奇异性,因此,积分∫vG(r, r′)dv′和∫v∇∇′G(r, r′)dv′存在奇异性,传统积分方程法采用等效体积法进行近似计算,降低了积分的计算精度,本文基于前期在重力无奇异解析计算的工作基础,利用散度定理转换强奇异值体积分为一系列弱奇异性的面积分公式,借助弱奇异性的面积分公式的解析计算表达式(Ren et al., 2012, 2017a, 2017b),从而高精度计算并矢Green函数中存在奇异性的积分.首先,令

|
(19) |
那么积分∫vG(r, r′)dv′可以写为

|
(20) |
对于式(20)中的第一项,由于积分核函数一阶连续可导,可以通过高斯数值积分高精度计算,第二项由于核函数在r=r′时存在奇异性,本文使用散度定理将体积分转换为面积分.忽略系数,将其写成统一的形式∫vRqdv′,其中q=±1.结合恒等式(Ren et al., 2017c):

|
(21) |
那么,积分可以写为
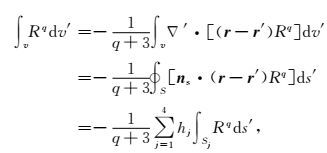
|
(22) |
其中,ns为四面体各个面的法向方向,hj=nsj·(r-r′)表示点r到第j个面的距离.需要注意的是,hj可以为负值.那么只需要考虑如何解析计算Kq=∫SjRqds′.
同样地,积分∫v∇∇′G(r, r′)dv′可以写为
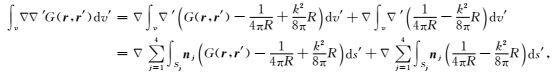
|
(23) |
式(23)中第一项的积分核函数一阶连续可导,可以通过高斯数值积分高精度计算.第二项的积分核函数在r=r′时存在奇异性,本文借助其解析计算表达式来高精度计算.忽略系数,将其写成统一的形式


当获得异常体内的电场值后,任意一点的电场值只需要通过式求解计算.任意一点处的磁场通过式得到

|
(24) |
其中,HP为电导率为σ1的均匀半空间的磁场.利用观察站的电场值和磁场值,获得测点处的视电阻率和相位.
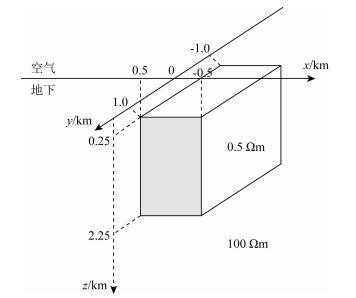
3 测试结果 3.1 正确性及高对比测试测试平台为:Intel(R) Core(TM) i5 CPU 3.30 GHz,8G内存.为验证程序的正确性,采用COMMEMI 3D-1标准测试模型(Zhdanov et al., 1997)进行验证,模型如图 1所示.均匀半空间的电阻率为ρ1=100 Ωm,低阻异常体的电阻率为ρ2=0.5 Ωm.异常体埋藏在地下x=[-0.5 km, 0.5 km]、y=[-1 km, 1 km]和z=[0.25 km, 2.25 km]处.边界处的电场变化较大,异常体边界附近采用密网格进行剖分,内部采用相对较粗的网格进行剖分,剖分成2401个四面体单元.计算频率为0.1 Hz.61个测点均匀分布在地表(x=[-3000 m, 3000 m]).
|
图 1 3D-1模型示意图 Fig. 1 Illustration of 3D-1 model |
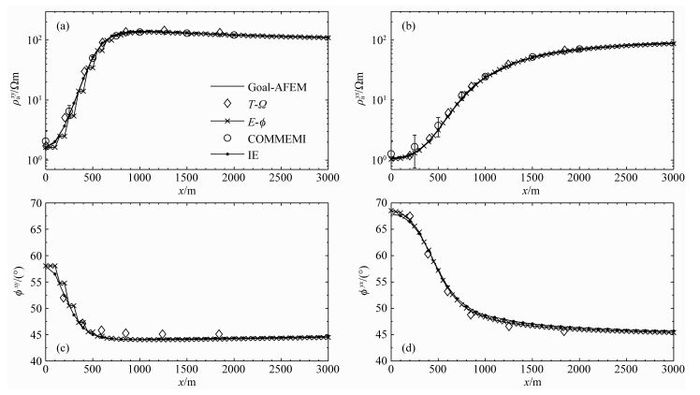
将本文方法计算的视电阻率和相位结果与其他4种方法的计算结果进行对比,如面向目标的自适应有限单元法(Ren et al., 2013)、T-Ω有限单元法(Mitsuhata and Uchida, 2004)、E-φ有限单元法(Farquharson and Miensopust, 2011)和已有积分方程法(COMMEMI)(Zhdanov et al., 1997).由于计算结果沿着剖面是对称的,所以只需要对比半条剖面的计算结果.面向目标的自适应有限单元的结果是基于网格依次迭代产生,因此具有非常高的精度,可被用于做参考值.对比图 2可知,本文结果和其他几种方法的计算十分吻合,与面向目标的自适应有限单元法计算结果非常一致,视电阻率相对误差小于3.1%,相位绝对误差小于0.1°.而传统COMMEMI积分结果则和面向目标的自适应有限单元法结果具有较大偏差.因此,本文的积分方程法计算结果对于传统积分方程法计算结果存在较大的改善.改善的主要原因是本文采用了精确的并矢量Green函数奇异值积分解析解.本文只使用了7203个未知数,便得到了高精度的计算结果,突出了积分方程法只需要对异常体剖分、未知数少的特点.但是,需要指出的是,由于积分方程法合成的是密实方程组,求解方程组比较耗时.
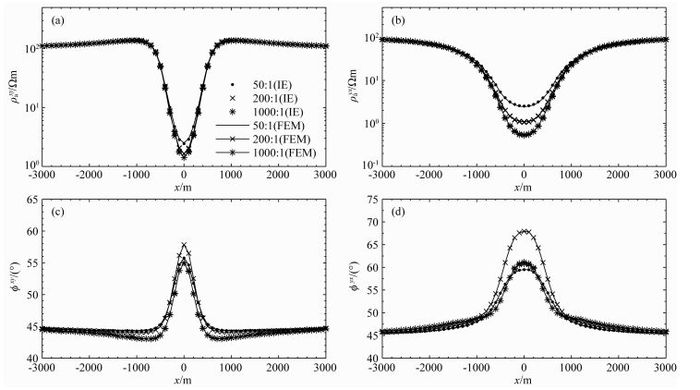
电导率高对比度模型是积分方程法的固有缺陷.采用如图 1所示模型,测试积分方程对不同对比度模型的模拟能力,均匀半空间电阻率为ρ1=100 Ωm,低阻异常体电阻率分别为ρ2=20 Ωm、0.5 Ωm、0.1 Ωm,对应的对比度分别为50:1、200:1、1000:1.
|
图 2 五种方法计算结果对比 Fig. 2 Forwarding results of five methods (a) ρaxy; (b) ρayx; (c) φxy; (d) φyx. |
图 3中,离散点为本文积分方程正演计算结果,实线为采用面向目标的自适应有限单元法结果.两种方法的计算结果十分吻合,视电阻率相对误差和相位绝对误差如表 1所示,对比度为1000:1的正演模型,ρaxy的相对误差小于3.6%,ρayx的相对误差小于4.8%,φxy绝对误差小于0.11°,φyx的绝对误差小于0.12°,表明本文方法能够处理电导率高达1000:1模型问题.图 3还可以看出,随着异常体电阻率的减小,视电阻率的最小值变小.对比度达到1000:1时的ρaxy与对比度为200:1差异不是特别大.相对于ρaxy,ρayx更能够接近异常体的真实电阻率,但是,由于体积效应,二者的视电阻率值都大于异常体的真实电阻率.
|
图 3 不同电导率对比度模型正演结果示意图 Fig. 3 Forwarding results of different conductivity contrast models (a) ρaxy; (b) ρayx; (c) φxy; (d) φyx. |
|
|
表 1 不同电导率模型积分方程和有限单元法正演计算误差 Table 1 Differences between the results of IE and FEM on different conductivity contrast models |
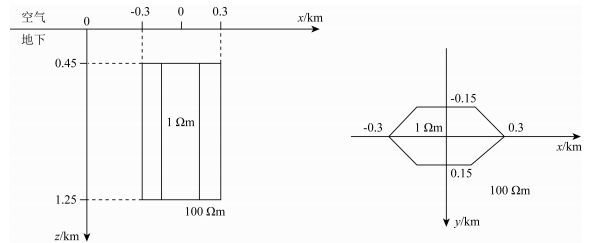
为了体现模拟复杂模型的能力和测试收敛性,建立了具有复杂几何结构的六棱柱低阻模型,如图 4所示.均匀半空间电阻率为ρ1=100 Ωm,六棱柱电阻率为ρ2=1 Ωm.计算频率为1 Hz,测点个数为41,均匀分布在地表(x=[-2000 m, 2000 m]).
|
图 4 六棱柱模型示意图 Fig. 4 Illustration of the hexagonal prism |
对六棱柱区域进行局部网格加密,获得单元个数为834、1541、2667和3840个的四种从疏到密的网格,如表 2及图 5所示.
|
|
表 2 四种网格计算参数 Table 2 The parameters of four grids |

|
图 5 四种疏密程度的网格剖分示意图 Fig. 5 Four meshes with different densities |
图 6展示了积分方程法采用上述四种网格剖分计算得到的视电阻率和相位结果.以最密的网格(3840个四面体)为参照,稀疏网格剖分正演结果视电阻率相对误差和相位绝对误差如表 2所示,最稀的网格(834个四面体)的ρaxy的相对误差小于0.05%,ρayx的相对误差小于0.035%,φxy绝对误差小于0.075°,φyx的绝对误差小于0.005°.总体来说,四种网格结果十分接近,可以说明本文提出的积分方程法具有很好的收敛性,同时说明,积分方程法具有非常快的收敛性,当结果达到一定精度时,加密网格不会有较大幅度精度的提高.

|
图 6 四种网格剖分正演结果示意图 Fig. 6 Forwarding results using four different grids (a) ρaxy; (b) ρayx; (c) φxy; (d) φyx. |
(1) 本文采用四面体单元进行网格剖分,实现了地下复杂异常体的三维大地电磁正演模拟,借助奇异值积分的解析计算方法,给出了基于四面体单元的并矢Green函数无奇异性高精度计算方法,提高了传统积分方程的计算精度,并通过算例验证了本文方法的正确性和适合处理复杂模型的能力.
(2) 本文的研究成果为地下复杂模型的大地电磁积分方程快速、高精度正演研究提供了基础.同时,本文采用的奇异值积分解析计算方法同样适用于直流电法、可控源电磁法等的积分计算.
附录A
下面给出积分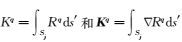

|
(A1) |
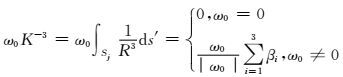
|
(A2) |
其中,∂iS, i=1, 2, 3表示面S的三条边,Ri+和Ri-分别表示点r到∂iS两个端点的距离,si-和si+分别表示点r在∂iS的两个端点的垂向距离,K-3为式Kq=∫SjRqds′在q=-3时的一个特殊情况.βi的计算表达式如下:
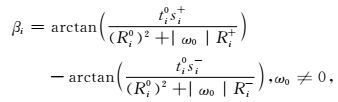
|
(A3) |
其中,|ω0|为点r到三角面S的距离,需要注意的是,ω0可以为负值.
|
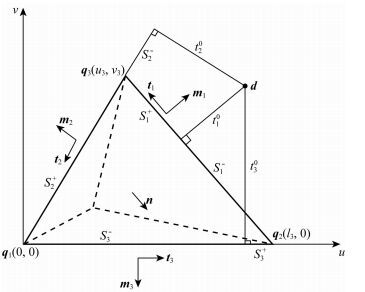
图 A1 局部坐标系 Fig. A1 Local coordinate system |
符号说明如图A1所示.以四面体的一个三角面S为例,三角形的面积为T,面外方向方向为n.建立局部坐标系,以面S的一个顶点为坐标原点,以改点所在的一条边为坐标轴,建立局部坐标系uov,点d为点r在面S上的投影,三角面S的三个顶点q1、q2、q3可以表示为(0, 0)、(l3, 0)和(u3, v3),每边的长为li, i=1, 2, 3.每条边的外方向方向为mi, i=1, 2, 3,每边的切向方向为ti, i=1, 2, 3,有n=mi×ti, i=1, 2, 3.点r到三条边的距离表示为ti0, i=1, 2, 3.具体计算表达式如下:

|
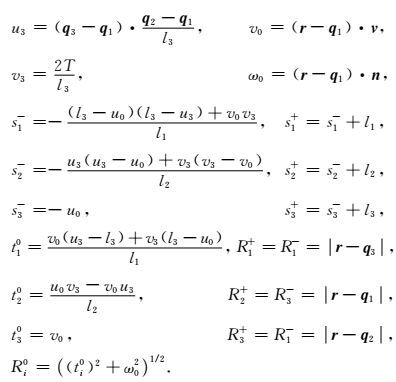
|
借助如下迭代计算公式:

|
(A4) |
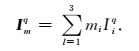
|
(A5) |
那么,积分Kq=∫SjRqds′和Kq=∫Sj∇Rqds′可以表示为
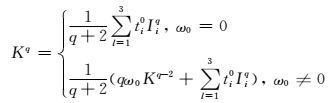
|
(A6) |
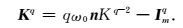
|
(A7) |
Abubakar A, Habashy T M.
2005. A green function formulation of the extended born approximation for three-dimensional electromagnetic modelling. Wave Motion, 41(3): 211-227.
DOI:10.1016/j.wavemoti.2004.05.011 |
|
Ansari S, Farquharson C G.
2014. 3D finite-element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids. Geophysics, 79(4): E149-E165.
DOI:10.1190/geo2013-0172.1 |
|
Chen G B, Wang H N, Yao J J, et al.
2009. Modeling of electromagnetic responses of 3-D electrical anomalous body in a layered anisotropic earth using integral equations. Chinese J. Geophys., 52(8): 2174-2181.
DOI:10.3969/j.issn.0001-5733.2009.08.028 |
|
Chen G B, Bi J, Wang J B, et al.
2011. A novel fast algorithm of electromagnetic dyadic Green's function in horizontal layered medium. Acta Physica Sinica, 60(9): 307-312.
|
|
Chen G B, Bi J, Zhang Y, et al.
2013. High-order generalized extended Born Approximation algorithm for 3D electromagnetic responses modeling in anisotropic medium. Acta Physica Sinica, 62(9): 094101.
|
|
Du H K, Ren Z Y, Tang J T.
2016. A finite-volume approach for 2D magnetotellurics modeling with arbitrary topographies. Studia Geophysica et Geodaetica, 60(2): 332-347.
DOI:10.1007/s11200-014-1041-9 |
|
Farquharson C G, Miensopust M P.
2011. Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction. Journal of Applied Geophysics, 75(4): 699-710.
DOI:10.1016/j.jappgeo.2011.09.025 |
|
Gao G, Torres-Verdín C.
2006. High-order generalized extended born approximation for electromagnetic scattering. IEEE Transactions on Antennas and Propagation, 54(4): 1243-1256.
DOI:10.1109/TAP.2006.872671 |
|
Hohmann G W.
1975. Three-dimensional induced polarization and electromagnetic modeling. Geophysics, 40(2): 309-324.
DOI:10.1190/1.1440527 |
|
Kalinkin A, Anders A, Anders R.
2015. Schur Complement Computations in Intel? Math Kernel Library PARDISO. Applied Mathematics, 6(2): 304-311.
DOI:10.4236/am.2015.62028 |
|
Kruglyakov M, Geraskin A, Kuvshinov A.
2016. Novel accurate and scalable 3-D MT forward solver based on a contracting integral equation method. Computers & Geosciences, 96: 208-217.
|
|
Li Y, Hu X Y, Yang W C, et al.
2012. A study on parallel computation for 3D magnetotelluric modeling using the staggered-grid finite difference method. Chinese J. Geophys., 55(12): 4036-4043.
DOI:10.6038/j.issn.0001-5733.2012.12.015 |
|
Liu C, Ren Z, Tang J.
2008. Three-dimensional magnetotellurics modeling using edge based finite-element unstructured meshes. Applied Geophysics, 5(3): 170-180.
DOI:10.1007/s11770-008-0024-4 |
|
Lu L Y, Zhang B X, Pao G S.
2003. Modeling of three-dimensional magnetotelluric response for a linear earth. Chinese J. Geophys., 46(4): 568-575.
|
|
Mackie R L, Madden T R, Wannamaker P E.
1993. Three-dimensional magnetotelluric modeling using difference equations-theory and comparisons to integral equation solutions. Geophysics, 58(2): 215-226.
DOI:10.1190/1.1443407 |
|
Mitsuhata Y, Uchida T.
2004. 3D magnetotelluric modeling using the T-Ω finite-element method. Geophysics, 69(1): 108-119.
DOI:10.1190/1.1649380 |
|
Nabighian M N. 1987. Electromagnetic Methods in Applied Geophysics: Voume 1, Theory. SEG Books.
|
|
Newman G A, Gasperikova E, Hoversten G M, et al.
2008. Three-dimensional magnetotelluric characterization of the Coso geothermal field. Geothermics, 37(4): 369-399.
DOI:10.1016/j.geothermics.2008.02.006 |
|
Ren Z Y, Kalscheuer T, Greenhalgh S, et al.
2012. Boundary element solutions for broad-band 3-D geo-electromagnetic problems accelerated by an adaptive multilevel fast multipole method. Geophysical Journal International, 192(2): 473-499.
|
|
Ren Z Y, Kalscheuer T, Greenhalgh S, et al.
2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling. Geophysical Journal International, 194(2): 700-718.
DOI:10.1093/gji/ggt154 |
|
Ren Z Y, Kalscheuer T, Greenhalgh S, et al.
2014. A finite-element-based domain-decomposition approach for plane wave 3D electromagnetic modeling. Geophysics, 79(6): E255-E268.
DOI:10.1190/geo2013-0376.1 |
|
Ren Z Y, Tang J T, Kalscheuer T, et al.
2017a. Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method. Journal of Geophysical Research: Solid Earth, 122(1): 79-109.
DOI:10.1002/2016JB012987 |
|
Ren Z Y, Chen C J, Pan K, et al.
2017b. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts. Surveys in Geophysics, 38(2): 479-502.
DOI:10.1007/s10712-016-9395-x |
|
Ren Z Y, Zhong Y Y, Chen C J, et al.
2017c. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts up to cubic order. Geophysics.
DOI:10.1190/geo2017-0219.1 |
|
Si H.
2015. TetGen, a Delaunay-based quality tetrahedral mesh generator. ACM Transactions on Mathematical Software (TOMS), 41(2): Article No. 11.
DOI:10.1145/2629697 |
|
Tan H D, Yu Q F, Booker J, et al.
2003. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method. Chinese J. Geophys., 46(5): 705-711.
|
|
Tang J T, Zhou C, Wang X Y, et al.
2013. Deep electrical structure and geological significance of Tongling ore district. Tectonophysics, 606: 78-96.
DOI:10.1016/j.tecto.2013.05.039 |
|
Ting S C, Hohmann G W.
1981. Integral equation modeling of three-dimensional magnetotelluric response. Geophysics, 46(2): 182-197.
DOI:10.1190/1.1441188 |
|
Unsworth M.
2003. Studying continental dynamics with magnetotelluric exploration. Earth Science Frontiers, 10(1): 25-38.
|
|
Wannamaker P E, Hohmann G W, SanFilipo W A.
1984. Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations. Geophysics, 49(1): 60-74.
DOI:10.1190/1.1441562 |
|
Wannamaker P E.
1991. Advances in three-dimensional magnetotelluric modeling using integral equations. Geophysics, 56(11): 1716-1728.
DOI:10.1190/1.1442984 |
|
Xiong Z H.
1992. Electromagnetic modeling of 3-D structures by the method of system iteration using integral equations. Geophysics, 57(12): 1556-1561.
DOI:10.1190/1.1443223 |
|
Xu Y X, Yang B, Zhang S, et al.
2016. Magnetotelluric imaging of a fossil paleozoic intraoceanic subduction zone in western Junggar, NW China. Journal of Geophysical Research: Solid Earth, 121(6): 4103-4117.
DOI:10.1002/2015JB012394 |
|
Yin C C, Zhang B, Liu Y H, et al.
2017. A goal-oriented adaptive algorithm for 3D magnetotelluric forward modeling. Chinese J. Geophys., 60(1): 327-336.
DOI:10.6038/cjg20170127 |
|
Yla-Oijala P, Taskinen M.
2003. Calculation of CFIE impedance matrix elements with RWG and n×RWG functions. IEEE Transactions on Antennas and Propagation, 51(8): 1837-1846.
DOI:10.1109/TAP.2003.814745 |
|
Zhang H, Li T L, Dong R X, et al.
2005. Computation of Green's tensor integrals for electromagnetic problems using Gaussian quadrature and continued fraction. Progress in Geophysics, 20(3): 667-670.
|
|
Zhdanov M S, Varentsov I M, Weaver J T, et al.
1997. Methods for modelling electromagnetic fields results from COMMEMI—the international project on the comparison of modelling methods for electromagnetic induction. Journal of Applied Geophysics, 37(3-4): 133-271.
DOI:10.1016/S0926-9851(97)00013-X |
|
Zhdanov M S, Dmitriev V I, Fang S, et al.
2000. Quasi-analytical approximations and series in electromagnetic modeling. Geophysics, 65(6): 1746-1757.
DOI:10.1190/1.1444859 |
|
Zhdanov M S, Lee S K, Yoshioka K.
2006. Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity. Geophysics, 71(6): G333-G345.
DOI:10.1190/1.2358403 |
|
陈桂波, 汪宏年, 姚敬金, 等.
2009. 用积分方程法模拟各向异性地层中三维电性异常体的电磁响应. 地球物理学报, 52(8): 2174–2181.
DOI:10.3969/j.issn.0001-5733.2009.08.028 |
|
陈桂波, 毕娟, 汪剑波, 等.
2011. 水平层状介质中电磁场并矢Green函数的一种快速新算法. 物理学报, 60(9): 307–312.
|
|
陈桂波, 毕娟, 张烨, 等.
2013. 各向异性介质三维电磁响应模拟的Ho-GEBA算法. 物理学报, 62(9): 094101.
|
|
李焱, 胡祥云, 杨文采, 等.
2012. 大地电磁三维交错网格有限差分数值模拟的并行计算研究. 地球物理学报, 55(12): 4036–4043.
DOI:10.6038/j.issn.0001-5733.2012.12.015 |
|
鲁来玉, 张碧星, 鲍光淑.
2003. 电阻率随位置线性变化时的三维大地电磁模拟. 地球物理学报, 46(4): 568–575.
|
|
谭捍东, 余钦范, BookerJ, 等.
2003. 大地电磁法三维交错采样有限差分数值模拟. 地球物理学报, 46(5): 705–711.
|
|
殷长春, 张博, 刘云鹤, 等.
2017. 面向目标自适应三维大地电磁正演模拟. 地球物理学报, 60(1): 327–336.
DOI:10.6038/cjg20170127 |
|
张辉, 李桐林, 董瑞霞, 等.
2005. 利用高斯求积和连分式展开计算电磁张量格林函数积分. 地球物理学进展, 20(3): 667–670.
|
|
 2017, Vol. 60
2017, Vol. 60


