在山地勘探中,相对精确的近地表速度模型对后续的处理流程至关重要.初至波走时层析技术的提出较好地解决了这一问题(Brenders and Pratt, 2007).因为初至波走时主要反映了近地表纵波速度的变化,同时初至波在地震记录中比较稳健且容易辨别(景月红,2009;刘玉柱等,2010),因此该方法目前已经在工业界广泛应用.
初至波走时层析可以基于射线理论(Nolet,1987)或有限频理论(刘玉柱等,2009).虽然有限频层析反演精度高,但由于其计算量较大,目前工业上仍以射线层析为主.初至波走时层析在高频近似假设下,反演方法的主要区别在于是否需要进行射线追踪.SIRT、LSQR等方法基于射线追踪建立大型层析方程组,通过求解层析方程组获得模型的更新量,然后迭代获得反演结果(刘玉柱等,2007).这类方法的优点是物理意义明确,求解方法灵活,缺点是层析方程高度病态,求解不稳定.Taillandier等(2009)将波形反演中的伴随状态法应用于走时层析中,用两次程函方程的正演模拟实现梯度的计算.相对于基于射线追踪的层析成像方法,伴随状态法层析具有以下特点:(1) 不需要进行射线追踪;(2) 计算量依赖于模型大小而不依赖于检波点数量(Leung and Qian, 2006;谢春等,2014);(3) 单炮检对的梯度不是射线而是具有一定的宽度(Li et al., 2013),形态上类似于菲涅尔体层析的核函数(Liu et al., 2009).
目前,该方法可以反演各向同性与各向异性(Waheed et al., 2016)条件下的近地表速度.但是该方法的一阶方向反演结果在地表起伏剧烈的情况下并不理想.在射线类走时层析中,一阶方向的反演结果主要存在两个问题.第一个问题是由于地表起伏所引起的射线聚焦效应,此时梯度反映的不再是模型中速度修改量的相对大小,而是射线的疏密程度.第二个问题是当初始模型中速度的纵向增速低于真实模型速度的纵向增速时,速度修改量将集中在浅层,进而形成“屏蔽层”,使得射线无法射入深层,导致反演失败(Taillandier et al., 2009).二阶方向可以解决以上两个问题,但伴随状态法走时层析二阶方向的实现非常困难且不经济(Bretaudeau et al., 2014).
因此,本文提出了一种针对伴随状态法的简单易行的预条件实现方式.在改进的散射积分法的实现框架下,通过将走时残差置为定值,再次进行反演即可获得类似于射线密度的矩阵,并以此矩阵的逆作为层析的预条件,使得梯度分布更加合理,反演结果更加稳定.
2 基本原理 2.1 伴随状态法走时层析方法简介与传统走时层析类似,伴随状态法初至波走时层析目标函数为
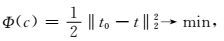
|
(1) |
其中,t表示在当前模型下计算出的理论走时,t0表示实际观测到的走时,c表示介质的速度.在高频近似假设下,走时满足程函方程:
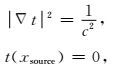
|
(2) |
其中,xsource表示震源点坐标.程函方程表示在震源点处初至波走时为0,其他位置的初至波走时满足(2) 式中的第一项.通过初始条件即可以求出空间内每一点的初至波走时.
可以利用伴随状态法求取最优化问题的思路来获得使目标函数下降最快的梯度方向,从而避免Fréchet导数的计算.将状态方程(2) 与伴随变量引入目标函数(1) 后形成新的目标函数:
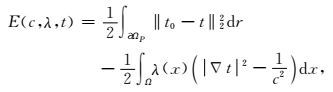
|
(3) |
其中,λ是拉格朗日因子,它可以保证当目标函数(3) 取得最小值时,程函方程的解与观测走时相等.同时,在最优化过程中,t、λ和c相互独立,所以当目标函数达到最小值时,变量满足以下三个关系:
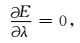
|
(4) |
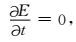
|
(5) |
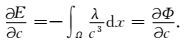
|
(6) |
根据(5) 式可以得到

|
(7) |
对(7) 式第二项应用高斯公式,将体积分转化为面积分然后合并得

|
(8) |
要使(8) 式始终成立,则两个积分需要始终为0,则在地表处有

|
(9) |
其中,n表示边界的外法向方向;在介质内部,λ满足
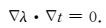
|
(10) |
利用(9) 式的边界条件求解得到边界上的λ值,再利用(10) 式求解全空间内的λ值,最后利用(6) 式即可获得目标函数对模型的梯度.迭代反演即可以求得最终的反演结果.反演过程可以表示如下:
a.拾取初至波到时;
b.利用当前模型计算出理论走时,并计算走时差;
c.利用(9) 式计算出地表处的λ值;
d.求解(10) 式,计算出全空间内的λ值;
e.求解(6) 式,计算出梯度方向,更新模型;
f.判断是否满足终止条件,如不满足,重复b—f过程.
2.2 预条件实施方法伴随状态法最速下降方向会导致反演陷入局部极值,而在初至波走时射线类反演中,利用射线密度矩阵的逆实施预条件是一种很有效的方法.伴随状态法走时层析由于不需要计算射线路径,所以无法直接求得射线密度,导致难以实现此类预条件.为此,本文提出了一种简单易行的计算类射线密度矩阵的方法.出于表示的方便性,本文在散射积分法初至波走时层析(李勇德等,2016)的框架下进行解释.
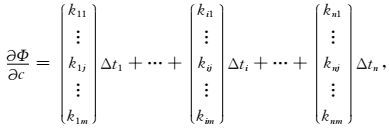
|
(11) |
(11) 式为散射积分法初至波走时层析中梯度的表达式,右端的每一项表示一个检波器的走时差与该检波器对应射线路径的乘积.如果假设每一个检波器走时差相等,即可将走时差提取公因式,等号右端变为

|
(12) |
该式中Hj表示穿过第j个网格的所有射线路径长度的和.需要说明的是,Benaïchouche等(2015)在伴随状态法的框架下给出了本文类似的方法,但他们认为该方法获得的是近似Hessian的对角线元素.根据本文上述的理论分析可知,(12) 式并不等同于近似Hessian矩阵对角元素(李勇德等,2016),而是将平方求和变为直接求和.所以,这是一种近似Hessian矩阵对角元素的进一步近似,但物理性质却得到了保持,而且数值上类似于射线密度.利用该方法求得的矩阵的逆作为伴随状态法初至波走时层析的预条件,既可以去除射线密度的影响,又不增加算法的复杂度.由于快速扫描法(Zhao,2005)的利用,增加的计算时间也不多.但求逆会出现很小的数作为分母的情况,所以需要增加阻尼因子,最终模型中第j个单元格速度的更新方向如(13) 式所示:

|
(13) |
其中,l表示迭代次数,αl表示步长,δ表示一个很小的数(本文采用预条件矩阵最大值的千分之四).新的预条件伴随状态法射线走时层析的反演步骤可以表示如下:
a.拾取初至波到时;
b.利用初始模型计算出理论走时,计算走时差;
c.利用(9) 式计算出地表处的λ;
d.求解(10) 式,计算出全空间内的λ;
e.求解(6) 式,计算出一阶梯度方向;
f.将走时差设定为某一定值,重复c—e步骤,获得射线密度矩阵;
g.根据(13) 式对一阶梯度方向进行预条件,并对模型进行更新;
h.判断是否满足终止条件,如不满足,重复b—h步骤.
3 数值实验为了验证方法的有效性,设计了一个二维平地表简单模型和一个二维复杂起伏地表模型进行测试.炮点和检波点均位于地表,基于相同的走时正演方法生成“观测数据”,然后利用预条件伴随状态法走时层析进行反演.为了方便对比,同时也利用传统的伴随状态法走时层析进行反演.
3.1 二维平地表简单模型简单模型是一个包含球状高速异常体的梯度模型,如图 1a所示,模型包含601×151个网格,网格间距为10 m×10 m,初始模型是不包含高速异常体的梯度模型.
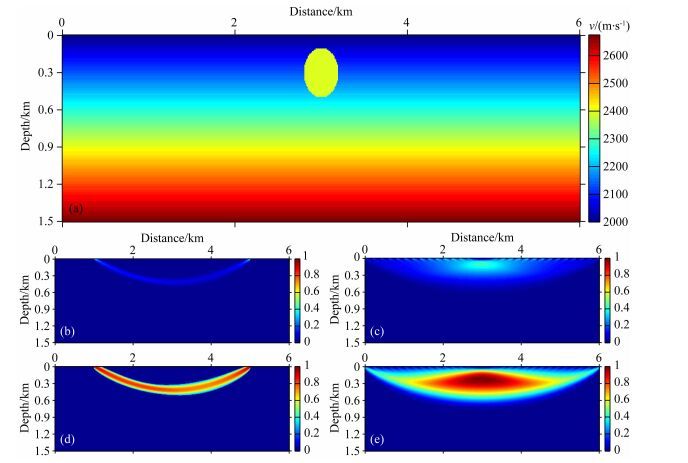
|
图 1 二维简单模型 (a)真实模型;(b)单炮检对所对应的梯度;(c)多炮叠加的梯度;(d)单炮检对所对应的预条件梯度;(e)多炮叠加的预条件梯度. Fig. 1 Comparisons of the inversion results of a 2D simple model (a) True model; (b) Gradient of the first round computed for one source-reciever; (c) Gradient of the first round computed for all source-reciever; (d) Preconditioned gradient of the first round computed for one source-reciever; (e) Preconditioned gradient of the first round computed for all source-reciever. |
伴随状态法走时层析所求得的梯度中炮检两端会存在极大值,如图 1b所示为某单炮检对所对应的梯度.在炮检对足够多的情况下,该效应会在一定程度上被减弱(图 1c).由于炮检两端的异常,速度修改最大值并不在异常体所在位置,而是分布在炮检点所在的位置.通过对梯度实施预条件,无论是单炮检对(图 1d)还是多炮叠加(图 1e)的梯度都得到了明显的改善,速度修改最大的位置处于异常体的真实位置.
3.2 二维起伏地表复杂模型为了验证该方法的反演能力,本文设计了二维复杂起伏地表模型进行试验.该模型被离散为4001×151个网格,每一个网格大小为10 m×10 m.本文仅反演近地表速度结构,故仅展示0~0.7 km深度范围内的速度变化情况(图 2a).该模型地表起伏剧烈,起伏落差近450 m,横向速度变化明显.利用弹性波方程模拟地表地震记录,并拾取Z分量初至波走时作为观测数据.第一炮位于横向坐标5 km处,炮点间隔40 m,共619炮.每炮201个检波器均匀放置在炮点两侧,水平间隔为20 m.中间放炮,两边接收.本文所采用的初始模型(如图 2b)与真实模型差距较大,传统伴随状态法实现的最速下降法走时层析明显陷入了局部极值(如图 2d所示),且在浅部形成了明显的“屏蔽层”,导致后续反演中初至波无法进入深部,因此反演失败.然而,利用本文提出的预条件最速下降法走时层析,反演结果得到了明显的改善.为了定量对比本文提出的预条件方法在反演中的作用,抽取距离地表 100 m、200 m、300 m处的速度曲线(图 3).由于模型左右两端并没有炮点覆盖,无法得到正确结果,因此仅显示了水平方向10~30 km范围内的速度模型.可以看到,在浅部传统最速下降法反演结果在真实模型附近存在抖动.与此同时,由于“屏蔽层”的产生,传统最速下降法无法获得正确的深部反演结果.
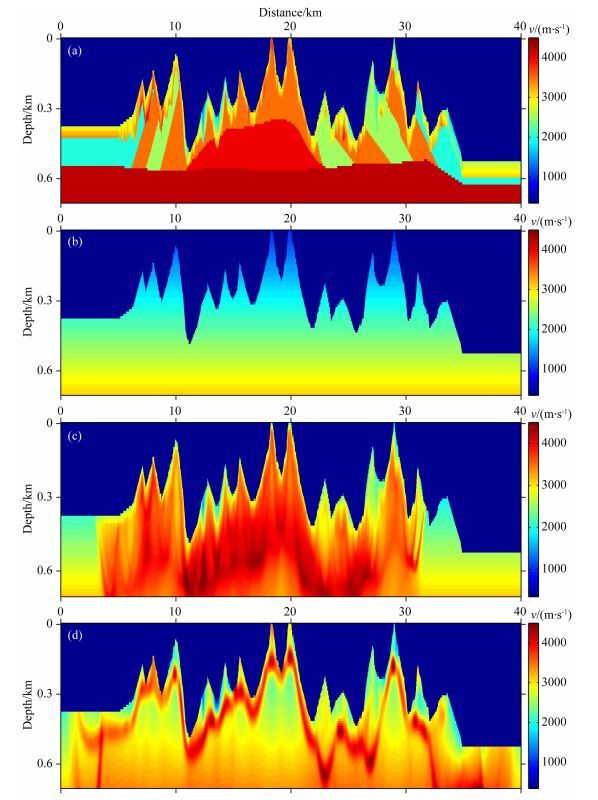
|
图 2 0.7 km深度以内的(a)真实模型、(b)初始模型、(c)预条件最速下降法40次迭代反演结果与(d)传统最速下降法150次迭代反演结果 Fig. 2 Zoomed views of the (a) true model, (b) starting model and inversion results using (c) preconditioned adjoint-state method after 40th iterations and (d) adjoint-state method after 150th iterations |

|
图 3 地表下(a)100 m、(b)200 m、(c)300 m深度处的速度曲线对比 初始模型(粉色)、真实模型(黑色)、预条件最速下降法反演结果(红色)、传统最速下降法反演结果(蓝色). Fig. 3 Comparisons of the horizontal profiles of the inversion results using preconditioned adjoint-state method and adjoint-state method at depths of (a) 100 m, (b) 200 m and (c) 300 m Starting model (pink); True model (black); Results using preconditioned adjoint-state method (red) and conventional adjoint-state method (blue). |
为了验证本文提出的预条件伴随状态法走时层析对实际资料的反演能力,将其应用于四川巴中的某条二维测线.测线长度为77 km,模型被离散为7700×300个网格点,网格大小为10 m×10 m.由于地表起伏,炮点并不完全均匀,间距为100~300 m不等.每炮480个检波器以25 m间隔均匀分布在炮点两侧.利用拾取的初至波走时数据进行预条件伴随状态法走时层析,反演结果如图 4所示.该地区地表起伏剧烈,局部最大落差近500 m.通过反演结果可以看出,近地表速度较高.基于反演获得的近地表模型计算静校正量.层析静校正叠加剖面如图 5a所示.图 5b为仅进行高程静校正的叠加剖面.可以看出,相对于常规高程静校正叠加剖面,预条件最速下降法层析静校正叠加剖面中同相轴更加清晰且连续.这说明,本文提出的预条件伴随状态法走时层析可以获得可靠的近地表速度结构.

|
图 4 预条件伴随状态法初至波层析结果 Fig. 4 Inversion result using preconditioned adjoint-state method |
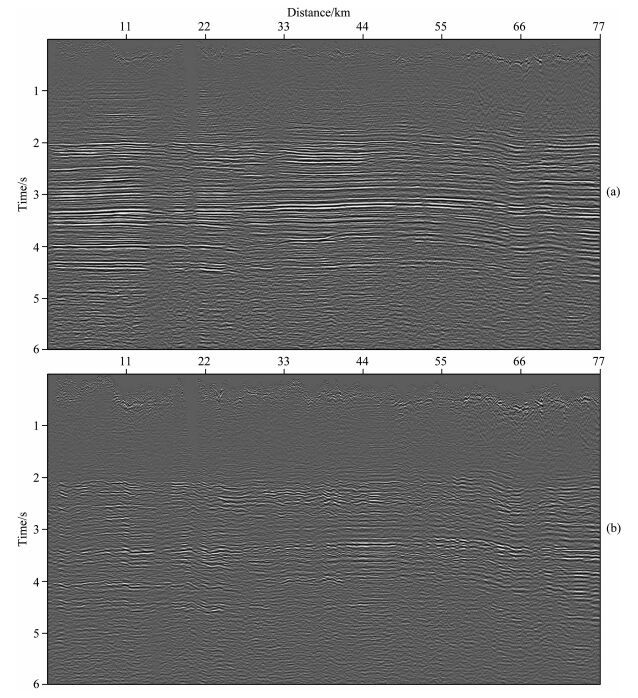
|
图 5 实际资料叠加剖面 (a)预条件伴随状态法层析静校正;(b)传统高程静校正. Fig. 5 Stack results using (a) preconditioned adjoint-state model statics and (b) elevation statics |
本文在改进的散射积分法初至波走时层析的实现框架下提出了一种新的预条件伴随状态法初至波走时层析方法.这种方法保留了伴随状态法的优点,通过增加一次反演的计算量得到类似于射线密度的矩阵.理论模型测试与实际资料处理表明,利用该矩阵的逆实施预条件,梯度中炮检两端的异常值消失,即使在初始模型不理想的情况下也不会在浅层形成“屏蔽层”,保障了后续反演的顺利进行.
Benaïchouche A, Noble M, Gesret A. 2015. First arrival traveltime tomography using the fast marching method and the adjoint state technique.//77th EAGE Conference and Exhibition 2015.
|
|
Brenders A J, Pratt R G.
2007. Efficient waveform tomography for lithospheric imaging:Implications for realistic, two-dimensional acquisition geometries and low-frequency data. Geophysical Journal International, 168(1): 152-170.
DOI:10.1111/gji.2007.168.issue-1 |
|
Bretaudeau F, Brossier R, Virieux J, et al. 2014. First-arrival delayed tomography using 1st and 2nd order adjoint-state method.//84th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 4757-4761.
|
|
Jing Y H. 2009. Seismic first break travel-time tomography and its application in near-surface velocity model building[Master thesis] (in Chinese). Xi'an:Chang'an University.
|
|
Leung S, Qian J L.
2006. An adjoint state method for three-dimensional transmission traveltime tomography using first-arrivals. Communications in Mathematical Sciences, 4(1): 249-266.
DOI:10.4310/CMS.2006.v4.n1.a10 |
|
Li S W, Fomel S, Vladimirsky A.
2013. First-break traveltime tomography with the double-square-root eikonal equation. Geophysics, 78(6): U89-U89.
DOI:10.1190/geo2013-0058.1 |
|
Li Y D, Dong L G, Liu Y Z.
2016. First arrival traveltime tomography based on an improved scattering-integral algorithm. Chinese Journal of Geophysics, 59(10): 3820-3828.
DOI:10.6038/cjg20161026 |
|
Liu Y Z, Dong L G, Xia J J.
2007. Normalized approach in tomographic imaging of first breaks travel time. Oil Geophysical Prospecting, 42(6): 682-685, 698.
|
|
Nolet G. 1987. Seismic wave propagation and seismic tomography.//Nolet G, ed. Seismic Tomography. Dordrecht:Springer.
|
|
Liu Y Z, Dong L G, Li P M, et al.
2009. Fresnel volume tomography based on the first arrival of the seismic wave. Chinese Journal of Geophysics, 52(9): 2310-2320.
DOI:10.3969/j.issn.0001-5733.2009.09.015 |
|
Liu Y Z, Dong L G, Wang Y W, et al.
2009. Sensitivity kernels for seismic Fresnel volume tomography. Geophysics, 74(5): U35-U46.
DOI:10.1190/1.3169600 |
|
Liu Y Z, Ding K Y, Dong L G.
2010. The dependence of first arrival travel time tomography on initial model. Oil Geophysical Prospecting, 45(4): 502-465.
|
|
Taillandier C, Noble M, Chauris H, et al.
2009. First-arrival traveltime tomography based on the adjoint-state method. Geophysics, 74(6): WCB1-WCB10.
DOI:10.1190/1.3250266 |
|
Waheed U, Flagg G, Yarman C E.
2016. First-arrival traveltime tomography for anisotropic media using the adjoint-state method. Geophysics, 81(4): R147-R155.
DOI:10.1190/geo2015-0463.1 |
|
Xie C, Liu Y Z, Dong L G, et al.
2014. First arrival traveltime tomography based on the adjoint state method. Oil Geophysical Prospecting, 49(5): 877-883.
|
|
Zhao H K.
2005. A fast sweeping method for eikonal equations. Mathematics of Computation, 74(250): 603-627.
|
|
景月红. 2009. 地震初至波走时层析成像与近地表速度建模[硕士论文]. 西安: 长安大学
http://cdmd.cnki.com.cn/Article/CDMD-11941-2009210878.htm |
|
李勇德, 董良国, 刘玉柱.
2016. 基于改进的散射积分算法的初至波走时层析. 地球物理学报, 59(10): 3820–3828.
DOI:10.6038/cjg20161026 |
|
刘玉柱, 董良国, 夏建军.
2007. 初至波走时层析成像中的正则化方法. 石油地球物理勘探, 42(6): 682–685, 698.
|
|
刘玉柱, 董良国, 李培明, 等.
2009. 初至波菲涅尔体地震层析成像. 地球物理学报, 52(09): 2310–2320.
DOI:10.3969/j.issn.0001-5733.2009.09.015 |
|
刘玉柱, 丁孔芸, 董良国.
2010. 初至波走时层析成像对初始模型的依赖性. 石油地球物理勘探, 45(4): 502–465.
|
|
谢春, 刘玉柱, 董良国, 等.
2014. 伴随状态法初至波走时层析. 石油地球物理勘探, 49(5): 877–883.
|
|
 2017, Vol. 60
2017, Vol. 60


