近场波动问题建模的核心在于确立近场及构建无限域.近场,即目标区和对该区域内波动有显著影响的邻近介质区.将近场以外介质分布及所在区域简化为无界、规则域,即无限域.无限域内介质分布规则,不存在向近场散射波动能量的局部非均匀性,近场辐射外行波将完全进入无限域,在无穷远处能量衰减为无穷小.无限域反映了近场与远区介质之间能量交互的主要特征(廖振鹏,2002).
近场波动数值模拟需引入人工边界将无限域截断,形成有限计算区,并设置人工边界条件(Artificial Boundary Condition, ABC)模拟计算区外部无限域.应用高精度人工边界条件,人工边界可设置于近场与无限域交界处,或距近场较近位置(Bangerth et al., 2004).与之对比,应用低精度人工边界条件,须外推人工边界足够远距离以提高无限域模拟的精度,导致近场波动数值模拟效率低下.已建立的高精度ABC主要有:1.满足无限域波动方程外行波解假定导出的弹簧-阻尼-质量ABC(Du and Zhao, 2010),旁轴ABC及其辅助变量实现形式(Clayton and Engquist, 1977;Guddati and Tassoulas, 2000),Higdon ABC及其辅助变量实现形式(Higdon, 1986; Hagstrom and Warburton, 2004);2.建立可描述体波、面波和导波的单向波形式表达式,以离散形式直接模拟外行波穿过边界,如透射边界(Liao et al., 1984);3.在人工边界外设置吸收层,通过改变无限域内介质衰减特性或变换无限域内波动方程以实现外行波在层内的快速衰减.代表性工作有:衰减层(Cerjan et al., 1985),黏滞性阻尼层(Sochacki et al., 1987),瑞利阻尼层(Sarma et al., 1998),Caughey阻尼层(Semblat et al., 2011),完美匹配层(Bérenger, 1994).完美匹配层(Perfectly Matched Layer, PML)与其他吸收层不同,其层内行波阻抗等同于计算区行波阻抗,且与波的频率、入射角以及PML层内衰减参数的取值大小无关,因此计算区外行波能无反射地进入PML,无须采用缓变衰减参数以减小波在参数变化位置处产生的反射,这使得相同精度要求下,PML设置层厚远小于其他吸收层,计算效率显著提升.
Chew和Weeden(1994)将PML解释成无限域内场方程在复坐标域的解析延拓,建立了构建PML的复坐标延伸技术,极大推进了PML的研究与应用.Chew和Liu(1996)首次将PML应用于近场弹性波动问题数值模拟.其研究工作表明PML具有数值离散方案易于构建、精度高、数值稳定性较好等优点,清晰揭示了PML的潜在应用前景.针对一阶速度-应力形式无限域弹性波动方程:Collino和Tsogka(2001)建立了分裂形式PML,给出了计算区外行波能无反射地进入PML的清晰论证,基于时空二阶交替网格差分法和速度应力有限元建立了PML离散方案.Komatitsch和Martin(2007)建立了复频移、非分裂卷积形式PML,采用时空二阶以及时间二阶空间四阶交替网格差分法进行数值离散,给出了PML应用于近场弹性波动数值模拟的长持时稳定算例.针对二阶位移形式无限域弹性波动方程:Komatitsch和Tromp(2003)首次建立了分裂形式PML,给出了PML的勒让德谱元离散方案.Basu和Chopra(2004)建立了非分裂形式PML及其线性有限元离散方案.Matzen(2011)构建了非分裂频移卷积PML,结合线性有限元,给出了PML应用于近场弹性波动数值模拟的长持时稳定算例.在此基础上,Xie等(2014)给出了PML应用于近场弹性波动勒让德谱元数值模拟的长持时稳定数值算例.
PML场方程与界面条件通常分别采用复坐标延伸技术变换强形式无限域内波动方程和界面条件得到.二者构建过程相互独立,可能出现场方程和界面条件匹配不合理而引发的数值失稳、计算精度低下等问题.Zhang和Shen(2010)提出PML自由边界条件应采用复坐标延伸技术变换无限域自由边界条件得到,其文中算例表明直接在PML内采用无限域自由边界条件将引发数值失稳.Duru和Kreiss(2014)基于复坐标延伸技术给出了两类不同的PML自由边界条件,其中一类因与PML场方程不匹配引发了数值失稳.针对PML层内介质分界面条件,Xie等(2016)在构建流固耦合PML及其勒让德谱元离散方案的过程,采用复坐标延伸技术建立了PML流固界面条件.文中指出在PML内采用无限域流固界面条件,将导致计算精度低下及数值失稳.基于上述认识,本文提出采用复坐标延伸法变换无限域弱形式波动方程以构建完美匹配层的方法.因弱形式波动方程耦合了波动方程及界面条件,保证了对无限域波动方程及界面条件进行相同形式的解析延拓,规避了变换后所得场方程与界面条件之间的匹配不合理问题.新方法可直接给出弱形式匹配层,在此基础上亦可还原得到匹配层场方程与界面条件的强形式.弱形式便于建立近场波动有限元模拟方案,强形式便于建立近场波动有限差分模拟方案.
文中第一节给出无限域内弹性波动方程及其弱形式.第二、三节在简要介绍复坐标延伸技术基础上,采用该技术变换弱形式弹性波动方程构建弱形式完美匹配层,进而结合勒让德谱元建立弹性介质近场波动谱元模拟方案.第四节利用算例阐明该方案的精度及数值稳定性.最后给出本文工作小结.
2 无限域弹性波动方程及其弱形式近场弹性波动问题常采用的无限域为水平层状弹性半空间(廖振鹏,2002).域内二阶位移形式弹性波动方程为
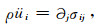
|
(1) |
式中ρ为介质密度,üi为xi方向加速度,σij为外法线矢量ni平面上应力沿xi方向的分量.∂j表示xj方向空间偏导数,∂j=∂/∂xj.
依据弹性介质本构关系:

|
(2) |
对各向同性弹性介质,弹性模量cijkl仅与拉梅常数有关.

|
(3) |
λ为拉梅第一常数,μ为介质剪切模量.域内介质分界面上位移及应力满足连续条件:

|
(4) |

|
(5) |
nj为连续介质分界面外法线单位向量的分量.初始位移和速度为0:

|
(6) |
地表自由边界条件为
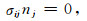
|
(7) |
nj为自由边界外法线单位向量分量.可以证明,由(1)—(7) 式构成的初边值问题具有唯一解(Durán et al., 2011).
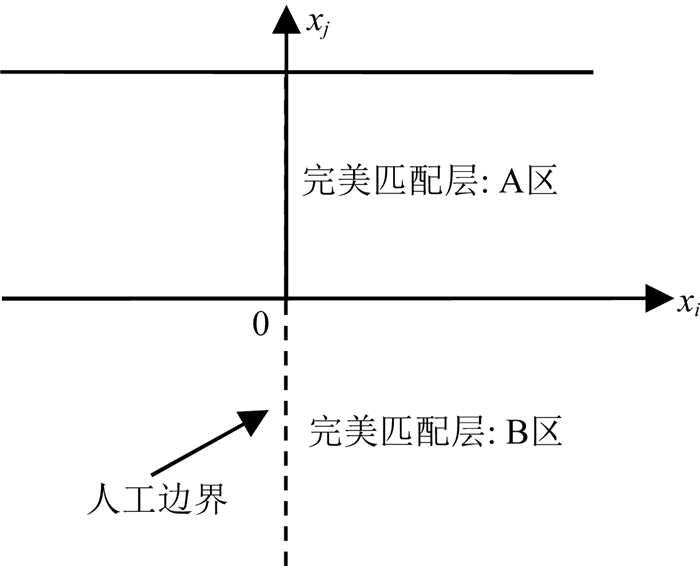
引入人工边界将无限域截断,形成有限的计算区(图 1).由(1) 式可得计算区外部无限域中A区弱形式波动方程为

|
(8) |

|
图 1 基于人工边界截断无限域所得有限计算区示意图 Fig. 1 Definition of the finite computational domain, which is obtained by truncating the infinite domain with absorbing boundary |
wi为权函数,ΩA为计算区外部无限域A区所处范围. ΓMIΩA为介质分界面,ΓFBΩA为自由地表,ΓABΩA为人工边界.nj为外法线矢量分量,njdΓ=dΩ/dxj.对于二维情形dΩ=dx1dx2,三维情形dΩ=dx1dx2dx3.由A区地表自由边界条件(7) 式可得
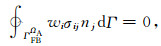
|
(9) |
由于ΓMIΩA,ΓMIΩB外法线单位向量方向相反,由A区和B区之间界面条件(4)(5) 式可得
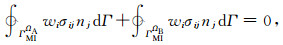
|
(10) |
由此得到无限域弱形式波动方程:
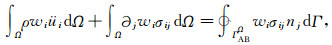
|
(11) |
Ω为计算区外部无限域, ΓABΩ为人工边界.
3 弱形式完美匹配层采用复坐标延伸技术构建PML的核心概念为解析延拓,即将无限域波动方程中实数坐标替换为复坐标,所得方程与原方程具有一致的行波解,不同之处仅在于延伸后所得方程行波解的空间自变量为复数,原方程行波解的空间自变量为实数.在实坐标系下考察延拓后所得方程的解具有空间衰减特征,将复坐标系下PML经实-复坐标转换可得实坐标系下PML.显然,对存在界面及物理边界情形,须对原波动方程、界面及边界条件进行相同形式解析延拓.这正是本文提出采用复坐标延伸技术变换弱形式波动方程以构建PML的基本出发点.
下面首先建立复坐标系,其次将频域弱形式波动方程进行解析延拓得到复坐标系下PML.基于复-实坐标变换给出实坐标系下弱形式PML的频域表达.利用傅里叶反变换,给出弱形式时域PML.
不失一般性,考虑计算区外部无限域中A区弱形式PML构建.假定坐标原点位于A区左下角(图 2),将人工边界外实坐标系进行解析延拓得到
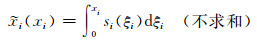
|
(12) |
|
图 2 无限域内弱形式完美匹配层构建示意图 Fig. 2 Sketch for the construction of weak-form PML in infinite-domain |
si为解析延拓函数.除标注不求和外,文中均采用Einstein求和约定.基于傅里叶变换将(8) 式变换至频域

|
(13) |
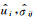

|
(14) |
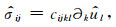
|
(15) |
x为坐标矢量,t为时间变量,

|
(16) |
式中

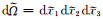
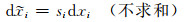
|
(17) |
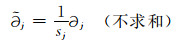
|
(18) |
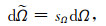
|
(19) |
二维情形:sΩ=s1s2,三维情形:sΩ=s1s2s3.将(17)—(19) 式代入(16) 式整理得到

|
(20) |
式中

|
(21) |
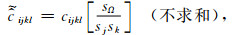
|
(22) |
(20) 式右端项分别为边界及界面积分的解析延拓.结合(9) 式, (10) 式可知

|
(23) |
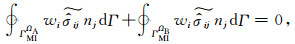
|
(24) |
由此可建立无限域弱形式频域PML为
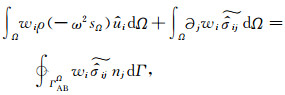
|
(25) |
将(20) 式,(23) 式,(24) 式,(25) 式还原成对应的强形式频域PML为

|
(26) |
界面及地表自由边界条件为
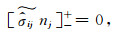
|
(27) |
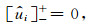
|
(28) |
应用傅里叶反变换,基于(25) 式可得弱形式时域PML:
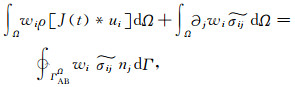
|
(29) |
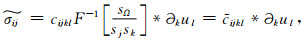
|
(30) |

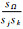
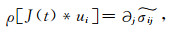
|
(31) |
界面条件为
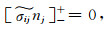
|
(32) |

|
(33) |
自由边界条件为

|
(34) |
在二维情形,仅考虑自由边界,采用复频移解析延拓函数(Kuzuoglu and Mittra, 1996),(31) 式与(34) 式等同于Duru和Kreiss (2014)针对强形式建立的可长持时稳定实现的PML场方程与自由边界条件.由于对强形式波动方程与自由边界条件分别做复坐标延伸,Duru和Kreiss亦得到了其他形式的PML,但其数值实验表明这类PML将引发数值失稳.其原因在于基于强形式构建PML具有一定的随意性,难以保证对波动方程与边界条件进行相同形式的解析延拓.而基于弱形式构建PML则规避了这一问题,可直接得到匹配的波动方程与边界条件.
4 基于勒让德谱元的弱形式时域PML时空离散方案勒让德谱元(Legendre spectral element method)兼具谱方法及集中质量有限元的优点:具有无穷阶收敛特性;质量阵为对角阵无需求解线性方程组.近年来谱元法被广泛应用于大型、复杂弹性波动数值模拟(Komatitsch and Tromp, 1999).
弱形式PML可直接采用谱元法进行离散,但需首先建立为此需建立J(t)与
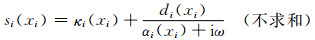
|
(35) |
di(xi)为ni外法线方向行波衰减因子,κi(xi)为坐标缩放系数,αi为频移参数.采用(35) 式构建PML为复频移PML,而传统PML采用的复坐标延伸函数为si(xi)=1+di(xi)/(iω).
基于(35) 式,可给出J(t)的解析表达式.这里仅给出αx1≠αx2≠αx3情形的J(t)表达式:

|
(36) |
进而可得

|
(37) |
详尽的J(t)和
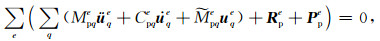
|
(38) |
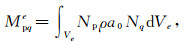
|
(39) |
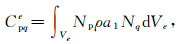
|
(40) |
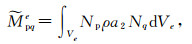
|
(41) |
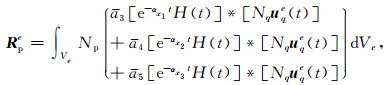
|
(42) |
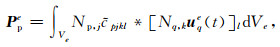
|
(43) |
其中uqe为单元q节点上的位移矢量.Nq表示单元q节点上插值函数,Nq, k为单元q节点上插值函数对xk的偏导数.经组装可得全部节点的运动方程组:
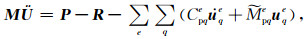
|
(44) |
M为全局对角质量阵,全局矢量ü, P, R分别由üpe, Ppe, Rpe组装得到.考虑计算区内部荷载,须在(44) 式右端补充全局荷载向量.
对(44) 式进行数值积分常采用Newmark-Beta预估-校正方法(Komatitsch and Tromp, 1999).考虑到P,R元素中所包含卷积项
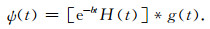
|
(45) |
Xie等(2014)给出了与Newmark-Beta法相匹配的二阶精度离散卷积公式

|
(46) |
ψn表示ψ在nΔt时刻的取值.若对(44) 式采用高阶精度数值积分,如低频散、低耗散龙格库塔法(Berland et al., 2006),需引入与卷积项ψ(t)对应的辅助微分方程:
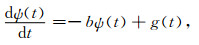
|
(47) |
(47) 式亦可采用低频散、低耗散龙格库塔方法进行数值积分.
5 数值算例Zeng等(2011)探讨了PML在浅地表勘探近场波动问题(二维Lamb波传播问题)中的应用,文中采用空间四阶、时间二阶交替解耦格式离散波动方程及PML,自由边界递推格式由Kristek等(2002)给出.作者指出若介质泊松大于等于0.39,PML将引发数值失稳.失稳最早出现于PML自由边界与其截断边界的交点位置,随后迅速扩散至其他区域.介质泊松比越大,失稳出现时间越早,失稳增长速度越快.失稳与PML构建过程中所采用复坐标延伸函数的具体形式无关,但复频移PML出现失稳的时间比传统PML晚.针对泊松比大于等于0.4情形,复频移PML失稳开始时间早于P波从源点行进至PML所需时长.为此,作者应用黏滞性阻尼层以替代PML.为保证吸收精度,文中采用的阻尼吸收层厚度为常规PML层厚的20倍.本节将重复Zeng等(2011)一文中算例,结合算例阐明:通过合理设置PML层内参数取值,弱形式复频移PML,结合勒让德谱元可给出稳定的数值结果.
Zeng等(2011)考虑二维直角坐标系(x, z)下均匀介质弹性半空间,介质密度ρ=1500 kg·m-3, P波波速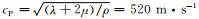
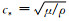

|
(48) |
式中振幅A=1×108 N,f0=50 Hz,t0=0.04 s.初始位移、速度为0.为保证施加荷载的完整性,起始计算时间取为-0.04 s.
采用四阶谱元对模型进行空间离散,离散后所得方程采用Newmark-Beta预估-校正法(β=0, γ=1/2) 做数值积分,卷积项数值积分采用(46) 式.参照谱元模拟精度要求及内域稳定条件,单元尺寸设置为0.25 m×0.25 m.时间步长取0.00005 s.在人工边界外施加6单元层厚PML,亦即PML层厚为1.5 m.
复频移延伸函数(35) 式中参数取值参照Collino和Tsogka(2001)给出:

|
(49) |
xi为沿着完美匹配层与内域交界面法线方向层内点与交界面的法线距离.Lxi为完美匹配层沿xi方向的厚度.
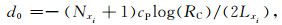
|
(50) |
Nxi=2,Cxi=1,RC=0.001.依据Zhang和Shen (2010)
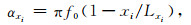
|
(51) |
f0为震源时间函数的中心频带,f0=50 Hz.αi的引入将使得行波在PML内的衰减快慢程度与频率有关.同时可提高PML对大角度入射波的吸收效果.进一步改善PML对Rayleigh波行进至PML外侧边界反射回来掠入射波动的吸收精度,参考Zhang和Shen (2010),令
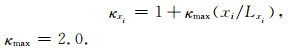
|
(52) |
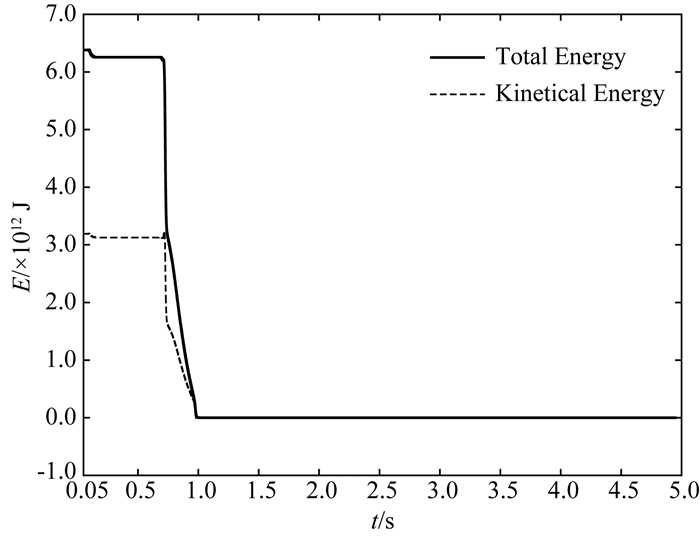
图 3给出计算区域内所有节点能量:
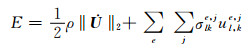
|
(53) |
|
图 3 除PML层内节点外,计算区内所有节点动能和总能量随时间衰减曲线 Fig. 3 Decay of total energy and the kinetical energy with time in the main computational domain (i.e. the domain without the six PML layers) |
随时间的变化曲线.式中第一项为动能,第二项为势能.从图中可以看出,待荷载加载完毕(0.02 s左右)及在P波到达PML之前计算区内部能量趋于平稳.第一个显著下降段开始于P波进入PML时刻,之后随着P波及首波(Head wave (Shan and Ling, 2016))持续进入PML,能量持续下降.由于首波携带能量较弱,在第二个能量显著下降段开始之前,计算区内能量基本不随计算时长增加而变化.第二个下降段开始于S波进入PML时刻,随着后续Rayleigh波进入PML,能量持续衰减.图中给出了100000时步的计算结果,总时长为5 s.依图所示,算例数值稳定.计算时间总长远大于P波从源点行进至PML层内所需时长:约为0.096 s,以及S波从源点行进至PML层内所需时长:约为0.73 s,对应时步数为14600步.图 4给出位于(48 m, 0 m), (48 m, -30 m)以及(48 m, -48 m)观测点x和z方向的位移时程.同时给出采用一阶精度黏性ABC(Lysmer and Kulemeyer, 1969)的计算结果及大区域解.结果表明,复频移PML能高效吸收计算区辐射的外行P波,S波以及首波,同时可有效吸收外行Rayleigh面波.通过优化层内参数取值可进一步提高PML吸收精度.
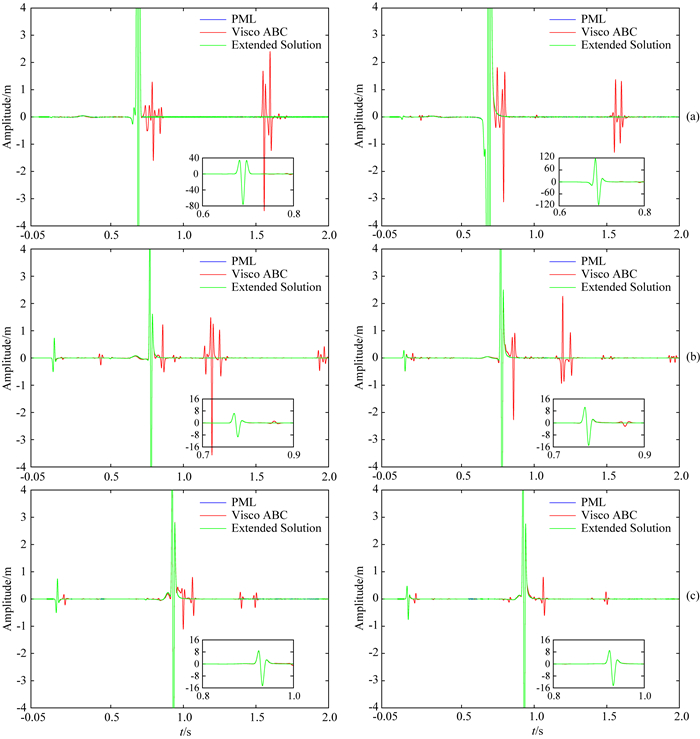
|
图 4 (a),(b)和(c)分别给出(48 m, 0 m), (48 m, -30 m), (48 m, -48 m)处观测点位移时程.左边一栏为x方向位移时程,右边为z方向位移.图中蓝色实线表示基于PML的计算结果,红色实线为基于黏性边界的计算结果,绿实线为大区域解.为清晰观察边界引入的误差,每个框图幅值范围设置为[-4 m, 4 m],右下角的子框图补充了幅值超出4 m以外的位移时程 Fig. 4 Time evolution of the x component (left) and z component (right) of the displacement vector at the receiver located (a) at (48 m, 0 m), (b) at (48 m, -30 m), and (c) at (48 m, -48 m) of the extended solution of the problem (green curve), the numerical solution with PML(blue curve) and with Visco ABC (red curve) (Lysmer and Kulemeyer, 1969). The subfigures, show the total range of displacement in specified time interval |
本文提出采用复坐标延伸技术变换弱形式无限域波动方程以构建弱形式时域PML及其强形式的方法.因弱形式波动方程耦合了波动方程及界面条件,规避了变换后所得场方程与界面条件之间的不合理匹配问题.新方法可直接应用于模拟无限域内存在复杂界面条件PML的构建,如流固PML及流-固-多孔介质PML.这对推进考虑海洋的地球波动数值模拟具有重要价值(赵成刚等, 1998).
基于弱形式复频移时域PML,结合谱元给出了近场弹性介质波动数值模拟方案,并将该方案应用于高泊松比介质的浅地表勘探波动正演问题数值模拟.数值算例表明,该方案可给出稳定的数值结果,并能有效吸收外行P波,S波,首波以及面波.该方案可应用于基于全波场反演方法的浅地表勘探.
值得一提的是,本文并没有深入探讨PML的稳定性,文中构建所得弱形式PML应用于各向异性介质波动数值模拟同样可能存在失稳问题.最近Chang等(2014)探讨了频域PML的物理实现方案,为各向异性介质PML的稳定实现提供了新思路.关于PML的数值稳定性值得进一步深入研究.
致谢本文部分研究工作是谢志南在法国国家科学院力学与声学实验室访问期间完成的,感谢合作教授Dimitri Komatitsch和Paul Cristinin提供的支持与帮助.感谢廖振鹏研究员一直以来对作者工作的支持.
Bangerth W, Grote M, Hohenegger C.
2004. Finite element method for time dependent scattering:nonreflecting boundary condition, adaptivity, and energy decay. Computer Methods in Applied Mechanics and Engineering, 193(23-26): 2453-2482.
DOI:10.1016/j.cma.2004.01.021 |
|
Basu U, Chopra A K.
2004. Perfectly matched layers for transient elastodynamics of unbounded domains. International Journal for Numerical Methods in Engineering, 59(8): 1039-1074.
DOI:10.1002/(ISSN)1097-0207 |
|
Bérenger J P.
1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics, 114(2): 185-200.
DOI:10.1006/jcph.1994.1159 |
|
Berland J, Bogey C, Bailly C.
2006. Low-dissipation and low-dispersion fourth-order Runge-Kutta algorithm. Computers and Fluids, 35(10): 1459-1463.
DOI:10.1016/j.compfluid.2005.04.003 |
|
Cerjan C, Kosloff D, Kosloff R, et al.
1985. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics, 50(4): 705-708.
DOI:10.1190/1.1441945 |
|
Chang Z, Guo D K, Feng X Q, et al.
2014. A facile method to realize perfectly matched layers for elastic waves. Wave Motion, 51(7): 1170-1178.
DOI:10.1016/j.wavemoti.2014.07.003 |
|
Chew W C, Weedon W H.
1994. A 3D perfectly matched medium from modified Maxwell's equations with stretched coordinates. Microwave and Optical Technology Letters, 7(13): 599-604.
DOI:10.1002/(ISSN)1098-2760 |
|
Chew W C, Liu Q H.
1996. Perfectly matched layers for elastodynamics:a new absorbing boundary condition. Journal of Computational Acoustics, 4(4): 341-359.
DOI:10.1142/S0218396X96000118 |
|
Clayton R, Engquist B.
1977. Absorbing boundary conditions for acoustic and elastic wave equations. Bulletin of the Seismological Society of America, 67(6): 1529-1540.
|
|
Collino F, Tsogka C.
2001. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media. Geophysics, 66(1): 294-307.
DOI:10.1190/1.1444908 |
|
Du X L, Zhao M.
2010. A local time-domain transmitting boundary for simulating cylindrical elastic wave propagation in infinite media. Soil Dynamics and Earthquake Engineering, 30(10): 937-946.
DOI:10.1016/j.soildyn.2010.04.004 |
|
Durán M, Muga I, Nédélec J C.
2011. The outgoing time-harmonic elastic wave in a half-plane with free boundary. SIAM Journal on Applied Mathematics, 71(2): 443-464.
DOI:10.1137/100786137 |
|
Duru K, Kreiss G.
2014. Numerical interaction of boundary waves with perfectly matched layers in two space dimensional elastic waveguides. Wave Motion, 51(3): 445-465.
DOI:10.1016/j.wavemoti.2013.11.002 |
|
Guddati M N, Tassoulas J L.
2000. Continued-fraction absorbing boundary conditions for the wave equation. Journal of Computational Acoustics, 8(1): 139-156.
DOI:10.1142/S0218396X00000091 |
|
Hagstrom T, Warburton T.
2004. A new auxiliary variable formulation of high-order local radiation boundary conditions:corner compatibility conditions and extensions to first-order systems. Wave Motion, 39(4): 327-338.
DOI:10.1016/j.wavemoti.2003.12.007 |
|
Higdon R L.
1986. Absorbing boundary conditions for difference approximations to the multi-dimensional wave equation. Mathematics of Computation, 47(176): 437-459.
|
|
Komatitsch D, Tromp J.
1999. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophysical Journal International, 139(3): 806-822.
DOI:10.1046/j.1365-246x.1999.00967.x |
|
Komatitsch D, Tromp J.
2003. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation. Geophysical Journal International, 154(1): 146-153.
DOI:10.1046/j.1365-246X.2003.01950.x |
|
Komatitsch D, Martin R.
2007. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics, 72(5): SM155-SM167.
DOI:10.1190/1.2757586 |
|
Kristek J, Moczo P, Archuleta R J.
2002. Efficient Methods to Simulate Planar Free Surface in the 3D 4th-Order Staggered-Grid Finite-Difference Schemes. Studia Geophysica et Geodaetica, 46(2): 355-381.
DOI:10.1023/A:1019866422821 |
|
Kuzuoglu M, Mittra R.
1996. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microwave and Guided Wave Letters, 6(12): 447-449.
DOI:10.1109/75.544545 |
|
Liao Z P, Wong H L, Yang B P, et al.
1984. A Transmitting boundary for transient wave analyses. Scientia Sinica (Series A), 27(10): 1063-1076.
|
|
Liao Z P. 2002.
Introduction to Wave Motion Theories in Engineering. (2nd ed). Beijing: Science Press.
|
|
Lysmer J, Kulemeyer R L.
1969. Finite dynamic model for infinite media. Journal of Engineering Mechanics Division, 95(4): 859-878.
|
|
Matzen R.
2011. An efficient finite element time-domain formulation for the elastic second-order wave equation:a non-split complex frequency shifted convolutional PML. International Journal for Numerical Methods in Engineering, 88(10): 951-973.
DOI:10.1002/nme.v88.10 |
|
Sarma G S, Mallick K, Gadhinglajkar V R.
1998. Nonreflecting boundary condition in finite-element formulation for an elastic wave equation. Geophysics, 63(3): 1006-1016.
DOI:10.1190/1.1444378 |
|
Semblat J F, Lenti L, Gandomzadeh A.
2011. A simple multi-directional absorbing layer method to simulate elastic wave propagation in unbounded domains. International Journal for Numerical Methods in Engineering, 85(12): 1543-1563.
DOI:10.1002/nme.v85.12 |
|
Shan Z D, Ling D S.
2016. An analytical solution for the transient response of a semi-infinite elastic medium with a buried arbitrary cylindrical line source. International Journal of Solids and Structures, 100-101: 399-410.
DOI:10.1016/j.ijsolstr.2016.09.012 |
|
Sochacki J, Kubichek R, George J, et al.
1987. Absorbing boundary conditions and surface waves. Geophysics, 52(1): 60-71.
DOI:10.1190/1.1442241 |
|
Xie Z N, Komatitsch D, Martin R, et al.
2014. Improved forward wave propagation and adjoint-based sensitivity kernel calculations using a numerically stable finite-element PML. Geophysical Journal International, 198(3): 1714-1747.
DOI:10.1093/gji/ggu219 |
|
Xie Z N, Matzen R, Cristini P, et al.
2016. A perfectly matched layer for fluid-solid problems:Application to ocean-acoustics simulations with solid ocean bottoms. Journal of the Acoustical Society of America, 140(1): 165-175.
DOI:10.1121/1.4954736 |
|
Zeng C, Xia J H, Miller R D, et al.
2011. Application of the multiaxial perfectly matched layer (M-PML) to near-surface seismic modeling with Rayleigh waves. Geophysics, 76(3): T43-T52.
DOI:10.1190/1.3560019 |
|
Zhang W, Shen Y.
2010. Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling. Geophysics, 75(4): T141-T154.
DOI:10.1190/1.3463431 |
|
Zhao C G, Du X L, Cui J.
1998. Review of wave propagation theory in saturated and unsaturated porous medium and its numerical methods. Advances in Mechanics (in Chinese), 28(1): 83-92.
|
|
廖振鹏. 2002.
工程波动理论导论(第二版). 北京: 科学出版社.
|
|
赵成刚, 杜修力, 崔杰.
1998. 固体, 流体多相孔隙介质中的波动理论及其数值模拟的进展. 力学进展, 28(1): 83–92.
DOI:10.6052/1000-0992-1998-1-J1998-124 |
|
 2017, Vol. 60
2017, Vol. 60

