21世纪以来，利用重力卫星数据监测全球质量变化的研究得到了极大的发展，尤其是2002年GRACE卫星发射以来，利用高精度轨道和星间观测数据监测全球质量变化取得了巨大成功，在全球陆地水储量变化、极地冰川和高山冰川消融、全球海洋质量变化和地震重力变化等领域的研究中做出了突出贡献，因此利用重力卫星数据监测全球质量变化具有重要意义(Tapley et al.，2004 ，Wahr et al.，2004).

利用重力卫星观测数据监测全球地表质量变化的主要方法为球谐函数法，即利用时变重力场模型计算地表质量变化(Wahr et al.，1998).该方法首先利用重力卫星观测数据恢复展开至一定阶次的时变重力场模型，这项工作主要采用确定重力场模型的理论方法，比较常用和典型的时变重力场模型主要有CSR(Center of Space Research)、JPL(Jet Propulsion Laboratory)和GFZ(Geo Forschungs Zentrum)等机构计算的GRACE模型；然后对时变重力场模型进行地心改正等处理，扣除平均重力场模型后得到这些时变重力场模型位系数残差，即可计算出地表质量变化的时间序列.该方法使用简单，计算效率较高.针对时变重力场模型位系数的相关误差和空域信号的南北条带噪声，许多学者发展了众多去相关算法和滤波平滑技术，如常用的多项式拟合去相关算法和高斯滤波技术(Wahr et al.，1998; Swenson and Wahr，2006; 詹金刚等，2015).由于采用滤波技术导致的信号衰减和泄漏问题，许多学者发展了尺度因子和Forward-Modeling方法进行信号矫正处理(Baur et al.，2009; Landerer and Swenson，2012; Chen et al.，2015; Long et al.，2015; 吴云龙等，2015).虽然球谐函数法被广泛而成功地用于地表质量变化监测，但该方法的缺陷也比较明显，主要表现在难以有效提升信号的空间和时间分辨率，精确评估地表质量变化的不确定性比较困难，球谐位系数存在截断误差，信号泄漏误差改正依赖于所研究区域的大小和形状等(Baur et al.，2009; Chen et al.，2015)，因此有必要发展新的基于重力卫星数据监测地表质量变化的技术.

另一类方法称之为Mascon法(或质量瘤法)，该方法的基本思路最早用于确定月球重力场模型(Muller and Sjogren，1968).该方法是将研究区域划分为规则块体且假设每个块体内的质量均匀分布，然后用一系列的Mascon参数来描述相对平均重力场模型的地表质量变化，采用时间-空间约束方程对Mascon解进行约束处理(Rowlands et al.，2005; Luthcke et al.，2006).研究发现该方法可以有效提升利用重力卫星观测数据监测地表质量变化的时空分辨率(Rowlands et al.，2010).由于信号的空间相关性，Mascon的大小需要进行恰当的选择，目前的研究表明2°至4°的格网大小较为合适(Rowlands et al.，2010; Andrews et al.，2015).

部分学者根据牛顿万有引力定律的基本原理发展了点质量模型法，该方法直接建立了地表质量变化和卫星所受加速度(或引力位)的变化之间的关系，目前已发展出引力位点质量模型法(Han et al.，2005a，2005b; Tangdamrongsub et al.，2012)和径向点质量模型法(Baur and Sneeuw，2011; Baur，2013).引力位点质量模型法是建立地表质量变化与卫星所受引力位变化之间的关系，通过能量守恒法将卫星观测量转换为位能的形式，许多学者对该方法进行了广泛而深入的研究，并有效提取了地表质量变化信息，但将卫星的三维观测信息转换为标量的位能过程中损失了矢量信息.而径向点质量模型法是将卫星受到的地表质量点引起的加速度投影至径向方向，建立卫星所受径向加速度变化与地表质量变化之间的关系，而卫星高度处的扰动径向加速度可以利用时变重力场模型计算，Baur对该方法进行了详细分析并用于计算Greenland的长期质量变化(Baur and Sneeuw，2011; Baur，2013).由于引力方向和径向方向之间存在夹角，因此利用卫星观测数据计算地表质量变化是一个非线性问题，只能采用时变重力场模型计算扰动径向加速度.

由于现有点质量模型法存在缺陷，本文基于点质量模型法的基本原理，在三维直角坐标系中建立地表质量变化和卫星加速度变化的线性关系，同时采用短弧积分法处理卫星观测数据，建立完整的利用重力卫星观测数据监测地表质量变化的三维点质量模型法.本文的方法直接建立了地表质量变化和卫星观测数据之间的三维线性关系，避免了引力位点质量模型法和径向点质量模型法各自的缺点，当然本文的方法也可以采用时变重力场模型计算地表质量变化.通过合成手段模拟地表质量变化，并考虑南北条带噪声的情况下，对三维点质量模型法进行了完整的模拟分析，验证该方法的有效性.

相对于地球质量而言，可以将卫星质量视为单位质量，设地面某一质量点的质量为δm，卫星和地面质量点之间的距离为l，根据牛顿万有引力定律，卫星受到的地面质量点引起的引力为(本文假设地球质量变化集中于地表及其表面以下10 km左右的一个薄层，即地面点位于地球平均半径R的球面)(Heiskanen and Moritz，1967)：

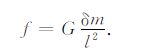
(1)

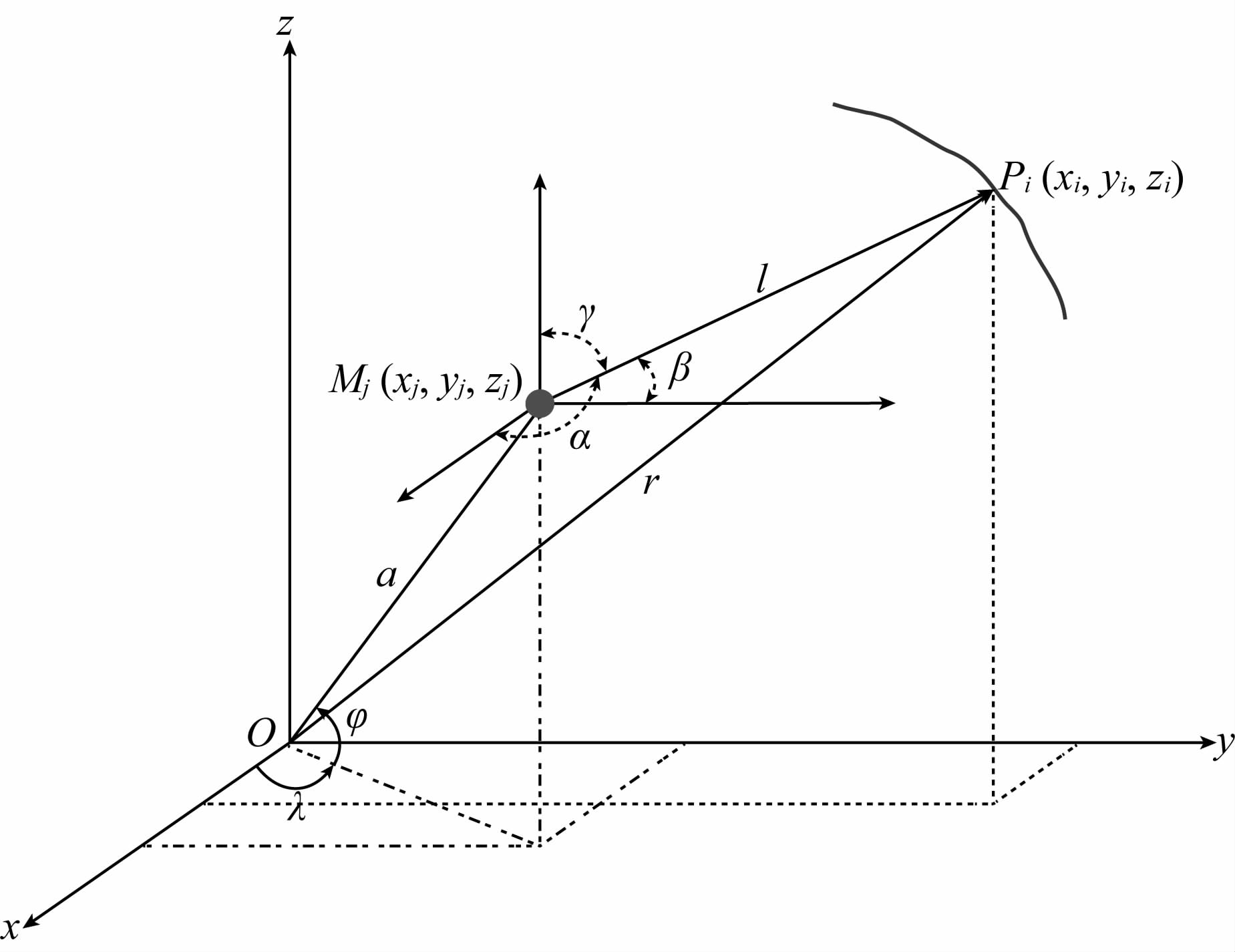
在三维直角坐标系中，设卫星在某时刻的位置为P_i(x_i，y_i，z_i)，地面点为M_j(x_j，y_j，z_j)，地面点和卫星之间的空间关系如图 1所示，点P和M之间的引力与三个坐标轴x，y，z之间的夹角分别为α，β，γ.由于将卫星视为单位质量体，本文不再具体区分卫星受到的引力和加速度之间的差别，两者在数值上做等价处理.

图 1

Fig. 1

图 1 三维点质量模型法示意图 Fig. 1 The illustration of three-dimensional point-mass modeling approach

将卫星与地面质量点之间的引力在三个坐标轴方向投影，可得卫星受到地面质量点作用的加速度分量为

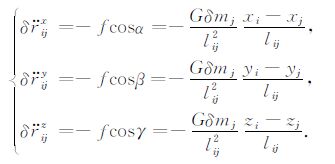
(2)

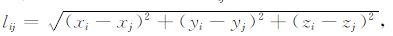
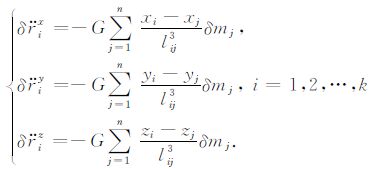
其中，设地面质量点的个数为n，卫星观测历元个数为k，由于在某一历元时刻卫星同时受地面所有质量点的引力作用，因此在该时刻由于地表质量变化而导致的卫星加速度变化可以表示为

(3)

式(3)即为三维点质量模型法的基本关系式，它将地表质量变化直接与卫星受摄运动的加速度相联系，因此如果知道卫星的摄动加速度，即可根据式(3)求解地表质量点的质量变化δm.卫星受到的总加速度可以分解为以下几部分：

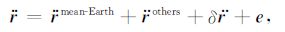
(4)

其中，${\ddot{r}}$为卫星受到的总加速度，为卫星受到的静态(平均)重力场引起的加速度，为卫星受到的固体潮、海潮、固体极潮、海极潮、三体引力摄动、相对论效应和非保守力摄动引起的加速度，为由于地表质量变化引起的卫星摄动加速度，e为加速度残差.其中，和可以通过精确的参考力模型计算，且非保守力加速度可以利用卫星的加速度计观测数据计算.下一步的问题可归结为利用卫星的观测数据计算其受到的总加速度，此过程与利用卫星观测数据确定地球重力场模型的方法一致.基于卫星观测数据确定地球重力场模型的常用方法有动力学积分法、加速度法、短弧积分法、天体力学法和能量守恒法等(苏勇，2016；游为，2011)，由于能量守恒法是将卫星观测数据转换为能量的形式，适用于处理引力位点质量模型法的求解，而不适用于本文的三维点质量模型法求解(Visser et al.，2003)，因此除了能量守恒法的其余方法均可用于三维点质量模型法的求解.本文采用短弧积分法建立卫星观测数据与其所受加速度之间的关系，考虑到GRACE卫星观测模式用于监测地球质量变化的巨大成功，因此本文主要考虑轨道和星间观测数据求解地表质量变化.

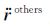
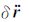
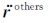
本文不加推导地给出短弧积分法的基本观测方程，对于轨道观测数据有如下关系(Mayer-Gürr et al.，2005; Mayer-Gürr，2006)：

(5)

对于星间距离变率则有如下关系(Mayer-Gürr，2006)：

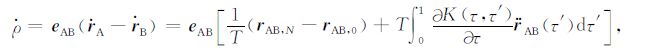
(6)

式(5)和(6)中，r和${\dot{r}}$分别为卫星的轨道坐标和速度向量，r₀和r_N为弧段的边界向量，τ和τ′为归一化的时间变量，T为弧段长度，下标A和B分别表示两颗卫星，${\dot{\rho }}$为双星星间距离变率，e_AB为星间单位向量，K(τ，τ′)为积分核函数.对于短弧积分法的详细计算已有许多文献进行了深入研究，本文不再细述(Mayer-Gürr，2006).

至此，联合式(3)—式(6)即可建立完整的基于卫星轨道和星间距离观测数据计算地表质量变化的三维点质量模型法.基于高斯-马尔科夫模型建立求解地表质量变化的观测方程：

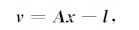
(7)

其中，A为设计矩阵，l为观测向量，x为未知参数向量，三维点质量模型法中表示地表质量点的质量变化，v为观测数据的改正向量.每个弧段的法方程为

(8)

由于利用卫星观测数据计算地表质量变化是一个向下延拓的过程，式(8)呈病态，直接求解无法得到稳定的解.针对利用卫星观测数据求解地表质量变化过程中的病态问题，通常的做法是采用时间-空间约束方程或正则化手段进行处理(Han et al.，2005a; Rowlands et al.，2005; Luthcke et al.，2006; Baur and Sneeuw，2011; Tangdamrongsub et al.，2012).本文采用最简单的零阶Tikhonov正则化方法，此时正则化的解可表示为(Koch，1999)：

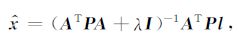
(9)

式中λ为正则化参数，I为正则化单位矩阵.最优正则化参数的确定采用L曲线法(Hansen，1992).

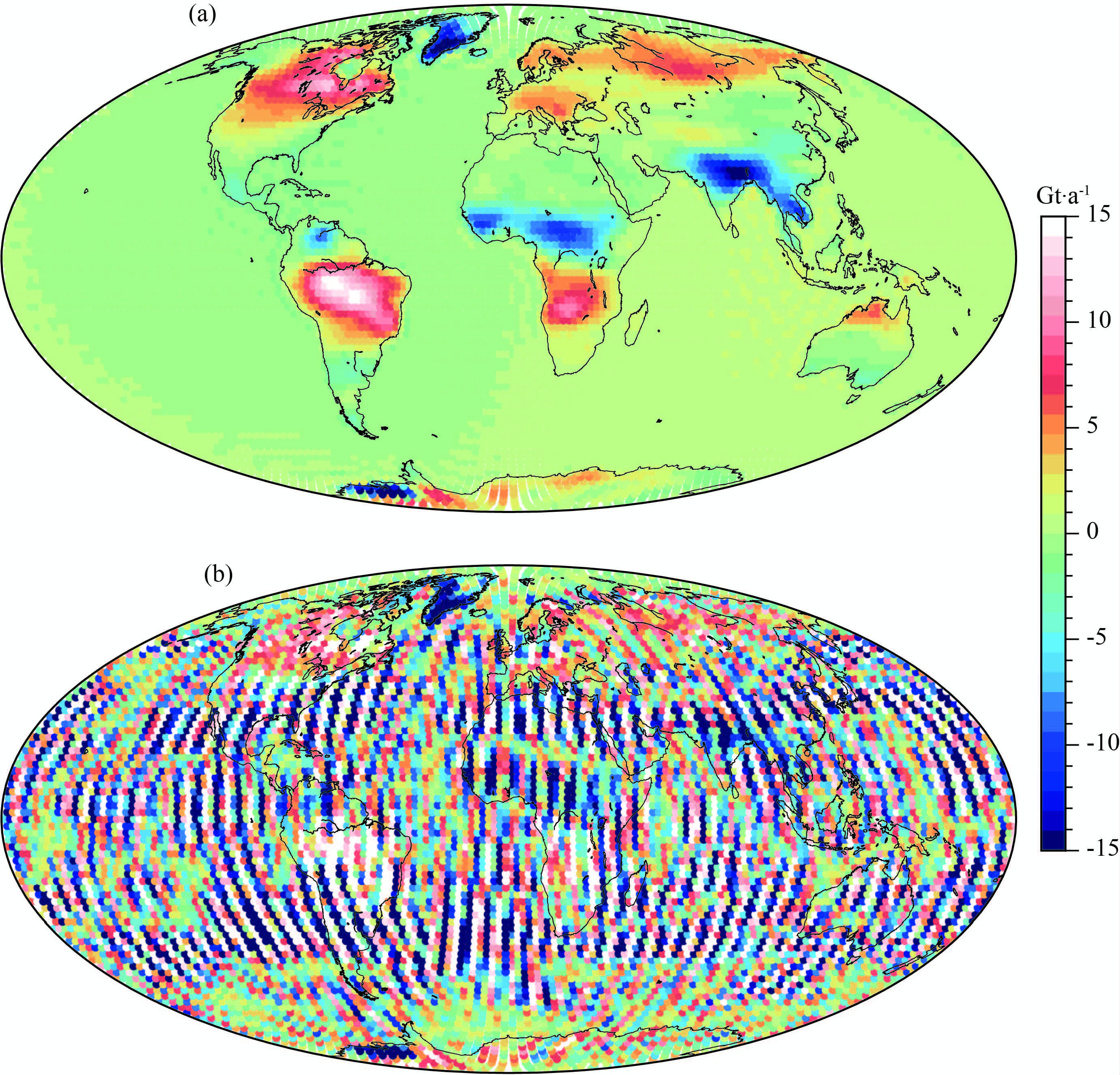
为了评估三维点质量模型法的效果，本文通过合成手段模拟全球质量变化情况.将空域信号转变为谱域球谐系数时，位系数的阶数越高，则截断误差越小；考虑到目前利用时变重力场模型研究质量分布时一般将模型截断至60阶左右，因此本文在合成全球质量变化时，球谐位系数也仅展开至60阶次，为了不考虑截断误差的影响，采用如下步骤合成全球质量变化：首先合成全球质量变化的空域格网点值，然后采用球谐分析手段将其转换至60阶次的球谐位系数模型，再采用球谐综合方法将合成的60阶次球谐位系数转换为空域的全球质量变化(如图 2a所示)，图中质量变化量的单位为十亿吨每年(Gt·a^-1)，最后将球谐综合得到的全球质量变化转化为60阶次的球谐位系数，得到合成的月时变重力场模型.同时为了模拟南北条带噪声的影响，在合成的无噪声月时变重力场模型中加入模拟的南北条带噪声，得到60阶次的含条带噪声的月时变重力场模型，如图 2b所示.经过以上步骤合成的空域全球质量变化及其对应的谱域60阶次月时变重力场模型之间不存在截断误差的影响，两者可以几乎无误差的相互转换.

图 2

Fig. 2

图 2 模拟的全球质量变化 (a)无条带噪声的全球质量变化；(b)含条带噪声的全球质量变化(即(a)+模拟的条带噪声). Fig. 2 Simulated model of global mass change a)Model without stripe noise；(b)Model with stripe noise，synthetic model by(a)add stripe noise model.

考虑有无条带噪声情况下的两种模拟时变重力场模型，以GGM05S模型的前60阶次作为静态重力场模型，同时考虑固体潮、海潮等因素的影响(具体采用的力模型和相关参数如表 1所示)，采用变步长的GAUSS JACSON(Berry and Healy，2004)积分器分别模拟了一个月的GRACE轨道和星间距离变率数据，历元间隔均为5 s，轨道积分的初始参数如表 2所示.

表 1(Table 1)

表 1 模拟GRACE轨道所采用的力模型 Table 1 Background force models for GRACE orbit simulation 力模型 模型 说明 静态重力场模型 GGM05S (Tapley et al.，2013) 截断至60阶次 固体潮 IERS 2010 (Petit and Luzum，2010) 考虑2，3和4阶次 海潮 EOT11a (Rieser et al.，2012) 截断至120阶次 固体极潮 IERS 2010 (Petit and Luzum，2010) 海极潮 Desai模型(Desai，2002) 截断至36阶次 N体引力 DE421 (Folkner et al.，2009) 仅考虑太阳和月亮

表 1 模拟GRACE轨道所采用的力模型 Table 1 Background force models for GRACE orbit simulation

表 2(Table 2)

表 2 模拟GRACE轨道的初始参数 Table 2 Initial parameters for GRACE orbit simulation 参数 GRACE-A GRACE-B 起始历元(简化儒略日) 53371.0 终止历元(简化儒略日) 53402.0 惯性系下的 初始坐标(m) X 3646542.573 3510572.982 Y 2859812.156 2745797.168 Z 5053108.148 5211060.593 惯性系下的 初始速度 (m·s-1) Vx 4301.430699 4438.532390 Vy 3621.305536 3729.046204 Vz -5141.152421 -4942.120949

表 2 模拟GRACE轨道的初始参数 Table 2 Initial parameters for GRACE orbit simulation

利用模拟的卫星轨道和星间距离变率，采用短弧积分法和三维点质量模型法计算全球质量变化，根据已有文献和本文的多次测试分析，选择积分弧长为30 min，由于模拟的卫星轨道和星间距离变率未加入观测误差，二者做等权处理.

地面质量点的分布规则需要适当选择，典型的规则格网可分为高斯格网(Gauss grid)、三角划分格网(Triangle grid)、等角格网(地理格网Geographical grid)、等个数格网(Equal-number grid)、等距离格网(Equi-distant grid)和等面积格网(Equal-area grid)等(Eicker，2008).最广泛使用的是等角格网，即在纬度和经度方向的格网大小一致，而高斯格网与其接近，但纬度方向并不是等角间隔，这两类格网在两极方向同一纬圈上的经度点个数越来越密，即空间分辨率从赤道往两极地区不断增大，等个数格网也面临着同样的问题.而相对来讲，等距离格网、等面积格网和三角划分格网在全球范围内均匀分布，但三角划分格网不易控制格网密度.同时等面积格网可以方便的将地面点的质量转换为以等效水高形式表示，本文采用等面积格网作为地面质量点的分布类型.由于每个质量点的质量作为待求未知参数，格网的个数即为未知参数的个数，由于所采用计算机硬件的限制，本文采用2°等面积格网，此时全球范围内共有10266个格网点.

基于模拟的两类轨道数据和星间距离变率数据，采用三维点质量模型法解算地表质量变化，除时变信号之外的力模型如表 1所示，下面将对解算结果进行详细分析.

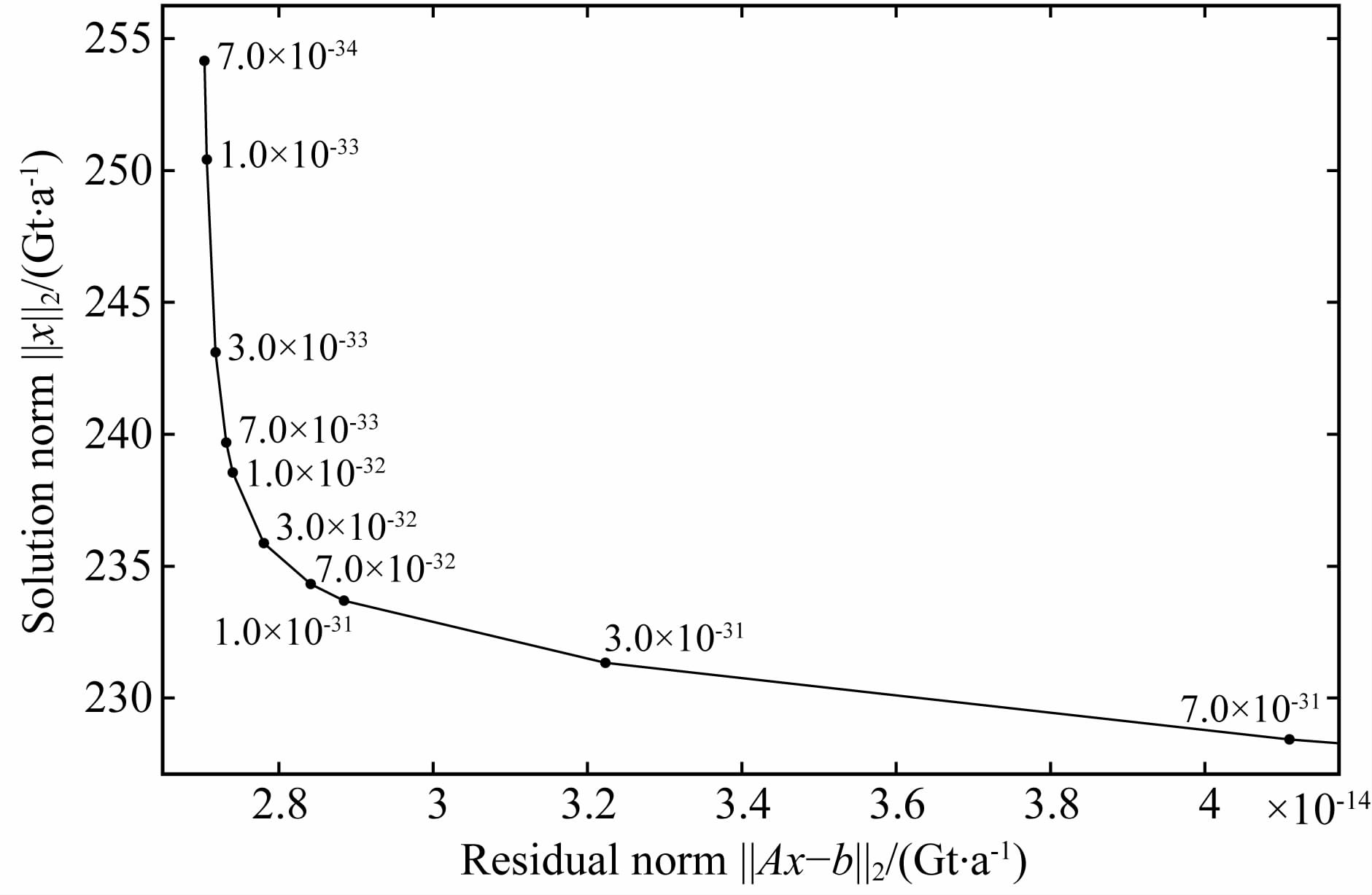
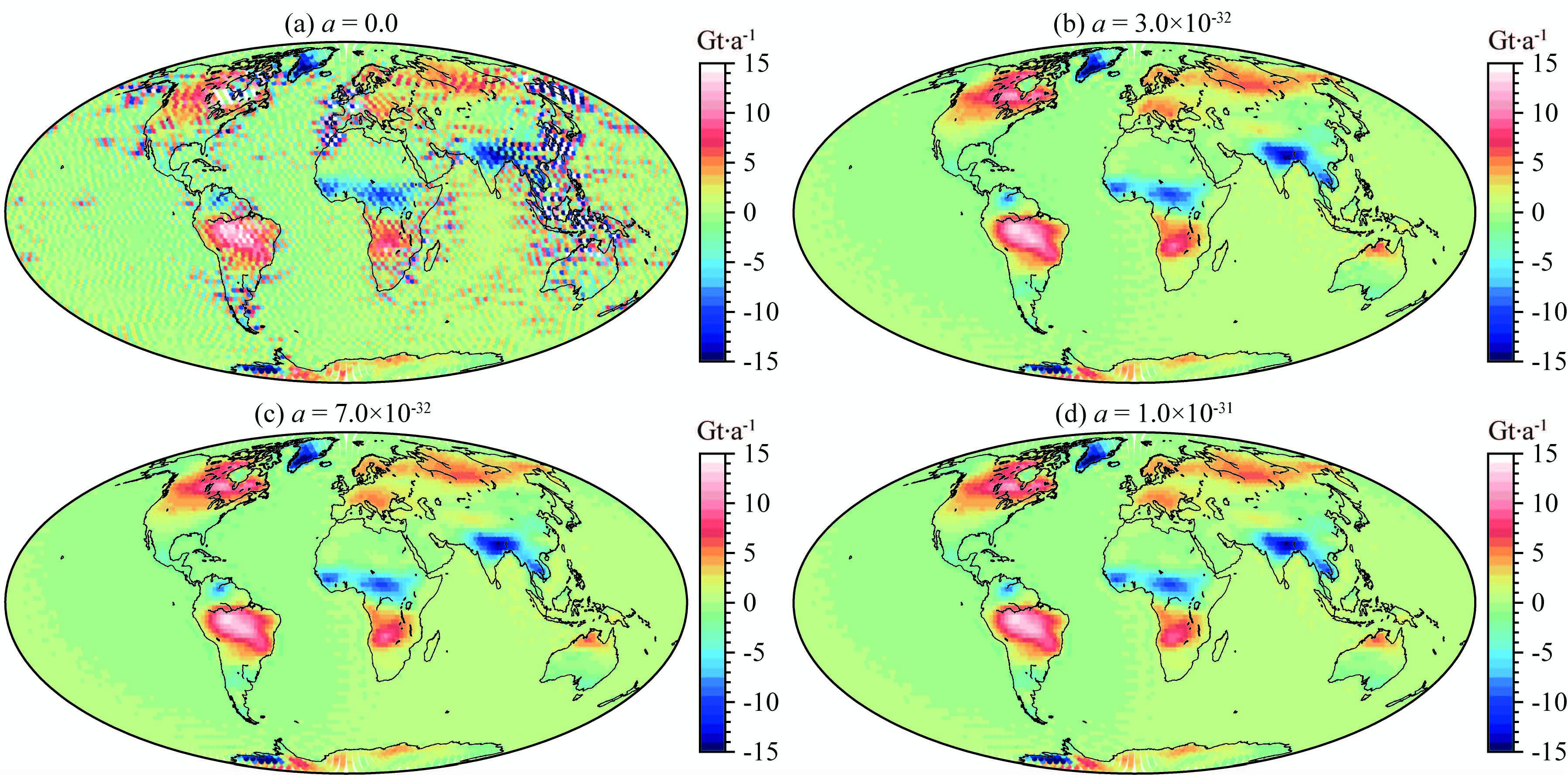
利用模拟的不包含南北条带噪声的时变重力场模型积分的轨道和星间距离变率数据，采用三维点质量模型法解算地表质量变化的最优正则化参数L曲线如图 3所示，当正则化参数取值分别为0、3×10^－32、7×10^－32和1×10^－31时的空域时变信号如图 4所示.理论上来讲，利用三维点质量模型法计算的地表质量变化与合成的无噪声地表质量变化应该是一致的，即当正则化参数取值为0时(图 4a所示)，空域信号应该与图 2a一致，但正如前文理论分析时所指出的原因，利用重力卫星观测数据解算地表质量变化是一个向下延拓的过程，无法得到稳定的解算结果.由图 3可以看出最优正则化参数的取值为7×10^－32，此时对应的空域信号如图 4c所示，正则化参数取值大于或小于最优值时均不能得到最优解(如图 4(b，d)所示).因此，由于向下延拓过程导致的病态问题，必须采用适当的正则化手段或约束条件才能得到合适的稳定解.

图 3

Fig. 3

图 3 无条带噪声时的正则化曲线 Fig. 3 The L-curve for 3D-PMA solutions with no stripe noise model

图 4

Fig. 4

图 4 无条带噪声情况下不同正则化参数的解算结果 Fig. 4 he solutions with different regularization parameters without stripe noise model

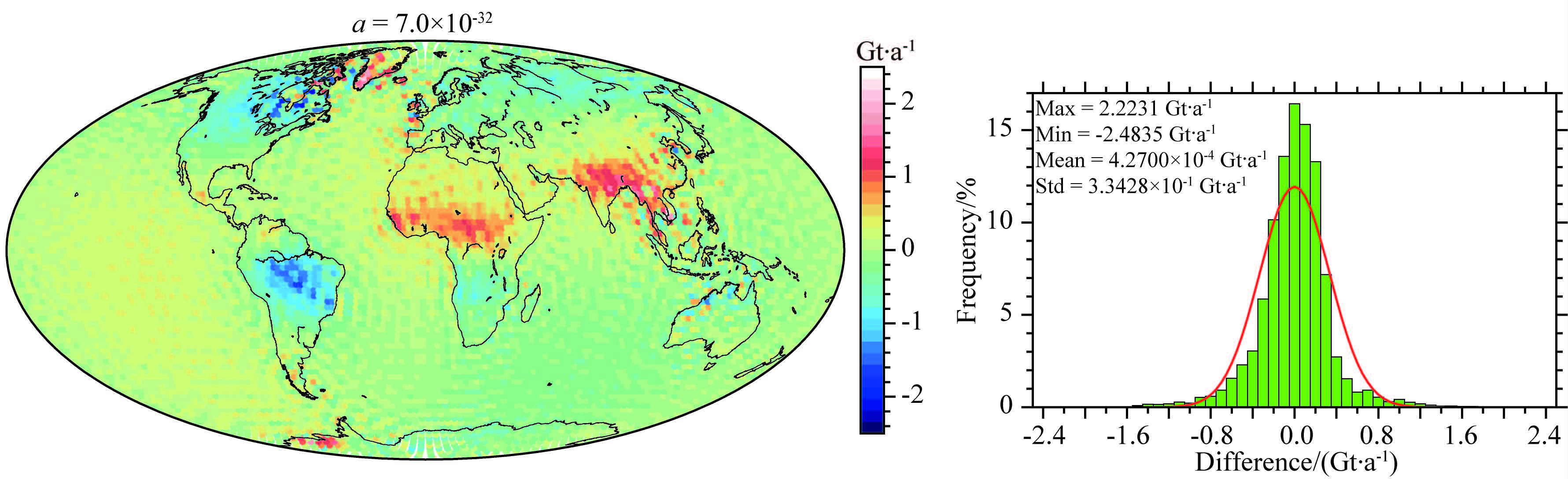
将采用最优正则化参数解算的地表质量变化与合成模型(图 2a)做差并进行统计分析，结果如图 5所示.由于采用正则化技术对病态问题进行约束的同时，对信号也进行了平滑处理，导致地表质量变化较大区域的信号出现了不同程度的被削弱现象(图 5左侧所示)，其统计直方图如图 5右侧所示，其中红线表示对应的正态分布曲线(下同)，可以看出，最优正则化参数解算的结果与合成模型的差值最大值约为2.2 Gt·a^-1，最小值约为-2.5 Gt·a^-1，均值约为4.3×10^－4 Gt·a^-1，标准差约为0.33 Gt·a^-1.通过以上分析可以看出，正则化技术不仅可以处理向下延拓导致的病态问题，而且可以对信号进行空域平滑，这将有利于处理含南北条带噪声的时变信号.

图 5

Fig. 5

图 5 最优正则化解与合成模型(图 2a)差值的统计 Fig. 5 The statistic of difference between optimal solution and synthetic model(Fig. 2a)

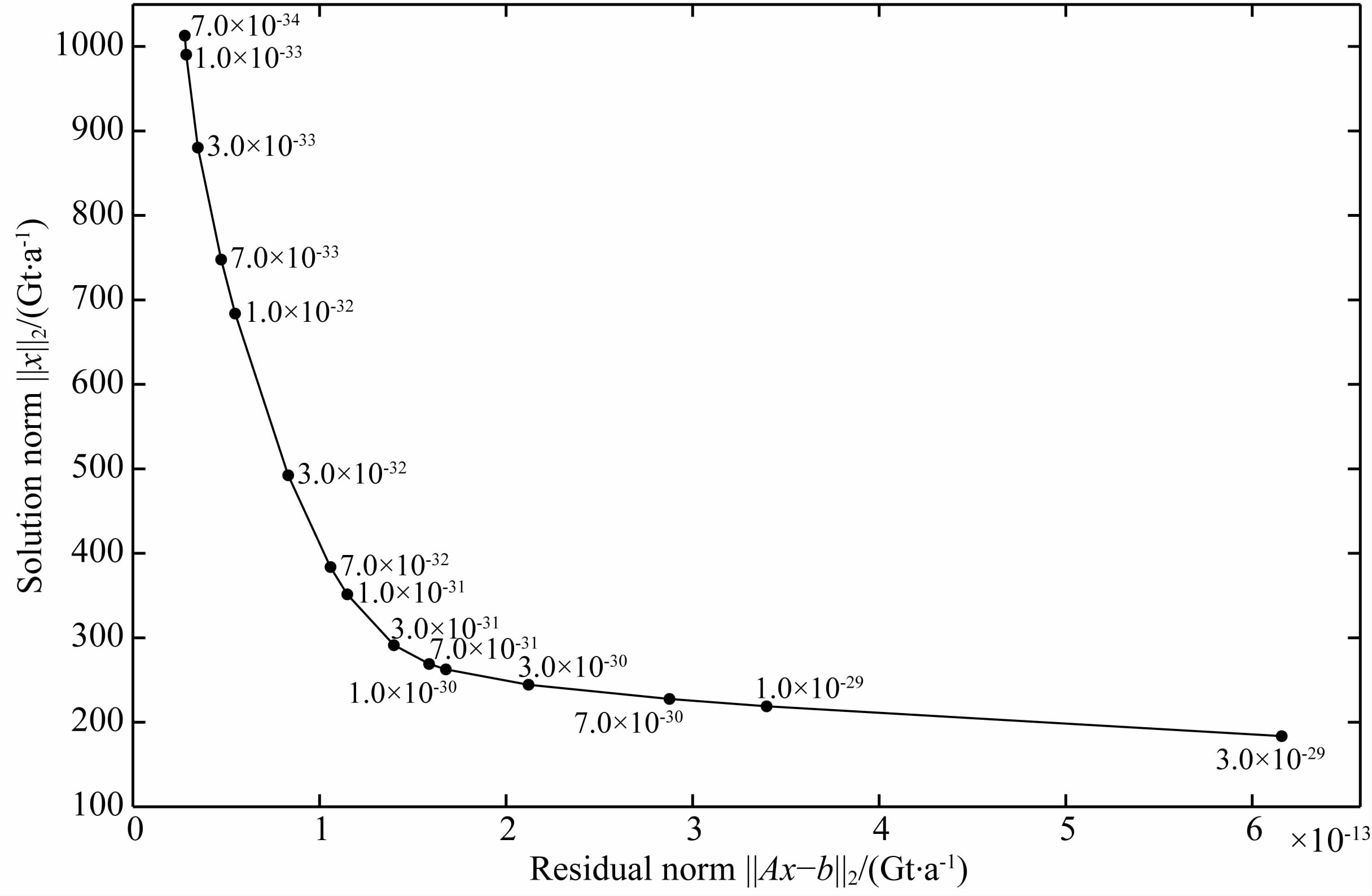
为了测试三维点质量模型法处理含南北条带噪声时的能力，利用合成的含南北条带噪声的时变重力场模型(如图 2b所示)模拟轨道和星间距离变率数据.此时，采用三维点质量模型法解算地表质量变化时的正则化曲线如图 6所示.根据L曲线法确定最优正则化参数的原则，此时的最优正则化参数应该在3×10^－31左右，但实际分析发现，采用L曲线法确定的最优正则化参数解算的结果仍然存在较为明显的南北条带噪声，也就是说采用L曲线法确定的最优正则化参数偏小.为了平衡条带噪声和平滑误差的影响，实验分析后取最优正则化参数为3×10^－30.

图 6

Fig. 6

图 6 有条带噪声时的正则化曲线 Fig. 6 The L-curve for 3D-PMA solutions with stripe noise model

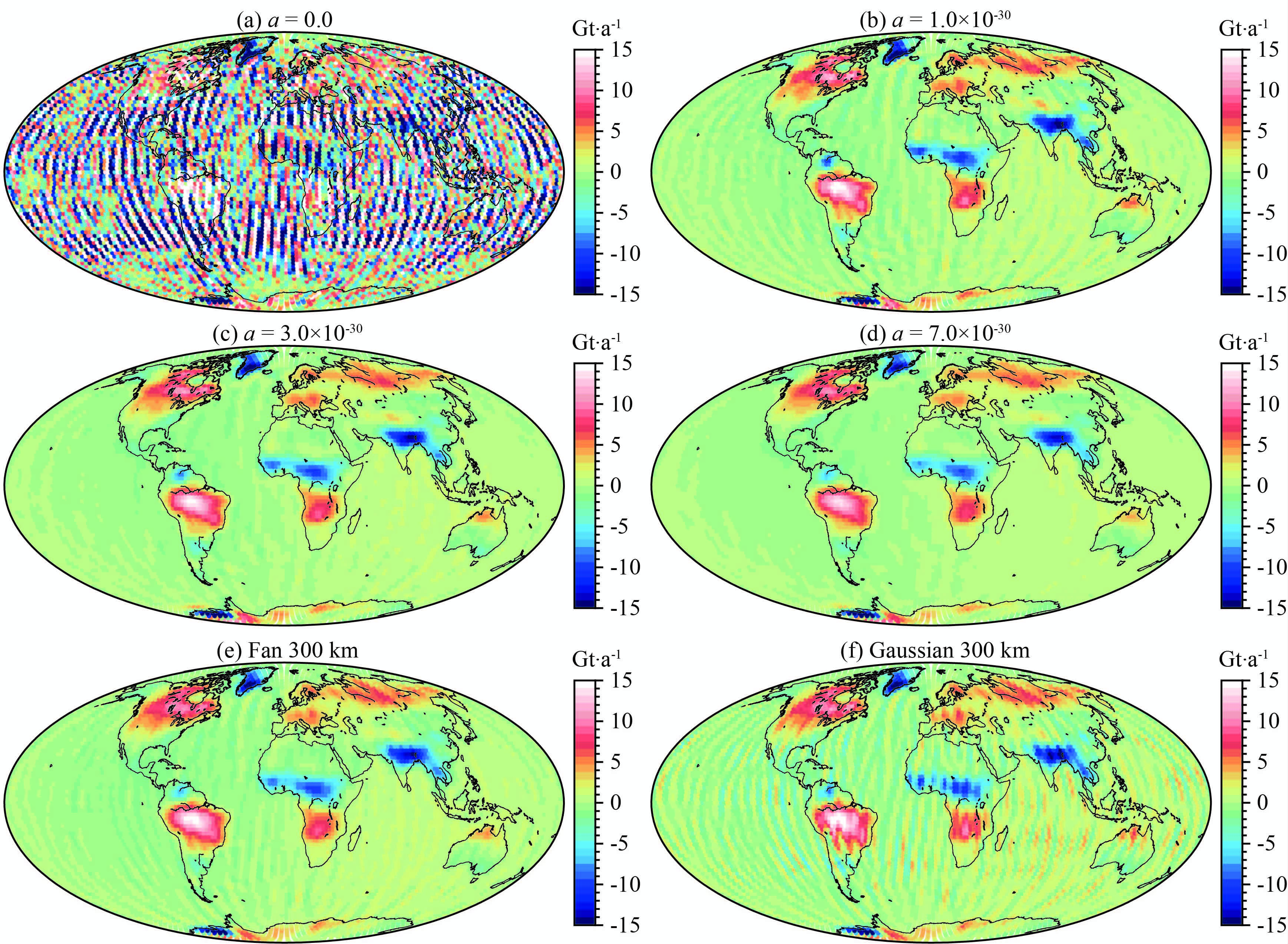
不同正则化参数时的空域结果如图 7所示.当正则化参数为0时，计算的结果同时受到南北条带噪声和向下延拓病态性的影响；随着正则化参数的不断增大，空域信号逐渐平滑，条带噪声和向下延拓病态的影响逐渐减弱，但空域信号的细节特征也逐渐被平滑.为了比较三维点质量模型法的结果，本文同时对模拟的含条带噪声的时变重力场模型位系数采用300 km的扇形滤波和高斯滤波处理，滤波后对应的空域信号如图 7(e，f)所示.对比后可以看出，300 km的扇形滤波和高斯滤波处理条带噪声的效果差于正则化参数为3×10^－30时的三维点质量模型法结果.直接对空域信号进行比较只能反映结果相互之间的平滑性，无法真实反映各方法的真实去条带噪声能力，这是由于空域信号看起来较平滑有可能是正则化参数或滤波半径过大而导致的，虽然平滑了较多的条带噪声，但同时可能也平滑了部分真实的信号.为了进一步比较，将采用最优正则化参数解算的地表质量变化以及滤波结果与合成无噪声模型(图 2a)做差并进行统计分析，结果如图 8所示.

图 7

Fig. 7

图 7 条带噪声情况下不同正则化参数的解算结果 Fig. 7 The solutions with different regularization parameters with stripe noise model

图 8

Fig. 8

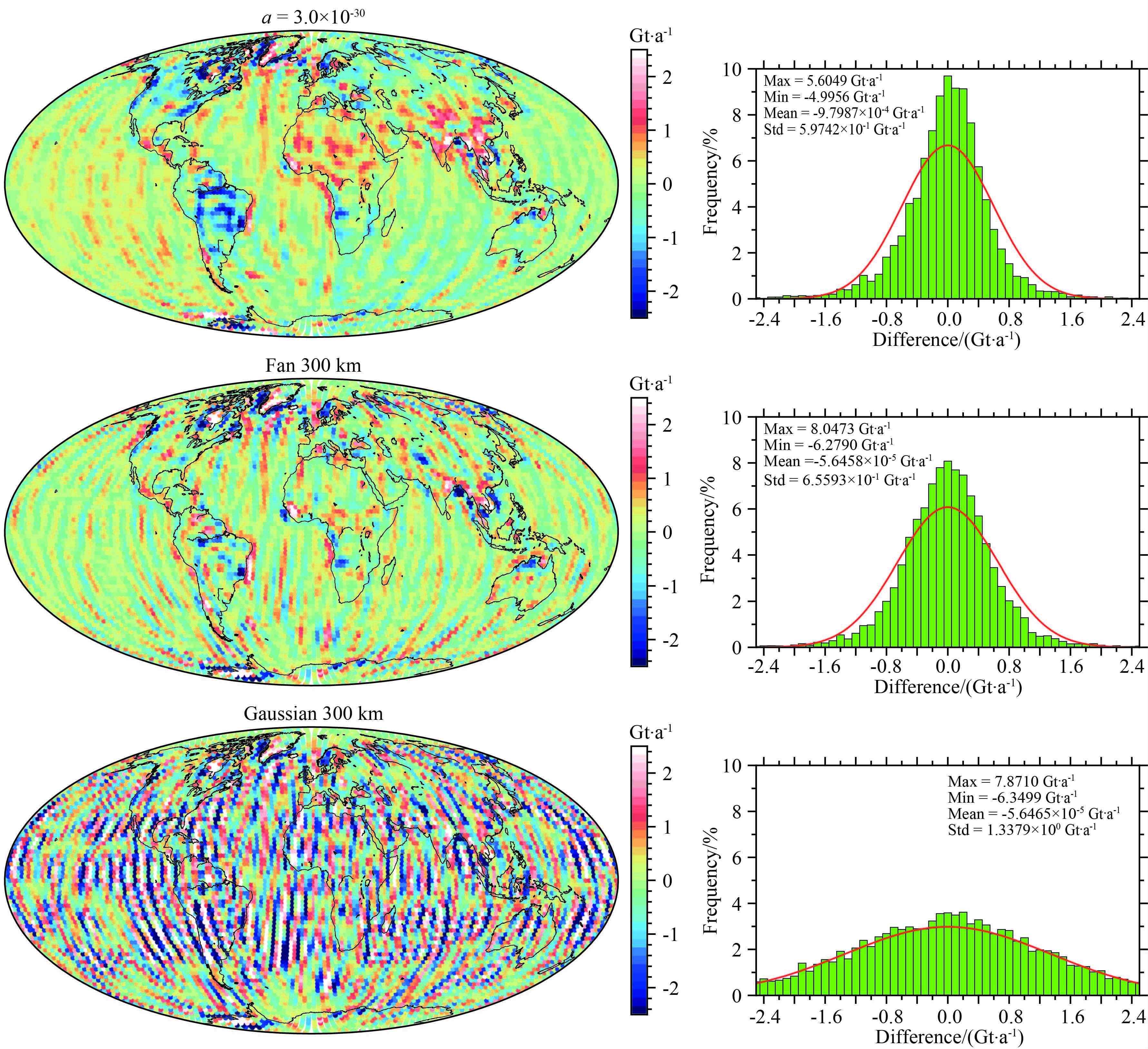
图 8 最优正则化3D-PMA解、扇形滤波和高斯滤波与合成模型(图 2a)差值的统计 Fig. 8 The statistic of difference between optimal 3D-PMA solution，Fan filter and Gaussian filter and synthetic model(Fig. 2a)

由图 8可以看出，各方法均无法完全平滑条带噪声的影响，相比较于300 km扇形滤波和高斯滤波的结果，最优正则化时的三维点质量模型法的效果最佳，高斯滤波的效果最差.从统计直方图的结果来看，也可以得出相同的结论.最优正则化参数解算的结果与合成无噪声模型的差值最大值约为5.6 Gt·a^-1，最小值约为-4.9 Gt·a^-1，均值约为－9.8×10^－4 Gt·a^-1，标准差约为0.60 Gt·a^-1，这些指标均优于300 km半径的扇形和高斯滤波的结果.需要说明的是，将三维点质量模型法的结果与扇形滤波和高斯滤波的结果进行比较，需要同时考虑两方面的问题：一是进行比较时，扇形滤波或高斯滤波的最优滤波半径的选取是否合适，本文只是采用大多数文献处理GRACE时变重力场模型时经常采用的数值，并未对最优滤波半径再次进行分析；但由于本文合成含条带噪声的时变信号时，南北条带噪声直接从GRACE真实时变重力场模型中分离提取，因此300 km左右大小的滤波半径可满足需求.二是三维点质量模型法的最优正则化参数的选取是否合适，本文采用与Baur and Sneeuw(2011)文中相同的基于L曲线确定最优正则化参数的方法；部分学者分析认为L曲线法确定的最优正则化参数会导致解过于平滑(Kusche and Klees，2002)，因而推荐采用基于均方根误差最小准则确定最优正则化参数的方法(Xu et al.，2006; Shen et al.，2012)；由于本文仅作模拟分析，而且最优正则化参数的选取采用L曲线法结合空域结果信号进行半经验选取，因此采用计算量较小、相对简单的L曲线法.

综上分析可知，三维点质量模型法可以有效利用卫星轨道或星间观测数据计算地表质量变化，正则化处理可以有效削弱向下延拓引起的病态问题并平滑处理条带噪声的影响.相比传统的球谐函数法以及点质量模型法，三维点质量模型法可避免球谐位系数截断误差导致的信号泄漏问题，函数模型和卫星轨道观测数据均为三维直角坐标系中给出，函数关系简单.但是采用正则化技术时，一方面不能完全平滑掉条带噪声的影响，另一方面会平滑掉有效的地表质量变化信号.

本文基于牛顿万有引力定律，在三维空间直角坐标系中导出利用重力卫星观测数据监测地表质量变化的三维点质量模型法，并详细介绍了该方法的基本原理和计算思路.由于在三维直角坐标系中直接建立卫星所受加速度变化与地表质量变化的线性关系，与传统的引力位点质量模型法和径向点质量模型法相比，该方法可直接利用重力卫星的轨道和星间观测数据或时变重力场模型计算全球质量变化.考虑到利用卫星观测数据计算地表质量变化的向下延拓过程以及观测数据噪声的影响，需要采用合适的空间约束方程或正则化技术对解算结果进行约束或平滑处理.

为了验证三维点质量模型法的有效性以及处理空域条带噪声的能力，利用合成全球质量变化模型模拟一个月的GRACE双星轨道和星间距离变率数据计算全球质量变化，对三维点质量模型法进行分析验证，采用零阶Tikhonov正则化技术处理病态问题，并将计算结果与扇形滤波和高斯滤波的结果进行比较分析.

模拟分析表明，三维点质量模型法可有效用于重力卫星观测数据监测全球质量变化，为利用重力卫星观测数据监测全球质量变化提供一种可选的途径.相比于传统的球谐函数法，该方法不存在截断误差导致的信号泄漏问题，可以更高的时空分辨率提取地表质量变化信号.但三维点质量模型法存在计算量大的缺点，例如计算全球2°等面积格网的地表质量变化，待求未知参数的个数约为10266个，这相当于求解球谐位系数展开至100阶次左右的月时变重力场模型.

感谢奥地利科学院空间研究所的Harald Wensberger博士在模拟GRACE轨道数据时提供的帮助.