2. 有色金属成矿预测教育部重点实验室, 长沙 410083
2. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education 410083, China
探地雷达(Ground Penetrating Radar,GPR)数值模拟是计算地球物理学的重要研究方向,通过对典型地质模型模拟结果的分析,可以加深对GPR传播规律与反射剖面的认识,有效指导GPR资料解释(曾昭发等,2010).在GPR正演模拟中,时域有限差分法(Finite Difference Time Domain,FDTD)具有直接时域计算、编程容易、节约存储空间和计算时间等优点而备受青睐(Irving and Knight,2006;Cassidy and Millington,2009;刘四新和曾昭发,2007;冯德山等,2010),但FDTD也存在两个明显的局限性:(a)时间步的选择要严格满足Courant 稳定性条件,需要占用大量计算资源,否则易产生网格色散和误差积累;(b)对网格剖分要求严格,通常只能是直交网格,不能与非结构化网格结合,对不规则目标、复杂的物性分界面拟合效果不好.为此,一些学者将有限单元法(FEM)引入到GPR正演模拟中:沈飚(1994) 率先推导了低损耗介质GPR有限元方程,并开展了台阶状模型的GPR正演;底青云和王妙月(1999) 推导了含衰减项的探地雷达波有限元方程,实现了复杂形体的GPR波的FEM正演;谢辉等(2003) 构建了20个节点等参单元的FEM,并对Pulse型GPR进行了模拟;戴前伟等(2012) 将双二次插值FEM法及三角剖分的FEM法应用于GPR正演,相比线性插值、矩形剖分FEM,具有更高的模拟精度.但这些文献中都是采用规则网格剖分,并没有充分发挥FEM的优势.
考虑到求解GPR波动方程时,需要丰富的时域信息,FEM的求解多在时域而非频域中开展,从而时域有限元(Finite-Element Time-Domain,FETD)方法得到了迅速发展,FETD继承了FEM可以灵活地选用插值基函数,时间步的选择较为宽松,能与非结构化网格结合、方便模拟复杂目标体的优点.但FETD又受限于自身的时间推进算法,在每个时间步都要求解系统矩阵方程,会消耗大量的计算时间.为了减小刚度矩阵规模,提高FETD的计算效率,可以通过发展高效的吸收边界条件和良好的网格剖分技术,使截断边界条件离目标较近,从而减小计算区域.众所周知,PML边界是吸收边界条件发展的里程碑,如何高效加载PML(Perfectly Matched Layer,PML)边界条件就成了当前FETD方法中的研究难点与热点.PML最初是由Berenger(1994) 提出的,通过在网格外边界加载一种非物理的吸收媒质,可以使电磁波在匹配层中无反射的通过并按指数规律衰减,但它的提出最初是基于FDTD算法(Berenger,1996),公式体系并不适用于FETD.Wu等(1997) 应用FETD开展电磁散射研究时引入了PML边界条件,并对比了各向异性完全匹配层与Berenger PML的吸收效果;Tsai等(2002) 将基于PML边界的无条件稳定扩展FETD求解有源非线性微波电路中,较好地处理了截断边界.Berenger PML需要电磁场分裂,增加了计算内存与数值实现的难度(葛德彪和闫玉波,2011),而且只对行波有吸收效果,对隐失波、低频波、掠角波无吸收效果(Berenger,1997,1999).为此,Sacks等(1995) 和Gedney(1996) 提出了单轴各向异性完全匹配层(Uniaxisal PML,UPML)并应用于FDTD,UPML边界无需对电磁场分裂,计算更简洁、易编程实现,因其在吸收系数中引入了线性的吸收因子,对隐失波、凋落波、低频波等干扰波有一定的吸收效果.Jiao和Jin(2001) 、Jiao等(2003) 、Rylander和Jin(2005) 、王洪华和戴前伟(2013) 等成功将UPML引入到电磁学计算的FETD中,使得FETD的计算进入新的发展阶段;Wang等(2006) 将各向异性介质PML引入到基于棱边的矢量时域有限元中.为了克服UPML低频区性能变差的缺点,Kuzuoglu和Mittra(1996) 提出了CFS-PML技术加强了对低频隐失波、大角度掠射波的吸收;Roden和Gedney(2000) 在CFS-PML基础上应用卷积技术提出了卷积完全匹配层(Convolutional PML,CPML),大大提高了运算效率.Movahhedi等(2007) 、Movahhedi和Abdipour(2009) 将复频移PML(CFS-PML)边界条件应用于Maxwell方程的时域矢量有限元的模拟中,并且开展了最优吸收效果的各项参数选取实验,有效地改善了截断边界反射;李义丰等(2010) 将CPML引入到二维声波有限元计算中,并在有限元计算软件COMSOL中完成数值计算;Correia和Jin(2006) 应用FETD开展了波导数值模拟中,对比了常规PML,CFS-PML,高阶PML优缺点,指出常规PML对传输波具有较好吸收效果,但对低频波、隐失波吸收效果不好;而CFS-PML虽然解决了隐失波的吸收问题,可它对传输波的吸收却大幅下降;高阶复合PML对隐失波和各个频段的传输波都能起到良好的吸收效果,但计算公式过于复杂,不便于编程实现;Donderici和Teixeira(2008) 将共形PML引入到FETD的Maxwell方程瞬变计算中,与常规PML相比,共形PML采用更少的PML区域及计算区域,减小未知量的同时,降低了每个时间步内的计算复杂度,从而节省计算时间.
为了实现圆形、曲面、球体等复杂形体雷达模型的高精度拟合,充分发挥有限元的优势,本文通过改变网格形状,采用不规则四边形网格的FETD开展GPR数值模拟,时间离散方式采用Gedney和Navsariwala(1995) 提出的隐式Newmark-Beta法,在保证稳定性的同时,降低时间步长,从而有效减少迭代步数.吸收边界采用对雷达传输波、隐失波、低频波等综合吸收效果较好的CPML边界条件,有效压制了来自截断边界处的反射波,极大地提升了FETD边界条件的处理效果.
2 GPR波动方程求解的FETD算法由电磁波传播理论可知(Taflove and Brodwin,1975),含衰减项的GPR时域二阶矢量波动方程为
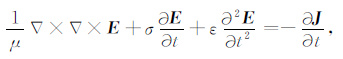
|
(1) |
式(1) 中,E为电场强度,ε为介电常数,μ为磁导率,σ为电导率,t为时间,J表示外加电流源.考虑二维TM(Ez,Hx,Hy)情形,则二阶矢量波动方程可以转化为Ez的二维标量波动方程:
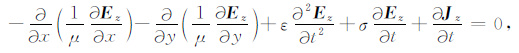
|
(2) |
采用Galerkin法推导FETD二维GPR波动方程.利用试函数v,可以得到
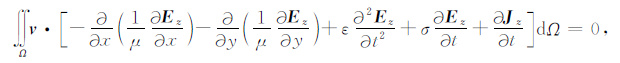
|
(3) |
对式(3) 中左边第1项采用Green公式变换,得到:
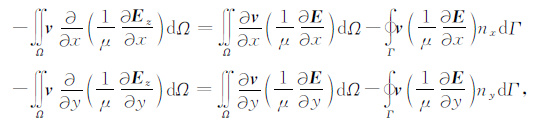
|
(4) |
在边界处采用完全匹配层,故式(4) 右端第二项为零.带入式(3) 得
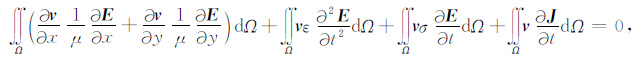
|
(5) |
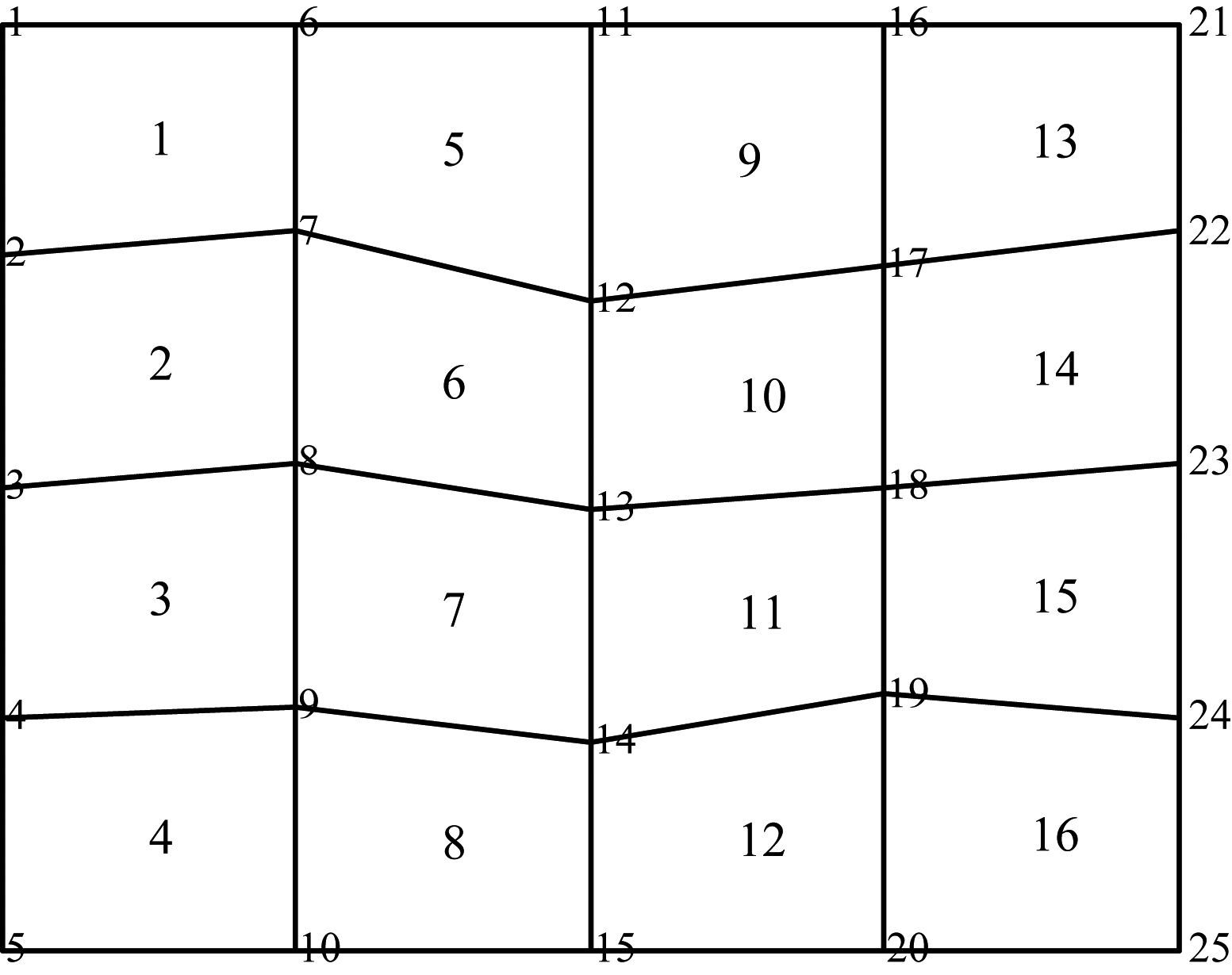
式(5) 为导出的二维FETD波动方程,为求解该方程,先将待求解区域采用图 1所示的非规则四边形进行离散.
|
图 1 网格剖分及节点编号示意 Fig. 1 Grid subdivision and node number |
将任一子单元映射到、准求解母单元(如图 2),单元形函数为(徐世浙,1994)
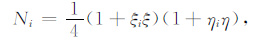
|
(6) |

|
图 2 母单元、子单元示意图 Fig. 2 Map of mother unit and sub unit |
两个单元的微分关系采用雅可比变换行列式表示为:
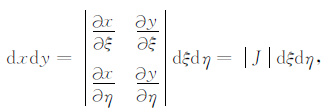
|
(7) |
其中雅可比变换行列式|J|可表示为
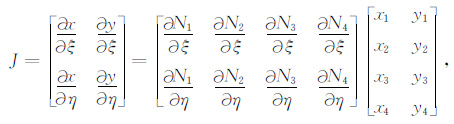
|
(8) |
将(6) 式带入有:
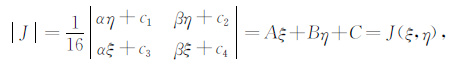
|
(9) |
其中
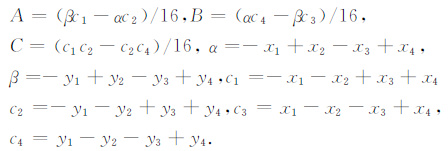
|
对式(5) 采用Galerkin法,利用形函数N作为展开和测试的基函数,单元内电场为:Ee(x,y)=NEe,带入式(5) ,可以得到表征电场波动方程的常微分方程式:
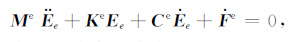
|
(10) |
公式(10) 中的矩阵表达式为
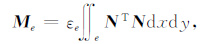
|
(11) |
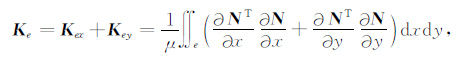
|
(12) |
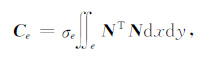
|
(13) |
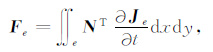
|
(14) |
将两者的微分关系带入可得矩阵中每一项的具体表达式:
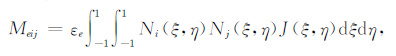
|
(15) |
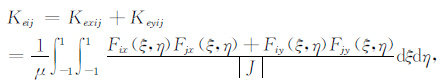
|
(16) |
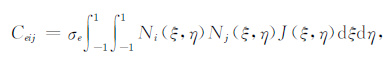
|
(17) |
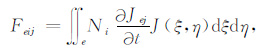
|
(18) |
其中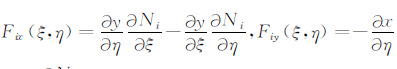
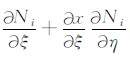
将单元列向量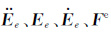

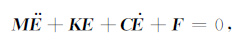
|
(19) |
式(19) 中M为质量矩阵,C为阻尼矩阵,K为刚度矩阵,${\dot{E}}$为时间的一次导数,${\ddot{E}}$为时间的二次导数,F为源项.采用Newmark-β求解方程组(19) ,式中的一阶及二阶导数可采用中心差分来近似(张新明等,2005):
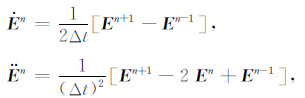
|
(20) |
Et用n-1,n和n+1时间步函数值的加权平均${\tilde{E}}$t来代替:
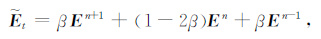
|
(21) |
将式(20) —(21) 带入式(19) 中可得

|
(22) |
其中:
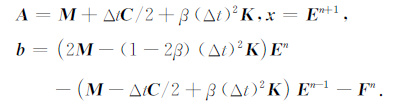
|
当β≥0.25时,方程(22) 表示的时间步进过程是无条件稳定的,因此是隐式算法,通常取β=0.25,此时的计算误差最小.
3 卷积完全匹配层原理根据电磁波场理论,时谐场的各向异性PML吸收边界的Maxwell方程通常表示为

|
(23) |
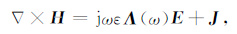
|
(24) |
式(23) 与(24) 中Λ(ω)具有单轴各向异性介质的特征,考虑一般的三维情形,它可表示为
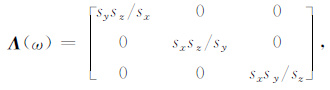
|
(25) |
对于常规Berenger PML吸收边界有

|
(26) |
si为坐标拉伸变量,其中σi在PML区域中控制波的衰减.与Berenger PML不同,Kuzuoglu和Mittra(1996) 提出的CFS-PML其si取值为
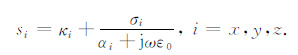
|
(27) |
式中σi为PML层内i方向电导率参数,κi值的引入是为了改善PML对倏逝波的吸收特性,αi值的引入则是为了改善PML对低频分量的吸收特性,σi和αi为大于零的正实数,κi≥1的正实数.在PML区域之外,αi=0,κi=1.在CFS-PML边界条件当中参数κi非常重要,必须要仔细地选取,而αi非常小甚至可以忽略,为了公式推导的简便,本文取αi=0.式(27) 可改写为
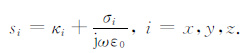
|
(28) |
联立式(23) (24) ,消去H,可以得到电磁波二阶矢量波动方程为

|
(29) |
式(29) 中:
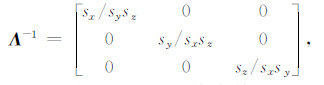
|
(30) |
将式(25) (30) 带入式(29) ,并将其表示为矩阵形式有
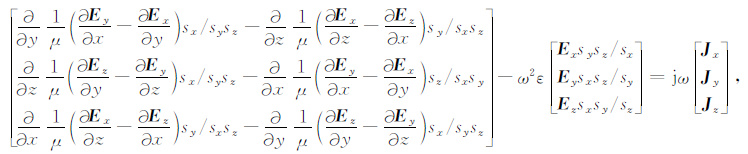
|
(31) |
对于二维TM波(Ez,Hx,Hy),有如下形式:
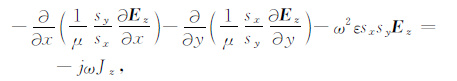
|
(32) |
其中si=κi+σi/jωε0,i=x,y.将上式关于CFS-PML变量展开有
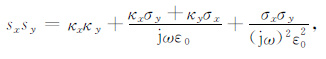
|
(33) |
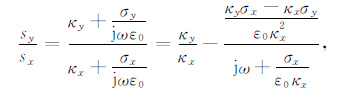
|
(34) |
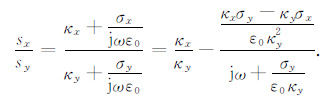
|
(35) |
可根据表 1的时频关系将等式(32) 从频率域变换到时间域:
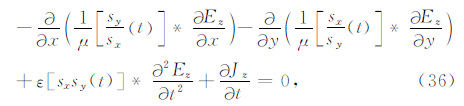
|
(36) |
|
|
表 1 时频函数对应关系 Table 1 The correspondence between the time domain function and frequency domain function |
其中:
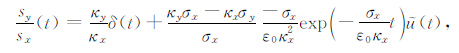
|
(37) |
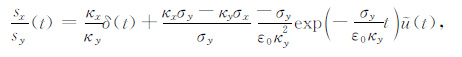
|
(38) |

|
(39) |
将式(37) —(39) 带入式(36) ,进一步展开得:
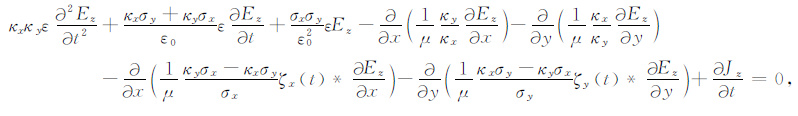
|
(40) |
其中: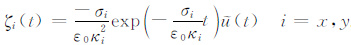
对式(40) 采用Galerkin法推导得到CPML边界的FETD波动方程:
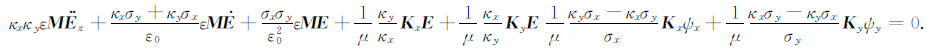
|
(41) |
式(41) 中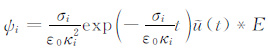
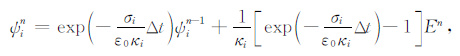
|
(42) |
CPML介质层参数的赋值由以下公式给出:
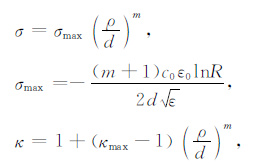
|
(43) |
其中d为吸收层厚度,ρ为单元中心到模拟区的距离,κmax是参数κ的最大值.其中反射系数R,指数阶数m,κmax的选取对吸收效果有重要的影响.
4 CPML边界条件最佳参数选取实验为了获得FETD求解GPR波动方程中CPML的最佳参数,采用图 3所示狭长模型,测试不同边界各参数对吸收效果的影响,观测区域为3.0 m×10.0 m,采用60×200的网格,网格间距为0.05 m,吸收层为20层.模型介电常数5.0,激励源位于上顶面中心,200 MHz的零相位Ricker子波,对该模型进行正演,采样时间间隔为0.1 ns,边界条件宽度都设置为1.0 m,时窗长度为70 ns.

|
图 3 狭长模型 Fig. 3 Model for the long and narrow |
观测点P1、P2与P3位置如图 3所示,采用扩大4倍模型获得观测点处的实测接收信号ES和参考模型信号Eref,并求取参考模型信号中振幅最大的值Erefmax,通过以下计算公式获得反射误差:
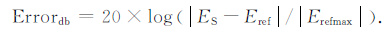
|
(44) |
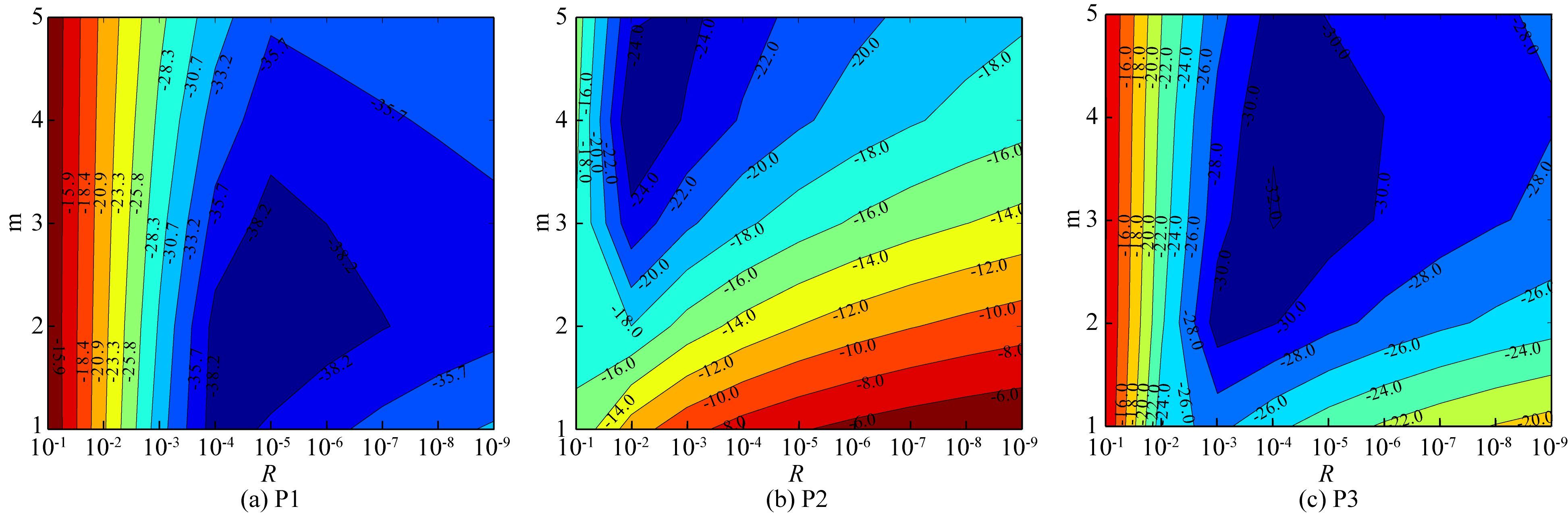
图 4为观测点不同参数m和反射系数R的最大反射误差分布图.通过分析观测点P1、P2与P3关于参数m和反射系数R的反射误差分布图可知,综合观测点P1、P2与P3,当m=3,R=1×10-4时反射误差达到最小.
|
图 4 参数m和反射系数R的最大反射误差分布图 Fig. 4 Maximum error of the parameters m and the reflection reflection coefficient R |
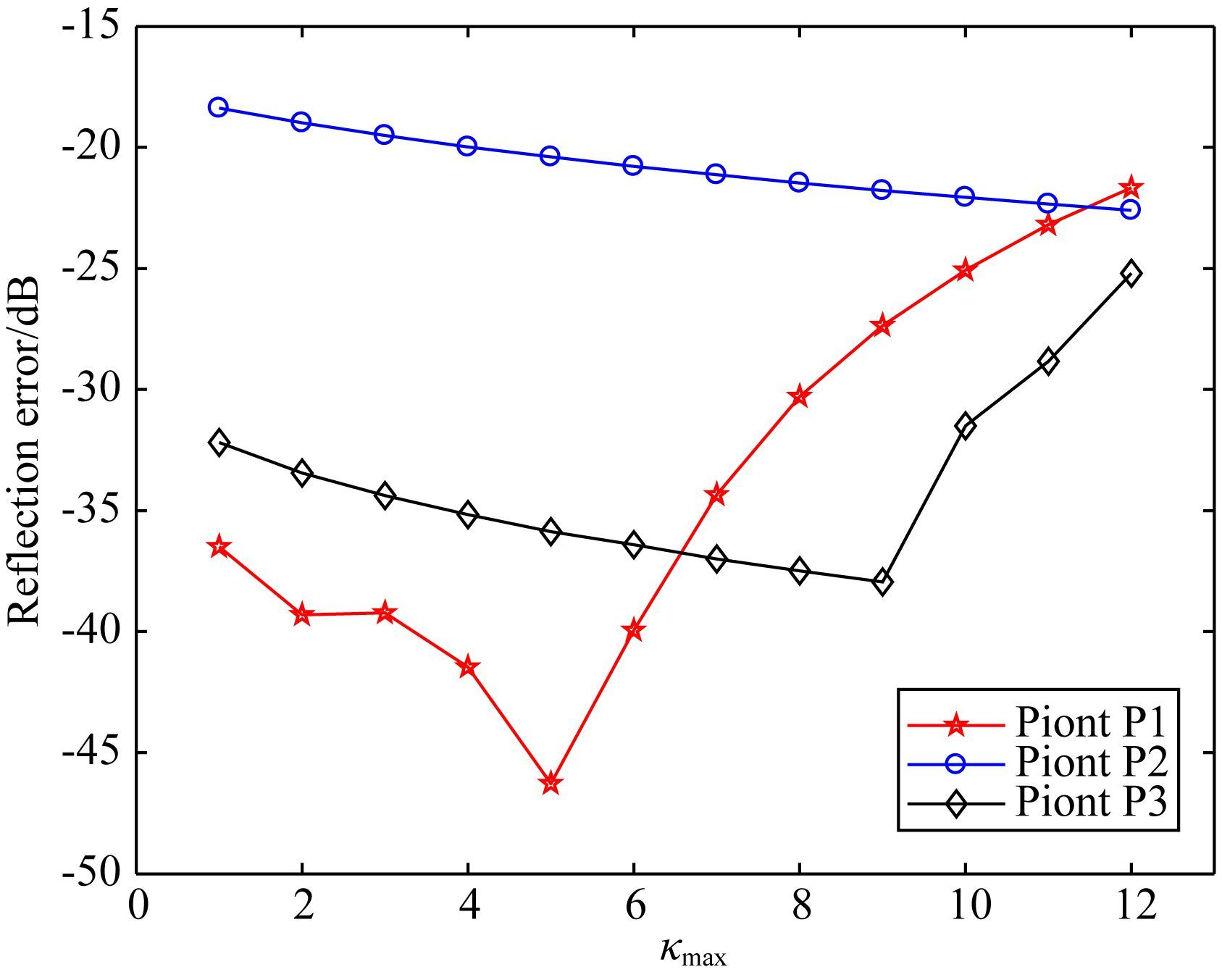
当m=3,R=1×10-4时分析参数κmax对反射误差的影响,模型与检波点设置同上,得到观测点P1、P2与P3关于参数κmax的反射误差分布如图 5所示.通过分析观测点P1、P2与P3关于参数κmax的反射误差分布图,综合观测点P1、P2与P3的误差结果,当κmax=6时反射误差达到最小.
|
图 5 观测点关于参数κmax的反射误差图 Fig. 5 Observation point about parameters κmax reflecting error |
图 6为3个观测点分别加载UPML与CPML边界条件的反射误差对比图.分析图 6可知,相比加载UPML边界,加载CPML边界的P1,P2,P3处的反射误差前期均有明显的减少,但后期会有少数点的反射误差增大,这是由于CPML边界中κ参数的离散化引起的震荡所致.整体而言,CPML边界条件的反射误差较小.

|
图 6 不同边界条件的反射误差对比 Fig. 6 Reflection error comparison of different boundary conditions |
为进一步分析两种边界条件的吸收效果,将图 7所示的两种边界不同时刻的波长快照进行对比.图 7a中35 ns的波场快照,此时UPML图中上边界仍有较小的反射,而图 7b中CPML对上边界的吸收效果很好.对比图 7c与图 7d的45 ns波场快照,可以发现UPML上界面两角点的反射较为明显,波形发生了畸变,而CPML有较为明显的改善.对比图 7e与图 7f的55 ns波场快照,UPML在后期仍有一些杂波,CPML出现了一些由κ参数的离散化所引起的震荡波,但数值非常小.

|
图 7 不同边界条件吸收边界波场快照对比 Fig. 7 Absorbing boundary wave field snapshot contrast different boundary conditions |
为了更好地说明CPML边界条件在GPR正演截断边界处对反射波的吸收效果,基于Matlab平台编写了CPML边界的FETD雷达正演程序.建立图 8所示的起伏地形地电模型,采用非规则四边形网格剖分,剖分网格为176×160,网格间距为0.0625 m,图中可见,非规则网格很好地拟合了起伏不平的光滑界面.最上部空气层为1 m,上层介电常数为7.0,电导率为0.002 S·m-1;背景介电常数为15.0电导率为0.01 S·m-1.矩形空洞上顶面埋深为4.5 m,宽度为1.25 m,厚度为1.25 m.考虑到二维GPR探测中常采用剖面法与宽角法两种数据采集方式,因此,应用FETD对该GPR模型进行正演时也基于剖面法和宽角法进行展开.

|
图 8 起伏地形地电模型 Fig. 8 Undulating terrain geoelectric model |
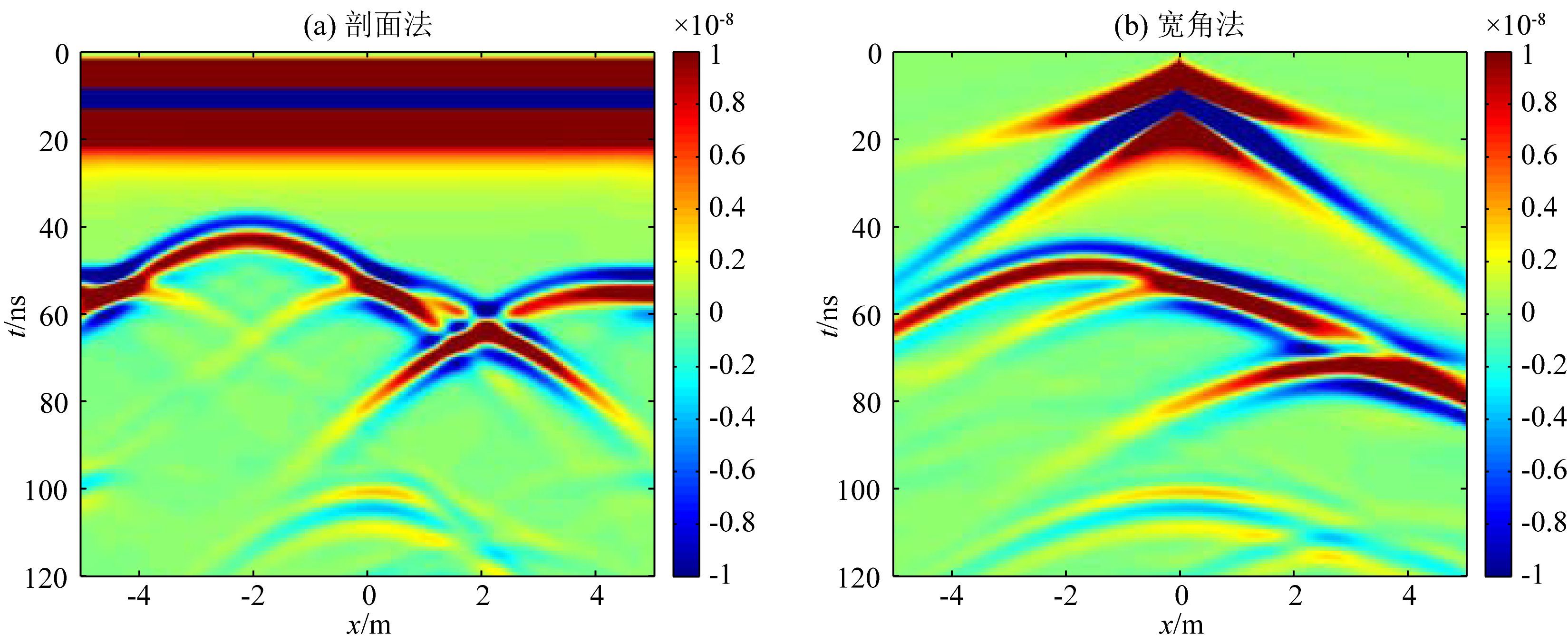
剖面法采用自激自收方式,自左向右同步移动.时间步长为0.1 ns,时窗长度为120 ns.激励源为100 MHz的零相位Ricker子波,位置均距地表 1个网格.模拟区域的外边界采用m=3,κ=6的CPML,层数为20层.图 9a为加载CPML边界条件、采用非规则四边形网格剖分的FETD算法正演所得的160道波形组成的雷达剖面图.图中可见,CPML对边界的截断效果比较理想,在正演剖面图中未出现人工截断边界的干扰.在60 ns的位置,从左至右有3处较为明显的绕射,分别对应隆起的左脚点、右脚点以及起伏界面的最低点,起伏界面的起伏形态与位置在剖面图中清晰可辨.而更深部埋深为4.5 m的空洞在100 ns处亦可见上下两处双曲绕射波,左瓣较为清晰,右瓣由于起伏界面最低点影响产生了形变.
|
图 9 起伏地形地电模型雷达正演剖面 Fig. 9 The forward modelling profile of GPR to Undulating terrain geoelectric model |
再考虑该地电模型宽角法的正演结果.将发射天线置于模拟区域的正上方,接收天线置于发射天线两侧,共记录160道波形.时间步长为0.1 ns,模拟时窗长度为120 ns,激励源仍为100 MHz的零相位Ricker子波,激励源的位置距离地表 1个网格.采用相同的吸收边界,图 9b即为宽角法接收到的正演剖面.
在图 9b正演剖面中,由于天线距地表有一定间距,故空气中的直达波与地表的直达波界面反射清晰可见,但是起伏地形分界面无法像剖面法那样明显,但是矩形空洞的异常的上界面位置与自激自收剖面基本一致.为了进一步加强对电磁波传播规律的理解,图 10为激发点位于0 m处不同时刻的波场快照.
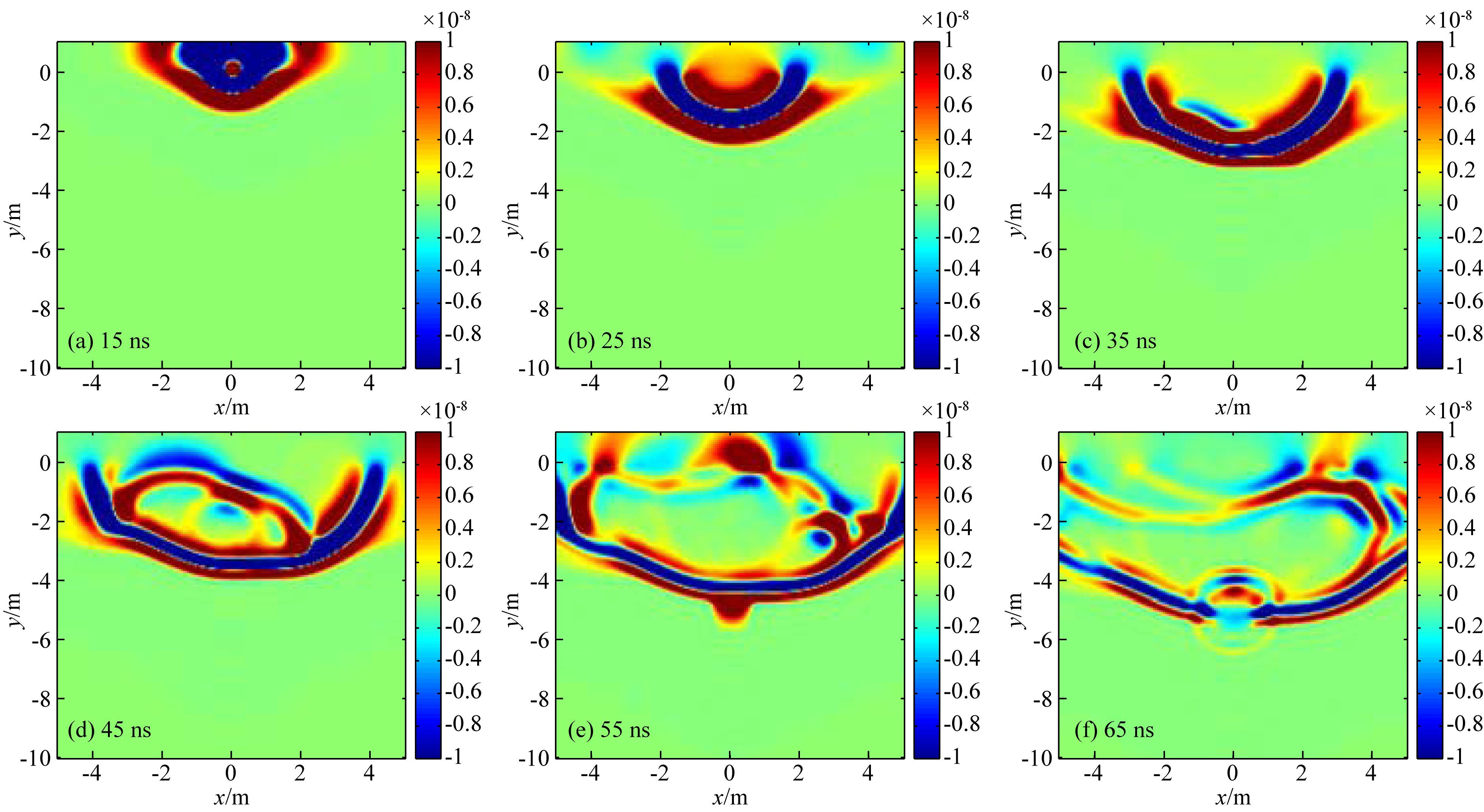
|
图 10 激发点位于0 m不同时刻波场快照 Fig. 10 Field snapshots of shot point is located at 0 m with different time |
图 10a中,电磁波在空气和地表的产生了分离,在空气中的波速较快,波长较长.图 10b中,电磁波进入地下,但是由于激发点与地表有一定间距,波前的两侧比中部较宽.图 10c中,波前遇到起伏界面发生反射.图 10d中,由起伏界面引起的反射波波速较快,波长较长,由于界面的起伏,波传播至界面的时间不一,透射波波前不规则.图 10e中,波前刚好传播至下界面中空洞处,可发现由于空气中波速较大,可发现波前在空洞处突入;同时由起伏界面引起的反射波传至地表,再次发生发射.图 10f中,可以看到两组波前,下面为激励源第一次经过界面产生的透射波,上面为界面反射波经地表反生引起的多次波.且由空洞引起的绕射波清晰可见.
6 结论(1) 采用递归积分实现了卷积完全匹配层的离散形式,并将CPML应用于电磁波二阶波动方程,根据CPML边界的电磁波二维波动方程推导了FETD矩阵方程形式,同时在时间导数离散上采用Newmark-β方法,有效地改进了算法稳定性.
(2) 以一个狭长模型为例,详细探讨了CPML边界条件中关键参数m,R以及κ的选取方法.实验表明:UPML中,当m=3,R=1×10-4时反射误差达到最小.CPML在κmax=6,m=3,R=1×10-4反射误差最小,对截断边界的反射波吸收效果总体最佳.同时,与UPML边界条件对比表明,CPML进一步提高了吸收效果,波场快照中杂波较少.
(3) 推导了FETD算法求解GPR波动方程详细步骤,编写了基于非结构化网格剖分的FETD算法正演程序,结合CPML吸收边界条件对1个复杂GPR地电模型进行了正演,结果表明:非规则四边形网格对于物性参数分布复杂或几何特征不规则的任意模型都能很好地拟合,网格剖分质量高,数据光滑程度好,具有良好的适应性,数值模拟结果能真实、客观地反映雷达波的实际探测波形特征.
致谢感谢编辑部和审稿专家的支持!
| Berenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 | |
| Berenger J P. 1996. Perfectly matched layer for the FDTD solution of wave-structure interaction problems. IEEE Transactions on Antennas and Propagation, 44(1): 110-117. DOI:10.1109/8.477535 | |
| Berenger J P. 1997. Numerical reflection of evanescent waves from perfectly matched layers.//IEEE Antennas and Propagation Society International Symposium. Montreal, Canada:IEEE, 3:1888-1891. | |
| Berenger J P. 1999. Evanescent waves in PML's:Origin of the numerical reflection in wave-structure interaction problems. IEEE Transactions on Antennas and Propagation, 47(10): 1497-1503. DOI:10.1109/8.805891 | |
| Cassidy N J, Millington T M. 2009. The application of finite-difference time-domain modelling for the assessment of GPR in magnetically lossy materials. Journal of Applied Geophysics, 67(4): 296-308. DOI:10.1016/j.jappgeo.2008.09.009 | |
| Correia D, Jin J M. 2006. Performance of regular PML, CFS-PML, and second-order PML for waveguide problems. Microwave and Optical Technology Letters, 48(10): 2121-2126. DOI:10.1002/(ISSN)1098-2760 | |
| Dai Q W, Wang H H, Feng D S, et al. 2012. Finite element method forward simulation for complex geoelectricity GPR model based on triangle mesh dissection. Journal of Central South University (Science and Technology) (in Chinese), 43(7): 2668-2673. | |
| Di Q Y, Wang M Y. 1999. 2D finite element modeling for radar wave. Chinese J. Geophys. (in Chinese), 42(6): 818-825. | |
| Donderici B, Teixeira F L. 2008. Conformal perfectly matched layer for the mixed finite element time-domain method. IEEE Transactions on Antennas and Propagation, 56(4): 1017-1026. DOI:10.1109/TAP.2008.919215 | |
| Feng D S, Chen C S, Dai Q W. 2010. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. Chinese J. Geophys. (in Chinese), 53(10): 2484-2496. DOI:10.3969/j.issn.0001-5733.2010.10.022 | |
| Ge D B, Yan Y B. Finite-Difference Time-Domain Method for Electromagnetic Waves (in Chinese).Xi'an: Xidian University Press, 2005: 67-81. | |
| Gedney S D. 1996a. An anisotropic perfectly matched layer-absorbing medium for the truncation of FDTD lattices. IEEE Transactions on Antennas and Propagation, 44(12): 1630-1639. DOI:10.1109/8.546249 | |
| Gedney S D. 1996b. An anisotropic PML absorbing media for the FDTD simulation of fields in lossy and dispersive media. Electromagnetics, 16(4): 399-415. DOI:10.1080/02726349608908487 | |
| Gedney S D, Navsariwala U. 1995. An unconditionally stable finite element time-domain solution of the vector wave equation. IEEE Microwave and Guided Wave Letters, 5(10): 332-334. DOI:10.1109/75.465046 | |
| Irving J, Knight R. 2006. Numerical modeling of ground-penetrating radar in 2-D using MATLAB. Computers & Geosciences, 32(9): 1247-1258. | |
| Jiao D, Jin J M. 2001. An effective algorithm for implementing perfectly matched layers in time-domain finite-element simulation of open-region EM problems. IEEE Transactions on Antennas and Propagation, 50(11): 1615-1623. | |
| Jiao D, Jin J M, Michielssen E, et al. 2003. Time-domain finite-element simulation of three-dimensional scattering and radiation problems using perfectly matched layers. IEEE Transactions on Antennas and Propagation, 51(2): 296-305. DOI:10.1109/TAP.2003.809096 | |
| Kuzuoglu M, Mittra R. 1996. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microwave and Guided Wave Letters, 6(12): 447-449. DOI:10.1109/75.544545 | |
| Li Y F, Li G F, Wang Y. 2010. Application of convolution perfectly matched layer in finite element method calculation for 2D acoustic wave. Acta Acustica (in Chinese), 35(6): 601-607. | |
| Liu S X, Zeng Z F. 2007. Numerical simulation for ground penetrating radar wave propagation in the dispersive medium. Chinese J Geophys. (in Chinese), 50(1): 320-326. | |
| Movahhedi M, Abdipour A, Ceric H, et al. 2007. Optimization of the perfectly matched layer for the finite-element time-domain method. IEEE Microwave and wireless components letters, 17(1): 10-12. DOI:10.1109/LMWC.2006.887240 | |
| Movahhedi M, Abdipour A. 2009. Complex frequency shifted-perfectly matched layer for the finite-element time-domain method. AEU-International Journal of Electronics and Communications, 63(1): 72-77. DOI:10.1016/j.aeue.2007.10.001 | |
| Roden J A, Gedney S D. 2000. Convolution PML (CPML):An efficient FDTD implementation of the CFS-PML for arbitrary media. Microwave and Optical Technology Letters, 27(5): 334-339. DOI:10.1002/(ISSN)1098-2760 | |
| Rylander T, Jin J M. 2005. Perfectly matched layer in three dimensions for the time-domain finite element method applied to radiation problems. IEEE Transactions on Antennas and Propagation, 53(4): 1489-1499. DOI:10.1109/TAP.2005.844423 | |
| Sacks Z S, Kingsland D M, Lee R, et al. 1995. A perfectly matched anisotropic absorber for use as an absorbing boundary condition. IEEE Transactions on Antennas and Propagation, 43(12): 1460-1463. DOI:10.1109/8.477075 | |
| Shen B. 1994. A study on wave eguation theory for ground-penetrating radar and forward modelling. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 16(1): 29-33. | |
| Taflove A, Brodwin M E. 1975. Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell's equations. IEEE Transactions on Microwave Theory and Techniques, 23(8): 623-630. DOI:10.1109/TMTT.1975.1128640 | |
| Tsai H P, Wang Y X, Itoh T. 2002. An unconditionally stable extended (USE) finite-element time-domain solution of active nonlinear microwave circuits using perfectly matched layers. IEEE Transactions on Microwave Theory and Techniques, 50(10): 2226-2232. DOI:10.1109/TMTT.2002.803442 | |
| Wang H H, Dai Q W. 2013. Finite element numerical simulation for GPR based on UPML boundary condition. The Chinese Journal of Nonferrous Metals (in Chinese), 23(7): 2003-2011. | |
| Wang S M, Lee R, Teixeira F L. 2006. Anisotropic-medium PML for vector FETD with modified basis functions. IEEE Transactions on Antennas and Propagation, 54(1): 20-27. DOI:10.1109/TAP.2005.861523 | |
| Wu J Y, Kingsland D M, Lee J F, et al. 1997. A comparison of anisotropic PML to Berenger's PML and its application to the finite-element method for EM scattering. IEEE Transactions on Antennas and Propagation, 45(1): 40-50. DOI:10.1109/8.554239 | |
| Xie H, Zhong Y H, Cai Y C. 2003. Application of finite element methods for electromagnetic fields in forward model of GPR. Henan Science (in Chinese), 21(3): 295-298. | |
| Xu S Z. The Finite Element Method in Geophysics (in Chinese).Beijing: Science Press, 1994. | |
| Zeng Z F, Liu S X, Feng X. Theory and Application of Ground Penetrating Radar (in Chinese).Beijing: Electronic Industry Press, 2010. | |
| Zhang X M, Liu K A, Liu J Q. 2005. A wavelet finite element method for the 2-D wave equation in fluid-saturated porous media. Chinese J. Geophys. (in Chinese), 48(5): 1156-1166. DOI:10.1002/cjg2.759 | |
| 戴前伟, 王洪华, 冯德山, 等. 2012. 基于三角形剖分的复杂GPR模 型有限元法正演模拟. 中南大学学报(自然科学版), 43(7): 2668–2673. | |
| 底青云, 王妙月. 1999. 雷达波有限元仿真模拟. 地球物理学报, 42(6): 818–825. | |
| 冯德山, 陈承申, 戴前伟. 2010. 基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟. 地球物理学报, 53(10): 2484–2496. DOI:10.3969/j.issn.0001-5733.2010.10.022 | |
| 葛德彪, 闫玉波. 电磁波时域有限差分方法.西安: 西安电子科技大学出版社, 2005: 67-81. | |
| 李义丰, 李国峰, 王云. 2010. 卷积完全匹配层在两维声波有限元计算中的应用. 声学学报, 35(6): 601–607. | |
| 刘四新, 曾昭发. 2007. 频散介质中地质雷达波传播的数值模拟. 地球物理学报, 50(1): 320–326. | |
| 沈飚. 1994. 探地雷达波波动方程研究及其正演模拟. 物探化探计算技术, 16(1): 29–33. | |
| 王洪华, 戴前伟. 2013. 基于UPML吸收边界条件的GPR有限元数值模拟. 中国有色金属学报, 23(7): 2003–2011. | |
| 谢辉, 钟燕辉, 蔡迎春. 2003. 电磁场有限元法在GPR正演模拟中的应用. 河南科学, 21(3): 295–298. | |
| 徐世浙. 地球物理中的有限单元法.北京: 科学出版社, 1994. | |
| 曾昭发, 刘四新, 冯晅. 探地雷达原理与应用.北京: 电子工业出版社, 2010. | |
| 张新明, 刘克安, 刘家琦. 2005. 流体饱和多孔隙介质二维弹性波方程正演模拟的小波有限元法. 地球物理学报, 48(5): 1156–1166. | |
 2017, Vol. 60
2017, Vol. 60


