2. 不列颠哥伦比亚大学地球、海洋与大气科学学院, 温哥华V6T 1Z4, 加拿大;
3. 中国海洋大学海洋地球科学学院, 青岛 266100
2. Department of Earth, Ocean and Atmospheric Sciences, University of British Columbia, Vancouver V6T 1Z4, Canada;
3. College of Marine Geosciences, Ocean University of China, Qingdao 266100, China
频率域可控源电磁法(controlled-source electromagnetic,CSEM) 由于优良的分辨能力而广泛应用于陆地和海洋矿产和油气资源勘探中(Constable,2010;Yang and Oldenburg,2012; Hu et al.,2013;Grayver et al.,2014).随着电磁勘探越来越多地深入到复杂地质环境中,一维和二维地质假设难以准确描述勘探目标体全方位的空间展布特征(Ledo,2005; Siripunvaraporn et al.,2005),电磁数据的三维反演越来越受到重视.CSEM的三维反演研究在最近十年取得了极大的进展,国内外一些学者陆续实现了有效的CSEM三维反演算法.例如Haber等(2007)实现了时间域CSEM三维反演;Commer和Newman(2008)、Plessix和Mulder(2008)实现了海洋CSEM三维反演;林昌洪等(2012)、翁爱华等(2012)和赵宁等(2016)针对陆地CSAMT勘探进行了三维反演研究;刘云鹤和殷长春(2013)则完成了航空CSEM数据的三维反演算法等等.尽管已有这些成功的研究工作,但越来越大的数据规模(例如最新的海洋CSEM发射与接收一体式的拖曳式测量) 以及越来越真实且复杂的地电模型假设(例如各向异性、高电性差异等) 对CSEM三维反演的可靠性、稳定性和计算效率仍然是巨大的考验,因此提升CSEM三维反演算法的性能在长时间内仍将是国内外电磁法学者的研究重点之一.
反演的性能在很大程度上取决于正演计算.对当前主流的正演方法包括有限差分、有限体积和有限单元法来说,大型稀疏线性方程组的求解是非常关键的一步.在早期计算机内存的限制下,迭代法是唯一可行的求解方程的方法,这是由于迭代解法只需计算和存储矩阵与向量的乘积,所需内存较少,运算速度较快,例如以上作者均采用了Krylov子空间迭代法.然而迭代解法的收敛性与系数矩阵的谱性质息息相关(Saad,2003),而模型的电导率变化范围大和网格尺寸的非均匀性都会使得系数矩阵的条件数非常大,从而可能导致迭代法的收敛性不佳、计算时间长,甚至不收敛.随着大型稀疏矩阵分解算法的持续优化(Amestoy et al.,2001,2006;Schenk and Gärtner,2006),以及计算机硬件技术的快速发展,使得在从工作站到并行集群上利用直接解法求解电磁法三维正演中的大型线性方程组成为可能.与迭代解法相比,对于同一线性方程组,直接解法需要消耗更多的计算内存,计算时间一般也会更长.尽管如此,直接解法相对于迭代解法有三个优点:一是求解精度更高(韩波等,2015);二是更加稳定,即其求解时间和精度基本不受系数矩阵的条件数影响,对强电性差异和含多尺度构造的模型同样适用;三是直接解法将线性方程组的求解过程分解为系数矩阵的分解和前代-回代(forward-backward substitution) 求解过程(Streich,2009),其中系数矩阵的分解虽然消耗大量的计算机内存和计算时间,但对于单一频率多个场源位置的问题,只需进行一次矩阵分解加上多次计算量极小的替代过程即可,而不像迭代解法对每个频率每个场源都要单独求解,因此直接解法特别适合具有多个场源的CSEM三维模拟(Oldenburg et al.,2013).正因为这些优点,基于矩阵分解的直接解法最近几年开始应用于CSEM三维反演计算(Grayver et al.,2013;Schwarzbach and Haber,2013).
正演中线性方程组的求解使用直接解法还是迭代解法,对反演中最优化算法的选择有直接影响.目前三维反演中广泛应用的NLCG法(Commer and Newman,2008;翁爱华等,2012;刘云鹤和殷长春,2013) 和QN法(Plessix and Mulder,2008;Schwarzbach and Haber,2013;翁爱华等,2015;赵宁等,2016),尽管模型的每一迭代更新非常容易计算,但由于仅利用了目标函数的一阶导数(即梯度) 信息,只具有线性收敛性(Wright and Nocedal,1999),模型往往需要更新很多次才能收敛.相较之下,高斯牛顿法(Grayver et al.,2013; Oldenburg et al,2013) 由于同时利用了目标函数的一阶导数和二阶导数(即Hessian矩阵) 信息,表现出近似二次收敛性(Nocedal and Wright,1999),所需的模型更新次数往往远少于NLCG和QN.当正演使用直接解法时,反演中每更新一次模型必然需要进行新的矩阵分解,即模型更新的次数越多,需要的矩阵分解次数也越多;由于矩阵分解要消耗大量的内存和时间,为减少反演迭代中矩阵分解的次数,相比NLCG和QN,高斯牛顿法是更好的选择.并且,每次高斯牛顿迭代的法方程可以使用预条件共轭梯度法(PCG) 求解,不仅可避免显式求解和存储灵敏度矩阵,减小计算量;而且还能够重复利用正演计算阶段所得到的矩阵分解结果,加快反演过程.
本文尝试利用最新优化的矩阵直接求解器,结合高斯牛顿最优化算法,实现相对可靠、稳定、高效且同时适用于陆地和海洋勘探场景的频率域CSEM三维反演算法.首先简要介绍了CSEM三维正演算法;接着详细介绍了反演算法的细节:包括目标函数的构建、灵敏度矩阵计算、法方程的求解、正则化函数及正则化参数的选取.最后通过典型三维理论模型的反演测试来验证所开发的算法的有效性.
2 三维正演计算CSEM三维正演基于电场总场的Helmholtz方程为
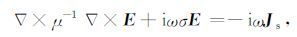
|
(1) |
其中, E 为电场强度(V·m-1),ω为角频率(rad/s),σ为介质电导率(S·m-1),μ为磁导率(H·m-1), Js 为外部激发场源的电流密度(A·m-2).使用拟态有限体积法(mimetic finite volume,MFV) 对(1) 式离散化.MFV方法的最大特点是能够对连续的微分算符进行精确的离散模拟,并确保离散化后的矢量场仍然满足其对应的连续形式的矢量性质及物理特性(Hyman and Shashkov,1999a,b),有效避免了伪解的产生.对于正交规则网格及各向同性介质来说,该离散化方法与常用的交错网格有限差分法相一致(Smith,1996).但MFV适用范围更广,其对于非正交网格同样适用(Hyman and Shashkov,1997).特别是对于具有高度电性差异及各向异性介质,MFV能够自然地得到对称的离散化形式(Hyman et al.,1997;Haber and Ruthotto,2014),这对于复杂三维介质的模拟十分有效.关于MFV的具体离散化过程的推导可参见以上几篇文献.
采用交错网格对(1) 式进行离散化得到待求解的线性方程组为
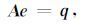
|
(2) |
其中系数矩阵A为大型稀疏正定对称复矩阵.本文通过调用基于多波前分解算法的MUMPS(Amestoy et al.,2001;Amestoy et al.,2006) 线性运算库对A进行LDLH分解后,再求解方程(2),即直接解法.对同一个模型的某一个频率,A是固定的,场源位置的改变仅仅会改变右端项q,因此只需进行一次矩阵分解,使得多个场源位置的CSEM正演计算量与单一场源相当.此外,直接解法还有精度高、稳定性好等优点,具体可参考Streich(2009)、Oldenburg等(2013)和韩波等(2015).
3 三维反演理论 3.1 目标函数的构建由于反演问题的不适定性,为获得稳定的最优解,CSEM三维反演的目标函数通常采用Tikhonov正则化方式来构建(Tikhonov and Arsenin,1977;Constable et al.,1987),目标函数可定义为
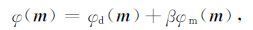
|
(3) |
其中 φd(m) 为数据拟合差函数, φm(m) 为模型正则化函数,β为Tikhonov正则化参数.为保证反演中模型参数的物理意义,模型参数m设为 m=lnσ. 数据拟合差函数可表示为
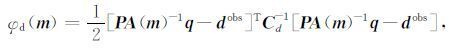
|
(4) |
其中dobs为观测的电磁场分量,Cd为数据协方差矩阵.P为观测矩阵,其将正演计算得到的网格采样点处的电磁场分量投影到测点处,观测矩阵采用“体积加权”的线性插值方式得到(韩波,2015).模型正则化函数为
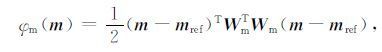
|
(5) |
其中mref为反演计算中参考模型,包括模型的先验信息.Wm为模型平滑矩阵.对于最小结构模型泛函,Wm为单位矩阵;对于平滑结构泛函,Wm为一阶差分矩阵.本文采用平滑结构泛函来构建模型正则化函数(Lelièvre and Oldenburg,2009),公式为
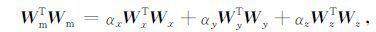
|
(6) |
其中Wx、Wy、Wz分别为x、y、z方向上的一阶差分矩阵.系数αx、αy、αz控制着模型结构在不同方向上的平滑程度.
对目标泛函(3) 在当前模型变量处进行二阶Taylor展开,并忽略高阶项,得到高斯-牛顿法(Gauss-Newton,GN) 的法方程(normal equation) 为
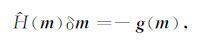
|
(7) |
其中g(m)为目标泛函的梯度向量, $\hat H$(m) 为目标泛函的正则近似海森矩阵.分别为:
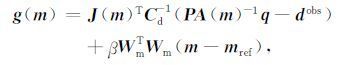
|
(8) |
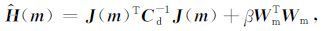
|
(9) |
其中J(m) 为CSEM的灵敏度矩阵.
3.2 法方程的求解为获得模型更新,在每次GN迭代中,都需求解(7) 式的法方程.直接求解(7) 式需要显式地计算和存储灵敏度矩阵以及海森矩阵.在梯度类反演算法中,灵敏度矩阵扮演着重要的角色.对于CSEM反演,利用隐式微分方法(Rodi and Mackie,2001;Egbert and Kelbert,2012),灵敏度矩阵可表示为

|
(10) |
其中P为(4) 式中的观测矩阵,A(m) 为(2) 式中的正演系数矩阵,u为正演得到的电磁场值.G(m,u) 为
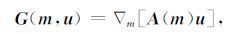
|
(11) |
从(10)(11) 式中可以看到,灵敏度矩阵的求解需要利用到所有发射场源(包括所有频率及发射场源位置) 的电磁响应,显式地求解涉及到大量正演计算.对于多频率多场源的三维CSEM反演来说,需要消耗大量的计算内存以及运算时间,现有计算资源往往无法满足要求.为避免显式的计算和存储灵敏度矩阵,通常采用预条件共轭梯度法(preconditioned conjugate gradient,PCG,Barrett et al.,1994) 来迭代求解(7) 式(Haber et al.,2007;Oldenburg et al.,2013;Schwarzbach and Haber,2013).在PCG算法中,只涉及到求解和存储灵敏度矩阵与模型向量的乘积,以及灵敏度矩阵转置与数据向量的乘积(林昌洪等,2012).图 1给出了求解灵敏度矩阵与模型向量乘积、以及灵敏度矩阵转置与数据向量乘积的算法,相关计算公式的详细推导,读者可参考林昌洪等(2012),本文不再赘述.具体的算法计算细节可见附录A.从图 1中可以看出灵敏度矩阵(或转置) 与向量的乘积相当于求解一次正演问题,因此每次PCG迭代需要求解两次正演问题.由于采用直接解法进行正演计算,在同一次GN迭代中,矩阵分解的结果可以多次重复利用.因此,相比于迭代法,直接解法在反演计算中的优势会更加明显(Oldenburg et al.,2013).

|
图 1 灵敏度矩阵及其转置与向量乘积算法 Fig. 1 Algorithms for matrix-vector products of Jocabian and its transpose with a |
当采用PCG来求解法方程(7) 时,GN反演过程的计算消耗将主要集中在PCG的迭代上.为减少反演的计算时间,一个可行的策略是降低法方程求解的精度来减少每次GN迭代中所需的PCG迭代次数,这就是所谓的非精确高斯牛顿法(Inexact Gauss-Newton,IGN,Nocedal and Wright,1999).对于IGN来说,只要法方程的残差(或目标函数的梯度) 随着PCG迭代不断降低,该算法的收敛性就能得到保证(Rieder,2001,2005).由于反演的非线性特征,对于线性化迭代反演来说,这种非精确求解不仅减小了计算量,而且避免了每次GN迭代中对法方程的过度求解(oversolving,Eisenstat and Walker,1996),使得在反演搜索过程中能有机会跳出局部极小陷阱.另外,PCG迭代求解具有正则化效应,并且PCG的迭代次数扮演着正则化参数的作用(van den Doel and Ascher,2007,2012),使得PCG在求解法方程过程中具有很好的稳定性.在三维反演中,一般PCG迭代次数取为十几次到几十次(Oldenburg et al.,2013).
对于PCG迭代中预条件子的选择主要有两种方式.一种方式是在每次GN迭代中,首先利用拟牛顿法(如L-BFGS) 来近似得到目标泛函Hessian矩阵的逆,将其作为PCG迭代的预条件因子(Oldenburg et al.,2013);另一种方式是在每次GN迭代中,先求解线性方程

|
(12) |
然后将(12) 式的解M作为PCG迭代的预条件子(Pidlisecky et al.,2007).在反演初始阶段,由于模型正则化项在目标函数中权重较大,(12) 式的解可视为(7) 式的近似解;并且由于模型协方差 WmTWm 的稀疏性质,能够以较小代价求得(12) 式的解.本文采用后一种方式来设置每次GN迭代中的PCG迭代的预条件因子,通过调用MUMPS线性运算库来直接求解(12) 式.
3.3 模型更新在利用PCG求得法方程(7) 的解后,需要进行线搜索来获得每次GN迭代的模型更新量,公式为
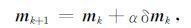
|
(13) |
步长α控制着模型更新大小,步长α的精确搜索需要求解关于α的单变量最优化问题 φ(mk+αδmk). 对于三维反演来说,精确线搜索往往因计算消耗巨大而无法进行.因此一般采用非精确线搜索方式来确定更新步长α.最常见的策略是采用(14) 式的弱Wolfe条件(Nocedal and Wright,1999) 来进行非精确线性搜索,得到更新步长α.公式为
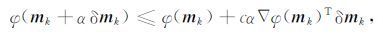
|
(14) |
其中常数c一般取10-4.
3.4 正则化策略及正则化参数的选取为了求解(3) 式的最优化问题,需要在反演迭代过程中选取合适的正则化参数.由于正则化参数起着平衡数据拟合和模型结构的作用,因此,正则化参数的选取必须兼顾反演的稳定性以及先验模型对反演结果的影响.一方面正则化参数必须设置的充分大来保证反演的稳定性;另一方面必须设置的足够小来减小先验模型对反演迭代搜索带来的偏差(Siripunvaraporn,2012;Grayver et al.,2013).对于Tikhonov正则化来说,可以通过数据拟合差和模型范数之间的差异准则(discrepancy principle) 来确定最优的正则化参数.在实际反演中一般通过采用所谓的松弛法(relaxation/cooling scheme) 来选取正则化参数(Newman and Alumbaugh,1997;Rodi and Mackie,2001):在反演的初期阶段,选取较大的正则化参数来确保反演的稳定性;随着反演的进行,逐渐减小正则化参数来降低模型正则化项的权重,使反演集中在数据的拟合上,直到达到最佳的数据拟合差.本文利用松弛法来自动选取GN迭代过程中正则化参数,其更新方式为
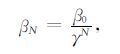
|
(15) |
其中γ为衰减因子,β0为初始正则化参数,N为当前GN迭代数.
4 理论模型合成数据反演测试为了验证所开发的CSEM三维反演算法的有效性,本文设计了两个三维模型来分别模拟陆地及海洋CSEM测量情况,并对这两个三维模型的合成数据进行了三维反演测试.本文所有计算均在一个小型并行机上完成.该小型并行机群系统配置有8个计算节点,每个计算节点含有2个4核Intel○R Xeon○R E5410型处理器,主频为2.33 GHz,每个计算节点配置有32G内存.操作系统为CentOS 5.5.
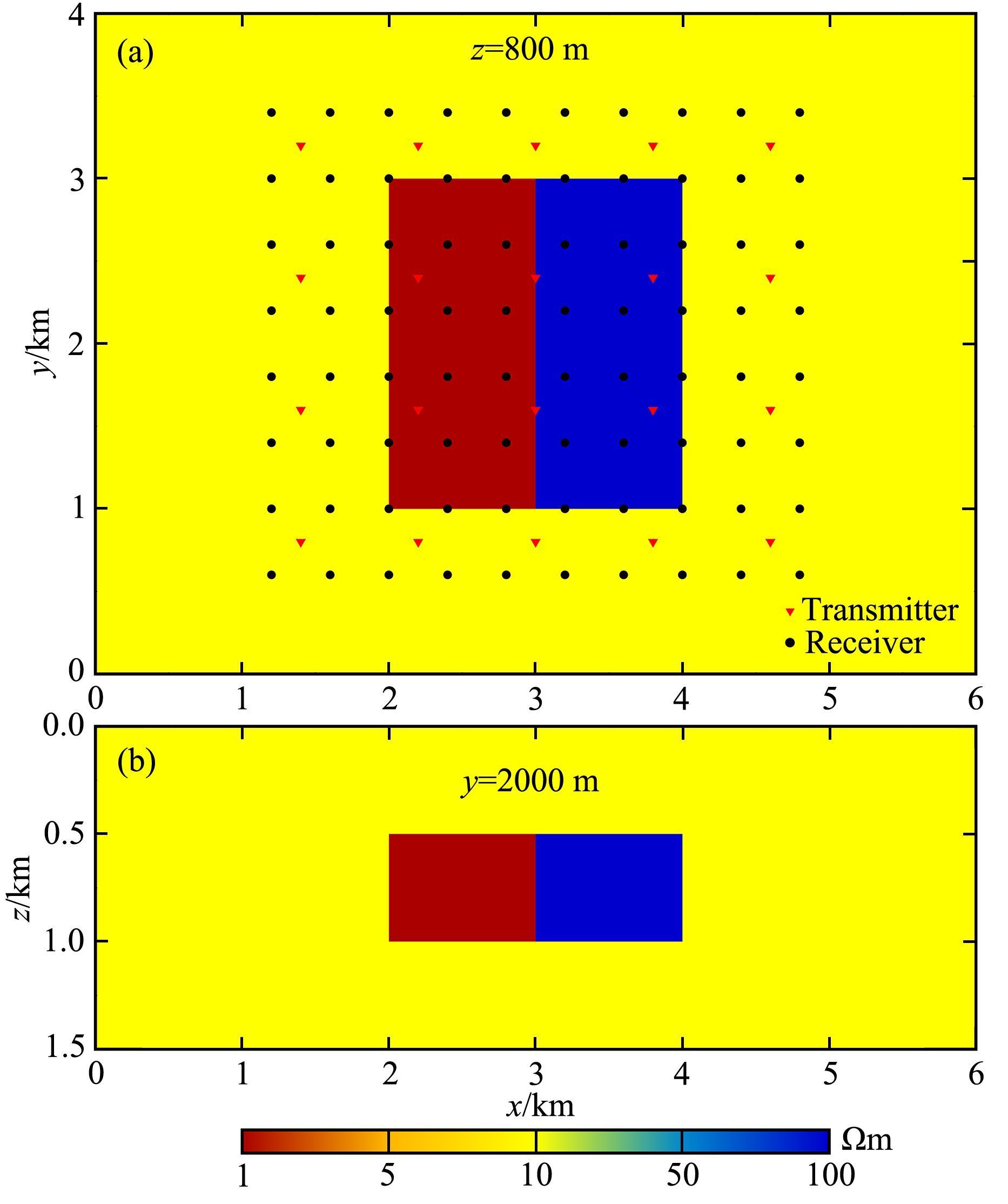
4.1 陆地三维模型首先考虑陆地CSEM测量情况,设计了如图 2所示的三维双棱柱体地电模型.其中高阻和低阻棱柱体尺寸均为1000 m × 2000 m × 500 m,顶部埋深为500 m,电阻率分别为100 Ωm和1 Ωm.两个棱柱体均埋藏在电阻率为10 Ωm的均匀半空间中.为得到高精度理论合成数据,模型核心区域被剖分为60 ×40 ×40的细密网格.为降低边界条件对计算结果的影响,在模型边界外各增加8个网格,网格增长因子为2.另外,计算模型区域包含10层空气层,空气层电阻率设为108 Ωm.整个正演计算的模型区域共划分成76×56×58的网格.观测系统包括20个发射站,场源间距为800 m,80个接收站,测点间距为400 m.发射站和测点均布设在地表处,如图 2所示.每个发射站均布设沿x方向极化的长度为100 m的水平接地导线源,发射频率为0.25 Hz和1 Hz.正演计算得到所有收发距大于600 m的电场Ex分量(包括实部和虚部) 作为理论合成数据,然后对理论合成数据添加3%的随机噪声得到反演观测数据.
|
图 2 陆地CSEM三维模型平面 (a) 水平切片图z=800 m;(b) 垂直剖面图y=2000 m.三角为发射场源位置,圆点为接收测站位置. Fig. 2 Planar views of 3D model for land CSEM survey (a)Horizontal slice at z=800 m;(b)Cross-section at y=2000 m. Triangles and circles indicate receivers and transmitters,respectively. |
为测试反演算法的稳定性,避免反演偏差,反演网格采用不同于合成数据所用的正演计算网格.反演核心区域划分为40×30×40的网格,其中场源处网格进行了局部加密.同样地,在核心区域外添加边界网格和空气层,整个反演计算区域划分成52×42×56的网格.反演初始正则化参数设置为0.01,衰减因子γ为2.GN迭代中的PCG迭代次数设为20次.目标拟合差设为1.反演初始模型及参考模型均采用电阻率为10 Ωm的均匀半空间.反演迭代中,空气层电阻率保存不变.整个反演共耗时约12.5小时.
图 3给出了三维反演所得到的最后地电模型结果.从图 3a和图 3b可以看出,反演结果较好地刻画出异常高低阻棱柱体的形态.其中对于低阻异常体的恢复要明显优于高阻异常体,这主要是由于CSEM对于高低阻异常体的灵敏度及分辨率不同引起的.图 3c给出了反演结果的三维图.对于低阻异常体来说,无论是异常体的电阻率还是异常体的位置分布,反演结果均与理论模型较为一致;对于高阻异常体,反演结果的最大电阻率数值约为50 Ωm,与真实模型有一定差距,另外,恢复的高阻体异常分布范围要小于真实模型分布区域.

|
图 3 陆地CSEM三维反演结果 (a) 水平切片图z=800 m;(b) 垂直剖面图y=2000 m;(c) 三维剖面图(电阻率大于20 Ωm或电阻率小于5 Ωm).图中三角为发射场源位置,圆点为接收测站位置,黑框表示真实模型位置. Fig. 3 Inversion results of land CSEM survey (a)Horizontal slice at z=800 m;(b)Cross-section at y=2000 m;(c)3D view. Cells with resistivity between 5 Ωm and 20 Ωm are cut-off. Triangles and circles indicate receivers and transmitters,respectively. Squares outline true locations of anomaly objects. |
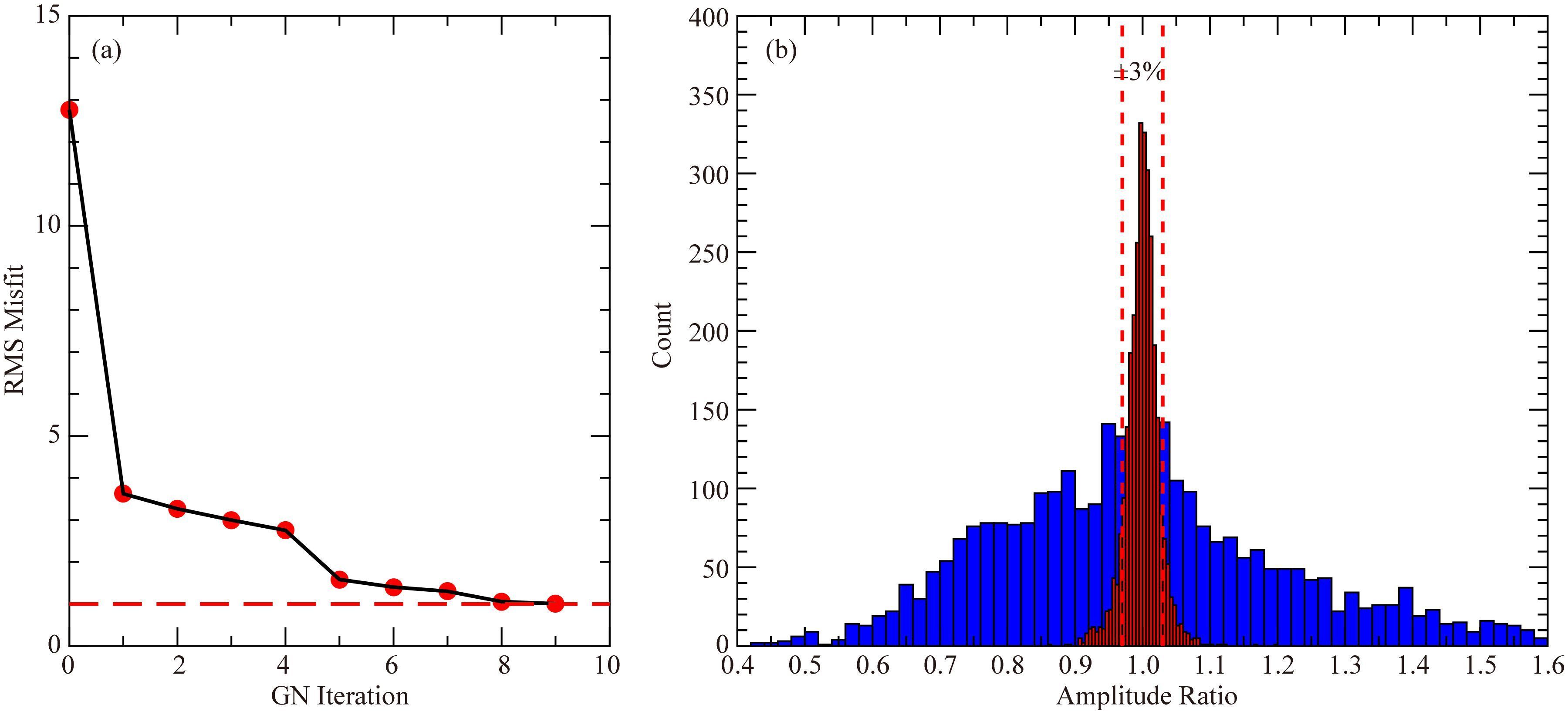
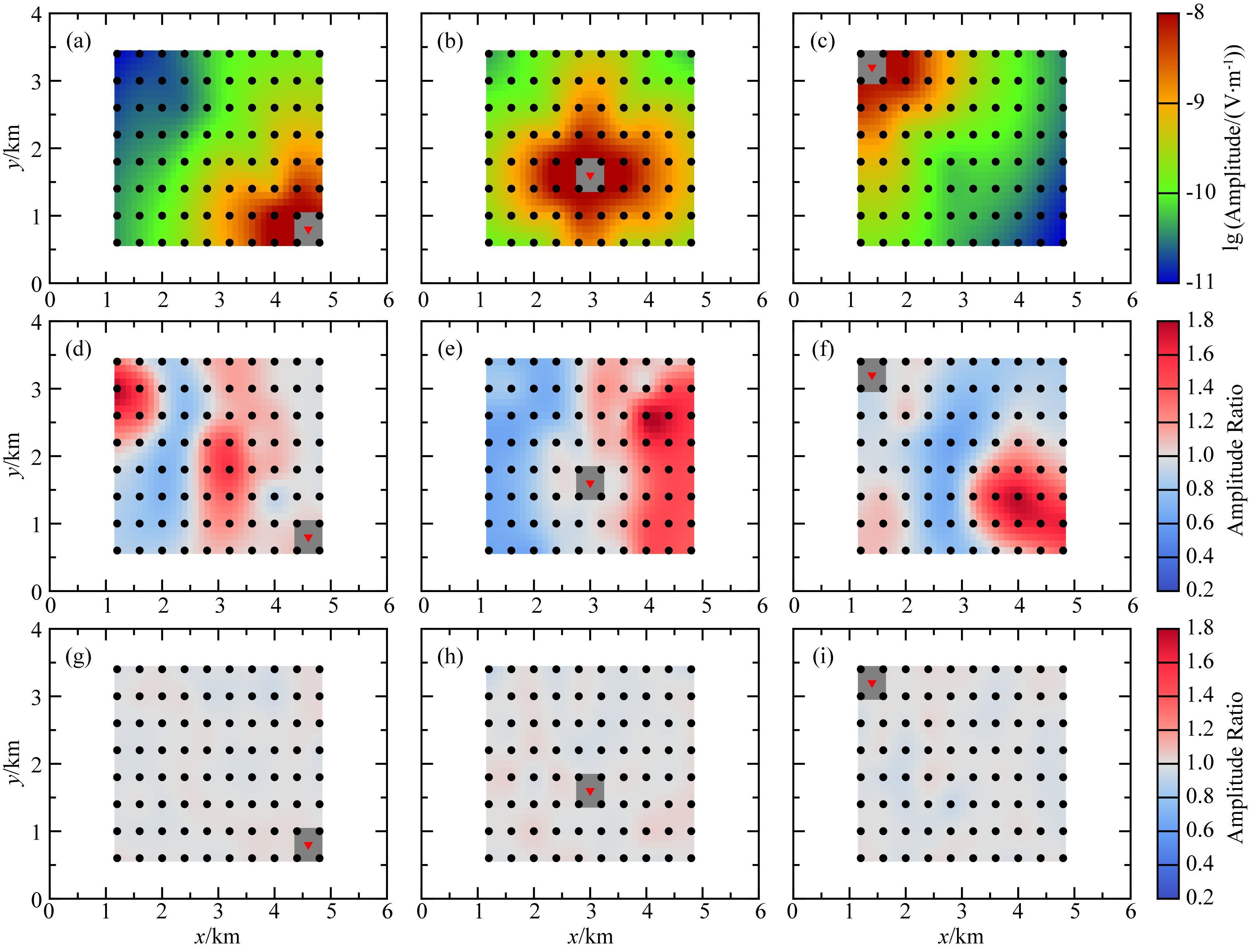
图 4a为反演过程中数据拟合差的变化.经过9次GN迭代,反演数据拟合差从最初的12.78逐渐收敛到最终的1.01,显示了GN反演算法优良的收敛性及稳定性.图 4b给出了反演合成数据与反演初始模型响应数据及反演最终迭代模型响应数据的振幅比率统计图.从中可以看出,反演结果对于所有频点和测点的数据总体拟合较为一致,最终的数据拟合误差降为所添加的随机误差范围之内(3%).与之对应,图 5显示了频率为1 Hz时,不同发射位置的所有测点的观测数据(图 5a—c)、观测数据与初始模型数据振幅比(图 5d—f)、以及观测数据与反演最终模型数据振幅比(图 5g—i).从图中可以看出,所有测点的数据拟合均匀一致,并未出现较明显的数据“过拟合”或“欠拟合”现象,表明GN算法具有良好的一致性.
|
图 4 陆地可控源三维反演数据拟合统计 (a) 数据拟合差RMS随迭代变化图,红色虚线为目标拟合差;(b) 反演合成数据与初始模型响应数据(蓝色) 和反演最终模型响应数据(红色) 振幅比率统计图,红色虚线为3%的数据误差区间. Fig. 4 Fitting statistics of 3D inversion (a)Data RMS misfit versus GN iteration for land CSEM survey. Red dashed line shows the desired data misfit at RMS=1;(b)Histogram of the amplitude ratios between observed data used for inversion and predicated data of initial iteration(blue) and of final iteration(red). The red dashed line indicates 3% data error interval. |
|
图 5 陆地CSEM频率为1 Hz时,(a—c) 不同发射位置的所有测点的观测数据振幅、(d—f) 观测数据与初始模型数据振幅比、(g—i) 观测数据与反演最终模型数据振幅比.红色三角为发射场源位置,黑色圆点为接收测站位置. Fig. 5 (a—c)Amplitudes of observed data.(d—f)Amplitude ratios between observed data and predicated data of starting model.(g—i)Amplitude ratios between observed data and predicated data of finial model for different transmitter locations with 1Hz transmission frequency for land CSEM survey. Triangles and circles denote receivers and transmitters,respectively. |
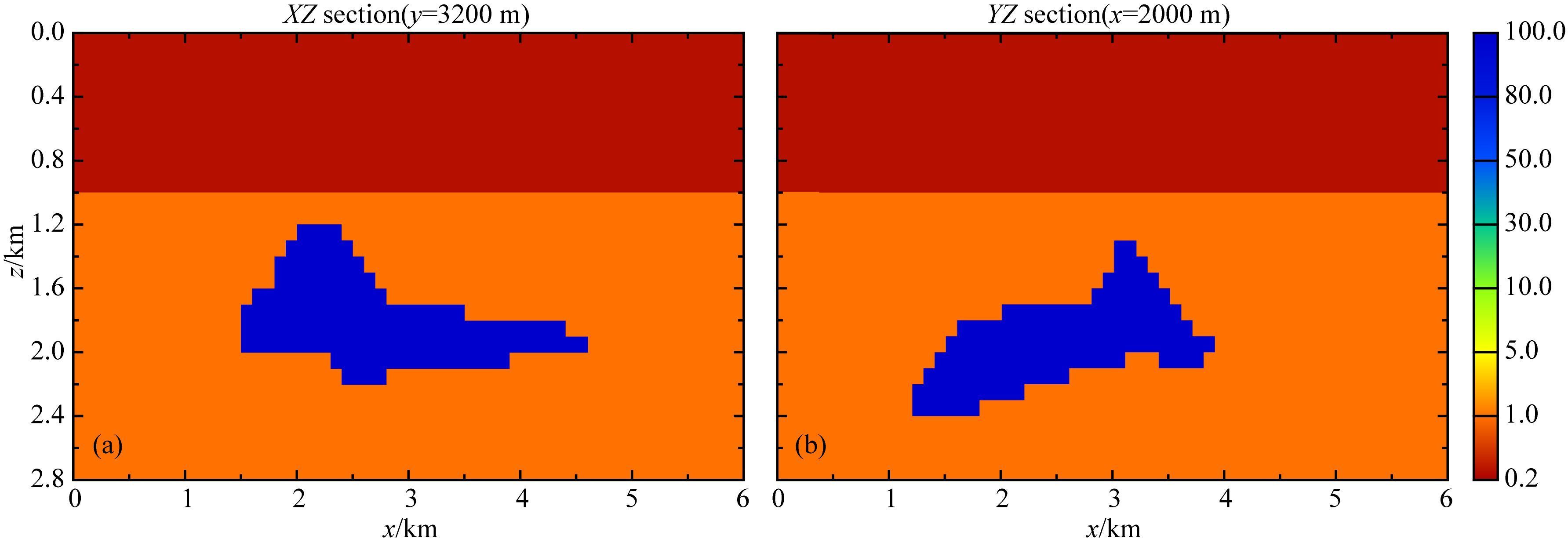
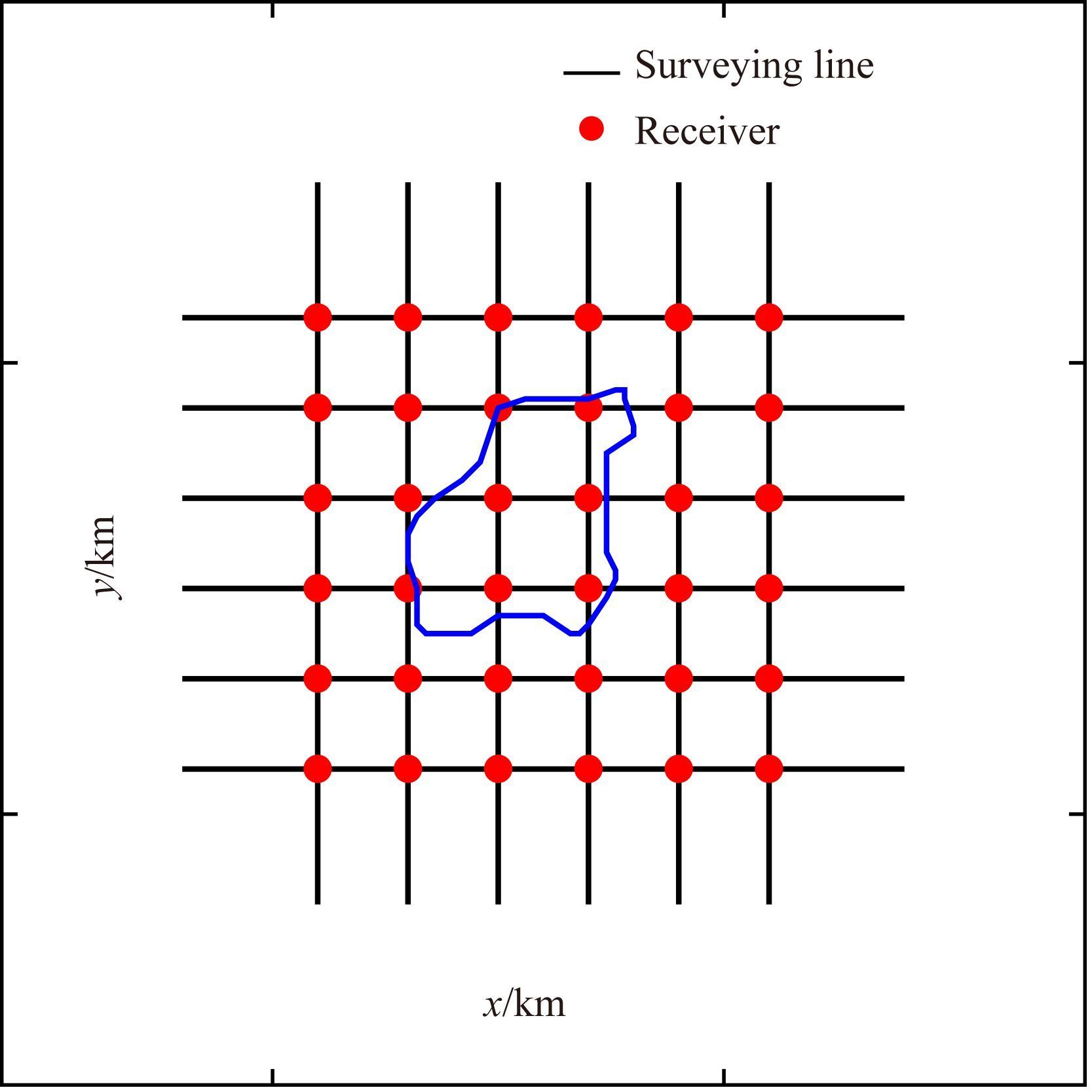
接着考虑海洋CSEM测量情况.为测试所开发的反演算法对于复杂模型的有效性,本文将地震勘探中常用于偏移成像算法测试的三维盐穹体(salt dome) 模型(Aminzadeh et al.,1997) 进行修改来模拟海洋可控源勘探情况.整个盐穹模型区域大小为6 km×6 km×2.8 km(含海水层),如图 6所示.盐穹体的电阻率设为100 Ωm.均匀海底沉积层电阻率为1 Ωm,海水层厚度为1 km,电阻率为0.33 Ωm.采用三维测网数据采集方式来模拟真实海洋可控源测量情况,如图 7所示.整个测量网格包括12条正交的测量线,每条测线长为6 km,测线间距为1 km.发射偶极子采用水平电偶极子(HED),偶极方向与测线方向一致,位于海底上方50 m处.发射偶极子每隔300 m向海底发射频率为0.25 Hz、0.75 Hz和1.25 Hz的电磁信号,共形成252个发射源位置.36个布设于海底的接收站在测区内呈均匀分布,同时接收电场x分量和y分量,测点间距为1 km.为得到用于反演的合成数据,与上述陆地三维模型剖分方式类似,正演网格剖分为92×92×54.正演计算得到所有场源的电场Ex分量和Ey分量.考虑到电磁数据的冗余情况,本文只利用与发射源偶极方向一致的电场分量(即对于沿x方向极化的偶极源只利用Ex分量,而对于沿y方向极化的偶极源只利用Ey分量) 作为反演数据,从而有效减少存储需求和反演计算量.对理论合成数据添加5%的随机噪声得到反演的观测数据.为避免反演中对振幅较小的数据的过度拟合,数据误差限设为5×10-15 V·m-1(Constable and Weiss,2006),总共形成23100个海洋可控源电场数据.反演网格采用不同于正演计算的网格,网格剖分为72×72× 46.反演初始正则化参数设置为0.01,为避免正则化因子下降过快,衰减因子γ为1.5.GN迭代中的PCG迭代次数设为15次.目标拟合差设为1.反演迭代中,空气层和海水层电导率均保持不变.
|
图 6 海洋可控源三维盐穹体模型剖面 (a)XZ剖面(y=3200 m);(b)YZ剖面(x=2000 m). Fig. 6 Planar views of 3D salt dome reservoir for marine CSEM survey section at y=3200 m;(b)YZ section at x=2000 m. |
|
图 7 海洋可控源三维观测系统平面 其中红色圆点为布设于海底的接收站,黑线为发射源的航行线,距海底50 m,蓝线为盐穹模型在深度为1750 m时的平面投影. Fig. 7 Sketch showing data acquisition geometry for marine CSEM survey Survey consists of thirty-two sea-bottom detectors denoted by red circles and twelve sail lines shown in black lines. The blue curve indicates the projection of the salt dome reservoir at the depth of 1750 m. |
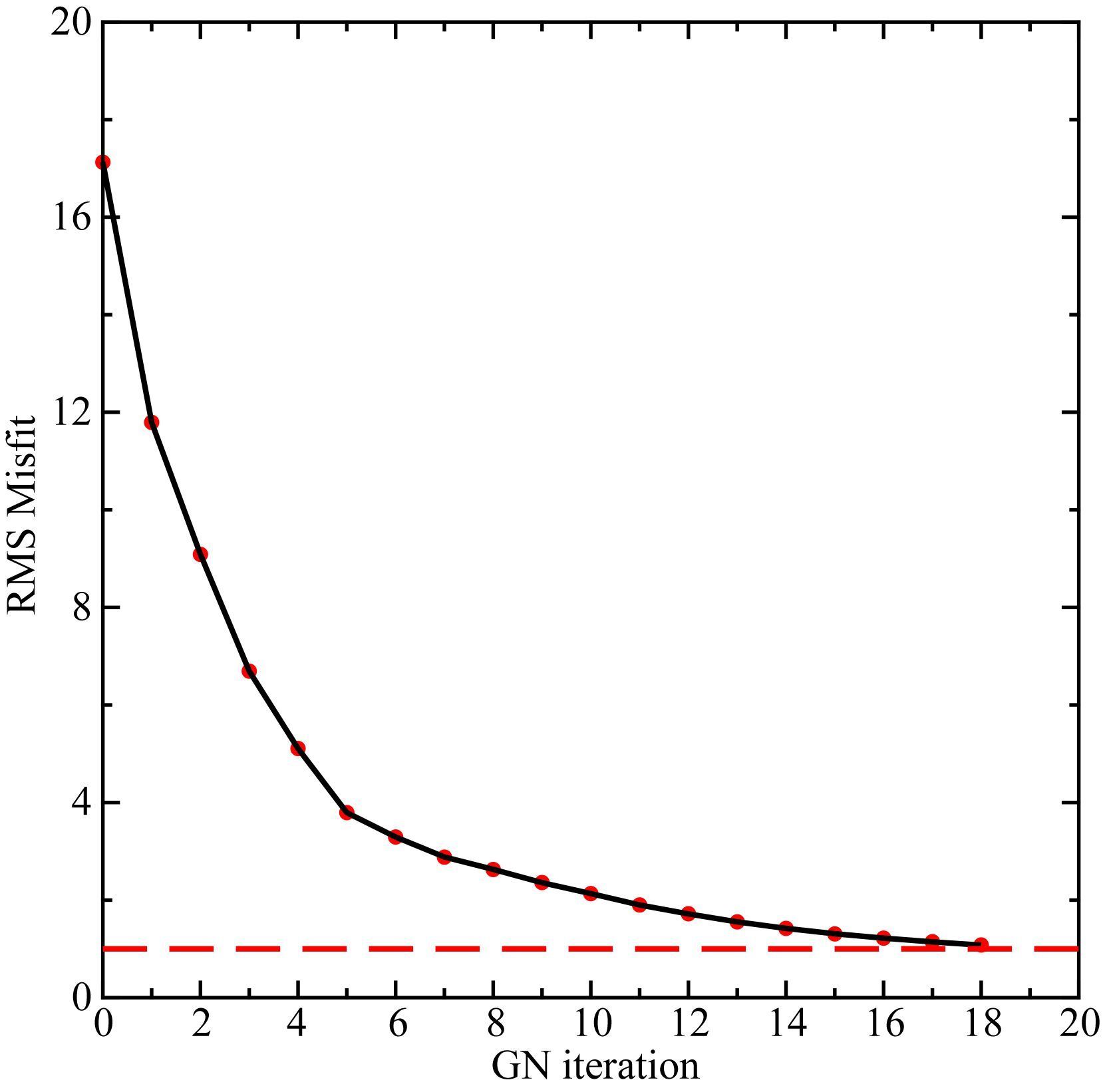
图 8给出了三维反演过程中数据拟合差的变化情况.整个反演共进行了18次GN迭代,反演数据拟合差从初始的17.13逐渐收敛到最后的1.07,显示了GN反演算法对于复杂模型同样具有优良的收敛性和稳定性.每次GN迭代耗时约1小时40分钟.
|
图 8 海洋可控源盐穹体模型反演数据拟合差 RMS随迭代次数变化(红色虚线为目标拟合差) Fig. 8 Data RMS misfit versus GN iteration for marine CSEM survey(The red dashed line shows the desired data misfit at RMS=1) |
图 9给出了盐穹体模型三维反演的不同剖面结果.可以看出,反演总体上很好地恢复了盐穹体模型在空间上的分布.对比反演结果中的高阻区域与盐穹体模型的真实区域(图中黑色曲线所圈定区域),可以发现根据反演结果能够有效地推断出盐穹体的结构特征,并估计出相应的边界位置.另外对于盐穹电阻率值的恢复,反演在盐穹核心区域处可达到80 Ωm以上(如图 9h,i),展示了海洋可控源电磁法对于高阻目标体优良的分辨能力.另一方面,由于盐穹模型的不规则特征,在某些区域内,反演结果并未能较好地刻画出真实的形态特征(如图 9a,g),这可能与本文所采用的平滑模型正则化泛函有关,若使用其他形式的模型正则化泛函有可能效果更好,这不在本文讨论范围以内.
本文实现了一种频率域CSEM三维反演算法.正演使用拟态有限体积法对控制方程离散化,并使用直接矩阵分解法求解离散所得的大型线性系统方程;反演中采用高斯牛顿最优化算法,并使用预条件共轭梯度法(PCG) 求解每次GN迭代所得到的法方程.以上这些技术的结合使用,使得本文的三维反演算法准确、稳定且高效,适用于陆地和海洋CSEM勘探场景,并且特别适合于多场源CSEM问题的模拟.理论模型的反演测试结果证明了本文算法的这些优点.
随着电磁勘探精度要求的提高,对地电模型的假设将越来越接近真实情况,此外数据规模也将越来越大,例如最新的海洋CSEM发射与接收一体式的拖曳式测量会带来数量极多的发射源和测点.这些因素都对CSEM的三维反演形成了巨大的挑战,因此需要不断地将最前沿的科学计算理论加以应用以提升CSEM三维反演算法的性能.本文算是在这方面做了一个较小的尝试,但还有大量的工作有待完成.
附录A Jv和JTw的计算Helmholtz方程离散后得到的线性方程组可表示为
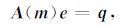
|
(A1) |
其中A为稀疏正定对称复矩阵,e为网格采样点处电场分量,q为场源项.为获得测点处的电场值,定义Nd×Ne阶观测矩阵P,假定其与模型参数无关,Nd、Ne分别为观测数据个数和电场采样点个数.则观测数据可表示为
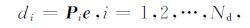
|
(A2) |
则数据的灵敏度矩阵J为
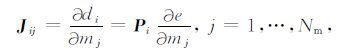
|
(A3) |
Nm为模型参数个数.
对(A1) 式取全微分可得

|
(A4) |
将(A4) 式代入到(A3) 式中可得
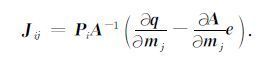
|
(A5) |
为求得灵敏度矩阵J与模型向量v的乘积,定义向量u为
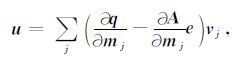
|
(A6) |
令向量y满足

|
(A7) |
结合(A5—A7) 式,可得到

|
(A8) |
为求得灵敏度矩阵转置JT与模型向量w的乘积,令向量z满足
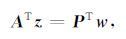
|
(A9) |
结合(A5) 和(A9) 式可得

|
(A10) |
对于总场公式来说,场源项与模型参数无关,则 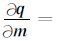
感谢加拿大英属哥伦比亚大学(UBC)Eldad Haber教授的指导及与GIF组内同学进行的有益讨论.另外特别感谢MUMPS线性运算库的开发者们的无私贡献.向匿名审稿人对本文提出的宝贵修改意见表示衷心感谢.
| Amestoy P R, Duff I S, L'Excellent J Y, et al. 2001. A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM Journal on Matrix Analysis and Applications , 23 (1) : 15-41. DOI:10.1137/S0895479899358194 | |
| Amestoy P R, Guermouche A, L'Excellent J Y, et al. 2006. Hybrid scheduling for the parallel solution of linear systems. Parallel Computing , 32 (2) : 136-156. DOI:10.1016/j.parco.2005.07.004 | |
| Aminzadeh F, Brac J, Kunz T. 1997. 3-D salt and overthrust models. SEG. | |
| Barrett R, Berry M, Chan T F, et al. 1994. Templates for the Solution of Linear Systems:Building Blocks for Iterative Methods. 2nd ed. Philadelphia:SIAM. | |
| Commer M, Newman G A. 2008. New advances in three-dimensional controlled-source electromagnetic inversion. Geophysical Journal International , 172 (2) : 513-535. DOI:10.1111/gji.2008.172.issue-2 | |
| Constable S. 2010. Ten years of marine CSEM for hydrocarbon exploration. Geophysics , 75 (5) : 75A67-75A81. DOI:10.1190/1.3483451 | |
| Constable S, Weiss C J. 2006. Mapping thin resistors and hydrocarbons with marine EM methods:Insights from 1D modeling. Geophysics , 71 (2) : G43-G51. DOI:10.1190/1.2187748 | |
| Constable S C, Parker R L, Constable C G. 1987. Occam's inversion:A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics , 52 (3) : 289-300. DOI:10.1190/1.1442303 | |
| Egbert G D, Kelbert A. 2012. Computational recipes for electromagnetic inverse problems. Geophysical Journal International , 189 (1) : 251-267. DOI:10.1111/j.1365-246X.2011.05347.x | |
| Eisenstat S C, Walker H F. 1996. Choosing the forcing terms in an inexact Newton method. SIAM Journal on Scientific Computing , 17 (1) : 16-32. DOI:10.1137/0917003 | |
| Grayver A V, Streich R, Ritter O. 2013. Three-dimensional parallel distributed inversion of CSEM data using a direct forward solver. Geophysical Journal International , 193 (3) : 1432-1446. DOI:10.1093/gji/ggt055 | |
| Grayver A V, Streich R, Ritter O. 2014. 3D inversion and resolution analysis of land-based CSEM data from the Ketzin CO2 storage formation. Geophysics , 79 (2) : E101-E114. DOI:10.1190/geo2013-0184.1 | |
| Haber E, Oldenburg D W, Shekhtman R. 2007. Inversion of time domain three-dimensional electromagnetic data. Geophysical Journal International , 171 (2) : 550-564. DOI:10.1111/gji.2007.171.issue-2 | |
| Haber E, Ruthotto L. 2014. A multiscale finite volume method for Maxwell's equations at low frequencies. Geophysical Journal International , 199 (2) : 1268-1277. DOI:10.1093/gji/ggu268 | |
| Han B. 2015 Three-dimensional parallel forward modeling and inversion of frequency-domain CSEM data[Ph.D. thesis](in Chinese). Wuhan:China University of Geosciences. | |
| HAN Bo, HU Xiang-Yun, HUANG Yi-Fan, et al. 2015. 3-D frequency-domain CSEM modeling using a parallel direct solver. Chinese J. Geophys. , 58 (8) : 2812-2826. DOI:10.6038/cjg20150816 | |
| Hu X Y, Peng R H, Wu G J, et al. 2013. Mineral exploration using CSAMT data:Application to Longmen region metallogenic belt, Guangdong Province, China. Geophysics , 78 (3) : B111-B119. DOI:10.1190/geo2012-0115.1 | |
| Hyman J, Shashkov M, Steinberg S. 1997. The numerical solution of diffusion problems in strongly heterogeneous non-isotropic materials. Journal of Computational Physics , 132 (1) : 130-148. DOI:10.1006/jcph.1996.5633 | |
| Hyman J M, Shashkov M. 1997. Adjoint operators for the natural discretizations of the divergence, gradient and curl on logically rectangular grids. Applied Numerical Mathematics , 25 (4) : 413-442. DOI:10.1016/S0168-9274(97)00097-4 | |
| Hyman J M, Shashkov M. 1999a. Mimetic discretizations for Maxwell's equations. Journal of Computational Physics , 151 (2) : 881-909. DOI:10.1006/jcph.1999.6225 | |
| Hyman J M, Shashkov M. 1999b. The orthogonal decomposition theorems for mimetic finite difference methods. SIAM Journal on Numerical Analysis , 36 (3) : 788-818. DOI:10.1137/S0036142996314044 | |
| Ledo J. 2005. 2-D versus 3-D magnetotelluric data interpretation. Surveys in Geophysics , 26 (5) : 511-543. DOI:10.1007/s10712-005-1757-8 | |
| Lelièvre P G, Oldenburg D W. 2009. A comprehensive study of including structural orientation information in geophysical inversions. Geophysical Journal International , 178 (2) : 623-637. DOI:10.1111/gji.2009.178.issue-2 | |
| Lin C H, Tan H D, Shu Q, et al. 2012. Three-dimensional conjugate gradient inversion of CSAMT data. Chinese J. Geophys. (in Chinese) , 55 (11) : 3829-3838. DOI:10.6038/j.issn.0001-5733.2012.11.030 | |
| Liu Y H, Yin C C. 2013. 3D inversion for frequency-domain HEM data. Chinese J. Geophys. (in Chinese) , 56 (12) : 4278-4287. DOI:10.6038/cjg20131230 | |
| Newman G A, Alumbaugh D L. 1997. Three-dimensional massively parallel electromagnetic inversion-I. Theory. Geophysical Journal International , 128 (2) : 345-354. DOI:10.1111/gji.1997.128.issue-2 | |
| Nocedal J, Wright S. Numerical optimization. New York: Springer, 1999 . | |
| Oldenburg D W, Haber E, Shekhtman R. 2013. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics , 78 (1) : E47-E57. DOI:10.1190/geo2012-0131.1 | |
| Pidlisecky A, Haber E, Knight R. 2007. RESINVM3D:A 3D resistivity inversion package. Geophysics , 72 (2) : H1-H10. DOI:10.1190/1.2402499 | |
| Plessix R é, Mulder W A. 2008. Resistivity imaging with controlled-source electromagnetic data:depth and data weighting. Inverse Problems , 24 (3) : 034012. DOI:10.1088/0266-5611/24/3/034012 | |
| Rieder A. 2001. On convergence rates of inexact Newton regularizations. Numerische Mathematik , 88 (2) : 347-365. DOI:10.1007/PL00005448 | |
| Rieder A. 2005. Inexact newton regularization using conjugate gradients as inner iteration. SIAM journal on numerical analysis , 43 (2) : 604-622. DOI:10.1137/040604029 | |
| Rodi W, Mackie R L. 2001. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion. Geophysics , 66 (1) : 174-187. DOI:10.1190/1.1444893 | |
| Saad Y. 2003. Iterative methods for sparse linear systems. Philadelphia:SIAM. | |
| Schenk O, Gärtner K. 2006. On fast factorization pivoting methods for sparse symmetric indefinite systems. Electronic Transactions on Numerical Analysis , 23 (1) : 158-179. | |
| Schwarzbach C, Haber E. 2013. Finite element based inversion for time-harmonic electromagnetic problems. Geophysical Journal International , 193 (2) : 615-634. DOI:10.1093/gji/ggt006 | |
| Siripunvaraporn W. 2012. Three-dimensional magnetotelluric inversion:an introductoryguide for developers and users. Surv. Geophys. , 33 (1) : 5-27. DOI:10.1007/s10712-011-9122-6 | |
| Siripunvaraporn W, Egbert G, Uyeshima M. 2005. Interpretation of two-dimensional magnetotelluric profile data with three-dimensional inversion:synthetic examples. Geophysical Journal International , 160 (3) : 804-814. DOI:10.1111/gji.2005.160.issue-3 | |
| Smith J T. 1996. Conservative modeling of 3-D electromagnetic fields, Part Ⅱ:Biconjugate gradient solution and an accelerator. Geophysics , 61 (5) : 1319-1324. DOI:10.1190/1.1444055 | |
| Streich R. 2009. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data:Direct solution and optimization for high accuracy. Geophysics , 74 (5) : F95-F105. DOI:10.1190/1.3196241 | |
| Tikhonov A N, Arsenin V I A K. 1977. Solutions of Ill-Posed Problems. Washington, D. C., USA:W. H. Winston and Sons. | |
| van den Doel K, Ascher U M. 2007. Dynamic level set regularization for large distributed parameter estimation problems. Inverse Problems , 23 (3) : 1271-1288. DOI:10.1088/0266-5611/23/3/025 | |
| van den Doel K, Ascher U M. 2012. Adaptive and stochastic algorithms for electrical impedance tomography and DC resistivity problems with piecewise constant solutions and many measurements. SIAM Journal on Scientific Computing , 34 (1) : A185-A205. DOI:10.1137/110826692 | |
| Weng A H, Li D J, Li Y B, et al. 2015. Selection of parameter types in Controlled Source Electromagnetic Method. Chinese J. Geophys. (in Chinese) , 58 (2) : 697-708. DOI:10.6038/cjg20150230 | |
| Weng A H, Liu Y H, Jia D Y, et al. 2012. Three-dimensional controlled source electromagnetic inversion using non-linear conjugate gradients. Chinese J. Geophys. (in Chinese) , 55 (10) : 3506-3515. DOI:10.6038/j.issn.0001-5733.2012.10.034 | |
| Yang D K, Oldenburg D W. 2012. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit. Geophysics , 77 (2) : B23-B34. DOI:10.1190/geo2011-0194.1 | |
| Zhao N, Wang X B, Qin C, et al. 2016. 3D frequency-domain CSEM inversion. Chinese J. Geophys. (in Chinese) , 59 (1) : 330-341. DOI:10.6038/cjg20160128 | |
| 韩波. 2015. 频率域可控源电磁法并行化三维正反演算法研究[博士论文]. 武汉:中国地质大学(武汉). http://epub.cnki.net/kns/detail/detail.aspx?QueryID=7&CurRec=1&recid=&FileName=1015709816.nh&DbName=CDFDLAST2016&DbCode=CDFD&pr= | |
| 韩波, 胡祥云, 黄一凡, 等. 2015. 基于并行化直接解法的频率域可控源电磁三维正演. 地球物理学报 , 58 (8) : 2812–2826. DOI:10.6038/cjg20150816 | |
| 林昌洪, 谭捍东, 舒晴, 等. 2012. 可控源音频大地电磁三维共轭梯度反演研究. 地球物理学报 , 55 (11) : 3829–3838. DOI:10.6038/j.issn.0001-5733.2012.11.030 | |
| 刘云鹤, 殷长春. 2013. 三维频率域航空电磁反演研究. 地球物理学报 , 56 (12) : 4278–4287. DOI:10.6038/cjg20131230 | |
| 翁爱华, 李大俊, 李亚彬, 等. 2015. 数据类型对三维地面可控源电磁勘探效果的影响. 地球物理学报 , 58 (2) : 697–708. DOI:10.6038/cjg20150230 | |
| 翁爱华, 刘云鹤, 贾定宇, 等. 2012. 地面可控源频率测深三维非线性共轭梯度反演. 地球物理学报 , 55 (10) : 3506–3515. DOI:10.6038/j.issn.0001-5733.2012.10.034 | |
| 赵宁, 王绪本, 秦策, 等. 2016. 三维频率域可控源电磁反演研究. 地球物理学报 , 59 (1) : 330–341. DOI:10.6038/cjg20160128 | |
 2016, Vol. 59
2016, Vol. 59


