2. 中石化上海海洋油气分公司, 上海 200120;
3. 阿美远东(北京)商业服务有限公司国际研发中心, 北京 100102;
4. 中石化石油物探技术研究院地震成像技术研究所, 南京 210014
2. Sinopec Shanghai Offshore Oil & Gas Company, Shanghai 200120, China;
3. Aramco Far East(Beijing) Business Services Co., Ltd, Beijing 100102, China;
4. Sinopec Geophysical Research Institute, Nanjing 210014, China
立体层析是一种极具特色的层析反演方法,该方法将局部相干同相轴在炮道集与检波点道集内的射线参数(或P参数)水平分量、以及炮点坐标和检波点坐标都纳入到反演的数据空间之中,重新定义了层析反演的数据分量和模型分量,使得数据的提取不再需要沿着连续的层位进行.这不仅使得数据空间的准备相比传统反射层析更为简单,也使得立体层析成为射线类层析反演方法中唯一一种可以同时反演速度结构、反射点位置与反射层局部形态的方法(Billette and Lambare,1998).国内外学者在立体层析反演的理论和实践方面做了很多工作(Prieux et al.,2013; 倪瑶等,2013;倪瑶等,2014;任丽娟等,2014;李振伟等,2014; Li et al.,2015).王宇翔等(2016)将结构张量算法用于P参数水平分量的搜索,实现了高密度的二维立体层析反演.Ni和Yang(2012)将正入射点(NIP)波层析与有限频相结合,得到一种结合有限频与NIP波层析的反演方法,为有限频立体层析方法奠定了理论基础.反观三维立体层析反演,国际上虽然偶有摘要类文章展示过实例研究(Chalard et al.,2000; and Lambaré,2005).但是对于其算法所涉及的理论推演从未有过系统的梳理.不同于前人在射线中心坐标系下基于降阶汉密尔顿算子,通过射线扰动理论建立三维层析(或FRECHET偏导数)矩阵,本文详细介绍在三维直角坐标系下、基于非降阶汉密尔顿算子,如何通过射线扰动理论导出三维立体层析反演所需的数据空间对模型空间的一阶线性关系,进而建立三维立体层析矩阵方程,并结合合理的规则化手段保证迭代收敛的稳定性.最后通过两个理论数据验证了上述理论推演的正确性.
2 三维立体层析矩阵详解首先对三维立体层析所涉及到的数据空间和模型空间各个分量给予详细介绍.图 1显示了三维立体层析数据空间各分量与模型空间各分量.对于三 维空间的一个射线对而言,地表能观测到的数据为d=(Sx,Sy,Sz,Rx,Ry,Rz,Tsr,Psx,Psy,Prx,Pry),其中Sx,Sy,Sz,Rx,Ry,Rz为炮检点的X、Y、Z坐标;Tsr为这个射线对的总走时;Psx,Psy,Prx,Pry为炮检点处的射线参数水平分量.这些数据分量与地下的模型空间m=(x0,y0,z0,θs,øs,θr,ør,V)有关,其中x0,y0,z0为地下反射点坐标,θs,øs代表从炮点一侧出射的地下张角与方位角,θr,ør代表从检波点一侧出射的地下张角与方位角,V代表地下介质速度信息.本文讨论的情形总假定Sz=Rz=常数,意味着这两个量不随模型空间而变化,于是数据空间分量可以从11个压缩为9个.地下的模型空间用标量表示则一共是8个分量(如果把V当做是一个分量).Billette和Lambaré(1998)已经给出了共炮点和共检波点道集内的局部相干同相轴的斜率等同于检波点处和炮点处慢度矢量的水平分量.这里不再重复其推导,仅强调该结论在三维下同样成立.这样,共炮点和共检波点道集上同相轴的斜率便可用来约束反射/绕射波在炮检点处的局部传播方向.事实上,立体层析反演中“立体”即与炮检点处的局部传播方向被引入数据空间,可以用于约束层析的反演密切相关.

|
图 1 三维立体层析数据空间各分量与模型空间各分量 Fig. 1 The model-space components and the data-space components in 3D stereotomography |
对于数据空间和模型空间中的所有信息,将其进一步写为

|
(1a) |

|
(1b) |
(1a)式表达了数据空间表示拾取到的n个数据点;(1b)式表达了模型空间中对应这n个数据点反射点坐标以及从这n个反射点出射到地表的射线初始信息.Billette和Lambaré(1998)、倪瑶等(2013)基于射线中心坐标系,推导了二维立体层析反演所需的模型空间各个分量扰动与数据空间各个分量扰动之间的线性关系,成功的建立了二维立体层析矩阵.三维立体层析矩阵的基本构建思路与二维并无区别,都是将从炮点S→反射点X→检波点R的反射过程分解为从X→S以及X→R这样两个透射过程.其中数据空间的残差Δd与模型空间残差Δm之间的关系由三维射线扰动理论建立: Δd=FΔm.
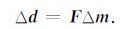
|
(2) |
(2)式代表了一个矩阵方程,其系数矩阵F即为三维立体层析矩阵或FRECHET偏导数矩阵.其完整形式表达如下:

|
(3) |
对于三维立体层析所需的Fréchet偏导数

|
(4) |
其次,根据费马原理,走时T在速度结构、激发点与接收点位置都固定时,已经是最小走时.因此可以认为散射角对走时T不存在一阶扰动影响.即可认为

|
(5) |
(5)式中σ的含义为针对各类数据的尺度加权因子,用于平衡不同类型的数据对于立体层析反演的误差泛函的贡献比例,避免由于物理量纲不同造成数据类型量级之间差别过大的问题,参数的大小需要通过做具体的测试得到.例如,对于本文中使用的测试数据,P参数关于模型空间的偏导数需要除以一个比较小的因子,基本上是10-5次方量级;走时t对于模型空间的偏导数,一般除以10-2次方量级;炮检点坐标对于模型空间的偏导数,一般除以1即可.对于不同的数据,这些因子有时也需要调整.需要指出,σ因子可以认为是Tarantola(1987)定义的数据误差泛函中数据协方差矩阵的一种特例.
3 三维笛卡尔坐标系下的射线扰动理论与三维立体层析矩阵建立立体层析反演的理论基础是射线扰动理论(Farra and Madariaga,1987).射线扰动理论的重要性在于,它在傍轴射线追踪和汉密尔顿传播算子的基础上,成功建立了速度扰动与描述射线传播的相空间各参数扰动量之间的一阶线性关系,这是建立立体层析矩阵的关键所在.Billette和Lambaré(1998)在射线中心坐标系下推导了二维立体层析所需的模型空间各个分量扰动与数据空间各个分量扰动之间的线性关系,并成功实现了二维立体层析反演.国际上已有的三维立体层析工作(Chalard et al.,2000,2005)依然沿用了Billette和Lambaré(1998)的研究思路,在三维射线中心坐标系下使用降价汉米尔顿算子推导出公式(5)所示矩阵中的各个偏导数关系.但是,三维射线扰动理论在射线中心坐标系下实现并非最佳,这是因为在三维射线中心坐标系下构造傍轴射线追踪所需的传播矩阵时,涉及到对垂直于中心射线的各个方向求关于速度的二阶导数计算.这个计算非常耗时,但是直角坐标系下的傍轴射线追踪则不存在上述问题.此外,与前人使用降阶汉密尔顿传播算子有所不同,本文采用了非降阶汉密尔顿传播算子实现三维射线扰动理论.采用非降阶汉密尔顿传播算子的理由是出于算法适应性方面的考量,使得算法可以自然的考虑回转波射线.
4 三维直角坐标系下非降阶汉密尔顿传播算子以及相应的傍轴射线系统三维直角坐标系下非降阶形式的各向同性汉密尔顿传播算子形式为

|
(6) |
则直角坐标系下的各向同性运动学射线追踪方程为
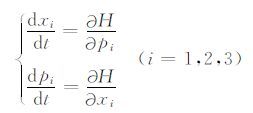
|
(7) |
其中积分变量为时间,其具体表达式为

|
(8) |
方程(8)为三维直角坐标系下非降阶形式的汉密尔顿运动学射线追踪方程组,由6个一阶微分方程组成.(X1,X2,X3,Px1,Px2,Px3分别对应X,Y,Z,Px,Py,Pz).如果使用降阶汉密尔顿传播子,其运动学追踪方程可以从6个降为4个.在直角坐标系下,常用的降阶方式是把垂直向下的Z方向(即X3方向)作为射线追踪的参考方向,这样在追踪时X3与Px3就无需求解微分方程,可以直接积分得到或基于其他四个追踪量换算得到.具体的推导过程请参阅文献(Cerveny,2001).这样做虽然使得方程组的数目减少,计算效率得到提高.但是一个限制就是射线在Z方向必须单调增加或者单调下降,无法考虑回转波射线.作者为了该算法将来能够考虑更复杂的射线路径(比如盐丘侧翼甚至盐丘底部的回转射线),在本文研究中没有采用降阶形式.同时我们发现二者的计算成本的差别并不明显.从(8)式出发,为得到射线初始位置的相空间扰动对射线末端相空间扰动的线性关系,需要对(8)式两边全微分,得到所谓的傍轴追踪系统:

|
(9) |
其中, Δζ=(Δx1,Δx2,Δx3,Δp1,Δp2,Δp3)T.
系数矩阵的表达式为

|
方程(9)即为三维直角坐标系下非降阶形式的运动学傍轴射线追踪系统.表达了射线场的初始扰动量与射线轨迹上任意一点的射线场扰动之间的线性关系.(9)式虽然建立了射线初始点的相空间扰动对射线末端的相空间扰动之间的线性关系,但是对于立体层析反演依然不够,必须还要建立速度扰动对射线轨迹上任一点的射线场扰动的一阶线性关系才可以建立完整的三维立体层析矩阵.这个一阶影响必须要通过射线扰动理论来建立.
5 三维直角坐标系下的射线扰动理论应用根据(Farra and Madariaga,1987),速度扰动对于射线传播汉密尔顿传播算子的线性影响表达为
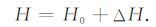
|
(10) |
其中扰动汉密尔顿传播算子,即

|
(11) |
从(6)式出发可得 

|
(12) |
对(10)式所代表的汉密尔顿传播算子做关于 Δζ=(Δx1,Δx2,Δx3,Δp1,Δp2,Δp3)T 的全微分,即可得到

|
(13) |
其中,
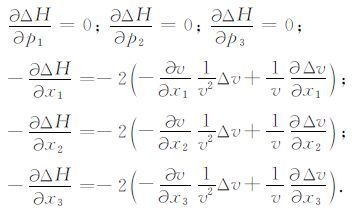
|
(14) |
根据Gilbert和Backus(1966),(13)式的传播矩阵形式的解为
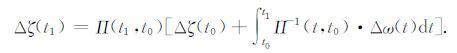
|
(15) |
其中射线传播矩阵是傍轴射线追踪的一组基本解,在使用三维非降阶汉密尔顿情形下为36个元素,即分别代入(1,0,0,0,0,0)、(0,1,0,0,0,0)、(0,0,1,0,0,0)、(0,0,0,1,0,0)、(0,0,0,0,1,0)、(0,0,0,0,0,1)这6组初始值,利用龙格库塔计算出的6组解构成的6×6矩阵.在射线路径的每一个点上都可以算出这样一个矩阵.以及其逆矩阵的具体形式为
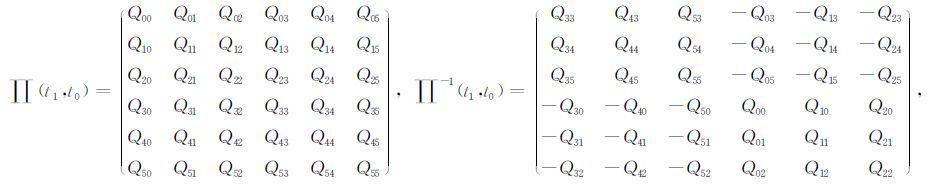
|
故式(15)的显示表达为

|
(16) |
其中,

|
根据式(16)即可以构建三维直角坐标系下数据空间分量 d=(Sx,Sy,Sz=0,Rx,Ry,Rz=0,Tsr,Psx,Psy,Prx,Pry) 中除了走时 Tsr 之外的所有分量与模型空间分量 m=(x0,y0,z0,θs,øs,θr,ør,V) 之间的一阶线性扰动关系.如炮点横坐标Sx、炮点 Psx 参数与模型空间各分量之间的一阶线性关系即可写出:
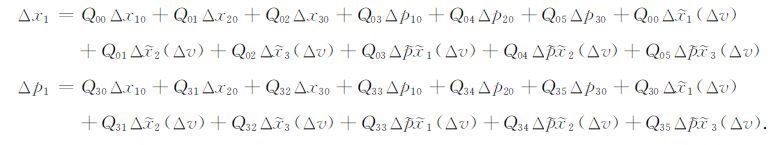
|
(17) |
其中,
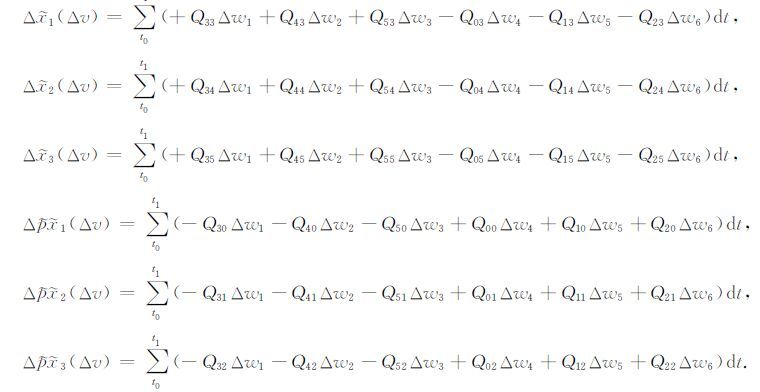
|
(18) |
数据空间其他分量对模型空间的偏导数均可以类似式(17)的形式写出.
在求解时,为了计算方便,我们实际上是将射线出射点处的射线参数 Px0,Py0,Pz0 (即(16)式中的 P10,P20,P30) 作为模型空间中的一部分在迭代过程中不断更新,而并不是直接更新 (θs,øs,θr,ør). 实践证明这样操作给计算带来了相当的方便,对反演精度没有造成任何负面影响.在反演结束后,只需用三维情形下P参数与速度V以及θs,øs,θr,ør之间的定量关系换算出θs,øs,θr,φr即可.该定量关系可参考相关文献(Audebert et al.,2002).
6 三维直角坐标系下走时 Tsr 与模型空间各分量之间的一阶扰动关系走时 Tsr 与模型空间分量之间的一阶扰动关系则可以通过以下推导来建立.考虑到 Tsr=ts+tr, 显然有:

|
(19) |
分析知

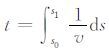

|
(20) |
其中,θ,ø代表炮点一侧的θs,øs或检波点一侧的θr,ør.由(20)式即可容易计算出走时t对模型空间各分量的偏导数 
三维立体层析所需的所有数据空间分量对模型空间分量的偏导数定量关系都已经得到.
7 理论数据敏感度测试在得到三维立体层析所需的数据空间各分量与模型空间各分量之间的一阶线性扰动关系之后,以下基于三维理论模型中的一个射线对信息,来测试不同数据分量与不同模型分量之间的敏感度.这些敏感度分析除了测试在前两节中推导的偏导数关系是否正确,也测试了在将来的反演中,各个模型分量是否能够通过求解立体层析矩阵获得足够的更新量.如果某个数据分量对于某个模型分量非常不敏感,那么二者之间的偏导数就没有必要求取了.
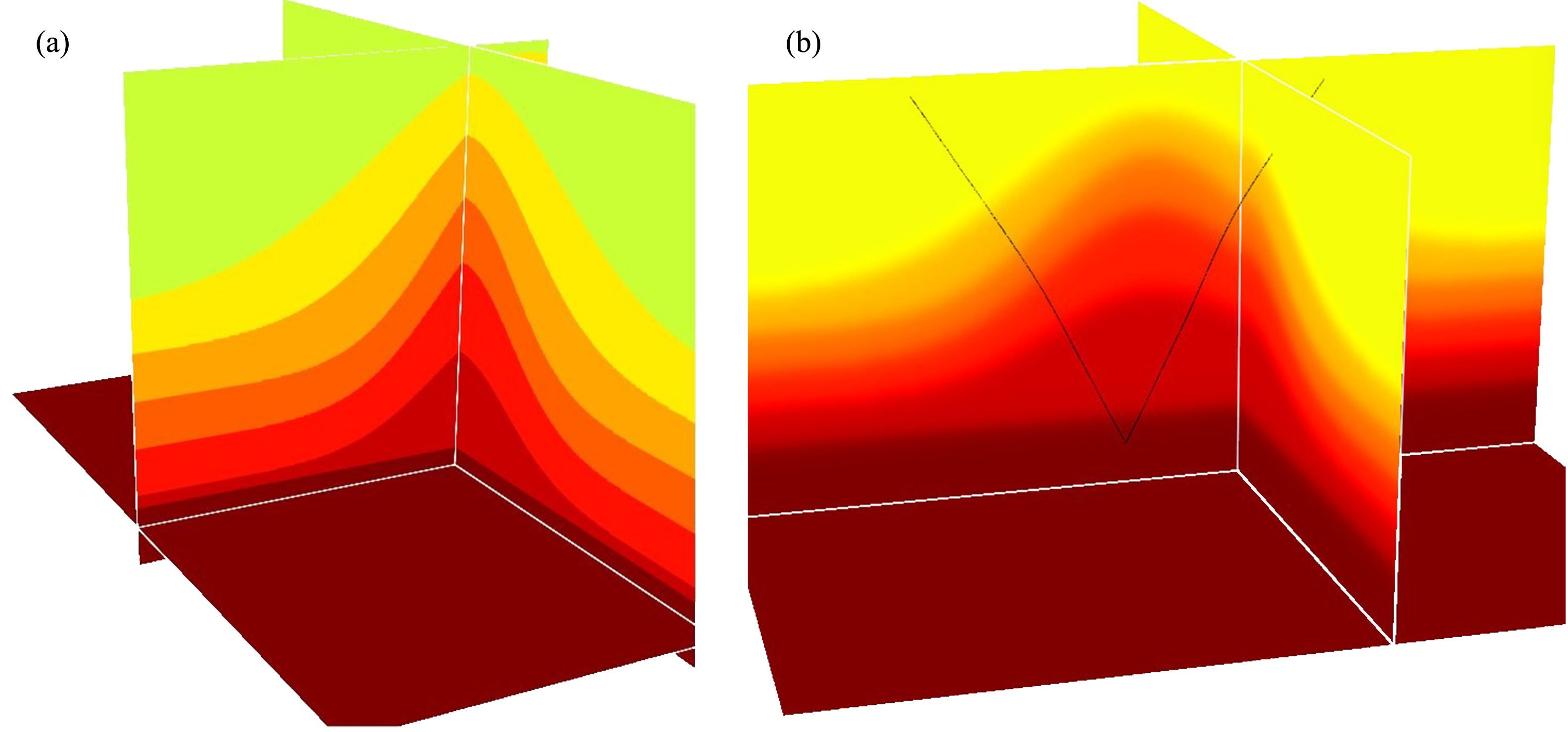
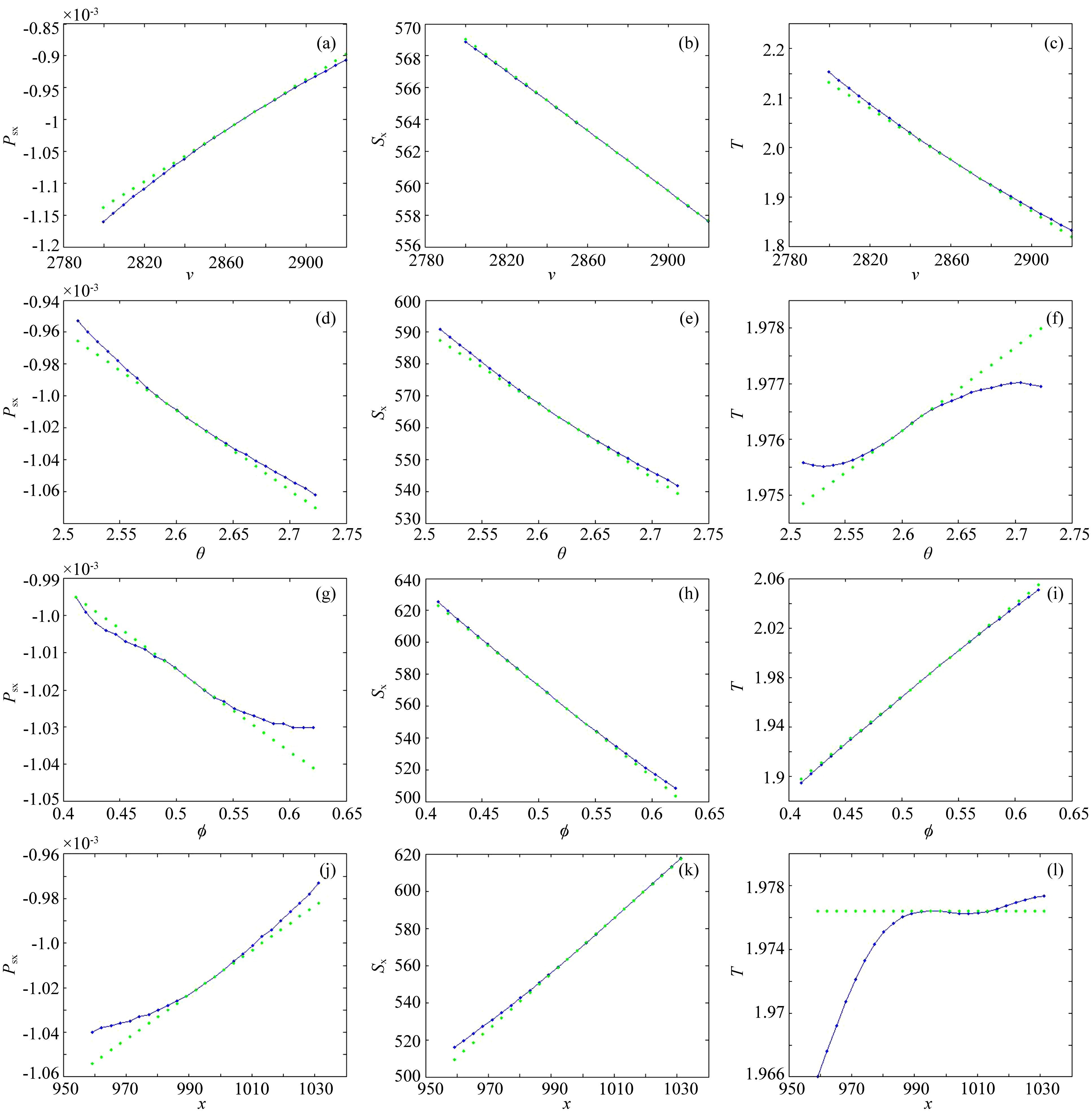
图 2a展示了一个盐丘速度模型,横向、纵向网格数为51×51×26,网格间距分别为横向dx=dy=40 m,纵向dz=40 m.图 2b是图 2a的光滑版本.可以看到图 2b中的一个射线对,从x0=1000 m,y0=1000 m,z0=500 m处,向上出射到Z=0 m的观测面,出射信息为Sx=560 m,Sy=550 m,Rx=820 m,Ry=740 m,Psx=-0.00011,Psy=-0.00015,Prx=0.00024,Pry=0.00009.我们选择了具有代表性的12对数据分量与模型分量展示其敏感度关系.这里的速度扰动是设置于炮点一侧的射线路径中间,其扰动幅度为15%.图 3展示了炮点一侧的P参数X分量Psx对v,x0,Θs,øs、 炮点X坐标Sx对v,x0,Θs,øs; 炮点一侧射线的走时Ts对v,x0,Θs,øs的敏感度分析图.在立体层析中,炮点和检波点具有互易性,因此所有的敏感度信息都适用于检波点的情形.同时所有X坐标的敏感度信息亦可以类比Y坐标和Z坐标的情形.因此更多的对比就不在正文中展现.图中蓝色线代表二者的变化关系,可以看到数据空间各分量对模型空间各分量有着良好的联动关系.绿色线为直线,代表在模型空间某点中,应用我们推导的扰动关系式(16)—(20)计算出的偏导数信息.可以看出绿色线和蓝色线在该点有很好的相切,代表前面推导的扰动关系正确无误.
|
图 2 在三维理论模型数据中测试三维立体层析所需的敏感度关系 (a)原始多层盐丘模型;(b)将图a所示模型光滑之后作为射线追踪初始模型. Fig. 2 Modeling of a single ray-pair for sensitivity test in a smooth synthetic multi-layer dome-like model (a)A true multi-layer dome model;(b)A smoothed model based on the model shown in Fig. 2a. |
|
图 3 数据空间炮点一侧分量对模型空间炮点一侧分量 δ(Ts,Sx,Psx)/δ(v,Θs,øs,x0) 敏感度分析 (a) Psx/v; (b)Sx/v;(c)ts/v;(d) Psx/Θs; (e) Sx/Θs; (f) ts/Θs;(g) Psx/s; (h) Sx/s; (i) ts/s; (j) Psx/x0; (k) Sx/x0; (l) ts/x0. Fig. 3 The sensitivity test of the Frechet derivatives for some selected data components(Ts,Sx,Psx)and some selected model components(v,Θs,øs,x0)of the 3D stereotomography |
三维立体层析矩阵相比二维情形显然更为稀疏,需要更强的规则化项保证方程能够收敛到一个合理的解.作者认为射线类层析反演方法通常用于偏移速度建模的阶段.在这个阶段,光滑性约束依然不失为一个重要的考量.在计算FRECHET偏导数的过程中,傍轴射线追踪本身就要求速度至少二阶可导.综合考虑各种光滑规则化项,本文采取了一种联合约束的策略:对速度场的二阶梯度求极小值作为一个约束项,对速度场的纵向光滑和横向光滑则作为另外两个约束项综合施加在误差泛函上.这种联合规则化项在实践中证明效果良好.考虑规则化项的、二范数意义下的三维立体层析反演可以归结为如下泛函的求极值问题:

|
(21) |
其中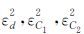
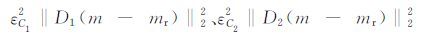
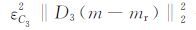
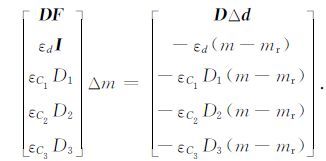
|
(22) |
本文利用最新的最小二乘QR(QR分解即将一个矩阵分解为一个正交阵Q与一个上三角阵R的乘积)方法(LSQR)(Paige and Saunders,1982)求解(22)式所示的矩阵方程组,该方法是一种迭代方法,可以在最小二乘意义下高效地求解大规模稀疏矩阵.
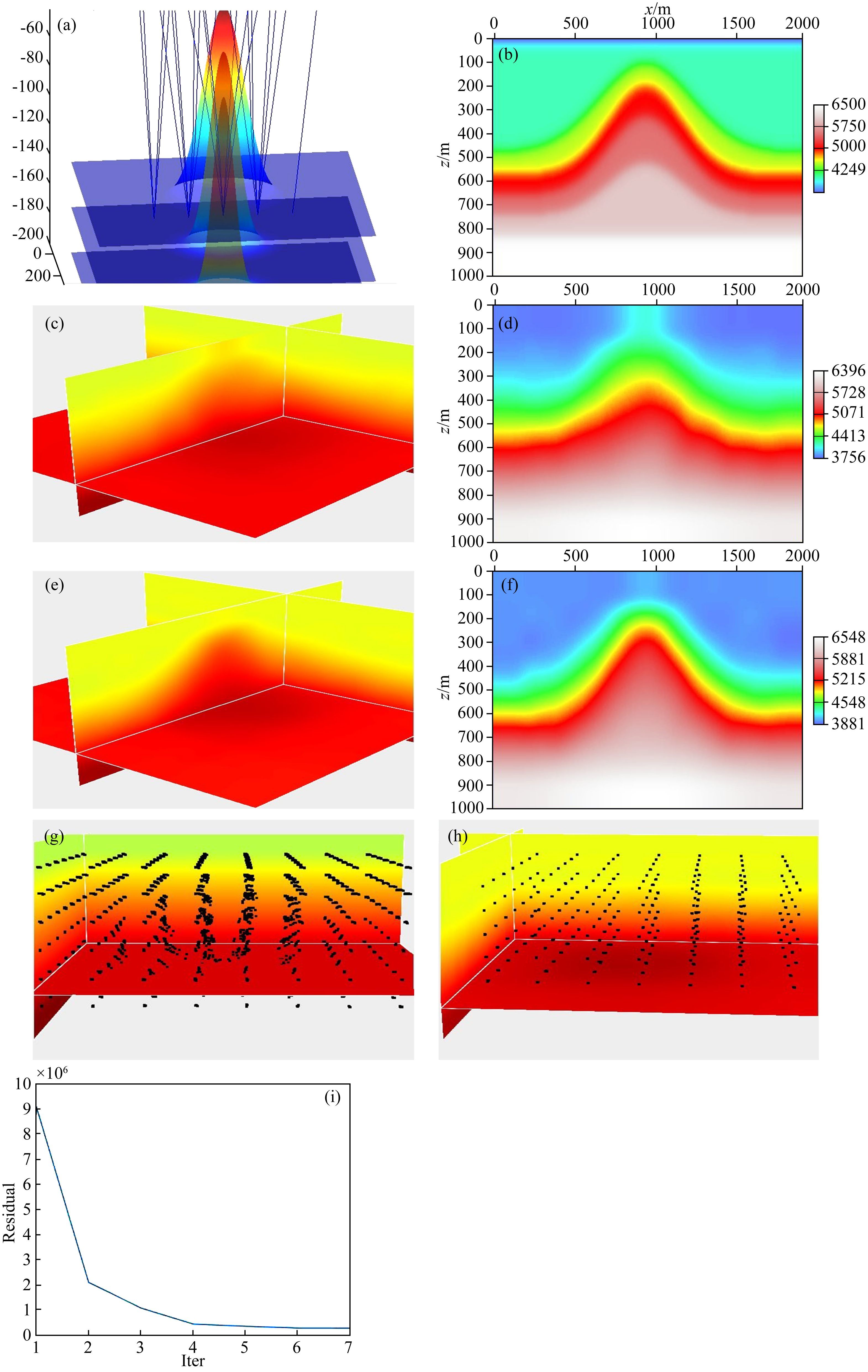
9 三维理论数据反演测试 9.1 实验一——反射点均匀分布透射实验实验一在如图 4a所示的盐丘光滑速度模型中进行.为了验证立体层析反演对强非均质性模型的适应能力,利用射线追踪为立体层析反演提供理想的数据输入.初始给定为梯度速度模型.输入数据分量与初始模型分量,便可开始立体层析的模型迭代更新过程.图 4(c,d)为第1次迭代更新后的速度场,可以看出,表层的速度得到了有效修改.随着迭代次数的增加,速度模型逐渐收敛,迭代8次后的速度模型如图 4(e,f)所示,地下盐丘的形状得到了较好的恢复.迭代8次后误差泛函下降缓慢,说明泛函的下降已接近极值处.迭代8次后的射线出射位置如图 4(g,h)所示,可以看见原本散乱分布的射线出射位置已经收敛到非常接近真实的射线出射点位置.从图 4i所示的目标泛函下降曲线中可看出迭代到第7,8轮时其残差已接近于0,证明了反演的正确性.
|
图 4 基于理论数据1的三维立体层析反演测试 (a)原始三维盐丘速度与射线联合显示;(b)原始盐丘速度模型切面(nx=101处);(c)第一次迭代后速度模型;(d)第一次迭代后速度模型切片显示;(e)第8次迭代后速度模型;(f)第8次迭代后速度模型切片显示;(g)第一次迭代后的模型空间反射点;(h)第八次迭代后的模型空间反射点;(i)目标泛函在迭代过程中的下降曲线. Fig. 4 The numerical test 1 with the 3D stereo-tomography algorithm presented in this paper (a)A joint display of true model and some simulated rays;(b)Depth slice through the true model(nx=101);(c)Inverted model after first iteration;(d)Depth slice through the inverted model(nx=101)after first iteration;(e)Inverted model after 8th iteration;(f)Depth slice through the inverted model(nx=101)after 8th iteration;(g)The reflector positions after first iteration;(h)The reflector positions after |
实验二沿用实验一的五层盐丘速度模型,横向、纵向网格数与网格间距均保持不变.同样使用射线正演数据作为数据空间,不同的是,把射线正演的出射点设在五层盐丘的层位上,绕着盐丘各层的法向方向出射(图 5a),这样更符合实际情况的反射点分布.注意对每个正演得到的数据点信息 (Sx,Sy,Rx,Ry,Tsr,Psx,Psy,Prx,Pry), 利用初始速度模型,从炮点(或检波点)出发,向地下作运动学射线追踪,仅用1/2走时就停下,即可得到该数据点所对应的初始模型参数(x0,y0,z0,θs,øs,θr,ør).这样便完成了对所有模型分量的初始化.
|
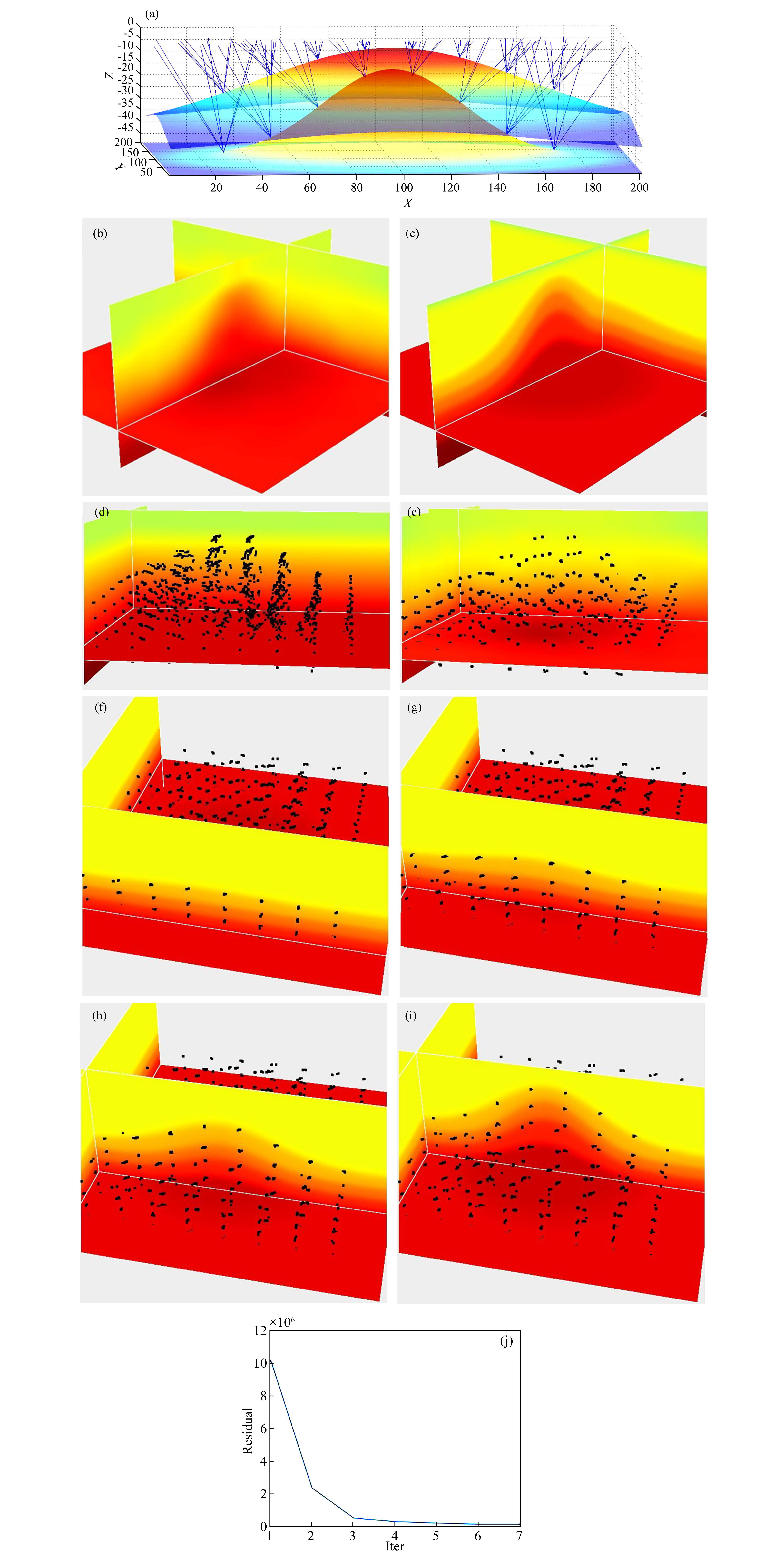
图 5 基于理论数据2的三维立体层析反演测试 (a)原始盐丘速度模型射线界面出射三维显示示意图;(b)第11次迭代后速度模型三维显示;(c)原始盐丘速度模型三维显示;(d)初始化后的射线出射点位置;(e)第11次迭代后的射线出射点位置;(f)迭代11次后第4层到第6层的射线出射点位置与真实层位贴合显示;(g)迭代11次后第3层到第6层的射线出射点位置与真实层位贴合显示;(h)迭代11次后第2层到第6层的射线出射点位置与真实层位贴合显示;(i)迭代11次后第1层到第6层的射线出射点位置与真实层位贴合显示;(j)目标泛函在迭代过程中的下降曲线. Fig. 5 The numerical test 2 with the 3D stereo-tomography algorithm presented in this paper (a)A joint display of true model and some simulated rays;(b)A 3D display of inverted model after 11st iteration;(c)A 3D display of true model;(d)The initialized ray starting position;(e)The ray starting points in inverted model after 8th iteration;(f)A joint display of ray starting points and the true position of interface(only for interfaces 4~6)after 11th iteration;(g)A joint display of ray starting points and the true position of interface(only for interfaces 3~6)after 11th iteration;(h)A joint display of ray starting points and the true position of interface(only for interfaces 2~6)after 11th iteration;(g)A joint display of ray starting points and the true position of interface(for all interfaces 1~6)after 11th iteration;(i)The decline of the cost function during the iterations. |
初始模型空间得到后,便可以从初始反射点位置出发,基于初始方位角与张角信息分别向炮点和检波点做运动学射线追踪,得到观测面上的三维立体层析数据分量,同时利用公式(16)计算Fréchet导数并建立层析方程组.对该方程组求解可以得到模型更新量.本次实验中采用的规则化因子分别为 εd=0.002 , εC1=0.02 , εC2=0.02 , εC2=0.01. 在迭代过程中也尝试了通过逐步下降规则化因子的方式,争取在保证反演稳定的同时恢复更多的模型细节.但规则化因子也不能下降到太小,太小可能会导致反演再次出现不稳定.
实验二再次证明了本文推导的三维立体层析算法的稳定性.图 5b是11次迭代后的速度模型结果,与图 5c所示原始模型比对有很好的相似度.图 5(d,e)分别显示了初始化模型空间射线出射点位置和迭代11次之后的射线出射点位置,可以看出射线出射点位置有很好的收敛.图 5(f—i)显示了迭代11次后、不同深度的射线出射点位置,按照从浅到深的顺序与真实模型的射线出射点位置的贴合对比.可以看出从浅到深反射点位置都基本归位,再次说明了三维立体层析反演对于强非均质性模型也具有很好的适应性.从图 5j所示的目标泛函下降曲线中同样也可看出迭代到最后时残差已非常小,也可证明反演的正确性.
9.3 规则化因子在反演中的作用
为了测试第5前两节中的三个约束项
ε2C1‖D1(m-mr)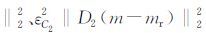

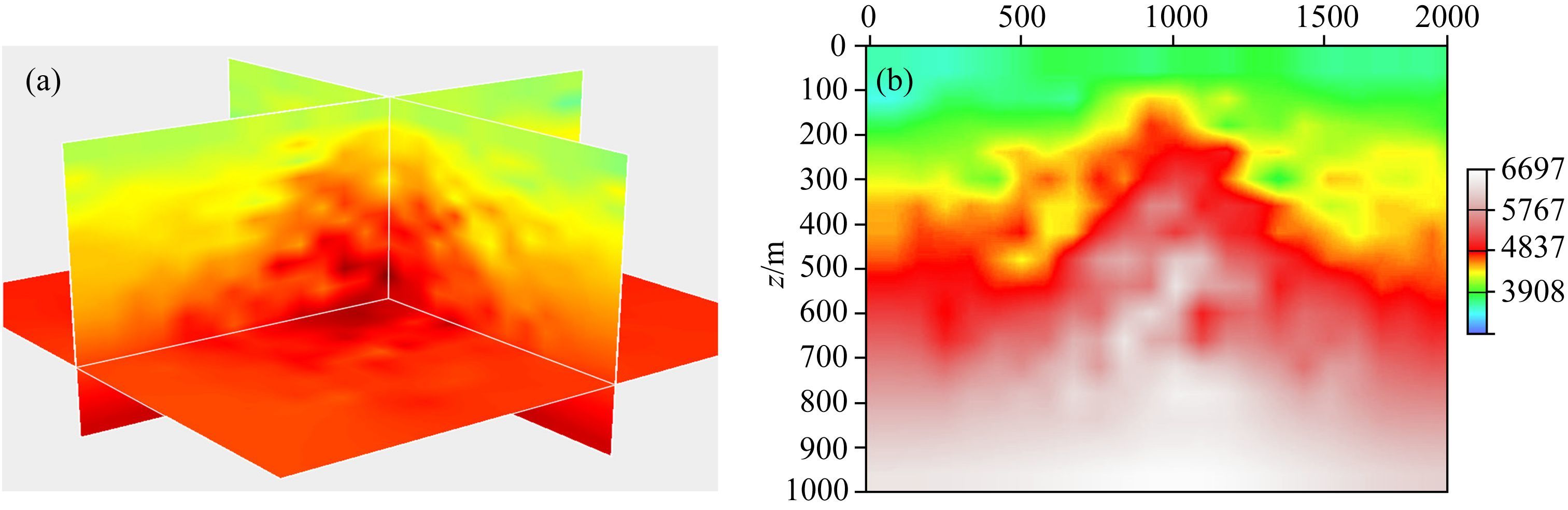
|
图 6 规则化因子对反演收敛性的影响分析 (a)无纵横向平滑因子的第8次迭代后速度模型;(b)无纵横向平滑因子的第8次迭代后速度切片显示. Fig. 6 The impact of regularization factors on the convergence of inversion (a)No any smoothing regularization factors applied on the cost function;(b)The depth slice through the model in Fig. 6a(nx=101). |
不同于前人在射线中心坐标系下基于降阶汉密尔顿算子建立三维立体层析矩阵,本文在三维直角坐标系下基于非降阶汉密尔顿算子,通过射线扰动理论导出了三维立体层析反演所需的数据空间对模型空间的一阶线性关系,进而建立三维立体层析矩阵方程.并结合合理的规则化手段以保证迭代收敛的稳定性.基于两个射线正演的无噪声理论数据验证了上述所有理论推演的正确性,为后续的三维立体层析应用奠定了理论基础.
致谢作者感谢国家自然科学基金面上项目(41274117, 41574098)对于本研究的支持.
| Audebert F, Froidevaux P, Rakotoarisoa H, et al. 2002. Insights into migration in the angle domain.//72th SEG Expanded Abstracts, 1188-1191. | |
| Billette F, Lambaré G. 1998. Velocity macro-model estimation from seismic reflection data by stereotomography. Geophysical Journal International. , 135 (2) : 671-690. DOI:10.1046/j.1365-246X.1998.00632.x | |
| Cerveny V. Seismic Ray theory. Cambridge: Cambridge University Press, 2001 . | |
| Chalard E, Podvin P, Lambaré G, et al. 2000. Estimation of velocity macro-models by 3D stereotomography.//70th SEG Expanded Abstracts, 2257-2260. | |
| Chalard E, Lambaré G. 2005. Status of 3D stereotomographic optimization.//75th SEG Expanded Abstracts, 2593-2596. | |
| Farra V, Madariaga R. 1987. Seismic waveform modeling in heterogeneous media by ray perturbation theory. J. Geophys. Res. , 92 (B3) : 2697-2712. DOI:10.1029/JB092iB03p02697 | |
| Gilbert F, Backus G E. 1966. Propagator matrices in elastic wave and vibration problems. Geophysics , 31 (2) : 326-332. DOI:10.1190/1.1439771 | |
| Li Z W, Yang K, Ni Y, et al. 2014. Migration velocity analysis with stereo-tomography inversion. Geophysical Prospecting for Petroleum (in Chinese) , 53 (4) : 444-452. | |
| Li Z W, Yang K, Xiong K, et al. 2015. Towards an edge-preserving stereotomography with a practical model regularization technique.//77th EAGE Conference & Exhibition. EAGE. | |
| Ni Y, Yang K. 2012. Slope tomography assisted by finite-frequency sensitivity kernel.//82th SEG Expanded Abstract. SEG, 1-5. | |
| Ni Y, Yang K, Chen B S. 2013. Stereotomography inversionmethod theory and application testing. Geophysical Prospecting for Petroleum (in Chinese) , 52 (2) : 121-130. | |
| Ni Y, Li Z W, Wang L X, et al. 2014. The preliminary practice of stereotomography.//The expanded abstract of the CPS/SEG Beijing 2014 International Geophysical Conference (in Chinese). | |
| Paige C C, Saunders M A. 1982. LSQR:An algorithm for sparse linear equations and sparse least squares. ACM Trans. Math. Softw. , 8 (1) : 43-71. DOI:10.1145/355984.355989 | |
| Prieux V, Lambaré G, Operto S, et al. 2013. Building starting models for full waveform inversion from wide-aperture data by stereotomography. Geophysical Prospecting , 61 (Suppl. 1) : 109-137. | |
| Ren L J, Sun X D, Li Z C. 2014. The stereotomography based on eigen-wave attributes.//The expanded abstract of the CPS/SEG Beijing 2International Geophysical Conference (in Chinese). | |
| Tarantola A. Inverse Problem Theory:Methods for Data Fitting and Model Parameter Estimation. Amsterdam: Elsevier, 1987 . | |
| Wang Y X, Yang K, Yang X C, et al. 2016. A high-density stereo-tomography method based on the gradient square structure tensors algorithm. Chinese J. Geophys. (in Chinese) , 59 (1) : 263-276. DOI:10.6038/cjg20160122 | |
| 李振伟, 杨锴, 倪瑶, 等. 2014. 基于立体层析反演的偏移速度建模应用研究. 石油物探 , 53 (4) : 444–452. | |
| 倪瑶, 杨锴, 陈宝书. 2013. 立体层析反演方法理论分析与应用测试. 石油物探 , 52 (2) : 121–130. | |
| 倪瑶, 李振伟, 王立歆等. 2014. 立体层析反演的初步实践.//CPS/SEG北京2014国际地球物理会议摘要. | |
| 任丽娟, 孙小东, 李振春. 2014. 基于特征波属性参数的立体层析速度反演方法研究.//CPS/SEG北京2014国际地球物理会议摘要. | |
| 王宇翔, 杨锴, 杨小椿, 等. 2016. 基于梯度平方结构张量算法的高密度二维立体层析反演. 地球物理学报 , 59 (1) : 263–276. DOI:10.6038/cjg20160122 | |
 2016, Vol. 59
2016, Vol. 59

