2. 地球空间信息技术协同创新中心, 武汉 430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
星载加速度计数据包含了卫星在轨所受非保守力信息,通过分离太阳辐射光压(Solar Radiation Pressure,SRP)、地球反照辐射等其他非保守力后可以获得卫星所受的空气动力,进而可以用于热层密度反演.随着CHAMP、GRACE、GOCE等重力卫星计划的顺利实施,星载加速度计资料跨度可达一个太阳活动周期,这为研究热层密度提供了大量高精度、高时空分辨率的数据.Bruinsma和Biancale(2003),Bruinsma等(2004),Sutton等(2007),Doornbos等(2010),Doornbos(2012),汪宏波和赵长印(2009)研究了采用CHAMP、GRACE星载加速度计实测数据计算热层大气密度.这些成果极大地促进了热层密度对太阳耀斑、太阳风暴和地磁暴的响应(Bruinsma et al.,2006,2010; Lei et al.,2011; Liu et al.,2011; Sutton et al.,2005,2006)、热层大尺度行扰(Bruinsma et al.,2007a,Bruinsma and Forbes,2008,2009; Sutton et al.,2006)、太阳辐射变化等对热层密度的影响(Guo et al.,2007)、热层密度年内周期性变化(Guo et al.,2008)等方面的研究.
利用CHAMP、GRACE星载加速度计数据反演热层密度时首先要对加速度计数据进行校正.通常认为GFZ发布的CHAMP、GRACE卫星的加速度计数据在每个方向均存在尺度误差和偏差误差(Case et al.,2010).Gerlach等(2003),徐天河和杨元喜(2004)研究了采用能量守恒法进行加速度计校准,该方法通过能量守恒方程并采用现有重力场模型估计标校参数,但是严重依赖于先验重力场模型精度.Helleputte等(2008,2009)在精密定轨(Precise Orbit Determination,POD)过程中以加速度计数据代替非保守力,通过估计加速度计标校参数实现对CHAMP和GRACE卫星加速度计数据的校正.其认为如果加速度计校正参数精确确定,则联合高精度的保守力模型以及校正后的加速度计数据进行轨道积分后得到的轨道应接近于“真实轨道”,因此加速度计校正的好坏可以通过轨道精度来体现.由于采用该校正方法时尺度参数与偏差参数强反相关,van Helleputte等(2009)对尺度和偏差因子引入了强约束,另外为了补偿力学模型误差还估计了经验力参数.结果表明该方法定轨结果与JPL精密科学轨道(Precision Scientific Orbit,PSO)相比三维RMS(Root Mean Square)为3.5 cm,SLR检核RMS为2.3 cm,且将尺度因子固定为常数时可估计获得更为平滑的偏差序列.熊永清等(2011a)提出了利用CHAMP卫星精密轨道数据作为伪观测数据,通过轨道拟合的方式估计卫星初始状态向量和加速度计参数.该方法能够避免处理GPS数据的复杂性.为消弱尺度因子和线性偏差的相关性,熊永清等(2011b)在以上方法基础上联合多个单天法方程进行二次校标,其多天只解算一组共同的尺度因子,而线性偏差每个单天解算一组.
卫星空气动力系数CA也是限制反演精度的重要因素之一.CA通常与卫星的几何形状、表面材质物理性质(对大气粒子的吸附、反射或其他交互作用性质)以及大气状态,如:大气温度,大气中各种成分的浓度等因素有关,其可通过Cook模型(Cook 1965)、Sentman稀薄空气动力学方程(Sentman,1961)等模型进行计算.Cook模型中忽略了粒子随机热运动对卫星的作用.Koppenwallner(2008),Sutton(2009)的分析表明,对于CHAMP、GRACE这类卫星,其与气流方向平行的侧面面板较为细长,大气粒子的热运动会导致CA显著增大.因此这种情况下采用Cook模型计算的空气动力系数偏低,会导致反演得到的热层密度系统性偏大.Sentman方程(Sentman,1961)考虑了入射粒子的不规则热运动,并假设反射粒子全漫反射分布,被认为是目前适合用于计算CHAMP、GRACE卫星CA系数的模型(Sutton 2009).由于低轨卫星在轨飞行中,卫星表面会吸附一层氧原子,从而改变了卫星表面材料对大气粒子吸附、反射等性质,Moe等(2004,2005)在Sentman方程基础上引入能量调节系数α.能量调节系数决定了粒子是否保持其平均热能(α=0)或者获得卫星的表面温度(α=1),对CA有显著影响.考虑到大气中各种成分对CA的贡献是非线性的,Doornbos(2012)在其研究中分别计算各种大气成分对CA的影响并最终取其浓度加权平均值.
Bruinsma等(2003,2004)最早采用CHAMP卫星加速度计数据研究热层密度反演,其将校正后的加速度计数据扣除SRP等其他非保守力后得到“大气阻力观测值”,以该阻力观测值和由经验模型密度计算的阻力的比值作为尺度因子,对模型密度进行改正从而得到了“观测密度”.在此基础上,Bruinsma等(2004)分析了由太阳、地磁活动以及潮汐引起的热层密度变化.Sutton等(2007)则系统研究了利用CHAMP、GRACE加速度数据反演热层密度的方法,利用校正后的星固系X轴和Y轴加速度计数据解算热层密度和大气风速,并分析了加速度计校准误差、大气阻力/升力系数误差、先验风速模型误差、SRP误差等对反演结果精度的影响,其结果表明反演密度误差一般小于15%,但是在地磁活动剧烈期间会由于大气风速误差增加而增至30%.Doornbos(2012)在以上研究基础上,利用Angara软件对卫星表面力进行精化建模,并分析了多种密度反演方式.国内汪宏波和赵长印(2008)处理了CHAMP卫星2001年至2002年星载加速度计数据,并反演得到了沿轨热层密度.其利用反演密度对经验大气模型DTM94和MSIS90的精度进行了检核,结果表明在太阳活动峰年DTM94模型误差为30%~35%,MSIS90模型为25%~30%(汪宏波和赵长印,2008).
上述研究中,Bruinsma等(2003,2004),Sutton等(2007),汪宏波和赵长印(2008)采用单天估计一组偏差和尺度因子的策略进行加速度计校正.然而,根据van Helleputte等(2008,2009)的结果,利用该策略校正的加速度计数据进行轨道积分的精度仅在10 cm水平,表明其标校精度相对较低.Doornbos(2012)根据van Helleputte等(2009)的研究结果进行加速度计校正,其校正时为了补偿保守力模型误差每600 s估计一组切向、法向和径向经验力参数.然而,频繁调节的经验力参数同时还会吸收部分非保守力,从而导致校正参数可能出现偏差.Bruinsma等(2003,2004),汪宏波和赵长印(2008)在其研究中均采用Cook模型计算CHAMP卫星空气动力系数,这可能导致其反演的密度偏大.
本文在以上基础上研究了利用GRACE星载加速度计数据进行热层密度反演.在反演中,采用了与Van Helleputte等(2009)相同的方式对GRACE卫星加速度计进行标校,但是本文在不引入经验力参数的前提下,通过调整定轨中的动力学策略,达到了与前者一致的轨道精度水平,同时也保证了标校参数的完整性.通过与已有结果和模型的比较,对本文反演密度的精度进行了评价.
2 数据源与模型本文选择GRACE卫星2007—2009年L1b级的数据进行处理,其包括星载GPS数据(GPS),加速度计数据(ACC),姿态四元数数据(SCA),卫星质量数据(MAS),卫星机动数据(THR)等.数据的具体说明可参见文献(Case et al.,2010).在进行加速度标校时,本文采用IGS提供的最终GPS精密星历和30 s采样率钟差产品作为数据处理的时空基准,其轨道、钟差精度分别在2.5 cm(1D RMS)和75 ps(RMS)量级(http://igs.org/products).反演过程中,卫星姿态通过恒星照相仪SCA数据计算,卫星在轨质量通过MAS数据获取.为维持KBR仪器相互对准,GRACE卫星在轨运行时经常需要进行机动调整,由此引入的机动力需在反演时扣除,否则会引起密度反演误差.本文在处理时则依据THR数据剔除了机动时期的数据.
为了对反演密度的精度进行评价,本文将处理结果与Doornbos、Sutton博士反演的结果进行了比较.Doornbos、Sutton博士的数据成果均可以在线公开获取,其具体的处理方法与策略可以参考Sutton等(2007)与Doornbos(2012).同时还对比了经验密度模型,包括:NRLMSISE00模型(Picone et al.,2002)和HASDM模型(Bowman and Storz,2003).其中,NRLMSISE00模型由美国海军实验室在MSISE系列经验密度模型的基础上进行改进得到,是目前低轨空间物体轨道确定和预报,以及热层-电离层耦合等空间天气研究中常用的经验模型.其误差一般在10%~30%且随高度增加而增大,在400~500 km高度处约在25%水平(Macros et al.,2006).HASDM模型则由美国空军研究中心开发,其使用75~80个低轨空间物体的雷达跟踪数据在确定轨道的同时估计大气密度的改正值,并以球谐函数的形式每3 h估计一次Jacchia71模型中的拐点温度和夜间散逸层最低温度(Bowman and Storz,2003).HASDM模型在200~800 km高度范围的精度可达6%~8%(Storz et al.,2005).
3 加速度计校正 3.1 联合GPS与加速度计数据的校正方法GRACE卫星上搭载的SuperSTAR星载加速度计能以极高的精度测量卫星所受到的非保守力.SuperSTAR的X、Y轴(指向星固系下的Z、X轴)是高敏感轴,而Z轴(指向星固系Y轴)为低敏感轴,三轴的测量精度都认为可以达到10-9 m·s-2(Frommknecht et al.,2003).然而由于星上温度变化,仪器老化以及仪器开关切换等原因,会导致加速度计测量的加速度数据包含了偏差和尺度变化.因此在使用加速度计数据时,首先要对其进行校准.由于大气阻力的作用,切向的加速度计校正参数比较容易准确确定.法向与径向的尺度与偏差参数与卫星的初始状态向量强相关,且法向是约束最弱的方向(van Helleputte et al.,2008).
GRACE卫星搭载的GPS接收机能够提供大量连续的高精度观测数据,本文联合星载GPS和加速度计数据进行动力学定轨,并同时估计加速度计校正参数.定轨中动力学模型策略主要参照GFZ最新发布的Level 2数据处理标准0005版本(Dahle et al.,2012)并进行了一定调整.保守力方面选择精度尽量高的模型,其中地球非球形引力摄动采用EIGEN-6C模型计算,且静态重力场截至130阶,时变部分则截至50阶,海潮模型采用FES2004模型并截至40阶,固体潮、极潮、相对论等其他保守力则均采用IERS Conventions(2003)的推荐模型(McCarthy and Petit,2004).非保守力模型则以加速度计数据替代.在使用加速度计数据时,先由GFZ发布的初始校正参数(Bettadpur,2004)进行预校正,然后在定轨过程中同时估计X、Y、Z三方向的偏差参数,尺度参数则不予估计.这样处理实际上是将尺度因子固定为常数,而仅估计偏差因子.其原因是一方面GRACE卫星星上温度控制较为稳定,其尺度参数可以认为是常数而不随时间变化(Bruinsma et al.,2007);另一方面,由于偏差参数和尺度参数强相关,估计的偏差参数会补偿尺度参数先验值的误差.Bezděk(2010),熊永清等(2011b)的研究中也表明了这一现象.偏差参数一般采用分段常数模型估计.本文测试了多组不同分段间隔情况下定轨的精度,发现估计间隔为60 min时轨道精度最佳,因此采用每60 min估计一组偏差参数的策略.这也与GFZ的数据处理标准(Dahle et al.,2012)中的策略一致.对于GPS观测值,采用无电离层组合伪距(PC)和无电离层组合相位(LC)作为基本观测模型,观测误差主要考虑GRACE和GPS卫星天线相位偏心(phase center offset,PCO)以及GPS卫星天线相位中心变化(phase center variation,PCV)、相对论效应、相位缠绕误差等.模糊度参数未进行固定,而是直接采用浮点解.具体的数据处理策略见表 1.
|
|
表 1 利用GRACE星载GPS和加速度计数据进行精密定轨 Table 1 Data processing strategy for POD and accelerometer data calibration using GPS observations and accelerometer data |
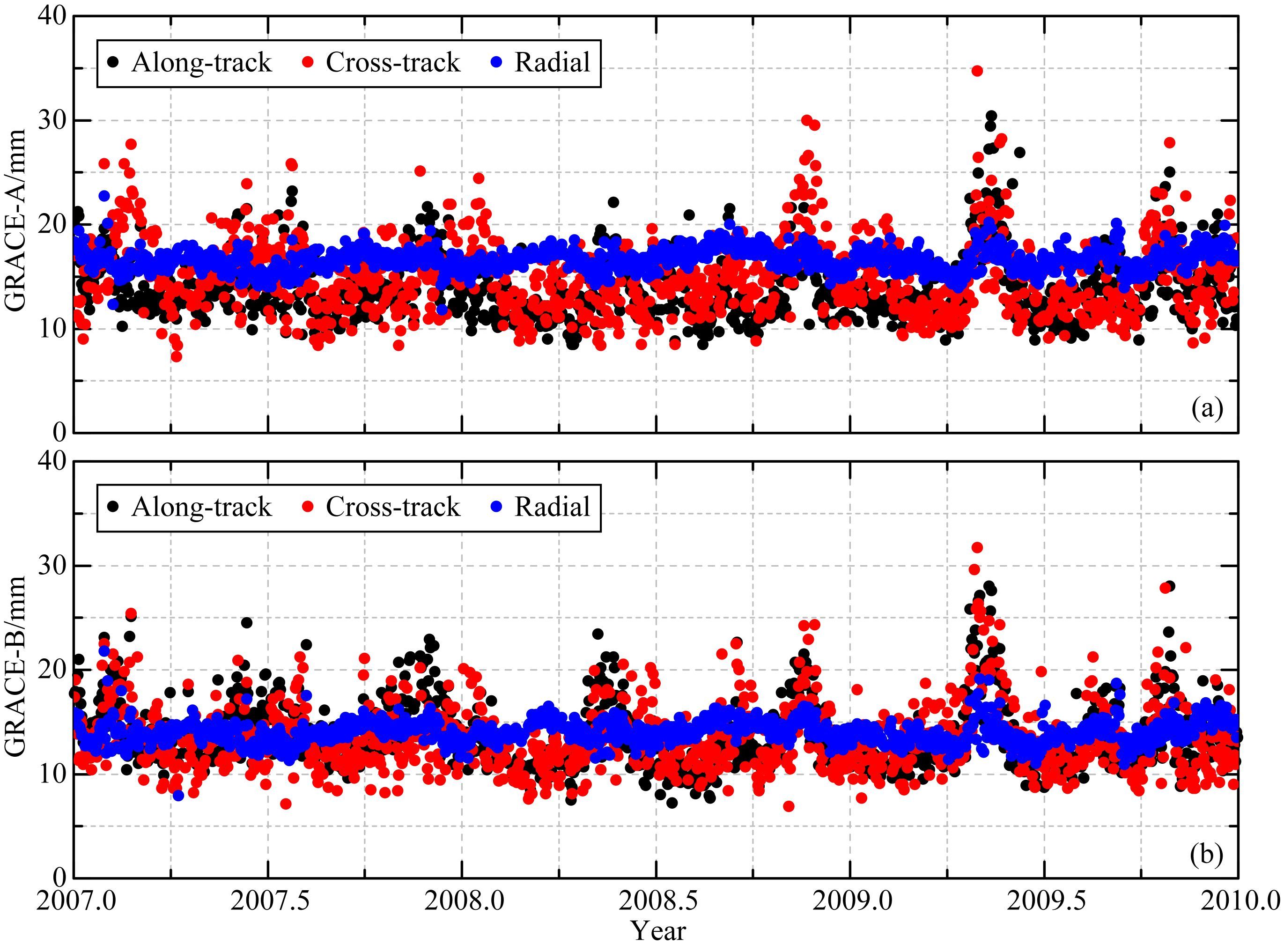
如前所述,利用校正后的加速度计数据结合保守力模型进行轨道积分,所得轨道的精度可以反映加速度计校正的精度.依据表 1中的数据处理策略,对GRACE卫星2007—2009年数据进行精密定轨处理,并将解算轨道与JPL PSO比较,统计每个定轨弧段的轨道差值RMS,其时序图见图 1.由图中可见,以JPL PSO为参考轨道,本文解算的GRACE-A/B卫星轨道在切向(Along-track)与法向(Cross-track)的RMS均主要在1.0~2.0 cm范围变化,而径向(Radial)RMS序列变化相对较为稳定,对于GRACE-A、B星均在1.5 cm左右变化.表 2为三方向轨道差值的平均RMS,其中径向平均RMS较法向与切向均略差,这可能是由于JPL PSO对GRACE卫星的天线PCV进行了改正,而本文并未考虑该影响.GRACE-A,B卫星三年轨道差值的平均3D RMS分别为2.6 cm和2.3 cm.
|
图 1 2007—2009年GRACE-A/B卫星与JPL PSO轨道比较的RMS序列 Fig. 1 RMS series of orbit differences with respect to the JPL PSO during 2007—2009 |
|
|
表 2 GRACE-A/B卫星与JPL PSO轨道比较的平均RMS统计 Table 2 RMS statistics of orbit differences of the GRACE-A/B satellite orbits w.r.t. JPL PSO orbits |
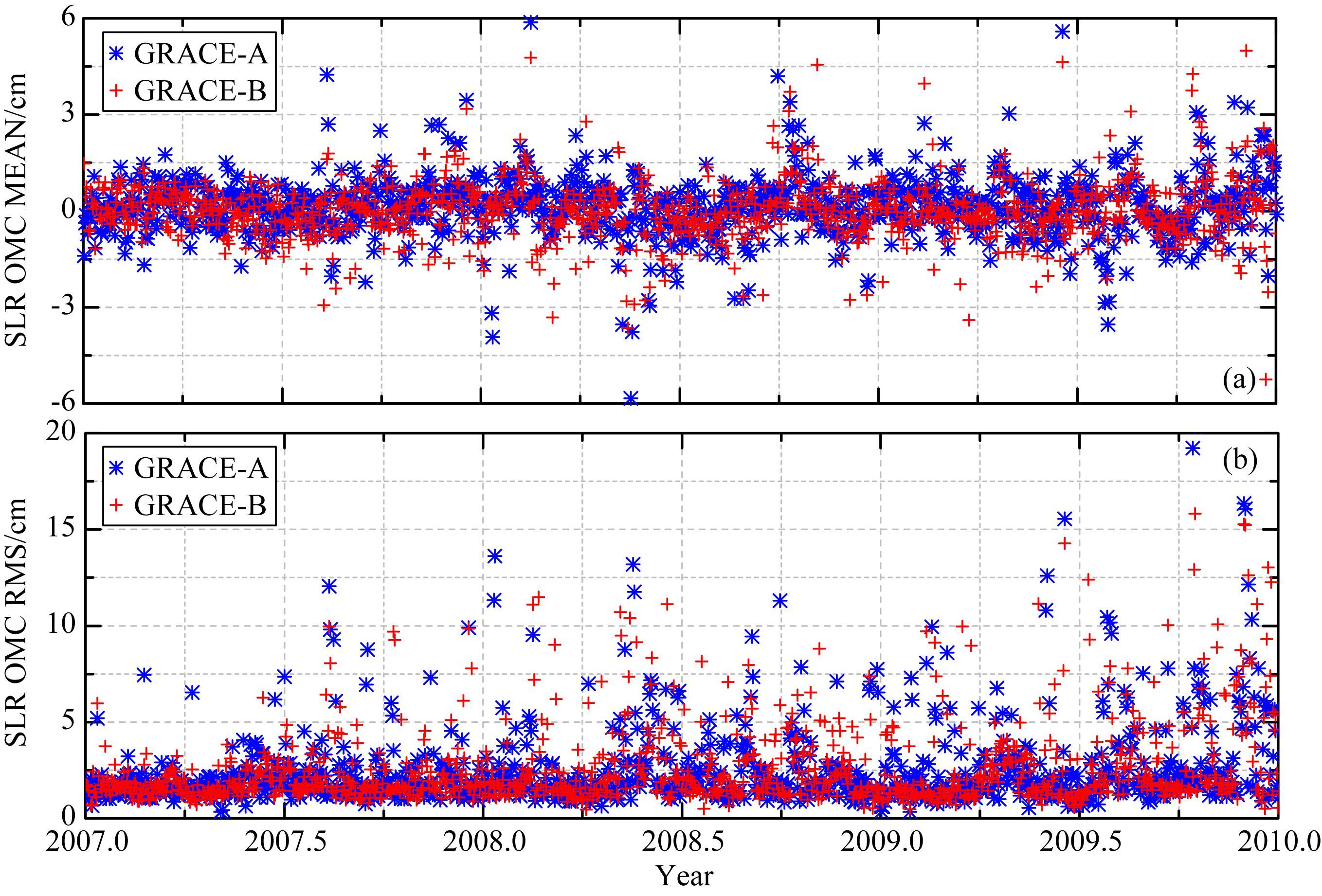
SLR技术常作为外部检核的方式用于轨道精度评价.采用NPT格式SLR数据对本文解算的GRACE卫星轨道进行检核,统计每个弧段SLR观测值残差(Observed Minus Computed,OMC)的平均值与标准差.统计时剔除高度角小于10°以及OMC绝对值大于50 cm的观测值,最终所有剔除的观测值约占总观测数量的2.5%,所有弧段的SLR OMC平均值与标准差时间序列见图 2.可见OMC平均值主要在±3 cm以内变化,未见明显系统偏差.标准差(Standard Deviation,STD)则均主要在5 cm以内.表 3为所有弧段SLR OMC平均值,STD和RMS的均值.同时对这三年JPL PSO轨道进行了SLR检核和精度统计.对比可见,SLR检核本文轨道的残差平均值均小于2 mm,JPL PSO则存在约1 cm的系统偏差.二者SLR检核RMS均在2.5 cm水平.
|
图 2 2007—2009年GRACE-A/B卫星SLR残差平均值(a)与标准差(b)序列 Fig. 2 The mean,STD series of the SLR OMC of GRACE-A/B satellites during 2007—2009 |
|
|
表 3 本文解算的GRACE-A/B卫星轨道以及JPL PSO轨道的SLR检核精度统计 Table 3 Mean,STD,RMS statistics of the calculated GRACE-A/B orbits from this paper and the JPL PSO |
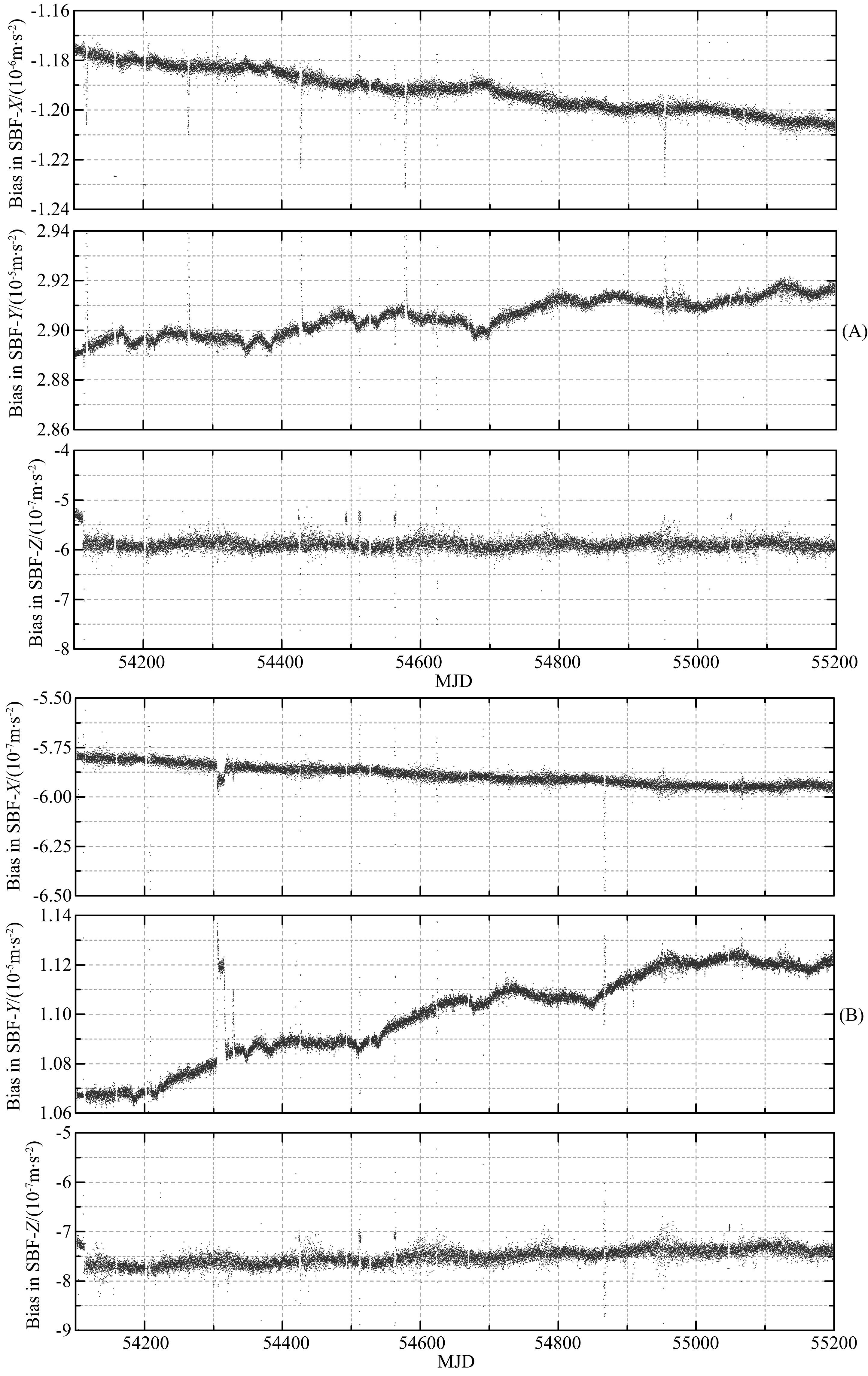
图 3为2007—2009年间GRACE-A和GRACE-B卫星加速度计偏差参数在星固系X,Y,Z方向的偏差时间序列.图中个别弧段估计得到的偏差出现明显跳变,其与卫星控制器切换以及卫星温度突变等原因相关(Bruinsma et al.,2007; Doornbos,2012).对于GRACE双星而言三个方向的偏差参数变化都非常平缓,且存在随时间的缓慢飘移,其主要由加速度计的老化导致,这也与Bruinsma等(2007)的结果一致.根据估计的偏差时序,对于GRACE-A/B卫星其在X方向偏差参数的年均变化分别仅为1×10-8 m·s-2和5×10-9 m·s-2.而在Y方向的偏差参数年均变化相比X方向明显较大,分别为9×10-8 m·s-2和1.84×10-7 m·s-2.
|
图 3 GRACE-A/B卫星2007—2009年加速度计偏差序列 (A)GRACE-A卫星;(B)GRACE-B卫星 Fig. 3 Time series of estimated bias parameters of GRACE-A/B satellites (A)GRACE-A satellite;(B)GRACE-B satellite |
本节介绍了利用X轴加速度计数据提取热层密度的基本方法,并分析了Cook模型和Sentman模型用于计算空气动力系数的差异,以及其他非保守力对反演的影响.基于这些分析,本节确定了密度反演的具体数据处理策略.
4.1 利用X轴加速度计数据反演热层密度 4.1.1 反演方法GRACE卫星在轨受到的非保守力主要包括空气动力、太阳辐射光压、地球反照辐射(Albedo)、地球长波辐射(IR,Infrared Radiation)等.其中,空气动力分为大气阻力与大气升力,大气阻力主要作用于沿轨方向,而大气升力则垂直于大气阻力方向.卫星所受到的总体空气动力r··a为所有面板的空气动力之和(Montenbruck and Gill,2000):

|
(1) |
式中, ρ 为大气密度,vr和 vr 分别为卫星与大气相对速度及其单位矢量,m为卫星质量,CA为整星总的空气动力系数,其在 vr 方向的分量一般称为阻力系数CD,垂直于 vr 方向的分量则称为升力系数CL,Aref这里是参考面积可以为任一给定正值, uL 方向为升力方向单位矢量,CD,i,CL,i系数分别为为面板i的大气阻力和升力系数.在计算时通常将每块面板CD,CL系数除以Aref 以使其无量纲.
GRACE卫星姿态相对稳定,其三轴旋转欧拉角较小一般在1°以内.由于大气阻力的作用,加速度计X轴分量信号强度大且校正精度较高(星固系X轴指向卫星沿轨方向),非常利于提取大气密度.利用校正后的加速度计数据扣除SRP等非保守力并投影至X轴方向,得到大气动力在X轴的分量aobs,X:
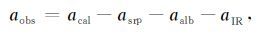
|
(2) |
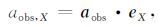
|
(3) |
其中,acal为校正后的加速度计数据(惯性系下),asrp为太阳辐射压力,aalb为地球反照辐射压力,aIR为地球红外辐射压力, eX 为惯性系转星固系旋转矩阵中X方向的单位向量.根据大气动力、热层密度和CA之间的函数关系(式1)反解热层密度:
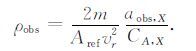
|
(4) |
由式(2)和(4)可知,利用校正后的加速度计数据反演密度时,需要对除空气动力外的其他非保守力进行准确建模和扣除,并准确计算卫星的空气动力系数.
4.1.2 空气动力系数模型CD,CL系数反映了卫星外表面与大气粒子之间的交互作用的强弱,并与卫星外表面材质物理特性以及大气粒子的成分等有关.精确确定CD,CL系数是目前反演热层密度的难点.由于CHAMP、GRACE这类卫星侧面面板较长,在Cook模型中被忽略的分子热运动会对其空气动力系数有较大影响.Sutton(2009)研究表明对于CHAMP卫星,相比采用Cook模型,采用Sentman方程后反演的热层密度与经验密度之间的标准差降低了约36%,偏差也由约56.4%~61.3%降低至21.2%~23.3%.
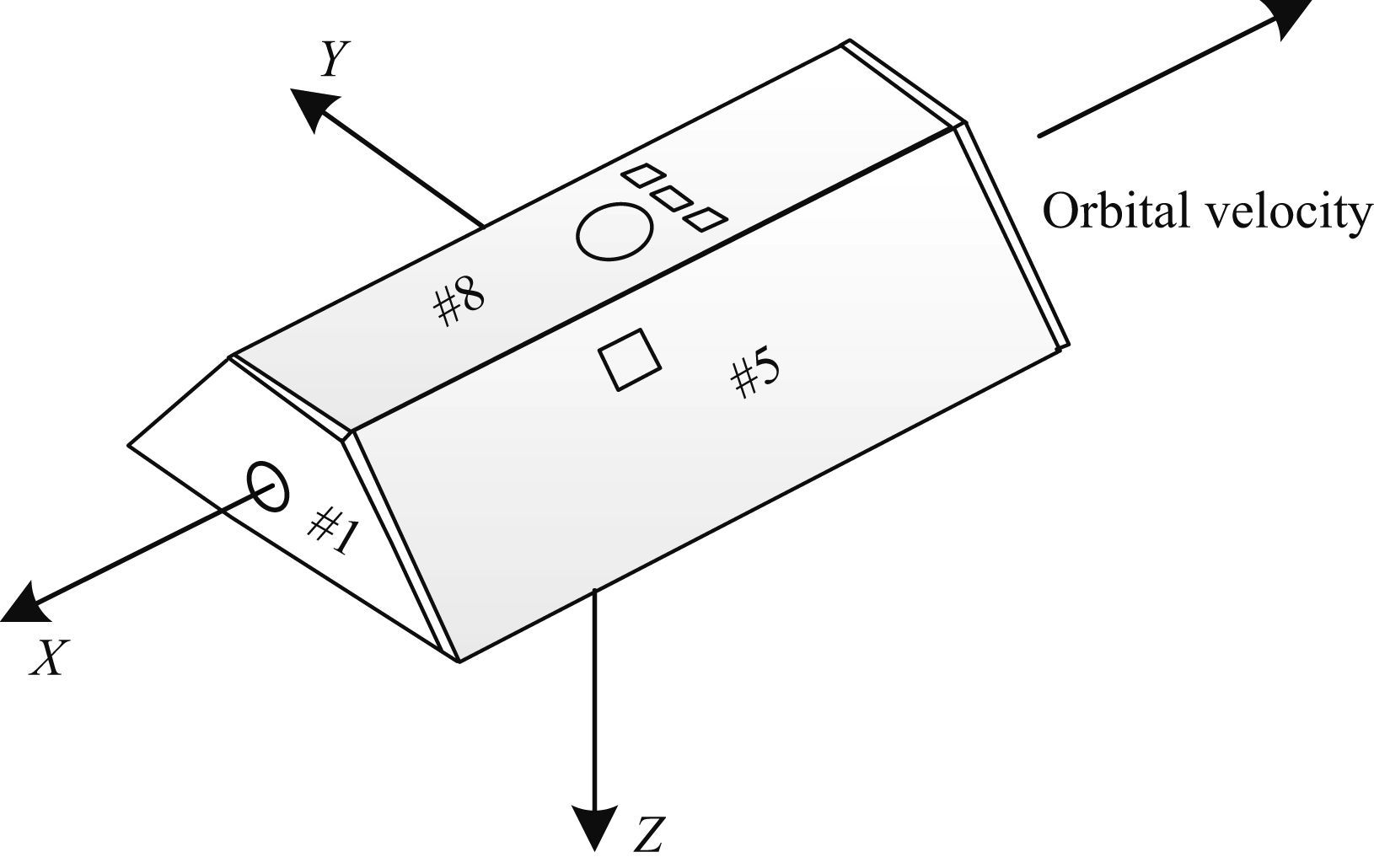
根据Bettadpur(2012)给出的GRACE卫星星体几何模型,图 4显示了GRACE-A卫星面板与星固系示意图.其中1,2号面板为卫星前后面,3,4,5和6号面板是卫星的侧面,7,8号分别为卫星底面和顶面,9号面板为卫星圆柱状底部的平面投影.对于9号面板因其法向方向不唯一(可沿卫星X-Y平面任意方向)且面积较小,故而未参与整星空气动力系数的计算.图 5为分别利用Sentman方程和Cook模型计算的GRACE-A卫星各个面板的CD系数.由图 4中可见,由于1,8号面板外法向与相对速度方向夹角θ>90°,因此在Cook模型中其CD系数始终为0.2号面板外法向正对大气气流方向(θ接近0°),其对卫星的空气动力系数贡献最大,Cook模型计算的结果与Sentman模型相差约为0.05.相差最大的面板为7号面板,Sentman模型计算的CD系数约高出Cook模型0.4~0.6,这是由于7号面板是GRACE卫星面积最大的面板,两种模型之间的差异通过面板面积被放大.对所有面板的空气动力系数求和,采用Cook模型和Sentman方程计算的整星空气动力系数分别为2.37和3.50,其差异可达32%(以Sentman模型结果为参考).
|
图 4 GRACE-A卫星面板与星固系示意图(Doornbos,2012) Fig. 4 Spacecraft body-fixed directions and panels of GRACE-A satellite |

|
图 5 GRACE-A卫星各面板大气阻力系数(α=0.93,2003年1月3日) Fig. 5 Drag coefficients of each panel of GRACE-A satellite based on Cook and Sentman models on 2003 Jan-3rd(fixed α=0.93) |
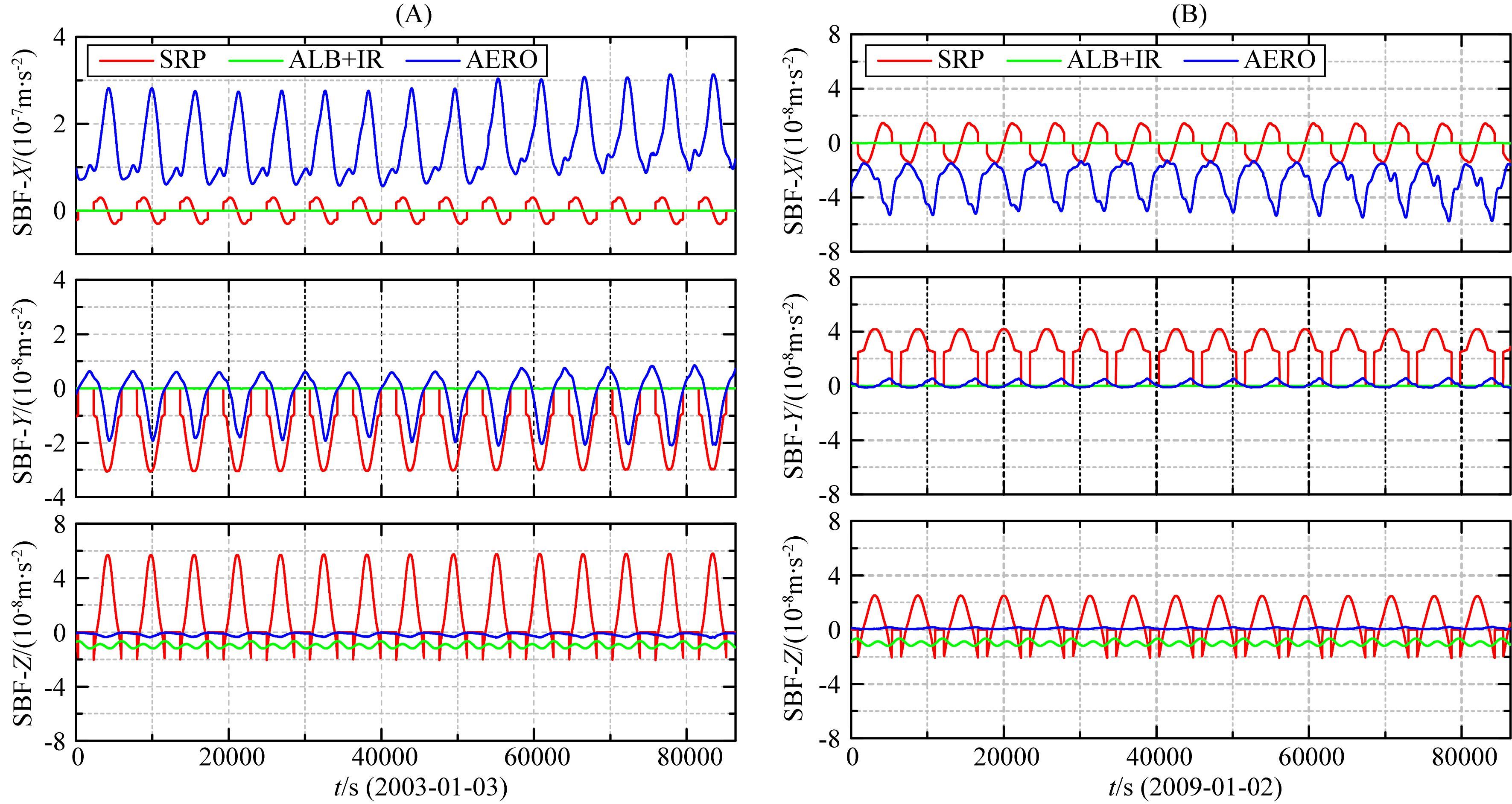
本文采用Box-wing模型计算SRP.地球反照辐射压力采用Bhanderi and Bak(2005)提出的模型计算,所需的地表反照辐射系数采用CERES网站提供的1°×1°格网分辨率的月平均地表反射系数,而地球长波辐射则参考Rim(1992)给出的经验模型.由于热层密度与太阳辐射强度相关,图 6分别给出了在太阳活动高年(2003年1月3日)和低年时期(2009年1月2日)GRACE-A卫星所受的太阳辐射压力(SRP),地球辐射压力(ALB+IR)以及空气动力(AERO)的比较.在热层反演中,最重要的是大气阻力在X轴方向的信号强度.图中可见,在太阳活动高年,由于热层密度较大,其所受大气阻力远大于太阳辐射压力,在X轴方向可以达到(0.8~3.2)×10-7 m·s-2,比太阳辐射压力高一个量级.而在太阳活动低年,大气阻力在X方向稍大于太阳辐射压力,二者均在10-8 m·s-2量级.并且图中可见在大气阻力X分量极小处,SRP的X分量与其大小几乎相等.因此,卫星所受SRP需要精确计算.而对于地球辐射压力,其量级通常较小在(1-2)×10-8m·s-2水平且主要作用于卫星径向(星固系Z轴方向),因此在实际反演计算中可以忽略.
|
图 6 不同太阳活动强度时期GRACE卫星空气动力与太阳辐射压力(A)、地球辐射压力(B)比较 Fig. 6 Comparison between aerodynamic,SRP and Earth radiation during different solar activity periods |
根据4.1节可知,加速度计校正,地球辐射压力,空气动力系数,卫星质量,大气风速等均能影响反演结果.大气阻力主要作用于卫星沿轨方向(即星固系X轴),从而使得加速度计数据X轴分量信号强度大得多也更容易校正,这为反演热层密度提供了有利条件.第3节中轨道精度的分析结果也验证了本文校正的结果具有较高精度.而地球辐射压力主要作用于卫星径向,在X轴的分量要比大气阻力低2~3量级,因此在反演中可以忽略.GRACE卫星质量年均变化1 kg左右,以GFZ公布的480 kg为参考质量,1 kg质量误差引起的密度偏差约为0.2%.在反演时也可采用GFZ发布的精确的卫星质量数据(MAS数据).大气风速误差(相对于旋转大气)对密度反演的影响比较复杂,其导致卫星与大气的相对速度在量级与方向上均会产生误差,从而引起卫星空气动力系数以及密度计算误差.Bruinsma等(2004)通过仿真分析表明大气风速与反演误差几乎呈线性关系,纬度分量在赤道地区每100 m·s-1误差约引起4%的误差,在两极地区影响可以忽略,而经线分量相反,在两极地区每100 m·s-1误差约引起5%的误差,在赤道地区则较小为2%.大气风速一般在几百米每秒量级,但是在空间环境扰动等时期,大气风速可以增大至千米每秒量级,因此在反演时应尽量减小其影响.
根据以上分析,本文按照表 4中的策略反演热层密度.其中,加速度计数据采用3.1节估计得到的每60 min一组的标校参数进行校正,SRP采用Box-wing模型计算,Albedo与IR均不予考虑.空气动力系数采用Sentman模型计算,因其对大气温度与卫星面板温度变化并不敏感,本文直接采用NRLMSISE00模型计算大气温度,卫星表面温度则采用Doornbos(2012)的推荐值273 K.调节系数是影响空气动力系数的重要参量,本文研究中采用Sutton博士的推荐值0.93.大气风速采用HWM93模型计算.此外,为避免卫星姿态调整机动时期引入的机动力的影响,本文根据THR产品(包含卫星机动记录数据)剔除了卫星点火机动时期的数据.
|
|
表 4 热层密度反演数据处理策略 Table 4 Data processing strategy of thermosphere density derivation |
采用第4节提出的策略处理得到了GRACE-A和GRACE-B卫星2007—2009年间的沿轨热层密度.为了对反演结果的精度进行评价,本节将反演得到的GRACE-A卫星2007—2009年沿轨密度与Doornbos(2012)等的反演结果,以及NRLMSISE00,HASDM等经验模型进行比较分析.
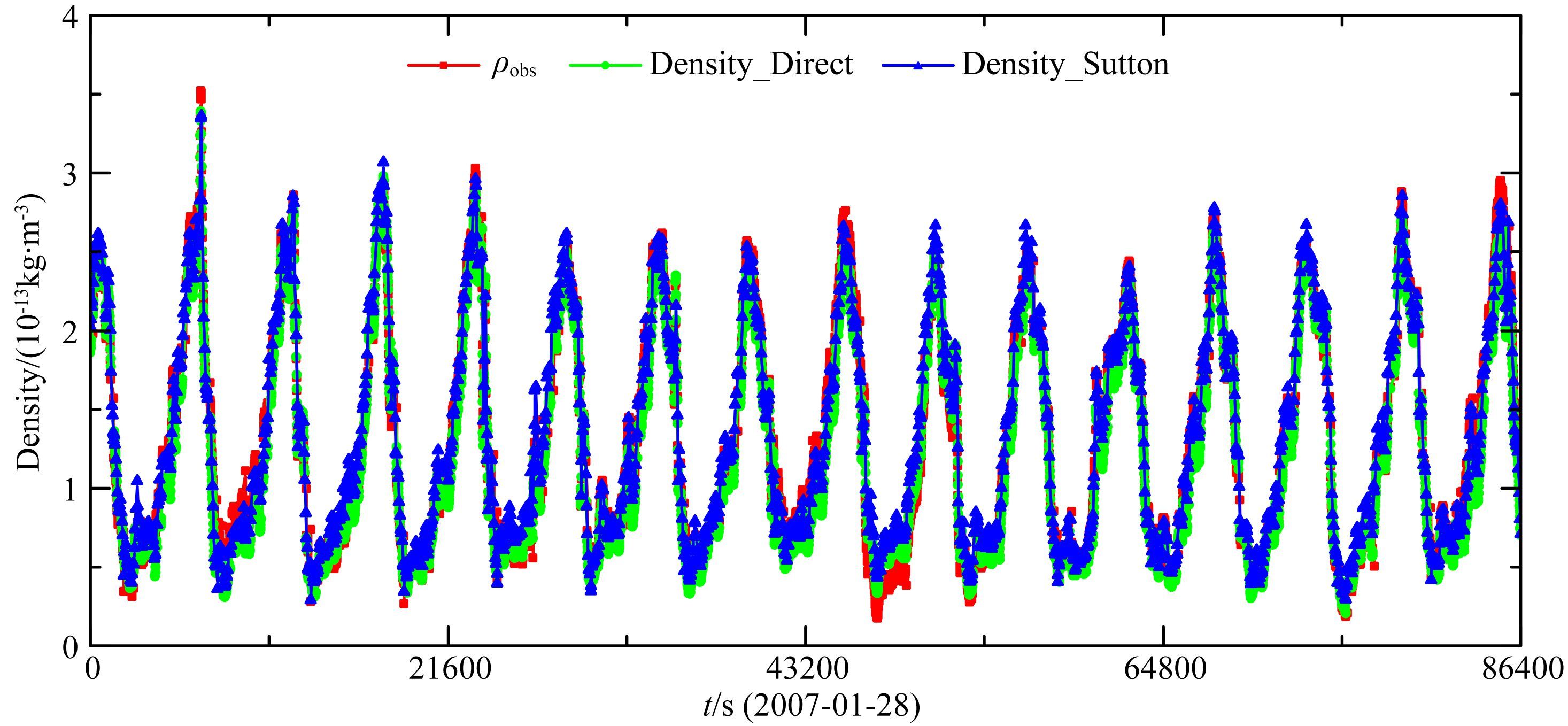
5.1 与Doornbos反演结果比较图 7为Doornbos,Sutton博士反演的2007年1月28日GRACE-A卫星沿轨密度与本文反演的结果进行对比,其中ρobs为本文反演结果,Density_Direct为Doornbos采用单轴法反演结果,Density_Sutton为Sutton博士反演得到的结果.Density_Direct的反演策略与表 4类似,其差异主要为:(1)加速度计校正参数采用van Helleputte等(2009)中的结果;(2)计算空气动力学系数时分别考虑各种气体粒子单独的贡献.Sutton博士的反演策略也与本文类似,但是其将反演结果根据卫星轨道纬度进行了合并(Sutton et al.,2007),因此其数据点时刻并不规则.由图中可见三者反演密度的变化趋势以及幅度均基本一致.
|
图 7 Doornbos,Sutton等研究与本文反演结果对比 Fig. 7 Densities comparison of this paper with respect to results from Doornbos and Sutton |
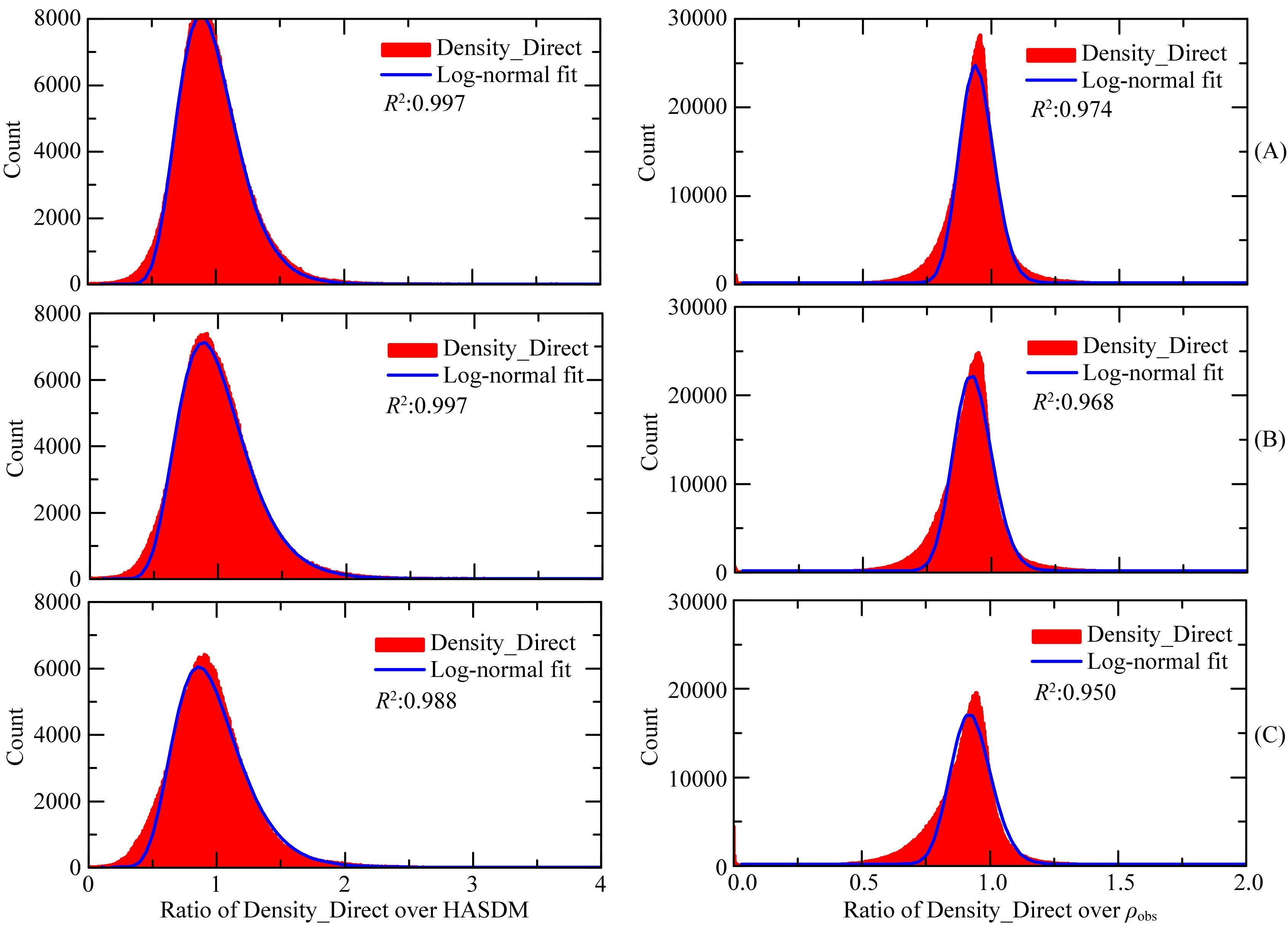
将本文反演结果ρobs与Density_Direct进行比较,对二者密度比值按年份进行对数正态分布拟合并统计bias和标准差;为了便于对照分析,将Density_Direct与HASDM模型也进行了比较,结果分别见图 8和表 5.其中年均比较数据点数约为2400000,统计密度比值的采样间隔设置为0.002.由图 8可见两组密度比值拟合的相关系数均达到了0.95以上,且Density_Direct与HASDM密度比值的拟合相关系数稍大一些.Density_Direct与ρobs,Density_Direct与HASDM的密度比值均主要分布在0.5~2.0区间内,但是Density_Direct与ρobs的比值分布更为集中,表明二者结果更为接近.由表 5可见,Density_Direct较HASDM模型、ρobs均偏小约4%~8%.Density_Direct与HASDM模型密度比值的STD在30%左右,与ρobs之间STD则均小于10%,表明本文反演结果与Doornbos的结果之间符合性较好.这主要是由于二者采用了相同的数据进行反演,且反演中采用的模型类似.
|
图 8 2007(A),2008(B)和2009(C)年Density_Direct与HASDM模型以及ρobs的密度比值的频数统计以及对数正态分布拟合 Fig. 8 Frequency number count and log-normal fit of ratios of Density_Direct over ρobs and HASDM model densities during year 2007(A),2008(B)and 2009(C),respectively |
|
|
表 5 2007—2009年Density_Direct与HASDM模型以及ρobs的密度比值的对数正态分布拟合统计 Table 5 Statistics of log-normal fit of ratios of Density_Direct over ρobs and HASDM model densities during year 2007,2008 and 2009,respectively |
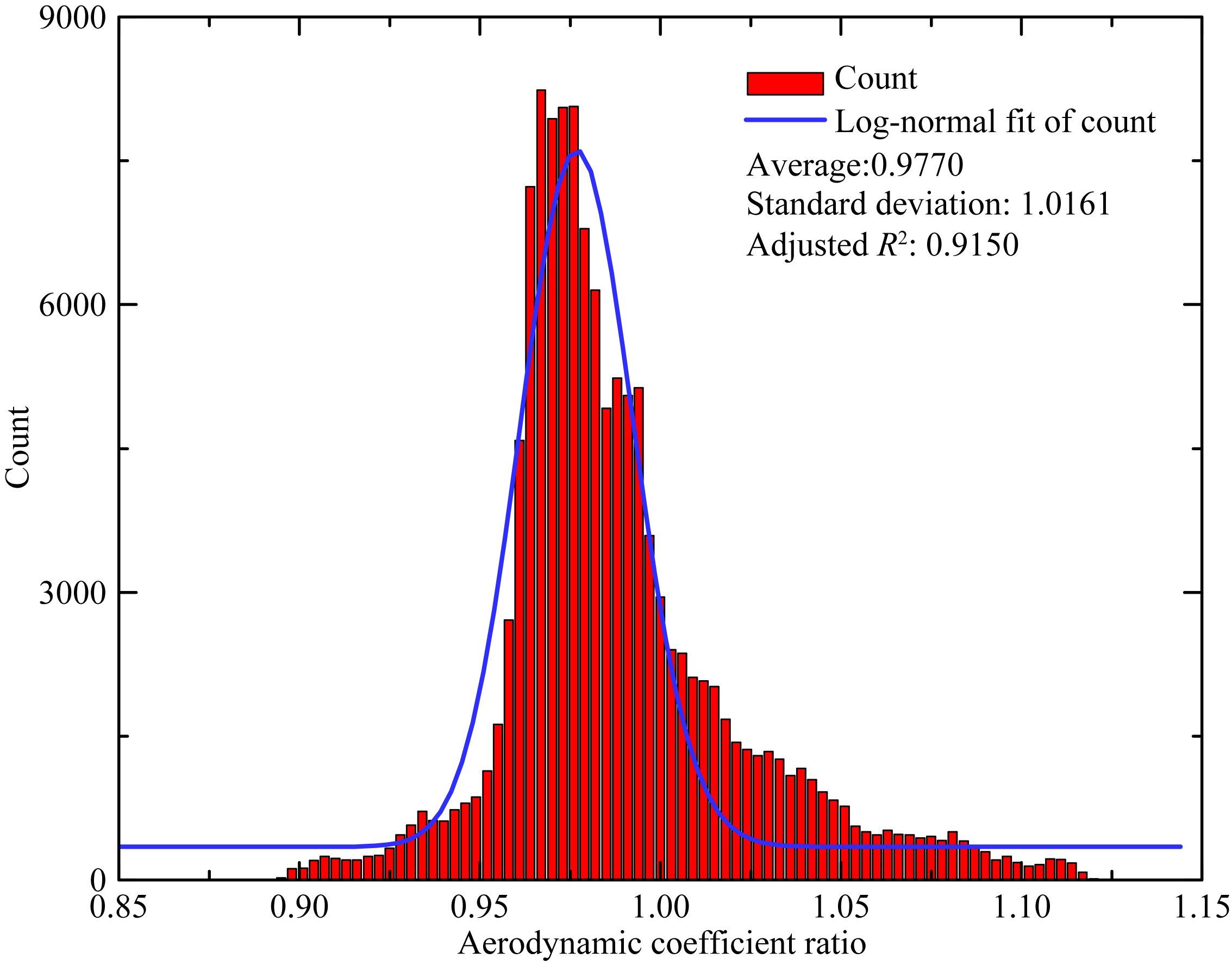
ρobs与Density_Direct之间的差异主要由计算空气动力系数与加速度计标校的策略不一致所造成.Doornbos在计算CA时分别考虑了每种气体粒子的贡献,而本文在计算时则是直接采用大气粒子的平均分子质量.图 9为2007年1月1—15日半个月内二者CA比值的频数统计,其中统计的空气动力系数数量为129600,采样间隔为0.005.对该频数分布进行对数正态拟合的平均值与标准差分别为0.977和1.016,拟合的相关系数为0.915.值得注意的是计算空气动力系数时所需要输入的数据或模型参数均可以很容易保持一致,因此空气动力系数差异的变化不大,其造成的反演密度差异也应在此水平.Doornbos(2012)通过仿真分析了加速度计校正误差对反演密度的影响,表明当X轴加速度计数据存在10 nm·s-2的偏差时,其造成的密度反演偏差和STD分别为-2.7%和1.5%.本文研究中将尺度参数固定为常数并每60 min估计一组偏差参数,而van Helleputte等(2009)则单天估计一组尺度与偏差参数且在切向、径向与法向均引入了经验力参数,二者标校参数的差异对密度反演造成的影响值得进一步研究.
|
图 9 Doornbos与本文计算的空气动力系数差异的频数统计和对数正态分布拟合 Fig. 9 Frequency count and log-normal fit of the differences of the aerodynamic coefficients between Doornbos and this paper |
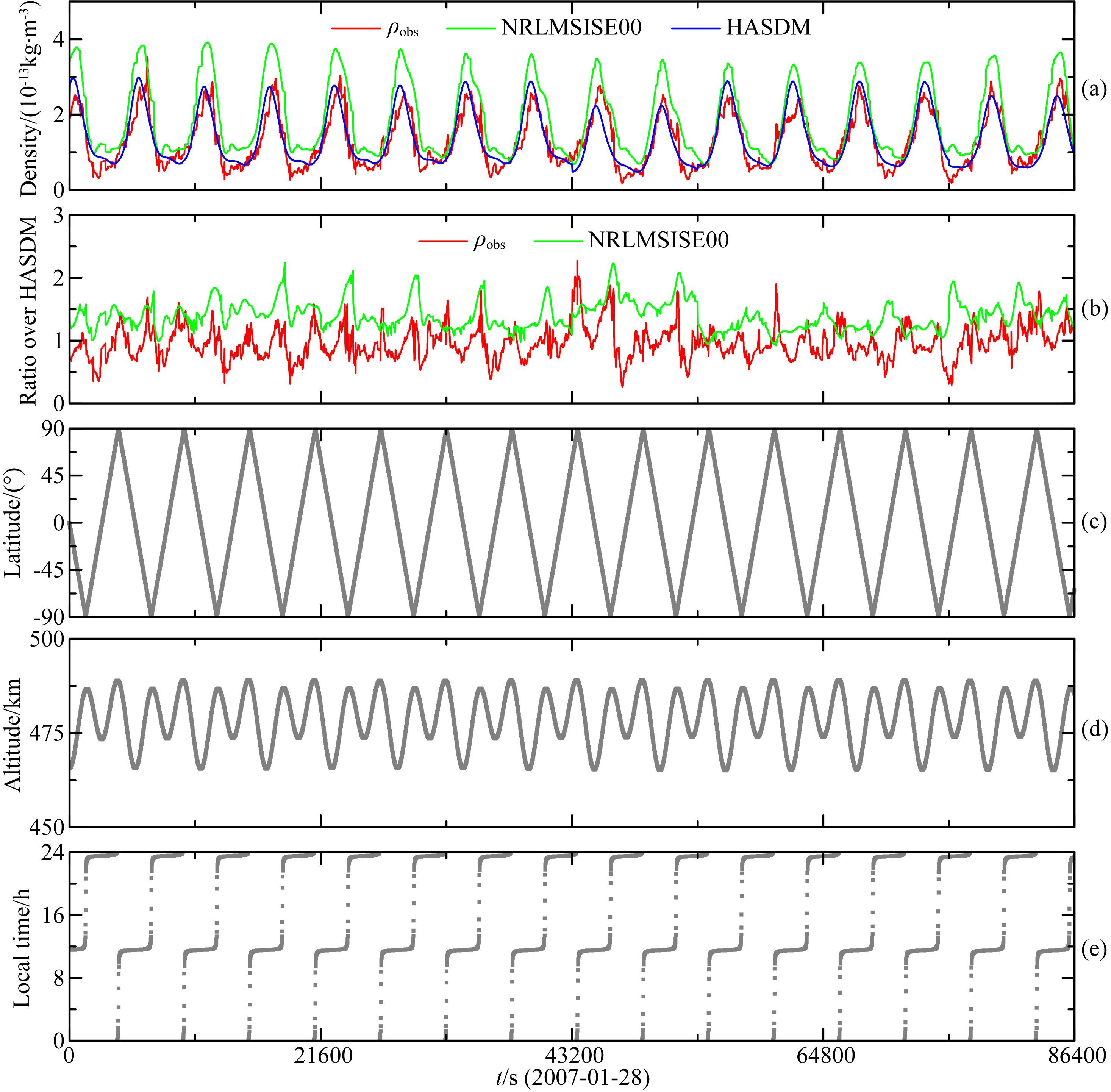
图 10为2007年1月28日GRACE-A卫星沿轨的反演密度ρobs,NRLMSISE00和HASDM模型密度以及密度比值.该天为地磁平静日,其全天Ap指数均小于10,平均Ap指数为5,F10.7指数和81天平均F10.7指数分别为79.0和84.5 sfu,表明太阳活动强度较低.为了便于比较,图中还给出了卫星轨道纬度,高度和当地时.图中可见轨道高度约在475 km左右.总体上ρobs与经验模型密度的变化趋势基本一致,但与HASDM更为接近,二者在密度峰值处大小非常接近.而NRLMSISE00模型预报密度较ρobs与HASDM均系统性偏大.ρobs与HASDM比值主要分布在0.5~1.5范围内,且在两极地区时出现较大幅度的跳变,其原因可能是在极地地区大气风速很容易增大至千米每秒量级,采用HWM93模型计算的大气风速可能会存在较大的误差,从而导致反演结果的误差增大.图 10中同时可见ρobs和NRLMSISE00模型密度在午夜时期均出现一个甚至多个峰值,这反映的是午夜密度极大(Midnight Density Maximum,MDM)现象.HASDM模型则未能反映出该变化.因此可以发现在午夜期间,ρobs、NRLMSISE00模型与HASDM模型的密度比值序列均存在峰值现象.
|
图 10 GRACE-A卫星2007年1月28日沿轨反演密度,NRLMSISE00和HASDM模型密度以及密度比值 (a)沿轨ρobs,NRLMSISE00和HASDM密度;(b)ρobs和NRLMSISE00分别与HASDM密度比值; (c)星下点纬度;(d)轨道高度;(e)星下点地方时. Fig. 10 The accelerometer-derived,NRLMSISE00 and HASDM model densities of GRACE-A satellite on January 16,2007,as well as their density ratios (a)Accelerometer-derived,NRLMSISE00 and HASDM model densities;(b)Ratio series of accelerometer-derived and NRLMSISE00 densities over HASDM model densities;(c)Orbit latitude;(d)Orbit altitude;(e)Local time of ground tracks. |
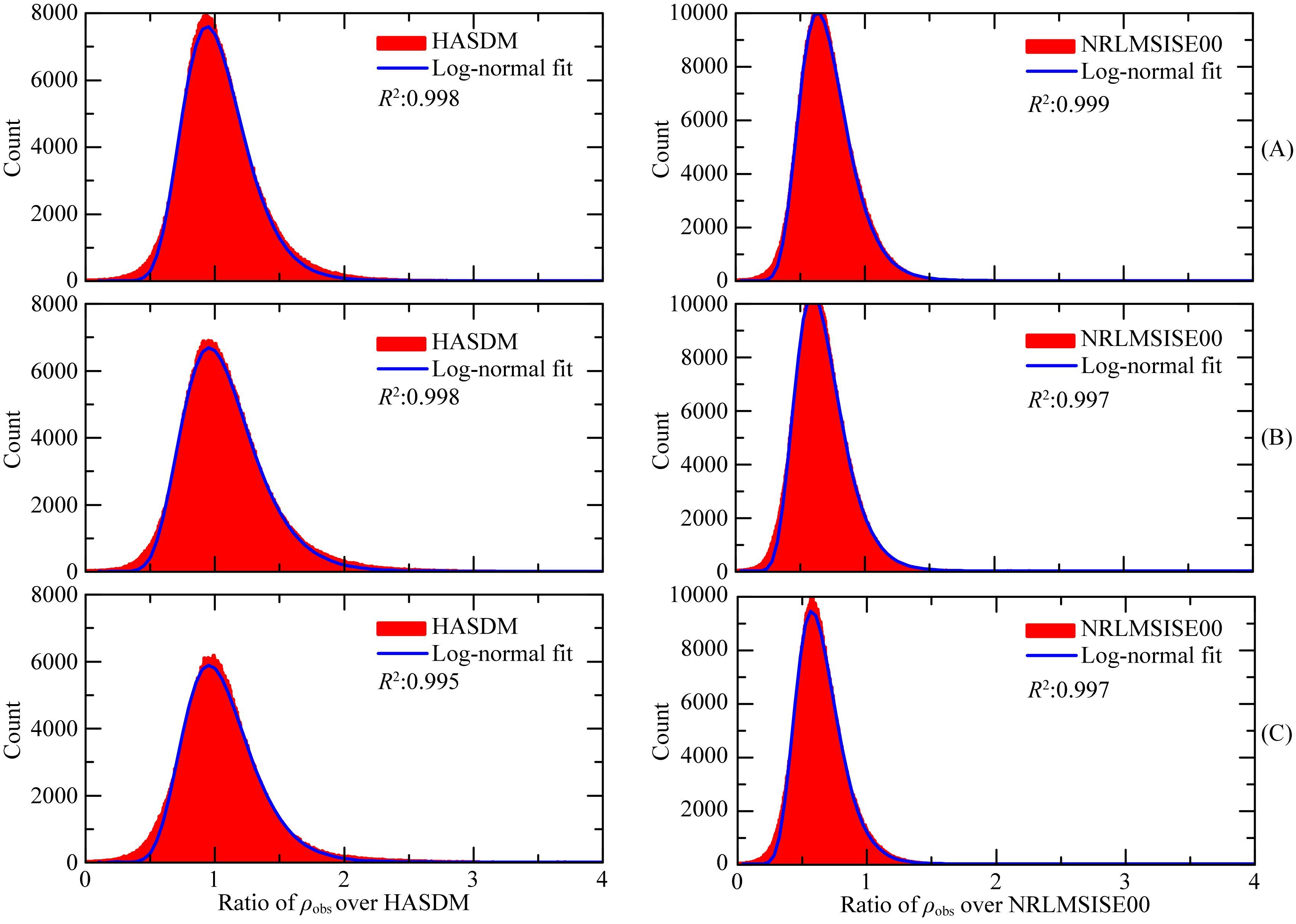
将本文反演的密度ρobs与NRLMSISE00模型预报密度以及HASDM模型比较并进行统计.图 11为2007—2009年密度比值的频数分布统计,以及对数正态分布拟合.图中可见,ρobs和NRLMSISE00模型以及HASDM模型之间拟合的相关系数均达到了0.99以上.表 6为密度比值的对数正态分布拟合的bias与STD.可见,ρobs与HASDM模型之间bias较小,均在4%以内,而与NRLMSISE00模型之间存在约30%~40%的年平均bias,其原因目前认为主要是由于2007—2009年太阳活动异常宁静从而导致NRLMSISE00模型产生了尺度性bias(Emmert et al.,2010; Solomon et al.,2010; Liu et al.,2011).STD统计结果来看,ρobs与NRLMSISE00以及HASDM的STD均在30%左右,但是其与HASDM模型之间的STD均要稍小于NRLMSISE00模型.值得注意的是,ρobs较HASDM模型系统性偏大,而Doornbos反演结果系统性偏小约4%~7%,二者与HASDM模型之间的STD均在30%左右.
|
图 11 2007(A),2008(B)和2009(C)年ρobs和NRLMSISE00模型与HASDM模型密度比值的频数统计以及对数正态分布拟合 Fig. 11 Frequency number count and log-normal fit of ratios of ρobs and NRLMSISE00 over HASDM model densities during year 2007(A),2008(B)and 2009(C)respectively |
|
|
表 6 2007,2008和2009年ρobs和NRLMSISE00与HASDM模型密度比值的对数正态分布拟合统计 Table 6 Statistics of log-normal fit of ratios of ρobs and NRLMSISE00 over HASDM model densities during year 2007,2008 and 2009 respectively |
以上的统计分析表明本文采用加速度计反演的热层密度与HASDM模型之间bias较小,而NRLMSISE00模型与本文反演密度以及HASDM均存在较大的bias.一般而言,不同密度模型或数据之间的bias主要来自于空气动力系数误差,以及对热层密度变化物理机制的错误模型化等,因此其常常与高度、纬度、地方时、太阳辐射和地磁活动强度等因素有关(Doornbos et al.,2008; 陈旭杏等,2013; Shi et al.,2015).本文利用加速度计数据反演密度时,分段加速度计校正参数的误差虽然会导致密度反演出现bias,但是从长时间来看加速度计标校误差是随机的(Sutton et al.,2007),而卫星空气动力系数误差则会导致显著的bias.一般而言,能量调节系数对空气动力系数CA的影响最为明显,调节系数越大CA越小.对于GRACE卫星而言,其调节系数一般认为在0.8以上,但是精确确定其调节系数目前仍然是一项挑战(Sutton,2009).类似的,对于NRLMSISE00,HASDM等经验模型,其使用的卫星阻力观测数据等同样存在由弹道系数误差所导致的bias.
另一方面,ρobs与目前公认精度最高的模型HASDM之间的标准差可达30%.其很大部分可能是由于HASDM采用的低阶球谐模型仅能在相对较大时空尺度上对热层密度的平均误差进行校正,而ρobs能够反映热层密度更高时空分辨率上的变化.Lechtenberg等(2013)将CHAMP和GRACE加速度计反演得到的密度与HASDM模型进行比较时发现二者总体上非常符合,然而前者能够反应热层密度变化的诸多高频变化现象,如:午夜密度极大,地磁极尖区密度增加,大气行扰等,而HASDM模型无法探测到以上变化.本文图 10中也显示出了类似的现象.其次,本文所研究的数据时段为2007—2009年,属于太阳活动低年时期,而Bowman和Storz(2003)对HASDM模型精度进行评价时采用的是2001—2002年的数据,属于太阳活动高年.在太阳活动低年时期由于太阳辐射较小导致热层密度为整个太阳活动周期内最低,因此大气阻力信号强度较弱.在考虑其他非保守力如SRP等误差不变的情况下,大气阻力减小从而会使得反演热层密度的相对误差增大.而另一方面,HASDM模型采用低轨空间物体阻力观测值来校正Jacchia71模型,其在太阳活动低年也同样存在因阻力信号减弱所致的阻力观测值相对误差增大的问题.这也是导致本文统计结果中ρobs与HASDM模型之间STD较大的原因之一.因此,采用整个太阳活动周期内的反演密度数据将有利于更准确地评价反演精度,特别是在不同太阳辐射强度条件下的反演密度精度.另外,对于反演得到的结果需要进行严格的质量控制和粗差剔除.现阶段本文仅仅根据THR产品对卫星点火时期的数据进行了删除,然而对于极区大气风速误差等导致的反演粗差仍然参与了比较,这也可能会对统计结果产生干扰.
6 总结本文介绍了利用加速度计数据反演热层密度的模型与方法,并对GRACE卫星2007—2009年的数据进行了处理与分析.首先利用星载GPS数据进行动力学精密定轨,并以加速度计数据代替非保守力,估计得到了该时段内GRACE卫星的加速度计标校参数.在此基础上利用校正后的加速度计数据扣除太阳辐射光压,并根据Sentman方程计算卫星空气动力系数,反演得到了2007—2009年沿GRACE卫星轨道的热层大气密度.本文研究的主要结论如下:
(1) 对不同太阳活动强度时期的卫星所受空气动力、太阳辐射压力,地球反照辐射等非保守力进行比较,结果表明在太阳活动高年卫星阻力信号较强,其在X轴分量比SRP高出一个量级;而太阳活动低年时期由于卫星阻力信号变弱,可能导致反演密度误差增加.
(2) 利用GRACE卫星2007—2009年的GPS与加速度计数据进行动力学定轨处理,通过轨道精度分析对加速度计校正精度进行了评价.结果表明,采用本文处理策略,利用GPS和加速度计数据定轨结果与JPL PSO在同一精度量级,GRACE-A/B星与JPL PSO轨道差值3D RMS平均值分别为2.6 cm和2.3 cm,SLR轨道检核的RMS平均值分别为2.4 cm和2.6 cm.通过该方法估计得到的三个方向的偏差参数变化都非常平缓,X方向偏差参数的年均变化在10 nm·s-2量级.
(3) 分析了利用GRACE卫星加速度计进行密度反演的数据处理策略,对反演结果进行分析与评估.对GRACE卫星2007—2009年的加速度计数据进行处理得到了该时期内沿GRACE卫星轨道的热层大气密度.将本文反演的结果与Doornbos解算的结果,经验密度模型NRLMSISE00和HASDM进行对比分析.结果表明本文反演结果与Doornbos结果之间存小于8%的系统性bias,二者STD统计值在10%以内,具有较好的符合性.二者之间的差异主要是由不同的加速度标校和空气动力系数计算策略造成.本文反演结果较HASDM偏大,bias在4%以内,而Doornbos结果较HASDM模型值偏小,bias在7%以内,二者与HASDM模型比较的STD均在30%左右.本文结果与NRLMSISE00模型之间存在约30%~40%的系统bias,这主要是由于NRLMSISE00模型在2007—2009年太阳活动异常宁静期间存在显著模型偏差所致.
致谢感谢ISDC提供GRACE卫星相关数据,以及IGS提供GPS精密轨道和钟差产品.感谢Doornbos和Sutton博士提供基于GRACE卫星加速度计反演的密度数据.感谢各基金项目对论文研究的支持.
| Bettadpur S V. 2004. Recommendation for a-priori bias & scale parameters for level-1B ACC data (Release 00). GRACE TN-04-02. | |
| Bettadpur S V. 2012. GRACE Product Specification Document, GRACE 327-720. The University of Texas at Austin. | |
| Bezděk A. 2010. Calibration of accelerometers aboard GRACE satellites by comparison with POD-based nongravitational accelerations. Journal of Geodynamics , 50 (5) : 410-423. DOI:10.1016/j.jog.2010.05.001 | |
| Bhanderi D D V, Bak T. 2005. Modeling Earth Albedo for Satellites in Earth Orbit.//AIAA Guidance, Navigation, and Control Conference and Exhibit. San Francisco, California:AIAA. | |
| Bowman B R, Storz M F. 2003. High Accuracy Satellite Drag Model (HASDM) review. Advances in the Astronautical Sciences , 116 : 1943-1952. | |
| Bruinsma S, Biancale R. 2003. Total densities derived from accelerometer data. Journal of Spacecraft and Rockets , 40 (2) : 230-236. DOI:10.2514/2.3937 | |
| Bruinsma S, Tamagnan D, Biancale R. 2004. Atmospheric densities derived from CHAMP/STAR accelerometer observations. Planetary and Space Science , 52 (4) : 297-312. DOI:10.1016/j.pss.2003.11.004 | |
| Bruinsma S, Forbes J M, Nerem R S, et al. 2006. Thermosphere density response to the 20-21 November 2003 solar and geomagnetic storm from CHAMPand GRACE accelerometer data. Journal of Geophysical Research:Space Physics , 111 (A6) : A06303. | |
| Bruinsma S, Biancale R, Perosanz F. 2007. Calibration parameters of the CHAMP and GRACE accelerometers. Poster presented at the GRACE Science Team Meeting. | |
| Bruinsma S L, Forbes J M. 2007. Global observation of traveling atmospheric disturbances (TADs) in the thermosphere. Geophysical Research Letters , 34 (14) : L14103. DOI:10.1029/2007GL030243 | |
| Bruinsma S L, Forbes J M. 2008. Medium-to large-scale density variability as observed by CHAMP. Space Weather , 6 (8) : S08002. | |
| Bruinsma S L, Forbes J M. 2009. Properties of traveling atmospheric disturbances (TADs)inferred from CHAMP accelerometer observations. Advances in Space Research , 43 (3) : 369-376. DOI:10.1016/j.asr.2008.10.031 | |
| Bruinsma S L, Forbes J M. 2010. Anomalous behavior of the thermosphere during solar minimum observed by CHAMP and GRACE. Journal of Geophysical Research:Space Physics , 115 (A11) : A11323. | |
| Case K, Kruizinga G L H, Wu S C. 2010. GRACE Level 1B Data Product User Handbook, JPL Publication D-22027. | |
| Chen X X, Hu X, Xiao C Y, et al. 2013. Correction method of the low earth orbital neutral density prediction based on the satellites data and NRLMSISE-00 model. Chinese J. Geophys. (in Chinese) , 56 (10) : 3246-3254. DOI:10.6038/cjg20131003 | |
| Cook G E. 1965. Satellite drag coefficients. Planetary and Space Science , 13 (10) : 929-946. DOI:10.1016/0032-0633(65)90150-9 | |
| Dahle C, Flechtner F, Gruber C, et al. 2012. GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 0005. Deutsches GeoForschungsZentrum GFZ. | |
| Doornbos E, Klinkrad H, Visser P. 2008. Use of two-line element data for thermosphere neutral density model calibration. Advances in Space Research , 41 (7) : 1115-1122. DOI:10.1016/j.asr.2006.12.025 | |
| Doornbos E, van Den Ijssel J, Luehr H, et al. 2010. Neutral density and crosswind determination from arbitrarily oriented multiaxis accelerometers on satellites. Journal of Spacecraft and Rockets , 47 (4) : 580-589. DOI:10.2514/1.48114 | |
| Doornbos E. Thermospheric Density and Wind Determination from Satellite Dynamics. Berlin Heidelberg: Springer, 2012 . | |
| Emmert J, Lean J, Picone J. 2010. Record-low thermospheric density during the 2008 solar minimum. Geophysical Research Letters , 37 (12) : 245-269. | |
| Frommknecht B, Oberndorfer H, Flechtner F, et al. 2003. Integrated sensor analysis for GRACE-development and validation. Advances in Geosciences , 1 : 57-63. DOI:10.5194/adgeo-1-57-2003 | |
| Gerlach C, Sneeuw N, Visser P, et al. 2003. CHAMP gravity field recovery with the energy balance approach:first results.//First CHAMP Mission Results for Gravity, Magnetic and Atmospheric Studies. Berlin Heidelberg:Springer, 134-139. | |
| Guo J P, Wan W X, Forbes J M, et al. 2007. Effects of solar variability on thermosphere density from CHAMP accelerometer data. Journal of Geophysical Research:Space Physics , 112 (A10) : A10308. | |
| Guo J P, Wan W X, Forbes J M, et al. 2008. Interannual and latitudinal variability of the thermosphere density annual harmonics. Journal of Geophysical Research:Space Physics , 113 (A8) : A08301. | |
| Koppenwallner G. 2008. Comment on special section:New perspectives on the satellite drag environments of earth, mars, and venus. Journal of Spacecraft and Rockets , 45 (6) : 1324-1327. DOI:10.2514/1.37539 | |
| Lechtenberg T F, McLaughlin C A, Locke T, et al. 2013. Thermospheric density variations:observability using precision satellite orbits and effects on orbit propagation. Space Weather , 11 (1) : 34-35. DOI:10.1029/2012SW000848 | |
| Lei J H, Thayer J P, Lu G, et al. 2011. Rapid recovery of thermosphere density during the October 2003 geomagnetic storms. Journal of Geophysical Research:Space Physics , 116 (A3) : A03306. | |
| Liu H X, Doornbos E, Yamamoto M, et al. 2011. Strong thermospheric cooling during the 2009 major stratosphere warming. Geophysical Research Letters , 38 (12) : L12102. | |
| Marcos F A, Bowman B R, Sheehan R E. 2006. Accuracy of Earth's thermospheric neutral density models.//AIAA/AAS Astrodynamics Specialist Conference and Exhibit,Guidance, Navigation, and Control and Co-located Conferences. Keystone, CO.:AIAA. | |
| McCarthy D D, Petit G. 2004. IERS conventions 2003. IERS Technical Note No. 32. Frankfurt am Main:Verlag des Bundesamts für Kartographie und Geodäsie. | |
| Moe K, Moe M M, Rice C J. 2004. Simultaneous analysis of multi-instrument satellite measurements of atmospheric density. Journal of Spacecraft and Rockets , 41 (5) : 849-853. DOI:10.2514/1.2090 | |
| Moe K, Moe M M. 2005. Gas-surface interactions and satellite drag coefficients. Planetary and Space Science , 53 (8) : 793-801. DOI:10.1016/j.pss.2005.03.005 | |
| Montenbruck O, Gill E. Satellite Orbits:Models, Methods and Applications. Heidelberg: Springer-Verlag, 2000 . | |
| Picone J M, Hedin A E, Drob D P, et al. 2002. NRLMSISE-00 empirical model of the atmosphere:Statistical comparisons and scientific issues. Journal of Geophysical Research:Space Physics , 107 (A12) : SIA 15-1-SIA 15-16. DOI:10.1029/2002JA009430 | |
| Rim H J. 1992. TOPEX Orbit Determination Using GPS Tracking System[Ph. D. thesis]. Austin:The University of Texas. | |
| Sentman L H. 1961. Free Molecule Flow Theory and its Application to the Determination of Aerodynamic Forces. DTIC Document. | |
| Shi C, Li W W, Li M, et al. 2015. Calibrating the scale of the NRLMSISE00 model during solar maximum using the two line elements dataset. Advances in Space Research , 56 (1) : 1-9. | |
| Solomon S C, Woods T N, Didkovsky L V, et al. 2010. Anomalously low solar extreme-ultraviolet irradiance and thermospheric density during solar minimum. Geophysical Research Letters , 37 (16) : L16103. | |
| Storz M F Bowman B R, Branson M J I, et al. 2005. High accuracy satellite drag model (HASDM). Advances in Space Research , 36 (12) : 2497-2505. DOI:10.1016/j.asr.2004.02.020 | |
| Sutton E K, Forbes J M, Nerem R S. 2005. Global thermospheric neutral density and wind response to the severe 2003 geomagnetic storms from CHAMPaccelerometer data. Journal of Geophysical Research:Space Physics , 110 (A9) : A09S40. | |
| Sutton E K, Forbes J M, Nerem R S, et al. 2006. Neutral density response to the solar flares of October and November, 2003. Geophysical Research Letters , 33 (22) : L22101. DOI:10.1029/2006GL027737 | |
| Sutton E K, Nerem R S, Forbes J M. 2007. Density and winds in the thermosphere deduced from accelerometer data. Journal of Spacecraft and Rockets , 44 (6) : 1210-1219. DOI:10.2514/1.28641 | |
| Sutton E K. 2009. Normalized force coefficients for satellites with elongated shapes. Journal of Spacecraft and Rockets , 46 (1) : 112-116. DOI:10.2514/1.40940 | |
| Van Helleputte T, Visser P. 2008. GPS based orbit determination using accelerometer data. Aerospace Science and Technology , 12 (6) : 478-484. DOI:10.1016/j.ast.2007.11.002 | |
| Van Helleputte T, Doornbos E, Visser P. 2009. CHAMP and GRACE accelerometer calibration by GPS-based orbit determination. Advances in Space Research , 43 (12) : 1890-1896. DOI:10.1016/j.asr.2009.02.017 | |
| Wang H B, Zhao C Y. 2008. Use CHAMP/STAR accelerometer data to evaluate atmospheric density models during solar maximum year. Acta Astronomica Sinica (in Chinese) , 49 (2) : 168-178. | |
| Xiong Y Q, Wang H B, Zhao C Y, et al. 2011a. A rapid and effective calibration method for CHAMP accelerometer. Progress in Astronomy (in Chinese) , 29 (2) : 228-237. | |
| Xiong Y Q, Wang H B, Xu X L, et al. 2011b. The calibration research for GRACE accelerometer. Scientia Sinica Physica, Mechanica & Astronomica (in Chinese) , 41 (11) : 1319-1327. | |
| Xu T H, Yang Y X. 2004. Calibration for CHAMP accelerometry data based on known Earth gravity field model. Acta Geodaetica et Cartographic Sinica (in Chinese) , 33 (3) : 200-204. | |
| 陈旭杏, 胡雄, 肖存英, 等. 2013. 基于卫星数据和NRLMSISE-00模型的低轨道大气密度预报修正方法. 地球物理学报 , 56 (10) : 3246–3254. DOI:10.6038/cjg20131003 | |
| 汪宏波, 赵长印. 2008. 用CHAMP加速仪数据校验太阳活动峰年的大气模型精度. 天文学报 , 49 (2) : 168–178. | |
| 熊永清, 汪宏波, 赵长印, 等. 2011a. CHAMP加速仪资料的快速校标研究. 天文学进展 , 29 (2) : 228–237. | |
| 熊永清, 汪宏波, 许晓丽, 等. 2011b. GRACE加速仪资料定标研究. 中国科学:物理学、力学、天文学 , 41 (11) : 1319–1327. | |
| 徐天河, 杨元喜. 2004. 利用现有重力场模型求定CHAMP卫星加速度计修正参数. 测绘学报 , 33 (3) : 200–204. | |
 2016, Vol. 59
2016, Vol. 59


