2. 有色资源与地质灾害探查湖南省重点实验室, 长沙 410083
2. Key Laboratory of Non-ferrous Resources and Geological Detection, Ministry of Hunan Province, Changsha 410083, China
混凝土是公路、桥梁、桩基、大坝、房屋等结构工程的主要材料,由硬化的水泥浆、砂、碎石、砾石、卵石等骨料,再加上充水或空气的孔隙等组成的非均匀多相复合凝聚体.简单来看,它是水泥砂装基体和骨料填充物组成的双相复合材料(张剑等,2004).混凝土的质量直接关系到生命及财产安全,始终是人们关注的焦点.混凝土质量无损检测方法有许多,探地雷达(GPR)是重要的检测方法之一.为了提高混凝土构筑物的GPR检测精度,需要开展GPR正演.传统的GPR正演常将混凝土简化为均匀介质或各向同性介质,这显然不符合混凝土介质的特点.考虑到混凝土介质中存在大量非均质的卵石、碎石或砂浆微小异常体,加上混凝土中骨料颗粒的几何尺寸不规则及位置随机分布,雷达波在其中传播时,必然会受到不均匀骨料的影响,造成大量小的不相干的扰动,易产生波形畸变、能量衰减、传播方向性差等现象,导致正演结果与实际探测结果在波场特征、幅值强弱、异常体可见性方面存在较大的偏差.需要开展以统计学理论为基础的双相随机介质模型来描述,使研究的对象更符合混凝土的真实情况(郭士礼,2013).
目前GPR正演算法主要有有限差分法(FDM,刘四新和曾昭发,2007;李静等,2010;冯德山等,2010)、有限单元法(FEM,底青云和王妙月,1999;Di and Wang,2004;冯德山等,2012),这些传统算法在求解特定奇异性问题时,难以完全消除局部大梯度所引起的振荡,影响求解精度.而小波有限元法利用小波函数或尺度函数作为插值函数构造单元,使问题的求解在一个嵌套序列中进行,根据实际需要任意改变分析尺度,在不改变网格剖分的前提下提高分辨率,使它可以在大梯度处采用小的分析尺度、高阶单元以提高分析精度,而在小梯度处采用大的分析尺度、较低阶单元以提高分析效率(何正嘉等,2006).在众多的小波当中,Daubechies小波(Daubechies,1998)因为具有紧支撑性、正交性等诸多优点,被广泛应用(Patton and Marks,1996;Chen et al.,2004,2006).Amaratunga等(1994)采用小波Galerkin法结合Dirichlet边界条件求解一维Helmholtz方程及二维Green方程(Amaratunga and Williams,1993),指出了小波嵌套空间能在不同尺度下求解的优势;Sarkar等(1994)将小波函数引入到传统有限元插值函数中求解Maxwell方程,所得的系数矩阵呈对角线的稀疏分布,具有条件数不随维数增加的优点;Mishra和Sabina(2011)应用小波Galerkin法求解一维谐波常微分方程及二维偏微分方程(Sabina and Mishra,2012).然而Daubechies小波没有显式表达,联系系数求解困难,影响了它的进一步推广.而区间B样条小波(B-spline wavelet on the interval,BSWI)是美国学者Chui & Quak(Chui and Quak,1992;Quak and Weyrich,1994)在求解边值问题时,为避免定义在整个实数轴上经典小波函数产生数值振荡现象而提出的.与其他小波函数相比,BSWI具有良好的数值逼近性和明显数学表达式,易于求导计算,能根据问题的求解精度要求灵活地选用小波基的尺度与阶次.而且,由于BSWI在空间域具有良好的局部化性质,能克服求解边值问题在边界上数值振荡这一缺陷,可以采用较少单元获得较高的精度,已引起国内外学者的广泛关注(Goswami et al.,1995;Xiang et al.,2007).
石钟慈(1979)采用三次B样条有限元解规则区域上板梁组合弹性结构的平衡问题,具有比常规有限元计算量少、精确度高的特点;梁旭彪等(1988)以矩形单元的B样条函数作为形函数,引入B样条重节点理论,成功地将B 样条有限元法应用于多种媒质场域内电磁场求解问题;金坚明等(2006)用张量积形式构造二维最小支集样条小波有限元,并将它用于求解弹性薄板小挠度问题;向家伟等(Xiang et al.,2008a;Xiang et al.,2008b)应用构造的一维、二维BSWI小波单元对杆、梁和板等结构件及轴承转子系统进行变形和振动分析;陈雪峰等(Chen et al.,2010)开展了二维BSWI多尺度小波自适应有限元分析;孙惠香等(2014)构造了三维BSWI小波单元,并将其应用于爆炸荷载作用地下箱形结构的动力响应的数值模拟.综上所述,尽管对BSWI的研究取得了一些成果,但在地球物理领域仍处于起步阶段.
目前开展随机介质GPR数值模拟的文献有:戴前伟和王洪华(2013)基于随机过程的谱分解和混合型自相关函数理论构造随机介质模型,采用无单元法对其进行了GPR波场正演;李静(2014)通过在局部随机位置引入高斯椭圆方程随机干扰因子,结合混合型自相关函数,建立了多参数耦合随机介质模型,并应用有限差分对该随机介质进行了正演.本文借助工程材料学中较为成熟的“数值混凝土概念”技术,将沥青混凝土视作随机介质,并将介电常数视为在空间上的随机分布特征,使其在物质组成,材料参数,骨料的形态及分布上与真实的混凝土在统计学意义上具有一致性(高政国和刘光廷,2003;余涛,2013),建立更符合实际的双相离散随机混凝土模型,更加真实地模拟雷达波的传播过程.
本文以双相离散随机介质来建立“数值混凝土”模型(余涛,2013;郭士礼,2013),采用BSWI算法对其进行GPR数值模拟,能有效地指导混凝土介质的GPR探测资料解释,同时,为目前GPR正演算法提供一种新的算法和思路.
2 区间B样条小波特性及二维张量积小波构造 2.1 区间B样条小波性质通过连接节点间的分段多项式,构成具有一定光滑性质的函数成为B样条函数,构造[0,1]区间上m阶j尺度B样条函数空间,首先将任意区间[a,b]上函数f(x)通过坐标变换ξ=(x-a)/(b-a)映射到标准[0,1]区间,再将[0,1]区间划分为相等2j份(j∈z,表示尺度),并在两端点外侧各添加m-1个重节点,节点总数为2j+m-1,节点序列xj用公式表示为

|
(1) |
节点序列形成的样条函数为m阶B样条函数,进一步利用m阶B样条函数的尺度函数Nm(x)构造[0,1]区间上m阶具有紧支性的j尺度空间vj[0,1].其中Nm(x)定义为
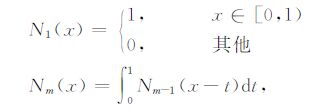
|
(2) |
m阶B样条尺度函数表示为
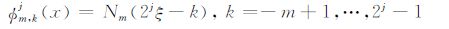
|
(3) |
其支撑区间为

|
(4) |
则可生成[0,1]区间上的多分辨分析.任意尺度为j的m阶BSWI尺度函数φm,kj(ζ),ζ∈[0,1]可用以下公式求出(何正嘉等,2006):

|
(5) |
BSWI21尺度函数有3个,其中0边界φ2-11,(ξ),1边界尺度函数φ2,11(ξ),内部尺度函数φ2,01(ξ),即

|
(6) |
BSWI22尺度函数有5个,其中0边界φ2,-12(ξ),1边界尺度函数φ2,32(ξ),内部尺度函数φ2,02(ξ),φ2,12(ξ),φ2,22(ξ),即

|
(7) |
求解二维GPR偏微分方程时,电场E及磁场H是关于时间变量t和空间变量x,y的函数,需要采用二维多分辨分析,构造二维小波最简单的方法是对一维小波多分辨逼近空间取张量积(何正嘉等,2006).假设m阶j尺度下L2(R2)空间中的二维张量积BSWI由一维多分辨逼近空间Vj1和Vj2张量积生成,则张量积空间Vj=Vj1⊗Vj2,尺度函数为
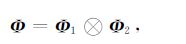
|
(8) |
式中,Φ1和Φ2分别为m阶j尺度下的一维BSWI尺度函数,表示为
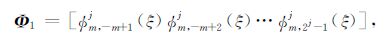
|
(9) |
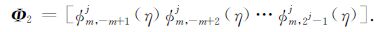
|
(10) |
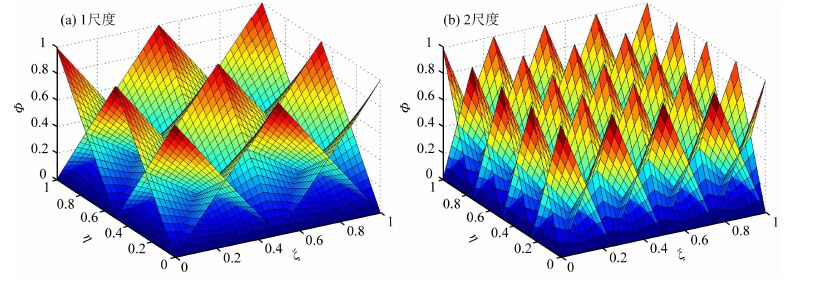
图 1为根据张量积构造的二维张量积BSWI2尺度函数.
|
图 1 二维张量积BSWI2尺度函数图 Fig. 1 The map of two-dimensional tensor product scaling function of BSWI2 |
由电磁波传播理论可知(Yee,1966),含衰减项的GPR波动方程为
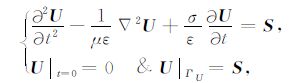
|
(11) |
式(11)中,当U表示电场值E时,S为激励源Se,当U表示磁场值H时,S为激励源Sh,ε为介电常数,μ为磁导率,σ为电导率,t为时间,ΓU表示模拟边界.本文采用满足Neumann边界条件的Galerkin原理(徐世浙,1994)来推导GPR小波有限元方程.首先,将待求解区域离散为若干个单元,对任一子单元,可以映射到标准BSWI求解单元.采用二维张量积BSWI尺度函数为插值函数构造小波单元,求解域被分成n×n网格,其中n=2j+m-2,j>j0,j0为保证至少具有一个内部小波的最小尺度,节点数为(n+1)×(n+1).本文采用的V1和V2尺度空间上的二阶区间B样条(BSWI2)小波单元的节点排列如图 2所示.

|
图 2 二维BSWI2小波单元 Fig. 2 Two-dimensional BSWI2 wavelet element |
在小波单元内未知场函数表示为

|
(12) |
Ue为单元内的电场值或磁场值,x,y为总体坐标系,ζ,η为局部坐标系.局部坐标与总体坐标的转换关系为:x=a·ζ,y=b·η,a与b分别为1个单元的长与宽.其中Ae表示单元上待求的小波插值系数列向量,表示为

|
(13) |
式中,

|
定义物理自由度列向量:

|
(14) |
式中uie=[u(ξi,η1)u(ξi,η2)…u(ξi,ηn+1)];ξi=(i-1)/n;ηi=(j-1)/n;i,j=1,2,…,n+1为标准求解域中各节点坐标值.将式(12)带入式(14)得
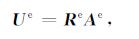
|
(15) |
式中,矩阵Re为
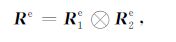
|
(16) |
式中
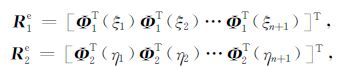
|
(17) |
联立式(12)和式(15),有
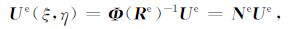
|
(18) |
令矩阵Re的逆矩阵为转换矩阵Te,即
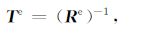
|
(19) |
则式(18)中形函数为
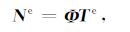
|
(20) |
式(18)可表示为
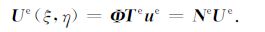
|
(21) |
利用Galerkin法,用形函数N做权函数,将(21)代入(11)式,两边同时乘以δU,在单元内积分得

|
(22) |
对式(22)中左边第2项采用Green公式变换,得到
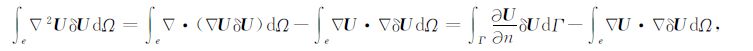
|
由于U丨Γ U=S,固有∇δU丨Γ U=0,则有

|
(23) |
左边第一项
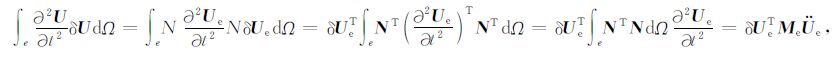
|
(24) |
得到

|
(25) |
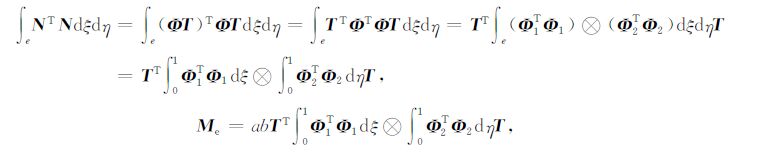
|
(26) |
左边第二项

|
(27) |
其中

|
(28) |
左边第三项
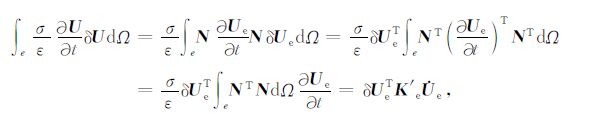
|
(29) |
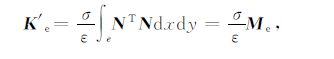
|
(30) |
右边项

|
(31) |
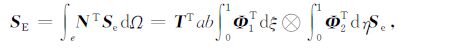
|
(32) |
令

|
(33) |
求出相关的尺度函数积分值和联系系数值即可求得单元矩阵值,现分别列出1尺度及2尺度相关值.1尺度:

|
2尺度:
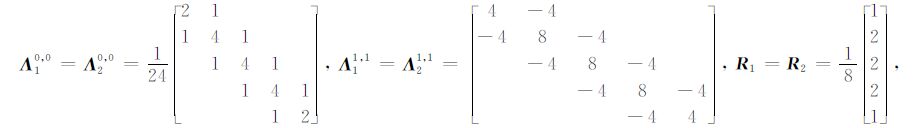
|
则
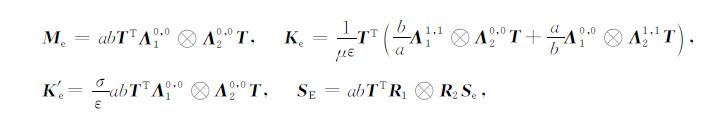
|
(34) |
其中2阶1尺度BSWI21的转换矩阵T为9×9单位矩阵,2阶2尺度BSWI22的转换矩阵T为25×25单位矩阵.根据式(24)、(27)、(29)、(31)得到BSWI单元积分
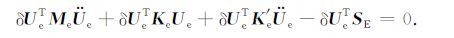
|
(35) |
将各单元的积分相加.相加前,将单元的场值列向量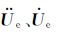
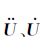
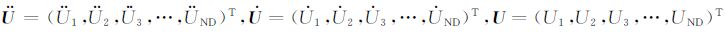
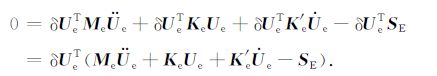
|
由于δUT≠0,故有
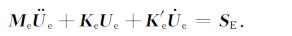
|
按照节点的总体序号,将单元系数矩阵中的各元位置放置在总体的相应行与列的交叉位置上,其余位置的元素为零,因为单元扩展后的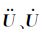

|
故有

|
(36) |
在求解方程组(36)时,式中的一阶及二阶导数可采用中心差分来近似逼近(张新明,2005):
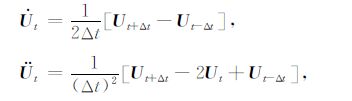
|
(37) |
(36)式可化为
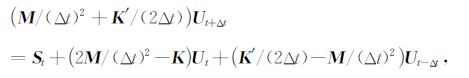
|
(38) |
当零时刻或-Δt时刻,场值为零,且St激励源为已知值.因此,可以通过解上面方程逐步求得不同时间层位上的场值,故式(38)可化简为
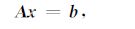
|
(39) |
其中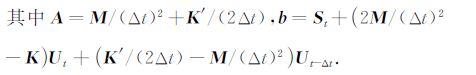
至此,可以得到含衰减项的GPR波动方程的数值解.由以上求解步骤可知,方程左端矩阵A的病态程度由M与Δt决定.因此,该GPR波动方程的算法精度由M确定,数值稳定性由Δt确定,若不考虑Δt而追求提高BSWI求解精度,可能会导致求解结果的不稳定.
4 BSWI算法实例分析 4.1 模型一 BSWI与FEM对比试验为了验证区间B样条小波有限元算法的正确性,选取图 3所示的10.0 m×10.0 m两层地电模型.上层介质厚度为6 m,上、下两层相对介电常数分别为3.5与16.0,电导率分别为0.001 S·m-1与0.1 S·m-1.模型中部有一矩状空洞异常体,长为2 m,高为1 m.波源为100 MHz脉冲零相位Ricker子波,时窗长度为100 ns,采样间隔为0.1 ns.

|
图 3 雷达模型一示意图 Fig. 3 The sketch map of GPR model 1 |
采用BSWI及FEM两种算法对该模型进行正演.FEM采用100×100个边长0.1 m的正方形网格剖分,吸收边界为20层.小波有限元选用图 1a所示的BSWI21以及图 1b所示的BSWI22尺度函数为基函数,每个0.2 m×0.2 m小网格为1个小波单元,共计50×50个小波单元,吸收边界为10层,其中BSWI21每个小波单元细分为2×2区间,BSWI22每个小波单元细分为4×4区间.在Intel(R)Core(TM)i5-3317U CPU@ 1.70 GHz,4.00 GB的内存物理地址扩展,Window 7操作系统笔记本计算该模型雷达单道数据.其中FEM、BSWI21 及BSWI22的计算时间分别为4.91 s、4.71 s、36.05 s.
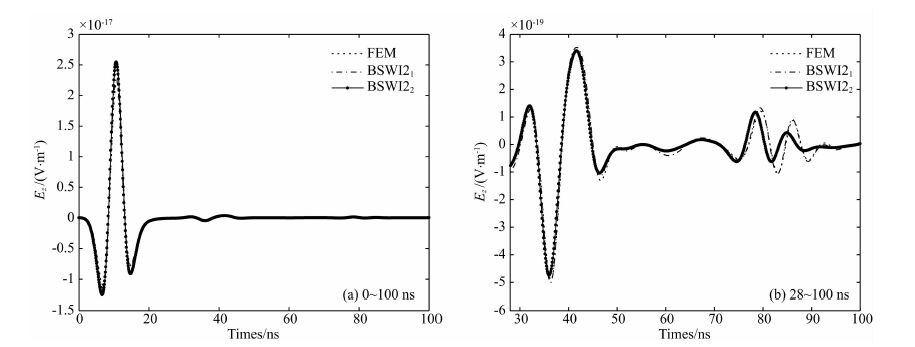
图 4a为FEM 、BSWI21 及BSWI22正演所得的单道数据对比图.图中可见,虚线的FEM、点划线的BSWI21 及实线的BSWI22计算结果重叠在一起,一致性较好,说明了BSWI计算结果的可靠性.图 4b为仅显示28~100 ns时的单道雷达波形,由于去掉了直达波的大振幅值,波场细节能得已体现,说明两种算法的计算结果之间仍存在细小的差别,但矩状异常体及两层介质的分界面在36 ns,60 ns,78 ns处都能得以体现,在28~70 ns区间,三者计算结果基本重合,BSWI22波形幅值存在细微差别.而在78 ns之后,BSWI22幅值与数值振荡都较其他两者小.
|
图 4 有限元、BSWI21 及BSWI22波形数据对比 Fig. 4 Contrasting between FEM BSWI21 and BSWI22 wavelet FEM of GPR waveform |
由此可见,尺度提升对解的精度与稳定性有一定的提高,但计算时间大大增加,其原因主要有:(1)尺度提升后,内部节点数急剧增多,内部节点数由1尺度下的1个增至2尺度的9个,形成的刚度矩阵,维数急剧增大,解方程的时间变长.(2)尺度提升后,若不改变采样间隔,高尺度需要更小的采样间隔,否则容易发散.1尺度时采用0.25 ns的采样间隔即可得到稳定中心差分解,2尺度则需取更小的0.01 ns的采样间隔才能得到稳定的解.而采样间隔的变小会引起求解时间的急剧增加.以BSWI4为例,保证存在内部小波的最小尺度为2,则二维小波单元总点数为49,内部节点数为25,虽然能在一定程度上提高解的精度,但对解的稳定性要求势必增高,求解时间也会大大增加.这也是没有采用更高阶区间B样条小波尺度函数插值的原因.
4.2 模型二 BSWI21与BSWI22尺度提升前后对比试验图 5所示为1.0 m×1.0 m矩形模型,分上下两层,分界面为包括“V”型和一个阶梯的起伏界面,上、下两层介电常数分别为8.0与15.0,电导率分别为0.0001 S·m-1与0.01 S·m-1.下层介质距地表 0.4 m处有一0.04 m×0.04 m矩状空洞异常体.波源频率为900 MHz,时窗长度为15 ns.

|
图 5 雷达模型二示意图 Fig. 5 The sketch map of GPR model 2 |
分别选用BSWI21(1尺度)和BSWI22(2尺度)对该模型进行正演,剖分为50×50网格空间,剖分后的小波单元长为0.02 m,吸收边界为20层.图 6a与图 6b分别为应用1尺度及2尺度正演所得的101道数据雷达剖面图.1尺度采样间隔为0.025 ns,所用时间为297.06 s.2尺度采样间隔为0.015 ns,所用时间为2908.47 s.

|
图 6 模型二雷达正演剖面图 Fig. 6 The section of GPR simulation |
分析图 6可知,纵坐标5 ns处的反射波较好地对应了上下介质分界面;横坐标0.4 m对应了“V”型中心,纵坐标7.5 ns对应阶梯状界面;横坐标0.5 m,纵坐标10 ns处绕射波较好地对应了空洞异常体上界面,矩状异常体下界面反射波能量较弱,在剖面图中反映并不太明显.由此可见,在增益倍数均相同条件下,图 6a与图 6b都能反映异常体的形态,但图 6a的1尺度下雷达反射及绕射波下面出现了较多的多次波,震荡波较为明显;而尺度提高后,雷达波形更简洁、能更清晰地体现异常体信息,对解的精度有较为明显的提高.
5 双相随机介质模型数值算例 5.1 双相随机介质建模欲建立二维双相离散随机骨料结构混凝土模型,骨料级配问题非常重要.本文采用目前最常见的理想级配曲线-最大密实度级配曲线(钟根全等,2008),即富勒曲线,其表达式为
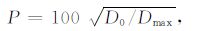
|
(40) |
式中,P为通过筛孔D骨料的质量百分比,Dmax为最大粒径.由富勒级配公式推导出二维截面内任意粒径的骨料出现的概率(Walraven and Reinhard,1991),其表达式为

|
(41) |
式中,D0为筛孔直径,Dmax为最大骨料粒径,Pk为骨料体积占总体积的百分比.由(41)式可求得模拟区域内截面上相应粒径骨料的颗粒数,即

|
(42) |
由本文采用椭圆为基本骨料形状,确定椭圆骨料形状及其位置需要5个随机参数:椭圆的长轴,短轴,倾角,形心坐标(x0,y0).骨料生成与投放的算法如下所示(余涛,2013):
(1) 根据级配曲线计算各粒径级颗粒数;
(2) 依据粒级参数,依次随机生成椭圆长轴,短轴,形心坐标以及倾角参数;
(3) 判断是否与已有椭圆骨料干涉,若发生干涉返回步骤(2);
(4) 输出该骨料参数;
(5) 判断该粒级是否完成,若未完成返回步骤(2);
(6) 判断是否存在下一粒级,若存在,改变粒级参数并返回步骤(2);
(7) 椭圆骨料生成完毕.
判断两个椭圆骨料是否干涉,先考虑椭圆的定义:椭圆上的点到其两个焦点的距离之和等于定长(长轴的长度).两个平面上任意两个椭圆,如果长轴较短的椭圆上的任意一点到另一椭圆两个焦点的距离之和大于长轴较长的椭圆的长轴长度,则这两个椭圆不会发生干涉.在编程实践中,任意点是取椭圆上有限个点代替,即是用椭圆的内接多边形逼近椭圆.
5.2 混凝土模型BSWI模拟算例图 7所示为含有3个空洞的模型图,大小空洞直径分别为0.2 m和0.08 m,模拟区域为1.0 m×1.0 m,背景介质都为混凝土,图 7a与图 7b不同之处为:前者将混凝土介质当成相对介电常数为5.45的均质介质,后者将混凝土看成双相随机介质,其中水泥砂浆相对介电常数为5.45,骨料相对介电常数为8.2,骨料所占模型百分比为0.45,最大和最小骨料粒径分别为0.05 m和0.008 m,两者电导率均为0.001 S·m-1.波源为1000 MHz脉冲零相位Ricker子波,采样时窗长度为12 ns.采用BSWI21模拟时,整个区域剖分为200×200个矩形网格,小波单元边长为0.005 m,吸收边界为20层,模拟过程中发射点与接收点同步移动,采样间隔为0.015 ns,共采样201道雷达数据.
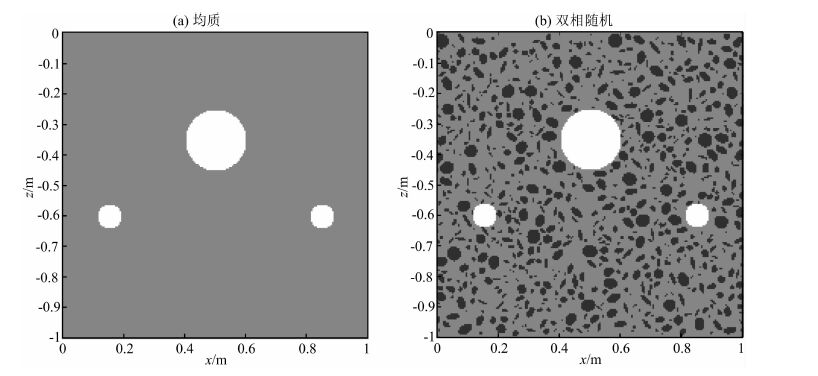
|
图 7 雷达模型图三 Fig. 7 The sketch map of GPR model |
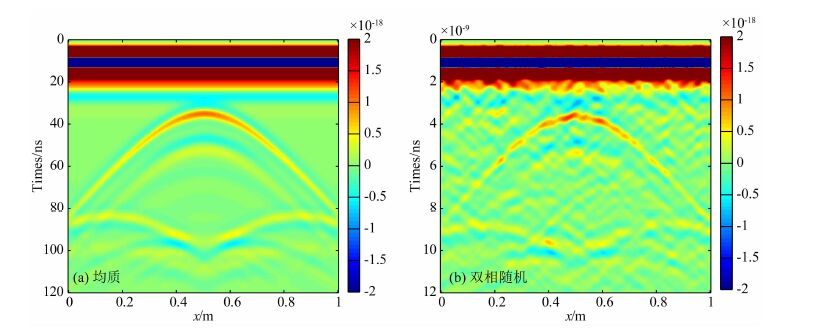
图 8a与图 8b分别对应背景为均质介质与双相随机介质的GPR正演剖面图,其中均质介质模拟耗时为8908.47 s.双相随机介质正演耗时为9137.56 s.图 8a可见上部大圆与两侧小圆引起的双曲绕射波非常圆滑、清晰,波形振幅强,双曲线弧顶位置能准确地指示空洞异常体的上界面.图 8b的双相随机介质中,雷达波受砾石、卵石等骨料的影响散射非常严重,波形发生扭曲,上部大圆的上界面产生的绕射波弧形欠光滑、波形振幅较弱、畸变严重、同相轴连续性较差,剖面中出现了较多的干扰杂波.而下界面与两侧小圆所引起的双曲线反射弧十分微弱,基本无法识别.避免了基于均匀介质理论可探测与识别的GPR异常体,但在实际工作中却无法探到的偏差,较好地解答了混凝土工程实测数据解释中遇到的困惑,给实测资料的合理解译提供了理论依据.实例证明,基于双相随机介质的混凝土模型所得的正演剖面与实测剖面更相符,更有利于指导雷达剖面的数据解译.
|
图 8 模型三雷达正演剖面图 Fig. 8 The section of model 3 GPR simulation |
(1) 编制了二维区间B样条小波有限元GPR正演程序,通过对比相同的剖分方式及节点数目条件下GPR单道波形图,BSWI算法能以较少的计算时间达到FEM相似的精度,证明BSWI算法的正确性.而将BSWI的尺度提升后,模拟得到的雷达波形更简洁、能更清晰地体现异常体信息,对解的精度有较为明显的提高,但计算时间大大增加.说明BSWI是区别于传统网格法和多项式法的另一种提高精度的细化方法,能在不改变网格剖分的前提下提高分辨率,为GPR波动方程求解提供新的思路.
(2) 将混凝土视为随机介质,构建了双相离散随机混凝土模型,使其在物质组成材料参数、骨料形态及分布上与真实的混凝土更具一致性.采用BSWI方法模拟了双相离散随机模型,与均质介质GPR正演剖面图相比,随机介质中GPR波形散射严重,波形扭曲,异常体绕射波弧形欠光滑、波形振幅较弱、剖面中出现了较多的干扰杂波.但随机介质模型的正演剖面能更真实地模拟雷达波的传播过程,与实测剖面特征更相符,更有利于指导雷达剖面的数据解译.
| Amaratunga K, Williams J R. 1993. Wavelet based Green's function approach to 2D PDES. Engineering Computations , 10(4): 349–367. | |
| Amaratunga K, Williams J R, Qian S, et al. 1994. Wavelet-Galerkin solutions for one-dimensional partial differential equations. International Journal for Numerical Methods in Engineering , 37(16): 2703–2716. | |
| Chen X F, Yang S J, Ma J X, et al. 2004. The construction of wavelet finite element and its application. Finite Elements in Analysis and Design , 40(5-6): 541–554. | |
| Chen X F, He Z J, Xiang J W, et al. 2006. A dynamic multiscale lifting computation method using Daubechies wavelet. Journal of Computational and Applied Mathematics , 188(2): 228–245. | |
| Chen X F, Xiang J W, Li B, et al. 2010. A study of multiscale wavelet-based elements for adaptive finite element analysis. Advances in Engineering Software , 41(2): 196–205. | |
| Chui C K, Quak E. 1992. Wavelets on a bounded interval.//Numerical Methods in Approximation Theory, Vol.9. Birkhäuser Basel, 53-75. | |
| Dai Q W, Wang H H. 2013. Element free method forward modeling of GPR based on random medium model. The Chinese Journal of Nonferrous Metals (in Chinese) , 23(9): 2436–2443. | |
| Daubechies I. 1998. Orthonormal bases of compactly supported wavelets. Communications on Pure and Applied Mathematics , 41(7): 909–996. | |
| Di Q Y, Wang M Y. 1999. 2D finite element modeling for radar wave. Chinese J. Geophys. (in Chinese) , 42(6): 818–825. | |
| Di Q Y, Wang M Y. 2004. Migration of ground-penetrating radar data with a finite-element method that considers attenuation and dispersion. Geophysics , 69(2): 472–477. | |
| Feng D S, Chen C S, Dai Q W. 2010. GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD. Chinese J. Geophys. , 53(10): 2484–2496. doi: 10.3969/j.issn.0001-5733.2010.10.022. | |
| Feng D S, Chen C S, Wang H H. 2012. Finite element method GPR forward simulation based on mixed boundary condition. Chinese J Geophys. , 55(11): 3774–3785. doi: 10.6038/j.issn.0001-5733.2012.11.024. | |
| Gao Z G, Liu G T. 2003. Two-dimensional random aggregate structure for concrete. Journal of Tsinghua University(Science and Technology) (in Chinese) , 43(5): 710–714. | |
| Goswami J C, Chan A K, Chui C K. 1995. On solving first-kind integral equations using wavelets on a bounded interval. IEEE Transactions on Antennas and Propagation , 43(6): 614–622. | |
| Guo S L. 2013. Research on GPR wave theory in random medium for detecting highway[Ph. D. thesis] (in Chinese). Wuhan:China University of Geosciences. | |
| He Z J, Chen X F, Li B, et al. Theory of the Wavelet Based Finite Element Methods and the Application in Engineering . (in Chinese) Beijing: Science Press, 2006 . | |
| Jin J M, Xu Y X, Xue P X. 2006. Minimum support spline wavelet finite element. Mathematica Numerica Sinica (in Chinese) , 28(1): 89–112. | |
| Li J, Zeng Z F, Wu F S, et al. 2010. Study of three dimension high-order FDTD simulation for GPR. Chinese J. Geophys. , 53(4): 974–981. doi: 10.3969/j.issn.0001-5733.2010.04.022. | |
| Li J. 2014. Ground penetrating radar detection and parameter inversion in stochastic effective medium[Ph. D. thesis] (in Chinese). Changchun:Jilin University. | |
| Liang X B, Jian B D, Ni G Z. 1988. The B-spline finite element method for electromagnetic field analysis. Journal of Zhejiang University (in Chinese) , 22(2): 100–110. | |
| Liu S X, Zeng Z F. 2007. Numerical simulation for Ground Penetrating Radar wave propagation in the dispersive medium. Chinese J. Geophys. (in Chinese) , 50(1): 320–326. | |
| Mishra V, Sabina. 2011. Wavelet Galerkin solutions of ordinary differential equations. Int. J. Math. Anal. , 5(9-12): 407–424. | |
| Patton R D, Marks P C. 1996. One-dimensional finite elements based on the Daubechies family of wavelets. AIAA Journal , 34(8): 1696–1698. | |
| Quak E, Weyrich N. 1994. Decomposition and reconstruction algorithms for spline wavelets on a bounded interval. Applied and Computational Harmonic Analysis , 1(3): 217–231. | |
| Sabina, Mishra V. 2012. Wavelet-Galerkin solutions of one and two dimensional partial differential equations. Journal of Emerging Trends in Computing and Information Sciences , 3(10): 1373–1378. | |
| Sarkar T K, Adve R S, García-Castillo L E, et al. 1994. Utilization of wavelet concepts in finite elements for an efficient solution of Maxwell's equations. Radio Science , 29(4): 965–977. | |
| Shih C T. 1979. On spline finite element method. Mathematica Numerica Sinica (in Chinese) , 1(1): 50–72. | |
| Sun H X, Xu J Y, Kang T, et al. 2014. The three-dimension spline wavelet finite element construction and application on antiknock of underground box structure. Journal of Xi'an University of Architecture & Technology (Natural Science Edition) , 46(6): 816–821. | |
| Walraven J C, Reinhardt H W. 1981. Theory and experiments on the mechanical behaviour of cracks in plain and reinforced concrete subjected to shear loading. Heron , 26(1A): 26–35. | |
| Xiang J W, Chen X F, He Z J, et al. 2007. The construction of 1D wavelet finite elements for structural analysis. Computational Mechanics , 40(2): 325–339. | |
| Xiang J W, Chen X F, He Z J, et al. 2008a. A new wavelet-based thin plate element using B-spline wavelet on the interval. Computational Mechanics , 41(2): 243–255. | |
| Xiang J W, Chen X F, Yang L F, et al. 2008b. A class of wavelet-based flat shell elements using B-spline wavelet on the interval and its applications. CMES-Computer Modeling in Engineering and Sciences , 23(1): 1–12. | |
| Xu S Z. The Finite Element Method in Geophysics . (in Chinese) Beijing: Science Press, 1994 . | |
| Yee K S. 1966. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media. IEEE Transactions on Antennas and Propagation , 14(3): 302–307. | |
| Yu T. 2013. Numerical simulation of ultrasonic wave propagation in concrete[Master thesis] (in Chinese). Changsha:Central South University. | |
| Zhang J, Jin N G, Jin X Y, et al. 2004. Numerical simulation method for polygonal aggregate distribution in concrete. Journal of Zhejiang University (Engineering Science) (in Chinese) , 38(5): 581–585. | |
| Zhang X M, Liu K A, Liu J Q. 2005. A wavelet finite element method for the 2-D wave equation in fluid-saturated porous media. Chinese J Geophys. (in Chinese) , 48(5): 1156–1166. | |
| Zhong G Q, Li L J, Liu F, et al. 2008. Numerical simulation of two-dimensional random aggregate in concrete. Concrete (in Chinese) (9): 70–73. | |
| 戴前伟, 王洪华. 2013. 基于随机介质模型的GPR无单元法正演模拟. 中国有色金属学报 , 23(9): 2436–2443. | |
| 底青云, 王妙月. 1999. 雷达波有限元仿真模拟. 地球物理学报 , 42(6): 818–825. | |
| 冯德山, 陈承申, 戴前伟. 2010. 基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟. 地球物理学报 , 53(10): 2484–2496. | |
| 冯德山, 陈承申, 王洪华. 2012. 基于混合边界条件的有限单元法GPR正演模拟. 地球物理学报 , 55(11): 3774–3785. | |
| 高政国, 刘光廷. 2003. 二维混凝土随机骨料模型研究. 清华大学学报(自然科学版) , 43(5): 710–714. | |
| 郭士礼. 2013. 基于随机介质的高速公路探地雷达检测理论研究[博士论文]. 武汉:中国地质大学. | |
| 何正嘉, 陈雪峰, 李兵, 等. 小波有限元理论及其工程应用. 北京: 科学出版社, 2006 . | |
| 金坚明, 徐应祥, 薛鹏翔. 2006. 最小支集样条小波有限元. 计算数学 , 28(1): 89–112. | |
| 李静, 曾昭发, 吴丰收, 等. 2010. 探地雷达三维高阶时域有限差分法模拟研究. 地球物理学报 , 53(4): 974–981. | |
| 李静. 2014. 随机等效介质探地雷达探测技术和参数反演[博士论文]. 长春:吉林大学. | |
| 梁旭彪, 简柏敦, 倪光正. 1988. 电磁场数值分析中的B样条有限元法. 浙江大学学报 , 22(2): 100–110. | |
| 刘四新, 曾昭发. 2007. 频散介质中地质雷达波传播的数值模拟. 地球物理学报 , 50(1): 320–326. | |
| 石钟慈. 1979. 样条有限元. 计算数学 , 1(1): 50–72. | |
| 孙惠香, 许金余, 康婷, 等. 2014. 三维样条小波单元构造及其在地下箱型结构抗爆数值模拟中的应用. 西安建筑科技大学学报(自然科学版) , 46(6): 816–821. | |
| 徐世浙. 地球物理中的有限单元法. 北京: 科学出版社, 1994 . | |
| 余涛. 2013. 超声波在混凝土中传播的数值模拟[硕士论文]. 长沙:中南大学. | |
| 张剑, 金南国, 金贤玉, 等. 2004. 混凝土多边形骨料分布的数值模拟方法. 浙江大学学报(工学版) , 38(5): 581–585. | |
| 张新明, 刘克安, 刘家琦. 2005. 流体饱和多孔隙介质二维弹性波方程正演模拟的小波有限元法. 地球物理学报 , 48(5): 1156–1166. | |
| 钟根全, 李丽娟, 刘锋, 等. 2008. 混凝土二维随机骨料的数值模拟. 混凝土 (9): 70–73. | |
 2016, Vol. 59
2016, Vol. 59

