2. 中国石油大学(北京)海洋石油勘探国家工程实验室, 北京 102249
2. National Engineering Laboratory for Offshore Oil Exploration, China University of Petroleum, Beijing 102249, China
叠前地震数据相对于叠后资料保留了更多的地下地质信息,基于叠前地震数据的AVO反演可以提供更可靠、更准确的岩性信息和流体信息,因此叠前AVO反演技术在实际生产中得到了广泛应用(张芝铭等,2015).利用叠前AVO三参数反演可以获取纵波速度、横波速度和密度信息,其反演精度对储层预测与油气藏描述有至关重要的影响.基于Zoeppritz近似公式的反演方法要求地震数据入射角度较小,通常在30度以内,但小偏移据地震振幅对密度信息变化敏感度较差,精确反演密度信息通常需要入射角度大于30度的中远偏移距地震振幅信息,而且Zoeppritz近似公式在计算PS波反射系数时误差较大,限制了PP波和PS波联合反演对反演精度的改善,因此基于Zoeppritz近似公式的反演方法限制了叠前反演精度的提高,尤其是密度信息.而基于精确Zoeppritz方程的反演方法可以克服这一矛盾问题,且方便实现PP波与PS波的联合反演,进一步提高纵波速度、横波速度尤其是密度信息的反演精度与稳定性(石玉梅等,2010;Khare and Rape,2007;Behura et al.,2007;Tarantola,1986).
由于精确Zoeppritz方程与三个弹性参数之间是复杂的非线性关系,通常采用非线性反演或者是广义线性反演作为优化算法.杨培杰和印兴耀(2008) 提出了基于支持向量机的非线性反演方法,该方法的正演过程是直接求解非线性的Zoeppritz方程.Zhu和McMechan(2012) 、Zhi等(2013) 均提出基于精确Zoeppritz方程的AVO反演方法,他们将PP波和PS波反射系数改写为关于速度比和密度比的函数来构建反演目标函数进行求解.张丰麒等(2013) 提出了基于精确Zoeppritz方程三变量柯西分布先验约束的广义线性AVO反演,实现了纵波速度、横波速度和密度三个参数的间接反演.基于统计理论的贝叶斯反演,通过引入模型参数的先验信息作为反演的正则化约束条件,有效的降低了反演的不适定性(Downton et al.,2001).Downton(2005) 针对二项和三项AVO波形反演,提出采用三种不同的长尾巴分布来描述三参数反射系数,相对高斯分布,长尾巴分布能产生稀疏脉冲反演的效果,提高反演的分辨率.Alemie和Sacchi(2011) 通过对比分析认为三参数反射系数服从三变量柯西分布更为合理,并引入相关矩阵来消除三参数反射系数之间的统计相关性,进一步降低了反演的不适定性,提高反演结果的精度.PS波地震资料包含丰富的密度信息,通过多波AVO联合反演将PP波和PS波数据优势互补,提高AVO三参数反演的精度(Margrave et al.,2001;Stewart,1990).Stewart(1990) 首先提出了由多波反射系数求弹性参数的PP波和PS波联合反演的框架方程.陈天胜等(2006) 、冯晅等(2008) 基于Aki-Richards近似公式提出了多波联合线性AVO直接反演方法,计算效率比较高.Zhi等(2013) ,提出了基于精确Zoeppritz方程的PP-PS波联合反演.付雷等(2008) 将多波联合线性AVO直接反演方法应用到实际资料的反演中,取得了比较理想的反演结果.
本文在前人研究的基础上,基于贝叶斯理论,利用精确Zoeppritz方程建立了多波联合非线性AVO反演理论框架.利用Taylor展开得到反演目标函数的二阶非线性近似,进而求解得到模型参数的更新迭代公式,实现对纵波速度、横波速度和密度三个参数的直接反演.
2 理论与方法 2.1 正演模型理论利用精确Zoeppritz方程进行正演,不仅可以避免Zoeppritz方程近似公式带来的计算误差,而且可以直接对纵波速度、横波速度以及密度三个弹性参数进行反演,公式为
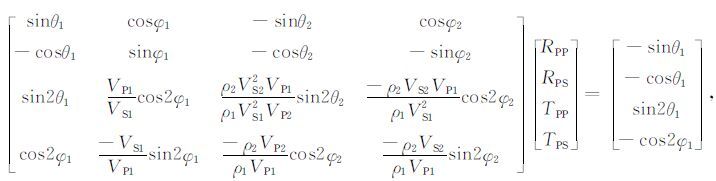
|
(1) |
从精确Zoeppritz方程可以看出,RPP和RPS均是关于VP,VS,ρ这三个弹性参数的复杂函数.根据褶积模型,模型参数与叠前地震数据的关系可表示为
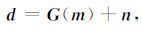
|
(2) |
式(2) 中, d T=(d1,d2,…dM)T为叠前观测地震数据, m T=(m1,m2,…ml)T为模型参数,G 为正演算子,G(m)为将正演算子 G 作用于模型参数 m 时得到的合成地震记录,n 为观测地震记录中的噪声.
2.2 反演目标函数构建根据贝叶斯理论,在叠前地震反演中,事件B为模型参数mT=(m1,m2,…m3N)T,事件A为叠前观测地震数据 d T=(d1,d2,…dNd)T.在已知叠前地震数据的情况下,反演地下介质弹性参数的问题可以归结为求解
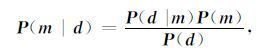
|
(3) |
式中 P(d)为观测数据的边缘概率分布,在已知观测数据的情况下是一个归一化因子,可以看作常数,它保证后验概率分布函数P(m|d)的积分和为1,P(d|m)为似然函数,P(m)为先验概率分布.
研究中假设观测地震数据中的噪声n服从高斯分布,那么似然函数可以表示为:
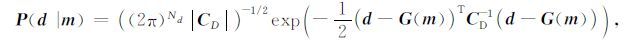
|
(4) |
上式中,矩阵 C D是噪声的协方差矩阵,Nd是观测数据的长度.对于多波地震数据,似然函数可以推广为
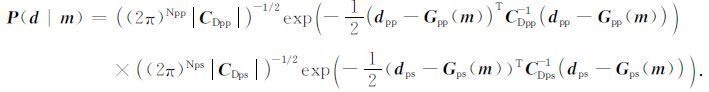
|
(5) |
贝叶斯反演通过引入模型参数的先验分布来构建反演的正则化约束项,从而提高反演的适定性.大量的研究表明,在有地质背景的情况下,三参数之间存在一定的统计相关性,Castagna等(1985) 发现了纵波和横波速度之间存在的线性关系,Gardner等(1974) 研究了纵波速度和密度之间的关系,Potter等(1998) 讨论了横波速度和密度之间的关系.Downton(2005) 提出通过对三参数的协方差矩阵进行特征值分解,进而达到对三参数进行去相关,使其符合同一时间采样点三参数之间统计独立不相关这一假设.Alemie和Sacchi(2011) 等通过对比多变量高斯分布和三变量柯西分布作为先验约束时的反演结果,提出了基于三变量柯西分布的高分辨率三参数AVO反演方法.杜向东(2014) 基于纵波和横波速度之间存在统计相关性的事实利用基于三变量柯西约束的AVO反演进行了横波精细估算,取得很好的效果.
图 1为二维t分布图,从图中可以看出,柯西分布的两个相关变量的概率密度拥有更窄的分布,具有相对较好的确定性.因此,结合前人的研究,选择三变量柯西分布作为本文反演问题的先验约束,提高了纵波速度、横波速度尤其是密度信息反演结果的稳定性和精度.
三变量柯西分布是t分布的一种特殊情况,根据Alemie和Sacchi的研究,三变量柯西分布不仅能够很好的融合三参数的相关性,还能恢复大的待反演参数值,具体表达式为

|
(6) |
式(6) 中, Φ i=(D i)T Ψ -1 D i,Ψ 是3×3的协方差矩阵,它包含三个AVO参数之间统计相关性,N是模型参数的长度,D 是3×3N的矩阵,具体形式为
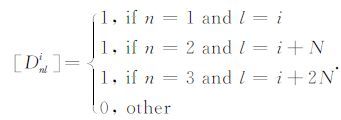
|
(7) |

|
图 1 二维高斯分布和柯西分布的对比 Fig. 1 Comparison of Cauchy distribution with Gaussian distribution(2D) |
根据贝叶斯理论,模型参数的后验概率密度分布函数满足如下关系式:
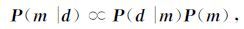
|
(8) |
略去与模型参数后验概率密度函数形状无关的常量并结合多波联合反演可得到
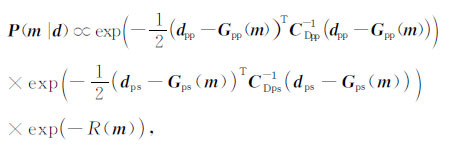
|
(9) |
式(9) 中,
通过蒙特卡洛的方法求解式(9) 可以得到模型参数的后验概率分布函数,用于评价反演模型参数的不确定性.但蒙特卡洛反演方法计算量比较大,通常取 P(m |d)最大值对应的模型参数作为最优解,也就是模型参数的最大后验概率解.求解式() 最大后验概率解也就等价于求解下式目标函数 J(m)1的最小值所对应的解:
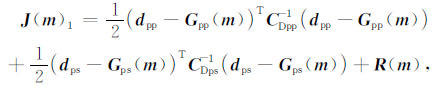
|
(10) |
假设地震数据中随机噪声之间相互独立,并服从高斯分布,则目标函数中的协方差矩阵可以简化为对角阵,即 C D=σn2 I,其中σn2表示噪声的方差,I 是Nd×Nd的单位矩阵,Nd是观测数据的长度.在上述目标函数中,设PP波地震数据的噪音方差为σpp,PS波地震数据的噪音方差为σps,则上式可以简化为:
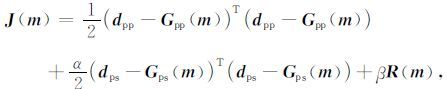
|
(11) |
式(11) 中,α=σpp/σps,β=σpp.
对目标函数 J(m)在 m 0处进行Taylor二阶展开:
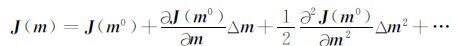
|
(12) |
其中, J(m)关于m的一阶偏导数为:
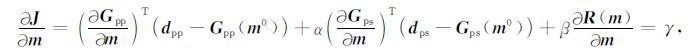
|
(13) |
J(m)关于m的二阶偏导数为:
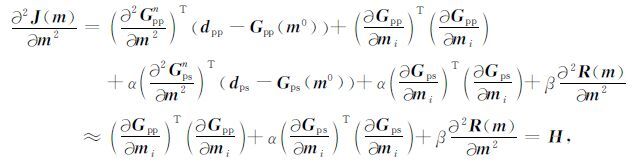
|
(14) |
γ和H 中正演算子关于模型参数的一阶偏导数可借助Aki和Richards(1980) 推导的不同入射波情况下的反射和透射表达式来求解,其表达式为
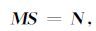
|
(15) |
假设 c j=\[c1 c2 c3 c4 c5 c6\]=\[α1 α2 β1 β2 ρ1 ρ2\] 为第j个界面两侧地层的弹性参数,c1-c6分别为地层分界面上下两侧的纵波速度、横波速度和密度.将式(15) 两边同时对ci求导得:
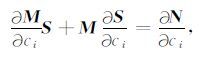
|
(16) |
整理可得:

|
(17) |
根据上式结果,将等式右边对应行和列相乘便可以得到第j个界面的纵波反射系数和转换横波反射系数关于界面两侧纵波速度、横波速度以及密度的一阶偏导数,然后在将地震子波与之进行褶积,就得到了基于Zoeppritz方程的正演算子关于模型参数m的一阶偏导数.
最终,根据上述推导,可以得到模型参数的更新迭代公式
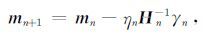
|
(18) |
式中,γn和H n分别表示目标函数关于模型参数m的一阶偏导数和二阶导偏数.ηn为第n次模型参数更新时的步长因子,通常取值为0到1之间.
虽然以上公式是基于多波地震数据的贝叶斯非线性公式,但如果把下标ps 改为x代表多分量地震的水平分量,下标pp改为z代表地震数据的垂直分量,则上述公式可以直接推广到多分量地震数据的贝叶斯反演中.
3 合成数据试算为了检验研究反演算法的可行性和抗噪性,利用图 2所示的模型参数进行反演算法试算.基于图 2给出的弹性参数利用精确Zoeppritz方程分别计算出不同时间采样点、不同角度处(以4°为间隔,4°到40°之间的10个角度)的纵波反射系数和转换横波反射系数,并与30 Hz的雷克子波进行褶积运算合成叠前角道集,如图 3所示.为了检验反演算法的抗噪性,在合成叠前角道集上加入信噪比为4的随机噪声,并利用该算法进行反演,检验方法的抗噪性.
|
图 2 真实模型参数(实线)和初始模型参数(虚线) Fig. 2 Real model data(solid line)and initial model data(dotted line) |

|
图 3 合成叠前角道集 Fig. 3 Synthetic angle gathers |
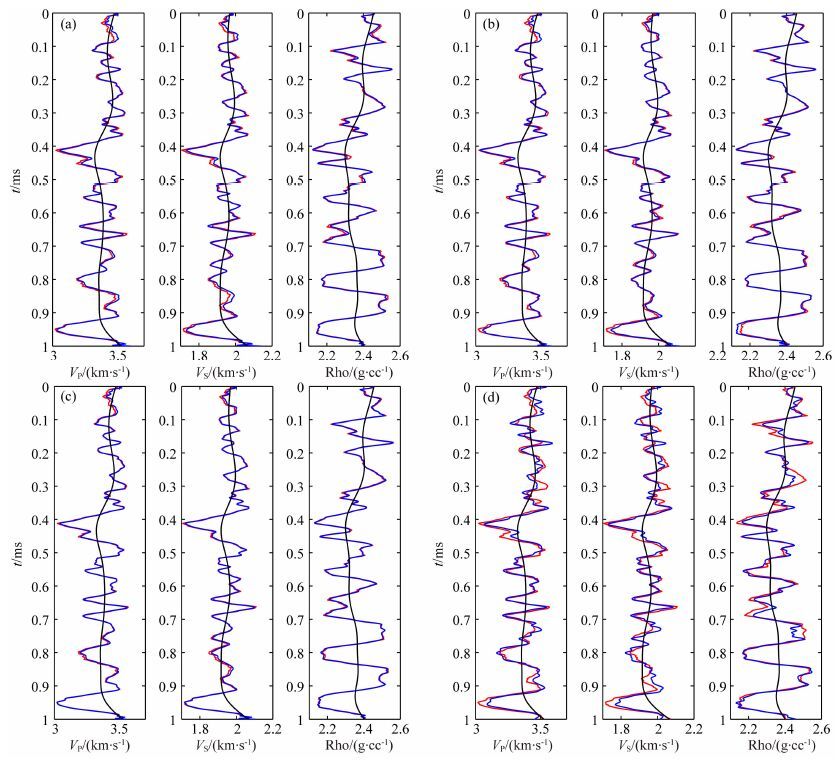
利用合成叠前角道集数据分别进行了如下四种反演:基于柯西先验约束的PP波独立反演、基于柯西先验约束的PS波独立反演、基于柯西先验约束的PP波和PS波联合反演、信噪比为4 ∶ 1时基于柯西先验约束的PP波和PS波联合反演.其反演结果分别如图 4(a—d)所示.初始模型参数是通过对真实模型参数进行多次光滑平均得到的,如图 2所示的虚线.图 4(a)是基于三变量柯西分布的PP波单独反演结果,从反演结果来看,该反演算法不仅能够直接反演纵波速度、横波速度和密度,而且具有很高的精度.仅利用PS波数据同样可以直接反演出纵波速度、横波速度和密度,如图 4(b)所示,但与利用纵波数据单独反演一样,存在反演精度不够高的问题.因此,考虑使用纵横波联合反演,提高反演精度.从图 4(c)中可以看出,PP波和PS波数据联合反演进一步的增强了反演结果的稳定性,对反演结果精度的提高具有明显的促进作用.
|
图 4 四种反演结果,其中红线代表真实模型参数,黑线代表初始模型参数,蓝线代表反演结果 (a)PP波单独反演;(b)PS波单独反演;(c)PP-PS联合反演;(d)含噪声时PP-PS联合反演. Fig. 4 Four inversion results. The red line indicates the true model date,the black line indicates the initial model date,and the blue line indicates the initial model date. (a)PP wave inversion;(b)PS wave inversion;(c)joint PP and PS wave inversion; (d)joint PP and PS wave inversion with noise. |
为了检验该反演算法的抗噪性,对信噪比为4的含噪叠前角道集进行PP波和PS波数据联合反演,从图 4(d)中的反演结果可以看出,随机噪声对反演结果影响较大,尤其是在0.4、0.9、0.95 s等模型参数极大(或极小)或者反射较弱的地方,影响尤为严重,但整体还是吻合很好.总体上,可以看出该反演算法具有较高的抗噪能力.
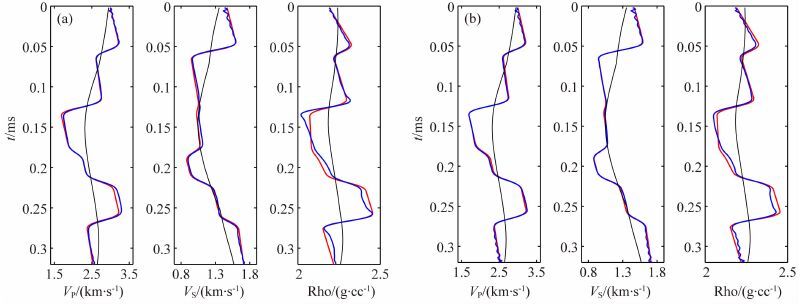
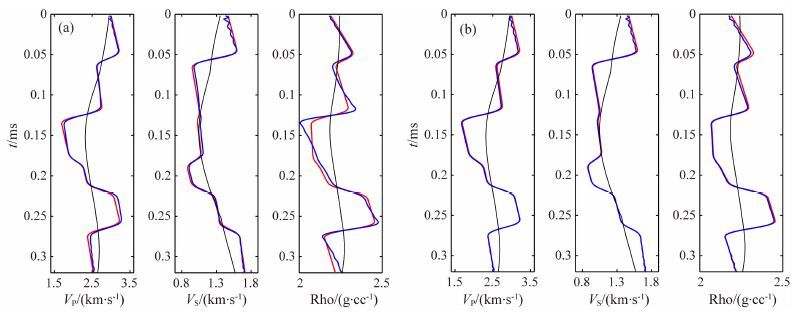
为了进一步分析基于精确Zoeppritz方程反演方法的优点,基于四类AVO响应地质模型,构建如图 5红线所示模型数据并合成对应角道集数据,然后分别利用基于Aki-Richards近似公式和精确Zoeppritz方程的反演方法进行反演试验,并将反演结果进行对比分析.图 5是利用0~30°PP波角道集单独反演的结果.图 6是利用0~45°PP波角道集单独反演的结果.图 7是利用0~45°PP波和PS波角道集联合反演的结果.在图 5、6、7和8中红线代表真实模型参数,黑线代表初始模型参数,蓝线代表反演结果.
从图 5中的反演结果对比可以看出,当仅利用角度范围为0~30°的近中偏移距PP波资料单独反演时,虽然利用Aki-Richards近似公式计算反射系数存在一定的误差,但在较小的角度范围内,计算得到的反射系数误差较小,其反演结果与基于精确Zoeppritz方程的反演结果相比差别不大.对比图 5和图 6可以看出,当利用包含大偏移距地震振幅信息的0~45°PP波角道集资料单独反演时,由于引入了大偏移距地震振幅信息,基于精确Zoeppritz方程反演得到的纵波速度、横波速度尤其是密度的精度得到了很大的提高.随着入射角度的变大,近似公式计算得到的纵波反射系数误差越来越大,虽然引入了大偏移距信息,但由于存在较大误差,使得基于Aki-Richards近似公式的反演结果精度没有得到较大改善,从误差系数分析来看密度项参数的反演结果精度甚至变差了.从上述结果可以看出在利用大偏移距信息方面,基于Zoeppritz方程的反演方法明显优于基于近似公式的反演方法.研究进行了大偏移距资料的联合反演对比,对比图 6和图 7可以看出,联合反演进一步提高了研究方法反演结果的精度.联合反演在一定程度上能够提高反演结果的稳定性和精度,但由于近似公式计算得到的横波反射系数误差较大,使得基于近似公式的反演结果精度虽然有所提升,但和新方法反演结果精度相比,差距很大,尤其是实际反演中很难准确估计的密度项参数反演结果.
|
图 5 利用0~30°PP波角道集资料单独反演结果 (a)基于Aki-Richards近似公式的反演结果;(b)基于精确Zoeppritz方程的反演结果 Fig. 5 Inversion using 0°~30°PP wave angle gathers data alone (a)The inversion results based on Aki-Richards approximation formula; (b)The inversion results based on exact Zoeppritz equations. |
|
图 6 利用0~45°PP波角道集资料单独反演结果 (a)基于Aki-Richards近似公式的反演结果;(b)基于精确Zoeppritz方程的反演结果. Fig. 6 Inversion using 0°~45°PP wave angle gathers data alone (a)The inversion results based on Aki-Richards approximation formula; (b)The inversion results based on exact Zoeppritz equations. |

|
图 7 利用0~45°PP-PS波角道集资料联合反演结果 (a)基于Aki-Richards近似公式的反演结果;(b)基于精确Zoeppritz方程的反演结果. Fig. 7 Joint inversion using 0°~45°PP and PS wave angle gathers data (a)The inversion results based on Aki-Richards approximation formula; (b)The inversion results based on exact Zoeppritz equations. |
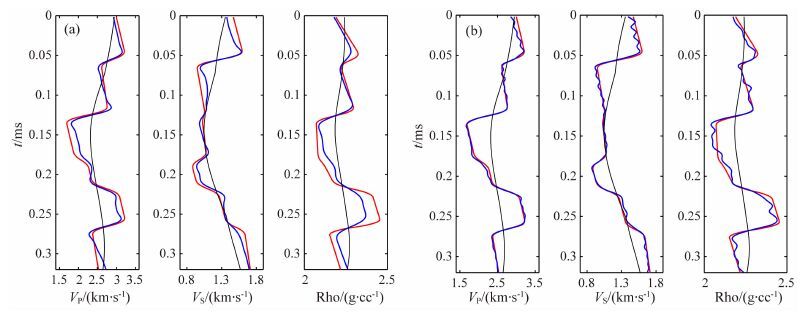
为了对比分析两种反演方法的抗噪性,在合成角道集上加入信噪比为4的随机噪声,图 8为两种反演方法在加入随机噪声情况下的反演结果,从图中可以看出,加入随机噪声之后,基于Aki-Richards近似公式的反演结果与真实模型数据的吻合程度明显变差,而基于Zoeppritz方程的反演结果还是能够很好的和真实模型参数吻合,尤其是纵波速度和横波速度.综上所述,研究方法在利用大偏移距信息、联合反演以及抗噪方面相比于基于近似公式的反演方法具有极大的优势.
|
图 8 利用0~45°PP-PS波角道集资料(信噪比为4:) 合反演结果 (a)基于Aki-Richards近似公式的反演结果;(b)基于精确Zoeppritz方程的反演结果 Fig. 8 Joint inversion using 0°~45°PP and PS wave angle gathers data(S/N=4) (a)The inversion results based on Aki-Richards approximation formula; (b)The inversion results based on exact Zoeppritz equations. |
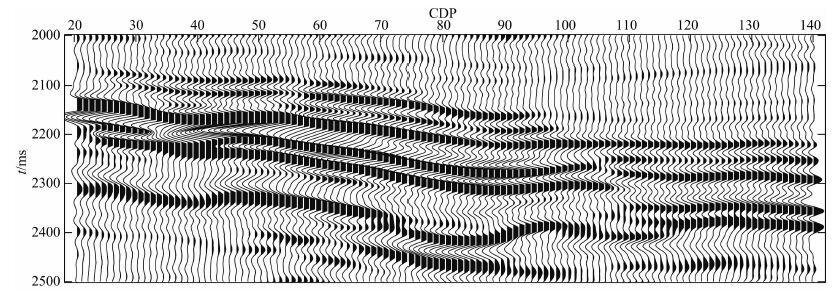
实际数据取自国内X工区,该工区位于凹陷构造带上,断层非常发育,图 9给出了实际数据叠加剖面.实际角道集资料的角度范围为3~34°,且其处理经过了球面扩散补偿、吸收衰减补偿、地表一致性振幅校正、地表一致反褶积、噪声压制、动校正以及叠前时间偏移等环节.
|
图 9 X工区实际叠加剖面 Fig. 9 Real data stack section of X work area |
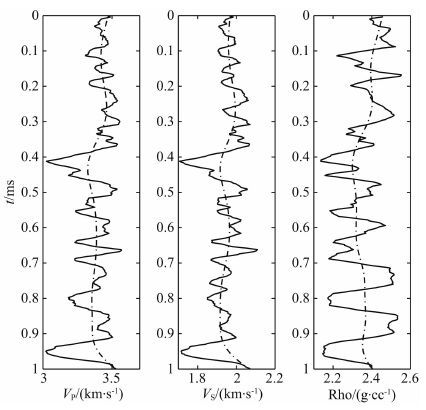
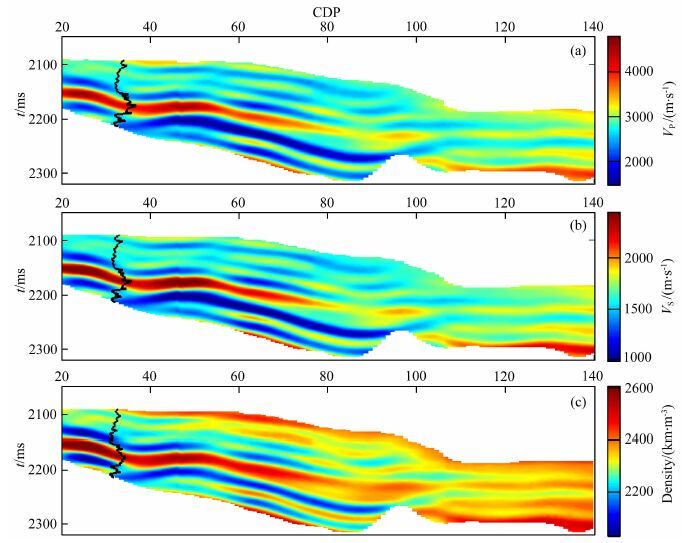
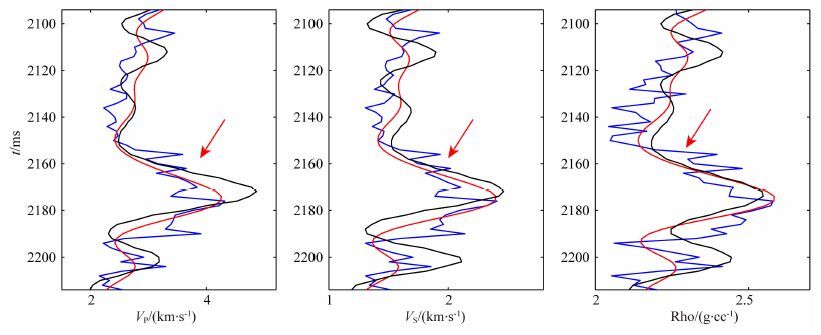
图 10是利用研究方法反演X工区实际数据得到的纵波速度、横波速度和密度剖面,图中的黑色曲线为对应位置的实际测井曲线.从图中可以看出,反演结果与测井曲线吻合良好,具有很高的精度,充分证明了该反演方法在实际资料应用中的可行性和有效性.为了进一步验证研究方法的反演精度,将井旁道的新方法反演结果与基于近似公式的反演软件反演结果进行对比分析,如图 11所示.从图中可以看出,相比于黑色曲线,红色曲线与蓝色实际测井曲线吻合更好,尤其是在图中红色箭头所示的目标储层位置,说明新方法反演结果与实际测井曲线吻合更好,并且黑色曲线所示的反演结果是商业化反演软件的反演结果,必然是经过很多优化处理的,但从反演结果对比可以看出其精度低于研究方法的反演结果精度,充分体现了研究方法的优越性.对于非常规油气藏勘探而言,纵波速度、横波速度尤其是密度信息反演结果精度的提升对流体饱和度计算和TOC含量计算等都至关重要.研究提出的基于精确Zoeppritz方程的反演算法,能够通过提取大偏移距地震振幅信息和纵横波联合反演来提高三个弹性参数反演结果的精度,但上述实际数据反演结果表明,即使由于实际资料的限制,在仅利用包含近中偏移距地震振幅信息的PP波资料单独反演的情况下,其反演结果较基于近似方程反演结果具有更高的精度.
|
图 10 实际数据反演剖面,纵波速度(a),横波速度(b),密度(c),图中黑线为实际测井曲线. Fig. 10 The section of inversion results from real data.(a)P-wave velocity section. (b)S-wave velocity section.(c)Density section. |
|
图 11 新方法反演结果与反演软件反演结果的对比,其中蓝色曲线代表真实井曲线,红色曲线代表新方法反演结果,黑色曲线代表反演软件反演结果,红色箭头所示位置为目标储层的位置. Fig. 11 The inversion result comparison between the new method and software. Blue curves represent real well logs,red curves represent the inversion results of the new method,black curves represent the software inversion results,the red arrows show the positions of target reservoirs. |
5.1 研究提出的基于精确Zoeppritz方程的非线性AVO三参数反演方法很好的避免了近似公式带来的计算误差,特别是在大角度(或大偏移距)的情况下.通过结合贝叶斯理论,引入模型参数的先验分布作为反演的约束项,并假设模型参数的先验信息服从柯西分布,大大降低了反演的不适定性,提高了反演结果的精度.在反演过程中不需要对精确Zoeppritz 方程进行改写,实现了对纵波速度、横波速度和密度三个弹性参数的直接反演,减少了间接求解带来的误差.通过合成数据试验和实际数据测试可以看出,该方法不仅可以直接反演纵波速度、横波速度和密度,而且具有很高的精度,尤其是常规反演很难确定的密度项参数,对储层流体识别具有重要意义.
5.2 从基于合成数据的Aki-Richards近似公式反演结果和研究方法反演结果对比可以看出,研究方法在利用大角度(或大偏移距)地震振幅信息、联合反演以及抗噪方面都优于基于近似公式的反演方法.但是,研究方法在达到或者超过临界角的地震数据应用方面还存在一定的问题,因此如何将该方法推广到临界角的情况,使其能应用于地质构造更加复杂的实际数据反演中,是本文研究方法继续改进和完善的一个重要方向,且该方法的联合反演是在纵横波资料时间域匹配良好前提下进行的,同时也没有考虑各向异性等影响因素.
| Aki K, Richards P G. 1980. Quantitative Seismology: Theory and Methods, Vol. 1. San Francisco, CA: W. H. Freeman & Co. | |
| Alemie W, Sacchi M D. 2011. High-resolution three-term AVO inversion by means of a trivariate Cauchy probability distribution. Geophysics , 76(3): R43–R55. | |
| Behura J, Kabir N, Crider R, et al. 2007. Density extraction from P-wave AVO inversion: Tuscaloosa Trend example.// 2007 SEG Annual Meeting. San Antonio, Texas: Society of Exploration Geophysicists, 1466-1470. | |
| Castagna J P, Batzle M L, Eastwood R L. 1985. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks. Geophysics , 50(4): 571–581. | |
| Chen T S, Liu Y, Wei X C. 2006. Joint amplitude versus offset inversion of P-P and P-SV seismic data. Journal of China University of Petroleum (in Chinese) (in Chinese) , 30(1): 33–37. | |
| Downton J E, Pickford S, Lines L R. 2001. Constrained three parameter AVO inversion and uncertainty analysis.// 2001 SEG Annual Meeting. San Antonio, Texas: SEG, 251-254. | |
| Downton J E. 2005. Seismic Parameter Estimation from AVO inversion [Doctor's thesis]. Calgary: University of Calgary. | |
| Du X D. 2014. Shear wave velocity delicate estimation based on Trivariate Cauchy constraint AVO inversion. Progress of Geophysics (in Chinese) , 29(2): 681–688. doi: 10.6038/pg20140228. | |
| Feng X, Shu M C, Wang Z G, et al. 2008. Joint AVO inversion using P-P and P-SV seismic data. Progress in Geophysics (in Chinese) (in Chinese) , 23(5): 1556–1559. | |
| Fu L, Wang J M, Kong X B, et al. 2008. Study on application of multi-wave AVO analysis in Xincheng area. Oil Geophysical Prospecting (in Chinese) (in Chinese) , 43(1): 88–92. | |
| Gardner G H F, Gardner L W, Gregory A R. 1974. Formation velocity and density: The diagnostic basics for stratigraphic traps. Geophysics , 39(6): 770–780. | |
| Khare V, Rape T. 2007. Density inversion using joint PP/PS data: Sensitivity to the angle range.// 2007 SEG Annual Meeting. San Antonio, Texas: SEG, 965-969. | |
| Margrave G F, Stewart R R, Larsen J A. 2001. Joint PP- and PS-seismic inversion. The Leading Edge , 20(9): 1048–1052. | |
| Potter C C, Dey A K, Stewart R R. 1998. Density prediction using P-and S-wave sonic velocity. CREWES Research Report (University of Calgary) , 10: 320. | |
| Shi Y M, Yao F C, Sun H S, et al. 2010. Density inversion and porosity estimation using seismic data. Chinese J. Geophys. (in Chinese) , 53(1): 197–204. doi: 10.3969/j.issn.0001-5733.2010.01.022. | |
| Stewart R R. 1990. Joint P and P-SV inversion. CREWES Research Report , 2: 112–115. | |
| Tarantola A. 1986. A strategy for nonlinear elastic inversion of seismic reflection data. Geophysics , 51(10): 1893–1903. | |
| Yang P J, Yin X Y. 2008. Prestack seismic inversion method based on support vector machine. Journal of China University of Petroleum (in Chinese) (in Chinese) , 32(1): 37–41. | |
| Zhang F Q, Wei F J, Wang Y C, et al. 2013. Generalized linear AVO inversion with the priori constraint of trivariate Cauchy distribution based on Zoeppritz equation. Chinese J. Geophys. (in Chinese) , 56(6): 2098–2115. doi: 10.6038/cjg20130630. | |
| Zhang Z M, Zhang M X, Hu Y S. 2015. Application of prestack inversion to volcano rock reservoir prediction in the area Yingshan-Shuangcheng fault depression. Progress of Geophysics (in Chinese) , 30(2): 621–627. doi: 10.6038/pg20150219. | |
| Zhi L X, Chen S Q, Li X Y. 2013. Joint AVO inversion of PP and PS waves using exact Zoeppritz equation.// 2013 SEG Annual Meeting. Houston, Texas: SEG, 457-461. | |
| Zhu X F, McMechan G. 2012. AVO inversion using the Zoeppritz equation for PP reflections.// 2012 SEG Annual Meeting. Las Vegas, Nevada: SEG, 1-5. | |
| 陈天胜, 刘洋, 魏修成. 2006. 纵波和转换波联合AVO反演方法研究. 中国石油大学学报(自然科学版) , 30(1): 33–37. | |
| 杜向东. 2014. 基于三元柯西约束AVO反演的横波精细估算方法. 地球物理学进展 , 29(2): 681–688. | |
| 冯晅, 舒梦珵, 王兆国, 等. 2008. P-P波和P-SV波联合AVO反演研究. 地球物理学进展 , 23(5): 1556–1559. | |
| 付雷, 王建民, 孔祥波, 等. 2008. 多波AVO分析在兴城地区的应用研究. 石油地球物理勘探 , 43(1): 88–92. | |
| 石玉梅, 姚逢昌, 孙虎生, 等. 2010. 地震密度反演及地层孔隙度估计. 地球物理学报 , 53(1): 197–204. | |
| 杨培杰, 印兴耀. 2008. 基于支持向量机的叠前地震反演方法. 中国石油大学学报(自然科学版) , 32(1): 37–41. | |
| 张丰麒, 魏福吉, 王彦春, 等. 2013. 基于精确Zoeppritz方程三变量柯西分布验约束的广义线性AVO反演. 地球物理学报 , 56(6): 2098–2115. | |
| 张芝铭, 张明学, 胡玉双. 2015. 叠前反演预测火山岩储层——以莺山—双城断陷为例. 地球物理学进展 , 30(2): 621–627. | |
 2016, Vol. 59
2016, Vol. 59


