2. Modeling and Imaging Laboratory, Earth & Planetary Sciences Department, University of California at Santa Cruz, CA 95064, USA;
3. 西安交通大学, 海洋石油勘探国家工程实验室, 西安 710049
2. Modeling and Imaging Laboratory, Earth & Planetary Sciences Department, University of California at Santa Cruz, CA 95064, USA;
3. National Engineering Laboratory for Offshore Oil Exploration, Xi'an Jiaotong University, Xi'an 710049, China
地震信号中低频信息的缺失导致对大尺度背景构造的反演非常困难,由此也导致了全波形反演对 初始模型的高度依赖性(Virieux and Operto,2009). 在传统方法中,初始模型一般通过其他技术提供,如走时反演(包括基于射线的走时反演和基于波动方程的走时反演;利用首次到达波的走时反演和利用反射波的走时反演)和速度分析.在全波形反演领域,人们通过使用大偏移距数据和多尺度反演的方法来减小全波形反演对初始模型的依赖性(Bunks et al.,1995; Pratt et al.,1996; Ravaut et al.,2004; Sirgue and Pratt,2004; Plessix et al.,2010; Sirgue et al.,2010; Fichtner and Trampert,2011; Vigh et al.,2011; Baeten et al.,2013; Brittan et al.,2013). 多尺度反演方法首先从数据中的最低频率出发反演模型的大尺度分量.近年来发展起来的低频陆上震源系统(频率可低至1.5 Hz)使得多尺度全波形反演方法可以使用一维线性模型作为初始模型(Baeten et al.,2013).他们指出,地震数据中的低频部分(1.5~2.0 Hz)对于正确地反演大尺度背景模型是非常关键的.然而通常情况下,这种低频震源是不具备的,要获取5 Hz以下的地震数据是非常困难的,因此怎样获得一个良好的初始模型仍然是全波形反演中的难点问题.Shin和Cha(2009)提出拉普拉斯域全波形反演方法,可以为全波形反演提供一个光滑的初始模型.近年来一种新的趋势是通过给全波形反演的目标函数中引入额外项从而将其他一些反演方法加入到全波形反演的框架中来,比如引入走时反演(Mora,1989; Clément et al.,2001; Xu et al.,2012; Ma and Hale,2013; Wang et al.,2013)和速度分析(Almomin and Biondi,2012; Biondi and Almonin,2012,2013; Tang et al.,2013).
我们提出了一种地震包络反演的方法(Wu et al.,2013,2014),通过利用包络中丰富的低频信息为全波形反演提供一个良好的初始模型.为了实现包络反演方法,首先需要提取信号的包络.对信号包络的提取是一个非线性的过程,这种非线性操作可以将信号包络中所包含的对介质扰动的大尺度响应从原始地震信号中分离出来,从而起到抑制反演中的局部极小值的作用,能够在缺乏低频信息的情况下为全波形反演提供一个良好的初始模型.本文研究包络反演对局部极小值的抑制作用,并通过目标函数形态的对比来展现这一特性.对Marmousi速度模型和Overthrust速度模型的反演证明了该方法的有效性.
2 方法原理 2.1 时域全波形反演回顾全波形反演通过匹配观测波场和模拟波场来反演地下介质参数.常用的L2范数的目标函数为
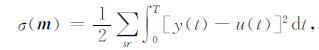
|
(1) |
其中u是观测波场,y是模拟波场, m 是模型参数.
在常密度声波方程情况下,速度v为模型参数,计算目标函数对速度的梯度,可以得到:
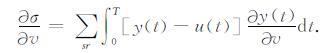
|
(2) |
引入算子 J(雅可比矩阵)和向量 η,公式为
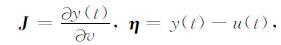
|
(3) |
则方程(2)可以被写为
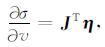
|
(4) |
其中雅可比矩阵 J 也被称为偏微商波场,即Fréchet微商.公式(4)中的梯度可以通过计算正传波场和反传波场的零延时相关得到.
2.2 包络反演方法为了实现包络反演,需要首先获得地震信号的包络.我们通过希尔伯特变换来提取地震信号的包络,一个不含有负频率成分的信号被称为解析信号,一个解析信号(t)可以由实信号f(t)和它的希尔伯特变换H f(t)构成,公式为
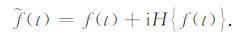
|
(5) |
希尔伯特变换的定义为
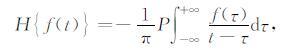
|
(6) |
其中P被称为柯西主值.信号f(t)的包络求解表达式为
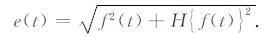
|
(7) |
在包络反演中,我们将目标函数定义为
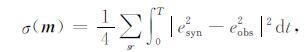
|
(8) |
其中 m 是模型参数,esyn和eobs分别是模拟波场和观测波场的包络.使用上述定义的希尔伯特变换,我们可以将公式(8)改写为
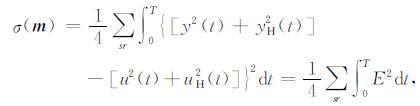
|
(9) |
其中y和u分别代表模拟波场和观测波场,yH和uH分别代表他们的希尔伯特变换,E代表包络信号残差.考虑波场速度v作为模型参数,计算目标函数(9)对模型参数的导数,可以得到结果(Wu et al.,2013,2014):
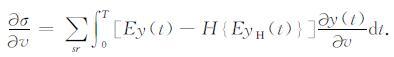
|
(10) |
仍然引入偏微分波场算子 J 和残差向量 η,其中
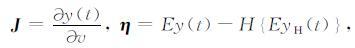
|
(11) |
因此公式(10)可以被改写为
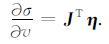
|
(12) |
从上式可以看到,包络反演中目标函数对模型参数的梯度与传统全波形反演中目标函数对模型参数的梯度具有同样的形式,区别仅在于残差向量的不同.包络反演同样可以通过反传算法来实现.因为包络反演中残差向量 η 与信号的包络有关,因此我们可以使用信号包络中的低频信息来反演模型的大尺度分量.
3 目标函数形态对比本小节通过比较包络反演和传统全波形反演目标函数的形态特征来展现包络反演对局部极小值的压制作用.实验中分别使用Marmousi速度模型和Overthrust速度模型进行测试.
根据公式(1)和公式(8)的定义可以看出,目标函数是关于速度模型的范函,而速度模型是在一个多维空间中变化的.为了便于展现目标函数的形态特征,我们将该多维空间简化成一个两维空间,简化过程如下.首先将真实模型记作vtrue(x),将该真实模型分解为一个背景速度模型和基于该背景模型的扰动速度模型.背景模型是一个一维线性模型,速度 大小从Vmax线性增长到Vmin.将该背景模型称为真实背景速度模型v0true(x),通过 vtrue(x)和v0true(x)相减可以得到真实的扰动速度模型δvtrue(x).设置扰动强度参数α,通过改变α可以得到一系列的速度扰动δv(x)=αδvtrue(x).对于真实模型来说,α=100%.所简化的两维空间中的两个参数分别为扰动强度α和背景模型的最大速度Vmax.首先保持Vmin不变,令Vmax变化,这样就得到一系列的背景速度模型;同时改变扰动强度α,这样就得到一系列的扰动速度模型;将背景速度和扰动速度相加就可以得到一系列的测试模型.通过计算来自于真实模型和来自于测试模型的地震数据和包络,就可以得到目标函数随着这两个参数的变化情况,从而刻画出目标函数的形态特征.
(1) Marmousi模型
首先对Marmousi模型进行测试,如图 1所示.对于Marmousi模型来说,在v0true(x)中,Vmin=1.5 km·s-1,Vmax=5.5 km·s-1,如图 2所示.保持Vmin=1.5 km·s-1不变,令Vmax从2.5 km·s-1变化到7.5 km·s-1;令扰动强度α从10%变化到300%.

|
图 1 Marmousi速度模型 Fig. 1 Marmousi velocity model |
|
图 2 对应于Marmousi模型的一维线性初始速度模型 Fig. 2 1D linear initial model for the Marmousi model |
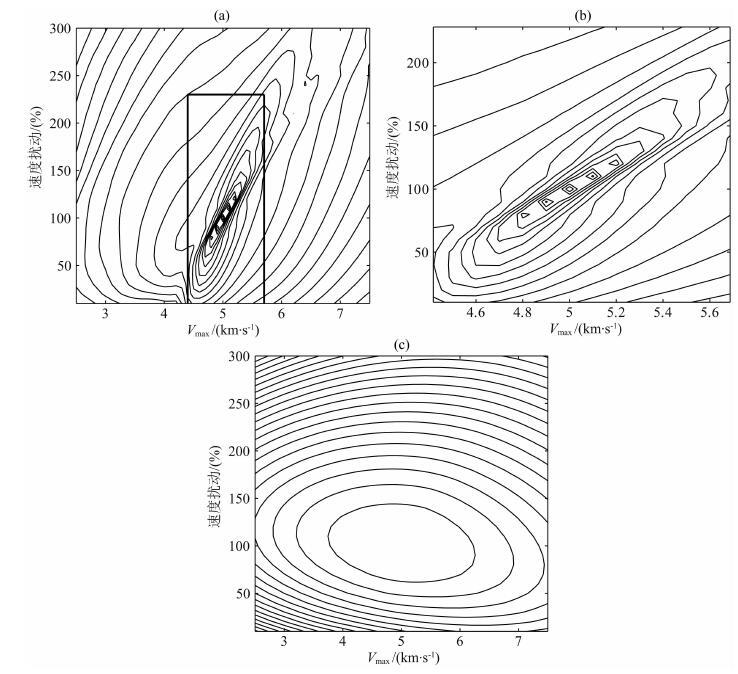
数随着上述两个参数变化的形态特征.图中横坐标是Vmax,纵坐标是扰动强度,振幅经过了归一化处理.其中图 3a是传统全波形反演的目标函数,为了便于观察,将图中粗线边框中的部分放大显示,如图 3b所示.从图中可以看出,传统全波形反演的目标函数中除了全局极小值以外,还有很多局部极小值,它们都有可能导致错误的反演结果.图 3c显示了包络反演的目标函数,可以看出,该目标函数非常平 滑,而且只有一个全局极小值,而不含有局部极小值.
|
图 3 Marmousi速度模型的目标函数形态对比(a)传统全波形反演目标函数;(b)对(a)中红色边框部分的放大显示;(c)包络反演目标函数. Fig. 3 Comparison of misfit function configurations for the Marmousi velocity model(a)Conventional full waveform inversion;(b)Enlarged box in the red border in(a);(c)Misfit function of envelope inversion. |
(2) Overthrust模型
接下来对Overthrust模型进行测试,如图 4所示.对于Overthrust模型来说,在v0true(x)中,Vmin=2.5 km·s-1,Vmax=6 km·s-1,如图 5所示.保持Vmin=2.5 km·s-1不变,令Vmax从3 km·s-1变化到8 km·s-1;扰动强度α仍然从10%变化到300%.
|
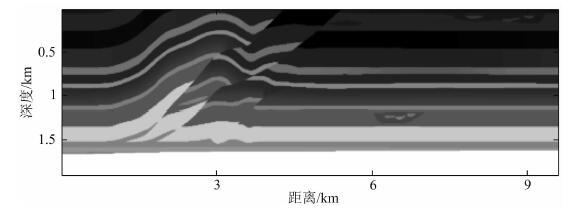
图 4 Overthrust速度模型 Fig. 4 Overthrus velocity model |
|
图 5 对应于Overthrust模型的一维线性初始速度模型 Fig. 5 1D linear initial model for the Overthrust model |
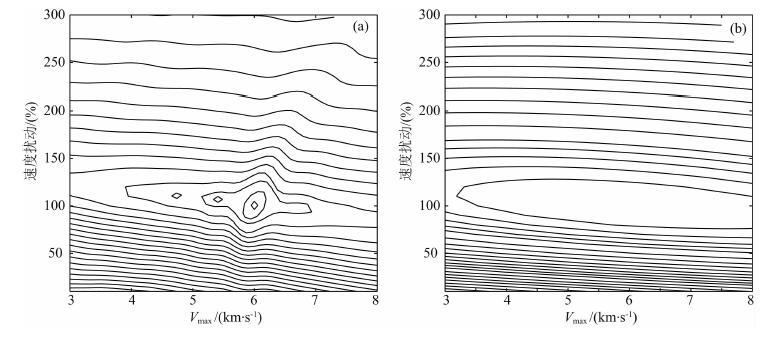
图 6显示了包络反演与传统全波形反演目标函数随着上述两个参数变化的形态特征.图中横坐标是Vmax,纵坐标是扰动强度,振幅经过了归一化处理.其中图 6a是传统全波形反演的目标函数,从图 中可以看出,传统全波形反演的目标函数中除了全局极小值以外,还有很多局部极小值,它们都有可能导致错误的反演结果.图 6b显示了包络反演的目标函数,可以看出,该目标函数非常平滑,而且只有一个全局极小值,而不含有局部极小值.
|
图 6 Overthrust速度模型的目标函数形态对比(a)传统全波形反演目标函数;(b)包络反演目标函数. Fig. 6 Comparison of misfit function configurations for the Overthrust velocity model(a)Conventional full waveform inversion;(b)Misfit function of the envelope inversion. |
从上述实验结果可以看出,包络反演具有避免局部极小值的能力,后文将通过反演结果进一步对此进行证明.
4 反演结果这一部分将给出包络反演的结果,并使用由包 络反演得到的结果做为新的初始模型来进行全波形反演,证明包络反演方法的有效性.仍然对Marmousi 速度模型及Overthrust速度模型进行测试.本文所使用的优化方法为共轭梯度法(Mora,1987).
(1) Marmousi速度模型
首先对Marmousi速度模型(图 1)进行测试,并且从线性初始模型(图 2)出发进行反演.反演中使用10 Hz主频的Ricker子波作为震源子波.
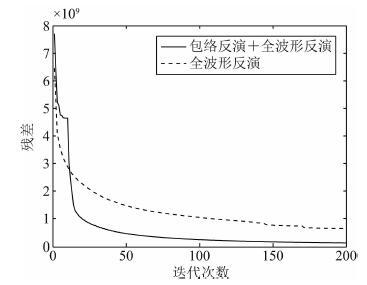
首先使用全频带的Ricker子波来产生地震数据并进行反演.图 7显示了从线性模型出发的包络反演结果.可以看到,使用包络反演可以得到模型的大尺度分量,该反演结果可以做为全波形反演的新的初始模型.图 8中显示了由该新的初始模型出发得到的全波形反演结果.作为对比,在图 9中我们给出了直接从线性初始模型出发得到的全波形反演结果.我们可以看出,由于线性初始模型与真实模型相 距太远,图 9中的结果已经陷入了局部极小值,而图 8 中的结果则很接近真实模型.使用包络反演与传统全波形反演相结合的方法可以得到更好的反演结果.图 10显示了目标函数随着迭代次数的下降曲线,其中实线为包络反演与全波形反演相结合的下降曲线,曲线中的拐点表示从包络反演向全波形反演过渡的点,拐点之前为包络反演,从拐点开始为使用包络反演的结果作为新的初始模型的全波形反演.图中虚线为传统全波形反演的下降曲线.可以看出,使用包络反演与全波形反演的数据残差更小,说明该方法可以得到更接近于实际模型的反演结果.

|
图 7 从线性模型出发的Marmousi模型包络反演结果 Fig. 7 Envelope inversion result starting from the linear initial model for the Marmousi model |

|
图 8 从图 7中结果出发的Marmousi模型全波形反演结果 Fig. 8 Full waveform inversion result for the Marmousi model using the result in Fig. 7 as new initial model |

|
图 9 从线性模型出发的Marmousi模型全波形反演结果 Fig. 9 Full waveform inversion result for the Marmousi model starting directly from the linear initial model |
|
图 10 Marmousi模型的误差数据残差下降曲线 Fig. 10 Reduction of data residual for the Marmousi model |
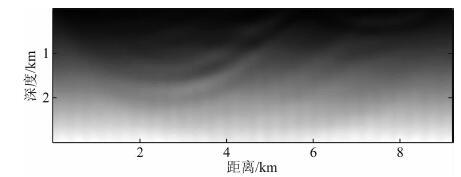
为了进一步验证包络反演的有效性,我们去除Ricker子波中5 Hz以下的频率成分,并使用去除低频的Ricker子波产生地震数据进行反演.图 11显示了从线性模型出发的包络反演结果.可以看到,在这种情况,使用包络反演仍然能得到模型的大尺度分量.使用该结果做为新的初始模型进行全波形反演,图 12中显示了最终的全波形反演结果.可以看到,该结果与图 8中的结果很接近.作为对比,我们直接从线性模型出发进行全波形反演,图 13显示了反演结果.可以看到,在缺少低频的情况下,传统全波形反演的结果变得更差.
|
图 11 使用去除低频Ricker子波的Marmousi模型包络反演结果 Fig. 11 Envelope inversion result for the Marmousi model using the low-cut Ricker wavelet |

|
图 12 用图 11作为初始模型的Marmousi模型全波形反演结果 Fig. 12 Full waveform inversion result for the Marmousi model using the result in Fig. 11 as new initial model |

|
图 13 使用去除低频Ricker子波的Marmousi模型的传统全波形反演结果 Fig. 13 Conventional full waveform inversion result for the Marmousi model using the low-cut Ricker wavelet |
(2) Overthrust速度模型
接下来对Overthrust速度模型(图 4)进行测试,并且从线性初始模型(图 5)出发进行反演.使用10 Hz主频的Ricker子波作为震源子波.
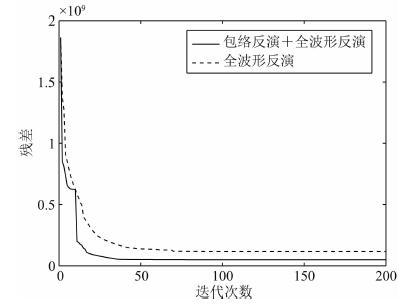
首先使用全频带的Ricker子波来产生地震数据并进行反演.图 14显示了从线性模型出发的包络反演结果,从图中可以看出模型的大尺度分量.使用该反演结果可以作为新的初始模型,图 15中显示了由该新的初始模型出发得到的全波形反演结果.作为对比,在图 16中我们给出了直接从线性初始模型出发得到的全波形反演结果.可以看出,图 16中的结果已经陷入了局部极小值,而图 15中的结果则很接近真实模型,说明使用包络反演与传统全波形反演相结合的方法可以得到更好的反演结果.图 17显示了目标函数随着迭代次数的下降曲线,其中实线为包络反演与全波形反演相结合的下降曲线,虚线为传统全波形反演的下降曲线.可以看出,使用包络反演与全波形反演的数据残差更小,说明该方法可以得到更接近于实际模型的反演结果.

|
图 14 从线性模型出发的Overthtust模型包络反演结果 Fig. 14 Envelope inversion result starting from the linear initial model for the Overthrust model |

|
图 15 从图 14中结果出发的Overthrust模型全波形反演结果 Fig. 15 Full waveform inversion result for the Overthrust model using the result in Fig. 14 as new initial model |

|
图 16 从线性模型出发的Overthrust模型全波形反演结果 Fig. 16 Full waveform inversion result for the Overthrust model starting directly from the linear initial model |
|
图 17 Overthrust模型的误差数据残差下降曲线 Fig. 17 Reduction of data residual for the Overthrust model |
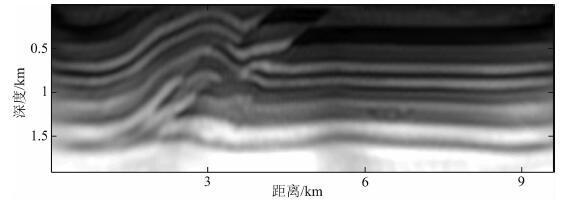
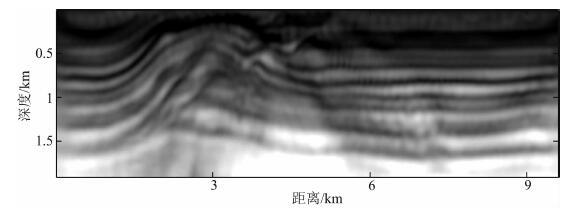
为了进一步验证包络反演的有效性,我们去除 Ricker子波中5 Hz以下的频率成分,并使用去除 低频的Ricker子波产生地震数据进行反演.图 18显示了从线性模型出发的包络反演结果.可以看到,在这种情况,使用包络反演仍然能得到模型的大尺度分量.使用该结果作为新的初始模型进行全波形反演,图 19中显示了最终的全波形反演结果.可以看到,该结果与图 15中的结果很接近.作为对比,我们直接从线性模型出发进行全波形反演,图 20显示了反演结果.可以看到,在缺少低频的情况下,传统全波形反演的结果变得更差.

|
图 18 使用去除低频Ricker子波的Overthrust模型包络反演结果 Fig. 18 Envelope inversion result for the Overthrust model using the low-cut Ricker wavelet |
|
图 19 用图 18作为初始模型的Overthrust模型全波形反演结果 Fig. 19 Full waveform inversion result for the Overthrust model using the result in Fig. 18 as new initial model |
|
图 20 使用去除低频Ricker子波的Overthrust模型的传统全波形反演结果 Fig. 20 Conventional full waveform inversion result for the Overthrust model using the low-cut Ricker wavelet |
通过上面的例子可以看出,使用包络反演可以为全波形反演提供一个光滑的初始模型.包络反演和全波形反演相结合的方法可以产生比传统全波形反演更好的反演结果.
5 结论(1) 本文讨论了包络反演对局部极小值的抑制作用.包络反演方法可以压制反演中的局部极小值,能够在缺乏低频信息的情况下为全波形反演提供一个良好的初始模型.文中通过对目标函数形态的对比展现了包络反演抑制局部极小值的能力,并通过对Marmousi速度模型和Overthrust速度模型的反演证明了该方法的有效性.
(2) 本文给出了包络反演方法应用于模型数据时的结果,对于实际数据而言情况较为复杂.由于该方法对观测数据和计算数据的包络进行匹配,因此在应用于实际数据时,需要首先对子波的振幅进行估计,从而更好地进行匹配.该方法目前在对岩丘进行反演时仍存在一定的问题,需要进一步优化和改善.
 2016, Vol. 59
2016, Vol. 59


