根据中国地震台网信息,2014年11月22日16时55分31秒(北京时间)于四川省甘孜藏族自治州康定县发生了MS6.3级地震,震中位于30.3°N/101.8°E,震源深度20 km(本文称其为M1) .3天后,于2014年11月25日23时19分11秒(北京时间)在当地又发生了MS5.8级地震,震中位于30.2°N/101.75°E,震源深度16 km(本文称其为M2) .我们将上述两次地震称为康定双震.余震分布以及当地的构造特征似乎表明,康定双震发生于NW-SE方向展布的鲜水河断裂带(图 1).

|
图 1 康定双震序列及其构造背景以及周边GPS速度场,其中(b)为(a)中方框展示区 (a)青藏高原及其周边的构造(白色线条)和GPS速度场(蓝色箭头)(GPS速度场来自于中国地壳运动观测网络和中国陆态网络2009、2011和2013年的全部数据与2012和2014年的部分数据);(b)康定双震序列、附近断层和台站分布.五角星为康定双震M1和M2以及经验格林函数地震G1,圆圈为主震M1发生至2015年3月31日ML>2的余震(震中位置参数来自中国地震台网地震目录),沙滩球为GCMT震源机制解.白线为附近主要断层.绿色三角形为震中距小于150 km的台站. Fig. 1 Kangding earthquake-doublet sequence and its tectonic settings and GPS-velocity field,where Fig. 1b shows the area framed with red box in Fig. 1a (a)Tectonic settings of Tibet Plateau and its surrounding regions(white solid lines)and GPS -velocity field(blue arrows),which are determined with all the observation data of the years 2009,2011 and 2013,as well as some of the data of the years 2012 and 2014,from CMONOC(Crustal Movement Observation Network of China).(b)Distribution of the Kangding earthquake-doublet sequence,nearby faults and local stations. Stars refer to epicenters of the Kangding earthquake-doublet M1 and M2 and the empirical green function earthquake G1,respectively,gray circles refer to the aftershocks with magnitudes ML>2 till Mar. 31,2015(Epicenter parameters of the aftershocks are from the CENC(China Earthquake Network Center)),beach balls refer to the focal mechanisms from GCMT. White solid lines refer to the main faults. Green triangles refer to the used broad-band stations with epi-distances less than 150. |
根据已有经验,康定双震的震源尺度应在10左右,反演远场直达P波很难获得具有方向优势的破裂过程图像.同时,由于震级较小,远场P波信号相对较弱,对反演结果必然造成负面影响.因此,较好的选择是区域面波和经验格林函数技术.跟远场体波相比,区域面波具有更高的分辨能力(Lay and Wallace,1995);跟合成格林函数相比,经验格林函数是对路径效应的更好近似.然而,康定双震余震相对较少,且没有能够充当经验格林函数事件的地震.于是,本文从中国地震台网地震目录中找到发生于2010年4月27日的一次ML4.8地震作为经验格林函数事件.
一个理想的格林函数事件必须满足如下条件:(1) 与主事件相比,格林函数事件的震级足够小,以致于它的震源时间函数可视为一狄拉克-δ函数;(2) 格林函数事件的震源位置与主事件相同;(3) 格林函数事件与主震具有相同的震源机制.然而,完全满足上述条件是不可能的.现实的做法是选择近似满足上述条件的地震.
因此,本文的重点首先是确认格林函数事件,然后是利用经验格林函数分析反演康定双震的震源破裂特征.具体地讲,(1) 利用逆时成像技术(许力生等,2013a,b)对康定双震和选用的经验格林函数地震进行重新定位,并利用广义极性振幅技术(严川和许力生,2014)反演康定双震和经验格林函数地震的震源机制;然后,利用经验格林函数技术分别提取M1和M2的视震源时间函数,并利用视震源时间函数的方位依赖性分析M1和M2的优势破裂方向;最后,利用视震源时间函数反演方法(Chen and Xu,2000; Xu et al.,2002; 张勇,2008)反演M1和M2的震源破裂过程,并讨论它们的可能成因.
2 震源位置与机制的确认无论是M1和M2还是G1都已经有震源的位置、震级的大小、甚至震源机制(表 1至表 4),但为了严谨起见,还是对它们进行重新定位和震源机制反演.
|
|
表 1 事件M1和M2以及G1的震源位置 Table 1 Source locations of the events M1 and M2 as well as G1 |
|
|
表 2 事件M1的震源机制 Table 2 Focal mechanisms of the event M1 |
|
|
表 3 事件M2的震源机制 Table 3 Focal mechanisms of the event M2 |
|
|
表 4 事件G1的震源机制 Table 4 Focal mechanisms of the event G1 |
中国地震台网公布的震源位置是常规定位的结果,通常具有较大误差或不确定性.为了获得尽可能准确和较小不确定性的震源位置,本文特别采用了新发展的非线性定位技术——逆时成像技术(许力生等,2013a,b),同时选用了为龙门山断裂带挑选的速度模型(王椿镛等,2002;Wang et al.,2003),重新确定康定双震M1和M2以及格林函数事件G1的震源位置.逆时成像技术利用互相关技术测量到时,提高了测量的客观性和准确性;并采用聚束能量作为目标函数,避免了最小二乘解对于少数或者个别出格数据敏感的缺点.关于龙门山断裂带的速度模型有不少研究结果,但本研究使用了经多个模型对比筛选后得到的模型(许力生等,2013b).
在确定震中位置时选用的台站距震中越近越好,但对于M1和M2以及G1而言,震中附近的台站过少.为了保证具有一定的台站数量,本研究选取了震中距150范围内的地震台.如图 1b所示,这些台站的方位覆盖较好,最小震中距约40 km.
表 1比较了三次地震的定位结果.经重新定位,主震M1的发震时刻比常规定位结果提前5 s,震源深度比常规定位结果浅约4 km,震中位置位于常规定位结果的西南约12.5 km.主震M2的发震时刻比常规定位结果提前3 s,震源深度比常规定位结果深约1 km,震中位置位于常规定位结果的西南约4 km.经验格林函数事件G1的发震时刻比常规定位结果提前4 s,震源深度比常规定位结果浅约8 km,震中位置位于常规定位结果北西约12 km.
我们无从知道常规定位的不确定性,但本文确定的发震时刻的不确定性约0.1 s,主震M1和M2的经度和纬度的不确定性均为0.001°,而G1的不确定性为0.002°,主震M1的震源深度比常规定位浅约4 km,但不确定性约5 km,主震M2的震源深度与常规定位结果基本一致,不确定性为2.4 km,G1的两个深度相差较大,约8 km,但不确定性也较大,约13 km.
图 2展示了三次地震定位前后的位置以及余震分布.重新定位后三次地震更呈线性排列,与余震的空间分布更一致.M1和M2的震中比较接近,二者相距约11,而M1和M2距G1略远,约40~50 km.M1和M2的震源深度比较接近,约16 km,而G1的深度较浅,约2 km.
|
图 2 事件M1和M2以及G1重新定位前(蓝色)、后(红色)的震中位置比较(参看图 1b) Fig. 2 Epicentral comparison of the events M1 and M2 as well as G1 after being relocated(red)with before (blue)(for details,see Fig. 1b) |
M1和M2与G1震源位置的差异必然给视震源时间函数乃至震源破裂过程带来负面影响,但影响的大小取决于震中距的大小,震中距越大,影响越小.
2.2 震源机制的重新确认为了确认康定双震和经验格林函数地震的震源机制解,本研究特别选用了震中距在150范围内的台站的垂直向P波初动信息以及三分向带有极性的P波最大振幅信息,利用广义极性振幅技术反演了这些地震的震源机制.广义极性振幅技术是充分吸纳初动符号法(Hardebeck,2002)和振幅类方法(Ebel and Bonjer,1990)的精髓形成的一种新方法(严川和许力生,2014),我们已经用这种方法反演了大量小震和微震的震源机制(严川,2015).
反演所用的格林函数采用反射率方法(Wang,1999)来计算,所用的速度模型与前面定位时采用的模型一致.
表 2,表 3和表 4分别展示了三次地震的震源机制.主震M1的震源机制与USGS的体波反演结果比较接近,与GCMT结果比较一致,也与中国地震局地球物理研究所发布的结果比较一致,但与USGS的矩心矩张量反演结果和W-phase反演结果差别较大.主震M2的震源机制与USGS的体波反演结果、GCMT结果以及中国地震局地球物理研究所发布的结果都比较一致.经验格林函数地震G1的震源机制与GCMT发布的结果比较相似.
图 3集中给出了这3次事件震源机制解的几何图像.参考余震和当地断裂的展布特征(图 1),可以断定北西—南东方向的节面为实际的发震断层面.

|
图 3 事件M1(a)、M2(b)和G1(c)的震源机制,红色节面为本研究确定的结果,灰色节面为表 2-4给出的其他结果 Fig. 3 Focal mechanisms of the events M1(a),M2(b)and G1(c). Gray nodes are from other sources shown in tables 2-4,red ones are from this study |
需要特别强调的是,M1的实际发震断层面为330°/84°/19°的节面,而G1的实际发震断层面为318°/77°/3°,这两个断层面参数相对一致.然而,M2的实际发震断层面为153°/68°/-11°,其倾向恰与G1的相反,前者倾向西南,后者倾向东北,不过它们的倾角都相对较陡.这种震源机制的差异会在下文的视震源时间函数的提取中反映的更加明显.
3 视震源时间函数提取与破裂方向性分析根据震源位置和震源机制的确认结果,经验格林函数地震G1与康定双震M1和M2震源位置相对较近,且震源机制相似,因此,可以尝试利用G1提取M1和M2的视震源时间函数.
由于过小的震中距不满足震源为点源的假设,进而导致震源位置不同的负面影响凸现出来,而且地震记录随着震中距增加信噪比逐渐降低,所以,本研究从中国地震台网仅选取了震中距3°~9°范围内的宽频带波形记录(郑秀芬等,2009).考虑到M1和M2与G1均为走滑型地震,Love波质量优于Rayleigh波质量,本研究选择了Love波视震源时间函数来分析康定双震的震源破裂的优势方向以及它们的震源破裂过程.
3.1 主震M1首先,将主震M1和经验格林函数地震G1的T分向记录进行0.02~0.1 Hz的带通滤波以去除频率过低和过高的噪声;然后,利用2.5~4.2 km·s-1的群速度窗截取T分向的基阶Love波波形;最后,利用PLD技术(Bertero et al.,1997; Piana and Bertero,1997; 张勇等,2009)提取视震源时间函数.
需要说明的是,在利用PLD技术提取视震源时间函数之后,不但要根据合成波形和观测波形的一致性剔除一致性较差的视震源时间函数,而且要根据方位相近或相邻的视震源时间函数的相似性剔除相似性较差的视震源时间函数.
图 4a展示了筛选后的视震源时间函数.可以看出,这些视震源时间函数的形状具有一定的方位依赖性,表明主震M1的断层具有一定的破裂尺度,而且破裂具有一定的优势方向.

|
图 4 事件M1(a)和M2(b)的视震源时间函数,横坐标为时间,纵坐标为观测点方位角,红色点为峰值点 Fig. 4 The ASTFs of the events M1(a)and M2(b). Horizontal axes show time while vertical axes show azimuths of the stations. And red dots are peak-points |
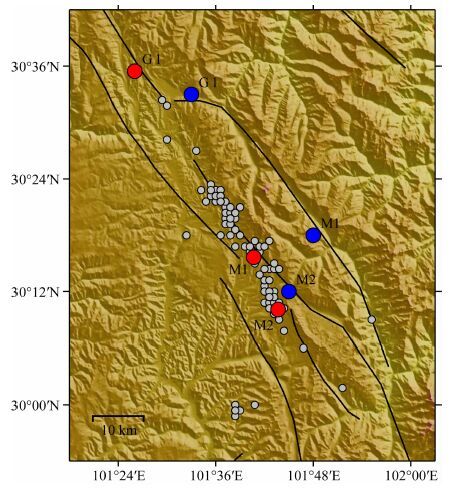
为了从提取的视震源时间函数更直观地认识主震M1破裂的方向性特征,利用哈佛大学测定的主震M1的标量矩1.9×1018N·m对提取到的视震源时间函数进行标定,然后投影到如图 5a所示的极坐标中.从图中可以发现,在西北和西南方向,地震矩释放较快且地震矩释放速率峰值较大,而在东北和东南方向,地震矩释放速率较慢且地震矩释放速率峰值较小,表明主震M1的破裂优势方向在西南和西北.不过需要说明的是,在西南方向几乎没有观测台站,所以朝向西南的破裂优势方向在此并不能确认.
|
图 5 事件M1视震源时间函数的极坐标展示(a)与破裂优势方向分析(b)(参考许力生等,2014a).子图(b)中绿色点为测量值,红色曲线为拟合结果.三角形为破裂优势方向及其相反方向.红色和蓝色虚线分别为1σ和2σ曲线 Fig. 5 The polar-coordinate exhibition of the ASTFs(a)and the analysis of dominant rupture direction(b)for the M1(see Xu et al.,2014a,for details). Green dots are the measured values and red curve is the simulated one,and purple triangles in subplot(b)indicate the dominant direction and its opposite direction.Red and blue dashed lines are 1σ and 2σ curves,respectively |
为了定量确定这次地震破裂的总体优势方向,本文计算了震源时间函数峰值对应的时刻TP,并用正弦型函数TP(θ)=a+bsin(cθ+θ0)拟合了它随方位角θ的变化(a为平均绝对延迟时间,b为相对延迟时间最大幅度,c为周期调制系数,θ0为初始相位),并计算了1倍标准差(1)和2倍标准差(2)曲线.拟合结果为TP(θ)=3.3+1.48sin(1.03θ-13.7) ,拟合曲线及其标准差曲线如图 5b所示,TP最大值位于101°,最小值位于276°,表明这次地震破裂的总体优势方向为276°.从图中可以看到,大部分观测值都在1倍标准差范围内,几乎所有的观测值都在2倍标准差范围内.
3.2 主震M2类似地,如图 4b所示,利用G1提取了主震M2的视震源时间函数.同样,这些视震源时间函数的形状具有一定的方位依赖性,意味着主震M2的地震断层也具有一定的破裂尺度,而且破裂具有一定的优势方向.
根据哈佛大学测定的结果,主震M2的标量矩为5.5×1017N·m.利用这个测量值对视震源时间函数进行标定,并投影到如图 6a所示的极坐标中.从图中可以看出,在~350°-30°、~80°-120°以及~230°-300°方位缺少观测台站,在西北和东北方向,地震矩释放较快且地震矩释放速率峰值较大,而在东南和西南方向,地震矩释放速率较慢且地震矩释放速率峰值较小,表明主震M2是从初始破裂点开始朝向北北西和北东方向传播.

|
图 6 事件M2视震源时间函数的极坐标展示(a)与破裂优势方向分析(b)(参考图 5 Fig. 6 The polar-coordinate exhibition of the ASTFs(a)and the analysis of dominant rupture direction(b)for the M2(see Fig. 5) |
同样,为了定量确定这次地震破裂的总体优势方向,我们计算了视震源时间函数峰值对应的时刻TP,并利用上文提到的正弦型函数拟合了它随方位角的变化.拟合结果为TP(θ)=3.42+1.63×sin(1.35θ-183.5) ,拟合曲线及其标准差曲线如图 6b所示,TP的最大值位于203°,最小值位于336°,表明这次地震破裂的总体优势方向为336°.同样,大部分观测值在1倍标准差范围内,几乎所有的观测值在2倍标准差范围内.
4 震源破裂过程的反演视震源时间函数的方位依赖性是震源断层尺度有限性和震源破裂方向性的反映.在上一节,借助于视震源时间函数的极坐标展示分析了破裂的优势方向.需要说明的是,上述结果只是破裂传播总体方向在水平面内的投影效果,并不是破裂在断层面内传播的实际方向.下面采用视震源时间函数反演方法反演这两次地震的震源破裂过程.
4.1 主震M1根据重新定位和震源机制反演结果,我们选取震源位置30.261°N,101.678°E,15.9 km为主震M1的起始破裂点,以走向330°和倾角84°的平面为破裂面,从初始破裂点沿断层走向330°方向20 km处作为断层的西北边界,沿150°方向20 km处作为断层的东南边界;从地表沿断层面向深部延展25 km作为断层的底边界.将整个断层面划分成1 km×1 km的网格,作为反演震源破裂过程的初始模型.
为了保持反演系统的线性关系,同时为了减少反演参数,需要事先给定合适的最大破裂速度以及子断层破裂的最长持续时间.经过多次尝试,最终给定的最大破裂速度为2.5 km·s-1,子断层震源时间函数最大持续时间为3 s.
为了使反演结果更加稳定并具有物理意义,在反演方程中需要引入空间和时间光滑约束(Yagi et al.,2004; 张勇,2008).具体地,本文采用了二维拉普拉斯时间和空间光滑算子,并经验性地给定了空间光滑和时间光滑的相对权重.另外,反演方程中还引入标量地震矩最小约束(张勇,2008),目的是弱化或抑制资料误差导致的空间上离散且幅度较小的位错.
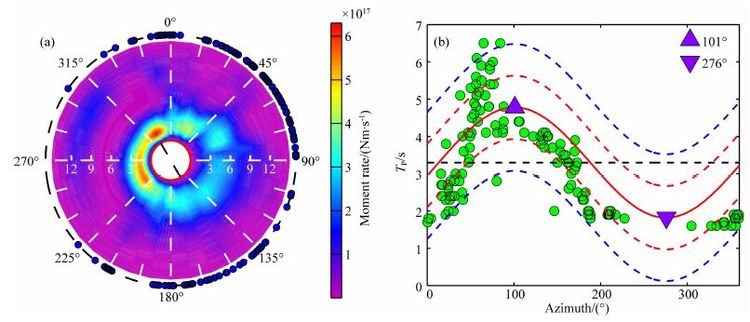
图 7展示了反演所用的台站以及反演结果.从反演得到的震源时间函数看,主震M1震源过程持续~11 s,大部分能量集中在前8 s.根据反演得到的静态位错分布,主要的位错发生在震中及震中西北10 km之间,呈单侧破裂,最大位错达~0.52 m.然而,在震中的西北方向较深区域以及震中东南较浅的区域似乎都有较弱的错动,表明主震M1从初始破裂点开始朝向浅表以及沿断层走向(N30°W)方向发生破裂,同时在相反的方向也发生了扩展.图 7d以快照的方式展示10 s前破裂的传播过程.

|
图 7 反演主震M1破裂过程时使用的台站以及反演结果 (a)震中(红色五角星)与台站(三角形)分布.红色三角形用于震源破裂过程反演,红色和绿色三角形用于视震源时间函数的提取,蓝色三角形为没能成功提取视震源时间函数的台站;(b)反演得到的地震矩率函数;(c)反演得到的静态位错分布; (d)随时间变化的滑动率快照.图(c)和(d)中五角星为起始破裂点位置. Fig. 7 Locations of the M1 and its stations used in inverting the rupture process as well as the inverted results (a)Distribution of the epicenter(red star)and its stations(triangles). Red triangles are the stations used for the rupture process inversion,red plus green ones are those used for the ASTF-retrieval,blue ones are those where the ASTFs failed to be retrieved;(b)The inverted moment-rate function;(c)The inverted static slip distribution;(d)Snapshot of the inverted time-dependent slip rate. In subplots(c)and(d),red stars show the initial points. |
利用反演得到的同震滑动模型计算了合成波形,并与观测波形进行了比较,如图 8所示,平均相关系数达到0.87,这表明得到的同震位错模型能够较好地解释观测资料.

|
图 8 事件M1的合成地震图与观测地震图的比较,每个子图左侧是台站名和相关系数,右侧是震相和台站方位角(单位:°) Fig. 8 Comparison of the observed waveforms with the symthetic ones for the M1. On the left side of each subplot are station code and coefficients, respectively, and on the right are phase and station-azimuth(Unit:°), respectively |
根据重定位和震源机制反演结果,以震源位置30.168°N,101.728°E,16.8 km为主震M2的起始破裂点,以走向153°,倾角68°的节面为实际破裂面,以初始破裂点沿断层面向西北15 km处为断层西北边界,向东南5 km处为断层东南边界,沿断层面向下距地表 3 km处为断层的上边界,沿断层面向下距地表 24 km处为断层的下边界.同样,将1 km×1 km作为子断层尺度,以2.5 km·s-1作为最大破裂速度和3 s作为子断层最大持续时间.其他约束条件与M1相同.
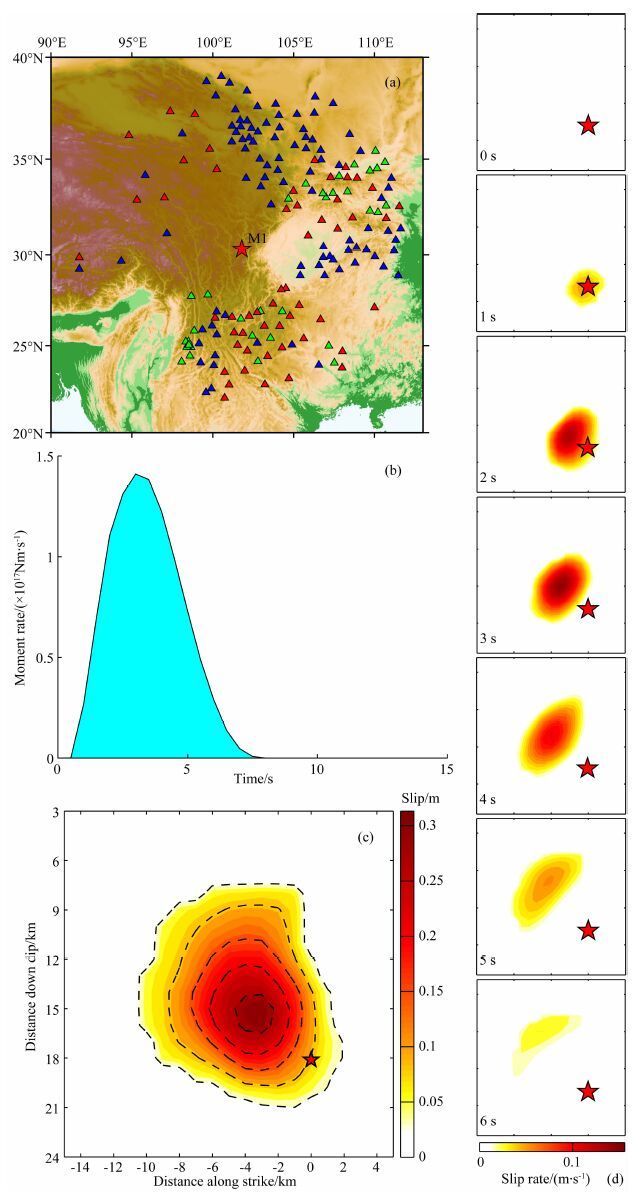
图 9展示了反演所用的台站和反演结果.根据反演得到的地震矩率函数,主震M2的震源持续时间~7 s,比M1的时间略短.根据静态位错分布图像,破裂区相对简单,似乎只有一个凹凸体,破裂区集中在震中与震中西北约10 km之间,呈单侧破裂,最大位错达~0.33 m,比M1略小.同时,可以注意到破裂区有明显向浅部扩展的趋势.总体看来,主震M2从初始破裂点开始朝向浅部以及沿断层面走向相反的方向(N27°W)发生破裂,而且自下向上的扩展优于水平方向的扩展,这一点从图 9d以快照方式展示的6 s前破裂传播的细节看得更清楚.
|
图 9 反演主震M2破裂过程时使用的台站以及反演结果(参看图 7) Fig. 9 Locations of the M2 and its stations used in inverting the rupture process as well as the inverted results(see Fig. 7) |
同样,利用反演得到的同震滑动模型计算了合成波形,并与观测波形进行了比较.如图 10所示,平均相关系数达到0.90,说明反演得到的M2的同震滑动模型亦能够很好地解释观测资料.

|
图 10 事件M2的合成地震图与观测地震图的比较(参考图 8) Fig. 10 Comparison of the observed waveforms with the synthetic ones for the M2(see Fig.8) |
经验格林函数方法是提取震源信息的重要方法之一,它可以有效地消除地震记录中的路径效应.然而,前提是经验格林函数事件必须非常理想.康定双震既没有较大的前震也没有较大的余震,我们不得不从以前发生的地震中寻找经验格林函数事件.经过筛选,最终选择了2010年4月27日的一次ML4.8地震.
为了确认这次ML4.8地震是否能够作为康定双震的经验格林函数事件,本文对康定双震和这次ML4.8地震进行了震源位置和震源机制反演.结果表明,这次地震可以作为康定双震的经验格林函数事件,但不是很理想.震源位置相对较远,震源机制也有相当的不一致性.无法从体波提取高质量的视震源时间函数,主要原因就是位置和震源机制的差异所致,因为体波周期相对较短,对震源位置或震源机制的差异更敏感.事实上,即便是周期较长的面波,也无法从所有台站提取满意的视震源时间函数,图 7和图 9中那些蓝色的台站就是因为无法得到满意的视震源时间函数而丢弃的,而主要原因就是主事件与格林函数事件的震源机制的差异,因为这些台站位于震源机制解的节面附近.其次还有震源位置差异的原因.尤其是M2事件,它的机制与G1的差别更明显,所以为此而丢弃的台站更多.
尽管G1不是理想的经验格林函数事件,但本研究仍然选择了G1,因为无法找到更好的事件.不过,从结果看,利用震中距较大的台站和周期较长的面波是可行的.较大的震中距和较长的周期允许忽略相对较小的震源位置差异,大部分令人满意的视震源时间函数允许忽略相对较小的震源机制差异.
事实上,我们尝试过从体波提取视震源时间函数,但始终没有得到足够令人满意的结果,原因就是震源位置和/或震源机制的差别以及较低的信噪比.并且也尝试过从Rayleigh波提取视震源时间函数,但令人满意的结果十分有限,原因是走滑断层引起的Rayleigh波相对较弱.这也是在研究2014年鲁甸MS6.5这个走滑型地震时选择Love波的原因(许力生等,2014a).
我们曾利用经验格林函数方法研究过不少地震(Xu et al.,2002; 张勇等,2009,2010;许力生等,2014a,2014b;张旭和许力生,2015).根据实际经验,匹配经验格林函数事件的关键在于主事件与格林函数事件的相对大小以及所使用的波长.波长越大,震中距越大,格林函数事件匹配兼容性越强.Vallée(2007) 还曾发现,两个震中相距650的MW7.2~7.3地震在远场距离上产生的100~2000 s的Rayleigh波是十分相似的,他还成功地利用一个MW7.2地震的Rayleigh波反演得到了震源断层长达1200 km的2004年苏门答腊巨震的震源破裂过程.
在反演震源破裂过程时,我们也尝试过3 km×3 km和2 km×2 km的子断层.权衡反演结果与资料拟合情况,最终选择了1 km×1 km的子断层尺寸,因为反演结果不仅具有较好的空间分辨能力,而且能较好地解释观测资料.
为了尽可能准确认识康定双震的破裂时间和能量释放过程,把视震源时间函数和震源破裂过程反演得到的震源时间函数放在一起进行比较分析.如图 11所示,M1地震的持续时间约11 s,但能量释放最快的时刻在4 s,开始较快,结束相对较慢,这很可能是地震过程后期较弱的双侧破裂所致(图 7c).M2地震的持续时间约7 s,能量释放最快的时刻在3.5s,开始较快,结束也较快,这对应着一个比较简单的凹凸体破裂(图 9c).

|
图 11 反演得到的事件M1(a)和M2(b)的震源时间函数(红色实线)、平均视震源时间函数(绿色实线)以及在所有台站提取的视震源时间函数结果(灰色实线).振幅均归一化 Fig. 11 The STFs from the rupture process inversion(red solid lines),the ASTFs averaged with all the ASTFs(green solid lines)and those retrieved from all the stations(gray solid lines)for the M1(a)and the M2(b). They all are normalized |
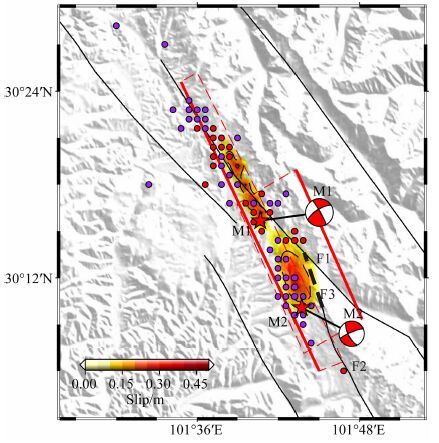
如果把康定双震的同震位错投影到地表,并把M1发生后至2015年3月31日前发生的ML>2.0的余震放在一起,如图 12所示,可以发现M1事件应该是鲜水河断裂带F1断层滑动所致,而M2事件并不发生在已有的断层上.M2似乎是F1断层和F2断层之间新断层或者隐伏断层F3的贯穿所致.值得强调的是,M1与M2不在同一个断层面上,M1的断层倾向东北,而M2的断层倾向西南,一定程度上反映了当地构造的复杂性.M2事件发生后,应力的调整使后续的余震不但发生在M2附近,而且也发生在M1附近.
|
图 12 事件M1和M2断层面上的位错在地表的投影与ML>2.0的余震分布,红色五角星为M1和M2重新定位后的位置,沙滩球为本研究确定的震源机制.红色圆圈为M1发生后至M2发生前的余震,紫色圆圈为M2发生后的余震.黑色实线为关注区域内的主要断层. 黑色虚线为推断的事件M2的断层. 红色实线为断层面与地表的交线 Fig. 12 The static slip distribution of the events M1 and M2 projected on ground surface with aftershocks of ML>2. Red dots are the aftershocks of the M1 but before the M2,and purple ones are those after the M2. Red stars refer to the locations of M1 and M2,and beach balls are their focal mechanisms determined in this study. Black solid lines are the major faults,the black dashed line is the deduced fault for the M2,and red solid lines indicate the intersection of the fault planes with ground surface |
康定双震发生在鲜水河断裂带与龙门山断裂带交接处的鲜水河断裂带,当地的GPS速度场表明这里的物质都在向东或东南移动(图 1b).然而,鲜水河断裂带北侧块体由于受四川盆地阻拦而速度相对较缓,而南侧由于相对自由而速度相对较快(图 1b).这样的速度差异很容易引起断层的左旋运动,而康定双震恰是左旋错动,因此,可以认为康定双震是由于鲜水河断裂带两侧块体的差速运动所致.
6 结论根据Love波视震源时间函数综合分析和反演结果,M1地震持续时间约11 s,能量释放最快的时刻在4 s,M2地震的持续时间约7 s,能量释放最快的时刻在3.5 s;M1地震的主要破裂区为单侧破裂,水平方向扩展约10 km,垂直方向约8 km,但在后期,扩展呈双侧破裂,在西北方向向深部扩展,在东南方向向浅部扩展,在水平面内总体破裂方位为276°;M2地震几乎是纯粹的单侧破裂,水平方向扩展约10 km,垂直方向扩展约11 km,在水平面内总体破裂方位为336°;M1地震的最大位错约0.52 m,M2地震的最大位错约0.33 m.
综合康定双震的震源位置、震源机制、破裂特征、余震的空间分布以及当地的断层空间展布特征,M1地震是当地已有断层的错动所致,而M2似乎是两条已有断层的贯穿所致.M2地震断层F3可能是新断层,也可能是隐伏断层.
致谢中国地震局地球物理研究所国家数字测震台网数据备份中心(doi:10.7914/SN/CB)为本研究提供地震波形数据,陈正松博士提供了图1中GPS速度场资料,在此一并表示感谢.
| Bertero M, Bindi D, Boccacci P, et al. 1997. Application of the projected Landweber method to the estimation of the source time function in seismology. Inverse Problems , 13(2): 465–486. | |
| Chen Y T, Xu L S. 2000. A time-domain inversion technique for the tempo-spatial distribution of slip on a finite fault plane with applications to recent large earthquakes in the Tibetan Plateau. Geophys. J. Int. , 143(2): 407–416. | |
| Ebel J E, Bonjer K P. 1990. Moment tensor inversion of small earthquakes in southwestern Germany for the fault plane solution. Geophys. J. Int. , 101(1): 133–146. | |
| Hardebeck J L. 2002. A new method for determining first-motion focal mechanisms. Bull. Seismol. Soc. Amer. , 92(6): 2264–2276. | |
| Lay T, Wallace T C. Modern Global Seismology. New York: Academic Press, Inc, 1995 . | |
| Piana M, Bertero M. 1997. Projected Landweber method and preconditioning. Inverse Problems , 13(2): 441–463. | |
| Vallée M. 2007. Rupture properties of the giant Sumatra earthquake imaged by empirical Green's function analysis. Bull. Seismol. Soc. Amer. , 97(1A): S103–S114. | |
| Wang C Y, Mooney W D, Wang X L, et al. 2002. Study on 3-D velocity structure of crust and upper mantle in Sichuan-Yunnan region, China. Acta Seismologica Sinica (in Chinese) (in Chinese) , 24(1): 1–16. | |
| Wang C Y, Chan W W, Mooney W D. 2003. Three-dimensional velocity structure of crust and upper mantle in southwestern China and its tectonic implications. J. Geophys. Res. , 108(B9). doi: 10.1029/2002JB001973. | |
| Wang R J. 1999. A simple orthonormalization method for stable and efficient computation of Green's functions. Bull. Seismol. Soc. Amer. , 89(3): 733–741. | |
| Xu L S, Chen Y T, Teng T L, et al. 2002. Temporal-spatial rupture process of the 1999 Chi-Chi earthquake from IRIS and GEOSCOPE long-period waveform data using aftershocks as empirical Green's functions. Bull. Seismol. Soc. Am. , 92(8): 3210–3228. | |
| Xu L S, Du H L, Yan C, et al. 2013a. A method for determination of earthquake hypocentroid: time-reversal imaging technique I—Principle and numerical tests. Chinese J. Geophys. (in Chinese) , 56(4): 1190–1206. doi: 10.6038/cjg20130414. | |
| Xu L S, Yan C, Zhang X, et al. 2013b. A method for determination of earthquake hypocentroid: Time-reversal imaging technique—An examination based on people-made earthquakes. Chinese J. Geophys. (in Chinese) , 56(12): 4009–4027. doi: 10.6038/cjg20131207. | |
| Xu L S, Zhang X, Yan C, et al. 2014a. Analysis of the Love waves for the source complexity of the Ludian MS6. 5 earthquake. Chinese J. Geophys. (in Chinese) , 57(9): 3006–3017. doi: 10.6038/cjg20140925. | |
| Xu L S, Yan C, Zhang X, et al. 2014b. Rupture histories of the 2014 Yingjiang double earthquakes. Chinese J. Geophys. (in Chinese) , 57(10): 3270–3284. doi: 10.6038/cjg20141015. | |
| Yagi Y, Mikumo T, Pacheco J, et al. 2004. Source rupture process of the Tecomán, Colima, Mexico earthquake of 22 January 2003, determined by Joint inversion of teleseismic body-wave and near-source data. Bull. Seismol. Soc. Am. , 94(5): 1795–1807. | |
| Yan C, Xu L S. 2014. An inversion technique for the mechanisms of local and regional earthquakes: generalized polarity and amplitude technique (I)—principle and numerical tests. Chinese J. Geophys. (in Chinese) , 57(8): 2555–2572. doi: 10.6038/cjg20140816. | |
| Yan C. 2015. Inversion methods for the focal mechanisms of small earthquakes and the stress field and their application (in Chinese) [Ph. D. thesis]. Beijing: Institute of Geophysics, China Earthquake Administration. | |
| Zhang X, Xu L S. 2015. Inversion of the apparent source time functions for the rupture process of the Nepal MS8. 1 earthquake. Chinese J. Geophys. (in Chinese) , 58(6): 1881–1890. doi: 10.6038/cjg20150604. | |
| Zhang Y. 2008. Study on the inversion methods of source rupture process (in Chinese) [Ph. D. thesis]. Beijing: Peking University. | |
| Zhang Y, Xu L S, Chen Y T. 2009. PLD method for retrieving apparent source time function and its application to the 2005 Kashmir MW7. 6 earthquake. Chinese J. Geophys. (in Chinese) (in Chinese) , 52(3): 672–680. | |
| Zhang Y, Xu L S, Chen Y T. 2010. Source process of the 2010 Yushu, Qinghai, earthquake. Sci. China Earth Sci. , 53(9): 1249–1251. | |
| Zheng X F, Ouyang B, Zhang D N, et al. 2009. Technical system construction of Data Backup Centre for China Seismograph Network and the data support to researches on the Wenchuan earthquake. Chinese J. Geophys. (in Chinese) , 52(5): 1412–1417. doi: 10.3969/j.issn.0001-5733.2009.05.031. | |
| 王椿镛, MooneyW D, 王溪莉, 等. 2002. 川滇地区地壳上地幔三维速度结构研究. 地震学报 , 24(1): 1–16. | |
| 许力生, 杜海林, 严川, 等. 2013a. 一种确定震源中心的方法: 逆时成像技术(一)——原理与数值实验. 地球物理学报 , 56(4): 1190–1206. | |
| 许力生, 严川, 张旭, 等. 2013b. 一种确定震源中心的方法: 逆时成像技术(二)——基于人工地震的检验. 地球物理学报 , 56(12): 4009–4027. | |
| 许力生, 张旭, 严川, 等. 2014a. 基于勒夫波的鲁甸MS6. 5地震震源复杂性分析. 地球物理学报 , 57(9): 3006–3017. | |
| 许力生, 严川, 张旭, 等. 2014b. 2014年盈江双震的破裂历史. 地球物理学报 , 57(10): 3270–3284. | |
| 严川, 许力生. 2014. 一种地方与区域地震震源机制反演技术: 广义极性振幅技术(一)——原理与数值实验. 地球物理学报 , 57(8): 2555–2572. | |
| 严川. 2015. 小震震源机制与应力场反演方法及其应用研究[博士论文]. 北京: 中国地震局地球物理研究所. | |
| 张旭, 许力生. 2015. 利用视震源时间函数反演尼泊尔MS8.1地震破裂过程. 地球物理学报 , 58(6): 1881–1890. | |
| 张勇. 2008. 震源破裂过程反演方法研究[博士论文]. 北京: 北京大学. | |
| 张勇, 许力生, 陈运泰. 2009. 提取视震源时间函数的PLD方法及其对2005年克什米尔MW7. 6地震的应用. 地球物理学报 , 52(3): 672–680. | |
| 张勇, 许力生, 陈运泰. 2010. 2010年青海玉树地震震源过程. 中国科学: 地球科学 , 40(7): 819–821. | |
| 郑秀芬, 欧阳飚, 张东宁, 等. 2009. "国家数字测震台网数据备份中心"技术系统建设及其对汶川大地震研究的数据支撑. 地球物理学报 , 52(5): 1412–1417. | |
 2016, Vol. 59
2016, Vol. 59


