随着勘探开发的不断深入，地震勘探逐渐进入岩性油气藏勘探阶段，对地震资料处理以及反演提出了更高的要求.全波形反演可以精确描述地下介质参数空间分布，但是其巨大的计算量以及对初始模型的依赖性，成为其广泛应用的瓶颈(Virieux and Operto，2009).为了克服其计算量大的缺陷，GPU加速技术、相位编码技术以及震源编码技术被相继利用，达到提高计算效率的目的(Ben-Hadj-Ali et al.，2009; Larner et al.，1981; Luo et al.，2012; Moghaddam et al.，2013).由于计算量大的限制，大多数反演方法局限于二维情况，且属于基于Fréchet导数的线性或拟线性方法，对初始模型具有一定的依赖性.为了减弱对初始模型的依赖性，许多学者做了大量的研究.Bunks等(1995)应用多尺度反演策略：大尺度反演的结果作为小尺度反演的初值，减弱了对初始模型的依赖性；Ren等(2014)应用第二代小波多尺度方法，实现了品质因子以及速度的反演；Shin等(2008;2009)提出了Laplace域以及Laplace-Fourier域全波形反演，其可为波形反演提供初始速度模型；Wu等(2014b)提出了包络反演方法，在低频缺失的情况下，可为全波形反演提供可靠的初始速度模型；在包络反演理论基础上，Luo和Wu(2015)讨论了包络反演在降低目标函数局部极小值以及抗噪性方面的特性；另外，Chi等人也同时研究了包络反演方法以及其为全波形反演方法提供初始模型的应用潜力(Chi et al.，2014).上述方法在减弱初始模型依赖性方面，均是设计对初始模型不敏感的目标函数，但是在更新迭代时，均基于Born近似，采用线性或拟线性方法，原因之一是其计算效率较高，因为基于蒙特卡洛的完全非线性方法，计算量大，目前无法在大规模计算中使用.

但是线性方法有其局限性，因此Wu和Zheng(2014)从理论上分析了Born近似(线性Fréchet导数)的弊端，证明很多情况下高阶Fréchet导数是不可以被忽略的，因此引入了非线性偏导数的概念.考虑到波传播以及反演过程的非线性性质，Weglein等(2003)研究了逆散射级数方法以及在地球物理勘探中的应用；但是Born级数以及逆Born级数的收敛性在很大程度上不能保证，因此为了改善收敛性，众多学者做了大量研究.Jakobsen(2012)利用量子物理中重整化方法得到改善的Born级数，改善了原Born级数的收敛性；Kouri和Vijay(2003)以及Yao等(2014)利用重整化技术将Lippmann-Schwinger方程从Fredholm积分转化为在1D介质复平面具有绝对一致收敛性的Volterra级数；Kouri等(2004)基于Volterra逆散射级数，提出了若干策略以得到更好的声波散射预测；Lesage等(2013)利用反射以及透射数据，用重整化的Volterra积分来描述逆声散射级数.该非线性模拟以及非线性反演，在重整化的框架下，改善了散射级数以及逆散射级数的收敛性.

本文基于Wu和Zheng(2014)建议的非线性反演方法以及Wu等(2014a，2015)提出的对逆散射级数进行重整化的逆薄板算子，对逆传播算子理论及其快速算法做进一步研究.在二维常密度声波正演方程中，首先引入传输矩阵(T-matrix)，得出扰动数据与T-matrix的线性关系；其次，根据解析关系，得到T-matrix与速度扰动的非线性关系，这种非线性关系可用Born级数表示；最后，在T-matrix已知的前提下，通过逆散射级数对速度扰动进行估计，为了保证收敛性，应用De Wolf近似，推导出了逆薄板传播算子(Inverse Thin-Slab Propagator，ITSP)，以得到地下参数准确而高效的非线性估计.我们已对高斯球高速异常体模型进行了收敛性分析(Wu et al.，2014a，2015)，本文对二维常密度声波方程利用ISTP方法对椭球高速异常体、高斯球低速异常体以及既含高速异常体又含低速体异常体的双扰动椭球模型进行测试，验证本文方法的有效性.

对于二维常密度声波方程，如公式(1)所示：

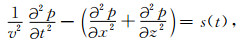
(1)

其中p为压力场，v为地下速度分布，s为震源项.方程的解可由Lippmann-Schwinger积分方程进行表征：

(2)

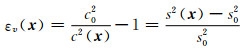
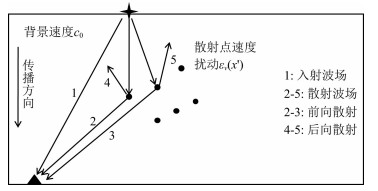
其中，在某一角频率ω下，p(x)是总波场，p⁰(x)是入射波场，g₀(x;x′)是背景介质对应的格林函数，波数k=ω/c₀，ε_v(x′)为速度扰动函数，定义为，c₀为背景介质的速度，s₀为背景介质的慢度.公式(2)的物理涵义可以由图 1进行阐释，总波场p(x)是入射波场p⁰(x)以及所有散射波场之和，且与传播方向相同的散射波为前向散射，与传播方向相反的散射波为后向散射；另外散射波场依赖于总波场p(x)，其计算可以通过迭代或者级数的方式进行计算.

图 1

Fig. 1

图 1 波传播示意图 Fig. 1 Cartoon of seismic wave propagation

公式(2)可以写成矩阵、向量形式：

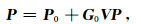
(3)

其中P为总波场(从震源x_s出发的向量)，P₀为背景波场(向量)，G₀为包含波数以及格林函数信息的矩阵，V为实值对角矩阵，包含速度扰动的信息.则利用循环迭代方式得总波场P的递推公式：

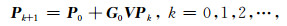
(4)

将总波场P写成级数的形式：

(5)

公式(5)对应的级数即为Born级数.右端第一项为入射场，第二项为一阶散射，第三项为二阶散射，后面的为高阶散射.将所有高次项叠加便可以得到包含各阶散射的合成地震记录，但Born级数不能保证收敛性，在扰动强度较大或扰动区域较大时，得到的Born级数发散，不能得到期望的合成地震记录.在扰动较弱时，通常对其进行线性近似，忽略高阶项的影响，取其前两项得Born近似，如公式(6)所示：

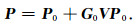
(6)

在扰动强度以及扰动范围较小时，其具有较高的精度；扰动强度以及扰动范围较大时，其精度较低，与有限差分得到的离散解相差较大.目前大多数反演方法都是基于Born近似理论，因此对初始模型具有一定的依赖性，只有在扰动相对较小时，才能得到合理的解估计.

为了提高Born级数的收敛性，引入传输矩阵(T-matrix)的概念，使得：

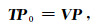
(7)

其中T为复值传输矩阵，包含总波场P中各阶散射的信息.由于传输矩阵T的引入，使得总波场P中的各阶散射信息被转移到传输矩阵T之中，基于传输矩阵T对速度扰动进行非线性估计.由于各阶散射的影响，传输矩阵T的结构与速度扰动V不同，其非对角线元素表征了不同扰动点之间的散射信息.将公式(7)反代入公式(3)中得：

(8)

则总波场P与速度扰动V之间的非线性关系转变为与传输矩阵T之间的线性关系，T的估计问题可以通过线性优化方法进行求解；在正演模拟时，与Born级数方法相比，公式(8)具有较好的收敛性.传输矩阵T与速度扰动V之间的关系为

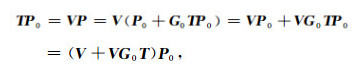
(9)

由于P₀是从震源x_s出发到达散射点x′的向量，由于震源x_s的任意性，使得向量P₀是任意的，且满足公式(9)，公式(9)两端同时约去P₀，得传输矩阵T与速度扰动V之间的非线性关系，隐式公式如(10)所示：

(10)

传输矩阵T与速度扰动V的相互关系可显示表达为

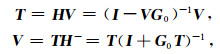
(11)

其中H为传播算子，将速度扰动V转化为包含各阶散射的传输矩阵T；H^－为逆传播算子，将包含各阶散射的传输矩阵T恢复为速度扰动V.正演计算时，已知速度扰动V，利用公式(11)计算传输矩阵T，再基于公式(8)合成地震记录；在反演计算时，可借助线性反演理论，基于公式(8)，估计复值传输矩阵T，再利用公式(11)进行速度扰动估计.但是当扰动区域较大时，利用矩阵求逆方法估计速度扰动计算量较大，与矩阵规模的三次方成正比，难以满足大规模计算的要求(Wang et al.，2014).

本文假设传输矩阵T已知，估计速度扰动V.由于矩阵求逆的计算量较大，当‖G₀T‖<1时，公式(11)中的矩阵求逆可通过级数的形式进行计算：

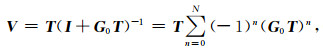
(12)

公式(12)实际上为逆Born级数，可以通过迭代的方式进行计算，递推公式为

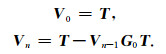
(13)

其中V_n是速度扰动第n次迭代的估计值.在收敛的前提下，随着迭代的进行，速度扰动的估计值V_n逐渐退化为实值对角矩阵，因此，我们主要关注估计值的对角元素，即

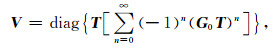
(14)

当速度扰动强度较大或扰动范围较大时，逆Born级数(公式(12)—(14))并不能保证收敛性，因此引入De Wolf近似方法(De Wolf，1971; Wu and Huang，1995; Wu and Zheng，2014; Wu et al.，2007)，进行收敛性的改善.

公式(11)在‖G₀T‖<1的前提下，可以展开为逆Born级数；但是在较强扰动或扰动范围较大时，‖G₀T‖<1假设不成立，导致逆Born级数式(12)以及迭代公式(13)的收敛性不能得到保证，这是逆Born级数的主要弊端.Wu和Zheng(2012;2014)指出可以将散射算子分解为前向散射以及后向散射算子，再对前向散射算子进行正则化处理，可以将关于传输矩阵T的逆Born级数转变为具有收敛性的De Wolf级数.因此，将传输矩阵T分解为前向散射(透射波)以及所有的后向散射(包含反射波在内的所有多次反射波)：

(15)

其中T_f是对应于前向散射的传输矩阵，T_b是对应于所有后向散射的传输矩阵.为简化问题，仅仅考虑只产生前向散射的光滑介质，应用于强反差复杂介质的T-matrix方法将是下一步的研究目标.则

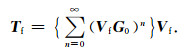
(16)

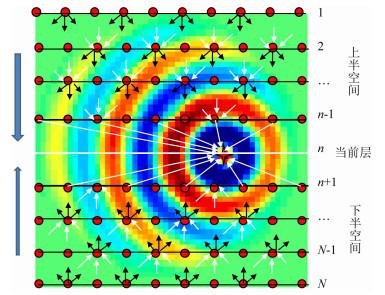
前向散射传输矩阵T_f按扰动点(图 2中红色十字星)所在层的位置可以分成三部分：上半空间速度扰动产生的干涉、下半空间速度扰动产生的干涉以及当前层速度扰动产生的干涉，如图 2所示，则

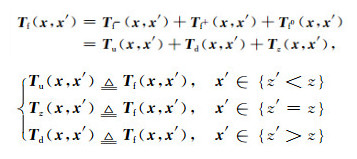
(17)

然后根据T_u，T_z和T_d对逆传播算子H^－进行分解得，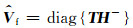

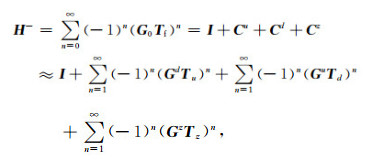
(18)

其中I为单位算子；C^u，C^d，C^z分别为对应于T_u，T_d和T_z的前向散射校正算子，且有

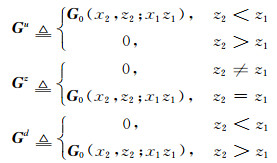
(19)

由于观测孔径的影响，T_z一般比较小，甚至不可能得到，因此在数值试验时忽略当前层的影响.C^u的第n次校正项为

(20)

则公式(18)—(19)可以总结为

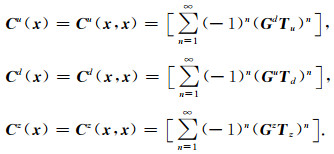
(21)

公式(18)转化为

(22)

对公式(18)进行直接计算，计算量较大.基于重整化的薄板法(Thin-Slab Propagator，TSP)思想(Wu and Wu，2006)，对于逆散射级数式(18)，我们推导出了相应的薄板法公式，称之为逆薄板传播算子(Inverse Thin-Slab Propagator，ITSP).由公式(22)知

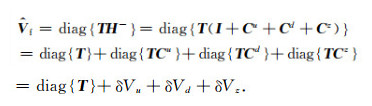
(23)

首先分析δV_u的估计问题.由公式(23)知

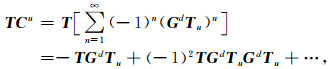
(24)

以积分或加和的形式将上式写成核算子的形式，上部散射对第m个薄板的校正值为

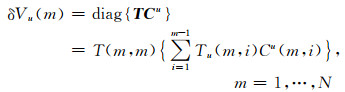
(25)

核函数表达式为

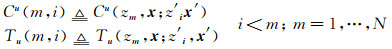
(26)

利用ITSP方法计算第m层校正值为

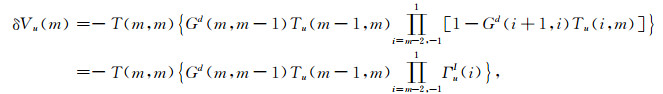
(27)

其中Γ_u^I(i)为第i层的逆薄板传播算子(ITSP)：

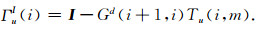
(28)

可以看出，在逆薄板法(ITSP)每一步中，均对之前薄板(第m个薄板之前)的多次逆散射进行了部分叠加，该重整化策略消除了逆散射级数的发散性问题，图 2显示了用于高斯球高速异常体模型测试(Wu et al.，2014a; Wu et al.，2015)的ITSP的示意图：第n层的红色十字表示要恢复的速度扰动点，该点对应的T-matrix(主频20 Hz)的实部为该示意图的背景图(红色表示正值，蓝色表示负值).为了恢复给定点的速度扰动，需要已知其所对应的T-matrix，其分布于整个速度扰动区域.

图 2

Fig. 2

图 2 逆薄板法示意图 Fig. 2 Schematic cartoon for ITSP (inverse thin-slab propagator)

与计算上部散射校正值一样，基于ITSP方法得到下部散射校正值：

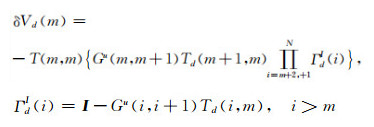
(29)

另外，当前层的校正值为

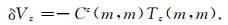
(30)

逆薄板传播算子(ITSP)是一个消除散射的算子，它逐渐将T-matrix中包含的散射信息消除，逐渐退化为速度扰动对应的对角矩阵V.因此，为了恢复某一层的速度扰动，需要知道T-matrix的各个元素T_u(i，m)，T_d(i，m)和T_z(m，m)，其估计问题将是下一步的研究内容.T_z一般比较小，甚至不可能得到，因此数值试验时忽略当前层的影响.

我们已对高斯球高速异常体模型进行了收敛性测试，该试验指出了逆Born级数的缺陷，且验证了ITSP方法的可行性.为了进一步验证ITSP方法的有效性，本文设计了椭球高速异常体、高斯球低速异常体以及既包含高速异常体又包含低速异常体的双扰动椭球模型.一系列数值试验分析验证了ITSP方法的可行性以及有效性.

椭球高速异常体模型如图 3所示：椭球的长轴为500 m，短轴为300 m，背景速度为2000 m·s^-1，高速异常体位于介质中间，模型总规模201×201，异常体的规模31×51，空间分辨率为10 m.T-matrix是一个频率依赖的复值矩阵，其规模为N×N；由于异常体主要分布于模型中间，仅考虑异常体区域即可，N=1581.反演中利用的T-matrix为频率20 Hz的精确T-matrix信息，其对应全孔径测量时的情形，包含全孔径测量数据的全部信息.一般情况下，T-matrix可从有限孔径的观测数据中，利用线性反演方法得到，至于采集孔径对T-matrix估计精度的影响将在后续的研究中进行讨论.

图 3

Fig. 3

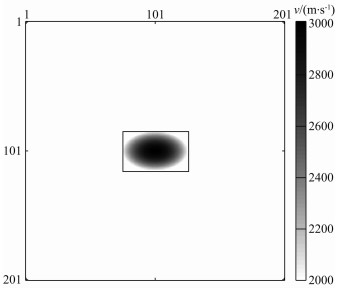
图 3 光滑椭球扰动模型(50%速度扰动) Fig. 3 The model of smooth ellipse ball with 50% perturbation

利用ITSP方法对速度模型的整个椭球扰动区域进行处理，估计得到速度分布以及它们的相对误差，如图 4(a—c)所示，分别为15%、20%和50%速度扰动时估计得到的速度分布以及相对误差，其中相对误差定义为绝对误差除以最大扰动量.可以看出，ITSP方法克服了逆Born级数的发散性问题，且精度较高，只经过一次扫描校正(一半来自上部，一半来自下部，示意图见图 2)，效率高.与高斯球高速异常体模型试验结果(Wu et al.，2014a; Wu et al.，2015)类似，在精确T-matrix已知的前提下，进行速度扰动估计，克服了逆Born级数的发散性问题，在全波形反演中具有较好的应用前景.

图 4

Fig. 4

图 4 不同扰动强度椭球高速异常体速度估计结果以及相对误差 (a) 15%； (b) 20%； (c) 50%. Fig. 4 The estimated velocity distributions and their relative errors for the high velocity anomalous ellipse ball model with different perturbation strengths

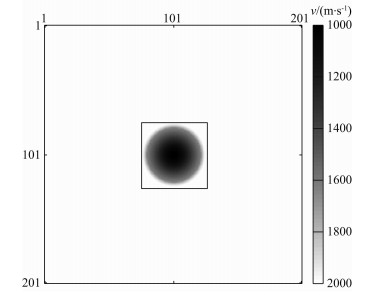
高斯球低速异常体模型如图 5所示：高斯球的半径为500 m，背景速度为2000 m·s^-1，低速异常体位于介质中间，模型总规模201×201，异常体的规模51×51，空间分辨率为10 m.T-matrix是一个频率依赖的复值矩阵，其规模为N×N；由于异常体主要分布于模型中间，仅考虑异常体区域即可，N=2601.与椭球高速异常体类似，反演中利用的T-matrix为频率20 Hz的精确T-matrix信息，其误差对后续速度扰动估计的影响将在后续的研究中进行讨论.

图 5

Fig. 5

图 5 高斯球低速异常体扰动模型(50%速度扰动) Fig. 5 The model of the low velocity anomalous Gaussian ball with 50% perturbation

与椭球高速异常体模型类似，利用ITSP方法对速度模型的整个扰动区域进行处理，得到速度分布以及它们的相对误差.如图 6(a—c)所示，分别为15%、20%和50%速度扰动时估计得到的速度分布以及相对误差，其中相对误差依然定义为绝对误差除以最大扰动量.反演结果表明ITSP方法精度较高，且只经过一次扫描校正，效率高.与高速异常体试验结果相比，反演的误差相对较大，特别是扰动较大时(图 6c)，但相对误差依然在允许范围之内.

图 6

Fig. 6

图 6 不同扰动强度高斯球低速异常体速度估计结果及相对误差 (a) 15%； (b) 20%； (c) 50% Fig. 6 The estimated velocity distributions and their relative errors for the low velocity anomalous Gaussian ball model with different perturbation strengths

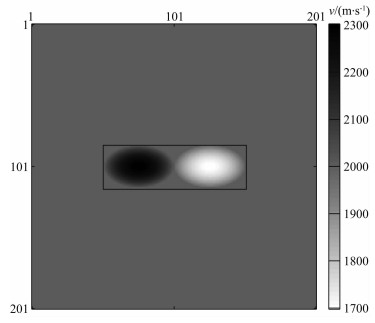
以上模型试验均为单一类型速度异常体模型(高速异常体或低速异常体)，本小节设计了既含有高速异常体，又含有低速异常体的双扰动椭球模型，如图 7所示，每个椭球的长轴为500 m，短轴为300 m，背景速度为2000 m·s^-1，双扰动异常体位于介质中间，模型总规模201×201，异常体规模为31×101，空间分辨率为10 m.T-matrix依然是一个频率依赖的复值矩阵，大小为N×N；由于异常体主要分布于模型中间，仅考虑异常体区域N=3131.类似于以上模型测试，反演中利用精确T-matrix，T-matrix的估计误差对速度估计的影响，将作为后续的研究课题.

图 7

Fig. 7

图 7 双扰动椭球模型(15%速度扰动) Fig. 7 The model of the high and low velocity anomalous ellipse ball with 15% perturbation

利用ITSP方法估计得到的速度分布及其对应的相对误差如图 8(a—c)所示，分别为速度扰动15%、20%以及50%对应的结果.与之前测试结果吻合，ISTP方法克服了逆Born级数的发散性问题，估计得到的解精度较高，且具有较高的计算效率.该测试基于精确T-matrix信息，ITSP方法的精度以及计算效率高，应用前景较好.

图 8

Fig. 8

图 8 不同扰动强度双扰动椭球异常体速度估计结果以及相对误差 (a) 15%； (b) 20%； (c) 50%. Fig. 8 The estimated velocity distributions and their relative errors for the high and low velocity anomalous ellipse ball model with different perturbation strengths

本文利用二维常密度声波方程，讨论了基于T-matrix的非线性速度扰动估计方法，在De Wolf近似的前提下，深入研究了逆薄板法(Inverse Thin-Slab Propagator，ITSP)，该算子摆脱了Born近似的束缚；由于考虑了多次散射项，克服了对初始模型的依赖性.在T-matrix已知的前提下，ITSP方法克服了Born级数的发散性问题，可对强速度扰动进行高精度的估计；由于其只经过一次扫描校正(一半来自上部散射的贡献、一半来自下部散射的贡献)，计算效率较高.不同扰动类型以及扰动强度的模拟数据分析验证了本文方法精度高、效率高的优点，但其依赖于T-matrix的估计精度，具体量化分析将在后续研究中进行讨论.本文方法基于二维常密度声波方程，但其可以推广至三维常密度声波方程中，与二维方法类似，三维方法也是逐层校正；不同的是，三维中的层面为平面，二维中的层面为线条.