随着野外采集技术、室内处理水平的提高和计算机技术的日益更新,各向异性介质逆时偏移技术已经成为理论研究的热点之一.各向异性介质的逆时偏移成像一般有两种方式:一是多波多分量成像,即求解各向异性介质的Christoffel方程得到P波和S波在频率域的偏振方向,从而求得空间域波场分离算子,进而分离出纯P波进行偏移成像(Dellinger and Etgen,1990; Yan and Sava,2009).但这种方式波场外推过程计算量和内存消耗巨大,而且需要的参数较多.另一方式是利用各向异性拟声波方程.Alkhalifah(1998)最先提出拟声波方程,他将P-SV波频散关系中对称轴方向上的SV波速度设为零,然后将它反变换到时间-空间域,得到拟声波方程,但是该方程为四阶微分方程.为了能提高计算效率、减少内存消耗,早期一些学者通过简化频散关系,将四阶微分方程分解成耦合的二阶微分方程组,从而得到计算效率更高的方案(Zhou et al.,2006; Du et al.,2008).虽然上述声学近似方程能够较为方便地实现波场的数值模拟和逆时偏移,但存在残留横波干扰问题,同时它也破坏了原刚度矩阵的正定性(Fletcher et al.,2009; Fowler et al.,2010; Zhang et al.,2011; 张岩和吴国忱,2013).针对各向异性介质逆时偏移不稳定的问题,Fletcher等(2009)通过引入非零的SV波方式来克服.虽然这种做法可以保持波场正反向传播的稳定,但在偏移过程中易产生一些假象,如非零SV波与P波的串扰假象.Zhang等(2011)则推导出稳定的TTI声波方程的自共轭微分算子,并通过能量守恒的方式证明了其方程在波场传播过程中是稳定的.Duveneck和Bakker(2011)从弹性波基本理论出发推导出更具有物理意义的各向异性声波方程,并且在TTI介质中考虑了角度(Thomson参数θ)的非均匀性,虽然能在一定程度上克服由角度变化引起的不稳定性,但还是不能完全解决残余横波的问题.
为了能得到纯P波波动方程,部分学者通过对各向异性介质P_SV波的频散关系进行化简分解,如因式分解法(Liu et al.,2009)、一阶近似法(Pestana et al.,2011; Zhan et al.,2012),从而导出解耦的P波和SV波的频散关系.但这种方式得到的波动方程存在一个高阶的拟微分算子,直接采用有限差分法求解是十分困难的,目前主要采用伪谱法实现数值模拟(Chu et al.,2011; Pestana et al.,2011),但计算量太大.Cheng和Kang(2012)、程玖兵等(2013,2014)通过对平面波形式的弹性波方程(即Christoffel方程)实施一种代表向波矢量方向投影的相似变换,推导出了一种适应任意各向异性介质、运动学上与原始弹性波方程完全等价,在动力学上突出qP波的新方程,即qP波伪纯模式波动方程.
另一方面,地下介质普遍存在黏滞性,表现为对地震波的吸收衰减作用,即地震波在介质中传播的同时,其高频成分容易丢失,而振幅则按指数规律衰减.目前关于黏弹介质的理论模型主要有:Kelvin-Voigt模型(Madja et al.,1985)、用连续频谱的弛豫时间表示的标准线性固体模型(Madja et al.,1985)、标准线性固体模型(Aki and Richards,1980)等.早期的标准线性固体模型是从流变学中引进而来(Emmerich and Korn,1987).Carcione等(1988)在此基础上提出了更为完善的基于广义Zener体的线性黏弹理论,并结合流变学理论,提出新的黏弹性介质中的本构方程,即将应力表示为松弛函数与应变的卷积,并将其推广到各向异性黏弹介质中.Robertsson等(1994)将交错网格有限差分算法应用到基于广义标准线性体模型的一阶速度-应力方程正演模拟中,并得到了不错的效果.
在成像方面,黏介质的偏移成像也随着黏介质理论的完善不断发展.由于它对地震波的衰减与吸收的补偿效应,使其成为实现“保幅偏移”的重要方式.早期业界广泛采用反Q滤波技术进行偏移成像,而这种技术只能进行一维的补偿,并不能准确地恢复波场的本来特征.进而由一维发展到二维,利用伪谱法实现黏声波方程的叠后深度偏移(Dai and West,1994).另一种实际生产中常用的方法就是结合射线理论,实现了克希霍夫反Q叠前偏移(Traynin et al.,2008; Xie et al.,2009).然而上述方法只能对地震波振幅有所补偿,并没有考虑黏滞地层对相位的影响.Fletcher等(2012)在波场延拓过程中同时对振幅和相位进行校正,实现了各向同性介质黏声波逆时偏移.基于带伪微分算子的常Q频散关系,Zhang等(2010)导出时间-空间域的各向同性黏声波动方程,该方程能很好地解决相位延迟问题,并将其应用于叠前逆时偏移;Suh等(2012)将Zhang等(2010)的理论扩展到各向异性介质中,弥补了黏拟声波的衰减效应.
然而对各向异性黏介质的保幅成像,我们往往只侧重于某一方面的研究,即各向异性或黏滞性,这使得成像效果都不理想.所以要想实现保幅成像必须同时考虑各向异性和黏滞性的影响,而这需要一个能准确描绘地震波在各向异性衰减介质中传播规律的方程.文中通过引入广义标准线性固体模型(GSLS)来模拟地震波的吸收衰减规律,并结合各向异性拟声波近似理论,推导出基于GSLS模型的各向异性衰减拟声波方程.理论模型的正演模拟和逆时偏移结果表明该方程能够同时兼顾地层的各向异性和黏滞性.
2 基于GSLS模型各向异性衰减拟声波方程 2.1 各向异性介质标准线性固体模型基本理论常规介质中的标量方程和弹性波方程均假设介质对地震波是无吸收衰减的,黏弹性波方程考虑了实际地下介质对波的黏滞吸收衰减作用;在各向同性介质下,由于各个方向的应力应变关系是一致的,所以每个方向上描述黏滞吸收衰减作用的松弛函数是一样的,也就是说在各向同性介质下只要引入两个松弛函数就能准确地描述介质的吸收衰减,一个松弛函数描述正应力与应变的松弛关系,另一个描述剪切模式下的松弛关系.然而在各向异性介质下,各个方向上应力应变关系不一致,所以以上方式很难适应该种介质.
针对各向异性黏弹介质,Carcione(1990)提出一种新的本构方程以及对应的时间域波动方程来描述地震波在非均匀各向异性衰减介质中的传播,即地震波在不同方向上的衰减特征均不同.其利用四个不同的松弛函数来表征地层的衰减特征,一个松弛函数描述准胀缩模型的非弹性性质,其他三个描述剪切模式的非弹性性质.
线性各向异性黏弹介质可以表示为最一般的本构关系(Carcione,1990):

|
(1) |
其中T=[T1,T2,T3,T4,T5,T6]=[σ11,σ22,σ33,σ32,σ13,σ12]为应力矢量(文中为了书写简便,用下标1表示X方向,2表示Y方向,3表示Z方向),S=[S1,S2,S3,S4,S5,S6]=[ε11,ε22,ε33,2ε32,2ε13,2ε12]是应变矢量,Ψ为各向异性黏弹介质下的弹性矩阵,该矩阵为6×6的对称矩阵,在该矩阵的一般形式中有21个独立的元素.应力、应变、弹性矩阵是由空间坐标(x,y,z)和时间变量决定的.方程(1)被称为 Boltzmann 叠加原则,或简称 Boltzmann 原理.根据上述Boltzmann原理,可将弹性矩阵表示如下:
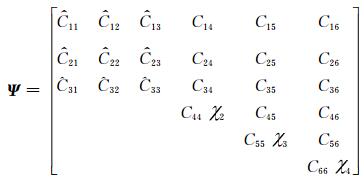
|
(2) |
其中
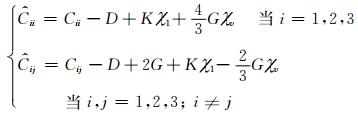
|
(3) |
方程(2)中Ĉii、Ĉij为各向异性黏弹介质的弹性系数,Cii、Cij为各向异性弹性介质的弹性系数,方程(3)中的变量K、D、G表述如下:
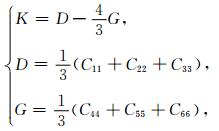
|
(4) |
其中χv为无量纲的松弛函数:当v=1时,表示准胀缩模式下的松弛函数,v=2,3,4是表示剪切模式的松弛函数.松弛函数个数的选择决定于介质的对称性,因为衰减函数的对称性与地层的对称性紧密相关,例如对于以Z轴为对称轴的横向各向同性介质,就有χv=χ2=χ3和C66χ4=(Ĉ11-Ĉ12)/2,用于保证横向各向同性.
广义标准线性固体(GSLS)模型是将一系列标准线性(SLS)固体并联在一起,其松弛函数与黏弹模量定义如下:
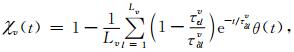
|
(5) |
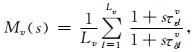
|
(6) |
其中L表示标准线性固体个数;τσl和τεl分别是第l个标准线性固体的应力松弛时间和应变松弛时间常数,每对弛豫时间常数描述了一个频散机制;θ(t)是单位阶跃函数;s是频率相关的函数,且有s=iω,其中ω是角频率,i是虚数单位.模量Mv(s)实质上就是d[χv(t)H(t)]/dt的时间傅里叶变换.
每个松弛函数对应的品质因子可定义为:

|
(7) |
其中Re表示实部,Im表示虚部.因此广义标准线性固体的品质因子为
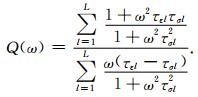
|
(8) |
方程(8)描述的Q-ω关系中,L越大,元组越多,Q-ω关系就越复杂,越远离单调递增或递减趋势,越能真实地描述介质的黏性性质.
2.2 基于GSLS模型TI介质衰减拟声波方程推导各向异性介质的波动方程是研究该介质下地震波正演、偏移成像、反演等的重要依据,本文将基于Carcione(1990)提出的各向异性黏弹性波的基本理论,即本构方程、运动微分方程还有几何方程,通过声学近似的方式推导出基于GSLS模型TI介质衰减拟声波方程.TTI介质可由VTI介质通过坐标变换而来,所以VTI介质可认为是TTI介质的一种特例.为了简化推导过程,本文先以VTI介质为例,之后再通过坐标变换的方法导出TTI介质下的波动方程.在观测坐标系下,其微分运动方程可写为:
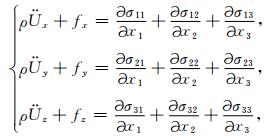
|
(9) |
其中σij(i,j=1,2,3)表示应力,Uk(k=x,y,z)表示位移分量,fk(k=x,y,z)表示震源项.根据2.1节的介绍,可以将黏弹VTI介质中的应力应变关系表示为:
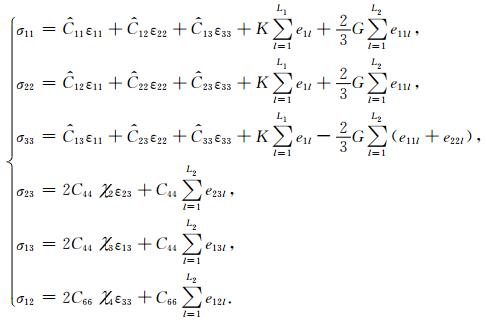
|
(10) |
其中e1l表示胀缩模式的记忆变量,eijl(i,j=1,2,3)为剪切模式下的记忆变量.
为能得到各向异性衰减拟声波方程,本文采用声学近似方法,即令对称轴方向上的横波速度为零,从而消除方程中的横波相关项.方程(11)为VTI介质弹性系数与Thomsen参数关系式(Thomsen,1986).
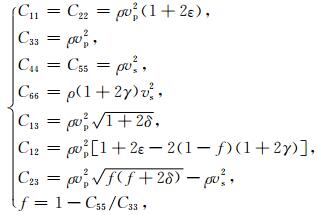
|
(11) |
其中vp,vs,ε,δ,γ为Thomsen参数.当令vs=0时,可得到新的关系式,如方程(12)所示.
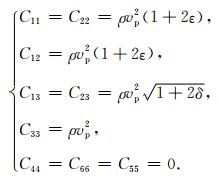
|
(12) |
由方程(12)可知C44=C66=C55=0,将其代入方程(10)中,即可达到消除横波项的目的.与此同时,求方程(10)的时间偏导,再将几何方程代入到求导后的方程中,即可得到声学近似下的应力应变微分关系,如方程(13)所示.
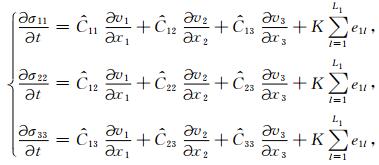
|
(13) |
方程(13)联立运动微分方程(9)得到VTI介质衰减拟声波方程:
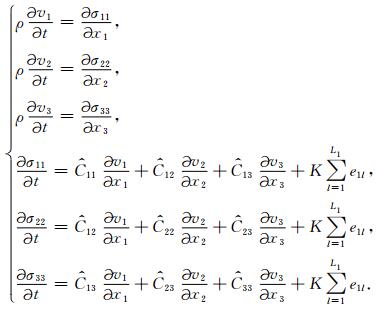
|
(14) |
由于VTI介质在XOY平面内是各向同性的,即在垂直于Z轴各方向的弹性刚度系数是相同的,所以其黏弹性刚度系数可以表示为:
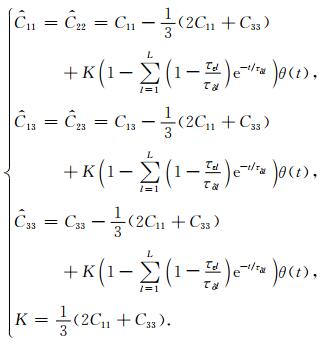
|
(15) |
根据广义标准线性固体(GSLS)的线性近似原理,可以将记忆变量的控制方程写为:

|
(16) |
在三维观测系统内,设TI介质的对称轴和XOZ平面内的观测系统Z轴的夹角为θ,这个角度称为极角;在XOY平面内与X轴的夹角为φ,称为方位角.这样只要对方程(14)进行相应的坐标变换,就能将VTI介质中的一阶方程转换到TTI介质中.设转换矩阵为C(详细的推导过程参考附录A):
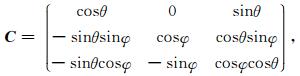
|
坐标系(x′,y′,z′)到(x,y,z)的转换可以表示为:

|
(17) |
其中Hx、Hy、Hz分别表示在x、y、z轴方向上的偏微分算子,(x′,y′,z′)表示VTI介质中的坐标,(x,y,z)表示转换到TTI介质中的坐标.
将方程(17)代入方程(14)中就可得到TTI介质中拟声波一阶速度-应力方程:
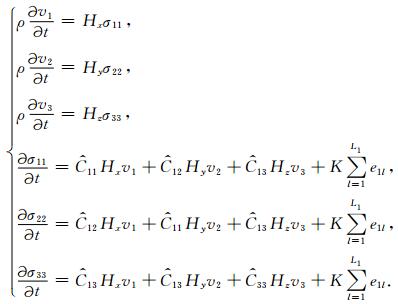
|
(18) |
方程(18)就是所要求解的TTI介质中的一阶速度-应力方程.可以看出方程中的拟声波以“矢量波”的形式存在于σ11、σ22、σ33等分量中,但这种声学近似下得到的“矢量波”有别于弹性介质中的矢量波,因为声学近似的假设已经破坏了波场的矢量性质,如旋度和散度特征(Fowler et al.,2010).关于标量波的选取问题,按照前人的惯例,本文将分量σ33视为准P波(Fletcher et al.,2009; Duveneck and Bakker,2011; Zhang et al.,2011).
3 模型试算由弹性波的基本理论推导出来的一阶速度-应力方程一直都是地球物理学家进行地震波正演模拟的重要方程.一方面它是二阶波动方程降阶的一种形式,使求解方程更为简便.另一方面它能很好地适应交错网格差分法,使网格间距可以取的更大,计算精度也会相应提高,从而降低对计算机内存的要求,缩短计算时间.故本文采用有限差分交错网格算法实现正演模拟和偏移成像(VTI介质方程(14)的差分格式请参考附录B).
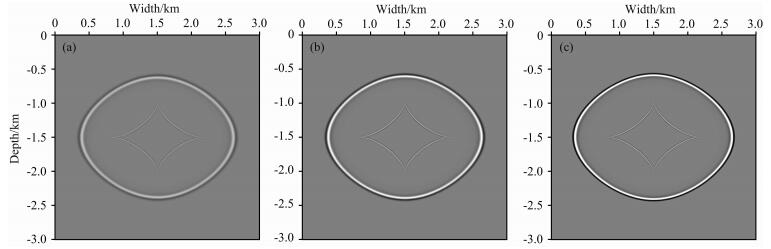
3.1 二维均匀各向异性介质模型正演模拟为了验证新推导的各向异性衰减拟声波的衰减特性及拟声波的运动学特征,选择简单的二维均匀各向异性介质模型进行正演模拟.模型参数:各向异性参数vp0=2000 m·s-1,ε=0.24,δ=0.1;模型大小为600×600,网格大小dx=dz=5 m;震源为主频40 Hz的雷克子波,时间采样间隔为0.5 ms;Q模型:分别为10、20、无穷大(完全弹性介质).如图 1为三个不同Q值的波场快照.图 2为模型中坐标为(1 km,1 km)点处的波形图和振幅谱.图 3为二维XOZ平面内绕Z轴旋转45°的TTI介质的正演结果.
|
图 1 Q为10(a)、20(b)、无穷大(c),t=4.8 s时的VTI介质波场快照 Fig. 1 Snapshots at 4.8 s of three different Q values ((a) 10, (b) 20, (c) infinity) of VTI media |
|
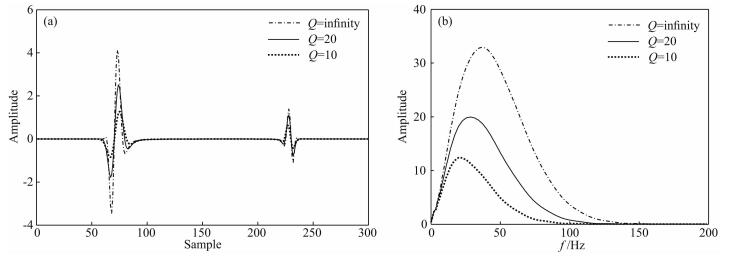
图 2 (1 km, 1 km)点处的波形图(a)、振幅谱(b) Fig. 2 Waveform (a) and amplitude spectrum (b) at point (1 km, 1 km) |
|
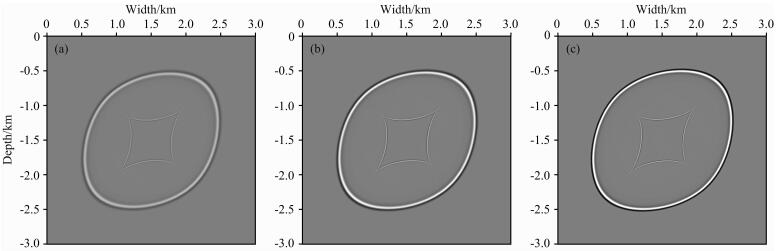
图 3 θ为45°,Q为10(a)、20(b)、无穷大(c),t=4.8 s时的VTI介质波场快照 Fig. 3 Snapshots at 4.8 s of three different Q values ((a) 10, (b) 20, (c) infinity) of TTI media,θ=45° |
从图 1与图 3的波场快照可见,一方面拟声波波前面呈现椭圆状,这符合各向异性介质下准P波的运动学特征,即准P波在各个方向上的相速度是不一致的;另一方面随着Q值的降低,衰减作用越明显,在波场快照中表现为同相轴变模糊,这也符合标准线性固体衰减模型的一般规律.结合图 2中的波形图和振幅谱可知,随着Q值的不断减小,吸收衰减越明显,振幅值不断减小,主频不断降低,并向低频靠近,同时频带宽度变窄,高频成分衰减更明显.说明本文的各向异性衰减拟声波方程能较为准确地描述黏声各向异性介质中地震波的运动学特征.
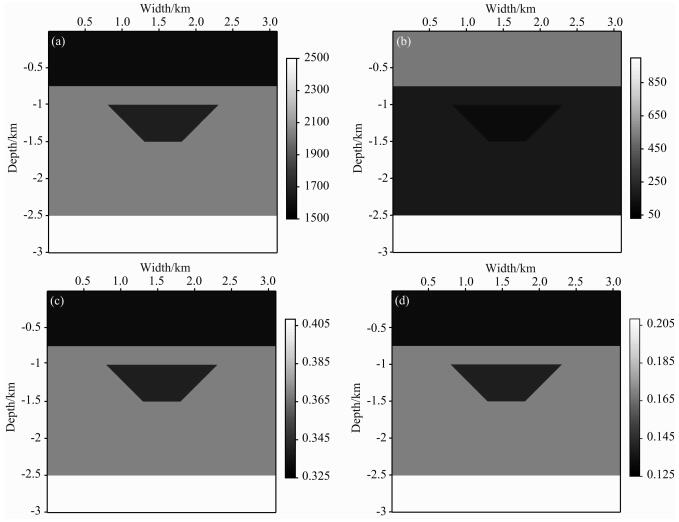
3.2 低速体模型正演模拟为了更好地研究各向异性黏介质下的拟声波特征,自制一个低速体模型,如图 4所示,分别为P波速度场(a)、Q模型(b)、ε模型(c)以及δ模型(d).Q模型是根据速度场构建的,Q值范围为30到50,中间存在强的衰减体,P波速度范围为1800 m·s-1到2500 m·s-1,ε和δ的范围分别为0.32到0.42以及0.12到0.22,震源为主频25 Hz的雷克子波,时间采样长度为3.5 s,时间采样间隔为0.5 ms,模型大小为620×601,网格间距为5 m.
|
图 4 P波速度场(a)、Q模型(b)、ε模型(c)以及δ模型(d) Fig. 4 P wave velocity (a), Q model (b), ε model (c) and δ model (d) |
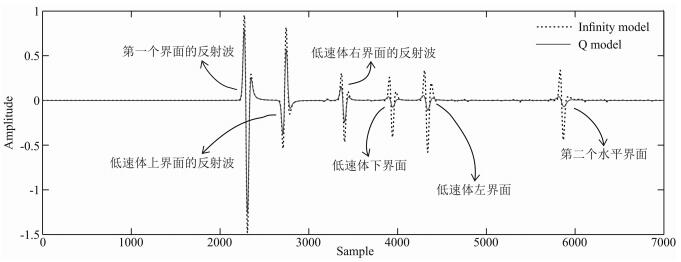
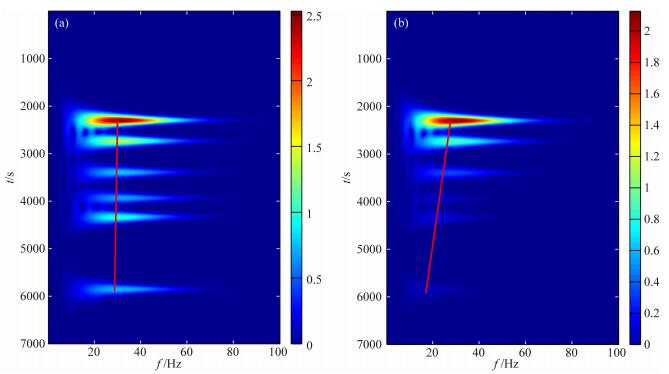
图 5a、5b分别为没有吸收衰减的炮记录和有衰减的炮记录,图 6为两个炮记录第340道的波形图,并在图中标明了各反射界面的反射波.本文采用时频谱的方式分析反射波的频率特征.较常规的频谱分析方法,其能够准确地描述不同界面反射回来的地震波时频特征,从而得到地震波在不同地层中的衰减规律;另一方面能与其对应的波形图相互佐证.得到时频谱的方法很多,如短时傅里叶变换,S变换等,本文采用广义S变换的方法,图 7为广义S变换的时频谱.

|
图 5 炮记录 (a) 完全弹性模型; (b) Q衰减模型. Fig. 5 Shot records (a) Elastic model; (b) Q attenuation model. |
|
图 6 炮集第340道的波形图 Fig. 6 Waveforms of 340th channel of shot records |
|
图 7 炮集第340道S谱 (a) 完全弹性介质; (b) Q衰减模型. Fig. 7 S wave spectrum of 340th channel in shot records (a) Completely elastic medium; (b) Q attenuation model. |
从炮记录可以看出,经过了强衰减体的反射波振幅有剧烈的减弱,同相轴的能量明显变弱,波形图上的振幅信息也证明了这一点.在时频谱中,黏介质中的反射波能量团比完全弹性介质小得多,随着深度的增加差距越大.另一方面黏介质反射波主频由高频向低频移动,高频的吸收更强烈,并且其频带逐渐变窄.综述分析,衰减的反射波振幅和频率特征都符合黏介质的一般衰减规律.
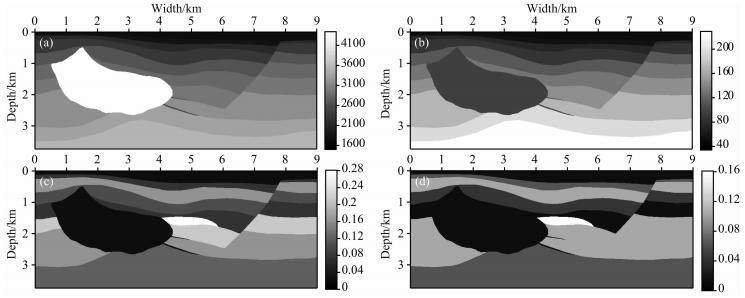
4 逆时偏移中的运用 4.1 VTI_HESS模型逆时偏移为验证文中推导的各向异性衰减标量波方程在逆时偏移中的可行性,文中选VTI_HESS模型进行试算,如图 8a、8b、8c、8d分别为P波速度、Q模型、ε模型以及δ模型.其中Q取值为30到500,深层有一个强的衰减体,与其相对应的速度谱上有一个高速体,P波速度取值为1500 m·s-1到4500 m·s-1,ε和δ的取值范围分别为0到0.28以及0到0.16,其中ε和δ的模型中有个各向异性的突变体(图中已经标出);采用25 Hz的雷克子波,总共600炮,炮间距为10 m,每炮检波器个数为600,检波器间隔5 m,时间采样长度为4.0 s,时间采样间隔为4 ms,成像条件为震源归一化互相关.
|
图 8 HESS_VTI模型:P波速度模型(a)、Q模型(b)、ε模型(c)以及δ模型(d) Fig. 8 P wave velocity (a), Q model (b), ε model (c) and δ model (d) of HESS_VTI model |
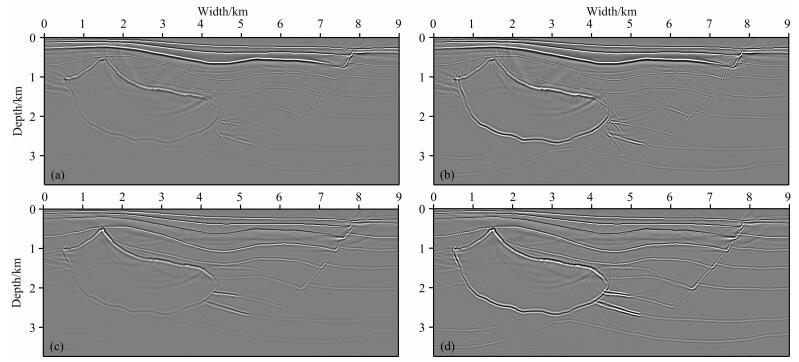
图 9a、9b、9c、9d分别是常规声波方程、各向同性黏声波方程、各向异性拟声波方程以及各向异性衰减拟声波方程的逆时偏移成像结果.通过对比看出,常规声波方程逆时偏移构造形态成像混乱,构造复杂区域绕射波没有完全收敛;特别是深部的各向异性突变体几乎不能显现;深部能量弱,成像效果差.各向同性黏声波方程逆时偏移只是对构造深部的振幅有所补偿,但没有解决常规声波方程逆时偏移的问题.这主要是因为各向同性介质下的声波方程不能完整地描述各向异性介质下标量波的传播规律,比如P波在各个方向上的传播速度不一致.所以该方法不能校正介质各向异性引起的绕射波不归位、能量不聚焦等现象,尤其是大倾角地区.各向异性拟声波方程逆时偏移对HESS模型断层构造成像清晰,在高陡倾角断层面处也有很好的成像效果,同相轴连续性较好,地下突变体轮廓明显.但由于没有考虑黏滞地层的吸收衰减,所以模型的深层成像效果不是很理想,主要是能量较弱,同相轴不清晰.而各向异性衰减拟声波方程逆时偏移既能很好地描述各向异性地震波传播规律,又考虑了地层的吸收衰减影响.从成像效果(图 9d)看出:同相轴清晰,深部能量强,振幅分布更加均衡.
|
图 9 HESS_VTI模型逆时偏移结果:常规声波方程(a),各向同性黏声波方程(b),各向异性拟声波方程(c)以及各向异性衰减拟声波方程(d) Fig. 9 Reverse time migration results of HESS_VTI model: (a) Conventional acoustic wave equation, (b) Isotropic viscoacoustic wave equation, (c) Anisotropic pseudo-acoustic wave equation, (d) Anisotropic viscoacoustic wave equation |
为验证文中推导的黏声波方程在TTI介质中的可行性,以逆冲模型的逆时偏移为例,如图 10a、10b、10c、10d、10e分别为P波速度、Q模型、ε模型、δ模型和θ模型,其中θ是指ZOX平面内的旋转角度.模型的各向异性体现在逆冲断层处.空间采样间隔10 m,横纵向采样点数都是401,时间采样间隔为1 ms,采用主频25 Hz的雷克子波作为震源.

|
图 10 逆冲模型:P波速度模型(a)、Q模型(b)、ε模型(c)、δ模型(d)θ模型(e) Fig. 10 P wave velocity (a), Q model (b), ε model (c), δ model (d) and θ model (e) of thrust model |
图 11a、11b、11c分别是各向同性黏声波方程、各向异性拟声波方程以及各向异性衰减拟声波方程的逆时偏移成像结果.采用各向同性黏声波方程逆时偏移所得的结果,能量聚焦较差,如图中箭头所示之处,可看到绕射波不收敛,层位成像混乱,从模型中可知,此处为TTI介质特性,用各向同性的偏移无法对其准确成像;另外,如方框所示,在各向异性介质的陡倾角下部,由于受到上覆介质各向异性影响,底部水平构造没有拉平,成像结果受到了严重的干扰.各向异性拟声波方程逆时偏移对逆冲模型断层构造成像清晰,在高陡倾角断层面处也有很好的成像效果,同相轴连续性较好.但由于没有考虑黏滞地层的吸收衰减,模型的深层成像效果不是很理想,主要是能量较弱,同相轴不清晰.只有当采用TTI介质逆时偏移算子时,能量才能够得到较好的聚焦,如图 11c所示,箭头所示的各向异性界面内,绕射波得到了很好的收敛,TTI介质的各向异性界面有了更清晰的刻画;如方框内所示,在各向异性陡倾角下部的水平界面也有了较好的刻画,呈现出水平的形态.总之,各向异性衰减拟声波逆时偏移既考虑了各向异性对地震波传播影响,又补偿了反射界面到检波器传播过程中产生的能量损失,使得深部层位成像更加清晰,振幅分布更加均衡,从而大大改善成像效果.

|
图 11 逆冲模型逆时偏移结果:各向同性黏声波方程(a),各向异性拟声波方程(b)以及各向异性衰减拟声波方程(c) Fig. 11 Reverse time migration results of thrust model:(a) Isotropic viscoacoustic wave equation, (b) Anisotropic pseudo-acoustic wave equation,(c) Anisotropic viscoacoustic wave equation |
文章从弹性波基本理论出发,引入GSLS模型模拟地震波的吸收衰减规律,并通过声学近似方式推导出各向异性衰减拟声波方程组.(1)本文将交错网格有限差分算法运用到正演模拟与偏移成像中,理论模型的正演模拟表明该方程既能描述各向异性介质的准P波运动学特征,又能表征地层的吸收衰减效应;(2)本文将各向异性黏声波方程引用到叠前逆时偏移技术中,采用归一化互相关成像条件.模型试算表明各向异性黏声波逆时偏移能对地震波的吸收进行补偿,校正介质的各向异性影响;其成像剖面更加清晰,深部能量得到加强,整体能量更为均衡,成像效果更加符合真实地层的构造特征.
本文的各向异性黏声波方程是基于声学近似推导而来,虽然能较为准确地表述准P波的运动学信息,但同时存在残留横波、动力学特征不准确等问题.另一方面,本文的黏声波逆时偏移只补偿了地震波在黏介质中的吸收衰减,并没有补偿地震波在透射与反射过程中的能量损失;另外还存在低频噪声、相位难以校正、波场逆时传播高频不稳定、深部幅值弱等问题.如何实现各向异性黏介质的保幅成像,仍有待于更进一步的研究.
附录A
TTI介质一阶方程可以由VTI介质一阶方程变换得到.设TI介质的对称轴和XOZ平面内的观测系统Z轴的夹角为θ,相应的旋转矩阵在三维体(x,y,z)内是:
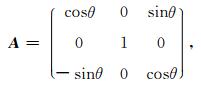
|
因此,可以将一个各向异性三维TTI介质拟声波方程由VTI介质方程经两个旋转变换得到,第一个是在(x,z)平面下的旋转矩阵,即A矩阵(二维情况下);第二个是(y,z)平面下的旋转矩阵B:
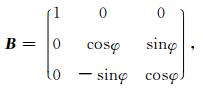
|
所以旋转矩阵可以表示为C=BA,
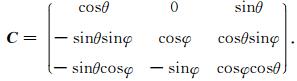
|
变量(x′,y′,z′)到(x,y,z)的偏微分变化可以表示为:
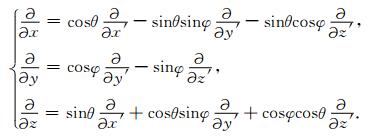
|
(A1) |
附录B
以VTI介质方程(14)为例,应力(σ11)、应变(v1)、记忆变量(e1l)的差分格式分别为
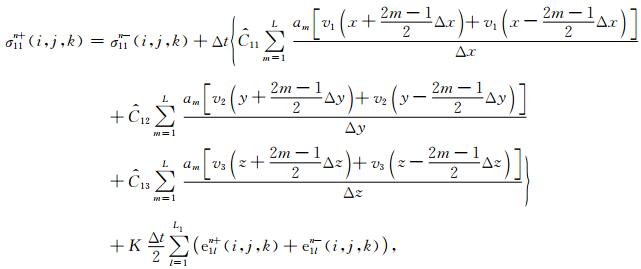
|
(B1) |

|
(B2) |
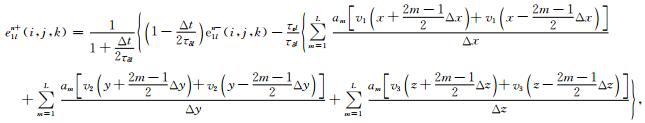
|
(B3) |
其中am为一阶导数的交错网格差分系数,2L表示其相应阶差分精度,其余σ22,σ33,v2,v3的差分格式可同理得到.τδl与τεl可由品质因子Q表示,如方程(B4)所示.另外本文方程的推导过程都是用弹性系数Cij(i,j=1,2,…,6)来描述介质的各向异性,而在模型试算部分笔者采用的是国际上较为常见的Thomsen(1986)参数(vp,vs,ε,δ)模型,这使得介质的弹性参数的物理意义更加明显,且VTI介质弹性系数与Thomson参数关系如方程(12).
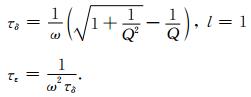
|
(B4) |
| Alkhalifah T. 1998. Acoustic approximations for processing in transversely isotropic media. Geophysics , 63(2): 623–631. | |
| Aki K, Richards P. 1980. Quantitative Seismology. W. H. Freeman and Company. | |
| Carcione J M, Kosloff D, Kosloff R. 1988. Viscoacoustic wave propagation simulation in the earth. Geophysics , 53(6): 769–777. | |
| Carcione J M. 1990. Wave propagating in anisotropic linear viscoelastic media: theory and simulated wavefields. Geophys. J. Int. , 101(3): 739–750. | |
| Cheng J B, Kang W. 2012. Propagating pure wave modes in general anisotropic media, Part I: P-wave propagator.//SEG Technical Program Expanded Abstracts. SEG, 1-6. | |
| ChengJ B, KangW, WangT F. 2013. Description of qP-wave propagation in anisotropic media, Part I: Pseudo-pure-mode wave equations. Chinese Journal of Geophysics , 56(10): 3474–3486. | |
| Cheng J B, Kang W. 2014. Simulating propagation of separated wave modes in general anisotropic media, Part I: qP-wave propagators. Geophysics , 79(1): C1–C18. | |
| Cheng J B, Chen M G, Wang T F, et al. 2014. Description of qP-wave propagation in anisotropic media, Part II: Separation of pure-mode scalar waves. Chinese Journal of Geophysics , 57(10): 3389–3401. doi: 10.6038/cjg20141025. | |
| Chu C L, Macy B K, Anno P D. 2011. An accurate and stable wave equation for pure acoustic TTI modeling.//SEG Technical Program Expanded Abstracts. SEG, 179-184. | |
| Dai N X, West G F. 1994. Inverse Q migration.//SEG Technical Program Expanded Abstracts. SEG, 1418-1421. | |
| Dellinger J, Etgen J. 1990. Wave-field separation in two-dimensional anisotropic media. Geophysics , 55(7): 914–919. | |
| Du X, Fletcher R P, Fowler P J. 2008. A new pseudo-acoustic wave equation for VTI media.//EAGE 70th Conference and Exhibition, Extended Abstracts, H033. | |
| Duveneck E, Bakker P M. 2011. Stable P-wave modeling for reverse-time migration in tilted TI media. Geophysics , 76(2): S65–S75. | |
| Emmerich H, Korn M. 1987. Incorporation of attenuation into time-domain computations of seismic wave fields. Geophysics , 52(9): 1252–1264. | |
| Fletcher R P, Du X, Fowler P J. 2009. Reverse time migration in tilted transversely isotropic (TTI) media. Geophysics , 74(6): WCA179–WCA187. | |
| Fletcher R P, Nichols D, Cavalca M. 2012. Wavepath-consistent effective Q estimation for Q compensated reverse-time migration.//EAGE 74th Conference and Exhibition, Extended Abstracts. | |
| Fowler P J, Du X, Fletcher R P. 2010. Coupled equations for reverse time migration in transversely isotropic media. Geophysics , 75(1): S11–S22. | |
| Liu F, Morton S A, Jiang S, et al. 2009. Decoupled wave equations for P- and SV-waves in an acoustic VTI media.//SEG Technical Program Expanded Abstracts, 2844-2848. | |
| Madja G, Chin R C Y, Followill F E. 1985. A perturbation theory for Love waves in an elastic media. Geophysical Journal of International , 80(1): 1–34. | |
| Pestana R C, Ursin B, Stoffa P L. 2011. Separate P-and SV-wave equations for VTI media.//SEG Technical Program Expanded Abstracts. SEG, 163-167. | |
| Robertsson J O A, Blanch J O, William W S. 1994. Viscoelastic finite-difference modeling. Geophysics , 59(9): 1444–1456. | |
| Suh S, Yoon K, Cai J, et al. 2012. Compensating visco-acoustic effects in anisotropic resverse-time migration.//SEG Technical Program Expanded Abstracts. SEG, 1-5. | |
| Thomsen L. 1986. Weak elastic anisotropy. Geophysics , 51(10): 1954–1966. | |
| Traynin P, Liu J, Reilly J M. 2008. Amplitude and bandwidth recovery beneath gas zones using Kirchhoff prestack depth Q-migration.//SEG Technical Program Expanded Abstracts. SEG, 2412-2416. | |
| Xie Y, Xin K F, Sun J, et al. 2009. 3D prestack depth migration with compensation for frequency dependent absorption and dispersion.//SEG Technical Program Expanded Abstracts. SEG, 2919-2923. | |
| Yan J, Sava P. 2009. Elastic wave-mode separation for VTI media. Geophysics , 74(5): WB19–WB32. | |
| Zhan G, Pestana R C, Stoffa P L. 2012. Decoupled equations for reverse time migration in tilted transversely isotropic media. Geophysics , 77(2): T37–T45. | |
| Zhang Y, Zhang P, Zhang H Z. 2010. Compensating for visco-acoustic effects in reverse-time migration.//SEG Technical Program Expanded Abstracts. SEG, 3160-3164. | |
| Zhang Y, Zhang H Z, Zhang G Q. 2011. A stable TTI reverse time migration and its implementation. Geophysics , 76(3): WA3–WA11. | |
| Zhang Y, Wu G C. 2013. Methods of removing pseudo SV-wave artifacts in TTI media qP-wave reverse-time migration. Chinese Journal of Geophysics , 56(6): 2065–2076. doi: 10.6038/cjg20130627. | |
| Zhou H B, Zhang G Q, Bloor R. 2006. An anisotropic acoustic wave equation for modeling and migration in 2D TTI media.//SEG Technical Program Expanded Abstracts. SEG, 194-198. | |
| 程玖兵, 康玮, 王腾飞. 2013. 各向异性介质qP波传播描述I: 伪纯模式波动方程. 地球物理学报 , 56(10): 3474–3486. | |
| 程玖兵, 陈茂根, 王腾飞, 等. 2014. 各向异性介质qP波传播描述II: 分离纯模式标量波. 地球物理学报 , 57(10): 3389–3401. | |
| 张岩, 吴国忱. 2013. TTI介质qP波逆时偏移中伪横波噪声压制方法. 地球物理学报 , 56(6): 2065–2076. | |
 2016, Vol. 59
2016, Vol. 59

