重力数据反演和重力梯度数据反演方法是位场反演方法的重要组成部分.在早期,因为重力数据获取和处理更加容易,对计算机的要求低,人们提出了很多用于重力数据反演的方法(Last and Kubik, 1983;Li and Oldenburg, 1998;Li and Chouteau, 1998;Portniaguine and Zhdanov, 1999;Chasseriau and Chouteau, 2003;Shamsipour and Marcotte, 2010;刘银萍等,2013).后来,随着FTG系统的出现,梯度数据的精度得到了很大的提高,人们将很多反演方法延伸到了梯度数据的反演(Li,2001;Zhdanov et al., 2004;Martinez et al., 2013;Geng et al., 2014).在实际测量中,重力数据是通过测量位场的垂直分量获得的,重力梯度数据则是通过测量重力场在三个方向的变化获得,在频率域对两种数据进行比较,可以发现,重力数据包含较多的低频信息,重力梯度数据则包含较多的高频信息.基于这一点,将两种数据结合进行联合反演得到的结果更加可信.但是,目前能够将重力和重力梯度数据联合反演的方法还比较少.Zhdanov等(2004)通过重力曲率将重力数据和梯度数据结合进行了反演计算.Wu等(2013)将目标体看作是质点,对其重力和重力梯度公式进行转换,实现了重力和重力梯度数据的联合反演.Capriotti等(2014)针对重力和重力梯度数据核函数随深度衰减速率不同的情况,通过灵敏度矩阵平衡两种衰减速率,实现了重力和重力梯度数据的联合反演.本文基于聚焦反演方法,提出一种能够实现重力和重力梯度数据联合反演的方法.
进行联合反演计算之前,首先需要计算各分量的灵敏度矩阵.一般将地下规则划分为一定数量的小长方体,分量种类的增加和小长方体数量的增加都会使灵敏度矩阵的计算时间增加.同时,存储矩阵所需要的内存也增加.Li等(2003)对灵敏度矩阵进行小波变换,对于变换后的矩阵,通过设置阈值,将低于阈值的部分设为0,从而形成稀疏矩阵,通过对其进行计算和存储,达到减少内存和计算量的目的,但是,这仍然需要先将灵敏度矩阵计算出来.姚长利等(2003)提出了几何格架的概念,他们将地下划分为规则的几何形体,计算模型的部分几何格架的值,随后利用其平移等效性特征推算其他几何格架的值.这样,仅需要计算和存储部分几何格架的值,就可以推算出所有几何格架的值,减少了计算量.与其类似,本文从重力和重力梯度正演公式的角度出发,提出一种快速计算灵敏度矩阵的方法.文中将正演公式看作是包含三个变量的函数式,统计这三个变量的值,将其依次代入公式中,求解得到构成灵敏度矩阵的值.按照一定的规律将数值存到另一矩阵中,依据小长方体的大小和位置信息,计算得到其对应数值在矩阵中的位置,取出该值构建灵敏度矩阵.这一方法对正演公式的变化量进行统计,避免了重复计算,从而缩短了计算时间.更重要的是,我们可以将计算得到的矩阵和小长方体的维度信息存储在数据库中,下次遇到相同的情况,可以直接进行提取.
对于重力和重力梯度数据的反演问题,文中选择有限内存BFGS拟牛顿法来进行求解.这是一种可以用来解决大规模反演问题的优化方法,在三维电磁反演中已经得到了广泛的应用(Newman and Boggs, 2004;Haber,2005;Avdeeva and Avdeev, 2006;Plessix and Mulder, 2008;Avdeev and Avdeeva, 2009;Zhang et al., 2012;刘云鹤和殷长春,2013).这一方法仅需要计算目标函数的梯度,其核心是通过几组修正向量来构建Hessian近似矩阵,从而降低了对内存的要求.
为了解决重力和重力梯度联合反演问题,还需要注意深度加权函数的选择.因为重力和重力梯度数据的核函数随深度增加是衰减的,直接对数据进行反演计算,会产生趋肤效应.而且,因为重力和重力梯度数据的核函数随深度增加其衰减速率不同,所以,通过近似核函数衰减速率提出的深度加权函数不能同时应用在重力和重力梯度数据上.因此,本文选择了Commer(2011)提出的基于异常体的分布的加权函数,这一加权函数需要异常体的大致埋深信息.对于异常体之上到地表的部分,给予较小的权值,对于异常体之下的深部则给予较大的权值.为了获得异常体的埋深信息,我们首先选择单一分量进行反演,随后依据反演结果对异常体的埋深进行评估.在本文中,我们通过再加权的方法将加权函数结合到拟合函数上.
本文首先对正演原理进行介绍,给出快速计算灵敏度矩阵的方法,之后引入反演方法,内容包括:稳定函数的选择及相应公式的推导,有限内存BFGS拟牛顿法的流程,深度加权引入,再加权优化求解,正则化参数的选取.文中通过模型试验对有限内存BFGS拟牛顿法的特点及正则化参数选取对反演过程的影响做了讨论,并探究重力和重力梯度数据联合反演的优势.最后,利用美国路易斯安娜州文顿岩丘的实测重力和重力梯度数据对方法进行验证.
2 正演介绍重力正演的目的是计算地下密度分布在地上引起的响应,本文在笛卡儿坐标系下进行计算.假定地下存在一个长方体,其长宽高分别沿X、Y、Z轴方向,其中Z轴竖直向下.长方体在三个方向的坐标变化范围是(x1,x2),(y1,y2),(z1,z2).观测点坐标为r=(x,y,z),则依据Zhdanov等(2004),可以得到重力数据的正演表达式为

|
(1) |
其中γ是万有引力常数,一般取γ=6.67×10-11m3/(kg·s2),ρ表示地下异常体的密度分布.重力梯度数据表达式为

|
(2) |
其中
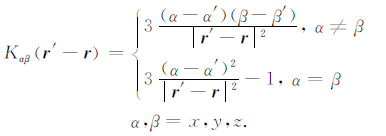
|
(3) |
为了进一步将重力和重力梯度数据的表达式简化,文中采用了Forsberg(1984)的方法,引入了一个三元组(an,bn,cn)l,其中n=1,2,将x-xn,y-yn和z-zn循环代入可以得到式(4)—(6):

|
(4) |
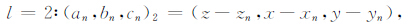
|
(5) |
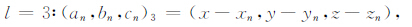
|
(6) |
其中,l=1,2,3分别对应x,y,z.因而有gz=g3,由式(1)和式(6)得到重力数据的正演表达式为
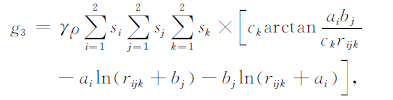
|
(7) |
其中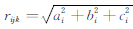
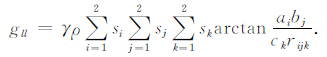
|
(8) |
类似的,对于l,l′=1,2,3且l≠l′,可以得到其他重力梯度分量的表达式如下:
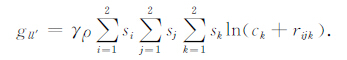
|
(9) |
假定测区的大小为Lx×Ly×Lz,地下被划分为N=nx×ny×nz个小长方体,每个小长方体的大小为dx×dy×dz.数据观测点规则分布,其在地面的投影位于小长方体的中心,观测点的坐标为(x,y,z),观测点个数为Nobs=nx×ny.假定密度ρ是单位密度,则由式(7)、(8)、(9)计算每个小长方体对观测点的影响,得到一个大小为Nobs×N的矩阵,用A表示,称之为灵敏度矩阵.用d表示观测数据,m表示地下密度分布,则正演的矩阵形式为
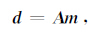
|
(10) |
式中,d的大小为Nobs×1,m的大小为N×1.
在正演计算中,灵敏度矩阵的计算消耗了大量时间,为此文中给出了快速计算灵敏度矩阵的方法.
因为地下规则划分,所以对于(an,bn,cn)l,n=1,2,有:

|
(11) |
式中d1,d2,d3是对应方向上的网格的大小,是常数.由此,式(7)、(8)、(9)包含三个变量a1,b1,c1,其统一的表达式为:
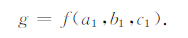
|
(12) |
令a1=x-x1,b1=y-y1,c1=c-c1,x1、y1、z1是小长方体中的点的坐标的最小值.快速计算灵敏度矩阵的方法的流程如下:
(1) 统计a1,b1,c1的取值,并分别用X、Y、Z表示.测区在三个方向坐标变化范围是0,Lx×0,Ly×0,Lz.对X,将其中的取值从小到大排列,有X=(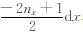
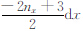
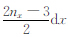
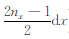
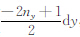
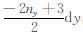
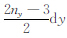
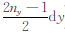
(2) 将X、Y、Z中不同的数据进行组合,组合种类为Nk=(2nx-1)×(2ny-1)×nz,则每个分量的数据量为Nk,将不同组合代入式(7)—(9),得到组成重力和重力梯度数据的灵敏度矩阵的值.
(3) 依据X、Y、Z中的数据计算出一个索引值,记录数据的存放位置.对于任意分量,创建一个矩阵Vα,其大小为Nk×1.对于第k次计算,X、Y、Z中数据对应的索引分别为ix,iy,iz,则数据在矩阵Vα中的位置ik由式(13)给出.

|
(13) |
(4) 依据计算得到的值来构建灵敏度矩阵.对于任意分量,其灵敏度矩阵记为A,Aij表示标记为j的小长方体对观测点i的影响.观测点坐标为(xi,yi,zi),小长方体上的点在三个方向坐标取值的最小值是(xj,yj,zj),则ix,iy,iz可用式(14)、(15)、(16)得到
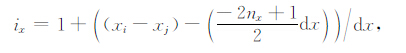
|
(14) |

|
(15) |
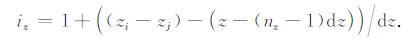
|
(16) |
将ix、iy和iz代入式(13)可以得到Aij的值在矩阵Vα中的位置,进而得出Aij的值.
在一般情况下,如果按照顺序依次计算某一分量的灵敏度矩阵,对于观测点数为nx×ny,地下划分为nx×ny×nz个小长方体的测区,需要代入公式计算n2x×n2y×nz次,本文中,仅需要代入公式计算(2nx-1)×(2ny-1)×nz次,计算的次数大大减少,从而节省了大量时间.另外,对于不同分量的计算,还可以进一步缩短时间.比如式(9)中,仅需要考虑X、Y、Z中的一部分,针对这些分量可以在此基础上进行改进,从而进一步缩短计算时间.
因为Vα中的值是按照一定规律存储的,其数值与网格大小有关,所以可以将常用到的几种网格大小得到的Vα单独存储,建立一个数据库,下次使用时,可以直接调用.
3 反演方法 3.1 稳定函数的选择通常,对于重力和重力梯度数据的线性反演问题,用下面的式子表示:
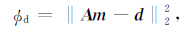
|
(17) |
这里,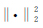
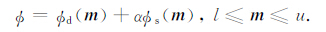
|
(18) |
这里α是正则化参数,ød是拟合函数,øs是稳定函数,l和u代表模型参数m的取值范围.对于正则化反演问题,我们可以通过数值优化算法来预测模型参数m的值,进而达到最小化目标函数的目的.
Last等(1983)提出了最小支撑(MS)函数,通过寻找具有最小体积的异常体来解释重力异常.基于这一函数,Portniaguine等(1999)提出了最小梯度支撑(MGS)算子并将其应用到了重力和可控源电磁数据反演中.MGS算子能够用来寻找具有大的梯度的结构体,并寻找其最小体积,对于具有陡峭边界的地质体,能够获得一个清晰、准确的边界.基于Zhdanov(2009)对该算子的改进,我们得到稳定函数的表达式为

|
(19) |
式(19)中
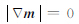
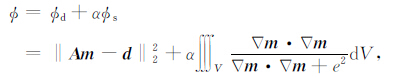 |
(20a) |
基于式(20),可以给出重力和重力梯度数据五个独立分量联合反演的目标函数的表达式为

|
(21) |
其中,Az是重力数据的灵敏度矩阵,Axy、Axz、Ayy、Ayz、Azz是重力梯度数据相应分量的灵敏度矩阵,dobsgz是重力数据,dobsgxy、dobsgxz、dobsgyy、dobsgyz、dobsgzz是重力梯度数据的五个独立分量.
3.2 有限内存拟牛顿法有限内存BFGS拟牛顿法(LBFGS)是一种适用于解决大规模优化问题的反演方法(Nocedal and Wright, 1999).这一方法仅要求计算目标函数的梯度.对于一般的拟牛顿法,比如BFGS拟牛顿法,需要存储大小为N×N的Hessian矩阵H,对于有限内存BFGS拟牛顿法,可以通过n(n取3~20之间的数)组修正向量来构建Hessian近似矩阵,需要的内存空间为2×n×N,大大减少了对内存的要求.这一方法已经被用来解决三维电磁(EM)反演问题(Newman and Boggs, 2004; Haber,2005;Plessix and Mulder, 2008)和一维和三维的大地电磁(MT)反演(Avdeeva and Avdeev, 2006;Avdeev and Avdeeva, 2009;Zhang et al., 2012).对于重力和重力梯度数据联合反演问题,与传统的重力和重力梯度数据反演相比,数据量增大,因此本文选择有限内存BFGS法来求解该问题.
已知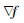
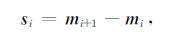
|
(22) |
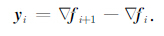
|
(23) |
令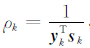
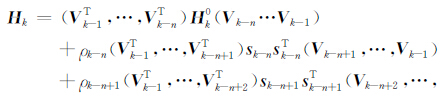 |
(24a) |
结合上面的信息,依据Nocedal等(1999),文中给出了有限内存BFGS拟牛顿法的流程:
(1) 设定模型参数m的初值m0=0及修正向量的组数n;
(2) 计算目标函数的梯度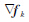
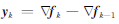
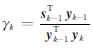
(3) 由式(23)构建Hessian近似矩阵Hk,对于初次迭代,Hk=Hk0,之后的迭代计算中,将通过修正向量{si,yi;i=k-n,…,k-1}和H0k来构建Hk;
(4) 计算搜索方向
(5) 通过Wolfe准则,搜索合适的步长βk,计算得到mk+1=mk+βkpk;
(6) 对目标函数的值和迭代次数进行判断,如果目标函数的值收敛或者达到迭代次数则终止循环,否则转到(2).
在有限内存LBFGS拟牛顿法中,为了保证其收敛,文中选择精确线搜索方法Wolfe准则,其表达式为
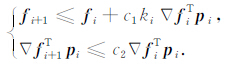
|
(25) |
其中0<c1<c2<1,一般取c1=10-4,c2=0.9.
同时,为了保证Hessian近似矩阵Hk是正定矩阵,向量sk和yk必须满足下面的条件
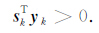
|
(26) |
为了保证这一条件,文中采用Ni和Yuan(1997)对sk进行修正,得到向量s′k,其表达式为
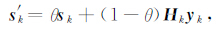
|
(27) |
其中
为了抵消趋肤效应,需要采用深度加权函数.依据Li等(1996),文中给出模型试验说明本文的加权方式.图 1所示为一个长方体模型,大小为500 m×500 m×500 m,顶面埋深为500 m,剩余密度为1 g·cm-3,为了与实际数据吻合,加入了10%的高斯噪声.

|
图 1 单个长方体模型和不同分量的反演结果的剖面图 (a) 模型三维立体图; (b) gz分量反演结果; (c) gzz分量反演结果; (d) z1=400时, gz和gzz联合反演结果; (e) z1=300时,gz和gzz联合反演结果; (f) z1=500时, gz和gzz联合反演结果. Fig. 1 Single prism model and profiles of inversion results of different components (a) 3D model; (b) Inversion result of gz component; (c) Inversion result of gzz component; (d) z1=400, inversion result of gz and gzz component; (e) z1=300,inversion result of gz and gzz component; (f) z1=500,inversion result of gz and gzz component. |
对于三维重力和重力梯度正演模型,其表达式的矩阵形式为式(10).由式(1)和(2),重力和重力梯度数据的核函数随深度增加是衰减的,因此会引起反演结果的趋肤效应.文中引入加权函数矩阵W来抵消这一影响.式(10)转换为

|
(28) |
同样式(17)转换为
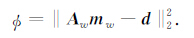
|
(29) |
在对式(29)进行求解前,需要选择加权函数.由式(1)和式(2),重力和重力梯度数据的核函数的衰减速率与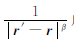
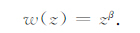
|
(30) |
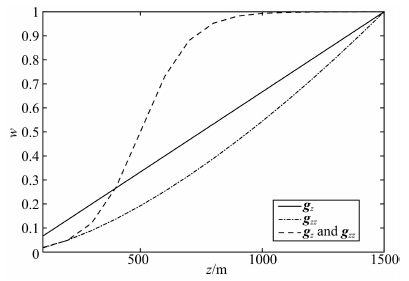
对于重力数据,取β=1,对w(z)进行归一化处理,得到w(z)随深度变化如图 2中的实线所示,将其应用到gz分量的反演计算中,得到结果如图 1b所示,图中显示反演结果克服了趋肤效应.对于重力梯度数据,取β=1.5,对w(z)进行归一化处理,得到w(z)随深度变化如图 2中虚点线所示.将其应用到gzz分量的反演计算中,得到结果如图 1c所示,图中显示趋肤效应被克服了.
|
图 2 不同深度加权函数随深度变化曲线 Fig. 2 Weighting functions varying with depth |
由图 1b和图 1c得出,对目标函数的拟合函数部分进行加权消除趋肤效应是可行的.因为重力数据和重力梯度数据具有不同的衰减速率,所以,从理论上来说,通过近似衰减速率得到的加权函数不能直接应用到重力和重力梯度数据联合反演中.Commer等(2011)提出了一种空间加权函数,Commer(2011)将其应用到了重力数据的反演计算中,这一函数需要了解模型的大致埋深,随后针对异常在垂直方向的分布规律,对于近地表的部分,给予较小的权值以达到阻尼的效果,对于可能存在异常的区域,则给予较大的权值.因为在理想条件下,对同一个地质体的重力和重力梯度数据分别进行反演计算,得到的模型是一致的.所以,这一基于模型分布提出的加权函数,可以用于重力和重力梯度数据的联合反演.其表达式为:
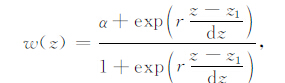
|
(31) |
其中α和r是常数,z1是与深度信息有关的常数,文中取α=0.001,r=1.其中α的值由Commer(2011)给出,是经验值.依据刘银萍等(2013),α也可以取其他很小的值,它的大小直接决定了近地表顶层压制作用的大小,其值越小,压制作用越大,反演结果越集中,反之亦然.对于参数r,其主要作用是保证当z→0时,w(z)的值是一个很小的值或者保证z→0时,w(z)≈α,从而影响近地表顶层压制作用的大小.由图 1b和图 1c,取z1=400,得到深度加权函数如图 2中虚线所示,将其应用到gz和gzz分量的联合反演中,得到图 1d.可以看到,反演结果克服了趋肤效应,能够准确反映出异常体的位置.
由此发现,通过式(29)对单一分量进行反演计算得到的异常体的深度值小于实际深度.这是因为没有其他约束条件,得到的反演结果(图 1b和图 1c)比较发散.但是将这一信息结合到式(31)中,将其作为深度加权函数应用到反演计算,得到的反演结果与真实模型一致.
为了进一步验证预测深度值z1对反演结果的影响,分别取z1=300和z1=500,得到反演结果如图 1e和图 1f.由图 1e,当z1=300时,异常体的位置略有上升,但是其高密度部分(>0.25 g·cm-3)与真实模型一致.当z1=500时,深度信息是准确的,图 1f中异常体的位置与真实模型一致.由此,虽然单一分量反演得到的异常体的深度信息与异常体实际埋深存在一定的差异,但是,将这一信息作为先验信息结合到深度加权函数中,进行实际的反演计算,得到的反演结果是可信的.即使预测的深度在一定范围内波动,也能得到可信的结果.同时,对比图 1d、图 1e和图 1f,可以发现,采用预测得到的深度值作为加权函数,得到的反演结果的密度的最大值更接近真实模型.
3.4 再加权优化求解将加权函数应用到目标函数中,则式(20)变为

|
(32) |
对于拟合函数部分,对mw求梯度得到
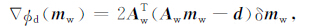
|
(33) |
对于稳定函数部分,对mw求梯度得到
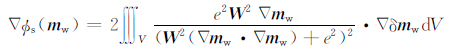 |
(34a) |
其中
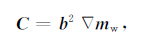
|
(35) |
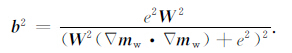
|
(36) |
对等式
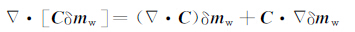
|
(37) |
进行积分计算,并重新排列得到
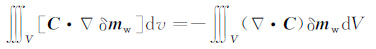 |
(38a) |
其中n是单位向量,指向区域V的外部,∂V是V的表面.依据齐次诺依曼边界条件
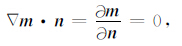
|
(39) |
可以得到

|
(40) |
则由式(34)、式(38)和式(40)得到
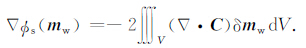
|
(41) |
由式(33)和式(41),得到目标函数的梯度的表达式为
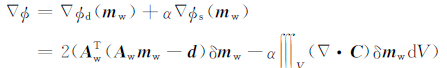 |
(42a) |
由式(20),模型参数m存在边界值,为了增强边界约束,将模型参数的边界信息加入到反演过程中,文中采用惩罚函数的方法,在每次迭代结束后,由mw计算模型参数m,对于超过边界值的部分,将边界值赋给相应的位置.
3.5 正则化参数的选取在反演计算过程中,需要确定正则化参数的值.Farquharson等(2004)对依据偏差原理、GCV准则和L曲线准则预测正则化参数的方法进行了对比.他们对同一数据加不同的噪声,在保证其他反演参数不变的情况下,将这三种方法应用到具有不同噪声水平的数据,结果显示依据GCV准则和L曲线准则获得的结果比依据偏差原理获得的结果更准确.进而得出,依据GCV准则和L曲线准则预测正则化参数的方法能够在反演计算中给出恰当的正则化参数的值.Portniaguine等(2002)给出了一种简单的数值方法,给定正则化参数的初值,在迭代计算中,正则化参数的值依次递减.Farquharson等(2004)给出的反演计算过程中的正则化参数的值,也符合这一规律.依据Zhdanov(2002),目标函数是关于正则化参数的单调函数,正则化参数的值减小,目标函数的值也减小.我们选择数值优化算法来求解目标函数时,一般是通过最小化目标函数来寻找最优解.对于每次迭代获得的解,如果正则化参数的值减小,则相应的目标函数的值也减小,加快了收敛速度.
本文采用有限内存BFGS拟牛顿法.依据3.2节中给出的该方法的流程,每次迭代结束,获得新的模型参数m之后,需要计算目标函数的梯度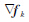
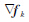
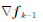
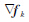
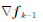

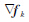
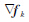
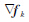
下面,在模型试验中,在保持其他参数设置不变的情况下,分别将α取1和Portniaguine等(2002)提出的正则化参数的计算方法应用到算法中,对含不同噪声水平的数据进行反演计算.Portniaguine等(2002)提出的正则化参数的计算方法如式(43)和式(44)所示.
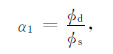
|
(43) |

|
(44) |
其中,拟合函数ød和稳定函数øs的表达式可以由式(32)得到,初次迭代计算后得到的正则化参数的表达式为式(43),随后的迭代计算中,则通过式(44)计算正则化参数的值.
4 模型试验首先通过单一模型试验来说明有限内存BFGS拟牛顿法的特点,随后通过组合模型试验1来比较正则化参数取值方式不同对反演结果的影响,并讨论不同噪声水平数据对正则化参数选取的影响,最后通过组合模型试验2来探究重力和重力梯度数据联合反演的优势.
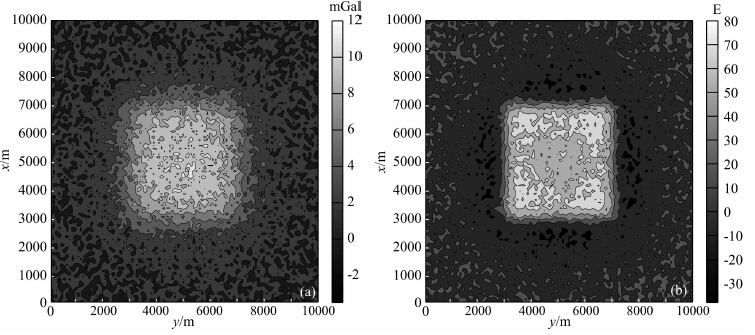
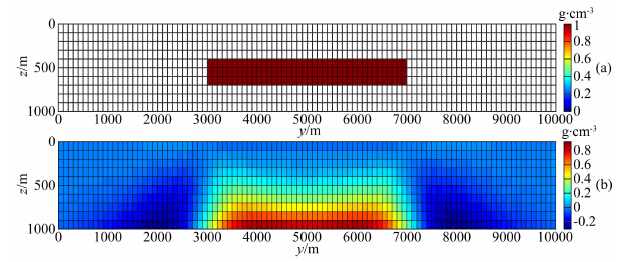
4.1 单一模型试验建立如下的模型:如图 3所示,模型由一个长方体组成,其大小为4000 m×4000 m×300 m.长方体的顶面埋深为400 m,剩余密度为1 g·cm-3.测区的大小为10000 m×10000 m×1000 m,地下被划分为100×100×10个小立方体,每个小立方体的大小为100 m×100 m×100 m,观测点的个数为100×100个.为了更贴近实际测量,加入占最大值10%的高斯噪声.图 4a和图 4b分别给出了观测数据gz和gzz的等值线图.

|
图 3 模型三维透视图,其大小为4000 m×4000 m×300 m,顶面埋深为400 m,其剩余密度为1 g·cm-3 Fig. 3 Perspective of the model. The size of the model is 4000 m×4000 m×300 m. The depth to the top of the model is 400 m.The density contrast of the model is 1 g·cm-3 |
|
图 4 (a) gz的等值线图,包含最大值10%的高斯噪声; (b) gzz的等值线图,包含最大值10%的高斯噪声 Fig. 4 (a) Contour map of gz, contaminated by 10% Gaussian noise; (b) Contour map of gzz, ontaminated by 10% Gaussian noise |
选择gzz数据,结合式(29)进行反演计算,其中加权函数采用式(30),β=1.5,得到反演结果在x=5000 m处的剖面如图 5b所示,图 5a为理论模型在x=5000 m处的剖面.由图 5b,异常分布在400 m以下的概率很大,这一信息与理论模型相符.由此得到式(31)的参数设置为α=0.001,r=1,z1=400.
|
图 5 (a) 模型在x=5000 m处的垂直剖面图,(b) gzz反演结果在x=5000 m处的垂直剖面图,结果显示异常体在地下400 m Fig. 5 (a) The vertical section of the synthetic model at x=5000 m, (b) the vertical section of gzz inversion result at x=5000 m, it shows that the anomalous body is located 400 m below the surface |
图 6a—6c分别给出了gz|gzz、gz|gxz|gyz|gzz和gz|gxy|gxz|gyy|gyz|gzz三组分量组合的反演结果,可以看出,三组分量的反演结果类似,与图 5a对比,图 6a—6c结果与理论模型相吻合.

|
图 6 (a) gz|gzz反演结果的垂直剖面,(b) gz|gxz|gyz|gzz反演结果的垂直剖面,(c) gz|gxy|gxz|gyy|gyz|gzz反演结果的垂直剖面,垂直剖面的位置为x=5000 m Fig. 6 (a) The vertical section of gz|gzz inversion result, (b) the vertical section of gz|gxz|gyz|gzz inversion result, (c) the vertical section of gz|gxy|gxz|gyy|gyz|gzz inversion result. The location of the vertical section is x=5000 m |
此处的模型试验中,单一分量的测点个数为10000,网格数为100000.在gz|gzz反演中,计算用到的测点数据个数为20000.相应的,在gz|gxz|gyz|gzz和gz|gxy|gxz|gyy|gyz|gzz反演中,计算用到的测点数据个数分别为40000和60000.对于gz|gzz,反演计算中迭代过程需要468.196 s,对于gz|gxz|gyz|gzz,反演计算中迭代过程需要694.870 s,对于gz|gxy|gxz|gyy|gyz|gzz,反演计算中迭代过程需要1623.908 s.对于图 3中的模型,每一分量的灵敏度矩阵大小为10000×100000,存储单一分量灵敏度矩阵需要存储空间为5.36 GB,采用文中提出的方法,存储组成灵敏度矩阵的值,需要的存储空间为1.6 MB.对于gz|gzz反演,式(21)中矩阵A的大小为20000×100000,对于gz|gxz|gyz|gzz反演,A的大小为40000×100000,对于gz|gxy|gxz|gyy|gyz|gzz反演,A的大小为60000×100000.与单一分量反演相比较,多分量组合反演的数据量和数据规模都大大增加,因此文中选择有限内存BFGS拟牛顿法对反演问题进行求解.
由3.2节中有限内存BFGS拟牛顿法的流程可知,在求解反演问题的过程中,使用多组修正向量来构建Hessian矩阵是该方法的关键点.Avdeev等(2009)指出有限内存BFGS拟牛顿法用n组修正向量来构建Hessian矩阵,它对内存的要求与2×n×N成正比,其中N代表网格数,这要求远远小于其他类型牛顿法的要求,其他类型的牛顿法对内存要求正比于N×M或N×N,其中M代表测点的个数.对图 3中模型,Hessian矩阵的大小为100000×100000,如果对这一矩阵进行存储,需要的空间大于30 GB.通过有限内存BFGS拟牛顿法,我们仅需要3.64 MB的内存空间,这里n=5.由此,与其他类型的牛顿法相比,有限内存BFGS拟牛顿法节省了大量内存空间.
4.2 组合模型试验1Farquharson等(2004)通过二维模型和三维模型对反演过程中正则化参数计算进行了论述,这里,建立类似的三维模型:如图 7a,模型由两个长方体组成,其中红色长方体大小为400 m×200 m×200 m,顶面埋深为400 m,剩余密度为1 g·cm-3,橘红色长方体大小为400 m×200 m×400 m,顶面埋深为400 m,剩余密度为0.8 g·cm-3.测区大小为1200 m×1200 m×1200 m,将地下划分为12×12×12个小长方体,每个小长方体大小为100 m×100 m×100 m,测点个数为12×12.为了观察不同噪声水平数据对正则化参数的影响,将最大值3%,5%和10%的高斯噪声分别加入到观测数据中.图 7b,7c和7d分别给出了含3%,5%和10%高斯噪声的gzz的等值线图.
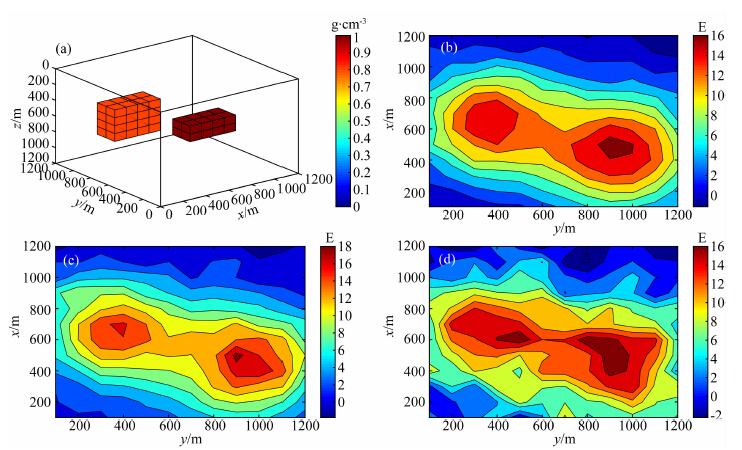
|
图 7 (a)模型的三维透视图,其中红色模型密度为1 g·cm-3,橘红色模型密度为0.8 g·cm-3; (b) gzz的等值线图,包含最大值3%的噪声; (c) gzz的等值线图,包含最大值5%的噪声; (d) gzz的等值线图,包含最大值10%的噪声 Fig. 7 (a) Perspective of the model. The red blocks have a density of 1 g·cm-3, the darker blocks have a density of 0.8 g·cm-3, (b) Contour map of gzz, contaminated by 3% Gaussian noise; (c) Contour map of gzz, contaminated by 5% Gaussian noise; (d) Contour map of gzz, contaminated by 10% Gaussian noise |
因为在4.1节中,gz|gzz分量组合能够得到清晰的反演结果且计算时间短,所以这里选择gz|gzz分量组合进行反演计算.加权函数参数取α=0.001,r=1,z1=400.
图 8a,8b分别给出了理论模型在z=500 m的横切面和x=500 m处的纵切面.图 8c—8h中的反演结果是在正则化参数取1的情况下,分别对含3%、5%和10%噪声水平的数据进行反演计算得到的.对比发现,三组数据反演得到的结果相近,与真实模型吻合.由此说明对不同噪声水平数据,正则化参数取1可行.通过式(43)和式(44)计算正则化参数,随后分别对三组数据进行反演计算,其他参数设置保持不变,得到的反演结果如图 9a—9f所示.与图 8c—8h比较,图 9中反演结果与图 8中反演结果一致,且图 9中的反演结果与实际模型吻合程度更好.由此说明,在实际计算中,依据式(43)和(44)计算正则化参数,能够得到更好的反演结果.
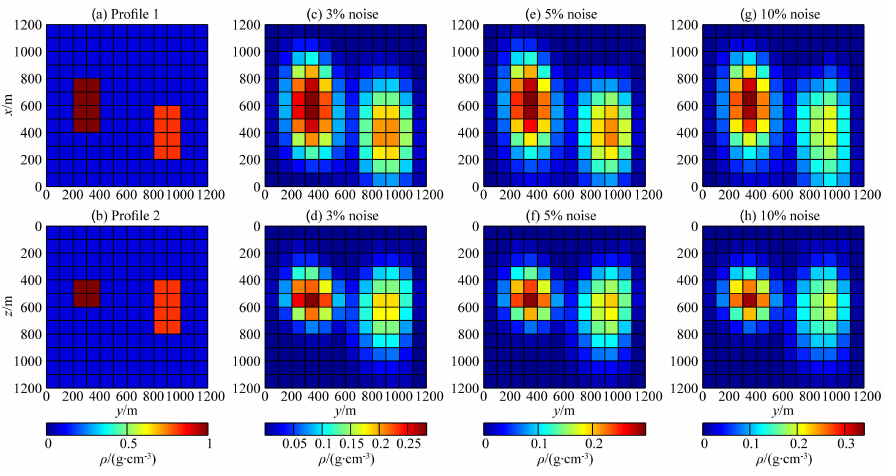
|
图 8 理论模型的横切面(a)和垂直切面(b),正则化参数取1,gz|gzz反演结果的横切面(c,e,g),gz|gzz反演结果的垂直切面(d,f,h).左边一列横切面的深度为z=500 m,右边一列垂直切面的位置为x=500 m Fig. 8 Depth section of the true model (a), vertical section of the true model (b), regularization parameter is set equal to 1, the depth section of the gz|gzz inversion (c,e,g), and vertical section of the gz|gzz inversion (d,f,h). The left column is at z=500 m. The right column is at x=500 m. |

|
图 9 依据式(43)和式(44)计算正则化参数,gz|gzz反演结果的横切面(a,c,e),gz|gzz反演结果的垂直切面(b,d,f).左边一列横切面的深度为z=500 m,右边一列垂直切面的位置为x=500 m Fig. 9 Regularization parameter was calculated based on equation (43) and (44). The depth section of gz|gzz incersion (a,c,e), the vertical section of gz|gzz inversion (b,d,f). The left column is at z=500 m, the right column is at x=500 m |
文中对正则化参数取值方式不同时,反演算法的收敛性进行比较.由图 10中的结果可以看出,当正则化参数随迭代过程变化时,目标函数的收敛速度更快,数据能够更好的拟合.
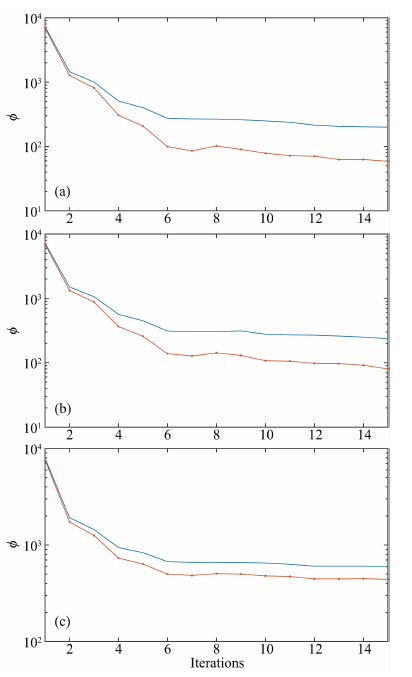
|
图 10 对包含不同噪声(a)3%,(b) 5%,(c) 10%的gz|gzz组合进行反演计算,得到的反演过程中目标函数的变化 实线表示正则化参数取1时的计算结果,带点的实线表示正则化参数变化时的计算结果. Fig. 10 Values of the objective function during inversion of gz|gzzcomponents. The noise level is (a) 3%, (b) 5%, (c) 10% of the maximum value Here, we set the regularization parameter equal to 1, the result is drawn with a solid line. Calculated the regularization parameter with equation (43) and (44), the result is drawn in solid line with points. |
下面,对比不同噪声水平数据对反演算法的收敛性影响.由图 11a,11b可知,对不同噪声水平数据进行反演计算,目标函数的收敛速度不同.图 11c则给出了正则化参数变化的情况下,对三组数据分别进行反演计算,得到的迭代过程中的正则化参数.可以看出,对于不同噪声水平的数据,正则化参数的值在每次迭代中是相近的.由此发现,不同噪声水平数据对正则化参数的取值影响很小.

|
图 11 (a)当正则化参数取1时,不同噪声水平的gz|gzz数据在反演过程中,目标函数的变化;(b)依据式(43)和(44)计算正则化参数时,不同噪声水平的gz|gzz数据在反演过程中,目标函数的变化; (c)当正则化参数变化时,在反演过程中计算得到的正则化参数 图中实线表示3%噪声,带点的实线表示5%噪声,带“+”的实线表示10%噪声. Fig. 11 (a) Setting the regularization parameter equal to 1, the value of the objective function for gz|gzz inversion with different noise. (b) Based on equation (43) and (44) to calculate the regularization parameter, the objective function during the gz|gzz inversion. (c) The regularization parameter during the inversion Here, the solid line represent 3% noise, the solid line with points represent 5% noise, the solid line with plus sign represent 10% noise. |
基于上面的讨论,可以发现,虽然依据式(43)和(44),在迭代过程中更新正则化参数,能够得到更好的反演结果,但是正则化参数取1时也能得出合理的反演结果.同时,基于3.5节中的分析,为了保持方程在迭代过程中的一致性,文中取正则化参数值为1.
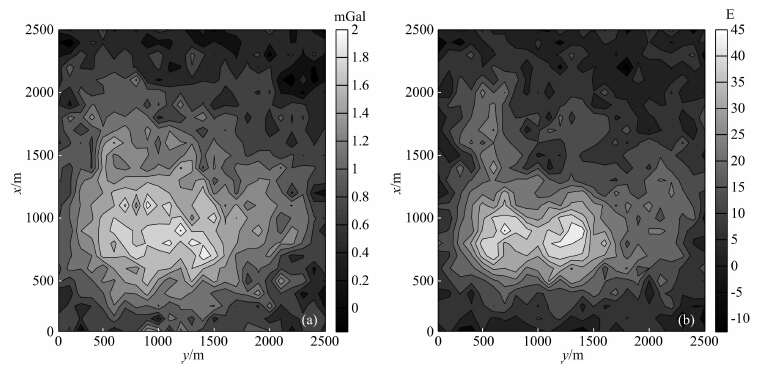
4.3 组合模型试验2建立如下模型:如图 12所示,模型由五个长方体组成,其中两个红色长方体大小为400 m×400 m×400 m,另一个红色长方体大小为200 m×200 m×200 m,它们的顶面埋深为400 m,剩余密度1 g·cm-3,两个橘红色长方体大小分别为1000 m×100 m×500 m和800 m×200 m×200 m,它们的顶面埋深为400 m,剩余密度为0.8 g·cm-3.测区的大小为2500 m×2500 m×1500 m.将地下划分为25×25×15个小长方体,每个小长方体大小为100×100×100,观测点的个数为25×25,为了更贴近实际测量数据,加入了占最大值10%的高斯噪声.图 13a和图 13b分别给出了观测数据gz和gzz的等值线图.
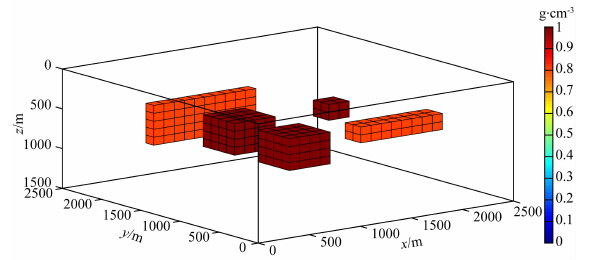
|
图 12 模型三维透视图,其中红色模型密度为1 g·cm-3,橘红色模型密度值为0.8 g·cm-3 Fig. 12 Perspective of the model. The red blocks have a density of 1 g·cm-3, the darker blocks have a density of 0.8 g·cm-3 |
|
图 13 (a) gz的等值线图,包含最大值10%的高斯噪声; (b) gzz的等值线图,包含最大值10%的高斯噪声 Fig. 13 (a) Contour map of gz, contaminated by 10% Gaussian noise; (b) Contour map of gzz, contaminated by 10% Gaussian noise |
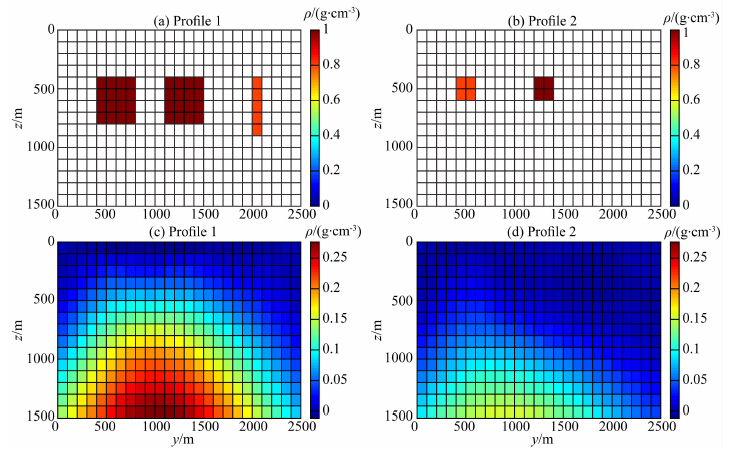
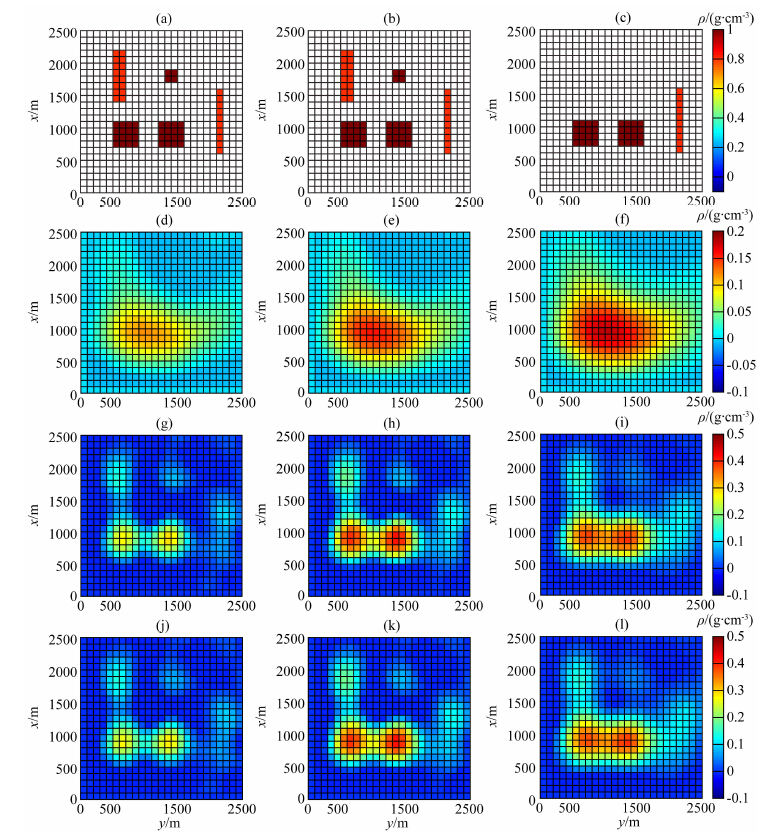
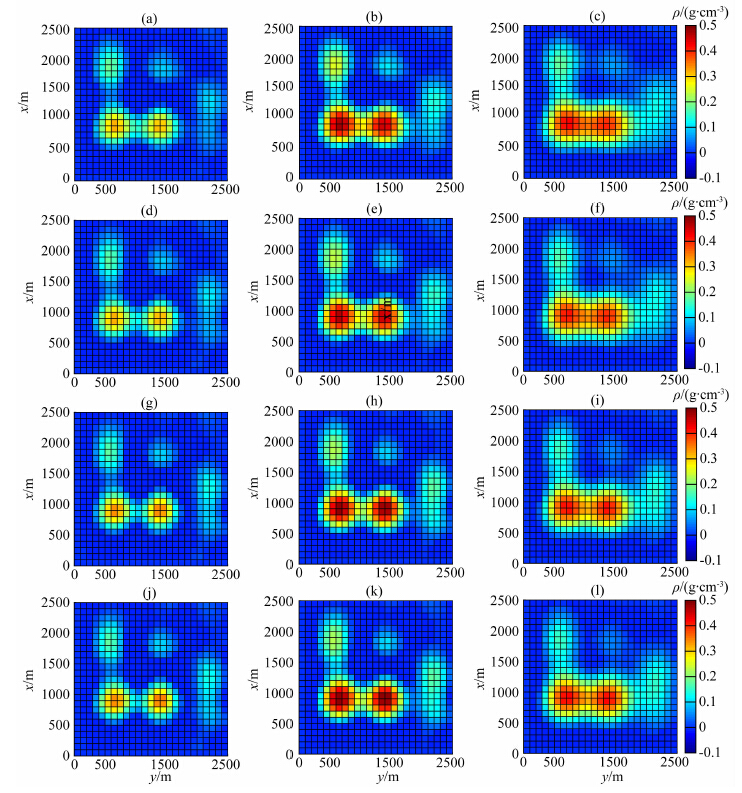
选择gzz数据,结合式(29)进行反演计算,其中加权函数采用式(30),β=1.5,得到反演结果在x=900 m和x=1800 m处的垂直剖面图,如图 14c和图 14d所示.图 14a和图 14b给出了模型在相同位置的垂直剖面图.由图 14c,异常体分布在400 m以下的概率很大,这一信息与实际模型分布一致,图 14d中的结果显示,异常分布在900 m以下.由图 13a和图 13b中异常值的分布,选择图 14c中的结果作为预测的异常体的深度信息,则加权函数参数取α=0.001,r=1,z1=400.将加权函数应用到不同重力和重力梯度分量组合的联合反演中,得到结果如图 15和图 16所示.
|
图 14 (a)模型在x=900 m处的垂直剖面图; (b) 模型在x=1800 m处的垂直剖面图; (c) gzz反演结果在x=900 m处的垂直剖面图,结果显示异常体在地下400 m; (d) gzz反演结果在x=1800 m处的垂直剖面图 Fig. 14 (a) Profile of the synthetic model at x=900 m; (b) Profile of the synthetic model at x=1800 m; (c) Profile of gzz inversion result at x= 900 m, it shows that the anomalous body is located 450m below the surface; (d) Profile of gzz inversion result at x= 1800 m |
|
图 15 理论模型的横切面(a,b,c),gz反演结果的横切面(d,e,f),gzz反演结果的横切面(g,h,i),gz|gzz反演结果的横切面(j,k,l).左边一列横切面深度为z=500 m,中间一列横切面的深度为z=600 m,右边一列横切面的深度为z=800 m Fig. 15 Top row is depth sections of true model (a,b,c), depth sections of gz inversion (d,e,f), depth sections of gzz inversion (g,h,i), and depth sections of gz|gzz inversion. The left column is at z=500 m, the central column is at z=600 m, the right column is at z=800 m |
|
图 16 gxz|gyz|gzz反演结果的横切面(a,b,c),gz|gxz|gyz|gzz反演结果的横切面(d,e,f),gxy|gxz|gyy|gyz|gzz反演结果的横切面(g,h,i),gz|gxy|gxz|gyy|gyz|gzz反演结果的横切面(j,k,l) Fig. 16 Depth sections of gxz|gyz|gzzinversion result (a,b,c), the depth section of gz|gxz|gyz|gzz inversion result (d,e,f), depth sections of gxy|gxz|gyy|gyz|gzz inversion results (g,h,i), depth sections of gz|gxy|gxz|gyy|gyz|gzz inversion result (j,k,l). The left column is at z=500 m, the centre column is at z=600 m, the right column is at z=800 m |
图 15a—15c分别给出了理论模型在z=500 m,z=600 m和z=800 m处的横切面图.图 15d—15f给出了gz反演结果,从图中,无法识别出不同的异常体.图 15g—15i给出了gzz反演结果,从图 15g中,可以识别出五个不同的异常体,其位置与真实模型的位置一致.对gz和gzz进行联合反演,结果如图 15j—15l所示,gz|gzz反演的结果与gzz反演结果类似.表 1中给出了高斯噪声的标准差和由不同反演结果得到的各分量的预测数据和观测数据的差的标准差.可以发现gz|gzz联合反演得到的各分量预测数据和观测数据的差的标准差(gxx:2.737,gxy:0.887,gxz:2.440,gyy:1.907,gyz:2.259,gzz:3.671,gz:0.177)大于gzz反演结果得到的各分量预测数据和观测数据的差的标准差(gxx:2.731,gxy:0.883,gxz:2.438,gyy:1.899,gyz:2.257,gzz:3.651,gz:0.177).这是因为gz分量的加入,识别出了gzz中与gz中包含信息不符的噪声成分.虽然,gz|gzz联合反演对模型的改进很小,但是gz|gzz联合反演得到的模型更加合理.
|
|
表 1 不同分量的高斯噪声的标准差和由各分量组合得到的反演结果的预测数据和观测数据的差的标准差(gz: mGal,gxx|gxy|gxz|gyy|gyz|gzz:E) Table 1 Standard deviations of Gaussian noise and the estimated standard deviation of the residual between the predicted data and observed data for the cases |
图 16a—16c给出了gxy|gyz|gzz反演结果的横切面,图 16d—16f给出了gz|gxz|gyz|gzz反演结果的横切面,这两组反演结果类似,且与理论模型相符.将图 16d与图 15j对比,可以发现,图 16d中的模型更加紧致,说明随着反演过程中数据分量的增加,反演模型得到了改进.
图 16g—16i和图 16j—16l分别给出了gxy|gxz|gyy|gyz|gzz和gz|gxy|gxz|gyy|gyz|gzz反演结果.这两组分量组合的反演结果与图 16a—16f类似.但是,由表 1可以得出,gz|gxy|gxz|gyy|gyz|gzz反演结果得到的预测数据和观测数据的标准差和高斯噪声的标准差最接近,说明gz|gxy|gxz|gyy|gyz|gzz反演得到的结果更加合理.
基于模型试验,可以得出,将重力和重力梯度数据联合反演,反演结果有一定程度的改进,虽然改进不大,但联合反演得到的结果更加合理.
图 17a—17g给出了不同分量组合反演过程中目标函数的变化,由图中可以得出,采用有限内存BFGS拟牛顿法最小化目标函数,能够实现较快的收敛.
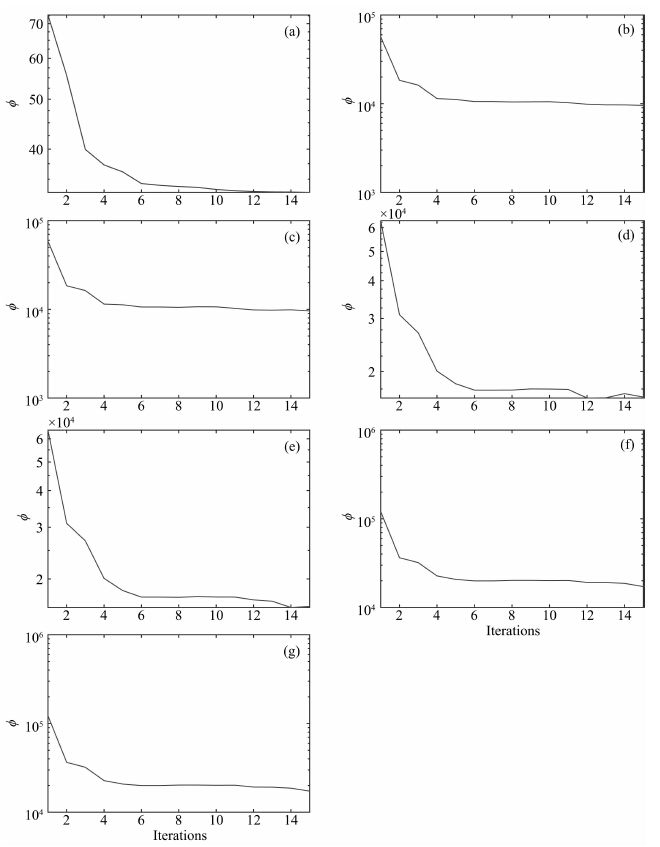
|
图 17 不同分量组合反演过程中目标函数的变化曲线:(a) gz,(b) gzz,(c) gz|gzz,(d) gxz|gyz|gzz,(e) gz|gxz|gyz|gzz,(f) gxy|gxz|gyy|gyz|gzz, (g)gz|gxy|gxz|gyy|gyz|gzz Fig. 17 The objective function during the inversion of different components:(a)gz,(b) gzz,(c) gz|gzz,(d) gxz|gyz|gzz,(e) gz|gxz|gyz|gzz,(f) gxy|gxz|gyy|gyz|gzz,(g) gz|gxy|gxz|gyy|gyz|gzz |
为了进一步说明方法的有效性,并说明重力和重力梯度数据联合反演在实际中的应用效果,文中将方法应用到美国路易斯安那州Vinton盐丘的重力数据和全张量重力梯度数据.Vinton盐丘是一个刺穿型盐丘,盐丘上覆一个巨大的岩盖,主要由石膏和硬石膏组成(Coker et al., 2007),其密度约为2.75 g·cm-3(Ennen,2012).盐丘周围主要是沉积岩层,密度约为2.2 g·cm-3.
数据由Bell Geospace公司在2008年测的,其中,重力数据在地面测得,全张量重力梯度数据则由FTG系统在飞机上测得.图 18a—18g展示了文中所用到的数据,其中图 18f为重力数据,图 18a—18e和图 18g是重力梯度数据.重力梯度数据经过地形改正获得,地形改正的值为2.2 g·cm-3(Oliveira and Barbosa, 2013).参考Geng等(2014),我们对数据做了一个带通滤波,达到增强数据信号的目的.对于重力数据,通过高通滤波去除背景场.选定了大小为4.2 km×4.2 km的测区,将地下划分为42×42×20个小长方体,每个长方体的大小为100×100×50.采用依次计算每个小长方体对观测点影响的方法计算gzz分量的灵敏度矩阵,需要8605.7 s,而通过本文提出的方法,仅需要344.3 s.
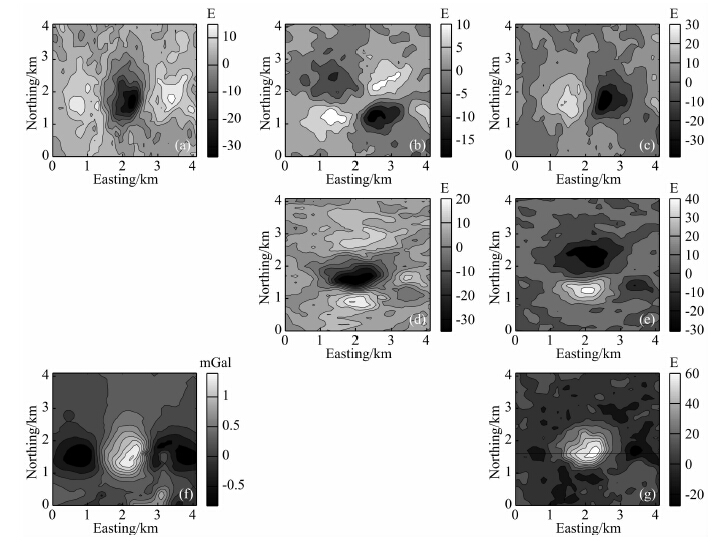
|
图 18 Vinton盐丘的观测数据 (a) gxx,(b) gxy,(c) gxz,(d) gyy,(e) gyz,(f) gz,(g) gzz. (g)中的黑线表示图19,图20,图21中垂直剖面的位置. Fig. 18 Observed data of Vinton salt dome (a) gxx, (b) gxy, (c) gxz, (d) gyy, (e) gyz, (f) gz, (g) gzz. Black line in (g) shows the location of the vertical profile in Figs.19,20, and 21. |
在模型试验中,首先对单一分量进行反演,由反演结果可以得到模型的深度信息,随后将这一信息结合到深度加权函数中,对实际数据,我们采用同样的步骤.首先,采用gzz数据,利用式(29)和(30)进行反演计算,得到结果如图 19,由图 19可以判断出异常体分布在200 m以下.这一信息与异常体的实际埋深有一定的差异,但是由3.3节的模型试验,我们发现,依据式(29)和(30)得到的异常体埋深的估计值,虽然与实际埋深有一定的差异,但是,将这一信息作为参数结合到深度加权函数中,得到的结果与理论模型一致.而且,当估计值在一定范围内波动时,将其应用到反演计算中,仍能获得可信的解.因此,这一深度信息可以应用于实际数据的计算.同时,这一信息与已知的地质信息相符,所以此处深度加权函数式(31)的参数取值为α=0.001,r=1,z1=200.图 20和图 21给出了不同分量组合反演得到的结果.剖面线的位置如图 18g中黑色实线所示.
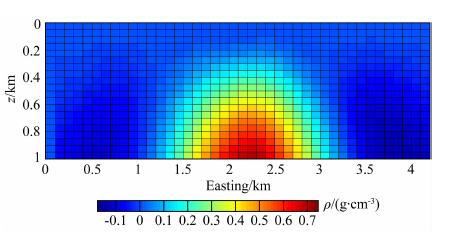
|
图 19 gzz反演结果的垂直剖面,剖面位置如图18g中黑线所示.由图中可知,岩盖位于地下200 m以下 Fig. 19 Vertical profile of gzz inversion result, the location of the profile is shown in Fig.18g. The cap-rock is located 200m below the surface |
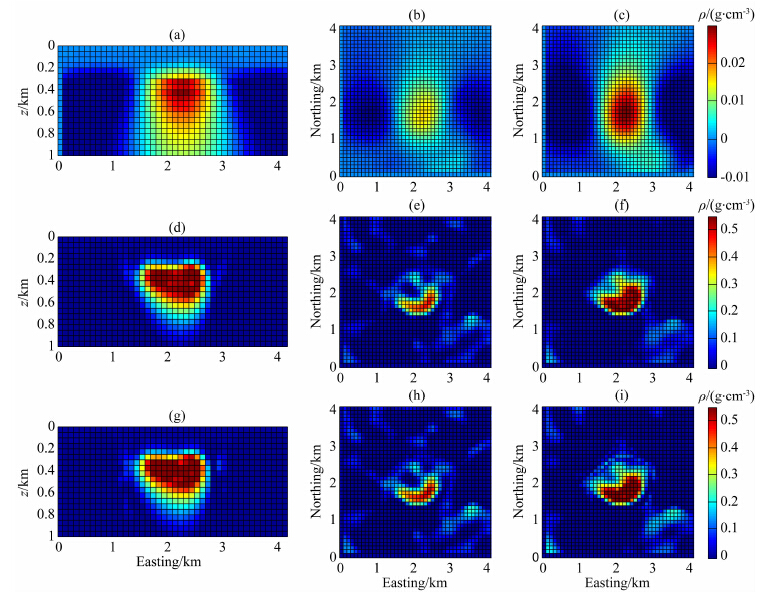
|
图 20 gz反演结果(a,b,c),gzz反演结果(d,e,f),gz|gzz反演结果(g,h,i),其中左侧一列为垂直剖面,剖面位置如图18g中黑线所示,中间一列为横切面,深度为z=250 m,右侧一列为横切面,深度为z=400 m Fig. 20 gz inversion result is shown in (a,b,c), gzz inversion result is shown in (d,e,f), gz|gzz inversion result is shown in (g,h,i). The Left column is vertical profile, the location of the profile is shown in Fig.18g. The central column is the depth section at z=250 m. The right column is the depth section at z=400 m |
|
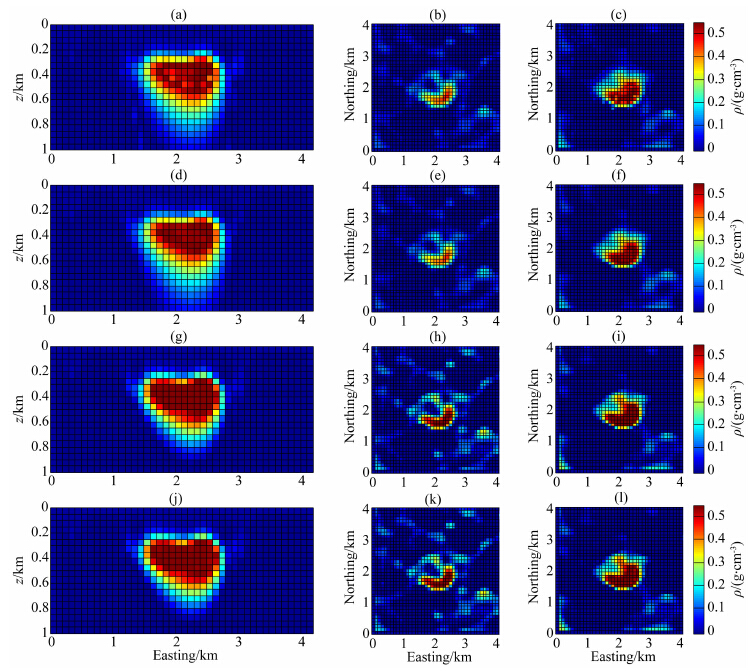
图 21 gxz|gyz|gzz反演结果(a,b,c),gz|gxz|gyz|gzz反演结果(d,e,f),gxy|gxz|gyy|gyz|gzz反演结果(g,h,i),gz|gxy|gxz|gyy|gyz|gzz反演结果(j,k,l).其中左侧一列为垂直剖面,剖面位置如图18g中黑线所示,中间一列为横切面,深度为z=250 m,右侧一列为横切面,深度为z=400 m Fig. 21 gxz|gyz|gzz inversion result (a,b,c), gz|gxz|gyz|gzz inversion result (d,e,f), gxy|gxz|gyy|gyz|gzz inversion result (g,h,i), gz|gxy|gxz|gyy|gyz|gzz inversion result (j,k,l). The left column is the vertical profile, the location of the profile is shown in Fig.18g. The central column is the depth section at z=250 m. The right column is the depth section at z=400 m |
图 20a—20c展示了gz反演结果.表 2列出了不同分量组合得到的反演结果的预测数据和观测数据的差的预测标准差,可以看出gz反演得到的gz分量的预测标准差小于其他组合反演得到的gz分量的预测标准差,而gz反演中梯度分量的预测标准差则大于其他分量组合反演得到的梯度分量的预测标准差,这是因为在反演计算中,参与反演过程的数据拟合的更好.所以,将多个分量联合反演,数据拟合的结果更好,反演结果更加合理.
|
|
表 2 对不同分量组合进行反演得到的结果计算得到的预测数据和实际观测数据之间的差的标准差(gz:mGal,gxx|gxy|gxz|gyy|gyz|gzz: E) Table 2 The standard deviations of the residual between the observed data and the predicted data obtained by the inversion of different combined components |
图 20d—20f展示了gzz反演结果.相比gz反演结果,gzz反演结果更加紧密.由图 20d可知,岩盖的中心埋深大约是400 m,其中高密度部分的在东西向上的长度大约是1400 m.这一结果与Thompson等(1928)中结果相符.由图 20e和图 20f还可以判断出,岩丘由东北到西南方向的延长,这一特征与该地区断层的走向吻合(Coker et al., 2007).所以,gzz反演结果是合理的.
对gz|gzz进行反演计算,结果如图 20g—20i所示.对图 20d和图 20g进行比较,发现图 20g更加紧密.对表 2中gz|gzz反演得到的各分量的预测标准差(第3列)和gzz反演得到的各分量的预测标准差(第2列)进行比较,可以得出gz|gzz反演得到的梯度分量的预测标准差增加了,这说明加入gz数据能够识别出与gz中包含信息不符的噪声,得到的结果更加合理.
图 21a—21c展示了gxz|gyz|gzz反演结果.图 21d—21f展示了gz|gxz|gyz|gzz结果.比较图 21a和图 21d发现,图 21d在图 21a的基础上更进一步优化,高密度部分更加连续.图 21g—21i展示了gxy|gxz|gyy|gyz|gzz反演结果,对比图 21g和图 21d,模型高密度部分更加紧密,更加连续,模型得到了进一步的优化.
图 21j—21l给出了gz|gxy|gxz|gyy|gyz|gzz反演结果,该结果与gxy|gxz|gyy|gyz|gzz反演结果类似.但是,对比表 2中由两组分量组合反演结果计算得到的各分量的预测标准差(第6行和第7行),可以发现,gz|gxy|gxz|gyy|gyz|gzz反演得到的各分量的预测标准差更小,说明gz|gxy|gxz|gyy|gyz|gzz反演中各数据拟合更好,反演结果更加合理.文中选择gz|gxy|gxz|gyy|gyz|gzz反演结果作为最终预测的模型.
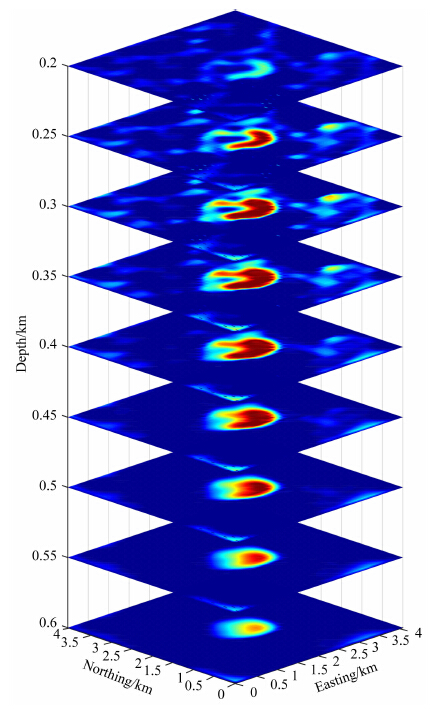
图 22给出了gz|gxy|gxz|gyy|gyz|gzz的横切面,横切面的深度从200 m变化到600 m,间隔为50 m.由图中可以看出,模型的南部的深度大约为200 m,由南向北,模型深度增大,这与Thompson等(1928)中的钻井数据相吻合,资料显示Vinton岩丘南部深度大约为200 m,向北部深度达到315 m.除此之外,模型的底部大约是600 m.Oliveira等(2013)给出的模型的深度是460 m,Geng等(2014)给出的深度是650 m.如果想要进一步确认准确的深度,需要更多的资料来约束反演,这里,我们认为,得出的模型是合理的.
|
图 22 gz|gxy|gxz|gyy|gyz|gzz 反演模型的横切面,切面深度变化范围是200 m到600 m,间隔为50 m Fig. 22 Depth sections of gz|gxy|gxz|gyy|gyz|gzz inversion results. The depth ranges from 200 m to 600 m. The interval is 50 m |
本文首先提出了一种可以快速计算重力和重力梯度灵敏度矩阵的方法,对于地下规则划分的情况,采用这一方法计算,能够大大地缩短计算时间.针对各分量联合反演数据量增大的问题,文中选择有限内存BFGS拟牛顿法求解目标函数,这一方法对内存要求相对较小,能够使目标函数较快地收敛.为了克服趋肤效应,文中介绍了加权方式和深度加权函数,并对目标函数的梯度的表达式进行了推导.本文得出,由单一分量反演获得的异常体埋深的估计值与异常体的实际埋深存在一定的偏差,但是将估计值应用到实际反演计算中,得到的反演结果与实际模型是一致的.而且,当估计值在一定范围内波动时,得到的反演结果也是可信的.通过第一组组合模型试验,发现正则化参数取1是可行的,不同噪声水平的数据对正则化参数的取值影响不大.通过第二组组合模型试验,发现将重力数据和重力梯度数据联合反演能够在一定程度上提高反演结果,但是结果的提升并不明显.这可能是因为重力数据包含较多的低频信息,而重力梯度数据包含较多的高频信息,因此,重力数据包含更多的深部信息,重力梯度数据包含更多的浅部信息.所以将重力数据和重力梯度数据联合反演浅部地质体,得到的反演结果与重力梯度数据反演结果相比,提升并不明显.在后续的研究中,我们将针对深部地质体进行讨论.将该方法应用到美国路易斯安那州的Vinton岩丘的FTG数据和重力数据,发现通过联合反演,模型得到了一定程度的提升,这说明在实际数据应用中,对于浅部地质体,联合反演是有一定意义的.反演得到的结果和已知的地质资料吻合,证明该方法可以用于实际数据的处理.
致谢感谢Bell Geospace公司提供数据.
| Avdeev D, Avdeeva A. 2009. 3D magnetotelluric inversion using a limited-memory quasi-Newton optimization. Geophysics , 74(3): F45–F57. | |
| Avdeeva A, Avdeev D. 2006. A limited-memory quasi-Newton inversion for 1D magnetotellurics. Geophysics , 71(5): G191–G196. | |
| Capriotti J, Li Y G. 2014. Gravity and gravity gradient data: Understanding their information content through joint inversions.// 2014 SEG Annual Meeting. Denver, Colorado, USA: SEG, 1329-1333. | |
| Chasseriau P, Chouteau M. 2003. 3D gravity inversion using a model of parameter covariance. Journal of Applied Geophysics , 52(1): 59–74. | |
| Coker M O, Bhattacharya J P, Marfurt K J. 2007. Fracture patterns within mudstones on the flanks of a salt dome: Syneresis or slumping? Gulf Coast Association of Geological Societies Transactions, 57: 125-137. , 57: 125–137. | |
| Commer M. 2011. Three-dimensional gravity modeling and focusing inversion using rectangular meshes. Geophysical Prospecting , 59(5): 966–979. | |
| Commer M, Newman G A, William K H, et al. 2011. 3D induced-polarization data inversion for complex resistivity. Geophysics , 76(3): F157–F171. | |
| Ennen C. 2012. Mapping gas-charged fault blocks around the Vinton Salt Dome, Louisiana using gravity gradiometry data [Master′s thesis]. Houston: University of Houston. | |
| Farquharson C G, Oldenburg D W. 2004. A comparison of automatic techniques for estimating the regularization parameter in non-linear inverse problems. Geophysics , 156(3): 411–425. | |
| Forsberg R. 1984. A study of terrain corrections, density anomalies, and geophysical inversion methods in gravity field modeling.// Report 355, Department of Geodetic Science and Surveying, The Ohio Stata University. | |
| Geng M X, Huang D N, Yang Q J, et al. 2014. 3D inversion of airborne gravity-gradiometry data using cokriging. Geophysics , 79(4): G37–G47. | |
| Haber E. 2005. Quasi-Newton methods for large-scale electromagnetic inverse problems. Inverse Problems , 21(1): 305–323. | |
| Last B J, Kubik K. 1983. Compact gravity inversion. Geophysics , 48(6): 713–721. | |
| Li X, Chouteau M. 1998. Three-dimensional gravity modeling in all space. Surveys in Geophysics , 19(4): 339–368. | |
| Li Y G, Oldenburg D W. 1996. 3-D inversion of magnetic data. Geophysics , 61(2): 394–408. | |
| Li Y G, Oldenburg D W. 1998. 3-D inversion of gravity data. Geophysics , 63(1): 109–119. | |
| Li Y G. 2001. 3-D inversion of gravity gradiometer data.// SEG Int′l Exposition and Annual Meeting. San Antonio, Texas. | |
| Li Y G, Oldenburg D W. 2003. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophysical Journal International , 152(2): 251–265. | |
| Martinez C, Li Y G, Krahenbuhl R, et al. 2013. 3D inversion of airborne gravity gradiometry data in mineral exploration: A case study in the Quadrilátero Ferrífero Brazil. Geophysics , 78(1): B1–B11. | |
| Liu Y H, Yin C C. 2013. 3D inversion for frequency-domain HEM data. Chinese J. Geophys. , 56(12): 4278–4287. doi: 10.6038/cjg20131230. | |
| Liu Y P, Wang Z W, Du X J, et al. 2013. 3D constrained inversion of gravity data based on the Extrapolation Tikhonov regularization algorithm. Chinese J. Geophys. , 56(5): 1650–1659. doi: 10.6038/cjg20130522. | |
| Newman G A, Boggs P T. 2004. Solution accelerators for large-scale three-dimensional electromagnetic inverse problems. Inverse Problems , 20(6): S151–S170. | |
| Ni Q, Yuan Y. 1997. A subspace limited memory quasi-Newton algorithm for large-scale nonlinear bound constrained optimization. Mathematics of Computation , 66(220): 1509–1520. | |
| Nocedal J, Wright S J. Numerical Optimization. New York: Springer, 1999 . | |
| Oliveira V C Jr, Barbosa V C F. 2013. 3-D radial gravity gradient inversion. Geophysical Journal International , 195(2): 883–902. | |
| Shamsipour P, Denis M, Michel C, et al. 2010. 3D stochastic inversion of gravity data using cokriging and cosimulation. Geophysics , 75(1): I1–I10. | |
| Plessix R E, Mulder W A. 2008. Resistivity imaging with controlled-source electromagnetic data: Depth and data weighting. Inverse Problems , 24(3): 1–22. | |
| Portniaguine O, Zhdanov M S. 1999. Focusing geophysical inversion images. Geophysics , 64(3): 874–887. | |
| Portniaguine O, Zhdanov M S. 2002. 3-D magnetic inversion with data compression and image focusing. Geophysics , 67(5): 1532–1541. | |
| Thompson S A, Eichelberger O H. 1928. Vinton salt dome, Calcasieu Parish, Louisiana. AAPG Bulletin , 12(4): 385–394. | |
| Tikhonov A N, Arsenin V Y. 1977. Solutions of Ill-Posed Problems. Washington, D.C.: W. H. Winston and Sons. | |
| Wu L, Ke X P, Hsu H, et al. 2013. Joint gravity and gravity gradient inversion for subsurface object detection. IEEE Geoscience and Remote Sensing Letters , 10(4): 865–849. | |
| Yao C L, Hao T Y, Guan Z N, et al. 2003. High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic algorithms. Chinese J. Geophys. (in Chinese) , 46(2): 252–258. | |
| Zhang L L, Koyama T, Utada H, et al. 2012. A regularized three-dimensional magnetotelluric inversion with a minimum gradient support constraint. Geophysical Journal International , 189(1): 296–316. | |
| Zhdanov M S. Geophysical Inverse Theory and Regularization Problems. New York: Elsevier, 2002 . | |
| Zhdanov M S, Ellis R, Mukherjee S. 2004. Three dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics , 69(4): 925–937. | |
| Zhdanov M S. 2009. New advances in regularized inversion of gravity and electromagnetic data. Geophysical Prospecting , 57(4): 463–478. | |
| 刘云鹤, 殷长春. 2013. 三维频率域航空电磁反演研究. 地球物理学报 , 56(12): 4278–4287. | |
| 刘银萍, 王祝文, 杜晓娟, 等. 2013. 基于Extrapolation Tikhonov正则化算法的重力数据三维约束反演. 地球物理学报 , 56(5): 1650–1659. | |
| 姚长利, 郝天珧, 管志宁, 等. 2003. 重磁遗传算法三维反演中高速计算及有效存储方法技术. 地球物理学报 , 46(2): 252–258. | |
 2016, Vol. 59
2016, Vol. 59

