2. 东方地球物理公司研究院大港分院, 天津大港 300280;
3. 中国石油天然气勘探开发公司, 北京 100034
2. Dagang Branch of GRI, BGP Inc., CNPC, Tianjin Dagang 300280, China;
3. China National Oil & Gas Exploration and Development Corporation, Beijing 100034, China
波动方程数值模拟是当前热门的逆时偏移、最小二乘偏移和全波形反演技术的基础.波动方程数值模拟的精度和效率在很大程度上决定了波动方程偏移和反演的精度和效率.当前,波动方程数值模拟的方法主要包括基于傅里叶变换的伪谱法,基于非规则网格剖分的有限元类方法以及基于差分近似的有限差分方法.伪谱法采用傅里叶变换计算空间偏导数,能完全压制由于空间离散造成的数值频散,但其缺点是计算效率较低(谢桂生等,2005),并且由于傅里叶变换的全局性,吸收边界的处理较为麻烦.有限元类方法剖分网格更灵活,能准确地模拟各种不规则边界,从而避免矩形网格剖分造成的阶梯绕射.然而,受制于巨大的计算量,目前有限元类方法在逆时偏移和全波形反演中很少使用.相比之下,有限差分法无疑是一种更灵活简便的数值算法,已被广泛用于各类偏微分方程的数值求解,在波动方程偏移和反演中也大受欢迎.
Alterman and Karal(1968)最早采用有限差分法模拟二维层状介质中的弹性波场,Kelly et al.(1976)则讨论了弹性波动方程数值模拟的两种有限差分方法,分别对应中心网格有限差分法和交错网格有限差分法.Virieux(1984,1986)正式将Yee(1966)的交错网格离散方法引入到波动方程数值模拟中,并求解一阶速度-应力形式的声波和弹性波动方程.早期的交错网格有限差分法仅采用二阶差分算子分别近似空间和时间偏导数项,当采用较大的网格间距时,数值频散严重,需要校正(吴国忱和王华忠,2005).为了提高有限差分数值模拟的精度,Levander(1988)采用四阶精度的差分算子近似空间偏导数,显著地改善了二阶差分算子的计算精度,形成了空间四阶精度、时间二阶精度的差分方法,本文将其简记为(4,2)差分法.与二阶差分方法相比,(4,2)差分方法更好地平衡了计算精度和计算效率,因此被广泛用于地震波场的数值模拟(Graves,1996;Moczo et al.,2000;Shi et al.,2012).为了进一步提高空间差分算子的精度,许多学者进一步讨论了高阶有限差分数值模拟方法(Holberg,1987;Fornberg,1987;Kristek et al.2010;Dong et al.,2013;杜启振等,2015).通过增加差分算子的长度,空间精度可以达到任意偶数(2M)阶(刘洋等,1988),本文将传统的高阶有限差分方法记为(2M,2).
尽管传统的高阶有限差分方法能有效地抑制空间频散,但长期以来很少有学者关注时间频散.事实上,地震波在时间和空间里传播,因网格离散造成的数值频散同时包括空间频散和时间频散,传统的高阶差分(2M,2)方法时间外推的精度只有二阶,当采用较大的时间步长时会出现明显的时间频散,甚至不稳定.近些年,许多旨在提高地震波场时间外推精度的数值模拟方法得以发展.这些方法主要包括基于傅立叶变换的矩阵低秩分解方法(Fomel et al.,2013;Song et al.,2013;Fang et al.,2014)和基于频散关系的时-空域有限差分方法(Finkelstein and Kastner,2007;Tan and Huang,2014).基于矩阵低秩分解的数值模拟方法在波场外推的每个时间步至少需要两次反傅里叶变换,计算量较大.因此,Song等(2013)和Fang等(2014)在矩阵低秩分解的基础上分别发展了基于中心网格和基于交错网格的有限差分方法,进一步提高了计算效率.Tan和Huang(2014)基于新的差分结构发展了时间四阶和六阶精度、空间任意偶数阶精度的交错网格有限差分方法,分别记为(2M,4)和(2M,6).频散分析表明(2M,4)和(2M,6)交错网格有限差分方法能显著地提高传统(2M,2)交错网格有限差分方法的精度,并且比传统方法具有更好的稳定性.国内学者董良国等(2000)在求解弹性波动方程的一阶速度-应力形式时将速度分量对时间的奇数阶偏导数转化成应力分量对空间的偏导数,发展了时间四阶精度、空间任意偶数阶精度的交错网格有限差分法.杨庆节等(2014)推导了可导函数任意次导数的任意阶精度的差分近似及相应的差分系数,进一步完善了董良国等(2000)的高阶差分法.
高阶差分算子的差分系数可利用泰勒多项式展开进行确定,也可采用一些优化的方法确定差分系数,如基于最小二乘的有限差分方法(Liu et al.,2014;张杰和吴国忱,2015),基于正则化的有限差分方法(Wang et al.,2014)以及基于非线性优化的有限差分方法(梁文全等,2015).时-空域有限差分方法的差分系数随速度而变换,当速度剧烈变化时,基于优化的方法需要对每个不同的速度值进行一次优化,引入了额外的计算量.相比之下,基于泰勒展开的方法给出了有限差分系数的解析表达式,使得计算差分系数的计算量基本可以忽略.
本文基于新的差分结构,发展了基于中心网格剖分的空间任意2M阶,时间四阶和六阶精度的有限差分方法,与Tan和Huang(2014)讨论的(2M,4)和(2M,6)交错网格有限差分法相比,本文的差分方法适用于离散二阶偏导数,因此适用于模拟二阶波动方程.当不考虑介质的密度变化时,本文研究的(2M,4)和(2M,6)中心网格有限差分方法具有更高的计算效率.
2 波动方程的差分离散格式2.1 时间四阶精度的差分方法地震波在二维声学介质中传播的控制方程为

其中t表示时间,xoz组成二维(2D)笛卡尔坐标系,v为地震波的传播速度,p为压力.采用如下差分格式离散方程(1),公式为
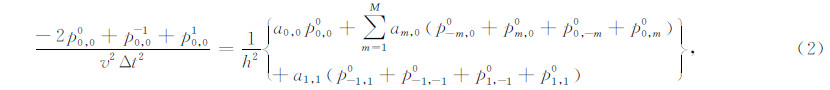
其中上标表示时间网格点的标号,下标表示空间网格点的标号,a0,0,a1,1和am,0(m=1,2,…,M)表示差分系数,h为网格大小,Δt为时间步长,M为空间差分算子长度.方程(2)为一种新的差分结构,与传统的差分结构相比,额外包含了非轴向的四个空间网格节点.Tan和Huang(2014)的研究表明,额外包含非轴向的四个网格节点刚好使得差分近似的截断误差为o(Δt4)+o(h2M)(符号o表示高阶无穷小),因此时间差分能达到四阶精度,空间差分能达到2M阶精度.本文将基于新的差分结构(2)并采用泰勒展开的方法确定方程(2)中的差分系数.对方程(2)两端做傅里叶变换,并利用傅里叶变换的时移性质可得到如下频散关系为

其中γ=vΔt/h为网格比,kx,kz为2D离散波数分量,ω为角频率.利用ω=vk替换ω并对方程(3)中的余弦函数做泰勒展开得到:
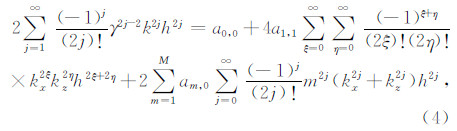
其中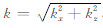 ,并根据二项式展开有
,并根据二项式展开有
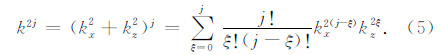
将方程(5)代入(4)并按h2j项整理得到

对比方程(6)两端h2j项的系数可得到:

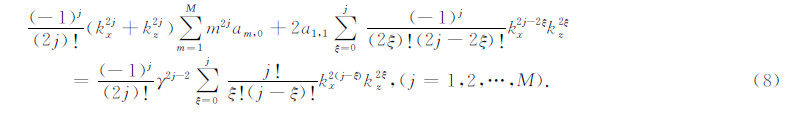
再对比方程(8)两端kx2j或者kz2j的系数得到:
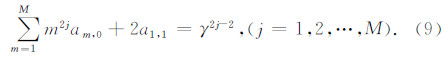
为获得时间外推的四阶精度,方程(8)两端混合项kx2kz2的系数应相等,由此得到:

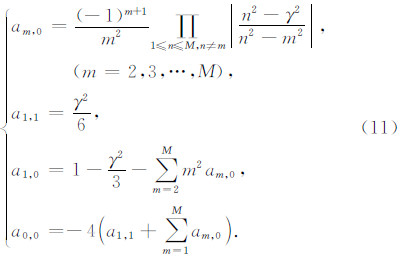
利用方程(11)中的差分系数,差分格式(2)能达到空间2M阶精度,时间四阶精度.
2.2 时间六阶精度的差分方法Tan and Huang(2014)发展了时间六阶精度的交错网格有限差分法,与其时间四阶精度的差分方法相比,其差分结构里又额外包含了八个网格节点.采用泰勒展开确定差分系数时,额外的网格节点使得求取差分系数的方程适定(即方程的个数刚好等于差分系数的个数),并且差分截断误差为o(Δt6)+o(h2M),因此时间差分能达到六阶精度,空间差分能达到2M阶精度.类似地,为发展时间六阶精度的中心网格差分方法,本文采用如下的差分格式为
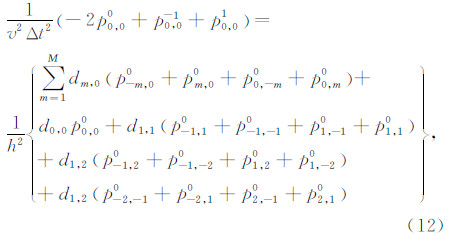
其中d0,0,d1,2和dm,0(m=1,2,…,M)为差分系数.类似地,对方程(12)两端做傅里叶变换,并利用其时移性质得到如下频散关系为
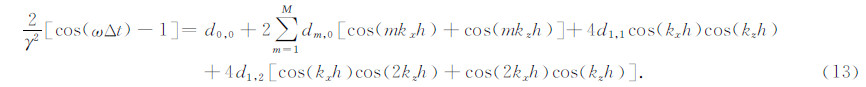
将ω=vk代入方程(13),并对方程(13)两端的余弦函数做泰勒展开得到
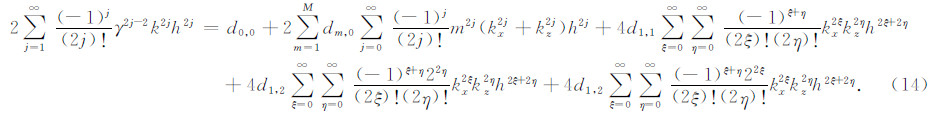
对比(14)式两端h2j项的系数可得到:
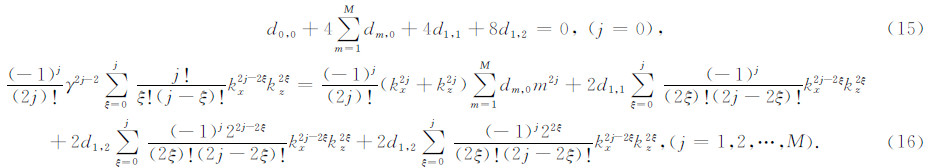
为获得2M阶的空间差分精度,方程(16)两端kx2j和kz2j项的系数应相等,考虑到对称性,对比kx2j项系数和对比kz2j项系数得到的方程相同,且为
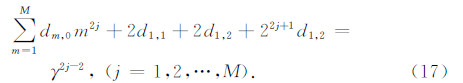
为获得时间外推的六阶精度,方程(16)两端混合项kx2kz2和kx4kz2或者kx2kz4项的系数应相等,由此得到如下两个方程为

联立方程(15)、(17)和(18)得到空间任意偶数阶,时间六阶精度的差分系数为
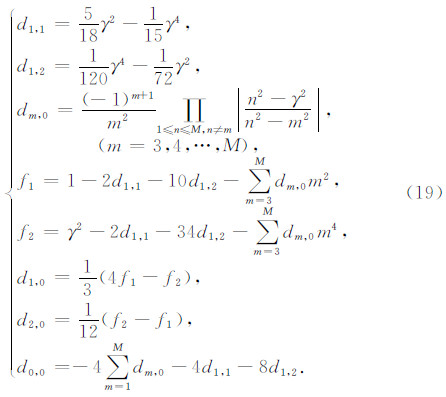
根据频散关系(3)和(13)求得角频率ω,进而得到数值相速度为vnum=ω/k,定义数值相速度和真实地震波传播速度之间的比值δ=vnum/v,用该比值来描述频散程度.该比值越接近于1,频散越小,越远离1频散越严重.另外,空间频散造成地震波的相位滞后,即δ<1;而时间频散则造成地震波的相位超前,即δ>1(Levander,1988;Tan and Huang,2014).据此可大致区分时间频散和空间频散.根据以上思路,时间四阶差分算子的δ的表达式为
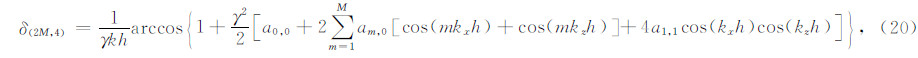
而时间六阶差分算子的δ的表达式为
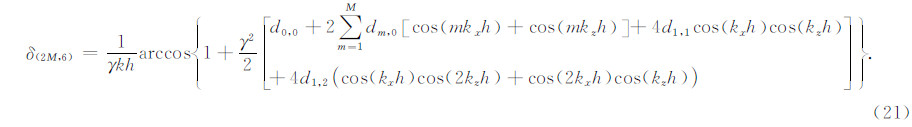
根据平面波传播理论,(kx,kz)=k(cosθ,sinθ),其中θ为波的传播方向与x轴的夹角.考虑到对称性,只需要考虑θ∈0,π/4范围内的数值频散.
图 1显示了当网格比取不同值时,传统时间二阶差分方法和本文推导的时间四阶、六阶差分方法的频散误差示意图,空间差分算子长度统一取为2M=16.当网格比取较小值γ=0.2时,传统的时间二阶差分方法仍然存在较明显的时间频散,如图 1a所示.当网格比增加到γ=0.4(实际上是时间采样步长增加一倍),传统的方法频散误差显著增加,如图 1b所示.相比之下,时间四阶精度的差分方法在γ=0.2时频散误差很小,当时间步长增加一倍时,频散误差也没有显著增加,如图 1c和图 1d所示.对比图 1d和图 1a也可得出结论,当传统方法的时间步长取为时间四阶精度差分方法的一半时,其频散误差仍然比时间四阶精度的差分方法大.图 1e和图 1f则分别显示了γ=0.2和γ=0.4时时间六阶精度差分方法的频散误差,很明显,时间六阶精度的差分方法压制时间频散的效果最好.图 1g和图 1h则分别显示了γ=0.6时本文研究的时间四阶和六阶精度差分算子的频散误差,在高波数部分四阶差分算子出现了较明显的频散,而六阶差分算子的精度更高,误差更小.对比图 1h和图 1a可以得出结论,即使传统时间二阶差分方法所取的时间步长为时间六阶差分方法的1/3,其频散误差仍然比后者严重.
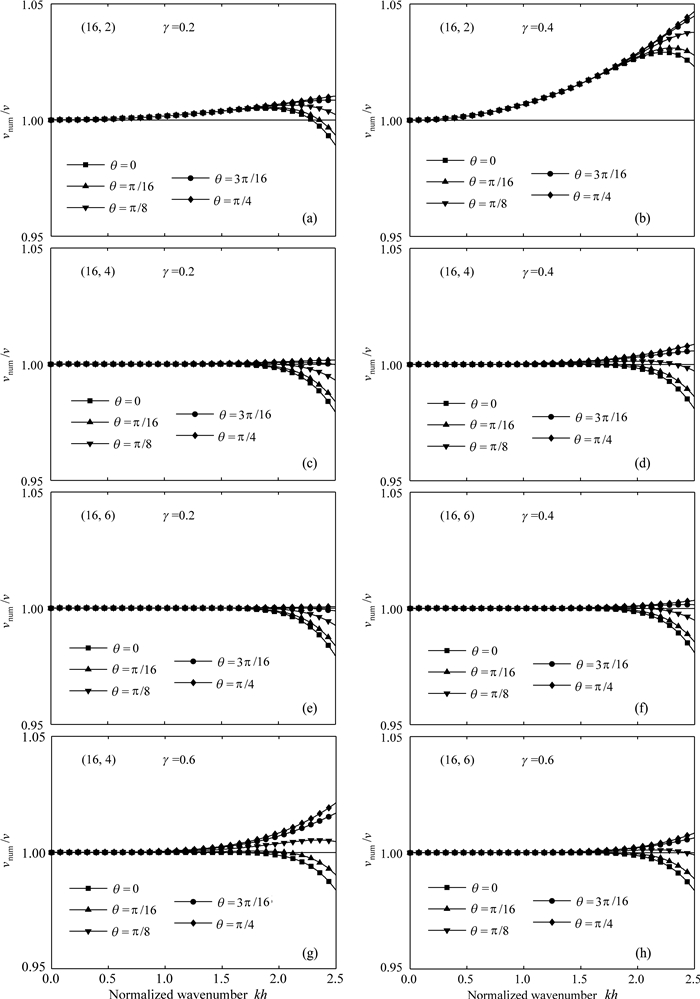 | 图 1 频散示意图 (a) 传统(16,2)方法,γ=0.2; (b) 传统(16,2)方法,γ=0.4; (c) 新的(16,4)方法,γ=0.2; (d) 新的(16,4)方法γ=0.4; (e) 新的(16,6)方法,γ=0.2; (f) 新的(16,6)方法γ=0.4; (g) 新的(16,4)方法γ=0.6; (h) 新的(16,6)方法γ=0.6.Fig. 1 Dispersion relations (a) The traditional (16,2) scheme with γ=0.2 and (b) with γ=0.4; (c) The new (16,4) scheme with γ=0.2 and (d) with γ=0.4; (e) The new (16,6) scheme with γ=0.2 and (f) with γ=0.4, (g) The new (16,4) scheme with γ=0.6, and the new (16,6) scheme with γ=0.6. |
本文讨论的时间四阶、六阶精度差分方法的稳定性条件可分别由频散关系(3)和(13)获得,本文以(2M,4)为例进行说明.由(3)得到如下不等式为
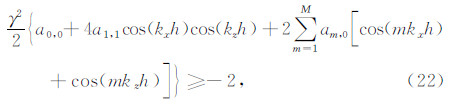
取尼奎斯特波数(kx,kz)=(π/h,π/h)代入方程(22)得到:
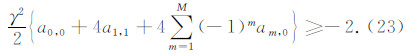
将方程(11)中a0,0的表达式代入(23)式,经过整理得到(2M,4)差分方法的稳定性条件为
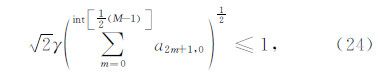
其中int表示直接截取浮点数的整数部分.同理可得到(2M,6)差分方法的稳定性条件为
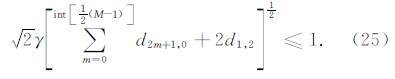
图 2进一步比较了取不同差分算子长度时,传统的时间二阶差分,本文所研究的时间四阶和六阶差分方法能取得的最大网格比.从图中可以看出,时间四阶和六阶差分方法显著地改善了传统二阶差分方法的稳定性,时间六阶差分算子的稳定性比时间四阶差分算子的稳定性略好.
 | 图 2 传统时间二阶差分方法,新的时间四阶、六阶差分方法取不同差分算子长度时对应的最大网格比Fig. 2 The allowed maximum Courant-Friedrichs-Lewy (CFL) number with ranging stencil length from 4 to 32, for the traditional temporal 2nd-order, and our temporal 4th- and sixth-order FD schemes. |
时间四阶和六阶精度差分算子基于新的差分结构,该差分结构除了包含轴向2M+1个离散点外,还包含少数的非轴向离散点,与传统的差分格式相比,引入了额外的计算量.然而,时间高阶差分方法改善了传统二阶方法的精度,在相同的精度下比较,传统方法需要使用更小的时间步长.整体而言,时间高阶差分方法能提高计算效率.通过一系列的频散分析可以得到,本文讨论的时间四阶差分算子采用约2.7倍于传统方法的时间步长时,仍然达到相似的精度;而时间六阶差分算子则可采用约4倍于传统方法的时间步长时,仍然能达到可比拟的精度.表 1列出了传统的时间二阶差分算子、本文讨论的时间四阶、六阶差分算子包含的离散点数,每个时间步内计算空间偏导数的浮点运算次数以及达到相似精度时所采用的时间步长.当差分算子长度2M=16时,与传统的时间二阶差分方法相比,本文发展的时间四阶差分算子和时间六阶差分算子的理论加速比分别为2.4和3.0.
| | 表 1 传统时间二阶差分算子与时间四阶、 六阶差分算子的计算效率比较 Table 1 Computational efficiency comparison between the traditional temporal 2nd-order FD scheme and our temporal 4th- and 6th-order FD schemes |
本文的第一个数值模拟例子模拟均匀介质中的声波波场,介质的地震波传播速度为2000 m·s-1,网格大小为20 m,采用主频为12.5 Hz的雷克子波作为震源,置于模型的中间,差分算子的长度2M=16.图 3显示了采用不同差分方法模拟得到的3.0 s的波场切片.图 3a采用传统的时间二阶差分算子计算,时间步长为5.0 ms,模拟结果出现了显著的相位扭曲,说明传统的时间二阶差分方法的精度低;图 3b是时间步长减半为2.5 ms时传统方法模拟的结果,其数值频散仍然比较明显;进一步减小时间步长为2 ms,传统的时间二阶精度差分法的精度有所提高,但仍然可见微弱的时间频散,如图 3c所示;图 3d显示的波场切片为传统的二阶方法模拟,采用的时间步长已经缩小4倍达到1.25 ms,未见明显的数值频散.图 3e和3f是分别采用本文发展的时间四阶、六阶差分方法模拟得到的波场切片,采用时间步长为5.0 ms.对比图 3b和3e可以发现,尽管传统的二阶差分方法采用的时间步长为时间四阶差分方法的一半,但其数值频散仍然比四阶方法严重;对比图 3c和3e可以发现,当四阶差分方法采用的时间步长为传统方法的2.5倍时,其压制数值频散的效果仍然更好,这与前文的频散分析结论是一致的.进一步对比图 3d和3f,两图中的波场均未见明显的数值频散,而此时时间六阶差分方法采用的时间步长为传统二阶方法的4倍,这与前文的频散分析结论也是一致的.
 | 图 3 采用不同差分方法模拟均匀介质中3 s时的波场切片,(a)传统时间二阶差分方法的模拟结果,时间步长5.0 ms,(b)传统时间二阶差分方法的模拟结果,时间步长2.5 ms,(c)传统时间二阶差分方法的模拟结果,时间步长 2.0 ms,(d)传统时间二阶差分方法的模拟结果,时间步长1.25 ms,(e)时间四阶差分方法模拟的结果,时间步长5.0 ms,(f)时间六阶差分方法模拟的结果,时间步长5.0 msFig. 3 Acoustic snapshots at 3.0 s computed by (a) the traditional temporal 2nd-order FD scheme with the time step of 5.0 ms, (b) with the time step of 2.5 ms, (c) with the time step of 2.0 ms, and (d) with the time step of 1.25 ms, (e) by our temporal 4th-order and (f) 6th-order FD schemes with the time step of 5.0 ms |
本文的第二个数值算例模拟在二维BP盐丘中传播的声波波场,图 4为相应的速度模型,该模型的最大速度差异比约为3.4.离散采用的网格大小为15 m,采用主频为12.5 Hz的雷克子波作为震源,位于(x,z)=(7500,300)m处,数值模拟采用的差分长度为2M=16.分别采用传统的时间二阶差分方法、本文发展的时间四阶、六阶差分方法模拟声波的传播.为对比各种差分方法模拟的结果,将传统时间二阶差分方法采用微小的时间步长0.15 ms模拟的地震记录作为参考解(见图 5).
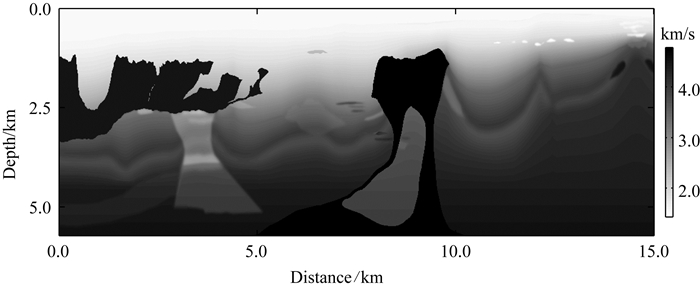 | 图 4 BP盐丘模型Fig. 4 BP salt model |
 | 图 5 传统时间二阶差分方法采用微小时间步长0.15 ms生成的参考地震记录Fig. 5 Reference seismic recording generated by traditional temporal 2nd-order FD scheme with a tiny time step of 0.15 ms |
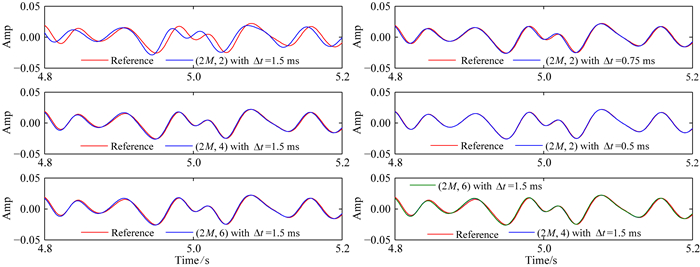 | 图 6 (x,z)=(12,0) km处的单道地震记录对比,时间段4.8~5.2 s,(a)时间二阶、四阶和六阶差分方法的模拟结果,采用相同的时间步长1.5 ms,(b)时间二阶差分方法采用0.75 ms,0.5 ms时间采样间隔的模拟结果,以及时间四阶、六阶差分方法采用1.5 ms采样间隔的模拟结果Fig. 6 Recorded seismograms at (x,z)=(12,0) km during 4.8~5.2 s, (a) computed by temporal 2nd-order, 4th-order and 6th-order FD schemes with the same time step of 1.5 ms, (b) computed by temporal 2nd-order FD scheme with the time step of 0.75 ms, 0.5 ms, and computed by the temporal 4th-order and 6th-order FD schemes with the time step of 1.5 ms |
图 6中对比了远偏移距接收点(x,z)=(12,0)km处的振动图,时间区段为4.8~5.2 s.图 6a上、中、下三个子图分别对比了传统时间二阶差分方法、本文发展的时间四阶、六阶差分方法模拟的地震道与参考道的波形差异,三种方法均采用1.5 ms的时间步长.由图可知,传统的时间二阶差分方法模拟的结果与参考解存在明显的差异,而本文发展的时间四阶、六阶差分方法与参考解吻合较好.图 6b上、中两子图显示了传统时间二阶差分方法模拟的地震道,时间步长分别采用0.75 ms和0.5 ms,分别为图 6a中时间步长的1/2倍和1/3倍.图 6b中的第三个子图则显示了时间四阶、六阶差分方法模拟的地震道.仔细对比图 6b中的三个子图,可发现采用1.5 ms时间步长的四阶、六阶差分方法模拟的结果几乎一致,并且与参考解的吻合程度略好于采用0.75 ms时间步长的二阶差分方法.然而,与理论的频散分析结论有些差异的是,当传统的时间二阶差分方法采用的时间步长为0.5 ms时(见图 6b中第二个子图),其吻合参考解的效果略微胜过采用1.5 ms时间步长的六阶差分方法.我们也对比了其他地震道,发现了一致的规律.这说明模拟非均匀介质中的地震波场,时间四阶精度搭配空间高阶精度的差分方法已经足够,而时间六阶差分算子的优势并未体现.
7 结论本文基于中心网格剖分发展了适用于二阶声波方程的时间四阶、六阶,空间任意偶数阶的有限差分数值模拟方法,并基于泰勒多项式展开推导了差分系数的解析表达式.与传统的时间二阶差分方法相比,本文发展的时间高阶差分方法具有更好的稳定性,允许更大的时间采样步长.频散分析表明本文发展的时间四阶、六阶精度的差分方法能显著地改善传统的时间二阶精度差分方法的精度,在相同的频散误差限下,本文发展的时间四阶、六阶精度差分方法允许更大的时间步长,因此提高了波场数值模拟的计算效率.在相似的频散条件下,理论的计算量分析表明本文发展的(16,4)和(16,6)差分算子的计算效率分别是传统(16,2)方法的2.4倍和3.0倍.然而,非均匀介质中波场模拟的数值实验证实,时间六阶精度差分方法模拟的结果与时间四阶精度差分方法模拟的结果几乎完全一致,考虑到时间四阶差分方法包含的浮点运算更少,因此,时间四阶精度搭配空间高阶精度更可取.此外,本文发展的时-空高阶差分方法可以很容易地推广至三维情况.
| [1] | Alterman Z, Karal F. 1968. Propagation of elastic waves in layered media by finite difference methods. Bull. Seism. Soc. Am., 58(1): 367-398. |
| [2] | Dong C H, Wang S X, Zhao J G, et al. 2013. Numerical experiment and analysis of the differential acoustic resonance spectroscopy for elastic property measurements. J. Geophys. Eng., 10(5): 1-10. |
| [3] | Dong L G, Ma Z T, Cao J Z, et al. 2000. The staggered-grid high-order difference method of one-order elastic equation. Chinese J. Geophys. (in Chinese), 43(6): 856-864. |
| [4] | Du Q Z, Guo C F, Gong X F. 2015, Hybrid PS/FD numerical simulation and stability analysis of pure P-wave propagation in VTI media. Chinese J. Geophys. (in Chinese), 58(4): 1290-1304. |
| [5] | Fang G, Fomel S, Du Q Z, et al. 2014. Lowrank seismic-wave extrapolation on a staggered grid. Geophysics, 79(3): T157-T168. |
| [6] | Finkelstein B, Kastner R. 2007. Finite difference time domain dispersion reduction schemes. J. Comput. Phys., 221(1): 422-438. |
| [7] | Fomel S. Ying L X, Song X L. 2013. Seismic wave extrapolation using lowrank symbol approximation. Geophys. Prospect., 61(3): 526-536. |
| [8] | Fornberg B. 1987. The pseudospectral method: comparisons with finite differences for the elastic wave equation. Geophysics, 52(4): 483-501. |
| [9] | Graves R W. 1996. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences. Bull. Seism. Soc. Am., 86(4): 1091-1106. |
| [10] | Holberg O. 1987. Computational aspects of the choice of operator and sampling interval for numerical differentiation in large-scale simulation of wave phenomena. Geophys. Prospect., 35(6): 629-655. |
| [11] | Kelly K, Ward R, Treitel S, et al. 1976. Synthetic seismograms: A finite-difference approach. Geophysics, 41(1): 2-27. |
| [12] | Kristek J, Moczo P, Galis M. 2010. Stable discontinuous staggered grid in the finite-difference modeling of seismic motion. Geophy. J. Int., 183(3): 1401-1407. |
| [13] | Levander A R. 1988. Fourth-order finite-difference P-SV seismograms. Geophysics, 53(11): 1425-1436. |
| [14] | Liang W Q, Wang Y F, Yang C C. 2015. Determination on the implicit finite-difference operator based on optimization method in time-space domain. Geophy. Prosp. Petroleum, 54(3): 254-259. |
| [15] | Liu H F, Dai N X, Niu F, et al. 2014. An explicit time evolution method for acoustic wave propagation. Geophysics, 79(3): T117-T124. |
| [16] | Liu Y, Li C C, Mu Y G. 1998. Finite-difference numerical modeling of any even-order accuracy. Oil Geophys. Prosp., 33(1): 1-10. |
| [17] | Moczo P, Kristek J, Halada L.2000. 3D fourth-order staggered-grid finite-difference schemes: Stability and grid dispersion. Bull. Seism. Soc. Am., 90(3): 587-603. |
| [18] | Shi R Q, Wang S X, Zhao J G. 2012. An unsplit complex-frequency-shifted PML based on matched Z-transform for FDTD modelling of seismic wave equations. J. Geophys. Eng. 9(2): 218-229. |
| [19] | Song X L, Fomel S, Ying L X. 2013. Lowrank finite-differences and lowrank Fourier finite-differences for seismic wave extrapolation. Geophy. J. Int., 193(2): 960-969. |
| [20] | Tan S R, Huang L J. 2014. An efficient finite-difference method with high-order accuracy in both time and space domains for modelling scalar-wave propagation. Geophy. J. Int., 197(2): 1250-1267. |
| [21] | Virieux J. 1984. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics, 49(11): 1933-1957. |
| [22] | Virieux J. 1986. P-SV wave propagation in heterogeneous media: Velocity stress finite-difference method. Geophysics, 51(4): 889-901. |
| [23] | Wang Y F, Liang W, Nashed Z, et al. 2014. Seismic modeling by optimizing regularized staggered-grid finite-difference operators using a time-space-domain dispersion-relationship-preserving method. Geophysics, 79(5): T277-T285. |
| [24] | Wu G C, Wang H Z. 2005. Analysis of numerical dispersion in wave-field simulation. Progress in Geophysics.(in Chinese), 20(1), 58-65. |
| [25] | Xie G S, Liu H, Zhao L G. 2005. Parallel Algorithm based on the multithread technique for pseudospectal modeling of seismic wave. Progress in Geophysics. (in Chinese), 20(1), 17-23. |
| [26] | Yang Q J, Liu C, Geng M X, et al. 2014. Staggered-grid finite-difference scheme and coefficients deduction of any number of derivatives. J. Jilin Univ. (Earth science edition), 44(1): 375-385. |
| [27] | Yee K S. 1966. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media. IEEE Trans. Antennas Propagat, 14(3): 302-307. |
| [28] | Zhang J, Wu G C. 2015, Seismic modeling method of two phase medium utilizing staggered grid with optimal difference coefficients. Progress in Geophysics. (in Chinese), 30(5), 2301-2311. |
| [29] | 董良国,马在田,曹景中等. 2000. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报. 43(6): 856-864. |
| [30] | 杜启振,郭成锋,公绪飞. 2015. VTI介质纯P波混合法正演模拟及稳定性分析. 地球物理学报. 58(4): 1290-1304. |
| [31] | 梁文全,王彦飞,杨长春. 2015. 基于优化方法的时间空间域隐格式有限差分算子确定方法. 石油物探.54(3): 254-259. |
| [32] | 谢桂生,刘洪,赵连功. 2005. 伪谱法地震波正演模拟的多线程并行计算. 地球物理学进展. 20(1): 17-23. |
| [33] | 刘洋,李承楚,牟永光. 1998. 任意偶数阶精度有限差分法数值模拟. 石油地球物理勘探. 33(1): 1-10. |
| [34] | 吴国忱,王华忠. 2005. 波场模拟中的数值频散分析与校正策略. 地球物理学进展. 20(1): 58-65. |
| [35] | 杨庆节,刘财,耿美霞等. 2014. 交错网格任意阶导数有限差分格式及差分系数推导. 吉林大学学报(地球科学版). 44(1): 375-385. |
| [36] | 张杰,吴国忱. 2015. 基于优化差分系数的双相介质交错网格正演模拟. 地球物理学进展.30(5): 2301-2311. |
 2016, Vol. 59
2016, Vol. 59


