地球物理学报  2016, Vol. 59 Issue (5): 1685-1695   PDF    
引用本文
陈世仲, 李小凡, 汪文帅. 2016. 地球自由振荡的保结构模拟. 地球物理学报, 59(5): 1685-1695, doi: 10.6038/cjg20160513   
Chen S Z, Li X F, Wang W S. 2016. Structure-preserving numerical simulation for Earth's free oscillations. Chinese J. Geophys. (in Chinese), 59(5): 1685-1695, doi: 10.6038/cjg20160513   
地球自由振荡的保结构模拟
陈世仲1,2,3, 李小凡1, 汪文帅4    
1. 中国科学院地质与地球物理研究所, 中国科学院地球与行星物理重点实验室, 北京 100029;
2. 中国科学院大学, 北京 100049;
3. 华北水利水电大学资源与环境学院, 郑州 450045;
4. 宁夏大学数学计算机学院, 银川 750021
收稿日期 2015-04-20, 2016-03-04 收修定稿
基金项目: 国家自然科学基金项目(41174047,40874024,41204041)资助.
作者简介: 陈世仲,男,1985年生.中国科学院地质与地球物理研究所在读博士研究生,主要从事地震波正反演及地球自由振荡等相关研究.E-mail:csz042@mail.iggcas.ac.cn
摘要: 大地震等诸多激励均能激发全球自由振荡现象,通常表现为驻波形式的全球整体振荡.现有的地震波数值模拟方法多为非保结构方法,无法压制长时程计算中的积累误差.本文采用优化的三阶辛格式谱元法,对地球自由振荡及全球尺度的地震波传播进行了长时程模拟.通过与传统的基于Newmark算法的谱元方法结果对比分析,明确验证了本文所得优化的三阶辛格式谱元法在模拟地球自由振荡等大规模长时程问题上的优越性和准确性.上述进展在方法论层面为今后探测、刻画全球尺度地球非均匀结构的驻波数值方法奠定了部分基础,并为相关研究领域提供了新的选择.
关键词: 地球自由振荡     保结构模拟     长时程追踪     三阶辛格式谱元法    
Structure-preserving numerical simulation for Earth's free oscillations
CHEN Shi-Zhong1,2,3, LI Xiao-Fan1, WANG Wen-Shuai4     
1. Key Laboratory of Earth and Planetary Physics, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Resources and Environment, North China University of Water Resources and Electric Power, Zhengzhou 450045, China;
4. School of Mathematics and Computer Science, Ningxia University, Yinchuan 750021, China
Abstract: Free oscillations of the Earth are usually as standing waves of entire globe, which can be excited by many factors such as a great earthquake. The oscillation types of this physical phenomenon depend on Earth's structure and physical parameters. Therefore, intrinsic characters of the Earth can be revealed by studying Earth' free oscillations. Numerical simulation is an effective way to research seismic waves travelling in different earth models. In essence, the numerical simulation of Earth's free oscillations is a long-term tracing of variable coefficient wave equation. The majority of numerical methods for seismic wave simulation are non-structure-preserving methods, which cannot suppress the accumulative error in long-time computation,e.g.,finite difference methods, pseudo-spectral methods, and finite element methods.In comparison, the symplectical methods based on the Hamilton system possess fine structure-preserving ability which makes them be suitable for the physical problem acquiring good precision in long-time simulation. The spectral element method combines the generality of the finite element method with the accuracy of spectral techniques. This method expands the solution in trigonometric series, of which a chief advantage is that the resulting method is of very high order. It also chooses high-degree piecewise polynomial basis functions, also achieving a very high order of accuracy. Symplectical methods introduced into spectral element methods may be an accurate and effective choice. In this research, a three-order symplectical spectral element method is modified for long-time simulation of Earth's free oscillations and seismic waves propagating in the global range. The event simulated is a great earthquake (Mw8.6) off the west coast of northern Sumatra on 11 April 2012. The PREM earth model is used for simulation. Our method and traditional spectrum element method using Newmark time scheme are chosen for simulation respectively with the same parameters and computation scales. The time step adopted by our method is 2.8 times that adopted by the Newmark method. Even under this extreme condition, the feasibility and effectiveness of this method have been proved by analysis of the simulation results, especially, by comparing with real seismic data processed with the same procedures and parameters. Those data are provided by the Incorporated Research Institutions for Seismology. This improvement can be a new and valid alternative to numerical methods for investigation on heterogeneity (especially lateral heterogeneity) in the globe range. Meanwhile, Earth's free oscillations influenced obviously by large inhomogeneous structure of Earth interiors has been confirmed by comparison of simulation results and real seismic data recorded by seismic networks.
Key words: Earth's free oscillations     Structure-preserving simulation     Long-term tracing     Three-order symplectical spectral element method    
1 引言

大地震、火山爆发、大气流动等地球内部运动均能激发地球作为类球体的本征振荡.地球自由振荡现象从基本特征来看，是在整个地球尺度上扰动的驻波(Bolt，2012).地球自由振荡信号包含了地球内部物质的物理特性，包括地球内部非均匀结构、地球自身物理状态等诸多重要的地球物理信息.因此，精确模拟、分析地球自由振荡是解读地球内部物质结构和特征的关键手段之一.

1829年，Poisson最早研究了完全弹性固体球的振动问题(Shearer，2009)对地球自由振荡的认识是从解析方法研究开始的，比如球谐展开.1882年，Lamb详细讨论了均匀球体模型的自由振荡规律(Lapwood and Usami，1981).1911年，Love在考虑重力作用的情况下，探讨了可压缩球体自由振荡现象(Bolt，2012).

理论研究表明，实际的地球自由振荡可以分解为若干阶特定的频率，称为地球自由振荡的本征频率，与本征频率相应的振动叫做本征振荡.每一种本征振荡都对应一种驻波，是地球的一种谐振形式.本征振荡分成两类：一类是球型振荡，通常用nSml表示.地球做球型振荡时，其质点位移既有半径方向的分量，也有水平分量.这是一种无旋转振动.另一类即环型振荡，通常用nTml表示.地球做环型振荡时，各质点只在以地心为球心的同轴球面上振动，位移无径向分量，地球介质只产生剪切形变，无体积形变，地球的重力场不受扰动(Lapwood and Usami，1981; Lillie，1999).理论上，地球的谐振振型有无穷多个，而实际振动则是这无穷多个振型的叠加.

地球自由振荡频谱特征受多种地球结构因素及状态的影响，包括：地球介质的横向非均匀性及径向非均匀性、各向异性、介质能量衰减效应、地球的自转、地球的椭率、地形以及断裂机制等因素.因此研究地球的本征振荡对研究地球内部结构及物理性质具有重要意义.

鉴于目前相关研究的匮乏，本文从波动理论出发，探寻求解地球自由振荡问题的方法，并依托大规模并行计算集群付诸实践.通过哈密尔顿体系运动方程的推导，结合谱元法，得出一个新的求解波动方程的三级三阶辛格式谱元算法(汪文帅等，2012b)，并将其应用于地球自由振荡及全球尺度地震波的长时程模拟.数值模拟结果与实际观测资料的对比分析表明，相对于采用Newmark算法的传统谱元方法，本文提出的算法具有良好的保结构特性，非常适合地球自由振荡及全球尺度地震波的长时程模拟这类有高精度长时程求解变系数偏微分方程需求的物理问题(陈世仲等，2012).本文的实验及分析还进一步证实，地球内部大尺度非均匀结构对地球自由振荡有着明显的影响(陈世仲等，2013).

2 地球自由振荡求解理论2.1 地球自由振荡波动方程建立

Alterman等(1959)将地球自由振荡满足的二阶偏微分方程本征值问题归化为一阶常微分方程组，奠定了现代计算机数值求解的基础.Dahlen(1968)采用“二阶扰动”理论研究了自转、椭球地球的简正模.方俊分别采用1066A模型和Harold Jeffreys的修正地球模型进行了环型和球型自由振荡简正模的计算，给出了1066A模型的环型和球型自由振荡本征周期较完整的理论计算值，并讨论了地球内部密度参数和弹性参数的变化对本征周期的影响(方俊，1990a; 1990b).Tsuboi等(1985)结合扰动技术和反演方法，利用牛顿方法及变分原理求解非线性方程，理论上分析了横向不均匀性地球自由振荡特征值的偏微分方程模型问题，并得出比一阶退化扰动理论更精确的特征频率和特征函数.随后，Tsuboi(1995)又根据变分原理计算了横向不均匀性和非弹性地球模型的基本模式，研究了地球自由振荡谱峰与横向不均匀性以及非弹性等之间的可能关系，即谱峰的中心频率随时间而改变.严珍珍等采用谱元法与并行计算数值模拟特大地震激发的弹性波在地球内部传播过程(Yan et al.，2014; 严珍珍等，2008; 严珍珍等，2012).

地震波的波动方程数值模拟实质上是求弹性地震波波动方程的数值解，模拟的地震波场包含了地震波产生和传播过程的所有运动学与动力学信息，所以波动方程数值模拟方法一直在地震模拟中占有重要地位.

类似地震波的波动方程数值模拟，数值模拟地球自由振荡，本质上也是求满足适当初边值条件的地球振动的常系数偏微分方程组的数值解.地球的一般弹性运动方程为

其中，f表示为外力和重力的扰动，一般情况大气的变化因素不予考虑，则只考虑重力的影响.

由地球自转的角速度为 ，自由振荡的最大周期是53.7 min，可得出角频率为 .因此，科里奥利加速度 相对于振动加速度 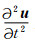来说影响是非常微小的.地球椭率为1/298，相对来说，地球椭率导致的地球自由振荡谱分裂的效应也较小.

据此，可对地球的一般弹性运动方程进行简化，以便与数值模拟求解.通常采取的简化包括：(1)忽略大气因素；(2)忽略科里奥利力；(3)忽略重力的影响；(4)忽略地球椭率，简化为球体；(5)忽略横向不均匀性，简化为圈层结构；等.

可得到，无震源激发情况下，简化的地球弹性运动方程：

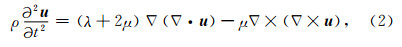
其中，λ，μ只与r有关.

欲求解式(2)，还需另加近似条件和边界条件：

(1)忽略大气因素，地球表面当作自由表面，即应力分量 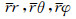在地球表面r=r0(r0为地球半径)的取值为 ；

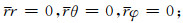(2)在地心r=0处正则，即u，v，w=0；

(3)在圈层的固-固边界上，应力和位移都连续；

(4)在固-液边界(核幔边界)上，边界的法向位移连续，即 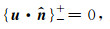，且应力连续；另外，因S波不能在液态介质传播，故边界的切向应力为0(Bullen and Haddon，1967).

2.2 波动方程理论求解

由震源项F激发的波动，在不考虑衰减、重力和科里奥利力的前提下，可将地球的弹性波动方程简化为

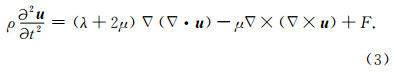
运用亥姆霍兹定理求解，可将F和u表示为

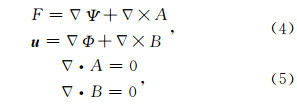
将(4)式、(5)式代入方程(3)，化简得到

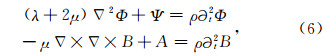
求解(6)，得出

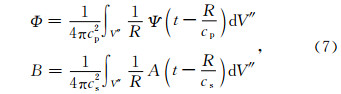
其中，

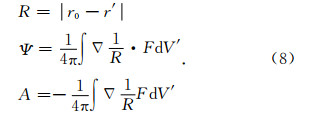
针对不同的震源机制F，求解积分，通过球谐函数展开，最终解出u.Lapwood和Usami(1981)曾讨论过f(t)=exp(iωt)和f(t)为单位阶跃函数时的解的表达式.亦可使用傅里叶变换，把方程从时间域变换到频域中求解.

2.3 三阶辛格式谱元数值求解波动方程

目前常用的波动方程数值模拟方法多为非保结构方法，如：有限差分法、伪谱法、时域非辛格式有限元法及时域非辛格式谱元法等.尽管这些方法简洁、易于实现、执行效率高，但存在固有的、数理逻辑上的局限性.尤其是其时间域离散化近似的非保结构性质，在一定程度和一定范围内对波动方程及解的结构破坏是无法避免的，其数值解对于理论解的明显偏离也是不可避免的.这一先天不足对于短时程计算问题并不明显，但对于地球自由振荡这类长时程数值模拟则极为明显.而辛算法则可有效解决此类问题，理论研究表明辛算法具有极佳的保结构特性.在长时间模拟的情况下，辛算法依然能够非常有效地控制累积误差的增长.因此，辛算法非常适合需要进行长时程模拟并对精度有较高要求的物理学数值模拟问题(Komatitsch and Tromp，1999).

对于波动方程空间域离散，谱元法的优越性毋庸置疑.该方法兼具有限元处理边界和结构的灵活性和伪谱法的高精度和快速收敛特性等优势，在单元上采用 Gauss-Lobatto-Legendre(GLL)积分并结合基于Legendre正交多项式的高阶拉格朗日型插值，使得质量矩阵对角化，避免了单元内高阶插值所带来的Runge现象.由于可以直接采用显格式算法，避开了大规模线性方程组的并行求解，大大简化了数值计算的计算量和实现方法，同时提高了模拟精度和算法的稳定性.

根据谱元法的原理，将波动方程在空间域离散，得到的微分方程组可写为

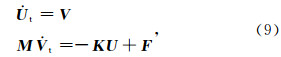
式中，U，V分别表示待求解的全局位移和速度向量，分别表示位移和速度关于时间的一阶微分，M为质量矩阵，K为刚度矩阵，F为震源项(Komatitsch and Tromp，2002).

将波动方程空间域离散后，在时间域可使用多种算法来进行离散，常用的非辛算法有差分算法、龙格库塔算法等.这些非辛算法普遍存在精度较低，长时程计算后数值频散明显.目前，在谱元法数值模拟研究领域，较为认可的时间域离散算法是Newmark算法，其从本质上来说，属于二阶保动量算法.理论研究表明，该方法在短时程的数值模拟中，体现出尚佳的性能，但该算法对积累误差和相位误差的控制一般，随着模拟时长的增加，二者均有比较明显的增加(Li et al.，2012; Zampieri and Pavarino，2006).

针对长时程高精度模拟的物理问题的需求，为更高效地获得更高精度的模拟结果，本文优化了Li等(2012)提出的新三阶辛算法(New Three-stage Third-order Symplectical Algorithm，NTSTO)，采用其进行时间域离散，并将其结合进行空间域离散的谱元法，进而得到一种新的具有时-空保结构特性的三阶辛格式谱元法.

对于微分方程数值求解，可进行如下三级三阶保辛算法：

将式(10)代入式(9)，同时考虑到谱元法所得的质量矩阵M为对角矩阵，非常便于线性方程求解，提高计算效率，从而可得到波动方程的三阶辛格式求解格式：

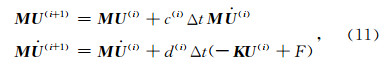
其中，Δt为时间步长，而c(i)、d(i)为辛条件系数(冯康和秦孟兆，2003)，i=1，2，3.

由于NTSTO算法具有良好的辛算法保结构特性，因此在进行时间域离散时，可采取相对大的时间步长计算.如此，即可保证模拟结果的准确性，同时又能弥补三阶算法比较耗时的不足.

而关于辛条件系数的选取，可根据不同的最优化原则进行.汪文帅等(2012a)采用相位最小误差原理，求取另一组辛条件系数，并通过多组数值试验，验证了NTSTO算法无论在内存消耗、稳定性及计算耗时，还是长时程跟踪能力都相当优越，而且可以有效地处理复杂几何形状和复杂介质.但其探讨的模型是物性参数和结构特点相对简单的二维模型，且模拟地震波时长较短(与地球自由振荡模拟相比而言)，其选择的辛条件系数足以达到研究要求.

然而，地球自由振荡研究所涉及的是具有复杂物性变化及横向非均匀结构的三维地球模型，且模拟地震波时程极长.如果仅考虑相位最小误差，数理逻辑角度将很难满足研究的需要.因此，本文根据最小均方误差原理，求取得到一组优化的辛条件系数：

代入此优化的条件系数，即得到优化的三阶辛谱元方法(New Three-stage Third-order Symplectical Spectral Element Method，NTSTO-SEM)，并将其应用于后续的地球自由振荡深入研究.

3 地球自由振荡数值模拟及分析3.1 震源及模型的选取

据地球自由振荡的特性可知，只有大地震才能产生比较明显的地球自由振荡现象.因此在进行自由振荡研究时，选取8级以上的地震作为震源.本文选取2012年4月11日16时38分(北京时间)在印度尼西亚苏门答腊西北海域(2.35°N、92.82°E)发生的8.6级强震(Magnitude 8.6-OFF THE WEST COAST OF NORTHERN SUMATRA. USGS于11 April 2012发布).

CMT公布的震源机制解为

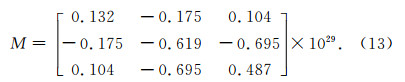
图 1所示为本次地震震中和全球168个台站所在位置以及CMT提供的本次地震的震源球.

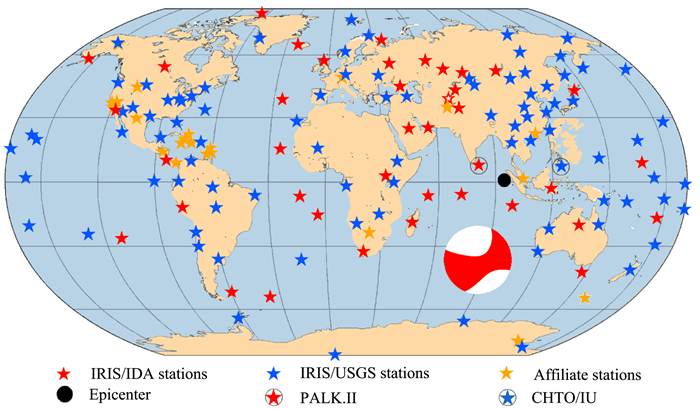图 1 震中和全球168个台站位置及震源球 Fig. 1 Epicenter, 168 stations on globe and earthquake mechanism

文中模拟采用Preliminary Reference Earth Model(PREM)地球模型.该模型是Dziewonski和Anderson(1981)提出的一维参考模型，引入黏滞衰减和各向异性的平均值，因此其上地幔部分是随频率变化的横向各向同性模型.

3.2 数值模拟方案

本次数值模拟使用了294个进程进行并行计算.参考全球地震台网(Global Seismographic Network，GSN)和中国地震台网(China Seismographic Network，CSN)公布的台站信息，在全球168个台站所处经纬位置分别设置地震波接收点.使用的谱元程序为Computational Infrastructure for Geodynamics(CIG)提供的SPECFEM3D_GLOBE(Komatitsch and Tromp，1999; Komatitsch et al.，1999).

基于PREM模型，考虑了地形和椭率，分别使用传统谱元法和NTSTO-SEM算法各模拟了地震波在全球表面传播500 min的整个过程.其中，在采用NTSTO-SEM算法计算时，为降低NTSTO算法的耗时，经过稳定性分析得出，NTSTO算法可取的最大时间步长为Newmark时间步长的2.8倍.详细地球模型参数、数值模拟参数及网格化参数如表 1所示.

表 1 数值模拟相关参数 Table 1 Simulation parameters

从理论角度分析，采用相同时间步长，三阶算法耗时约为二阶算法的1.5倍.本文在数值模拟时，NTSTO算法采用大时间步长.在相同震源、相同模型的情况下，采用Newmark离散的谱元法和NTSTO-SEM算法(下文简称Newmark算法和NTSTO算法)，分别模拟地震波在全球传播500 min，所消耗的时间分别为463h41min5s、486h32min34s，用时比约为1:1.04.该比例远低于1:1.5的理论值，表明本文推导的三阶辛格式谱元法在采用大时间步长运算时，可非常有效地弥补三阶算法耗时的不足.

3.3 数值实验结果分析

根据本次地震以水平错动为主要表现的特点，同时考虑研究横向非均匀的需要，选取了分布于地球表面不同位置的168个台站作为分析对象.文中分析的实际地震观测数据，均是按照模拟采取的震源和传播时长，从Incorporated Research Institutions for Seismology(IRIS)申请所得.限于篇幅，只列举其中2个特征台站CHTO.IU(98.94°E，18.81°N)和PALK.II(80.70°E，7.27°N)，将按照时间域波形和频率域频谱两类进行分析.

(1)时间域波形曲线分析

图 2所示为CHTO.IU台站模拟地震波Z分量波形对比图，图 3所示为PALK.II台站模拟地震波Z分量波形对比图.图 2、图 3中，红色曲线为台网观测数据，蓝色曲线为数值模拟的结果.辛算法的优势在于长时程模拟控制误差，为突出说明此特点，图 4和图 5分别选取图 2和图 3的时长200~500 min时段进行展示.

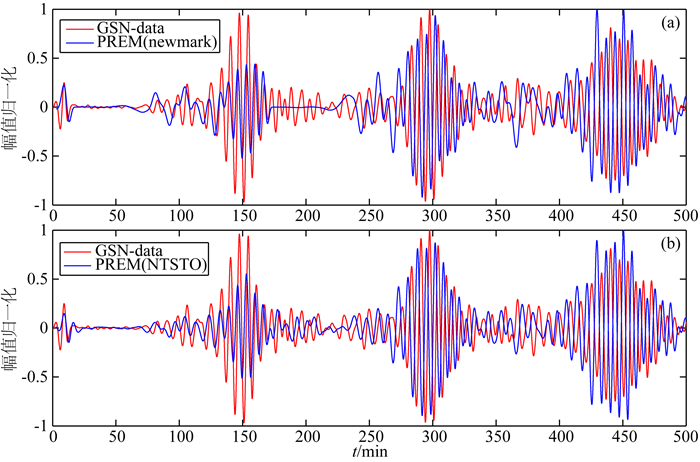图 2 CHTO.IU台站地震波Z分量波形对比
(a) 谱元法; (b) 三阶辛方法. Fig. 2 Z component of seismic wave of station CHTO.IU
(a) SEM; (b) NTSTO-SEM.

由图 2和图 3可见，在0~20 min的初始阶段，两种算法所得的波形曲线与实测数据的波形契合度均较好，而NTSTO算法的结果明显好于Newmark算法.但随着模拟时间的推移，与实测数据相比，两种算法所得地震波曲线均出现较明显的偏差.这是因为数值模拟采用的模型是PREM模型，不考虑衰减和横向非均匀等影响因素，模拟的结果与实际的观测数据必然存在差异.尽管如此，随着模拟时长的增长，如200 min之后，NTSTO算法所得的波形曲线与观测数据仍具有较好的对应性，并且保持稳定.从图 4和图 5中即可看出.

图 3 PALK.II台站地震波Z分量波形对比
(a) 谱元法; (b) 三阶辛方法. Fig. 3 Z component of seismic wave of station PALK.Ⅱ
(a) SEM; (b) NTSTO-SEM.

图 4 CHTO.IU台站地震波Z分量波形长时程对比
(a) 谱元法; (b) 三阶辛方法. Fig. 4 Z component of seismic wave of station CHTO.IU
(a) SEM; (b) NTSTO-SEM.

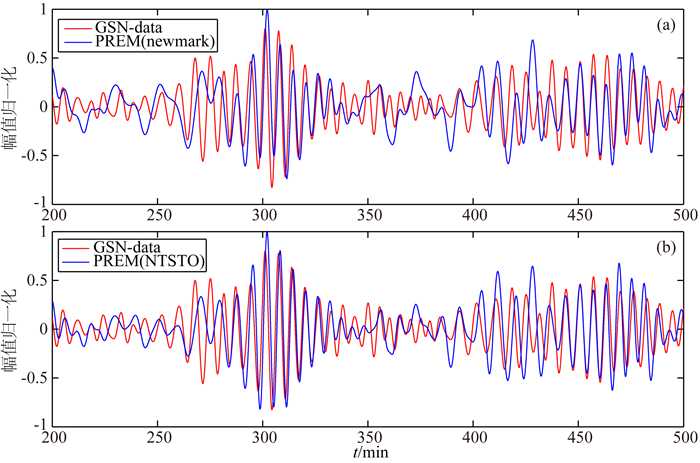图 5 PALK.II台站地震波Z分量波形长时程对比
(a) 谱元法; (b) 三阶辛方法. Fig. 5 Z component of seismic wave of station PALK.Ⅱ
(a) SEM; (b) NTSTO-SEM.

另外，对波形的频谱分析表明，模拟结果与观测数据存在相位差.在进行时域误差分析时，模拟结果与观测数据不能直接做定量分析，特别是幅值的差异.因为这类对比所出现的“误差”很大程度上来自模型与实际地球间的巨大差异，而目前阶段这一“误差”很难定量地从总误差中予以区分.因此，今后的研究应不断完善地球模型，使其更贴近实际地球介质构造.

(2)频率域频谱分析

因为自由振荡是本征频率问题，研究的主要是频率域问题.图 6所示为CHTO.IU台站模拟地震波Z分量频谱对比图，图 7所示为PALK.II台站模拟地震波Z分量频谱对比图.图 6和图 7中，红色曲线为台网观测数据频谱分析结果，蓝色曲线为数值模拟的频谱分析结果.

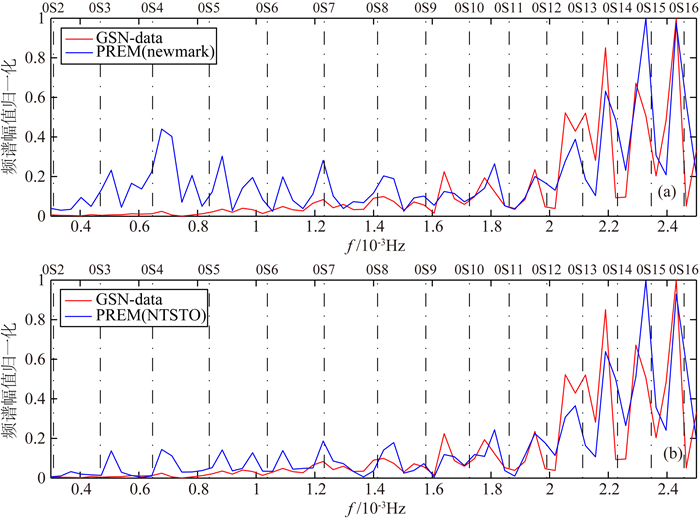图 6 CHTO.IU台站地震波Z分量频谱对比
(a) 谱元法; (b) 三阶辛方法. Fig. 6 Z component of spectrum of station CHTO.IU
(a) SEM; (b) NTSTO-SEM.

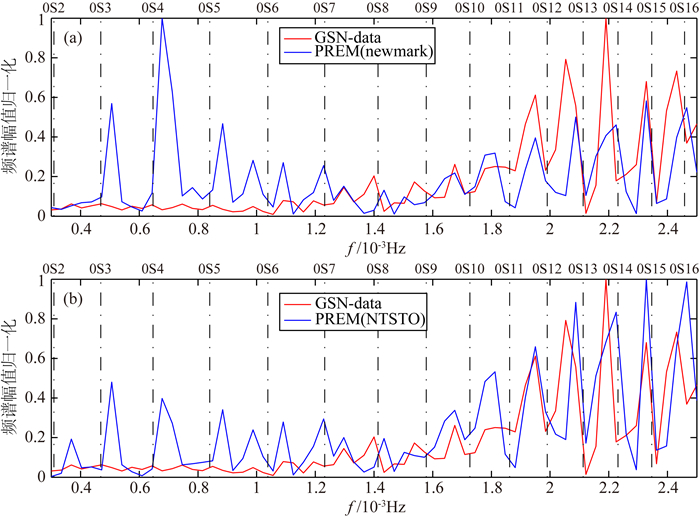图 7 PALK.II台站地震波Z分量频谱对比
(a) 谱元法; (b) 三阶辛方法. Fig. 7 Z component of spectrum of station PALK.Ⅱ
(a) SEM; (b) NTSTO-SEM.

不同振型的地球自由振荡的理论频率值通常被当作参照依据，故本文亦引用之.图 6和图 7中，上方横坐标轴分别为不同阶的球型振荡(从0S2到0S16)，连接上下横坐标轴的黑色虚线为各阶球型振荡对应的理论频率.理论研究表明，将无数个不同自由振荡振型进行叠加，即可得出地球振动波形(Bolt，2012; Lapwood and Usami，1981).但这些理论值是通过一维简化地球模型求解所得，此模型同地球实际的三维非均匀复杂结构(包括横向非均匀结构)有极大偏差，所以即使将这些理论值用于简正模求和，也无法得到真实可信的振动波形.故这些理论值对实际研究而言，仅可作为粗略的一级近似参考或约束.从图 6及图 7中也可发现，这些理论值大多与观测数据相去甚远.

表 2所示为CHTO.IU台站模拟结果和台网数据的频谱分析结果，表 3所示为PALK.II台站模拟结果和台网数据的频谱分析结果.两表中，第一列为台网数据识别出的谱峰频率值，第二列为Newmark算法模拟识别出的谱峰频率值，第三列为Newmark算法与观测数据的绝对误差；第四列为NTSTO算法模拟识别出的谱峰频率值，第五列为NTSTO算法与观测数据的绝对误差.

表 2 CHTO.IU台站模拟结果和台网数据的频谱分析(谱峰频率值) Table 2 Spectrum analysis of simulation and GSN data of station CHTO.IU (frequencies of spectral peaks)

表 3 PALK.Ⅱ台站模拟结果和台网数据的频谱分析(谱峰频率值) Table 3 Spectrum analysis of simulation and GSN data of station PALK.Ⅱ (frequencies of spectral peaks)

本文采用的是PREM模型，所以两个台站识别的振型频率值应基本一致.而实际地球是复杂的横向非均匀衰减结构，会造成两个台站观测数据识别的振型频率值略有差异或者部分缺失.因此，综合两个台站的观测数据，可得到最全的振型频率参考值.表 2和表 3第一列的加括号数据即两个台站观测数据的互补.

表 2和表 3共38组对比数据，只有1组数据，NTSTO算法的结果稍逊于Newmark算法.这还建立在前者的数据量明显少于后者以及观测数据的基础上，因为前者采用了大时间步长.如果计算条件允许，采用同样小步长，NTSTO算法的精度将远高于Newmark算法.

对比图 6和表 2、图 7和表 3，可明确看出，NTSTO算法所得结果在频谱的峰值对应性、幅值关系、能量分布等多方面都明显优于Newmark算法所得结果.尤其是在甚低频段，频率可识别度明显高于Newmark算法的结果，这点对于自由振荡的研究至关重要，见表 2和表 3的前两组数据.自由振荡的最长周期可达54 min，频率约为0.29 mHz.鉴于介质衰减等因素，长时间传播的情况下，信号的能量会大幅降低，超长周期信号很难有效识别.因此在图中，实测数据的甚低频段的频谱能量都非常低.

纵观时间域和频率域的结果，模拟结果与实际观测资料均未能完全契合，主要原因是实际地球的内部结构及其介质的物理性质远比PREM模型复杂得多，表明地球内部大尺度非均匀结构对地球自由振荡有着明显的影响.另外，信息量的缺失也是不可忽视的原因.由于计算平台限制及计算稳定性的约束，数值模拟无法达到台网地震仪的采样频率.从表 1可知，Newmark算法采取的最小时间步长为0.07315 s，NTSTO算法采用前者的2.8倍的大步长，最小时间步长仅为0.20482 s，而此次下载实测数据的地震仪器的采样率为50 sps，即采样间隔为0.05 s.因此，实测数据的有效信息远多于模拟结果的有效信息.其中，NTSTO算法的信息量仅相当于Newmark算法的约1/3，实测数据的约1/4.

尽管如此，NTSTO算法的结果依然与观测数据有良好的拟合关系，能够更准确识别自由振荡振型频率值.模拟的结果表明本文推导的三阶辛格式谱元法在采用大时间步长运算时，精度依然明显高于采用Newmark算法的传统谱元法.如果计算平台满足，采用与Newmark算法相同的小时间步长，模拟结果的准确性将极大提升，该算法的优越性将更加明显.同时，将其结合观测数据也可大幅增高观测记录中振型频率的可识别率，并且逐步完善对地球内部结构的认知.

4 结论

前人在数值模拟自由振荡方面的研究多集中于同自由振荡不同振型的理论值进行对比.前述已知，这些理论值所基于的模型与实际地球结构出入甚大.数值模拟结果与理论参考值对应好坏实际意义一般，应更关注同实际观测资料的对比分析.

本文提供了一种保结构模拟地球自由振荡的新方法，并应用此方法对2012年4月11日印度尼西亚苏门答腊8.6级地震激发的地球自由振荡进行了数值模拟.数值实验结果显示，无论是时间域理论地震记录，还是频率域波谱曲线分布，均与实际观测数据具有良好的对应.研究分析及数值结果证实，本文推出的方法具有保结构性质，可有效控制波动方程长时程模拟中的积累误差及相位误差.尽管数值结果与观测数据尚有差别，但这些差别主要源于波动方程空间离散时单元剖分较粗糙(限于计算平台的条件)及所采用地球模型与实际地球结构间的差异.

本文所涉及的工作将保结构计算(模拟)拓展至地球自由振荡研究领域，其方法适合有高精度长时程求解变系数偏微分方程需求的物理问题；在方法论层面上为探测、刻画全球尺度地球非均匀(特别是横向非均匀)结构的驻波数值方法奠定了部分基础，并为相关研究领域提供了新的选择.

致谢 非常感谢“中国科学院地质与地球物理研究所计算模拟实验室(Computer Simulation Lab，IGGCAS)”为本文研究提供高性能计算集群.同时，非常感谢IRIS提供地震数据以及CIG提供SPECFEM3D_GLOBE程序.

参考文献
[1] Alterman Z, Jarosch H, Pekeris C L. 1959. Oscillations of the Earth. Proc. Roy. Soc. Lond. Ser.-A, 252(1268): 80-95.
[2] Bolt B A. 2012. Seismology: Surface Waves and Earth Oscillations. Burlington, MA: Elsevier.
[3] Bullen K E, Haddon R A. 1967. Derivation of an Earth model from free oscillation data. Proc. Natl. Acad. Sci. U S A, 58(3): 846-852.
[4] Chen S Z, Li X F, Wang W S, et al. 2012. Simulation of the Earth's free oscillation based on a lateral inhomogeneous earth model.//28th Ann. Mtg., Chinese Geophysical Society (in Chinese). Beijing: Chinese Geophysical Society.
[5] Chen S Z, Li X F, Wang W S, et al. 2013. The Earth's Free Oscillation of Structure-preserving Simulation in Analysis of Lateral Heterogeneity of the Earth Structure on the Global Scale.//29th Ann. Mtg., Chinese Geophysical Society (in Chinese). Beijing: Chinese Geophysical Society.
[6] Dahlen F A. 1968. The normal modes of a rotating, elliptical earth. Geophys. J. Int., 16(4): 329-367.
[7] Dziewonski A M, Anderson D L. 1981. Preliminary reference Earth model. Phys. Earth Plan. Int., 25(4): 297-356.
[8] Fang J. 1990a. Parameter kenerls in linear inversion of the Earth lree oscillation (I). Science in China Series B (in Chinese), 1990, (2): 202-207.
[9] Fang J. 1990b. Parameter kenerls in linear inversion of the earth free oscillation (II). Science in China Series B (in Chinese), (3): 329-336.
[10] Feng K, Qin M Z. 2003. Symplectic Geometric Algorithms for Hamiltonian Systems (in Chinese). Hangzhou: Zhejiang Science and Technology Press.
[11] Komatitsch D, Tromp J. 1999. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophysical Journal International, 139(3): 806-822.
[12] Komatitsch D, Vilotte J P, Vai R, et al. 1999. The spectral element method for elastic wave equations—Application to 2-D and 3-D seismic problems. Int. J. Numer. Meth. Eng., 45(9): 1139-1164.
[13] Komatitsch D, Tromp J. 2002. Spectral-element simulations of global seismic wave propagation—I. Validation. Geophysical Journal International, 149(2): 390-412.
[14] Lapwood E R, Usami T. 1981. Free Oscillations of the Earth. New York: Cambridge University Press.
[15] Li X F, Wang W S, Lu M W, et al. 2012. Structure-preserving modelling of elastic waves: a symplectic discrete singular convolution differentiator method. Geophysical Journal International, 188(3): 1382-1392.
[16] Lillie R J. 1999. Whole Earth Geophysics: An Introductory Textbook for Geologists and Geophysicists. New Jersey: Prentice Hall.
[17] Shearer P M. 2009. Introduction to Seismology. 2nd ed. New York: Cambridge University Press.
[18] Tsuboi S, Geller R J, Morris S P. 1985. Partial derivatives of the eigenfrequencies of a laterally heterogeneous earth model. Geophys. Res. Lett., 12(12): 817-820.
[19] Tsuboi S. 1995. Free oscillations of a laterally heterogenous and anelastic earth. Pure Appl. Geophys., 145(3-4): 445-457.
[20] Wang W S, Li X F, Lu M W, et al. 2012a. Structure-preserving modeling for seismic wavefields based upon a multisymplectic spectral element method. Chinese J. Geophys. (in Chinese), 55(10): 3427-3439, doi: 10.6038/j.issn.0001-5733.2012.10.026.
[21] Wang W S, Li X F, Chen S Z, et al. 2012b. Spectral-element method for seismic wave equations in a 3-D spherical coordinate system.//28th Ann. Mtg., Chinese Geophysical Society (in Chinese). Beijing: Chinese Geophysical Society.
[22] Yan Z Z, Zhang H, Yang C C, et al. 2008. An initial study of the numerical simulation of the Earth's free oscillations process excited by earthquake. Advances in Earth Science (in Chinese), 23(10): 1020-1026.
[23] Yan Z Z, Zhang H, Fan X T, et al. 2012. Comparative analysis on the characteristics of low-frequency energy released by the Wenchuan earthquake and Kunlun Mountain earthquake. Chinese J. Geophys. (in Chinese), 55(12): 4218-4230, doi: 10.6038/j.issn.0001-5733.2012.12.033.
[24] Yan Z Z, Zhang H, Fan X T, et al. 2014. Comparative analysis of the characteristics of global seismic wave propagation excited by the Mw9.0 Tohoku earthquake using numerical simulation. Science China Earth Sciences, 57(7): 1626-1636.
[25] Zampieri E, Pavarino L F. 2006. Approximation of acoustic waves by explicit Newmark's schemes and spectral element methods. Journal of Computational and Applied Mathematics, 185(2): 308-325.
[26] 陈世仲, 李小凡, 汪文帅等. 2012. 基于横向非均匀地球模型的地球自由振荡模拟.//中国地球物理学会第二十八届年会. 北京: 中国地球物理学会.
[27] 陈世仲, 李小凡, 汪文帅等. 2013. 全球尺度地球内部横向非均匀结构研究中的地球自由振荡保结构数值模拟.//中国地球物理学会第二十九届年会. 北京: 中国地球物理学会.
[28] 方俊. 1990a. 地球自由振荡线性反演中的参数核(Ⅰ). 中国科学(B辑 化学 生命科学 地学), (2): 202-207.
[29] 方俊. 1990b. 地球自由振荡线性反演的参数核(Ⅱ). 中国科学(B辑 化学 生命科学 地学), (3): 329-336.
[30] 冯康, 秦孟兆. 2003. 哈密尔顿系统的辛几何算法. 杭州: 浙江科学技术出版社.
[31] 汪文帅, 李小凡, 鲁明文等. 2012a. 基于多辛结构谱元法的保结构地震波场模拟. 地球物理学报, 55(10): 3427-3439, doi: 10.6038/j.issn.0001-5733.2012.10.026.
[32] 汪文帅, 李小凡, 陈世仲等. 2012b. 三维球坐标系下的地震波方程的谱元解法.//中国地球物理学会第二十八届年会. 北京: 中国地球物理学会.
[33] 严珍珍, 张怀, 杨长春等. 2008. 地震激发地球自由振荡过程的数值模拟初步探索. 地球科学进展, 23(10): 1020-1026.
[34] 严珍珍, 张怀, 范湘涛等. 2012. 汶川与昆仑山强烈地震激发的地球自由振荡频谱的对比分析. 地球物理学报, 55(12): 4218-4230, doi: 10.6038/j.issn.0001-5733.2012.12.033.