2. 中国地震局地球物理研究所, 北京 100081;
3. 日本国际地震学与地震工程研究所, 日本 茨城 305-0802
2. Institute of Geophysics, Chinese Earthquake Administration, Beijing 100081, China;
3. International institute of seismology and earthquake engineering, Building Research Institute, 1 Tatehara, Tsukuba, Ibaraki 305-0802, Japan
 .
.In this paper, the stress Green's functions for a constant slip rate on a triangular fault are calculated. Theorectially, the mechanics of earthquake rupture process can be regarded as a transformation from static friction to dynamic one. For the dynamic rupture modeling, friction criterion plays a very important role. Because we only focus on the rupture propagation and neglect the nucleation and cessation, slip weakening friction law is applied in our study. Nonplanar fault geometries include many types as mentioned above, and here we just take the curved faults with different bending angles as examples to study the influences of fault geometries on the rupture propagation. After modeling, it is found whether rupture can continue to propagate after curventure part is controlled by many factors, such as bending angles, initial stress in and out of the asperity, the radius of the asperity, slip weakening distance and so forth. Simulation results show that the higher the initial stress in and out of the asperity is, the easier the rupture propagates. And the larger the radius of the asperity or the smaller the slip weakening distance is, the easier the rupture propagates beyond the bend part. Given the same initial conditions, when the inclination angle is bigger, it has more obvious inhibition effect and can be taken as a barrier. However, the curved fault with small inclination angle has similar rupture propagation characteristics, and does not show obvious inhibition effect.
作为零阶近似,地震断层可以用简单连续的平面形态来模拟.但是,实际断层并不是平面构造,而是复杂不连续的断裂组合带,有很多常见的断层弯折、分叉、阶跃、亚平行的分支等(薛霆虓等,2009).理论分析表明,这些断层几何结构的非连续会引起应力场的复杂变化,对断层破裂传播过程有重要影响.实际震例分析发现,地震破裂的成核、扩展以及终止也常常受断层几何结构的影响(Sibson,1986;Scholz,1990),其复杂性使得变形破坏过程复杂化(马瑾,1987).
Kato等(1999)以及马瑾等(1996)开展了相关实验,研究了弯折断层物理场的演化过程,并分析了几种典型断层与弯折断层的不同物理场演化特征.Shin和Teng(2001)讨论了1999年集集地震断层几何形态造成的断层附近静态位移场变化.Aochi等(2000a,b)研究了二维分支断层的动力破裂过程,结果表明,断层的复杂几何形态造成了断层面上的应力非均匀性,进而导致了动力学破裂传播的多样化.Aochi和Fukuyama(2002)成功模拟了1992年L and ers地震的动力学破裂过程,由于小的Kickapoo断层的存在,破裂产生了“跳跃”,使得其传播方向发生了改变.Zhang等(2014)利用有限差分方法模拟了由两条平行断层Ⅰ和Ⅲ以及一条跨跳断层II组成的复杂断层系的破裂过程传播,子断层I和II的夹角为26.5°.结果表明,当破裂应力降较小时,破裂无法越过子断层Ⅰ和Ⅱ的弯折部位继续传播,而当应力降较大时,破裂则可以越过子断层II,继续向子断层III传播.可见,复杂的非平面断层几何形态确实对断层破裂传播过程有重要影响.因此,研究具不同几何结构的断层系的变形破坏及演化过程,对理解地震机制有非常重要的意义(马瑾等,1996).
弯折断层是一种非常典型常见的断层几何结构,一般认为,大角度的弯折断层应力难以传递,相互作用比较困难,而小角度的弯折断层相互作用强烈,大震易于连发.而且断层弯折部位也常常是构造地震发生的区域,易于导致不同断层段发生错动,如安县附近断层走向的变化,可能是2008 年汶川8.0级地震造成北川严重损失的一个重要的原因.基于上述,本文欲模拟断层弯折对地震破裂传播的控制作用,定量分析初始应力场及断层弯折角度等对断层破裂传播的影响.
2 研究方法2.1 三维断层动力学破裂方程研究采用边界积分方程方法,该方法最早由Das和Aki(1997)引入断层破裂动力学模拟,是一种半数值半解析方法.对于断层的破裂传播问题,基于边界积分方程方法求解的出发点是位移表示定理,最终要建立的弹性动力学方程主要是寻找应力和滑动量之间的关系.常用的求解途径有两种,分别是位移边界积分方程方法(直接基于位移的积分表示求解)和牵引力边界积分方程方法(从位移表示定理出发,通过求空间导数得到应力的积分表示,并以此为问题求解).在牵引力边界积分方程方法中,积分方程是基于全空间格林函数建立的,求解的问题不限于平面断层,对于任意弯曲断层都成立.因此,从90年代以来,基于边界积分方程方法的断层破裂问题研究基本都是采用牵引力边界积分方程方法(Cochard and Madariaga,1994;Fukuyama and Madariaga,1995,1998;Chen and Aki,1996).
破裂发生的地震断层,是周围介质的边界,这是因为位移在断层面的两侧是不连续的.表示定理(Aki and Richards,1980)中,在无限弹性介质中位移场可以表示为断层面上滑动分布和积分核的时空卷积.边界积分方程在地震破裂动力学的应用起始于断层面上的基本弹性动力学积分方程(Tada,2009):
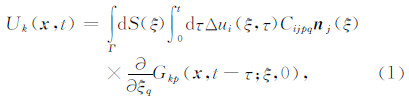
因为我们考虑的是动力学破裂问题,所以需要建立应力和断层面上滑动量的时空分布关系.当接收点接近断层表面Γ时,断层面上的应力T(x,t)可以表示为
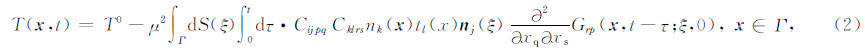
但这个方程仅仅是非常抽象和概念性的表示,如果将该理论应用到实际的地震学问题中,我们需要用更为实用的边界积分方程来描述这种复杂的破裂传播问题.对于三维问题而言,断层面垂直于x3坐标轴,滑动沿着x1和x2轴,也就是说滑动量有两个自由度Δu1和Δu2:
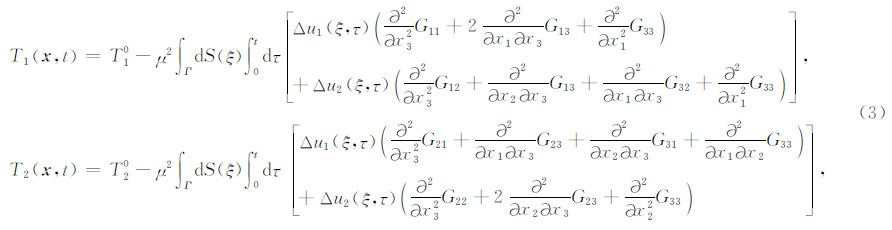
该方法最大的优势在于格林函数存在形式简单的闭合解析解,但代价是在应力的积分表示中,由于全空间格林函数本身当场点趋向于源点时存在弱奇异性,因此对它的二阶导数会出现高度奇异性.在动力学研究领域,通常采用分部积分的方法(Fukuyama and Madariaga,1995; Tada et al.,2000),将对格林函数的高阶导数降低一阶到滑动量上,从而达到去除高度奇异性的目的.尽管面积分仍有强奇异性,但利用全空间格林函数的解析解中含有Dirac函数的性质,最终回避了这个问题,并可以得到积分核的解析表达式.
采用积点法和箱形离散化方案对边界积分方程进行离散化处理,网格数目和时间步长数用NX和NT表示,第n个网格所在的断层面用Γn表示,第q个时间步长的结束点用tq(tq-1≤t≤tq)表示.经过离散化处理后,最终得到了适用于数值模拟的弹性动力学方程:
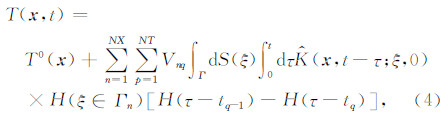
 (x,t-τ;ξ,0)为离散积分核,H(·)为赫维赛德阶跃函数.
(x,t-τ;ξ,0)为离散积分核,H(·)为赫维赛德阶跃函数.
破裂过程的时空演化由时间推进算法确定,在每一时间步长内,我们先确定破裂的区域,评估破裂尖端的剪应力,通过比较同一位置的剪应力与屈服应力的关系判断破裂是否能扩展.
2.2 摩擦本构关系地震力学过程可以被视为断层由静摩擦转为动摩擦的过程,对于震源破裂过程的动力学模拟,摩擦准则是求解震源动力学方程的关键.它控制着断裂的起始、发展和愈合,合理地理解摩擦准则对于破裂过程的控制作用能为我们更好地理解震源过程的多样性和非均匀性提供物理基础(张丽芬和姚运生,2013).
目前,较为常用的摩擦准则是滑动弱化准则(Ida,1972;Andrews,1976a,b)、速率弱化准则(Cochard and Madariaga,1994;Aagaard et al.,2001)和速率-状态依赖摩擦准则(Dieterich,1979;Scholz,1998).本研究只考虑破裂的扩展和停止,而忽略破裂成核和愈合的过程,所以采用滑动弱化准则.该准则最早由Ida(1972)提出,有很好的物理基础,Dieterich(1979)岩石破裂的实验结果表明,破裂点的应力降不是瞬时产生的,而是要经过一定的滑动距离,应力才能下降到动摩擦力,这与滑动弱化模型中应力与滑动距离成反比的假定一致.该准则数学上形式非常简单,便于数值操作,因此在震源动力学的模拟中被广泛使用(Andrews,1976a,b;Harris et al,1991,张海明,2004).在这个模型中,假定内聚力可以用位移间断的函数表示,内聚区的应力与破裂面之间的滑动距离有关.岩石摩擦实验表明,随着滑动量的增大,物质性质变弱,最终进入稳态滑动模式.在滑动弱化准则中,破裂尖端是应力集中的部位(Ohnaka,1992),当断层上一点的剪应力超过屈服应力强度τp时,该点开始破裂并发生滑动.随着位错Δu的增加,剪应力以线性方式下降,直至位错达到临界滑动弱化距离Dc后,剪应力下降到稳定的剩余应力水平τr:
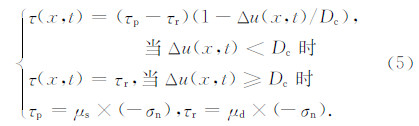
Courant-Friedrich-Lewy(CFL)比值是控制计算稳定性的重要参量,显式时间推进算法必须满足CFL条件(Fukuyama and Madariaga,1998;Tada and Madariaga,2001),确保在某一给定单元在时间t产生的波,在t+Δt之前不影响到其他相邻单元.为保证计算精度,同时兼顾计算速度,模拟计算中采用中心差分的时间积分方法.为了保证数值模拟的稳定性,研究中引入了CFL比值ωα=αΔt/Δx来表达场点的影响.对于序号为(i,j)的场点,只有Δt时间间隔内发出的波才能影响它,P波速度最大,因此,只有以场点为圆心,αΔt为半径的圆所覆盖的单元才对该场点有贡献.
例如,对于矩形网格而言,当αΔt≤Δx/2时,此圆落在当前网格内,这意味着只有当前网格对它本身有贡献.对于等边三角形,CFL则需要满足ωα≤  .而对于等腰直角三角形网格,则只有当αΔt≤
.而对于等腰直角三角形网格,则只有当αΔt≤  时,即ωα≤
时,即ωα≤ 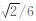 ,其他网格才不会对当前网格有干扰,以当前网格对它本身的贡献为主(图 1).
,其他网格才不会对当前网格有干扰,以当前网格对它本身的贡献为主(图 1).
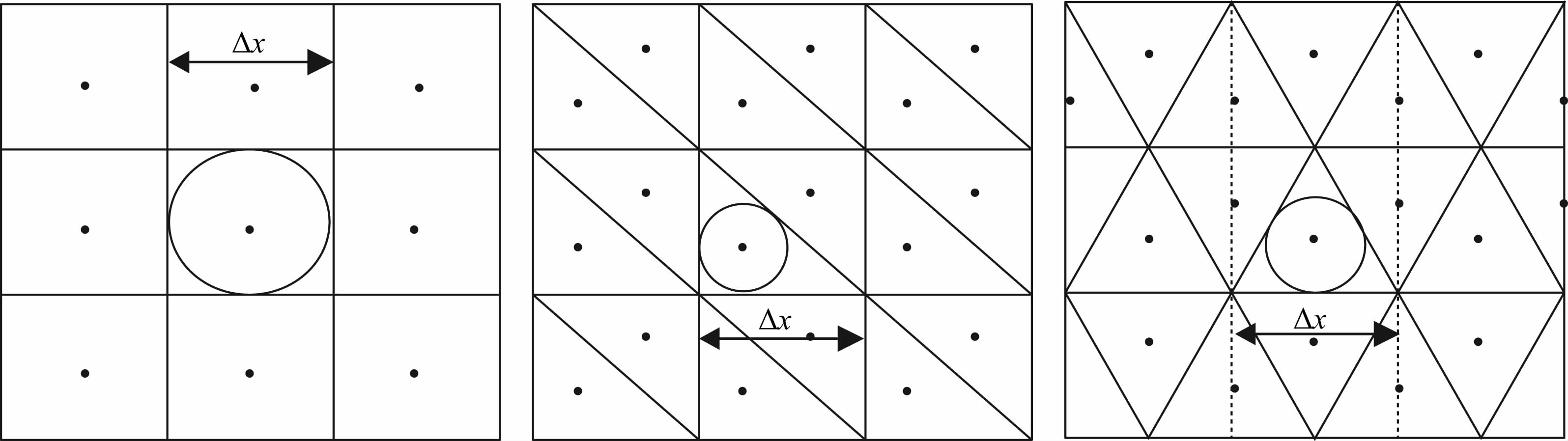 | 图 1 矩形网格和三角形网格的CFL比值对当前网格贡献分布示意图 Fig. 1 Schematic figure of CFL ratio of rectangle and triangular elements |
(1)格林函数验证
数值检验的第一步就是确定基于三角形网格的三维格林函数计算的正确性,应力格林函数是指在时间tq,三角形源在ξp处沿着j方向滑动而在接收点x1和时间tm产生的应力响应.在每一个三角形单元内,滑动都被设定以均匀滑动速率发生.为了验证格林函数计算的准确性,我们与Tada(2006)计算的应力分量进行了比较.震源区设置为1 km×1 km,用两个三角形ABC和CDA组成正方形震源,源区的点A为z=0平面的原点,局部坐标系中各源点坐标分别为:A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),接收点位于R(0.6,0.3,0.2)处.计算中,设定剪切波速β=3.0 km·s-1,纵波速度α=  ,时间步长设为0.01 s.本文计算了不同的应力分量格林函数,通过与Tada(2006)计算结果的对比(图 2,彩色图为本研究结果;黑白图为Tada(2006)结果),发现两者分别求解的三角形ABC、CDA和矩形ABCD的应力格林函数结果完全一致,说明该程序是正确的,可以用于离散积分核的计算及动力学破裂过程的数值模拟.
,时间步长设为0.01 s.本文计算了不同的应力分量格林函数,通过与Tada(2006)计算结果的对比(图 2,彩色图为本研究结果;黑白图为Tada(2006)结果),发现两者分别求解的三角形ABC、CDA和矩形ABCD的应力格林函数结果完全一致,说明该程序是正确的,可以用于离散积分核的计算及动力学破裂过程的数值模拟.
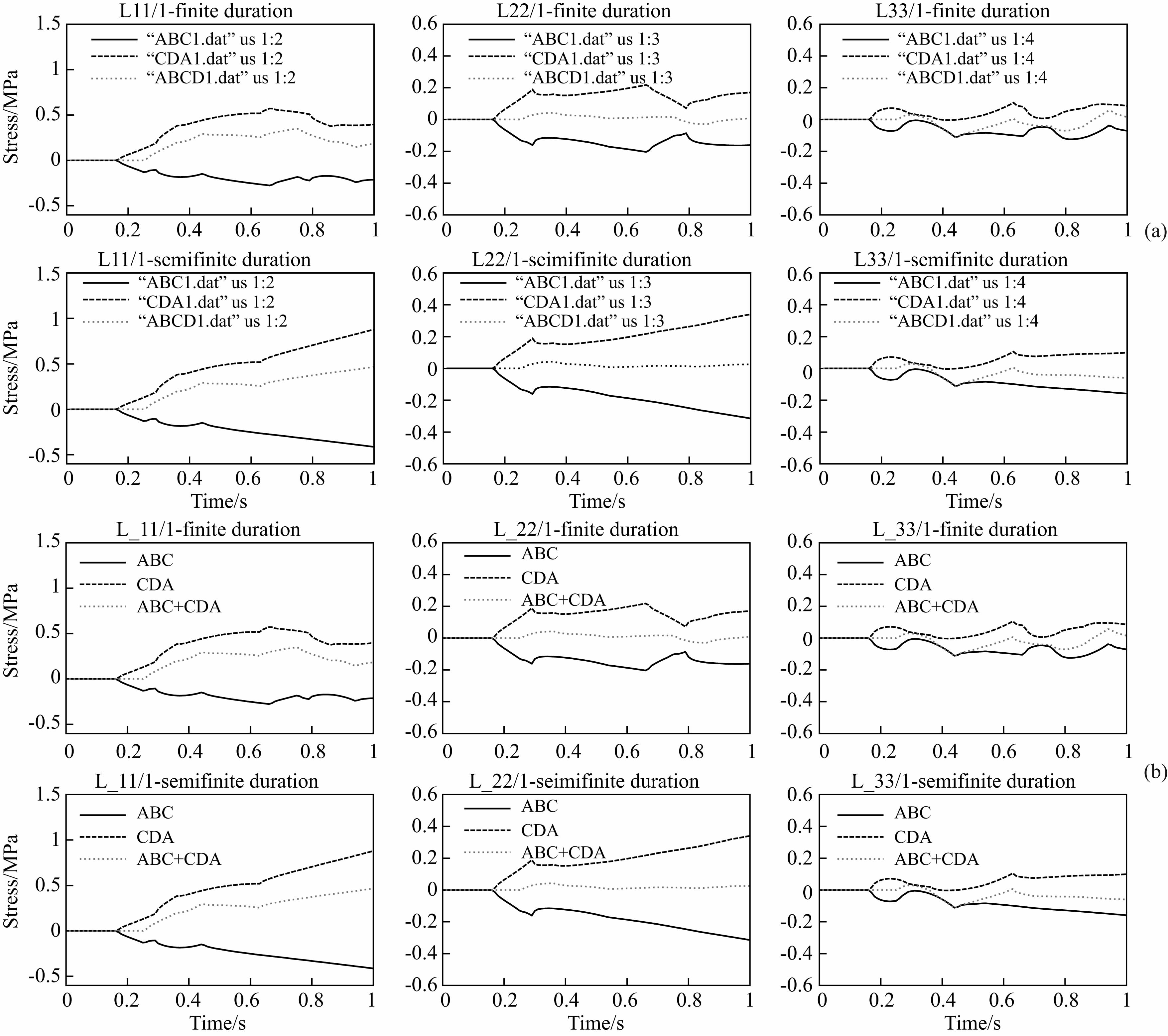 | 图 2 应力格林函数计算结果对比 (a) 本研究; (b) Tada(2006);黑色实线:三角形ABC的格林函数Lij/k;黑色虚线: 三角形CDA的格林函数Lij/k;灰色虚线:矩形ABCD的格林函数Lij/k. Fig. 2 Comparison of the stress Green′s function with semi-duration and finite duration (a) Present study; (b) Tada(2006). |
(2)典型算例对比
Madariaga等(1998)基于笛卡尔坐标下的交错网格有限差分方法,研究了三维断层自发破裂问题.在他的研究中,设定断层初始破裂区(凹凸体)的半径为10个网格空间步长,初始剪应力Tasp为1.6τp,其中τp为剪切破裂强度,取值80;凹凸体外初始剪应力Te为0.5τp;临界滑动弱化距离Dc为4.0,CFL系数取0.35.图 7分别给出了Madariaga等(1998)和本文的研究结果,通过比较过凹凸体中心切平面上点的滑动量随时间的变化图像,不难发现,二者的滑动位移分布基本一致.破裂从断层中心开始,之后以微小的速率向两侧对称传播.滑动量图像中心部位出现一个鼓包,这个过剩的滑动量是破裂起始于一个有限的凹凸体的最显著特征(图 3).在Madariaga等(1998)的研究结果中,当t=30时,滑动量的分布图像中出现了数据缺失的情况,初步分析是因为研究者考虑到随时间演化数值模拟的不稳定性而做了数据截断处理引起的.本研究中数值计算结果相对稳定,没有出现如图中的缺口,与同样利用边界积分方程方法的Aochi(1999)和张海明(2004)的研究结果基本一致.
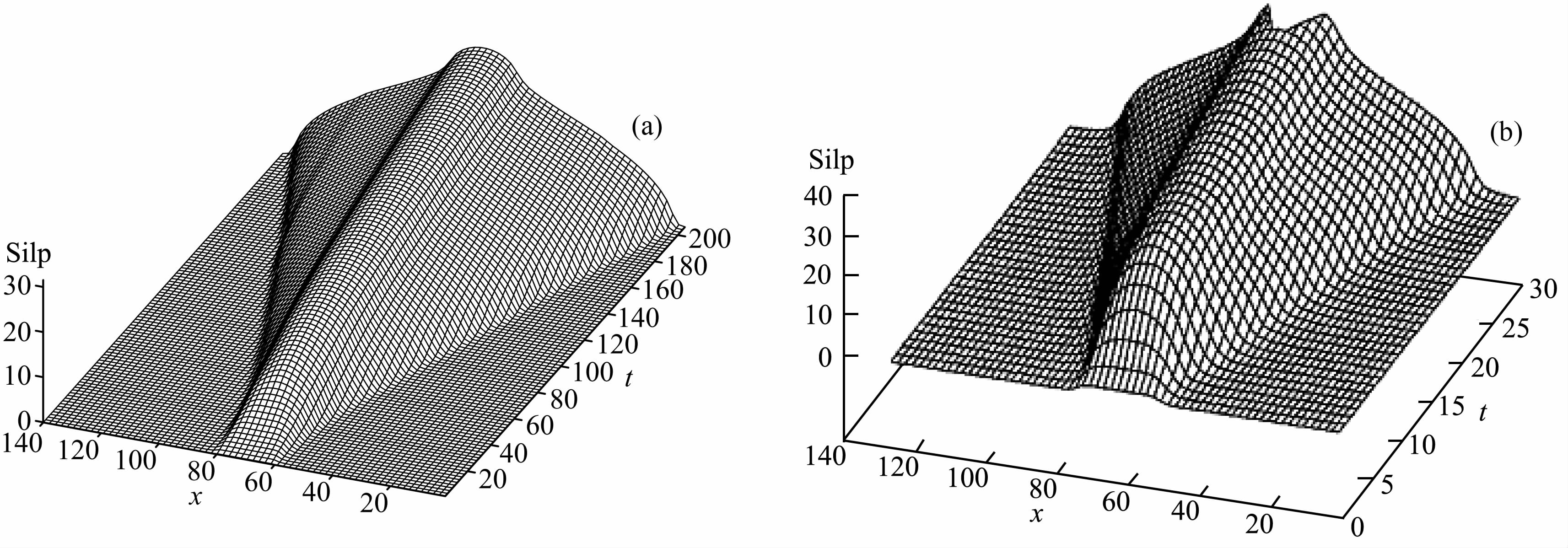 | 图 3 无限矩形断层的自发破裂滑动量对比 (a)本研究;(b)Madariaga et al.(1998). Fig. 3 Comparision of slip of rectangle fault (a)This study;(b)Madariaga et al.(1998). |
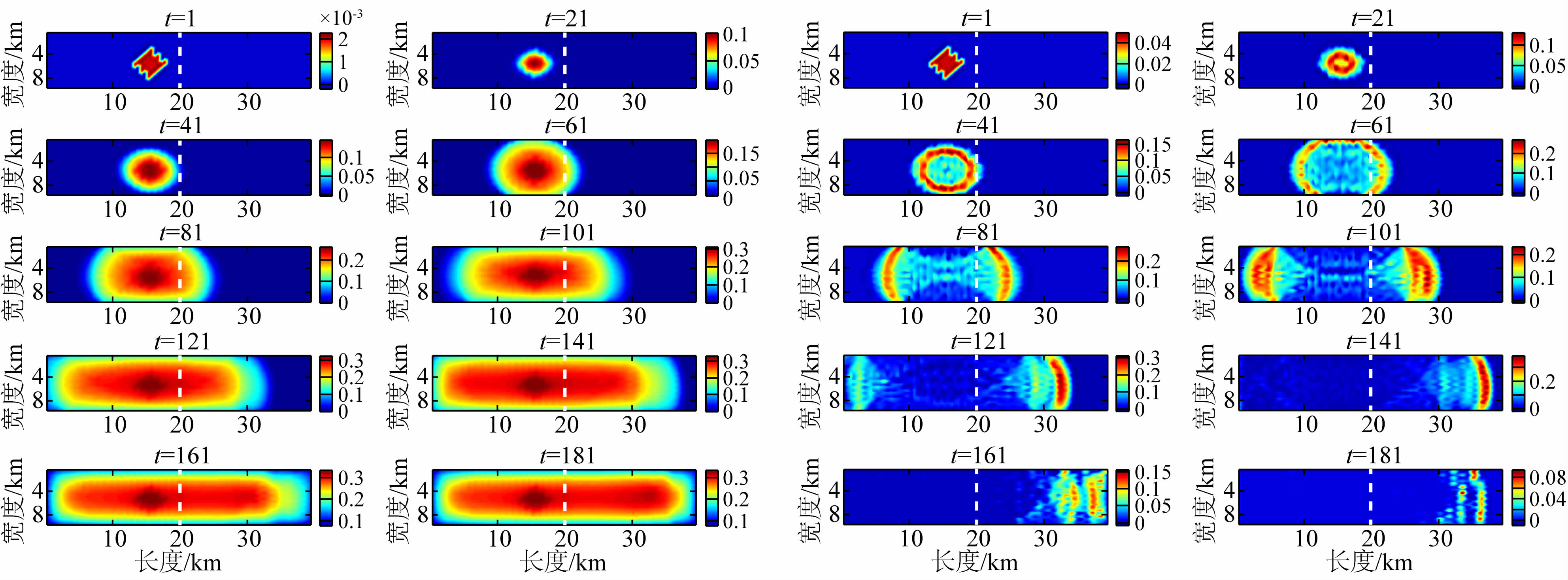 | 图 7 弯折角为10°的弯曲断层自发破裂滑动量(左图,色标单位m)和滑动速率(右图,色标单位m·s-1)瞬像 Fig. 7 Snapshot of slip(left figure) and slip rate (right figure)of spontaneous rupture propagation of 10°curved fault |
本研究还比较了给定时刻(Madariaga等(1998)中t=200;本研究中t=140),沿切平面方向的应力随位置的空间变化特征(图 4),两种方法的整体形态比较一致.在破裂前锋之外出现了类似于Madariaga等(1998)中的强应力扰动,这种现象在Aochi(1999)、Zhang等(2006)的研究中均有体现,分析认为这种强应力扰动是与S波有关的.通过上述比较,检验了所用研究方法的正确性.
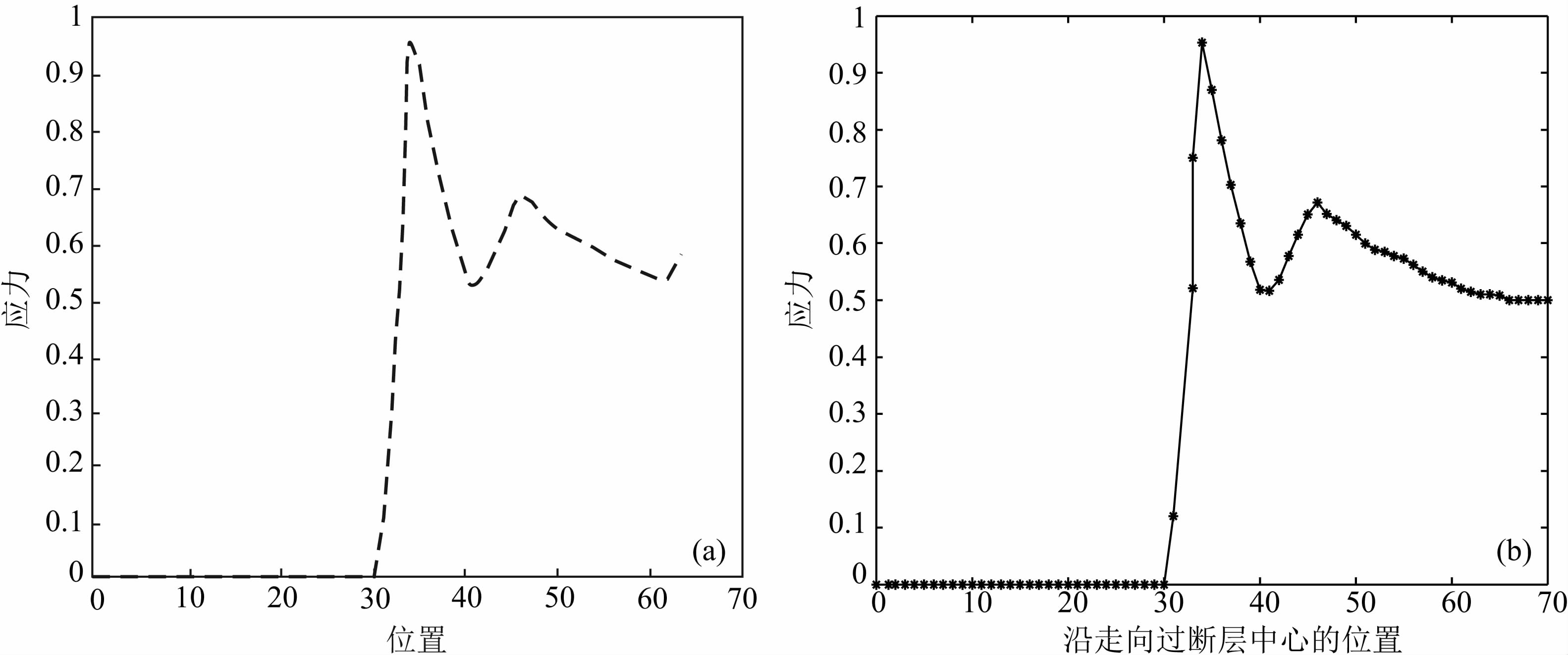 | 图 4 给定时刻矩形断层应力的空间分布对比 (a) Madariaga et al.(1998); (b) 本研究. Fig. 4 Comparison of stress distribution at a given time (a)Madariaga et al.(1998);(b)This study. |
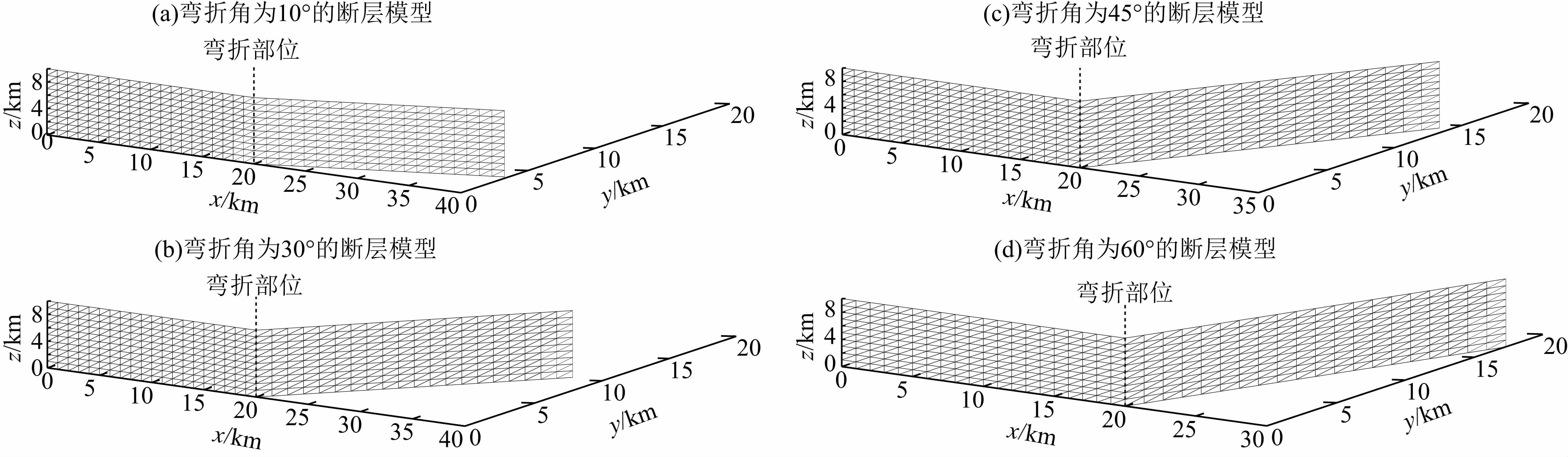 | 图 5 弯折角分别为10°、30°、45°和60°的弯曲断层模型 Fig. 5 Curved fault model with inclination angle of 10°、30°、45°and 60° |
对研究方法进行正确性检验后,我们考虑利用笛卡尔坐标系建立多种弯折断层模型来讨论其动力学破裂传播问题,主断层模型的左下角点设为坐标系的原点,整个断层系统位于无限均匀弹性介质中.
为研究断层破裂在经过弯折部位时的传播情况,本文根据不同的初始应力状态、不同的滑动弱化距离以及不同的弯折角度,进行了反复的数值实验,利用控制变量法来研究每一种因素对断层破裂越过弯折部位传播的影响,并对上述几种因素进行了不同的组合,形成多种模型,通过对比这些模型的模拟结果来探究这些因素的具体控制作用.
3.1 不同弯折角断层的破裂传播过程为检验断层弯折角度的影响,我们分别建立了平面断层模型和不同弯折角度的非平面断层模型进行比较,除了断层模型不同外,初始应力条件、滑动弱化距离等条件均相同.
1)模型1——弯折角为0°的平面断层
建立长度为20 km,宽为5 km、弯折角度为0°的三维垂直走滑平面断层模型,未考虑断层厚度,设置滑动沿走向方向.对断层模型进行离散化处理,网格大小为0.5 km×0.5 km,共划分400个三角形网格,时间步长取100.设定S波速度为3.0 km·s-1,纵横波速比为1.732,刚度模量为30 GPa.对于自发破裂传播问题,采用人为指定一个初始应力大于破裂强度的区域(即凹凸体),保证破裂首先在该区域发生,破裂在摩擦准则控制下自发扩展.本研究中给定破裂强度τp为1.0 MPa,凹凸体内的应力为1.2τp,凹凸体外的初始应力为0.8τp,剩余应力τr设定为0.
对于全空间平面断层而言(图 6),由于假定断层面上各处破裂强度是均匀的,因此,破裂在没有其他障碍体的情况下,破裂永不停止.实际模拟结果可以看到,有限矩形断层凹凸体内的初始应力高于破裂强度,使得破裂起始成核.随着破裂的传播,裂纹尖端的应力集中进一步触发周围各点,使得破裂沿走向方向以凹凸体为中心呈椭圆形向两侧对称扩展.在此模型设定的初始应力条件下,破裂速度前锋以亚剪切速度传播.t=50dt开始,切平面方向内的破裂前锋接触到断层面的上下边界(可以认为是障碍体)产生停止震相,停止震相继续向断层中心传播,t=80dt时,从断层上下边界反射回来的停止震相到达断层中心并相遇.随着应力的调整,滑动速率逐渐减小至零,在t=100dt时,破裂前锋到达断层的左右边界.
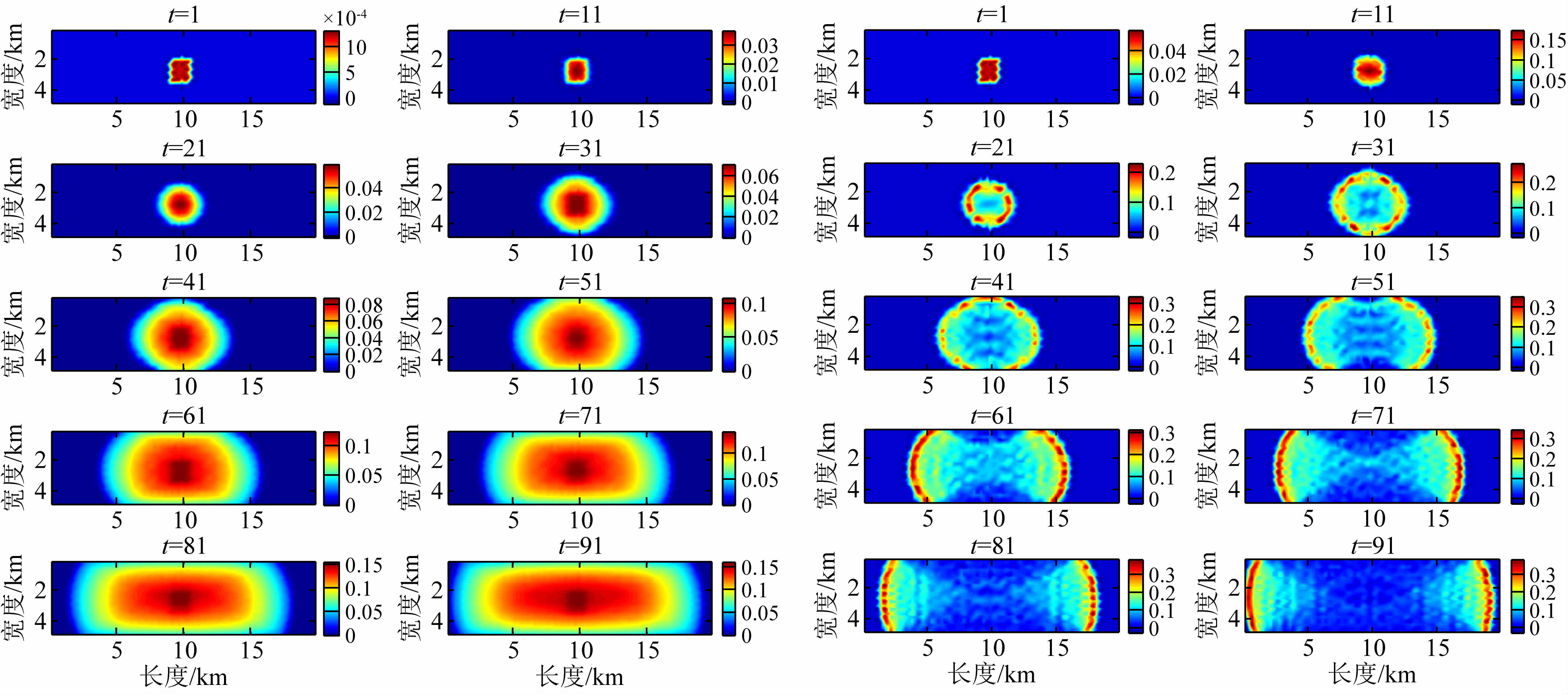 | 图 6 平面走滑断层自发破裂滑动量(左图,色标单位m)和滑动速率(右图,色标单位m·s-1)瞬像 Fig. 6 Snapshot of slip(left figure) and slip rate (right figure)of spontaneous rupture propagation of planar fault |
2)模型2——不同弯折角度的弯曲断层
建立长度为40 km,宽为10 km、弯折角度分别为10°、30°、45°和60°的三维非平面断层模型,未考虑断层厚度,设置滑动沿走向方向.对断层模型进行离散化处理,网格大小为1 km×1 km,时间步长取200.设定S波速度为3.0 km·s-1,纵横波速比为1.732,刚度模量为30 GPa.对于自发破裂传播问题,仍采用上述人为指定一个初始应力大于破裂强度的区域,保证破裂首先在该区域发生的方法,初始应力条件设置同上述平面断层.
非平面断层的数值模拟结果显示,对于弯折角度为10°的情况(图 7),弯折角较小,破裂的传播方式与平面断层的传播方式差别不大,沿断层走向以椭圆形式近对称向两侧扩展.成核后初始破裂阶段,滑动速率较小;随着破裂的不断扩展破裂前锋的滑动速率逐渐变大,在t=41 dt,破裂前锋就到达了20 km处的断层弯折部位,但由于弯折角度较小,而且成核区距离弯折部位很近,所以破裂越过弯折部位后继续传播.滑动速率逐渐增大,到t=141 dt时最大,之后破裂波前到达断层的右边界,由于反射回来的停止震相使得滑动速率逐渐减小为0,破裂停止.可见,即使在均匀介质中,凹凸体外的初始应力、破裂强度及Dc都相同的情况下,破裂传播过程中滑动速率也不是一个常量.
对于弯折角度为30°的情况(图 8),破裂的传播方式沿断层走向以椭圆形式近对称向两侧扩展.与弯折角为10°的相比,前者的破裂呈似对称传播.随着弯折角的增大,当弯折角为45°时(图 9),破裂越过弯折部位后,破裂的传播方式与平面断层的传播方式出现了明显差别,在弯折部位不再以近对称向两侧扩展,而是出现了明显的阻碍,破裂在传播至35 km左右停止.当弯折角为60°时(图 10),破裂传播的不对称特征更为清晰,大角度弯折对破裂传播的阻碍影响更为显著,破裂在传播至25 km左右即停止.
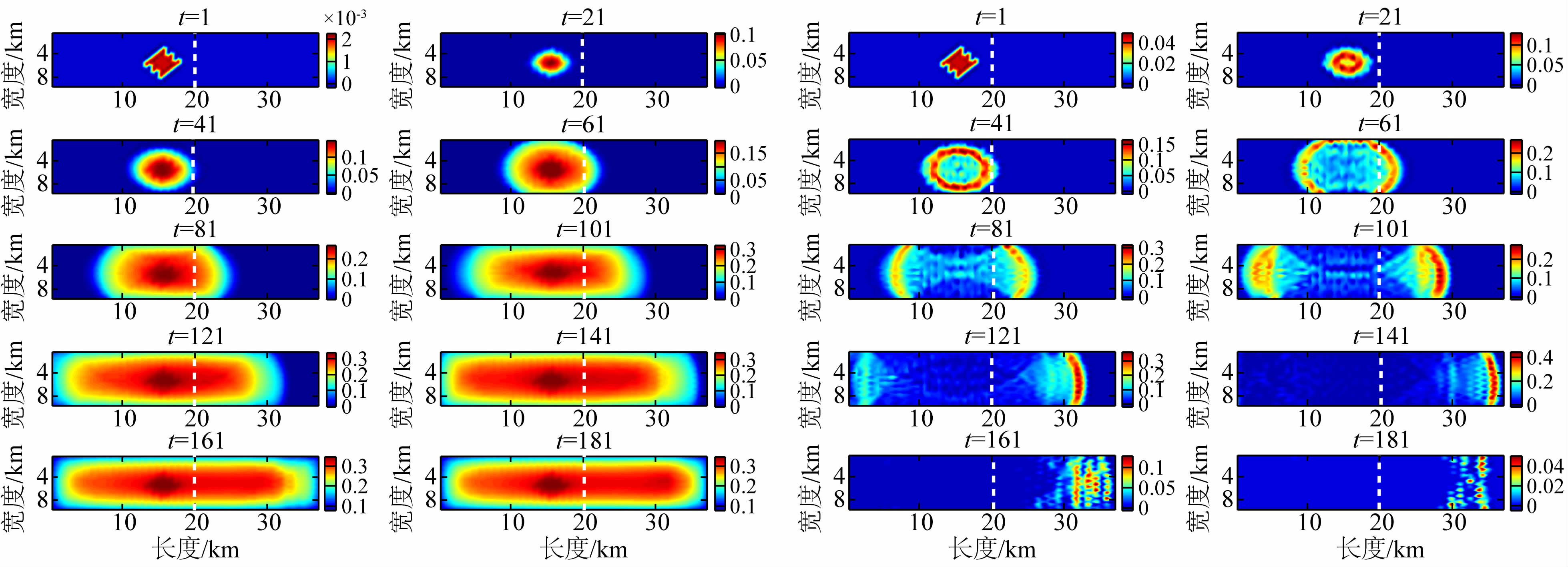 | 图 8 弯折角为30°的弯曲断层自发破裂滑动量(左图,色标单位m)和滑动速率(右图,色标单位m·s-1)瞬像 Fig. 8 Snapshot of slip (left figure) and slip rate (right figure)of spontaneous rupture propagation of 30°curved fault |
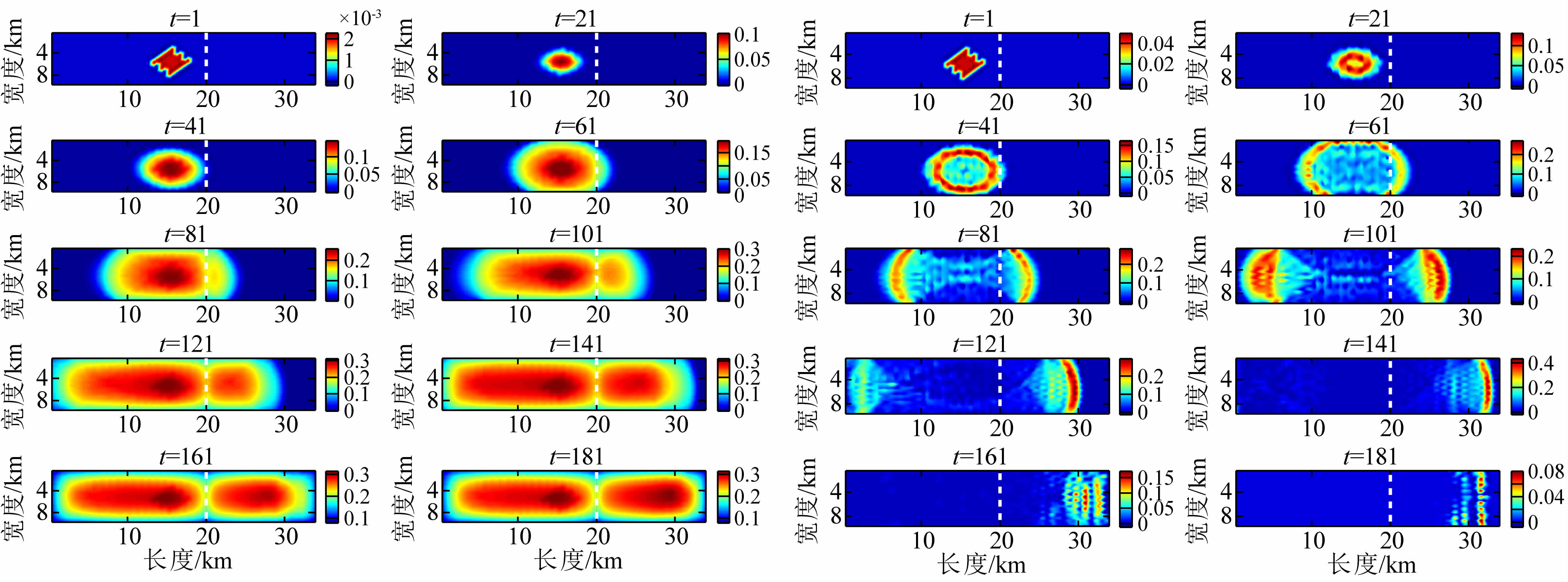 | 图 9 弯折角为45°的弯曲断层自发破裂滑动量(左图,色标单位m)和滑动速率(右图,色标单位m·s-1)瞬像 Fig. 9 Snapshot of slip (left figure) and slip rate (right figure)of spontaneous rupture propagation of 45°curved fault |
 | 图 10 弯折角为60°的弯曲断层自发破裂滑动量(左图,色标单位m)和滑动速率(右图,色标单位m·s-1)瞬像 Fig. 10 Snapshot of slip (left figure) and slip rate (right figure)of spontaneous rupture propagation of 60°curved fault |
通过上述不同弯折角非平面断层系统破裂行为的研究发现,破裂即使在均匀介质中沿着断层弯折之后也可能自动停止,强度或应力分布的不均匀性对于破裂的停止不是必须的,显示了局部的构造和断层的非平面结构在地震产生和破裂过程中的作用非常重要.对于弯折断层而言,较大的弯折对于破裂的传播行为有较大影响,可以视为障碍体.弯折之前破裂速度及断层面上的滑动分布均发生改变,这些主要是由于初始应力增加和应力降的非均匀性造成的,同时这又与断层几何形态引起的静态应力变化相关.薛霆虓等(2009)运用有限元法建立大尺度几何弯曲断层的二维模型,并利用接触单元技术模拟断层间的作用,探讨了具有一定几何形态断层对断层系统活动的影响.结果表明,几何弯曲的断层导致了应力的集中,而且在断层的地震事件中起到了抑制作用,但是也为孕育大震提供了条件.本研究还发现,随着弯折角的增大,在断层的弯折部位,滑动量表现出减小的特征,并且越过弯折之后,滑动量明显地分成了两个部分,这与Aochi(1999)对弯折断层的动力学破裂过程模拟结果也比较一致,当弯折角度较小时,滑动量的分布与平面断层差别不大,但随着弯折角的增大,障碍体对滑动量分布的影响更为显著.
3.2 破裂能否越过断层弯折部位的其他影响因素前述分析了由于弯折角度不同而导致断层破裂经过断层弯折部位时的不同情形,为了较全面地研究决定破裂越过断层弯折部位的主要控制因素,我们考察了初始应力场、摩擦本构关系、滑动弱化距离等对破裂传播过程的影响,模拟了十几种不同的模型,并进行了详细分析.本文主要研究断层弯折对破裂传播的影响,因此在这些模型中没有展示详细的破裂过程,表 1给出的10种典型情况,只显示断层弯折对破裂传播的阻止与否.
| | 表 1 不同初始应力场、凹凸体半径及滑动弱化距离对30°弯折断层破裂传播过程的影响 Table 1 Simulation results in different models in which initial stress fields,asperity radius and slip weakening distance are different |
① 比较模型1、2、3和模型4,我们可以看出,在其他条件相同时,滑动弱化距离Dc越小,断层破裂越容易穿越弯折部位,且滑动速率越快.对于模型1,破裂波前在t=20 dt时到达断层弯折部位,并越过弯折继续传播,t=80 dt时破裂前锋到达断层的左右边界,破裂停止.模型2,破裂波前在t=30 dt到达断层弯折部位后继续传播,t=130 dt破裂前锋到达断层的左右边界,破裂停止.模型3,破裂波前到达断层弯折部位的时间为t=50 dt,在t=200 dt破裂停止.模型4则因为滑动弱化距离较大,破裂在成核后不久(t=10 dt)就停止了.
② 比较模型2、5和模型6,可以看出,凹凸体内初始应力越高,破裂越容易越过弯折部位继续传播,且传播速度越快.
③ 比较模型2、7和模型8,可以看出,凹凸体外初始应力越高,破裂越容易越过弯折部位继续传播,且传播速度越快.
④ 比较模型2、9和模型10,可以看出,当凹凸体半径越大,破裂越容易越过断层弯折部位继续传播,反之破裂不传播或在很短时间内破裂即停止.
通过上述模型的对比,可以对凹凸体内、外的初始应力Tasp、Te,凹凸体半径Rasp和临界滑动弱化距离Dc对破裂的影响给出一些定性的认识.Tasp、Te、Rasp越大,或Dc越小,破裂越容易发生,也容易越过断层的弯折部位继续传播;反之,破裂较难越过弯折部位,甚至仅在成核后不久破裂即停止.可见,大地震破裂传播时间的长短与上述各因素均存在重要联系.当凹凸体半径越大,即震源尺度越大,破裂传播的时间相对较长;凹凸体(震源体)内的初始应力超过屈服应力强度越高,破裂越容易发生,并向外传播.
4 讨论与结论本文利用边界积分方程方法对弯折断层的破裂传播情况进行了分析,作为三维非平面断层数值模拟的例子,我们研究了均匀弹性介质中弯折断层的简单情况.本研究的模拟结果表明,断层弯折角对于破裂传播过程或是减速或是停止作用,而且由非平面断层几何形态伴随的动态应力改变引起的扰动不足以使得破裂传播停止.文中给出了决定破裂是否能越过弯折部位继续传播的控制因素,凹凸体内、外的初始应力Tasp、Te及凹凸体半径Rasp越大或临界滑动弱化距离Dc越小,破裂越容易发生,越容易越过断层的弯折部位;反之破裂难以发生,或在成核后不久就停止.实际的断层动力学破裂传播过程是非常复杂的,不单单受复杂断层几何形态的影响,复杂的介质、非均匀应力场分布及自由表面的存在等都是重要影响因素.本研究使用的边界积分方程方法有其局限性,仅能考虑均匀介质.且在本研究中我们也仅研究了全空间的情况,没有将自由表面的影响考虑在内,所以后续的研究会尝试其他数值模拟方法,探讨半空间非均匀介质中复杂断层模型的破裂传播问题,希望将地震孕育与震源破裂过程进行结合,使获得的破裂模型更符合实际.
致谢 十分感谢Hideo Aochi老师和Taku Tada老师的耐心指导,并感谢审稿老师所提出的问题以及对文章修改所给予的建设性意见.| [1] | Aagaard B T, Heaton T H, Hall J F. 2001. Dynamic earthquake ruptures in the presence of lithostatic normal stresses:implications for friction models and heat production. Bull. Seism. Soc. Am., 91(6):1765-1796. |
| [2] | Aki K, Richards P G. 1980. Quantitative Seismology Theory and Methods, Vol. I, W. H. San Francisco, California:Freeman and Company. |
| [3] | Andrews D J. 1976a. Rupture propagation with finite stress in antiplane strain. J. Geophys. Res., 81(20):3575-3582. |
| [4] | Andrews D J. 1976b. Rupture velocity of plane strain shear cracks. J. Geophys. Res., 81(32):5679-5687. |
| [5] | Aochi H. 1999. Theoretical studies on dynamic rupture propagation along a 3D non-planar fault system[Ph. D. Thesis]. Tokyo:University of Tokyo. |
| [6] | Aochi H, Fukuyama E, Matsu'ura M. 2000a. Spontaneous rupture propagation on a non-planar fault in 3-D elastic medium. Pure Appl. Geophys., 157(11-12):2003-2027. |
| [7] | Aochi H, Fukuyama E, Matsu'ura M. 2000b. Selectivity of spontaneous rupture propagation on a branched fault. Geophys. Res. Lett., 27(22):3635-3638. |
| [8] | Aochi H, Fukuyama E. 2002. Three-dimensional nonplanar simulation of the 1992 Landers earthquake. J. Geophys. Res., 107(B2):ESE 4-1-ESE 4-12. |
| [9] | Chen X F, Aki K. 1996. An effective approach to determine the dynamic source parameters. Pure Appl. Geophys., 146(3):689-696. |
| [10] | Cochard A, Madariga R. 1994. Dynamic faulting under rate-dependent friction. Pure Appl. Geophys., 142(3-4):419-445. |
| [11] | Das S, Aki K. 1977. A numerical study of two-dimensional spontaneous rupture propagation. Geophys. J. Int., 50(3):643-668. |
| [12] | Dieterich J H. 1979. Modeling of rock friction:1. Experimental results and constitutive equations. J. Geophys. Res., 84(B5):2161-2168. |
| [13] | Fukuyama E, Madariaga R. 1995. Integral equation method for plane crack with arbitrary shape in 3D elastic medium. Bull. Seism. Soc. Am., 85(2):614-628. |
| [14] | Fukuyama E, Madariaga R. 1998. Rupture dynamics of a planar fault in a 3D elastic medium:rate-and slip-weakening friction. Bull. Seism. Soc. Am., 88(1):1-17. |
| [15] | Harris R A, Archuleta R J, Day S M. 1991. Fault steps and the dynamic rupture process:2-D numerical simulations of a spontaneously propagating shear fracture. Geophys. Res. Lett., 18(5):893-896. |
| [16] | Ida Y. 1972. Cohesive force across the tip of a longitudinal-shear crack and Griffith's specific surface energy. J. Geophys. Res., 77(20):3796-3805. |
| [17] | Kato N, Satoh T, Lei X L, et al. 1999. Effect of fault bend on the rupture propagation process of stick-slip. Tectonophysics, 310(1-4):81-99. |
| [18] | Ma J.1987. Introduction of Tectonophysics. Beijing:Seismological Press |
| [19] | Ma J, Ma S L, Liu L Q, et al. 1996. Physical field evolution and instability properties of fault geometry. Acta Seismologica Sinica(in Chinese), 18(2):200-207. |
| [20] | Madariaga R, Olsen K, Archuleta R. 1998. Modeling dynamic rupture in a 3D earthquake fault model. Bull. Seism. Soc. Am., 88(5):1182-1197. |
| [21] | Ohnaka M. 1992. Earthquake source nucleation:a physical model for short-term precursors. Tectonophysics, 211(1-4):149-178. |
| [22] | Scholz C H. 1990. The Mechanics of Earthquakes and Faulting. New York:Cambridge University Press, 439. |
| [23] | Scholz C H. 1998. Earthquake and friction laws. Nature,391:37-42. |
| [24] | Shin T C, Teng T L. 2001. An overview of the 1999 Chi-Chi, Taiwan, earthquake. Bull. Seism. Soc. Am., 91(5):895-913. |
| [25] | Sibson R H. 1986. Rupture interaction with fault jogs.//Earthquake Source Mechanics, Geophys. Monogr. Ser. 37.Washington D C:AGU, 157-167. |
| [26] | Tada T, Fukuyama E, Madariaga R. 2000. Non-hypersingular boundary integral equations for 3-D non-planar crack dynamics. Computational Mechanics, 25(6):613-626. |
| [27] | Tada T, Madariaga R. 2001.Dynamic modelling of the flat 2-D crack by a semi-analytic BIEM scheme. Int. J. Numer. Meth. Engng., 50:227-251. |
| [28] | Tada T. 2006. Stress Green's functions for a constant slip rate on a triangular fault. Geophysical Journal International, 164(3):653-669. |
| [29] | Tada T. 2009. Boundary integral equation method for earthquake rupture dynamics.//Fault-zone Properties and Earthquake Rupture Dynamics. International Geophysics, 94:217-267. |
| [30] | Xue T X, Fu R S, Lin F. 2009. The simulation of activities of bend fault. Chinese J. Geophys.(in Chinese), 52(10):2509-2518, doi:10.3969/j.issn.0001-5733.2009.10.009. |
| [31] | Zhang H M. 2004. Theoretical study on the spontaneous propagation of 3-D seismic rupture on a planar fault in half space[Ph. D. thesis](in Chinese). Beijing:Peking University. |
| [32] | Zhang L F, Yao Y S. 2013. Review on numerical simulation of dynamic rupture process of earthquake source. Acta Seismologica Sinica(in Chinese), 35(4):604-615. |
| [33] | Zhang W B, Iwata T, Irikura K. 2006. Dynamic simulation of a dipping fault using a three-dimensional finite difference method with nonuniform grid spacing. J. Geophys. Res., 111(B5):B05301. |
| [34] | Zhang Z G, Zhang W, Chen X F. 2014. Three-dimensional curved grid finite-difference modelling for non-planar rupture dynamics. Geophys. J. Int., 199(2):860-879. |
| [35] | 马瑾.1987.构造物理学概论.北京:地震出版社. |
| [36] | 马瑾, 马胜利, 刘力强等. 1996. 断层几何结构与物理场的演化及失稳特征. 地震学报, 18(2):200-206. |
| [37] | 薛霆虓, 傅容珊, 林峰. 2009. 几何弯曲断层活动性的模拟. 地球物理学报, 52(10):2509-2518, doi:10.3969/j.issn.0001-5733.2009.10.009. |
| [38] | 张海明. 2004. 半无限空间中平面断层的三维自发破裂传播的理论研究[博士论文]. 北京:北京大学. |
| [39] | 张丽芬, 姚运生. 2013. 震源动力学破裂过程数值模拟研究. 地震学报, 35(4):604-615. |
 2016, Vol. 59
2016, Vol. 59

