近年来,面波多道分析技术(Song et al.,1989;Park et al.,1999;Xia et al.,1999)广泛应用于探测横波速度、动力学特征等环境与工程地球物理领域.该技术利用谱分析方法提取多道面波记录中的频散曲线,结合面波频散曲线的正演计算,继而反演得到地表横波速度结构.面波频散曲线的正演以弹性层状介质理论为基础,然而实际近地表物质具有黏弹性,研究面波在层状黏弹性介质中的传播特征,将为近地表面波勘探提供有益帮助.
黏弹性介质面波传播特征的研究分两个方面.一方面是通过面波波场正演模拟,在频率-速度域分析其能量谱特征;另一方面是通过求解面波频散方程,分析其频散和衰减特征.Zhang等(2011)利用伪谱法模拟黏弹性介质中Rayleigh波波场,通过对比频散能量谱特征表明,由于黏弹性介质的影响,相比弹性介质,Rayleigh波频散曲线存在明显变化.高静怀等(2012)使用有限差分法模拟复杂黏弹性介质中的Rayleigh波,指出黏弹性介质与弹性介质中面波的频散特性差异显著,强吸收情况下高阶面波能量所占比重较大.Lai和Rix(2002)基于围道积分和Cauchy留数定理,发展了一种求解Rayleigh波频散方程的方法,但当介质含低速层时,利用该方法求解会出现漏根.Cao和Dong(2010)结合Muller法和二维Newton法实现了层状黏弹性介质中Love波频散方程的快速求解.
英文文献中将面波相邻两条频散曲线的彼此靠近现象称为“osculation”现象,在“osculation”点,相邻两条频散曲线的相速度差达到最小.当地表下存在比较强的波阻抗差异或含有低速夹层时,Rayleigh波频散曲线通常会发生“osculation”现象(Zhang and Lu,2003;De Nil,2005;Levshin and Panza,2006;Tuan et al.,2011;Boaga et al.,2013).由此可知,频散曲线“交叉”现象为“osculation”现象的特例,即相邻两条频散曲线彼此交叉,在“交叉”点,相速度差为零.当地层含低速层时,实际提取到的Rayleigh波频散曲线经常会发生“之”字形回折(张碧星等,2000,2002;鲁来玉等,2006),而这种现象与频散曲线“交叉”现象密切相关.杨天春等(2004)通过计算表明某些情况下看似相交的频散曲线实际上不相交.凡友华等(2007)根据频散方程的高频近似分解公式定义了Rayleigh波的4种基本模式,即R模、S模、R型周期模和S型周期模.刘雪峰等(2009),Liu和Fan(2012)提出判定频散曲线相交与否的方法,即如果在加密搜根前后相同频率的两个点之间的相速度差在不断降低,就说明两条频散曲线相交,并基于“交叉”点附近的本征位移曲线特征,分析R模和S型周期模之间的耦合现象.本文利用Muller法(Muller,1956;Cao and Dong,2010;张凯,2011)求解层状黏弹性介质中Rayleigh波频散方程,根据Rayleigh波衰减曲线的连续性和本征位移曲线特征,分析其频散曲线“交叉”现象.
2 黏弹性介质地震波传播理论黏弹性介质对地震波的影响有两个方面(Zhou,2009):(1)振幅衰减--地震波能量的损失致使其振幅随传播距离而衰减;(2)速度频散--应力和应变的松弛致使地震波速度随频率而改变.对于均匀介质,一般用一个无量纲的参数Q衡量平面波振幅衰减和速度频散,Q即为品质因子,它表示一个周期内地震波所损耗的能量与原有能量的比值:

黏弹性均匀介质中平面波传播在频率域中表示如下:


实验数据表明,在地震勘探范围内(0.001~100 Hz)Q值几乎为恒定的(Hardin and Drnevich,1972;Liu et al.,1976;Shibuya et al.,1995).对于黏弹性介质,地震波复速度可表示为(Lai and Rix,2002):
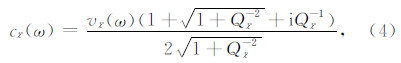
根据式(3)和(4)可得:
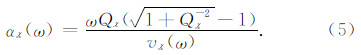
由于物理介质的传输响应具有因果关系,复速度的实部和虚部必须满足Kramers-Krönig频散关系,由此可以得到两者的一个显式关系(Aki and Richards,2002):
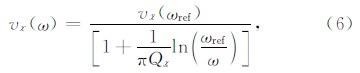
从式(4)和(6)可以看出,复速度由参数v(ωref)和Q唯一确定.当Q→∞,衰减系数α→0,黏弹性介质就会成为弹性介质.因此,黏弹性介质理论是弹性介质理论的一种推广.
3 Muller法黏弹性水平层状介质中的Rayleigh波频散方程跟复波数k、圆频率ω以及四组模型参数--横波复速度cS、纵波复速度cP、密度ρ和地层厚度h有关,可表示如下:
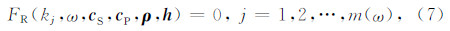
函数FR为一高度非线性函数,并不能推导出解析表达式,只能通过数值计算得出.对于弹性介质,速度cS、cP为实数,给定某个ω值,由k到函数FR的映射为实数域到实数域(即R→R).但对于黏弹性介质,速度cS、cP为复数,给定某个ω值,由k到函数FR的映射为复数域到复数域(即C→C).Buchen和Ben-Hador(1996)总结各种计算函数FR的方法,提出了一种高效的快速三角矩阵算法.该算法类似快速Schwab-Knopoff法(Schwab and Knopoff,1972),所不同的是采用三角矩阵形式来计算矩阵行列式.这种算法由一系列跟层参数有关的1×6的单行矩阵组成,令第1层矩阵X1=μ12[2t1,-t12,0,0,-4,2t1],其中μ1=ρ1cS12,t1=2-(ω/k)2/ cS12,通过简单的线性迭代关系依次求出X2,X3,…,Xn,则函数FR=Xn(2)+SnXn(3)-Rn(Xn(4)+SnXn(5)),其中Sn和Rn是跟第n层参数有关的常数.由于迭代关系为线性的,该算法适合推广到复数域,当模型中含有低速层时,能有效地求出Rayleigh波所有模式.本文基于快速三角矩阵算法,利用Muller法求取层状黏弹性介质中Rayleigh波频散方程的复根,再根据式(3)确定Rayleigh波频散和衰减曲线.
Muller法是一种迭代方法,给定三个初始点(k0,FR(k0))、(k1,FR(k1))和(k2,FR(k2)),构造一个抛物线经过这三点,用抛物线函数的零点作为方程根的近似值.Muller法的迭代公式为(Cao and Dong,2010):
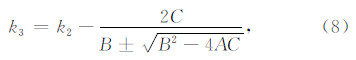

公式(8)中正负符号的选择应使得分母的模最大.
当精度达到要求时,迭代停止.图 1表示利用Muller法求解黏弹性介质Rayleigh波频散和衰减曲线流程示意图.分为以下几步:
 | 图 1 Muller法计算Rayleigh波频散和衰减曲线流程示意图 Fig. 1 Flow chart of calculating Rayleigh wave dispersion and attenuation curves by Muller′s method |
① 设最大迭代次数为M(30~50),n=0,TOL为精度值(10-12),从最小圆频率ωmin开始,令ω=ωmin;
② 根据Rayleigh波物理性质,确定其波数kR实部的范围[kRmin,kRmax];
③等间距分割区间[kRmin,kRmax],分割点组成数组Xj,j = 1,2,…,NUM,X1=kRmin,XNUM=kRmax,j的初始值为1;
④ 令k0=Xj+δi,k1=Xj+1+δi,k2=Xj+2+δi,代入式(8)进行迭代;
⑤ 如果迭代次数小于M且∣k3∣
⑥ 若j≤NUM-2,进入步骤④;若j>NUM-2,循环结束,得到圆频率ω下所有的复根k,判断所有根的实部real(k)是否在区间[kRmin,kRmax]内,对落在区间范围内的所有根按实部大小进行排序后,根据式(3)计算Rayleigh波相速度和衰减系数;
⑦ 令n=n+1,ω=ωmin+nΔω,进入步骤②,进行下一个频率的计算,直到所有给定的频率计算完毕.
假定第n层半空间的横波速度vS大于其他层的横波速度,Rayleigh波基阶模式的相速度的变化范围介于最大和最小的VR之间(VR表示把每层当作均匀半空间对应的Rayleigh波相速度),高阶模式的相速度介于最大和最小的vS之间.根据弹性和黏弹性介质的对应原理(Bland ,1960),黏弹性介质中Rayleigh波相速度存在的物理范围与弹性情况类似,但由于体波速度随频率而变,所以每次进入下一个频率点计算时都要执行步骤②,重新确定波数范围.步骤④中δ代表衰减系数的初值,随着频率增高,频散方程的根受模型第1层的影响变大,为了尽量使初值接近频散方程的根,本文将第1层Rayleigh波复波数的虚部赋值给δ.将第1层当作半空间,则Rayleigh波复波数满足方程:
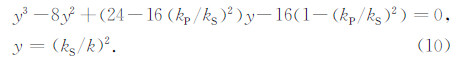
三次方程(10)存在三个根,分别为(Borcherdt,1974):
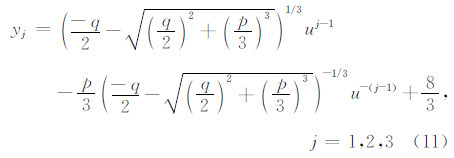
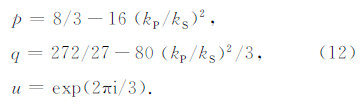
三个根中,有且仅有一个根满足Rayleigh波的物理条件(Romeo,2001).
为了验证算法的正确性,我们利用Muller法计算黏弹性均匀半空间(VP=1000 m·s-1,QP=30,VS=600 m·s-1,QS=15)Rayleigh波的相速度与衰减系数,并与式(11)解析解进行对比,如图 2所示,两者一致.
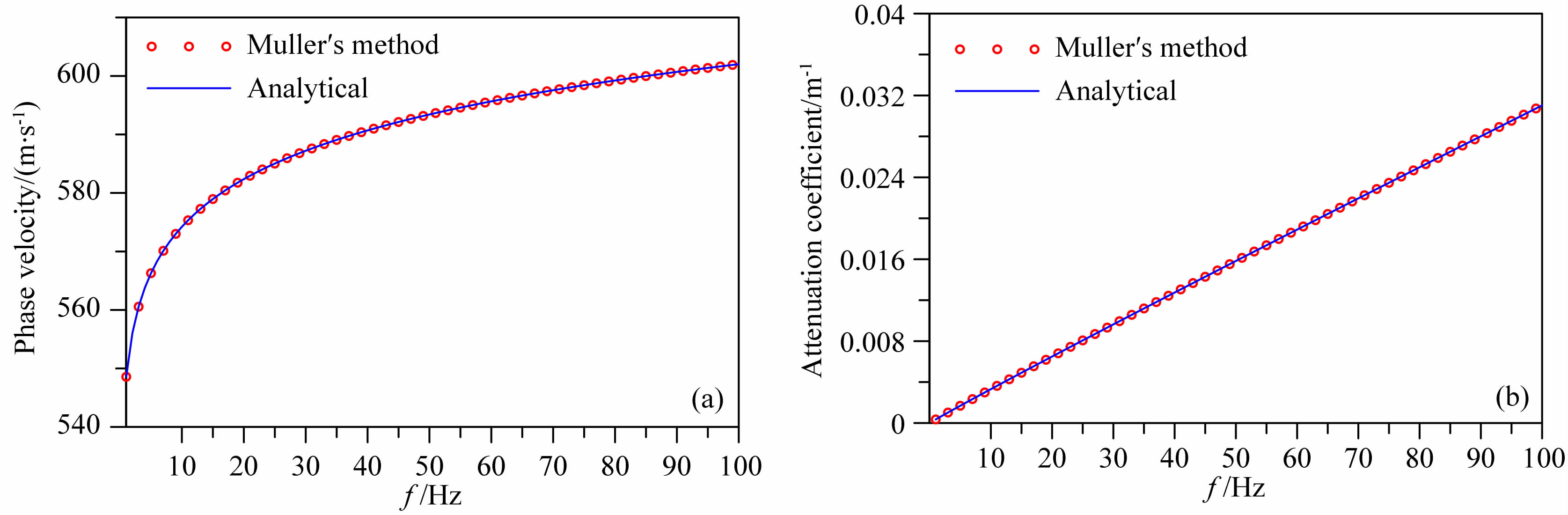 | 图 2 黏弹性半空间中Muller法计算结果与理论值的对比:(a)相速度,(b)衰减系数 Fig. 2 Comparison of phase velocities (a) and attenuation coefficients (b) between analytical solutions and numerical results by Muller′s method in a viscoelastic half-space |
为简单起见,本节中我们将层状模型设为二层,并假定地震波速度v和品质因子Q在所研究的频率范围内是恒定的.由黏弹性介质理论可知该假定并不失一般性.参考Levshin和Panza(2006)给出的弹性二层模型,表 1给出四种二层模型,四种模型中仅品质因子取值不同.该地质模型代表基岩上覆盖有一层第四系松散沉积层,两者波阻抗差异较大,基岩的波阻抗为松散沉积层波阻抗的3倍.根据岩石的物理性质,松散沉积物对地震波的衰减强于基岩对地震波的衰减,即松散沉积物的Q值小于基岩的Q值.根据黏弹性介质理论和岩石实验测试表明,岩石对横波的衰减强于对纵波的衰减,即岩石中横波的Q值小于纵波的Q值.因此表 1给出的岩石衰减特征并不失一般性,模型Ⅰ品质因子很大,可近似看作弹性介质,模型Ⅱ到模型Ⅳ品质因子依次减小,即表示黏弹性介质对地震波能量的损耗越来越强.
| | 表 1 二层模型的地层参数 Table 1 Two-layer model parameters |
一般地,层状黏弹性介质模型中Rayleigh波频散和衰减曲线都是连续曲线,我们据此判断频散曲线是否相交.利用Muller法分别得到表 1中四种模型Rayleigh波的频散和衰减曲线,如图 3-6所示.由Muller法求解出频散方程的根是按照相速度由小到大排列的,第1组根对应基阶模式,第2组根对应第一高阶模式,依次类推.选取其中的第1和第2组根进行分析.由Rayleigh波频散曲线连续的性质可知,频散曲线图 3a和4a中曲线A和曲线A′组成一条连续曲线,曲线B和曲线B′组成另一条连续曲线,即曲线A和曲线A′为同一模式,曲线B和曲线B′为同一模式.由第2组根所组成的频散曲线AA′与第1组根所组成的频散曲线BB′彼此并没有相交.因此,近似弹性介质模型Ⅰ和黏弹性模型Ⅱ中并没有发生频散曲线“交叉”现象.由此可知在相应的衰减曲线图 3b和4b中,曲线AA′为同一模式,曲线BB′为同一模式.由Rayleigh波衰减曲线连续的性质可以断定,衰减曲线AA′和BB′彼此相交,衰减曲线的交叉点即为“osculation”点.“osculation”现象产生的主要原因是因为介质中同时存在几种不同类型的导波或者相同的导波中存在弱耦合波场(Levshin and Panza,2006).在“osculation”点附近,Rayleigh波相邻模式对应的垂直分量的振幅急剧减小(Boaga et al.,2013).由图 3a和4a可见,相邻模式的Rayleigh波频散曲线在“osculation”点交换彼此的梯度(De Nil,2005).
 | 图 3 模型Ⅰ中Rayleigh波频散(a)和衰减曲线(b) Fig. 3 Dispersion (a) and attenuation (b) curves of Rayleigh wave in model Ⅰ |
 | 图 4 模型Ⅱ中Rayleigh波频散(a)和衰减曲线(b) Fig. 4Dispersion (a) and attenuation (b) curves of Rayleigh wave in model Ⅱ |
 | 图 5 模型Ⅲ中Rayleigh波频散(a)和衰减曲线(b) Fig. 5 Dispersion (a) and attenuation (b) curves of Rayleigh wave in model Ⅲ |
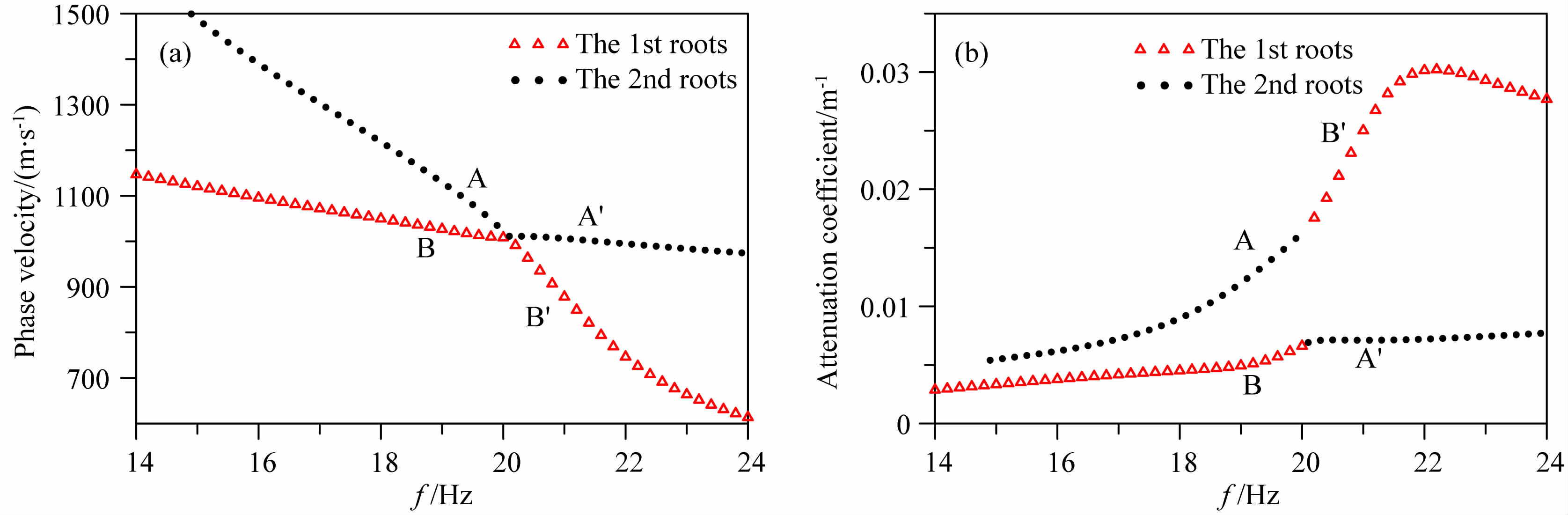 | 图 6 模型Ⅳ中Rayleigh波频散(a)和衰减曲线(b) Fig. 6 Dispersion (a) and attenuation (b) curves of Rayleigh wave in model Ⅳ |
通过依次减小Q值,得到图 5和6所示Rayleigh波的频散和衰减曲线.由Rayleigh波衰减曲线连续的性质可知,衰减曲线图 5b和6b中曲线A和曲线B′组成一条连续曲线,曲线B和曲线A′组成另一条连续曲线,即曲线A和曲线B′为同一模式,曲线B和曲线A′为同一模式.由此可知,在相应的频散曲线图 5a和6a中,曲线AB′为同一模式,曲线BA′为同一模式.由Rayleigh波频散曲线连续的性质可以断定,频散曲线AB′与BA′彼此相交.因此,黏弹性介质模型Ⅲ和Ⅳ中存在频散曲线“交叉”现象.另外,对比图 5b和6b,随着Q值越来越小,衰减曲线AB′与BA′在“交叉”点对应的频率处彼此分离得越来越远.
我们利用广义反射-透射系数法计算面波频散曲线上每一点对应的本征位移曲线来分析Rayleigh波的波动特性(Chen,1993).细分频率后可知,图 3中衰减曲线和图 6中频散曲线的交点均介于19.8 Hz和20.1 Hz之间.图 7和8分别给出模型Ⅰ和Ⅳ频散曲线中19.8 Hz和20.1 Hz的本征位移随深度的变化曲线,其中本征位移为垂直和水平分量绝对值分别与对应的垂直分量绝对值的比值.对于近弹性模型Ⅰ,图 3中曲线B和曲线B′为同一模式,对应的图 7a与7b中本征位移波动特性相似,而曲线A和曲线A′为同一模式,对应的图 7c与7d中本征位移波动特性相似.对于黏弹性模型Ⅳ,图 6中曲线B和曲线A′为同一模式,对应的图 8a与8d中本征位移波动特性相似,而曲线A和曲线B′为同一模式,对应的图 8c与8b中本征位移波动特性相似.对比图 7和8可知,与弹性介质相比,黏弹性介质中Rayleigh波的波动特性存在明显差异.
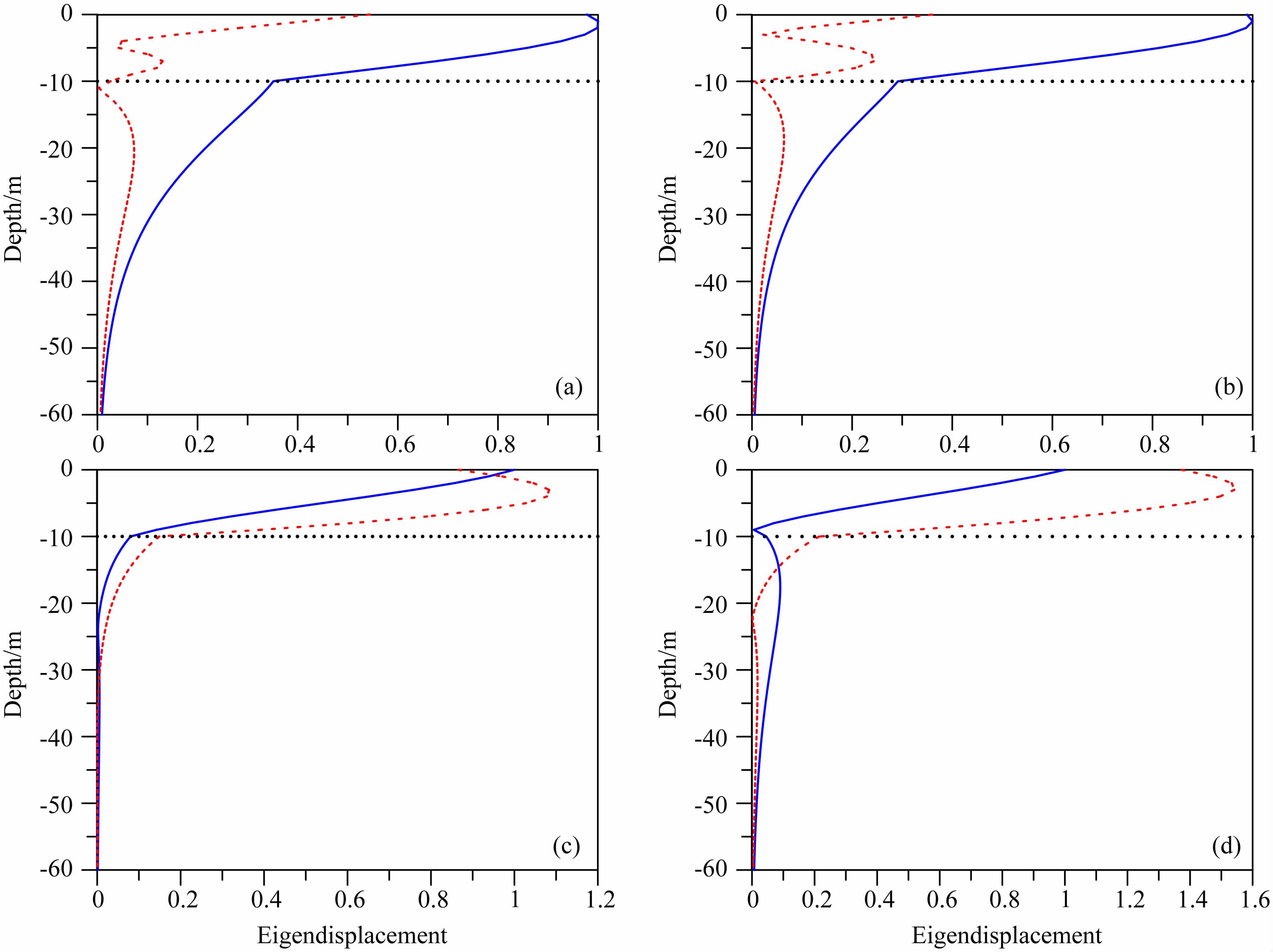 | 图 7 图3中归一化本征位移的绝对值随深度变化曲线 (a) 对应19.8 Hz处第一个根; (b) 对应20.1 Hz处第一个根; (c) 对应19.8 Hz处第二个根; (d) 对应20.1 Hz处第二个根. 图中实线代表本征位移垂直分量,虚线代表本征位移水平分量,点线代表第1层界面深度. Fig. 7 Normalized absolute values of eigendisplacements in Fig.3 (a) First root at 19.8 Hz; (b) First root at 20.1 Hz; (c) Second root at 19.8 Hz; (d) Second root at 20.1 Hz. Solid line is vertical component. Dashed line is horizontal component. Dotted line shows interface of two layers. |
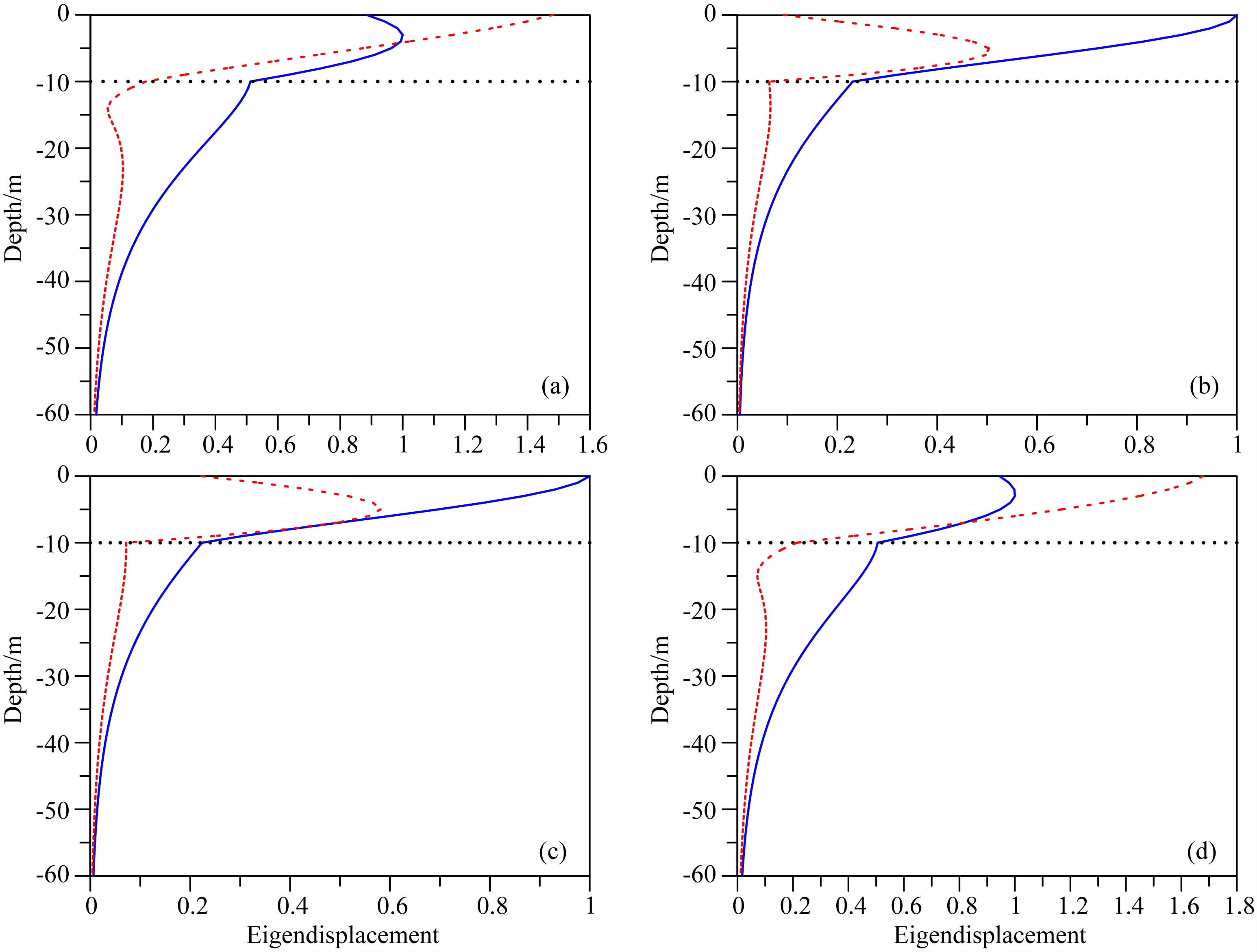 | 图 8 图 6中归一化本征位移的绝对值随深度变化曲线,其他说明同图 7 Fig. 8 Normalized absolute value of eigendisplacements in Fig. 6. Other explanations are same as Fig. 7 |
在对应的弹性模型中,由理论地震记录生成的频散能量谱可知(Ivanov et al.,2013),当频率小于“osculation”频率时,大部分能量集中在曲线A(第一高阶),而当频率大于“osculation”频率时,大部分能量停留在曲线B′(基阶).实际由地震记录提取的频散曲线为AB′,将AB′当作基阶(曲线BB′)进行反演会造成对基岩横波速度的过高估计.对于衰减比较强的黏弹性模型,实际提取的频散曲线AB′成为同一模式,对曲线AB′进行反演将会得到正确的横波速度结构.值得注意的是,实际资料中提取的频散曲线并不能判定“osculation”频率,这需要结合多分量地震数据,分析Rayleigh波极化椭圆率的变化特征与“osculation”频率的关系,据此判定是否产生“osculation”现象以及估测“osculation”频率(Boaga et al.,2013).
5 结论与讨论本文利用Muller法计算层状黏弹性介质Rayleigh波频散方程,通过对二层模型中Rayleigh波频散和衰减曲线连续性分析,并结合本征位移曲线特征的研究,结果表明与弹性介质相比,黏弹性介质中Rayleigh波的波动特性存在明显差异,随着Q值越来越小,即介质对地震波的损耗越来越强,将导致Rayleigh波频散曲线发生“交叉”现象.
岩石的Q值能够为岩性、物性及岩石饱和度等研究提供信息,实际介质中,尤其近地表介质,品质因子Q值可能会非常小,黏弹性介质对Rayleigh波波动特性的影响将更加明显.因此,有必要进一步开展黏弹性介质中利用面波衰减信息反演介质品质因子的研究.另外,由于层状黏弹性介质中频散方程的根为复数,我们可以在XYZ三维坐标系统中考虑复波数随频率的变化曲线,令复波数的实部为Y轴,复波数的虚部为Z轴,自变量频率为X轴.则求解的每一个复根都对应三维坐标空间中一个点,Rayleigh波频散和衰减曲线合并为三维坐标系统中的一条连续光滑曲线.在这种意义下四种模型中相邻两条三维曲线并没有彼此相交,但对于比较小的Q值模型Ⅲ和Ⅳ来说,相邻两条三维曲线在“osculation”点发生彼此交换现象.
| [1] | Aki K, Richards P G. 2002. Quantitative Seismology, 2nd ed. California:University Science Books(First edition published in 1980). |
| [2] | Bland D R. 1960. Theory of Linear Viscoelasticity. New York:Pergamon Press. |
| [3] | Boaga J, Cassiani G, Strobbia C L, et al. 2013. Mode misidentification in Rayleigh waves:Ellipticity as a cause and a cure. Geophysics, 78(4):EN17-EN28. |
| [4] | Borcherdt R D. 1974. Rayleigh-type surface wave on a linear viscoelastic half-space. The Journal of the Acoustical Society of America, 55(1):13-15. |
| [5] | Buchen P W, Ben-Hador R. 1996. Free-mode surface-wave computations. Geophys. J. Int., 124(3):869-887. |
| [6] | Cao Z L, Dong H F. 2010. Attenuation dispersion of Love waves in a viscoelastic multilayered half-space.//80th Annual Meeting of the Society of Exploration Geophysicists. Denver, Colorado:SEG, 2998-3002. |
| [7] | Chen X F. 1993. A systematic and efficient method of computing normal modes for multilayered half-space. Geophys. J. Int., 115(2):391-409. |
| [8] | De Nil D. 2005. Characteristics of surface waves in media with significant vertical variations in Elasto-dynamic properties. J. Environ. Eng. Geophys., 10(3):263-274. |
| [9] | Fan Y H, Chen X F, Liu X F, et al. 2007. Approximate decomposition of the dispersion equation at high frequencies and the number of multimodes for Rayleigh waves. Chinese J. Geophys. (in Chinese), 50(1):233-239. |
| [10] | Gao J H, He Y Y, Ma Y C. 2012. Comparison of the Rayleigh wave in elastic and viscoelastic media. Chinese J. Geophys.(in Chinese), 55(1):207-218, doi:10.6038/j.issn.0001-5733.2012.01.020. |
| [11] | Hardin B O, Drnevich V P. 1972. Shear modulus and damping in soil:measurement and parameter effects. ASCE Soil Mechanics and Foundation Division Journal, 98(6):603-624. |
| [12] | Ivanov J, Schwenk J T, Miller R D, et al. 2013. Dispersion-curve imaging nonuniqueness studies from multi-channel analysis of surface waves(MASW) using synthetic seismic data.//83th Annual Meeting of the Society of Exploration Geophysicists. Houston, Texas:SEG, 1794-1800. |
| [13] | Lai C G, Rix G J. 2002. Solution of the Rayleigh eigenproblem in viscoelastic media. Bulletin of the Seismological Society of America, 92(6):2297-2309. |
| [14] | Levshin A L, Panza G F. 2006. Caveats in multi-modal inversion of seismic surface wavefields. Pure and Applied Geophysics, 163(7):1215-1233. |
| [15] | Liu H P, Anderson D L, Kanamori H. 1976. Velocity dispersion due to Anelasticity:implications for seismology and mantle composition. Geophysical Journal International, 47(1):41-58. |
| [16] | Liu X F, Fan Y H, Chen X F. 2009. Research on the cross of the dispersion curves of Rayleigh waves and multi-modes coupling phenomenon. Chinese J. Geophys.(in Chinese), 52(9):2302-2309, doi:10.3969/j.issn.0001-5733.2009.09.014. |
| [17] | Liu X F, Fan Y H. 2012. On the characteristics of high-frequency Rayleigh waves in stratified half-space. Geophys. J. Int., 190(2):1041-1057. |
| [18] | Lu L Y, Zhang B X, Wang C H. 2006. Experiment and inversion studies on Rayleigh wave considering higher modes. Chinese J. Geophys.(in Chinese), 49(4):1082-1091. |
| [19] | Muller D E. 1956. A method for solving algebraic equations using an automatic computer. Mathematical Tables and Other Aids to Computation, 10(56):208-215. |
| [20] | Park C B, Miller R D, Xia J. 1999. Multichannel analysis of surface waves. Geophysics, 64(3):800-808. |
| [21] | Romeo M. 2001. Rayleigh waves on a viscoelastic solid half-space. The Journal of the Acoustical Society of America, 110(1):59-67. |
| [22] | Schwab F A, Knopoff L. 1972. Fast surface wave and free mode computations.//Bolt B A. Methods in Computational Physics. New York:Academic Press, 87-180. |
| [23] | Shibuya S, Mitachi T, Fukuda F, et al. 1995. Strain rate effects on shear modulus and damping of normally consolidated clay. Geotech. Test. J., 18(3):365-375. |
| [24] | Song Y Y, Castagna J P, Black R A, et al. 1989. Sensitivity of near-surface shear-wave velocity determination from Rayleigh and love waves.//59th Annual Meeting of the Society of Exploration Geophysicists. Expanded Abstracts, 509-512. |
| [25] | Tuan T T, Scherbaum F, Malischewsky P G. 2011. On the relationship of peaks and troughs of the ellipticity(H/V) of Rayleigh waves and the transmission response of single layer over half-space models. Geophys. J. Int., 184(2):793-800. |
| [26] | Xia J H, Miller R D, Park C B. 1999. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves. Geophysics, 64(3):691-700. |
| [27] | Yang T C, He J S, Lü S L, et al. 2004. Dispersion curves of Rayleigh wave in three-layer media. Geophysical and Geochemical Exploration(in Chinese), 28(1):41-45. |
| [28] | Zhang B X, Xiao B X, Yang W J, et al. 2000. Mechanism of zigzag dispersion curves in Rayleigh exploration and its inversion study. Chinese J. Geophys.(in Chinese), 43(4):557-567. |
| [29] | Zhang B X, Lu L Y, Bao G S. 2002. A study on zigzag dispersion curves in Rayleigh wave exploration. Chinese J. Geophys.(in Chinese), 45(2):263-274. |
| [30] | Zhang B X, Lu L Y. 2003. Guided waves in a stratified half-space. Acoust. Phys., 49(4):420-430. |
| [31] | Zhang K. 2011. Modeling and dispersion curve inversion of Rayleigh waves in viscoelastic media(in Chinese). Wuhan:China University of Geosciences. |
| [32] | Zhang K, Luo Y H, Xia J H, et al. 2011. Pseudospectral modeling and dispersion analysis of Rayleigh waves in viscoelastic media. Soil Dynamics and Earthquake Engineering, 31(10):1332-1337. |
| [33] | Zhou Y. 2009. Surface-wave sensitivity to 3-D anelasticity. Geophys. J. Int., 178(3):1403-1410. |
| [34] | 凡友华, 陈晓非, 刘雪峰等. 2007. Rayleigh波的频散方程高频近似分解和多模式激发数目. 地球物理学报, 50(1):233-239. |
| [35] | 高静怀, 何洋洋, 马逸尘. 2012. 黏弹性与弹性介质中Rayleigh面波特性对比研究. 地球物理学报, 55(1):207-218, doi:10.6038/j.issn.0001-5733.2012.01.020. |
| [36] | 刘雪峰, 凡友华, 陈晓非. 2009. Rayleigh波频散曲线"交叉"及多模式耦合作用研究. 地球物理学报, 52(9):2302-2309, doi:10.3969/j.issn.0001-5733.2009.09.014. |
| [37] | 鲁来玉, 张碧星, 汪承灏. 2006. 基于瑞利波高阶模式反演的实验研究. 地球物理学报, 49(4):1082-1091. |
| [38] | 杨天春, 何继善, 吕绍林等. 2004. 三层层状介质中瑞利波的频散曲线特征. 物探与化探, 28(1):41-45. |
| [39] | 张碧星, 肖柏勋, 杨文杰等. 2000. 瑞利波勘探中"之"形频散曲线的形成机理及反演研究. 地球物理学报, 43(4):557-567. |
| [40] | 张碧星, 鲁来玉, 鲍光淑. 2002. 瑞利波勘探中"之"字形频散曲线研究. 地球物理学报, 45(2):263-274. |
| [41] | 张凯. 2011. 黏弹性介质瑞雷波模拟及其频散曲线反演. 武汉:中国地质大学. |
 2016, Vol. 59
2016, Vol. 59

