全波形反演(Full Waveform Inversion,FWI)是在最优化理论框架下,通过拟合模拟数据与观测数据,使残差达到最小,从而获取具有高分辨率的地下物性参数(如纵横波速度、密度、阻抗或各向异性参数等)的反演方法.
Lailly(1983)和Tarantola(1984)最早在时间域建立了基于最小二乘目标泛函的全波形反演框架,利用激发点正传波场和接收点残差反传波场的互相关求解梯度方向.Pratt和Worthington(1990)将全波形反演扩展到频率域,只利用有限几个离散频率或频率组就可以方便地实现多尺度反演,提高了全波形反演的实用性.随着宽方位采集技术及高性能计算平台的发展,全波形反演已在诸多理论与实际资料中成功应用(Shipp and Singh,2002;Sears et al.,2008;Sirgue et al.,2010;李国平等,2011;刘国峰等,2012;刘玉柱等,2014).
多参数全波形反演是当前研究的热点,它不仅可以为复杂地质条件下的偏移成像提供更加准确的背景速度模型(Plessix et al.,2013),还可以为储层预测、岩性解释和油藏监测提供相应的岩石物性参数(单蕊等,2011;Prieux et al.,2013;石玉梅等,2014).相对于声波近似的单参数全波形反演,多参数全波形反演也面临巨大的挑战(董良国等,2013;杨积忠等,2014).地震数据对不同参数的敏感性在特定的传播角度上有一定的相似性,使得不同参数在反演过程中相互干涉,相互耦合,增加了反演的非线性程度;不同参数具有不同的物理量纲,对地震数据的影响量级也不同,在反演过程中如不能进行很好的校正,也会加剧反演的病态性(Operto et al.,2013;刘玉柱等,2015).
选择合适的参数化方式,制定合理的反演策略,是解决多参数全波形反演非线性问题的有效途径.Tarantola(1986)和Mora(1987)指出,在P波震源反射地震波形反演中,拉梅常数-密度是一种比较差的参数化方式;对近偏移距数据来说,阻抗是比较合适的参数,而对远偏移距数据来说,速度是比较合适的参数;不管利用哪种参数化方式,密度都不能被很好地估计.Köhn等人(2012)指出,在弹性波多参数全波形反演中,不管利用哪种参数化方式,拉梅常数、纵横波速度、阻抗都可以被较好地估计,而密度反演效果较差;利用速度-密度参数化方式、阻抗-密度参数化方式得到的反演结果要优于拉梅常数-密度参数化方式得到的反演结果.针对密度反演比较困难这一问题,部分学者提出了有利于密度反演的多参数全波形反演策略.Jeong等(2012)在频率域,首先以拉梅常数-密度为参数化方式,将密度固定为任意常数,通过单参数反演得到拉梅常数,然后将换算得到纵横波速度作为初始模型,进而以纵横波速度-密度为参数化方式,同时反演拉梅常数和密度,最后换算得到速度和密度,有效提高了密度的反演精度.Prieux等(2013)先利用大偏移距地震数据单参数反演速度参数,再利用全偏移距地震数据同时反演速度、密度参数,有效提高了密度反演的稳定性,但密度反演结果仍然不够理想.他们同时指出,利用速度-密度参数化方式反演得到的速度、密度和阻抗结果要好于利用速度-阻抗参数化方式得到的反演结果.杨积忠等(2014)基于变密度声波方程,以速度-密度为参数化方式,首先利用全偏移距地震数据对速度、密度进行同时反演,得到比较可靠的速度反演结果,然后以反演得到的速度和最初给定的密度作为初始模型,进一步对速度、密度进行同时反演,得到了比较准确的速度、密度反演结果.刘玉柱等(2015)在各向异性FWI研究中利用了相似的反演策略.
上述反演策略的本质在于考虑了地震数据对不同参数敏感性的差异,分层次、分阶段地实现对不同参数的反演,在一定程度上降低了多参数全波形反演的非线性程度.然而,这些反演策略并没有从根本上解决不同参数间的耦合问题,使得反演结果的分辨率和精度都受到不同程度的影响.在反演过程中引入Hessian算子的逆,是解决这一问题的重要途径(Operto et al.,2013).在多参数全波形反演中,Hessian矩阵,特别是高斯-牛顿近似Hessian矩阵是分块对角占优矩阵,主对角块元素反映了波场的几何扩散效应、数据的频带效应以及观测系统的孔径效应,而非主对角块元素则反映了不同参数之间的耦合效应(Operto et al.,2013).在反演过程中考虑近似Hessian矩阵的逆,能够消除上述效应对全波形反演的影响,提高收敛速度,使全波形反演获取较为准确的模型估计(Pratt et al.,1998;Operto et al.,2013).
由于巨大的计算和存储消耗,显式地计算与存储Hessian及其逆算子并不现实,使得全牛顿法和高斯-牛顿法不能得到广泛应用(Pratt et al.,1998;Sheen et al.,2006).截断牛顿类方法(包括全牛顿法和高斯-牛顿法)可以较好地估计Hessian算子的逆,近年来在全波形反演中逐步得到应用(Santosa and Symes,1988;Akçeliket al.,2002;Epanomeritakis et al.,2008;Hu et al.,2009;Bae et al.,2012;Métivier et al.,2013,2014;Wang et al.,2013;王义和董良国,2015). 通常情况下,截断牛顿类全波形反演利用一阶伴随状态法计算目标函数对模型参数的梯度,模型更新方向则通过共轭梯度法不完全求解线性牛顿类方程得到.在每一步内循环迭代过程中,利用二阶伴随状态法或有限差分法求解Hessian-向量乘,需额外求解两次正演问题,计算量较大,需要设计合理的预条件算子以减少内循环次数(Métivier et al.,2013).Liu等(2015)提出了一种基于Born敏感核函数计算目标函数梯度及高斯-牛顿方向的全波形反演方法,该方法在利用共轭梯度法不完全求解线性牛顿类方程的内循环过程中,将Hessian-向量乘转化为两次核函数-向量乘,无需额外求解正演问题,有效降低了计算量.
本文将Liu等(2015)提出的方法推广到声介质速度、密度双参数全波形反演中.以速度-密度为参数化方式,详细推导了Born近似下速度、密度对应的敏感核函数,并在均匀背景模型中分析了它们的性质,最后将其应用于速度、密度双参数全波形反演.球状异常体模型和Marmousi-2模型的数值实验充分证明了该方法的有效性.
2 反演方法全波形反演通过拟合模拟数据 d cal和观测数据 d obs,使波场残差δ d = d cal- d obs达到最小,进而获取地下介质的物性参数 m .目标函数可以表达为
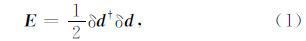
这里 代表共轭转置.由于全波形反演中涉及的数据量大、模型参数多,通常用局部最优化方法来求解(1)式.在给定的初始模型的基础上,通过求取模型更新量来迭代更新模型,如(2)式所示:
代表共轭转置.由于全波形反演中涉及的数据量大、模型参数多,通常用局部最优化方法来求解(1)式.在给定的初始模型的基础上,通过求取模型更新量来迭代更新模型,如(2)式所示:
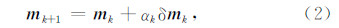
其中,δ m k为模型更新方向,αk为更新步长.步长α可以利用线性搜索或信赖域方法求取(Nocedal and Wright,2006).模型更新方向δ m k满足牛顿方程:
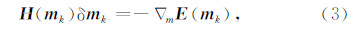
其中,▽ m E(m)为目标函数对模型参数的梯度,如公式(4)所示,H(m)为Hessian算子,是目标函数对模型参数的二阶导数,如公式(5)所示.

这里,K 为Fréchet微商,又称敏感核函数,它反映 了波场对模型参数的敏感程度.在Born近似条件下,要求背景模型与真实模型非常接近,数据残差 δ d 相对于背景波场非常小,因此Hessian算子的第二项可以忽略不计,这样Hessian 算子就退化为近似Hessian算子 H a:

同时,牛顿方程(3)退化为高斯-牛顿方程:
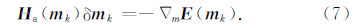
需要指出的是,Hessian算子的第二项为波场对模型参数的二阶导数与波场残差在检波点处零延迟的相关,反映了波场的二次散射效应,当波场中多次波较为明显时,考虑Hessian算子的第二项可以消除这些多次散射效应的影响,提高反演精度,而忽略Hessian算子的第二项,则会加剧多次散射的影响,使反演陷入局部极值.
由公式(4)直接求取梯度需要显式计算与存储Fréchet核函数,计算量与存储量较大,目前通常采用一阶伴随状态法来间接计算目标函数的梯度(Plessix,2006).由伴随状态法求得的梯度可以看成是激发点正传波场和接收点残差反传波场零延迟的互相关,而各参数之间辐射模式的不同导致了梯度在具体表达形式上的差异.假定整个观测系统中不重复的炮点个数为ns,不重复的检波点个数为nr,利用伴随状态法计算梯度所用的正演次数为2ns,与检波点个数无关.而在利用共轭梯度法求解线性方程组(3)或(7)时,虽然不需要显示构造Hessian算子并求逆,但在每一步内循环过程中,需利用二阶伴随状态法或有限差分法求解Hessian-向量乘 Hv(v 为模型空间的任意向量),需要额外求解两次正演问题.假定内循环的迭代次数为nCG,需要的正演次数为2ns×nCG,因此计算量很大(Métivier et al.,2013,2014;Wang et al.,2013).
Liu等(2015)提出了一种基于Born敏感核函数计算目标函数梯度与高斯-牛顿方向的全波形反演方法.该方法的核心思想是将公式(4)中的核函数-向量乘运算表示为具有明确物理意义的向量-标量乘的累加运算,在运算过程中只需存储单个炮检对的敏感核函数,避免了庞大核函数矩阵的存储.在计算高斯-牛顿方向的内循环过程中,将Hessian-向量乘 Hv 分解为两次核函数-向量乘 Kp 或 K  p(p 为模型空间或数据空间的任意向量),不需要额外求解正演问题,有效降低了计算量.假定数据个数为m,模型网格参数为n,那么 K 为m×n的矩阵,K
p(p 为模型空间或数据空间的任意向量),不需要额外求解正演问题,有效降低了计算量.假定数据个数为m,模型网格参数为n,那么 K 为m×n的矩阵,K  为n×m的矩阵,H 或 H a为n×n的矩阵.计算梯度方向与核函数-向量乘 Kp 的实现方式如下:
为n×m的矩阵,H 或 H a为n×n的矩阵.计算梯度方向与核函数-向量乘 Kp 的实现方式如下:
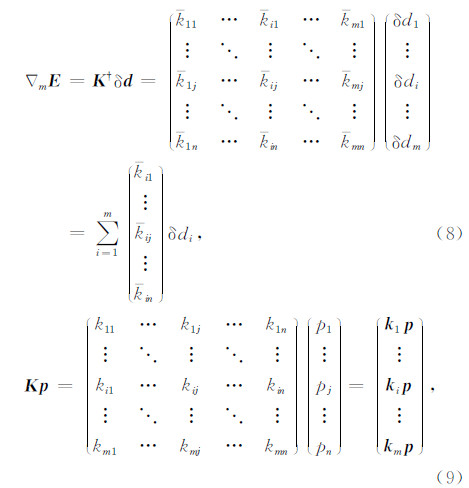
其中,kij为敏感核函数矩阵 K 的任意元素,它代表第i个数据元素对第j个模型网格参数的敏感性,上划线表示复数共轭,k i为第i个炮检对所对应的核函数向量.公式(8)中右端项求和运算中的每一个列向量代表任意一个炮检对所对应的敏感核函数的共轭,其物理意义可以解释为将数据残差沿炮检对 所对应的Born波路径进行反投影(Woodward,1992).
利用共轭梯度法求解公式(7)的流程如表 1所示.
| | 表 1 用共轭梯度法(CG)求解线性方程组 Ax = b 的流程 Table 1 A matrix-free conjugate-gradient (CG) algorithm for solving Ax=b |
这里,A 为近似Hessian矩阵 H a, x 为需要求解的模型更新方向δ m k,b 为负梯度方向- ▽ m E .假定整个观测系统中不重复的炮点个数为ns,不重复的检波点个数为nr,则利用上述方法计算梯度和求解高斯-牛顿方程所需的正演次数为ns+nr,相比于伴随状态法,正演计算量有效降低.
基于Born敏感核函数的全波形反演的基本流程如下.
(1)给定初始模型 m 0,输入观测数据 d obs;
(2)计算整个观测系统中炮点对应的格林函数 G(x,x s,ω)及不重复的检波点对应的格林函数 G(x,x r,ω),这里利用了格林函数的互易性原理 G(x r,x,ω)= G(x,x r,ω);
(3)计算波场残差δ d = d cal- d obs,d cal= f(ω) G(x r,x s,ω);
(4)利用公式(8)计算梯度方向;
(5)利用表 1对应的流程计算模型更新方向δ m k;
(6)利用线性搜索计算步长αk;
(7)更新模型 m k+1= m k+αkδ m k;
(8)判断是否满足结束条件,如果满足,保存更新后的模型,退出循环;如果不满足,进入下一轮迭代过程,重复步骤(2)—(7);
由上面介绍可知,基于Born敏感核函数的全波形反演方法的核心在于推导并计算各个模型参数所对应的敏感核函数.针对本文的速度、密度双参数全波形反演,附录A中详细推导了变密度声波方程中以速度-密度为参数化方式时所对应的敏感核函数.相应的联合模型更新方向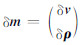 ,联合敏感核函数矩阵 K m=(K v K ρ),则高斯-牛顿方程(7)改写为:
,联合敏感核函数矩阵 K m=(K v K ρ),则高斯-牛顿方程(7)改写为:
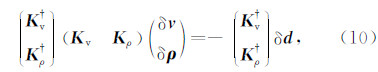
其中,

由公式(11)可知,近似联合Hessian矩阵 H a由四块组成,其中,左上角和右下角矩阵块的主对角元素为相同参数敏感核函数在相同空间位置零延迟的自相关,反映了波场的几何扩散效应;非主对角元素则为相同参数敏感核函数在不同空间位置零延迟的互相关,反映了数据的频带效应以及观测系统的孔径效应.而左下角和右上角的矩阵块则代表了不同参数敏感核函数零延迟的相关,反应了不同参数之间的相互作用,即所谓的耦合效应.当左下角和右上角矩阵块的元素为零时,不同参数间无耦合效应,公式(10)退化为单参数全波形反演:

利用共轭梯度法求解速度、密度双参数高斯-牛顿方程(10)即可得到联合模型更新方向.联合模型更新方向求得后可进一步利用联合核函数-向量乘方便地实现步长的计算(Liu et al.,2015).
3 敏感核函数分析为了详细分析敏感核函数的性质,本节利用公式(A25)计算了均匀介质中速度、密度的敏感核函数.模型中速度值为4000 m·s-1,密度值为2000 kg·m-3,模型大小为10 km×10 km,网格离散间距20 m.炮点位置(2000 m,5000 m),检波点位置(8000 m,5000 m),炮点、检波点格林函数对应的频率为10 Hz. 由于是在频率域中计算,同时展示了速度、密度敏感核函数的实部和虚部.
图 1a与图 1b显示的是速度敏感核函数的实部和虚部,图 1c与图 1d显示的是密度敏感核函数的实部和虚部,图 2显示的是速度、密度敏感核函数在x=5000 m处的纵向剖面.可以看出:(1)速度敏感核函数在垂直于波传播方向,能量由中心向两边逐渐减弱;而密度敏感核函数在垂直于波传播方向,中心能量最弱,向两边逐渐增强;(2)在中心区域,波场对速度的敏感性要强于对密度的敏感性;在这一区域,将波场残差沿波路径反投影得到的速度梯度的权重大于密度梯度的权重,不利于密度的反演,此时速度对密度反演的影响较大;(3)在远离中心射线区域,波场对速度的敏感性和波场对密度的敏感性有一定的相似性,在反演过程中,速度和密度在这一区域相互耦合,相互影响,难以同时反演.
 | 图 1 速度、密度敏感核函数:速度敏感核函数的实部(a)与虚部(b),密度敏感核函数的实部(c)与虚部(d).红色为正值,蓝色为负值,黄色为零Fig. 1 The sensitivity kernels for velocity and density: (a) real and (b) imaginary parts of velocity sensitivity kernel, (c) real and (d) imaginary parts of density sensitivity kernel. Red is positive, blue is negative, yellow is zero |
 | 图 2 速度、密度敏感核函数在x=5000 m处的纵向剖面:速度敏感核函数的 实部(a)与虚部(b),密度敏感核函数的实部(c)与虚部(d)Fig. 2 The vertical cross sections at position x=5000 m of sensitivity kernels: (a) real and (b) imaginary parts of velocity sensitivity kernel, (c) real and (d) imaginary parts of density sensitivity kernel |
本节数值实验基于球状异常体模型.速度模型如图 3a所示,背景均匀,速度值为3000 m·s-1,球状异常体中心位于(700 m,700 m)处,半径100 m,速度值为3300 m·s-1;密度模型如图 3c所示,背景均匀,密度值为2000 kg·m-3,球状异常体中心位于(1300 m,1300 m)处,半径100 m,密度值为2200 kg·m-3.采用四周观测方式,使得目标体在各个方向的照明均匀,进而消除观测系统的影响.共有152炮均匀分布于模型四周,炮间距为50 m,每一炮由152个检波点接收,检波点均匀分布于模型 四周,检波点间距为50 m.模型纵横向大小为2 km× 2 km,网格离散间距10 m.地震记录长度1.5 s,时间采样间隔1 ms,震源函数为7 Hz主频的Ricker子波.
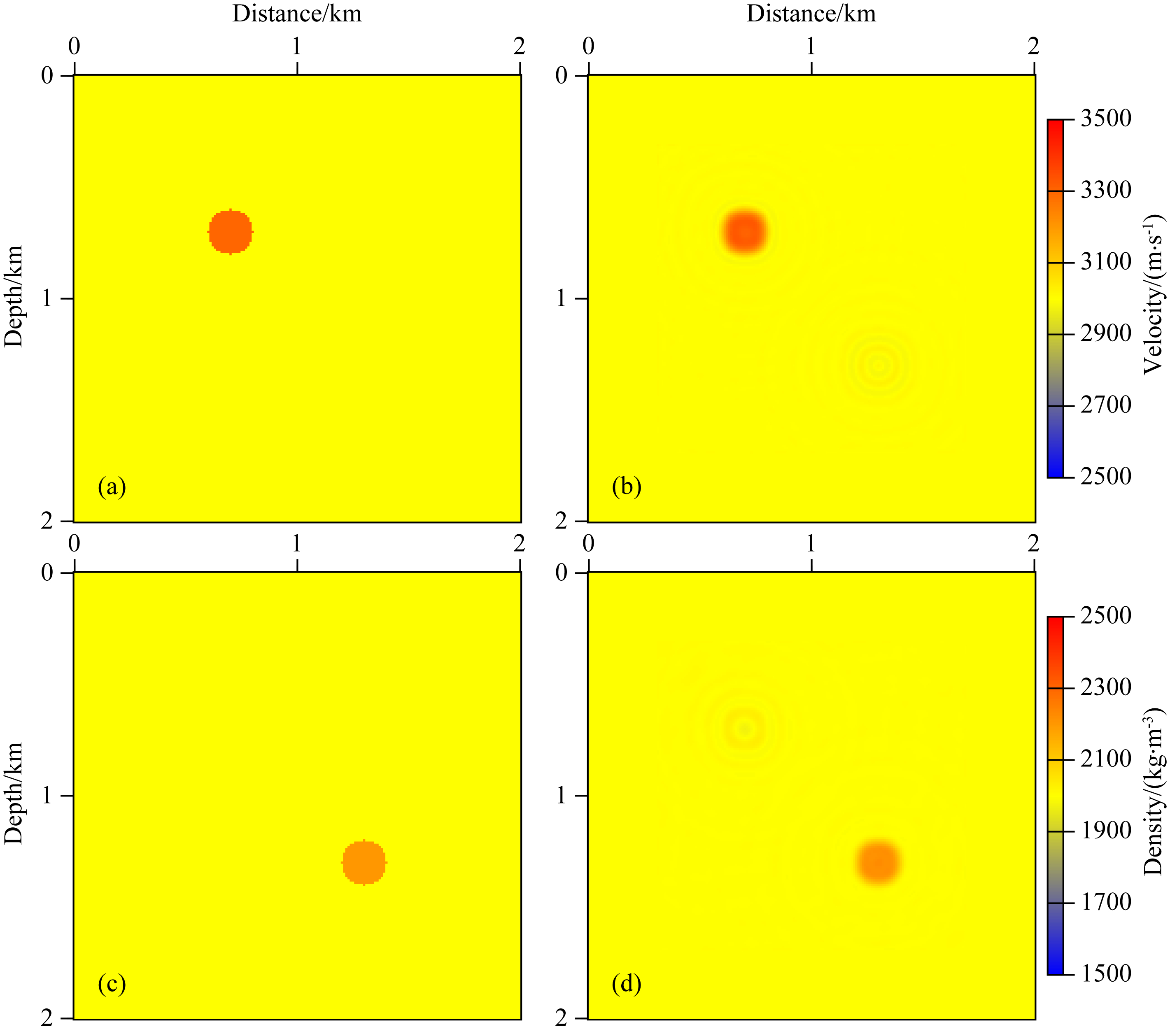 | 图 3 球状异常模型及多参数全波形反演结果 (a) 真实速度模型; (b) 速度反演结果; (c) 真实密度模型; (d) 密度反演结果. Fig. 3 The inclusion model and the final models obtained by multi-parameter full waveform inversion (a) The true velocity model; (b) The recovered velocity; (c) The true density model; (d) The recovered density. |
将速度和密度的均匀背景模型作为初始模型,对速度、密度进行同时反演.反演结果如图 3b和图 3d所示,图 4显示了反演结果的纵向剖面.可以看出,速度、密度反演结果与真实模型具有较好的一致性.对比杨积忠等(2014)对该双参数反演问题的反演策略研究中考虑速度、密度相互影响的数值实验的图 4—图 7可以发现,在本文数值实验中,速度异常并没有引起明显的密度异常,而密度异常存在的地方也没有影响速度的反演,说明通过引入截断高斯-牛顿法,考虑近似Hessian矩阵中反映速度、密度相互影响的非主对角块元素,可以有效解决反演过程中速度、密度之间的耦合效应,即使在不采用反演策略的情况下,仍能够得到比较可靠的反演结果.
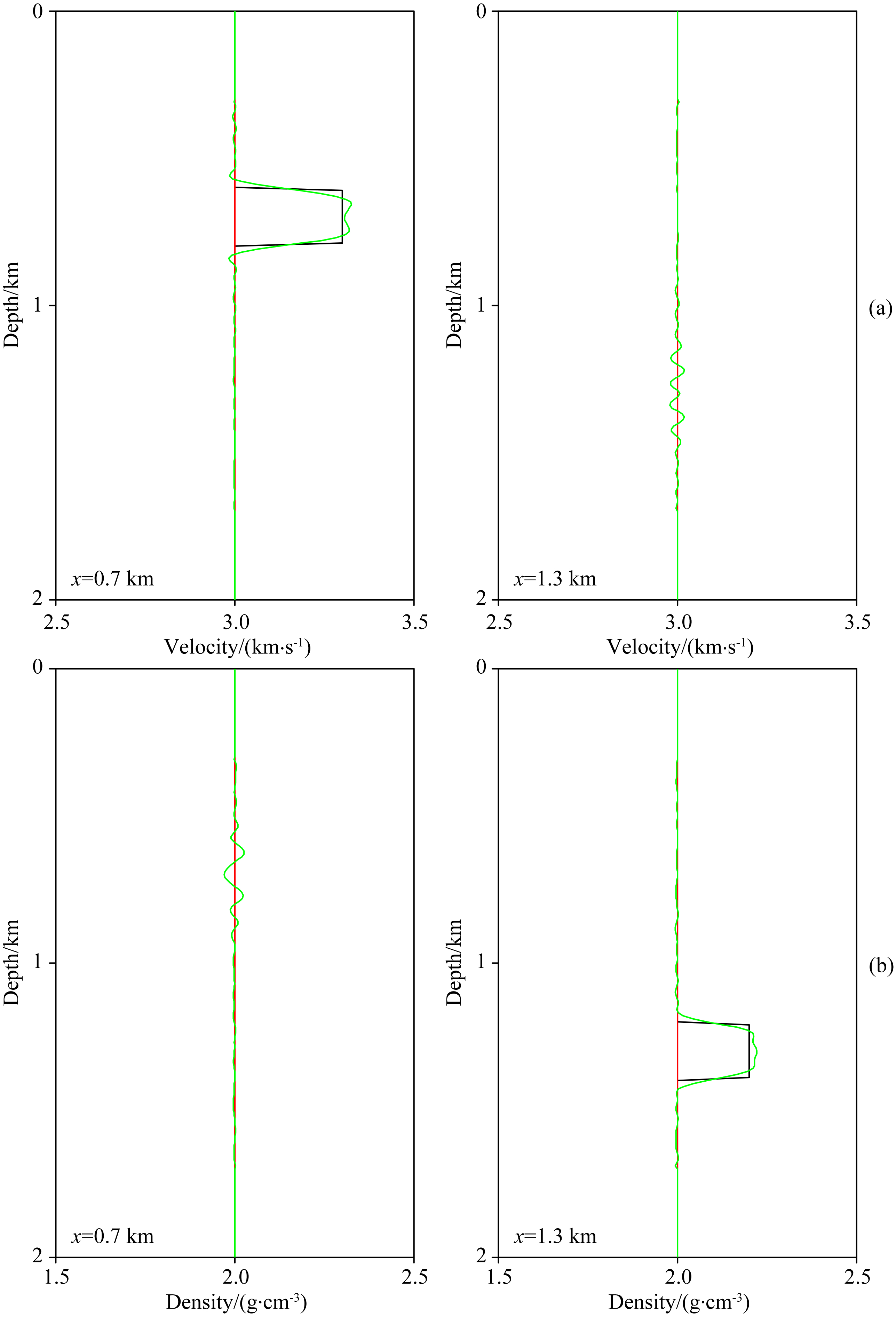 | 图 4 多参数全波形反演结果纵向剖面,分别位于水平方向0.7 km(左)和1.3 km(右)处的(a)速度反演结果与(b)密度反演结果. 黑线代表真实模型,红线代表初始模型,绿线代表反演结果,速度和密度的单位分别是km·s-1和g·cm-3 Fig. 4 Vertical profiles at horizontal positions of 0.7 km (left) and 1.3 km (right) of the models shown in Fig.1 for (a) P-wave velocity and (b) density. The black line indicates the true model, the red line denotes the initial model and the green line denotes the reconstructed model. The units of velocity and density are km·s-1, and g·cm-3, respectively |
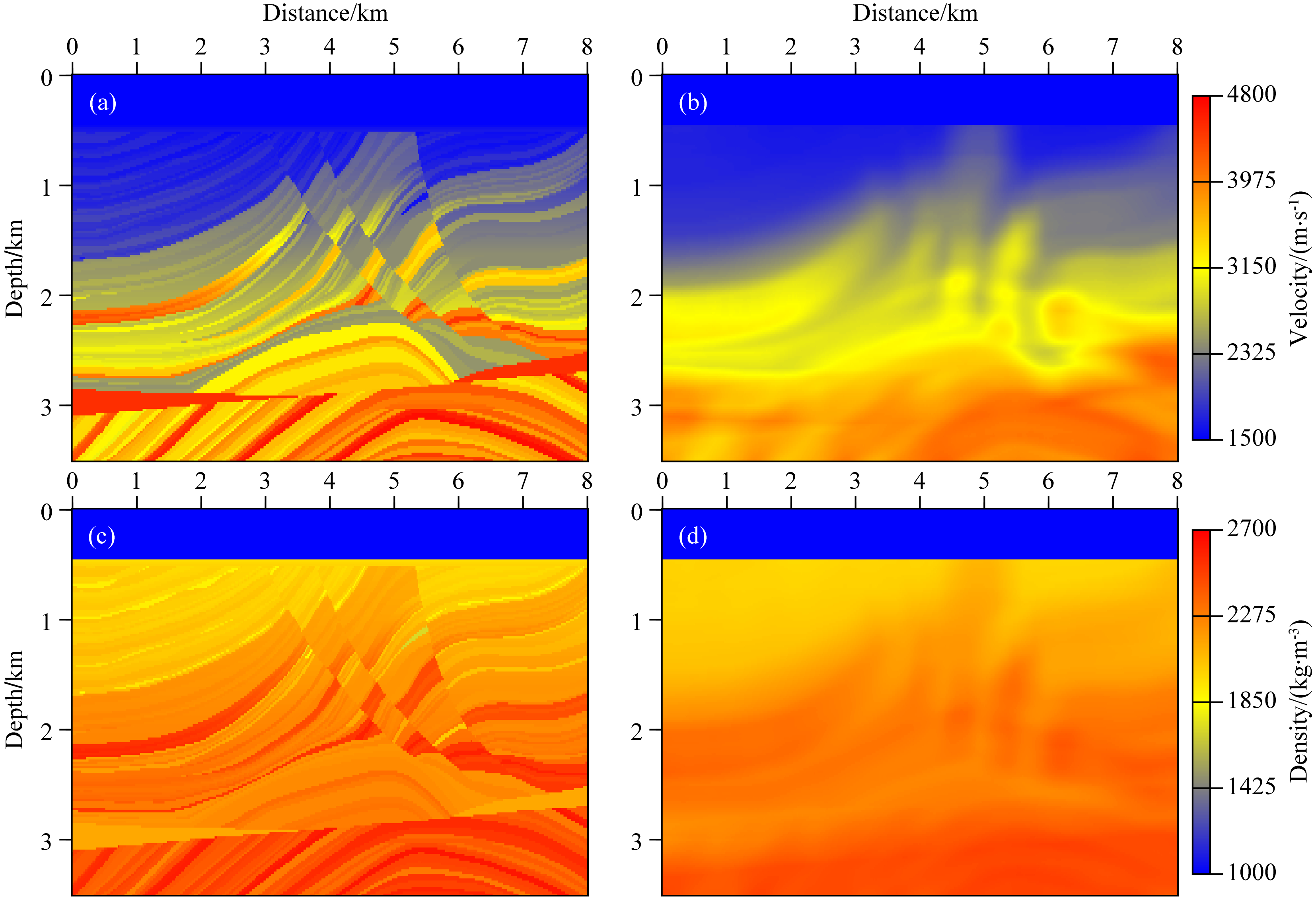 | 图 5 Marmousi-2模型 (a) 真实速度模型; (b) 初始速度模型; (c) 真实密度模型; (d) 初始密度模型. Fig. 5 The Marmousi-2 model (a) True velocity model; (b) Initial velocity model; (c) True density model; (d) Initial density model. |
 | 图 6 多参数全波形反演结果 (a) 速度; (b) 密度. Fig. 6 The final models obtained by multi-parameter full waveform inversion (a) Velocity; (b) Density. |
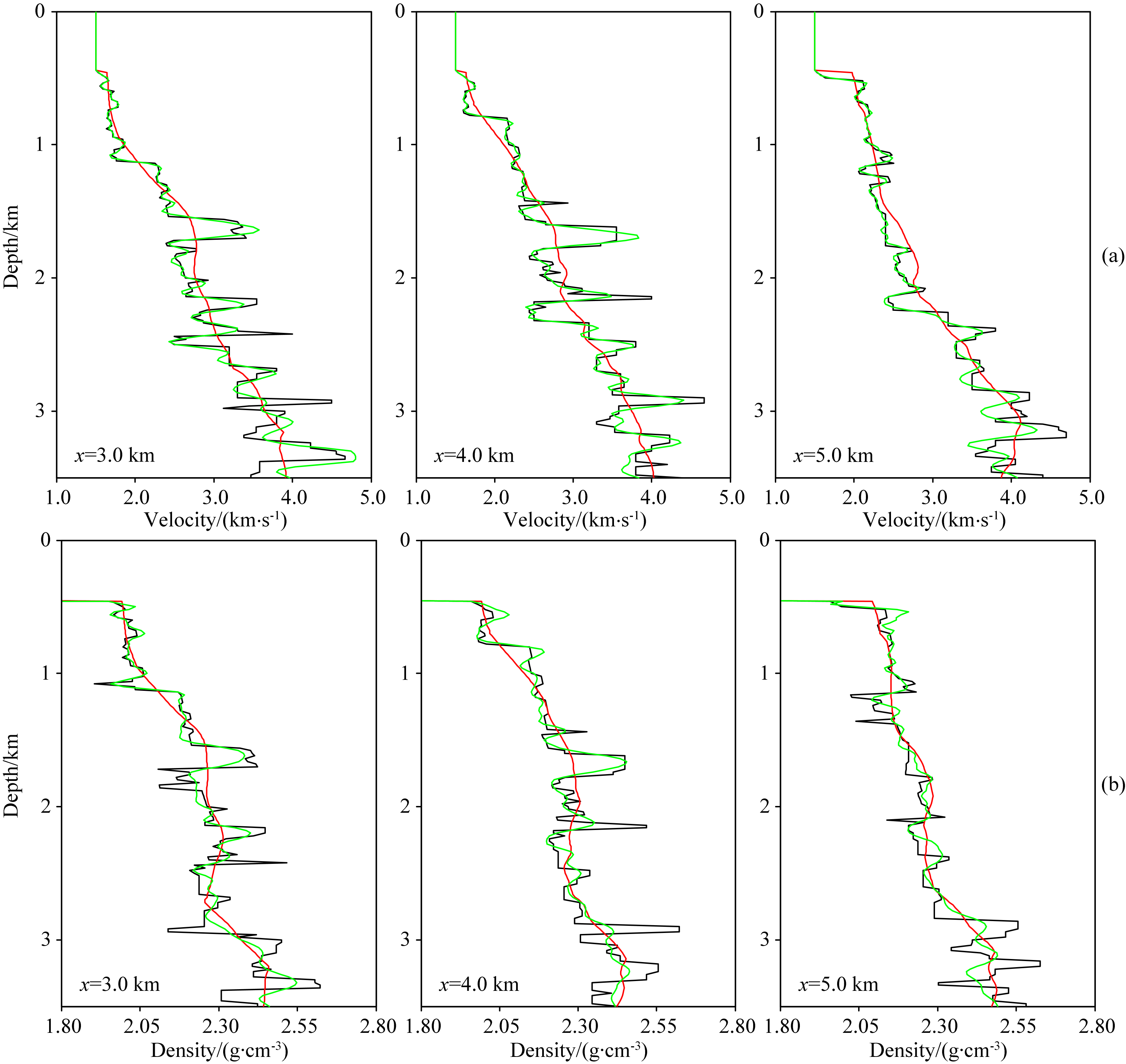 | 图 7 多参数全波形反演结果纵向剖面,分别位于水平方向3 km(左)、4 km(中)和5 km(右)处的(a)速度反演结果与(b)密度反演结果.黑线代表真实模型,红线代表初始模型,绿线代表反演结果,速度和密度的单位分别是km·s-1和g·cm-3 Fig. 7 Vertical profiles at horizontal positions of 3 km (left), 4 km (middle) and 5 km (right) of the models shown in Fig.5 for (a) P-wave velocity and (b) density. The black line indicates the true model, the red line denotes the initial model and the green line denotes the reconstructed model. The units of velocity and density are km·s-1, and g·cm-3, respectively |
为了测试本文方法在地表反射观测系统情况下 反演复杂模型的能力,本节实验将其应用于Marmousi-2 模型(Martin et al.,2006).模型大小为8 km×3.5 km,网格离散间距20 m.数值模拟79炮地表地震记录,第一炮位于水平方向100 m处,炮间距100 m,检波点分布于地表所有网格点上,数据记录长度8 s,时间采样间隔2 ms,震源函数选用主频为7 Hz的Ricker子波.
真实速度、密度模型和基于真实模型高斯平滑得到的初始速度、密度模型如图 5所示.对速度、密度进行同时反演,反演结果如图 6所示,图 7显示了反演结果的纵向剖面.可以看出,速度反演结果具有较高的分辨率与反演精度,密度反演效果相对略差,但仍与真实模型具有较好的一致性,说明密度反演相对于速度反演来说比较困难.对比杨积忠等(2014)对该双参数反演问题的反演策略研究中的图 21—图 26可以发现,在反演过程中考虑近似Hessian 算子的逆,可以有效地解决多参数全波形反演中不同参数间的耦合效应,即使在不采用反演策略的情况下,仍可以得到比较准确的反演结果,特别是密度反演精度的提高尤为显著.
5 结论准确地估计Hessian算子的逆,对多参数全波形反演具有至关重要的作用.本文将截断高斯-牛顿法用于声介质速度、密度双参数全波形反演,利用共轭梯度法不完全求解线性高斯-牛顿方程,间接考虑了近似Hessian算子的逆在多参数全波形反演中所起的作用.数值实验充分证明,在反演过程中引入近似Hessian算子的逆,能够有效解决多参数全波形反演中速度与密度的耦合问题,即使在不采用反演策略的情况下,仍能够获得比较准确的速度、密度反演结果.
本文基于Born近似,详细推导了变密度声波方程中速度、密度对应的敏感核函数,然后将计算梯度时所用的联合核函数-向量乘表示为具有明确物理涵义的向量-标量乘的累加运算,避免了庞大核函数矩阵的存储,而在利用共轭梯度法不完全求解双参数高斯-牛顿方程时将对应的联合Hessian-向量乘转化为两次联合核函数-向量乘,无需额外求解正演问题,有效降低了计算量,具有较好的应用前景.
虽然本文是在变密度声波方程基础上研究基于Born敏感核函数的全波形反演方法在多参数全波形反演中的应用,但该方法同样适用于其他多参数全波形反演.
附录A: 变密度声波方程速度、密度敏感核函数推导在频率域,变密度声波方程可以表达为
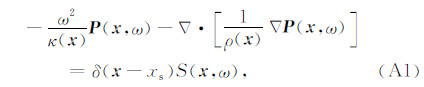
在背景模型中,满足
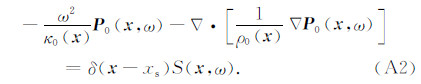
在Born近似条件下,有

分别对模量κ(x)和密度ρ(x)进行扰动,

相应地,
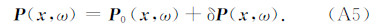
将(A4)、(A5)式带入(A1)式,得

其中,
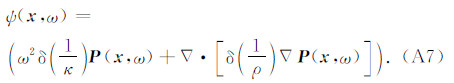
将(A5)式代入(A7)式,可得

在Born近似条件下,P 0(x,ω)>>δ P(x ,ω),因此(A8)式变为

方程(A6)的积分解为
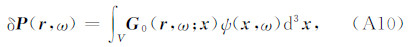
其中,G 0(r,ω; x)为背景模型的格林函数,满足方程
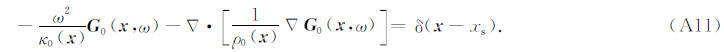
将(A9)式代入(A10)式,得
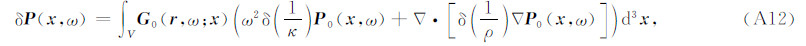
即
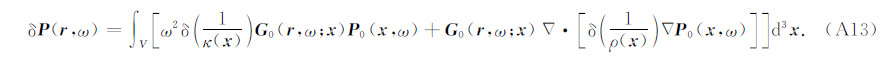
由于
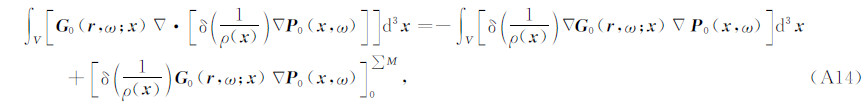
在均匀边界条件下,

所以,
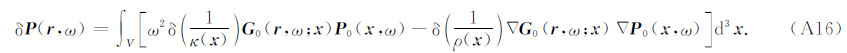
在Born近似条件下,波场扰动与模型扰动之间存在如下线性关系:
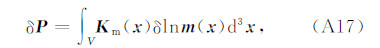
其中,δln m =δ m / m 为相对模型扰动,K m为敏感核函数.引入模量、密度敏感核函数:
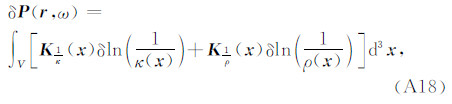
对比(A16)得到
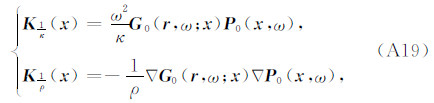
由于
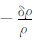 ,所以
,所以

其中
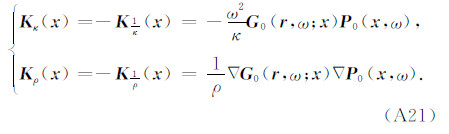
利用模量、速度、密度之间的关系:
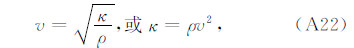
存在如下全微分关系:
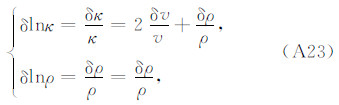
可得
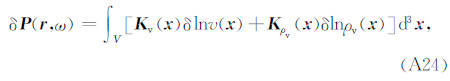
其中
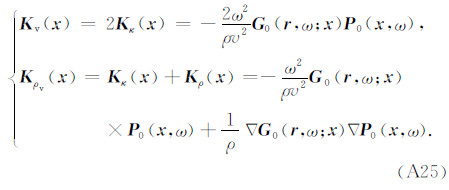
上式即为速度、密度敏感核函数表达式.
| [1] | Akçelik V, Biros G, Ghattas O. 2002. Parallel multiscale Gauss-Newton-Krylov methods for inverse wave propagation.//Proceedings of the ACM/IEEE 2002 Conference Supercomputing. IEEE:41. |
| [2] | Bae H S, Pyun S, Chung W, et al. 2012. Frequency-domain acoustic-elastic coupled waveform inversion using the Gauss-Newton conjugate gradient method. Geophysical Prospecting, 60(3):413-432. |
| [3] | Dong L G, Chi B X, Tao J X, et al. 2013. Objective function behavior in acoustic full-waveform inversion. Chinese J. Geophys.(in Chinese), 56(10):3445-3460, doi:10.6038/cjg20131020. |
| [4] | Epanomeritakis I, Akçelik V, Ghattas O, et al. 2008. A Newton-CG method for large-scale three-dimensional elastic full waveform seismic inversion. Inverse Problems, 24(3):034015. |
| [5] | Hu W Y, Abubakar A, Habashy T M. 2009. Simultaneous multifrequency inversion of full-waveform seismic data. Geophysics, 74(2):R1-R14. |
| [6] | Jeong W, Lee H Y, Min D J. 2012. Full waveform inversion strategy for density in the frequency domain. Geophysical Journal International, 188(3):1221-1242. |
| [7] | Köhn D, De Nil D, Kurzmann A, et al. 2012. On the influence of model parametrization in elastic full waveform tomography. Geophysical Journal International, 191(1):325-345. |
| [8] | Lailly P. 1983. The seismic inverse problem as a sequence of before stack migrations.//Conference on inverse scattering:theory and application. Society for Industrial and Applied Mathematics. Philadelphia, PA, 206-220. |
| [9] | Li G P, Yao F C, Shi Y M, et al. 2011. Pre-stack wave equation inversion and its application in frequency domain. Oil Geophysical Prospecting(in Chinese), 46(3):411-416. |
| [10] | Liu G F, Liu H, Meng X H, et al. 2012. Frequency-related factors analysis in frequency domain waveform inversion. Chinese J. Geophys.(in Chinese), 55(4):1345-1353, doi:10.6038/j.issn.0001-5733.2012.04.030. |
| [11] | Liu Y Z, Xie C, Yang J Z. 2014. Gaussian beam first-arrival waveform inversion based on Born wavepath. Chinese J. Geophys. (in Chinese), 57(9):2900-2909, doi:10.6038/cjg20140915. |
| [12] | Liu Y Z, Wang G Y, Yang J Z, et al. 2015. Multi-parameter full-waveform inversion for VTI media based on Born sensitivity kernels. Chinese J. Geophys.(in Chinese), 58(4):1305-1316, doi:10.6038/cjg20150418. |
| [13] | Liu Y Z, Yang J Z, Chi B X, et al. 2015. An improved scattering-integral approach for frequency-domain full waveform inversion. Geophysical Journal International, 202(3):1827-1842. |
| [14] | Martin G S, Wiley R, Marfurt K J. 2006. Marmousi2-an elastic upgrade for Marmousi. The Leading Edge, 25(2):156-166. |
| [15] | Métivier L, Brossier R, Virieux J, et al. 2013. Full waveform inversion and the truncated newton method. SIAM Journal on Scientific Computing, 35(2):B401-B437. |
| [16] | Métivier L, Bretaudeau F, Brossier R, et al. 2014. Full waveform inversion and the truncated newton method:quantitative imaging of complex subsurface structures. Geophysical Prospecting, 62(6):1353-1375. |
| [17] | Mora P R. 1987. Nonlinear two-dimensional elastic inversion of multi-offset seismic data. Geophysics, 52(9):1211-1228. |
| [18] | Nocedal J, Wright S J. 2006. Numerical Optimization. New York:Springer Science+Business Media, LLC. |
| [19] | Operto S, Gholami V, Prieux V, et al. 2013. A guided tour of multiparameter full waveform inversion with multicomponent data:From theory to practice. The Leading Edge, 32(9):1040-1054. |
| [20] | Plessix R E. 2006. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophysical Journal International, 167(2):495-503. |
| [21] | Plessix R E, Milcik P, Rynja H, et al. 2013. Multiparameter full-waveform inversion:Marine and land examples. The Leading Edge, 32(9):1030-1038. |
| [22] | Pratt R G, Worthington M H. 1990. Inverse theory applied to multi-source cross-hole tomography. Part 1:Acoustic wave-equation method. Geophysical Prospecting, 38(3):287-310. |
| [23] | Pratt R G, Shin C, Hicks G J. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophysical Journal International, 133(2):341-362. |
| [24] | Prieux V, Brossier R, Operto S, et al. 2013. Multiparameter full waveform inversion of multicomponent ocean-bottom-cable data from the Valhall field. Part 1:imaging compressional wave speed, density and attenuation. Geophysical Journal International, 194(3):1640-1664. |
| [25] | Santosa F, Symes W W. 1988. Computation of the Hessian for least squares solutions of inverse problems of reflection seismology. Inverse Problems, 4(1):211-233. |
| [26] | Sears T J, Singh S C, Barton P J. 2008. Elastic full waveform inversion of multi component OBC seismic data. Geophysical Prospecting, 56(6):843-862. |
| [27] | Shan R, Bian A F, Yu W H, et al. 2011. Pre-stack full waveform inversion for reservoir prediction. Oil Geophysical Prospecting (in Chinese), 46(4):629-633. |
| [28] | Sheen D H, Tuncay K, Baag C E, et al. 2006. Time domain Gauss-Newton seismic waveform inversion in elastic media. Geophysical Journal International, 167(3):1373-1384. |
| [29] | Shi Y M, Zhao W Z, Cao H. 2007. Nonlinear process control of wave-equation inversion and its application in the detection of gas. Geophysics, 72(1):R9-R18. |
| [30] | Shi Y M, Zhang Y, Yao F C, et al. 2014. Methodology of seismic imaging for hydrocarbon reservoirs based on acoustic full waveform inversion. Chinese J. Geophys.(in Chinese), 57(2):607-617, doi:10.6038/cjg20140224. |
| [31] | Shipp R M, Singh S C. 2002. Two-dimensional full wavefield inversion of wide-aperture marine seismic streamer data. Geophysical Journal International, 151(2):325-344. |
| [32] | Sirgue L, Barkved O I, Dellinger J, et al. 2010. Full waveform inversion:The next leap forward in imaging at Valhall. First Break, 28(4):65-70. |
| [33] | Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8):1259-1266. |
| [34] | Tarantola A. 1986. A strategy for nonlinear inversion of seismic reflection data. Geophysics, 51(10):1893-1903. |
| [35] | Wang Y, Dong L G, Liu Y Z. 2013. Improved hybrid iterative optimization method for seismic full waveform inversion. Applied Geophysics, 10(3):265-277. |
| [36] | Wang Y, Dong L G. 2015. Multi-parameter full waveform inversion for acoustic VTI media using the truncated Newton method. Chinese J. Geophys. (in Chinese), 58(8):2873-2885, doi:10.6038/cjg20150821. |
| [37] | Woodward M J. 1992. Wave-equation tomography. Geophysics, 57(1):15-26. |
| [38] | Yang J Z, Liu Y Z, Dong L G. 2014. A multi-parameter full waveform inversion strategy for acoustic media with variable density. Chinese J. Geophys.(in Chinese), 57(2):628-643, doi:10.6038/cjg20140226. |
| [39] | 董良国, 迟本鑫, 陶纪霞等. 2013. 声波全波形反演目标函数性态. 地球物理学报, 56(10):3445-3460, doi:10.6038/cjg20131020. |
| [40] | 李国平, 姚逢昌, 石玉梅等. 2011. 频率域叠前波动方程反演及其应用. 石油地球物理勘探, 46(3):411-416. |
| [41] | 刘国峰, 刘洪, 孟小红等. 2012. 频率域波形反演中与频率相关的影响因素分析. 地球物理学报, 55(4):1345-1353, doi:10.6038/j.issn.0001-5733.2012.04.030. |
| [42] | 刘玉柱, 谢春, 杨积忠. 2014. 基于Born波路径的高斯束初至波波形反演. 地球物理学报, 57(9):2900-2909, doi:10.6038/cjg20140915. |
| [43] | 刘玉柱, 王光银, 杨积忠等. 2015. 基于Born敏感核函数的VTI介质多参数全波形反演. 地球物理学报, 58(4):1305-1316, doi:10.6038/cjg20150418. |
| [44] | 单蕊, 卞爱飞, 於文辉等. 2011. 利用叠前全波形反演进行储层预测. 石油地球物理勘探, 46(4):629-633. |
| [45] | 石玉梅, 张研, 姚逢昌等. 2014. 基于声学全波形反演的油气藏地震成像方法. 地球物理学报, 57(2):607-617, doi:10.6038/cjg20140224. |
| [46] | 王义, 董良国. 2015. 基于截断牛顿法的VTI介质声波多参数全波形反演. 地球物理学报, 58(8):2873-2885, doi:10.6038/cjg20150821. |
| [47] | 杨积忠, 刘玉柱, 董良国. 2014. 变密度声波方程多参数全波形反演策略. 地球物理学报, 57(2):628-643, doi:10.6038/cjg20140226. |
 2016, Vol. 59
2016, Vol. 59



