2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
地震层析成像是地球内部物理学发展的一个重要环节,是研究地球内部非均匀结构和动力学过程的最重要工具.20世纪70年代以来,基于射线理论的地震层析成像发展迅速,加深了人们对地球内部结构的认识(Aki and Lee,1976),取得了一系列重大发现,如发现活火山前缘的低速体及对俯冲板块边界清晰成像等(Zhao et al.,1994;Bijwaard et al.,1998;Huang and Zhao,2006;Li et al.,2008).然而,传统的地震层析成像基于射线理论,假定地震波为无限高频,射线轨迹则依据费马最小走时原理,台站接收到的地震波走时差异只与射线路径上的速度结构有关,忽略了射线路径以外结构的影响,因而无法对非均匀性很强的复杂地质构造进行成像(Rawlinson et al.,2010).
波前愈合效应的发现使得全球层析成像从基于射线理论向基于有限频率理论过渡(Liu and Tromp,2008).图 1为射线理论与有限频理论对比卡通图.对于有限频率的地震波,射线路径上异常体引起的波前异常,会逐渐向射线路径旁边扩散,故使波前异常越来越不明显(江燕和陈晓非,2011).波前愈合造成初至波的幅度越来越小,直至堙没在噪声中,这就造成了从波形上读取初至走时的误差.有限频率层析成像的关键是计算“有限频率”敏感核,或者称之为“Fréchet”敏感核,获得有限频率敏感核的途径很多,包括面波格林函数法(Marquering et al.,1999)、体波射线理论(又称为香蕉-甜甜圈理论)(Dahlen et al.,2000;Hung et al.,2000)、面波射线理论(Zhou et al.,2004)、简正波理论(Zhao et al.,2000;Zhao et al.,2005)、伴随波场理论等(Montelli et al.,2004;Tromp et al.,2005).
 | 图 1 有限频率敏感核与射线理论争论的焦点在于全球尺度层析成像中的分辨率的提升(Liu and Gu,2012)Fig. 1 The heated debate centered on the resolution improvement of global tomographic models based on finite-frequency sensitivity kernels vs. simple ray approximation(Liu and Gu,2012) |
考虑到射线理论忽略了地震波频率对速度结构不同的解析能力,Woodward于20世纪90年代重新改写了不同频率的单频波走时异常与空间速度场变化的关系.90年代末,Marquering等基于Born近似理论提出了地震波三维有限频理论.2000年,Dahlen和Zhao两个研究组分别创建了球对称初始介质中的三维体波有限频走时kernel理论体系.Dahlen等(2000)使用WKBJ近似求得球对称初始介质中的格林函数和波场,它需要远场条件,并要求射线路径远离速度界面.在实际应用中,它还需要追踪出中心射线,才能用旁轴近似方法在射线中心坐标系中求出中心射线外的kernel值,所以不是严格的波动方程层析成像,或许称之为“射线有限频”理论更恰当(江燕和陈晓非,2011).Zhao等(2000)用normal model理论计算的体波波场在球对称初始介质中严格符合波动方程,故在速度界面附近更精确.
基于Born近似推导的有限频率敏感核在有限频理论中占有重要地位,但基于一阶 Born近似与相关走时一阶近似相结合的有限频率线性走时理论允许的最大速度扰动为10%,对于速度变化剧烈的区域无能为力(Mercerat and Nolet,2013; 江燕和陈晓非,2014).因而作者推导了基于二阶Born近似的有限频率敏感核,使得其能够适用于速度变化剧烈的区域,目前国内外尚未有基于二阶Born近似推导的有限频率敏感核的论文发表.
随着有限频理论的不断发展,有限频层析成像逐渐应用于研究多尺度的地球内部结构问题(Hung et al.,2005;Zhou et al.,2005; Gautier et al.,2008).国内研究人员也进行了一些有限频率层析成像的相关研究,但总体上还处于起步阶段(刘玉柱等,2009;杨峰等,2010;鲁来玉等,2011; 童平,2012).我国地质构造复杂,多旋回的构造背景和“块带镶嵌、多层叠覆”的构造特征使得我们需要相比于射线层析成像分辨率更高的有限频层析成像方法对深部构造进行精确刻画,故有限频层析成像在我国有着广阔的应用前景.
2 基于一阶Born近似的有限频敏感核对于速度为c的P波或S波,走时延迟的Fréchet 敏感核定义为走时延迟δT与速度扰动δc之间的线性积分关系(Tong et al.,2011):

其中,下标s,r和q分别代表震源、台站和地震波传播过程中经过的介质中某点,Kc(rq;rr;rs)是点rq处的Fréchet敏感核,积分区域是整个地球体积⊕.
地震波在均匀介质中传播,满足频率域的声波方程,对于震源以外的区域:
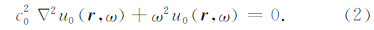
假定入射波场是平面波形式:

其中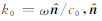 是波传播方向的单位矢量,并且 ▽ 2u0=-k02u0=-(ω2/c02)u0,将位移场和速度场均分解为背景场和扰动场的叠加:即u(r,ω)=u0(r,ω)+δu(r,ω)和c(r)=c0+δc(r ).对于震源区以外的扰动介质,方程(2)可以写成:
是波传播方向的单位矢量,并且 ▽ 2u0=-k02u0=-(ω2/c02)u0,将位移场和速度场均分解为背景场和扰动场的叠加:即u(r,ω)=u0(r,ω)+δu(r,ω)和c(r)=c0+δc(r ).对于震源区以外的扰动介质,方程(2)可以写成:

将方程(4)减去方程(2)并基于一阶Born近似略去二阶小量,得到散射场δu(r,ω)满足如下方程:
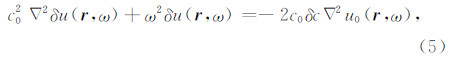
将 ▽ 2u0=-k02u0=-(ω2/c02)u0代入:
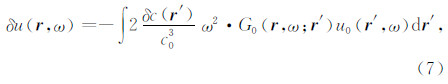
方程(6)有着如下形式的积分解:
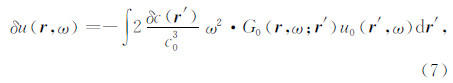
其中,G0(r,ω; r ′)为无扰动速度场c0中 r ′点在台站的格林函数,利用Rytov近似并结合方程(1),最终得到常速度模型中有限频率走时敏感核的解析表达式(Tsr,Tsq和Tqr分别表示震源至台站、震源至散射点和散射点至台站的走时)(童平,2012):
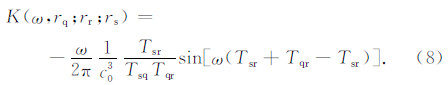
图 2为有限频率走时敏感核空间分布示意图,震源坐标(5 km,5 km),接收点坐标(15 km,45 km),地震波主频1 Hz,介质速度5 km·s-1.
 | 图 2 有限频走时敏感核分布图 五角星代表震源,三角形代表台站Fig. 2 The distribution of finite-frequency travel sensitivity kernel Star is source,triangle is station. |
在弹性介质中,声波方程的总波场可以用以下形式表示:
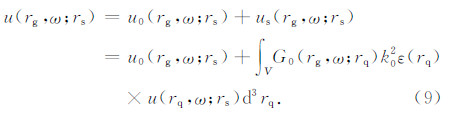
式中,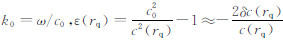 ,方程(9)就是著名的Lippmann-Schwinger方程,它表示非均匀介质中的地震波场可以看成背景介质中的地震波场和有扰动介质的散射波场总和.将方程(9)循环迭代,则可以得到Born散射序列:
,方程(9)就是著名的Lippmann-Schwinger方程,它表示非均匀介质中的地震波场可以看成背景介质中的地震波场和有扰动介质的散射波场总和.将方程(9)循环迭代,则可以得到Born散射序列:
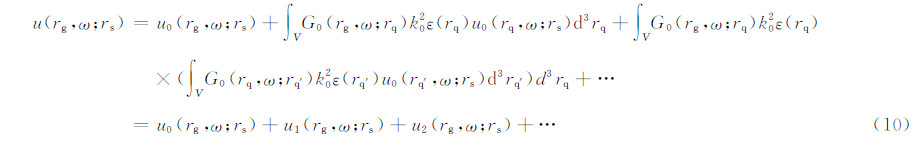
Born序列中第一项表示在背景介质中从源点到接收点传播的直达波场;第二项是积分形式,表示所有一次散射的地震散射波场叠加(rs→rq→rg),即通常所用到的一阶Born近似中的扰动场;第三项表示二次散射的地震波场叠加(rs→rq→rg),依此类推(注:此处二次散射是指经过了两个散射点的散射,并非直接由震源经第二散射点至台站的散射,与方程(10)中右边第三项相对应,本文中二次散射皆为此意),图 3为两次散射示意图.
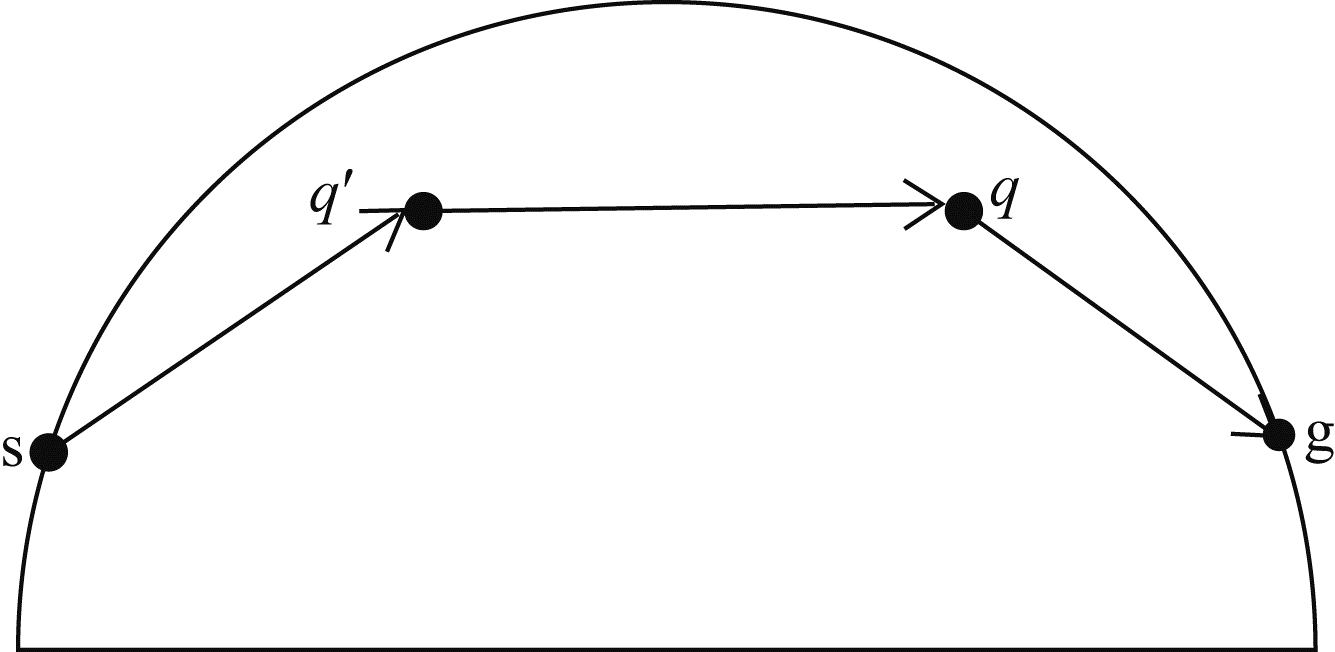 | 图 3 两次散射地震波传播示意图(震源s,台站g)Fig. 3 Seismic wave propagation with two scattering(source s,station g) |
当前有限频层析成像中,Fréchet敏感核的推导大都借助一阶Born近似,但这只适用于弱散射介质的情况,无法对速度扰动较大的介质进行准确成像.下面基于二阶Born散射推导均匀介质中Fréchet敏感核的解析表达式,并将其推广到非均匀介质中.
由方程(10)可知:

令:
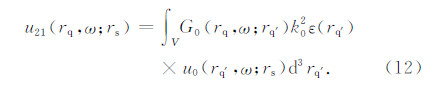
考虑背景场为均匀介质、脉冲点源激发这一特殊情况,三维均匀介质中,格林函数具有解析表达式:

将方程(13)代入方程(12)得

注意到方程(14)有一个关键量ω2,它代表了时间域的二阶微商.方程(14)是振荡积分,直接求解比较困难,我们利用傅里叶变换将其转换到时间域:
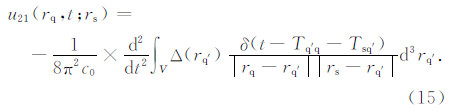
此处δ(t)是Dirac-delta函数,且
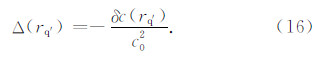
对于走时t>Tsg,定义散射体积Vt为0≤Δt≤t-Tsg,根据Zhao等(2005),散射体Vt的横截面可以写为
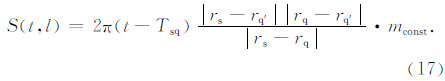
式中,mconst是单位为 km·s-1的单位量,为的是使方程(17)两边单位一致.假定扰动能够延伸并且光滑,我们可以取Δ(rq′)=Δ(l),因而方程(15)可以重写为走时和射线长度的积分:

取震源到q点(s→q)射线路径上平均扰动为δc,则:
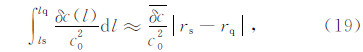
将式(19)代入方程(18)中得:
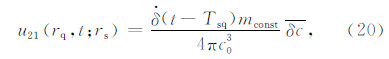
对(20)式利用傅里叶变换,转换到频率域:
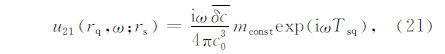
联合方程(11)、(21),得出二次散射场:
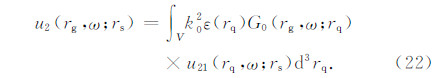
最终,总散射场δu(rg,ω;rs):
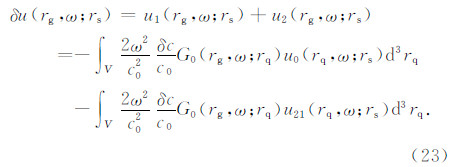
根据Rytov近似,走时扰动ΔT与散射场之间关系如下(Snieder and Lomax,1996;Spetzler and Snieder,2001):

将方程(23)代入方程(24),并根据方程(1)可得:
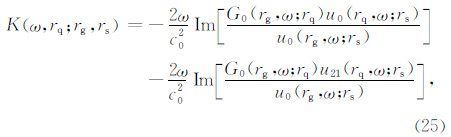
考虑震源为脉冲点源激发的情况,则:
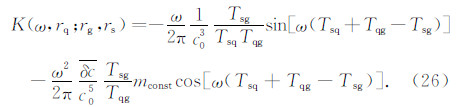
二阶Born近似 Fréchet敏感核可以看成一次散射的Fréchet敏感核和二次散射的Fréchet敏感核相加(注:此处的二次散射是指两个散射点,与之类似是三个散射点的三次散射、四个散射点的四次散射等,因为本文是基于二阶Born近似,故高于二次散射的情况暂不考虑),即:
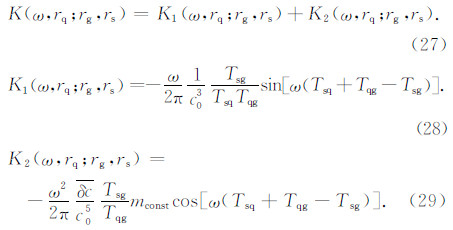
方程(26)、(29)中得到的有限频率敏感核中包含平均速度扰动项,这与基于一阶Born近似或其他方法得到的敏感核不同.推导有限频率敏感核的目的就在于其与模型参数(如速度等)的分离,以便进行反演.实际上,方程(26)和(29)中的平均速度扰动项并非变量,而是一个常数.在进行二阶Born近似有限频率反演时,可以根据研究区域之前的地球物理研究结果(如基于射线理论的层析成像结果等),预估平均速度扰动项的初值,而后在反演迭代的过程中根据上一次的迭代结果求出平均速度扰动值,然后进行下一次迭代.
二阶Born近似Fréchet敏感核(方程(26))只适用于均匀介质的情况,这极大地限制了它的实际应用,因为地球内部速度变化的是空间坐标的函数.因而需要对二阶Born近似Fréchet敏感核(方程(26))做适当的延拓才能应用到实际的地震层析成像中.假设背景速度c0(rq)具有三维变化时,方程(26)依然成立,则三维非均匀介质中二阶Born近似Fréchet敏感核解析表达式如下:
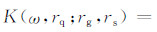
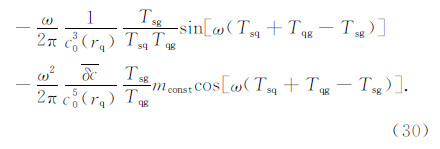
在介质速度变化平缓的情况下,用c0(rq)近似替代c0是可行的,方程(30)是由均匀介质中的解析表达式延拓而来,其在非均匀介质中的准确性还需要实际的反演成像结果验证.
4 二阶Born近似与一阶Born近似的Fréchet敏感核对比 4.1 Fréchet敏感核空间分布对比本文推导了基于二阶Born近似的走时延迟有限频率敏感核,并指出其为一次散射的Fréchet敏感核和两次散射的Fréchet敏感核之和.为了便于阐述,现将二阶Born近似走时Fréchet敏感核、一次散射的走时Fréchet敏感核和二次散射的走时Fréchet敏感核分别简写为总Fréchet敏感核、一次Fréchet敏感核和二次Fréchet敏感核.
(1)当平均速度扰动为1% 时(图 4),二次Fréchet敏感核总体上很微弱,只是在接收点附近出现极值.二次Fréchet敏感核与一次Fréchet敏感核一个很大的区别是二次Fréchet敏感核在震源至接收点的射线路径上取值并不为0,它不是中空的.总Fréchet敏感核同一次Fréchet敏感核差别很小,可近似认为二者相同.
 | 图 4 平均速度扰动1%时Fréchet敏感核空间分布对比 (a)一次Fréchet敏感核;(b)二次Fréchet敏感核;(c)总Fréchet敏感核. 地震波主频1 Hz,介质速度5 km·s-1,震源坐标(5 km,0 km),接收点坐标(15 km,45 km). Fig. 4 The comparison of Fréchet kernel when velocity perturbation is 1% (a)Primary scattering Fréchet kernel;(b)Two scattering Fréchet kernel;(c)Total scattering Fréchet kernel. Seismic wave frequency is 1 Hz,velocity is 5 km·s-1,source(5 km,0 km),receiver(15 km,45 km). |
(2)当平均速度扰动为2% 时(图 5),二次Fréchet敏感核依旧微弱,但相比于图 4中的二次Fréchet敏感核较强,接收点处出现极值的范围亦大于图 4. 总Fréchet敏感核同一次Fréchet敏感核相比并非中空,两者已经有明显不同.
 | 图 5 平均速度扰动2% 时Fréchet敏感核空间分布对比 图注说明同图 4. Fig. 5 The comparison of Fréchet kernel when velocity perturbation is 2% Figure note is the same as Fig. 4. |
(3)当平均速度扰动为5% 时(图 6),二次Fréchet敏感核已经较强,出现极值的范围已经很大,总Fréchet敏感核与一次Fréchet敏感核差别很大,即表明此时已经不能忽略二次散射的地震波.
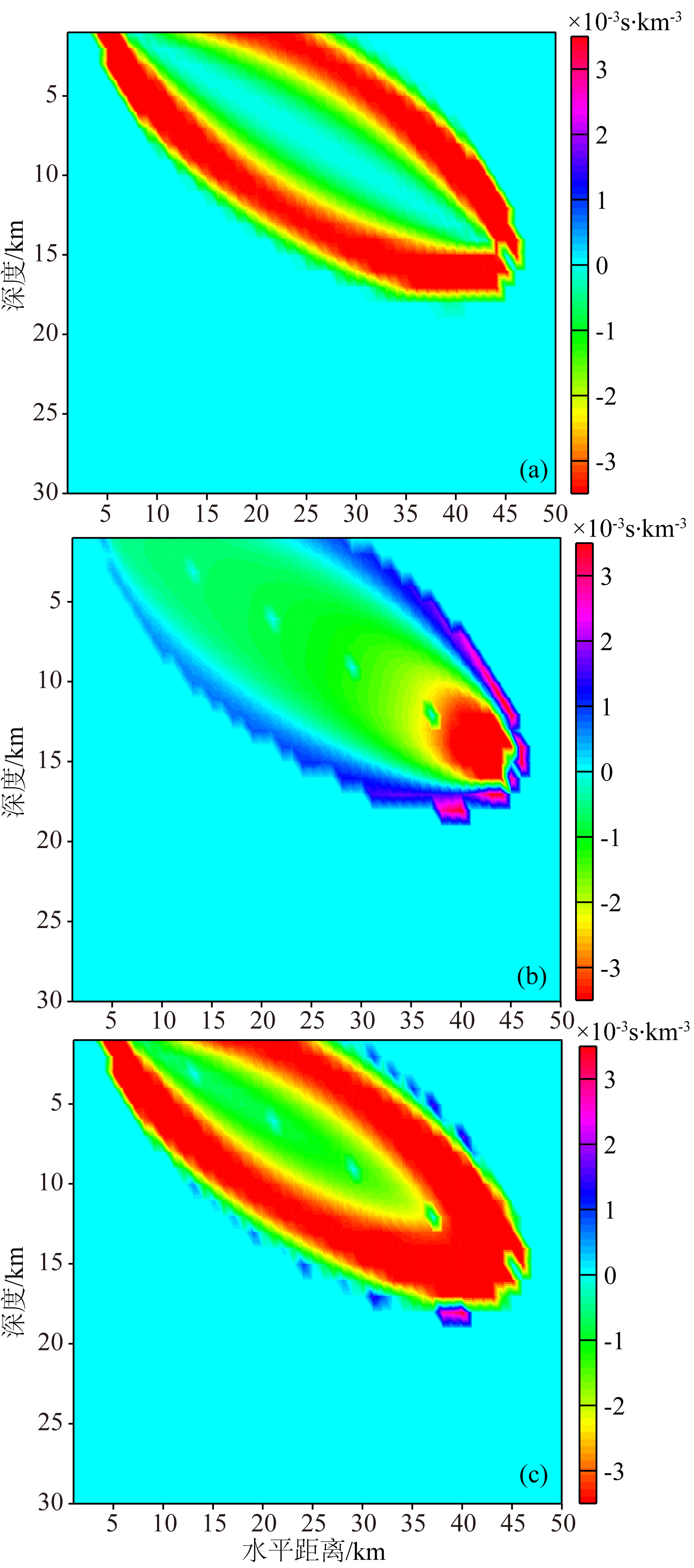 | 图 6 平均速度扰动5%时Fréchet敏感核空间分布对比图注说明同图 4.Fig. 6 The comparison of Fréchet kernel when velocity perturbation is 5% Figure note is the same as Fig. 4. |
(4)当平均速度扰动为10% 时(图 7),二次Fréchet敏感核已经很强,二次Fréchet敏感核的空间的积分值已经接近一次Fréchet敏感核的空间积分值,表明此时二次散射地震波的总能量已经接近一次散射地震波的总能量.总Fréchet敏感核同一次Fréchet敏感核已经完全不同.
 | 图 7 平均速度扰动10%时Fréchet敏感核空间分布对比图注说明同图 4. Fig. 7 The comparison of Fréchet kernel when velocity perturbation is 10% Figure note is the same as Fig. 4. |
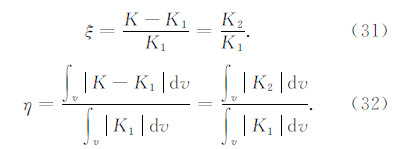
式中K,K1和K2分别表示总Frchet敏感核、一次Fréchet敏感核和二次Fréchet敏感核,积分项中v表示整个研究区域.误差函数ξ和η分别表征研究区域中每一点处和整个研究区域中二阶Born近似与一阶Born近似的Fréchet敏感核的差别.
图 8—11(仅以横坐标X=25 km为例计算了误差函数,其余各处计算结果与此类似,故不一一列出)可以看出,误差函数ξ和η随平均速度扰动的增加而增加.在平均速度扰动为1%时,η=0.077,并且ξ只在很小的范围内有较小的值,说明此时可以忽略二次散射;平均速度扰动为2%时,η值为0.15,此时已经不能忽略二次散射;而当平均速度扰动为5%时,η=0.38,ξ在较大范围内有较大的值,且由η值也可以看出此时二次散射与一次散射地震波的比值在1/3左右,表明此时已经不能忽略二次散射;平均速度扰动为10%时,η=0.77,二次散射地震波造成的走时异常与一次散射地震波已经很接近.
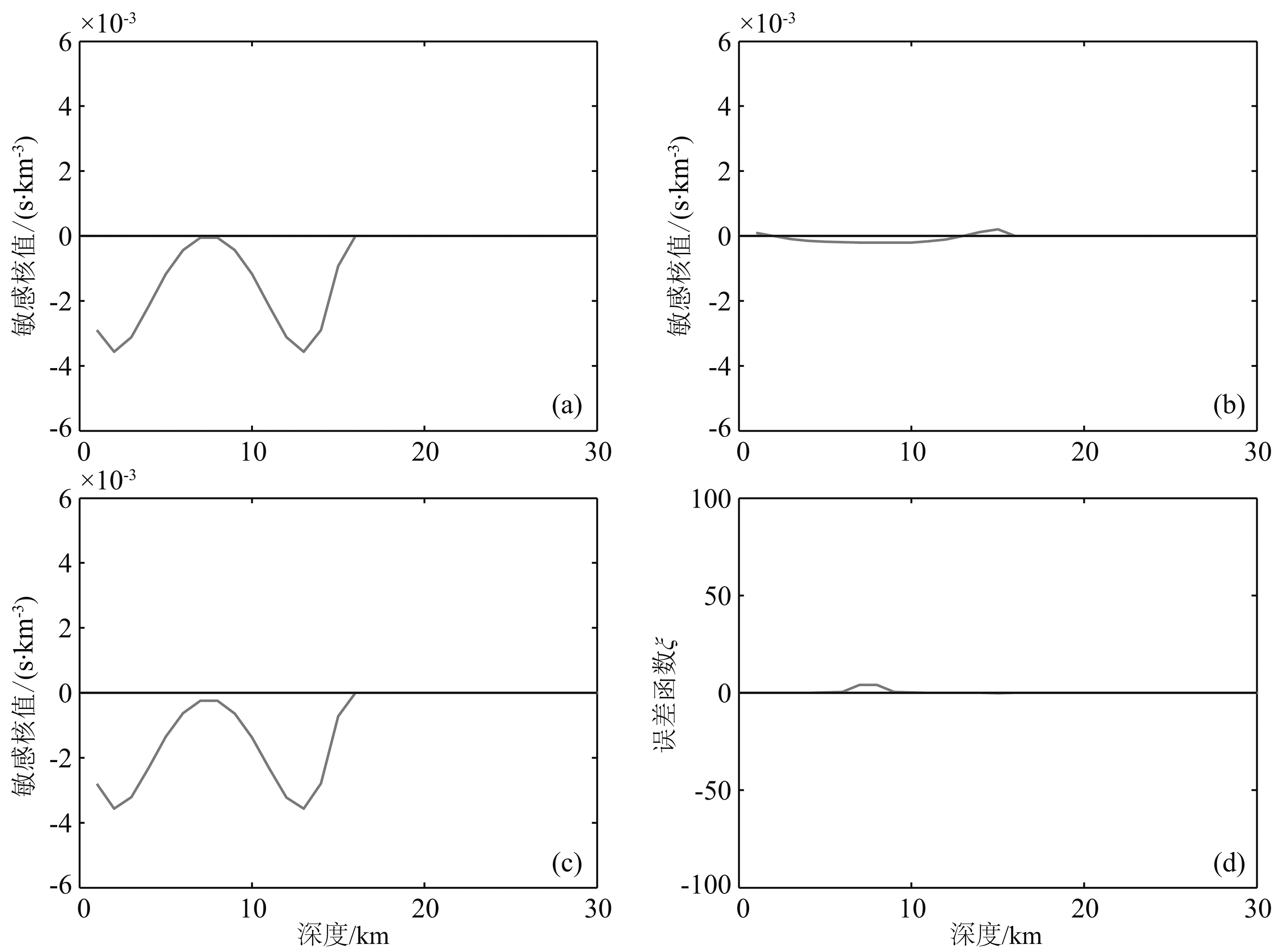 | 图 8 平均速度扰动1% 时Fréchet敏感核沿横坐标X=25 km处对比及误差函数 (a)一次Fréchet敏感核;(b)二次Fréchet敏感核;(c)总Fréchet敏感核;(d)误差函数ξ分布.震源坐标(5 km,0 km)、接收点坐标(15 km,45 km); 地震波主频1 Hz,介质速度5 km·s-1,η=0.077Fig. 8 The comparison of Fréchet kernel when velocity perturbation is 1% at X=25 km (a)Primary scattering Fréchet kernel;(b)Two scattering Fréchet kernel;(c)Total scattering Fréchet kernel;(d)Error function ζ. source(5 km,0 km)、receiver(15 km,45 km); Seismic wave frequency is 1 Hz,velocity is 5 km·s-1,η=0.077 |
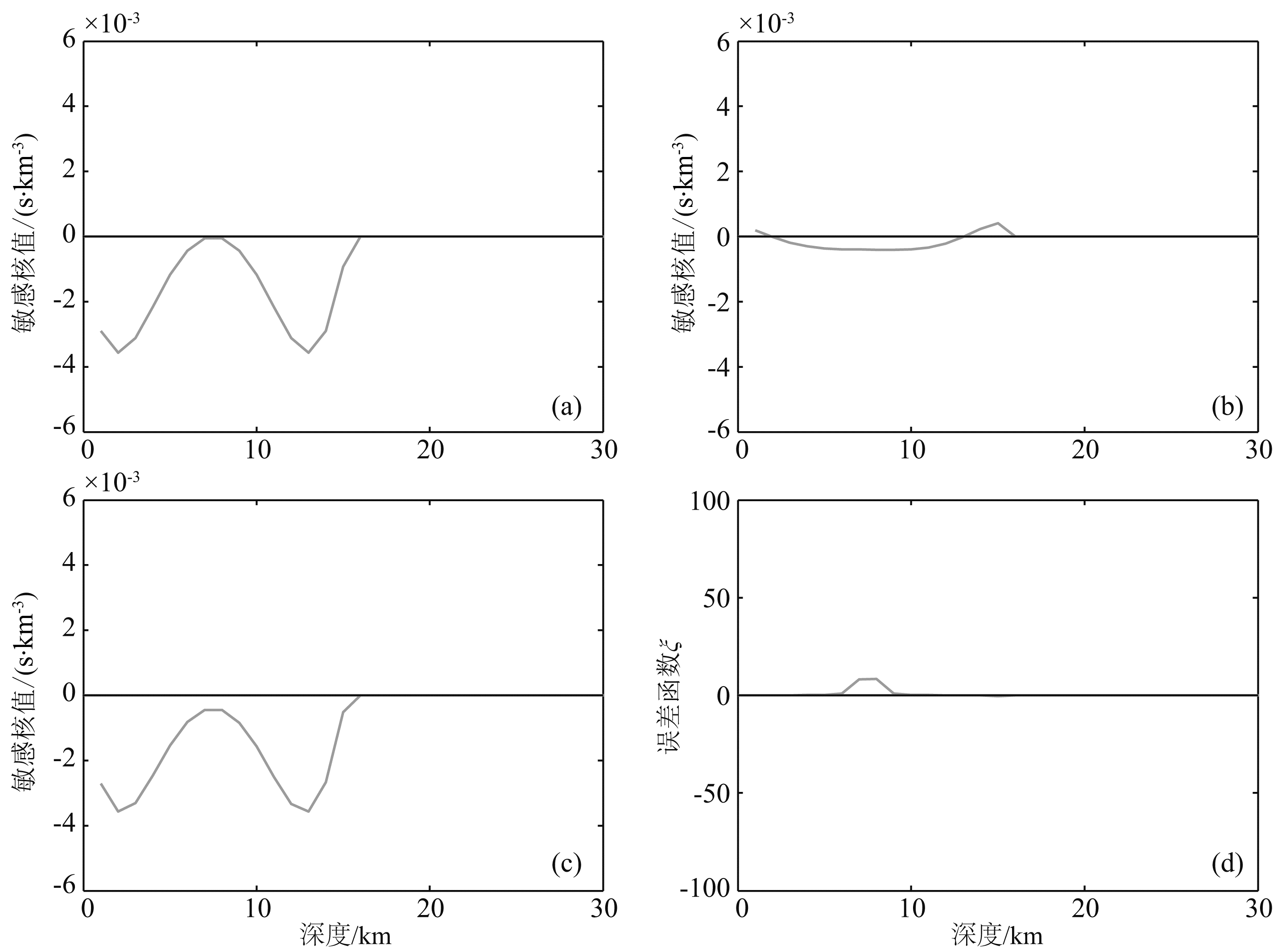 | 图 9 平均速度扰动2% 时Fréchet敏感核沿横坐标X=25 km处对比及误差函数 图注说明同图 8;η=0.15.Fig. 9 The comparison of Fréchet kernel when velocity perturbation is 2% at X=25 km Figure note is the same as Fig. 8; η=0.15. |
 | 图 10 平均速度扰动5%时Fréchet敏感核沿横坐标X=25 km处对比及误差函数图注说明同图 8;η=0.38.Fig. 10 The comparison of Fréchet kernel when velocity perturbation is 5% at X=25 km Figure note is the same as Fig. 8; η=0.38. |
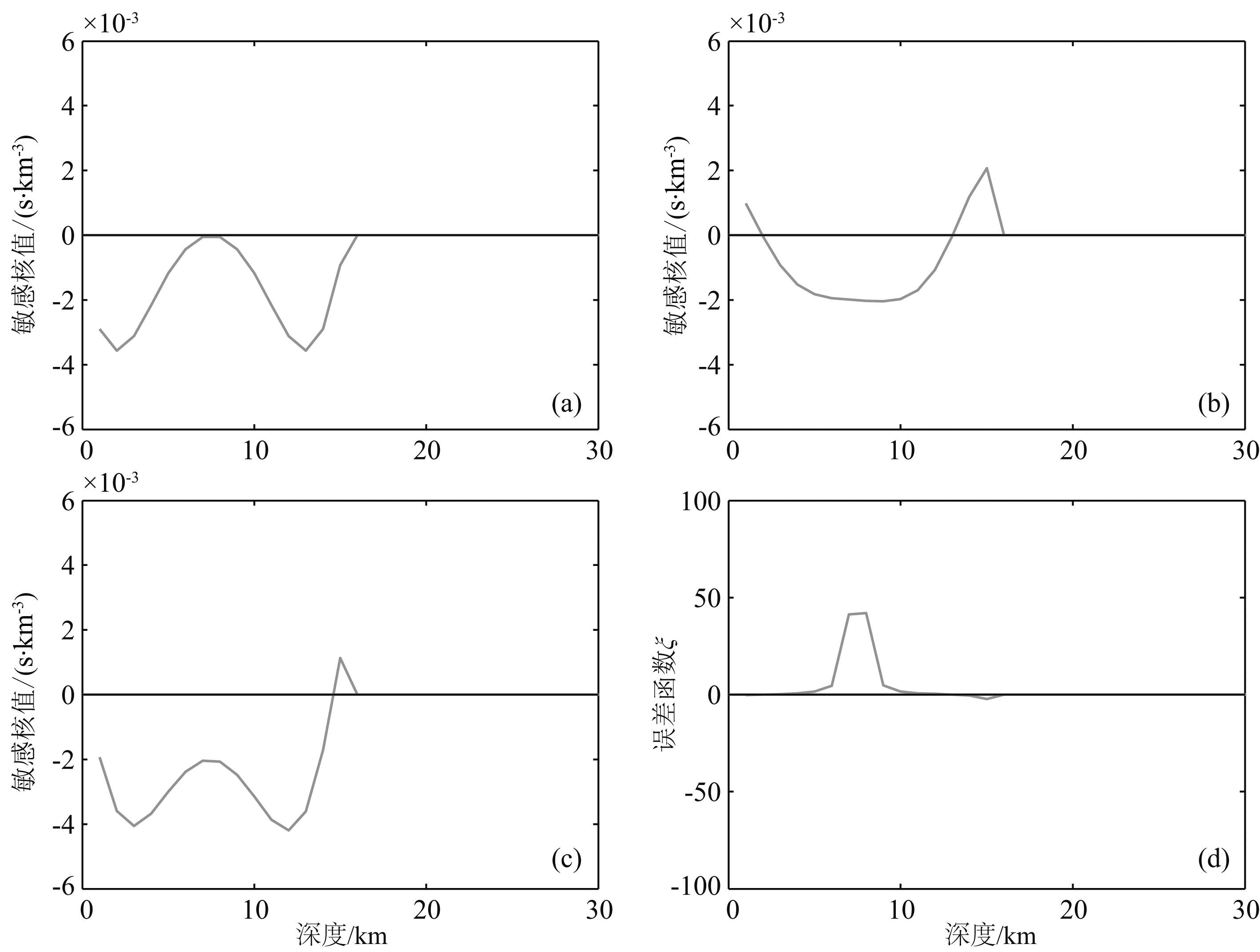 | 图 11 平均速度扰动10%时Fréchet敏感核沿横坐标X=25 km处对比及误差函数图注说明同图 8;η=0.77Fig. 11 The comparison of Fréchet kernel when velocity perturbation is 10% at X=25 km Figure note is the same as Fig. 8; η=0.77. |
江燕和陈晓非(2014)使用数值方法统计分析了Born近似相关走时误差,目标模型为高斯型三维随机介质.结果表明(见图 12),当最大速度扰动不超过1%时,Born近似相关走时误差可以忽略不计,当速度扰动超过2%时,Born近似相关走时误差较大,已不能忽略.本文的研究结果与其相一致.虽然一阶Born近似可适用的速度扰动很小,但将一阶 Born近似与相关走时一阶近似相结合获得的有限频率线性走时理论却适用于速度扰动小于10%的情况,具体解释参见文献江燕和陈晓非(2014)、 Mercerat等(2013).
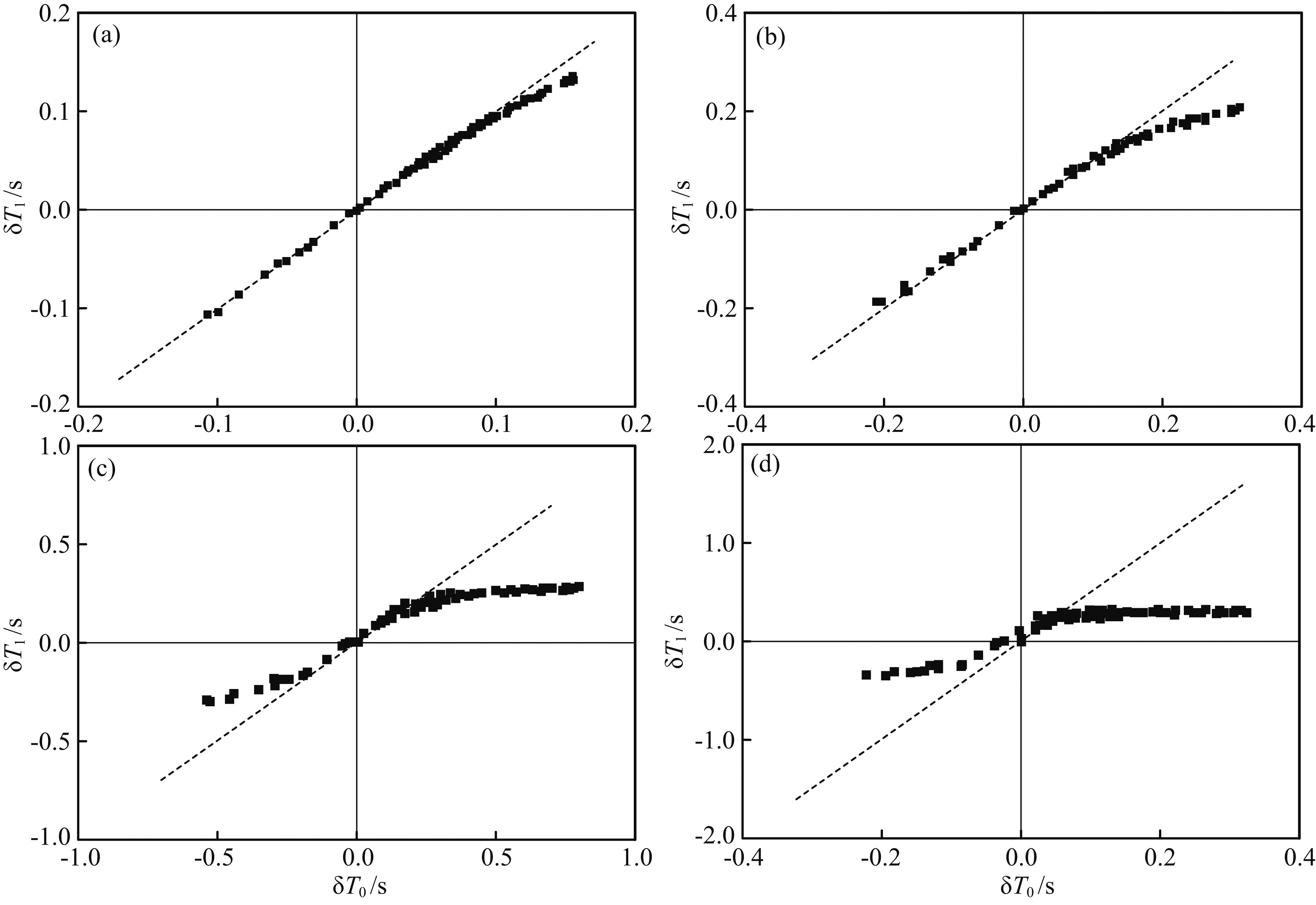 | 图 12 随机扰动情形下的一阶Born近似相关走时误差(a—d)最大速度扰动分别为1%,2%,5%,10% Fig. 12 The error of cross-correlation traveltime of Born approximation with r and om perturbations The maximum velocity perturbations of Figs(a—d)are 1%,2%,5% and 10%,respectively |
本文同样使用了数值统计方法分析二阶Born近似下的相关走时误差,目标模型也为三维高斯型随机介质(图 13).震源位于YOZ平面上,坐标为(0 km,50 km,50 km),接收点共100个,等间距(间距1 km)分布于X=100 km,Z=50 km的直线上,震源时间函数采用主频率为10 Hz的雷克子波,采用江燕和陈晓非(2014)相同的方法得到相关走时误差图(图 14). 由图 14可以看出,在最大速度扰动2%时,二阶Born近似相关走时误差可以忽略,当最大速度扰动超过5%时,Born近似相关走时误差较大,这表明了二阶Born近似相较于一阶Born近似能够更精确地描述高的速度异常.
 | 图 13 速度均值为3 km·s-1,最大速度扰动10%的高斯型三维随机介质Fig. 13 3D Gaussian r and om medium with the average of velocity is 3 km·s-1,the max velocity disturbance 10% |
 | 图 14 随机扰动情形下的二阶波恩近似相关走时误差(a—d)最大速度扰动分别为1%,2%,5%,10%.Fig. 14 The error of cross-correlation traveltime of second-order Born approximation with r and om perturbations The maximum velocity perturbations of Figs(a—d)are 1%,2%,5% and 10%,respectively. |
由二阶Born近似的敏感核(图 4—7)和公式(30)可以看出,二阶Born近似条件下有限频理论不同于射线理论之处为:射线路径上的速度异常对走时延迟贡献较小,而影响走时延迟最显著的速度异常位于射线路径周围区域(即第一菲涅尔带).此外,二阶Born近似走时有限频敏感核是实心的,这与一阶Born近似下有限频率敏感核“中空”不同.
5 讨论与结论现今地震层析成像理论与方法正由基于射线理论的层析成像向基于有限频率理论层析成像过渡,由于有限频率层析成像考虑了地震波的波前愈合效应,使得它更符合地震波在地下传播状态.普林斯顿大学的研究小组(Dahlen、Nolet和Hung等)基于体波射线理论,利用WKBJ近似推导出了三维体波有限频走时敏感核,将其应用到全球层析成像研究中发现了数个新的起源于核幔边界的全地幔柱,并发现射线理论对深部小尺度的速度异常幅值可能低估了30%到60%.Dahlen等(2000)的“射线有限频” 层析成像需要地震射线追踪,因而存在路径偏差,故并非严格的波动方程层析成像.此外,Zhao等(2000)基于Normal mode方法推导了三维体波有限频走时敏感核,Tromp等(2005)提出了基于伴随波场法(Adjoint-wavefield)有限频理论,Zhao等(2005)提出散射积分有限频(线性)理论等等.
进行有限频率层析成像的关键是推导和计算相应的有限频率敏感核(又称Fréchet敏感核),当前推导有限频率敏感核多基于一阶Born近似,但这只适用于弱散射介质情况,无法对地下速度变化剧烈的壳、幔介质结构准确成像.本文基于二阶Born近似推导了三维均匀介质中的走时有限频敏感核的解析表达式,并将其延拓到非均匀介质中.此外,我们经过数值计算,给出了基于二阶Born近似的走时Fréchet敏感核同基于一阶Born近似的Fréchet敏感核的对比图表明:当介质中速度扰动小于2% 时,基于二阶Born近似的有限频率敏感核与基于一阶Born近似的有限频率敏感核差别很小,可近似认为相同;当介质中速度扰动大于5% 时,基于二阶Born近似的有限频率敏感核与基于一阶Born近似的有限频率敏感核有较大不同,此时使用基于一阶Born近似的有限频率层析成像将无法得到准确成像图.
Dahlen等(2000)得到的走时Fréchet敏感核是“中空”的,即射线路径上的速度异常对走时延迟没有影响,这一度引起可很大的争议.他们得到的走时Fréchet敏感核“中空”的原因是走时Fréchet敏感核为走时差(Tsq+Tqg-Tsg)正弦的函数,射线路径上走时差为0,因而射线路径上的敏感度为0.本文推导的基于二阶Born近似走时有限频敏感核是实心的,这是同Dahlen等不同的地方,其原因乃是二次散射的走时敏感核是走时差(Tsq+Tqg-Tsg)余弦的函数,更深层的原因则是从震源到接收点的二次散射场是由震源到接收点的背景场的一阶微商与走时延迟的乘积.
本文推导出的基于二阶Born近似走时Fréchet敏感核在计算时需要事先预估整个研究区域的平均速度扰动,这在实际层析成像应用中虽然有难度,但是可以通过参考该区域以前的研究结果或相邻地区的速度扰动事先估计研究区域的平均速度扰动;同时我们将三维均匀介质中推导出的走时有限频敏感核直接延拓到三维非均匀介质中,有效性需要进一步确定.这些都是接下来需要进一步深化研究与探索问题.
| [1] | Aki K, Lee W H K. 1976. Determination of three-dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes:1. A homogeneous initial model. J. Geophys. Res., 81:4381-4399. |
| [2] | Bijwaard H, Spakman W, Engdahl E R. 1998. Closing the gap between regional and global travel time tomography. J. Geophys. Res., 103(B12):30055-30078. |
| [3] | Dahlen F A, Hung S H, Nolet G. 2000. Fréchet kernels for finite-frequency traveltimes-I. Theory. Geophys. J. Int., 141(1):157-174. |
| [4] | Gautier S, Nolet G, Virieux J. 2008. Finite-frequency tomography in a crustal environment:Application to the western part of the Gulf of Corinth. Geophysical Prospecting, 56(4):493-503. |
| [5] | Huang J L, Zhao D P. 2006. High-resolution mantle tomography of China and surrounding regions. J. Geophys. Res., 111(B9):B09305, doi:10.1029/2005JB004066. |
| [6] | Hung S H, Dahlen F A, Nolet G. 2000. Fréchet kernels for finite-frequency traveltimes-Ⅱ. Examples. Geophys. J. Int., 141(1):175-203. |
| [7] | Hung S H, Garnero E J, Chao L Y, et al. 2005. Finite frequency tomography of D" shear velocity heterogeneity beneath the Caribbean. J. Geophys. Res., 110(B7):B07305, doi:101029/2004JB003373. |
| [8] | Jiang Y, Chen X F. Born approximation paradox of linear finite-frequency theory. Acta Seismologica Sinica, 36(3):372-389. doi:10.3969/j.issn.0253-3782.2014.03.004. |
| [9] | Jiang Y, Chen X F. 2011. Review on the comparative study between finite-frequency tomography and ray-theoretical tomography. Progress in Geophys.(in Chinese), 26(5):1566-1575, doi:10.3969/j.issn.1004-2903.2011.05.008. |
| [10] | Li C, van der Hilst R D, Engdahl E R, et al. 2008. A new global model for P wave speed variations in Earth's mantle. Geochem. Geophys. Geosyst., 9(5):Q05018, doi:10.1029/2007GC001806. |
| [11] | Liu Q Y, Tromp J. 2008. Finite-frequency sensitivity kernels for global seismic wave propagation based upon adjoint methods. Geophys. J. Int., 174(1):265-286. |
| [12] | Liu Q, Gu Y J. 2012. Seismic imaging:From classical to adjoint tomography. Tectonophysics, 566-567:31-66. |
| [13] | Liu Y Z, Dong L G, Li P M, et al. 2009. Fresenl volume tomography based on the first arrival of the seismic wave. Chinese J. Geophys.(in Chinese),52(9):2310-2320. |
| [14] | Lu L Y, Ding Z F, He Z Q. 2011. Analysis of 3D sensitivity kernels of the finite frequency surface wave tomography in shallow subsurface.Chinese J. Geophys.(in Chinese),54(1):55-66. |
| [15] | Marquering H, Dahlen F A, Nolet G. 1999. Three-dimensional sensitivity kernels for finite-frequency traveltimes:the banana-doughnut paradox. Geophys. J. Int., 137(3):805-815. |
| [16] | Mercerat E D, Nolet G. 2013. On the linearity of cross-correlation delay times in finite-frequency tomography. Geophys. J. Int., 192(2):681-687. |
| [17] | Montelli R, Nolet G, Dahlen F A, et al. 2004. Finite-frequency tomography reveals a variety of plumes in the mantle. Science, 303(5656):338-343. |
| [18] | Rawlinson N, Pozgay S, Fishwick S. 2010. Seismic tomography:A window into deep Earth. Phys. Earth Planet. Inter., 178(3-4):101-135. |
| [19] | Snieder R, Lomax A. 1996. Wavefield smoothing and the effect of rough velocity perturbations on arrival times and amplitudes. Geopys. J. Int., 125(3):796-812. |
| [20] | Spetzler J, Snieder R. 2001. The effect of small-scale heterogeneity on the arrival time of waves. Geophys. J. Int., 145(3):786-796. |
| [21] | Tong P, Zhao D P, Yang D H. 2011. Tomography of the 1995 Kobe earthquake area:comparison of finite-frequency and ray approaches. Geophys. J. Int., 187(1):278-302. |
| [22] | Tong P. 2012. Seismic tomography methods and their applications[Ph.D. thesis](in Chinese). Beijing:Tsinghua University. |
| [23] | Tromp J, Tape C, Liu Q Y. 2005. Seismic tomography, adjoint methods, time reversal, and banana-doughnut kernels. Geophys. J. Int., 160:195-216. |
| [24] | Yang F, Huang J L, Yang T. 2010. Upper mantle structure beneath the Chinese capital region from teleseismic finite-frequency tomography. Chinese J. Geophys.(in Chinese), 53(8):1806-1816. |
| [25] | Zhao D P, Hasegawa A, Kanamori H. 1994. Deep structure of Japan subduction zone as derived from local, regional, and teleseismic events. J. Geophys. Res., 99(B11):22313-22329. |
| [26] | Zhao L, Jordan T H, Chapman C H. 2000. Three-dimensional Fréchet differential kernels for seismic delay times. Geophys. J. Int., 141(3):558-576. |
| [27] | Zhao L, Jordan T H, Olsen K B, et al. 2005. Fréchet kernels for imaging regional earth structure based on three-dimensional reference models. Geophys. J. Int., 95(6):2066-2080. |
| [28] | Zhou Y, Dahlen F A, Nolet G, et al. 2005. Finite-frequency effects in global surface-wave tomography. Geophys. J. Int., 163(3):1087-1111. |
| [29] | Zhou Y, Dahlen F A, Nolet G. 2004. Three-dimensional sensitivity kernels for surface wave observables. Geophys. J. Int., 158(1):142-168. |
| [30] | 江燕, 陈晓非. 2011. 有限频与射线层析成像比较研究综述.地球物理学进展, 26(5):1566-1575, dio:10.3969/j.issn.1004-2903.2011.05.008. |
| [31] | 江燕, 陈晓非. 2014. 有限频率线性理论的波恩近似佯谬. 地震学报, 36(3):372-389. |
| [32] | 刘玉柱, 董良国, 李陪明等. 2009. 初至波菲涅尔体地震层析成像. 地球物理学报, 52(9):2310-2320. |
| [33] | 鲁来玉, 丁志峰, 何正勤. 2011. 浅层有限频率面波成像中的3D灵敏度核分析. 地球物理学报, 54(1):55-66. |
| [34] | 童平. 2012. 地震层析成像方法及其应用研究[博士学位论文]. 北京:清华大学. |
| [35] | 杨峰, 黄金莉, 杨挺. 2010. 应用远震有限频率层析成像反演首都圈上地幔速度结构. 地球物理学报, 53(8):1806-1816. |
 2016, Vol. 59
2016, Vol. 59

