2. 山东省科学院激光研究所, 济南 250014;
3. 山东微感光电子有限公司, 济南 250103
2. Institute of Laser, Shandong Academy of Sciences, Ji'nan 250014, China;
3. Shandong Micro-sensor Photonics Limited, Ji'nan 250103, China
准确定位震源位置是利用微震监测系统对煤矿井下动力灾害进行监测预警的关键问题之一.通过在煤矿井下布置传感器,接收地下岩层破裂产生的震动波信号,结合传感器坐标、岩层波速等数据可实现震源位置反演.而传感器的布置受煤矿井下狭小巷道空间的制约,受此影响震源反演定位的误差将会大大增加.
针对煤矿井下工作面的微震监测,传感器只能安装在顺槽周围(叶根喜等,2008).为使传感器避免布置在同一水平面内,需要钻深孔安装,增加测点间垂向差值.但是长钻孔卡钻、塌孔等问题影响传感器的顺利安装.井下施工条件恶劣,深孔安装意味着施工难度的加大和成本费用的提高,同时钻孔深度是有限的.在地表进行矿井采空区安全监测和相邻矿井防盗采微震监测也面临同样问题.因而受限空间微震测点优化布置和已有测点监测数据非适定条件即病态条件下的震源高精度定位问题需要进行深入研究.
目前震源定位方法有十多种,空间定位精度在5~50 m之间(林峰等,2010;董陇军等,2011),其中线性定位法是其中的一类重要分支.震源坐标、传感器坐标与初始到时可以构成二次非线性方程组,把非线性方程组通过降维转化为线性方程组(李寅祺和祝永新,2009),可以用高斯消去法(李庆扬等,2008)求得精确解.但当线性方程组系数矩阵条件数很大时,用高斯消去法求方程解误差将会变大.当系数矩阵A的元素数值量级差别很大时,可采用行均衡或列均衡的方法,这时矩阵A的条件数可得到改善(刘建国,1999).Geiger法、联合定位法、相对定位法和双重残差法等线性定位方法都没有对因测点布置引起的病态问题进行研究(田玥和陈晓非,2002;金明培等,2014),且当只有有限测点监测到震动信号时,震源定位误差将大大增加.
微震震源定位是根据监测到时、波速等信息计算震源位置的反演问题,即数学中的反问题.Tikhonov和Arsenin (1977)和Phillips于20世纪60年代分别独立提出了求数学反问题稳定近似解的正则化方法.正则化方法包括截断奇异值分解、改进的截断奇异值分解、广义截断奇异值分解、衰减奇异值分解、最小熵原理、最大熵正则化、二次约束最小二乘法和截断完全最小二乘(Hansen,2007).目前应用较广的正则化方法是Tikhonov法.正则化参数是正则化理论中的重要参数,正则化参数的选择是正则化法的基础(王彦飞,2007).正则化参数λ控制赋予解范数和残差范数最小化的权重,平衡不稳定性和光滑性.正则化参数的选取分为两类:(1) 误差估计,即偏差原则(马成业等,2010),这种简单方法的主要问题是当选择的参数过大时,得到的是具有巨大正则化误差的过正则化解;(2) 从右端项提取必要的信息,包括L曲线准则,广义交叉验证(Generalized Cross-Validation,GCV)和近似最优准则.GCV有时会把相关噪声误认为是有效信号;而L曲线可以极好的分辨相关干扰(Hansen and O′Leary, 1993;Hansen,2001).逄焕东等(2004)针对微地震线性方程定位过程中的病态问题,采用Tikhonov正则化法进行迭代计算,发现Tikhonov正则化法比最小二乘法和正规解法收敛速度更快.曾小牛等(2015)利用λ和截止波数ωc的关系,得到了改进的正则低通滤波函数,成功应用于位场各阶垂向导数的换算.
最方便的图形化分析离散非适定问题的工具是L曲线,包括了全部的有效正则参数.L曲线是使解范数和残差范数同时最小化的折中方法,显示了这些量对正则化参数的依赖程度(Hansen,1997).Miller (1970)、Lawson and Hanson (1974)最早利用L曲线的方法处理非适定最小二乘问题.L曲线在联系Tikhonov正则化和病态问题时起到了核心作用.只有有限测点监测到震动信号且测点布置近乎在同一平面时,由测点坐标、到时等信息构造的震源求解矩阵很可能是病态的,基于L曲线准则的Tikhonov正则化法可提高此病态矩阵求解精度.
本文针对煤矿井下巷道受限空间微震监测中存在的传感器沿巷道、近乎平面布置问题,分析影响震源定位精度的因素,在对传感器布置进行优化的基础上,基于现场测试数据特点,对病态问题提出了先进行预处理再求正则解的方法.提出了对传感器安装位置原始坐标进行中心化的算法,以降低系数矩阵A、b之间的数值量级差距;构建了行平衡预处理的算子矩阵,以降低系数矩阵A的条件数;对经上述中心化和行平衡预处理后的数据进行奇异值分解(Singular Value Decomposition,SVD),利用L曲线法计算正则条件数,再计算Tikhonov正则解,并验证了正则解的适用性.
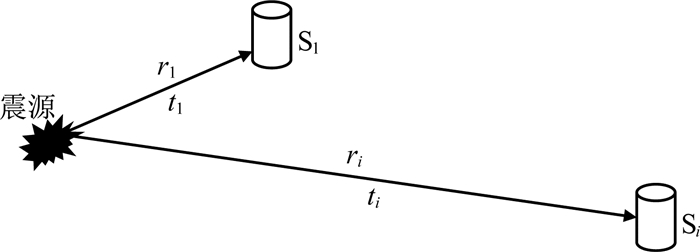
2 理论基础设未知震源大地坐标为(x,y,z),第i个传感器坐标为xi,yi,zi.如图 1所示,震源与第i个传感器Si之间的距离为
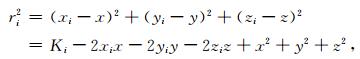
|
(1) |
|
图 1 震源与传感器位置关系 Fig. 1 The position relation between seismic source and sensors |
其中,Ki=xi2+yi2+zi2.
通过把二次非线性方程组降维变为一次线性方程组,可以求得震源坐标的精确解.设ri, 1为ri与r1差值,r1是距离震源最近传感器S1与震源之间的距离(李寅祺和祝永新,2009),则:
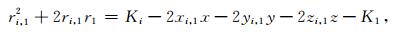
|
(2) |
其中,xi, 1=xi-x1,yi, 1=yi-y1,zi, 1=zi-z1,r1=(t1-t0)v,ri, 1=(ti-t0)v-(t1-t0)v=(ti-t1)v,如图 1所示,t1是地震波到达S1的时间,ti是地震波到达Si的时间,t0为微震发生的时间是未知量,r1是t0的函数,v为波速.写成矩阵的形式为
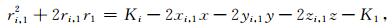
|
(3) |
为论述方便上式可以简写为

|
(4) |
对于线性方程组,设A为非奇异系数矩阵,则A的条件数为(李庆扬,2008):

|
(5) |
当A的条件数远大于1,即cond (A) > > 1时,则线性方程组是病态的,即A是病态矩阵.A的条件数越大,线性方程组越病态,用常规方法求得的解偏差越大(李庆扬等,2008;肖庭延等,2003).通常使用的条件数为cond (A)∞(刘建国,1999),因而本文在计算中采用式cond (A)∞计算线性方程组系数矩阵条件数.
3 病态问题处理方法测点布置是系数矩阵A病态与否的关键因素,为实现对目标区域岩体活动高精度监测,首先对测点布置进行优化;对优化后依然病态的问题,采用预处理加正则化处理的方法进行求解.
3.1 线性无关优化为实现震源三维空间定位,测点布置时,四个以上的测点不要布置在同一水平面上,因测点间z坐标相同,系数矩阵A的行列式detA=0,A为奇异矩阵,故A-1不存在,将导致方程组有无穷解或无解,即要保证detA > 0.
系数矩阵A的行向量或列向量的近似相关性,即向量间夹角非常小时,是矩阵病态的直接原因.因而测点在空间三个方向都要不等间距设置,尽量无序排列,以便于构建非奇异系数矩阵A,最终使基于直接法解线性方程组成为可能.即要满足:ai≠qaj和ci≠qcj,其中ai、aj是行向量,ci,cj代表列向量,q是任意实数.系数矩阵A两列或两行成比例,趋于完全重合时,条件数趋于正无穷大.
为监测足够宽广的区域,在测点平面坐标(xi,yi)基本确定的条件下,增大测点之间的安装深度差,可以有效降低矩阵A的条件数.
3.2 初始坐标中心化如果常数项b的微小变化,引起方程组AX=b解的巨大变化,此方程组即为病态方程组.设b有扰动δb,相应解X的扰动记为δx(刘建国,1999),则:

|
(6) |

|
(7) |
对某一确定的微震事件,ri, 1,xi, 1,yi, 1,zi, 1是定值,大小决定于测点间的相对位置关系,不受测点原始坐标取值大小的影响,但式(4)右端项可表示为

|
(8) |
从上式可以看出,x1,y1,z1的取值对b影响巨大.若初始坐标采用8位整数大地坐标表示x1、y1,将造成矩阵A和b之间数量级的巨大差距.因而需要把b转化成与A一样不受初始坐标影响的常数项,保证在正则化求解中减小解的误差.
对于给定的测点初始坐标(xi,yi,zi),本文提出了如下的中心化处理方法:

|
(9) |

|
(10) |
i=1,…,n.因为线性方程组中涉及到了5个测点坐标,因而只对参与计算的5个xi坐标进行算术平均.变换后均值为0,方差矩阵不变.以同样的方法对yi和zi进行中心化处理.用变换后的x′i,y′i,z′i计算式(4)右端项b.
3.3 行平衡预处理受制于监测范围宽广和节省成本简单快速安装的原因,xi, 1或yi, 1与zi, 1数量级通常相差巨大.采用如下方法对式(4)进行平衡化预处理,以降低系数矩阵的条件数.选择非奇异矩阵P∈Rn×n,使式(4)化为等价方程组:
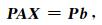
|
(11) |

|
(12) |
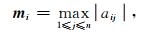
|
(13) |
式(12),是刘建国(1999)提出的,记为mmax.
本文提出了下面的基于2范数的对角矩阵构造法,记为m2,具体如下:

|
(14) |
ai为矩阵A的行向量,即A=[a1, a2, …, an]T,且存在‖PA‖2=1.在后面的数据处理部分,将比较两种方法的实际应用效果,选择最优的构造方法.
3.4 正则化反演式(4)中A是欧氏空间中的有界线性算子,是紧算子,当detA≠0时方程组存在唯一解,条件数较大时,问题是不适定的,即病态的.求解病态问题,需要在b变化不大的情况下,寻求稳定的近似解.正则化解xλ的定义(Tikhonov and Arsenin, 1977)为
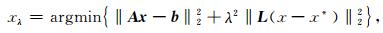
|
(15) |
λ为正则化参数,控制相对边界约束和残差范数最小化的权重,L为边界限制矩阵,x*为估计初值.
Tikhonov是直接化法,正则化模型即求解下面的最小二乘问题(ELDEN,1977):

|
(16) |
系数矩阵A的奇异值分解为

|
(17) |
ui是U中的行向量,vi是V中的行向量,i是行标.
标准形式的Tikhonov正则化模型,L=In,x*=0,正则解的计算方法(Hansen,2001)为
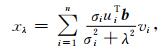
|
(18) |

|
(19) |
‖xλ‖2和‖Axλ-b‖2在判定λ时起到了重要的作用.过正则化作用于解时,将导致残差‖Axλ-b‖2太大;然而当欠正则化时,残差‖Axλ-b‖2较小,但是正则解将受数据误差的控制,导致‖xλ‖2将会很大.当两个量都需要控制时L曲线事实上是一条折中的曲线.
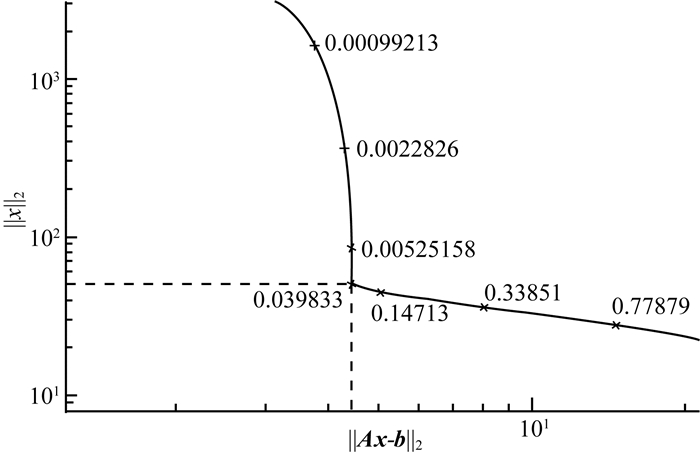
λ取为一组常量,代入式(18)和(19),求得xλ和b-Axλ,并以‖Axλ-b‖2为横坐标,以‖xλ‖2为纵坐标,得到L曲线.如图 2所示.
|
图 2 L曲线 Fig. 2 The L-curve |
L曲线准则,即在L拐角处最大曲率对应的正则化参数即为最优正则化参数.从图中无法直接得到精确的最优正则化参数,图 2中最优正则化参数为0.039833,通过如下方法求解其精确数值解.
计算L曲线的曲率k(Hansen and O′Leary,2001):

|
(20) |

|
(21) |
以k为纵坐标,λ为横坐标做图,曲率最大值对应的λ即为最优正则参数.
3.6 病态问题处理步骤测点布局阶段进行线性无关优化,从源头上避免病态问题.随着工作面推进,可用测点减少,剩余测点或优化后测点构成的系数矩阵不可避免的出现病态问题时,需要进行预处理和正则化求解.具体数据处理步骤如下:
(1) 选定初始到时最小的测点为基准点,另外选定4个测点,构建式(4);
(2) 计算系数矩阵A,并求cond (A)∞,若cond (A)∞ < 10,则用高斯消去法直接求解,并结束计算;假如cond (A)∞≥10,则执行步骤(3);
(3) 进行中心化预处理和行平衡;
(4) 进行正则化处理,得到正则近似解.
4 现场试验 4.1 测点布置某矿属特厚煤层矿井,采矿方法为综采放顶法,为适时监测岩体破裂,预测矿井动力灾害,在正在回采工作面安装了一套微震监测系统,共11个测点布置于轨道顺槽顶底板内,测点布置如图 3所示,黑色填充圆点表示安装在顶板的传感器,正方形代表安装在底板的传感器,标定炮孔在底板中.各测点坐标及P波初始到时数据如表 1所示.

|
图 3 测点布置图 (a)平面图(x-y坐标);(b)剖面图(y-z坐标). Fig. 3 Monitoring points arrangement graph (a) Planar graph (x-y coordinates); (b) Profile graph (y-z coordinates). |
|
|
表 1 测点坐标及到时数据 Table 1 Monitoring points coordinates and arrival time |
表 1中S1、S2…S11为各测点编号,xi、yi、zi为各测点三维坐标,ti为P波初至时刻.标定炮的空间坐标为(3899.89,5097.48,1009.30),S1为距离标定炮最近的基点,任取两个传感器Si和Sj,二者到标定炮的距离分别为di和dj,震动波到时分别为ti和tj,则基于上述两个传感器的波速计算公式为
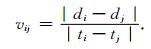
|
(22) |
分别取4组底板测点组合和4组顶板测点组合,选取间隔最大的测点、跨越轨顺的测点、间隔最近的测点等分别计算对应的波速vij,再对全部vij算术平均,得到波速为4.35 m·ms-1.具体如表 2所示.
|
|
表 2 波速计算 Table 2 The wave velocity calculation |
通过设计倾角、深度变化的钻孔实现测点三维方向差异性优化布置.但仍然受限于巷道狭小空间,底板测点z坐标最大间距仅为1.64 m,而顶板测点z坐标最大间距为10.56 m.但y方向测点间距最大值为174 m.对因空间布置引起的病态问题,需要进行分析处理.由于系统布置时未作线性无关优化,因而S1、S3、S7、S10基本在同一水平面内.在上述底板测点参与的震源定位反演中,下面四组数据出现了严重病态问题.各组合包含的测点编号为:组合一(S1、S3、S4、S7、S11),组合二(S1、S3、S9、S10、S11),组合三(S1、S3、S6、S7、S10),组合四(S1、S4、S7、S9、S11),其中S1为距离标定炮最近的基点.具体方程解如表 3所示.各组合分别采用m2、mmax构造的对角矩阵进行行平衡,计算的条件数如图 4所示.分别采用高斯消去算法(高斯消去)、正则化算法(正则化)、中心化处理后再求正则化解(中心化正则化)和
|
|
表 3 四组病态问题数据优化处理 Table 3 The optimization processing of four groups data with ill-posed problems |

|
图 4 各组合条件数 Fig. 4 Condition number of four groups |
中心化加行平衡预处理再求正则化解(预处理正则化)得到的四组解的误差如图 5所示.

|
图 5 不同算法解误差 Fig. 5 The error of different algorithms |
从图 4可以看出,各组合的三类条件数基本是递减的,行平衡处理前条件数最大,采用m2构造的对角矩阵计算的条件数降低最明显.从图 5可以看出,四种算法得到的解误差也呈递减变化规律,高斯消去解误差最大,预处理正则化法震源定位反演效果最好.
不做预处理,条件数较大,四组震源组合中,最小的条件数为6062.69,最大值为14834.2都属于病态方程组.直接用高斯消去法进行震源定位处理,得到的震源坐标误差最小为2411.34 m,最大为10558.34 m,结果都是没有意义的.
不做预处理,直接用L曲线计算正则化参数、用Tikhonov正则化算法计算得到正则解,相比高斯消去法,对应组合的解都得到了改善,误差最小为2370.15 m,最大为2514.29 m,仍然与实际结果相差巨大,没有应用价值.
通过分析初始系数矩阵A和b的特点发现,A中元素绝对值最大量级为102而b中元素绝对值最大量级为106,初步分析是数量级差别大造成的解的巨大误差.对四组数据进行中心化预处理,处理后矩阵A没有变化,因而条件数没有降低,右端项b量级明显降低,其元素绝对值最大量级为104,大多数为103.对中心化预处理后的数据,若用高斯消去法求解,定位误差将得不到改善.利用Tikhonov正则化解法,大大提高了定位精度,组合一和组合四定位误差缩小到10 m以内,最小定位误差仅为7.28 m,平均定位误差为14.4 m,定位结果已经达到可以实际应用的水平.
对上述四组数据进行中心化预处理后继续进行行平衡预处理,cond (A)∞得到明显改善,最大值由14834.2降为10818.如图 4所示,组合一、二、四采用m2构造的对角矩阵计算的条件数都比采用mmax构造的对角矩阵计算的条件数小,只有组合三的条件数二者基本接近,因而本文提出的以2范数构造对角矩阵进行行平衡预处理效果更好.但是方程组仍然是病态的,需要进行正则化处理.行平衡预处理后,组合一和组合二的Tikhonov正则解改善明显,组合一误差最小仅为3.09 m,组合三误差减小了0.1 m,只有组合四的误差增大了1.06 m.相比中心化正则化法定位精度得到了进一步提升,平均定位误差减小为11.6 m.测点布置、信号品质和平均速度等因素,都会对解误差产生影响.
5 结论(1) 采用线性方法进行震源定位反演,需要对测点布置做线性无关优化,4个以上的测点不要布置在同一水平面上,测点布置三维方向非等间距,做到无序排列,增大测点之间的安装深度差.
(2) 测点初始坐标取值是影响震源定位结果误差水平的最主要因素.基于微震数据的特点提出了中心化预处理法,在不影响系数矩阵A的情况下,极大的降低了常数项b的数量级,定位误差大大降低.中心化前没有任何意义的定位结果,中心化后得到的定位结果达到了可以实际应用的水平.
(3) 提出了基于系数矩阵A行向量2范数构建对角矩阵P对方程组进行行平衡预处理,有效降低了系数矩阵A的条件数.但是条件数的改善是有限度的,对于达不到优化预期的严重病态方程组,必须要进行正则化处理.
(4) 若直接利用微震监测数据求正则化解,则定位误差依然很大.本文提出的对微震监测数据进行预处理后求正则化解的方法,可极大的提高解的精度.最小定位误差可以达到3.09 m,四组数据中有三组的震源定位反演误差小于10 m,平均定位误差为11.6 m,达到了实际工程应用要求.
总之,测点优化布置、高质量采样信号、速度模型优化等因素是获得高精度震源位置的基础.本文从常规方法认为无效的无法处理的监测数据中提取出了有用的信息,在有限测点监测到信号的情况下,也能得到震源精确位置.本文为微震震源定位病态问题提供了一种全新的反演算法,促进了微震监测技术的发展.
| DongL J, Li X B, Tang L Z, et al. 2011. Mathematical functions and parameters for microseismic source location without pre-measuring speed. Chinese Journal of Rock Mechanics and Engineering, 30(10): 2057-2067. | |
| Eldén L. 1977. Algorithms for the regularization of ill-conditioned least squares problems. BIT Numerical Mathematics, 17(2): 134-145. DOI:10.1007/BF01932285 | |
| Hansen P C, O'Leary D P. 1993. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput., 14(6): 1487-1503. DOI:10.1137/0914086 | |
| Hansen P C. 1997. Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion. Philadelphia: SIAM. | |
| Hansen P C. The L-Curve and its Use in the Numerical Treatment of Inverse Problems.Southampton: WIT Press, 2001. | |
| Hansen P C. 2007. Regularization Tools Version 4. 0 for Matlab 7.3. Numerical Algorithms, 46(2): 189-194. DOI:10.1007/s11075-007-9136-9 | |
| Jin M P, Wang R J, Dai S G. 2014. Improvement and case test of linear method for single event seismic location. Acta Seismologica Sinica, 36(5): 757-759. | |
| Lawson C L, Hanson R J. 1974. Solving Least Squares Problems. Englewood Cliffs: SIAM. | |
| Li Q Y, Wang N C, Yi D Y. Numerical Analysis.(5th ed).Beijing: Tsinghua University Press, 2008. | |
| Li Y Q, Zhu Y X. 2009. Capsule in vivo environment's TDoA wireless location algorithm and simulation. Microcomputer Information, 25(22): 134-135. | |
| Lin F, Li S L, Xue Y L, et al. 2010. Microseismic sources location methods based on different initial values. Chinese Journal of Rock Mechanics and Engineering, 29(5): 996-1002. | |
| Liu J G. 1999. Matrix Condition Number and Ill-Posed Improvement [Master thesis] (in Chinese). Chongqing: Chongqing University. | |
| Ma C Y, Yang S L, Li S P. 2010. A regularization method of ill-conditioned linear equations. Journal of Gansu Science, 22(4): 33-35. | |
| Miller K. 1970. Least squares methods for ill-posed problems with a prescribed bound. SIAM J. Math. Anal., 1(1): 52-74. DOI:10.1137/0501006 | |
| Pang H D, Jiang F X, Zhang X M. 2004. Study on nonhomogeneous material's AE by image processing method. Rock and Soil Mechanics, 25(Z1): 60-62. | |
| Tian Y, Chen X F. 2002. Review of seismic location study. Progress in Geophysics, 17(1): 147-155. | |
| Tikhonov A N, Arsenin V Y. 1977. Solutions of Ill-Posed Problems. Washington: Winston. | |
| Wang Y F. Computational Methods for Inverse Problems and Their Applications.Beijing: Higher Education Press, 2007. | |
| Xiao T Y, Yu S G, Wang Y F. Numerical Solution of Inverse Problem.Beijing: Science Press, 2003. | |
| Ye G X, Jiang F X, Yang S H. 2008. Possibility of automatically picking first arrival of microseismic wave by energy eigenvalue method. Chinese J. Geophys., 51(5): 1574-1581. | |
| Zeng X N, Li X H, Jia W M, et al. 2015. A new regularization method for calculating the vertical derivatives of the potential field. Chinese J. Geophys., 58(4): 1400-1410. DOI:10.6038/cjg20150426 | |
| 董陇军, 李夕兵, 唐礼忠, 等. 2011. 无需预先测速的微震震源定位的数学形式及震源参数确定. 岩石力学与工程学报, 30(10): 2057–2067. | |
| 金明培, 汪荣江, 戴仕贵. 2014. 线性单事件地震定位方法的改进及应用尝试. 地震学报, 36(5): 757–759. | |
| 李庆扬, 王能超, 易大义. 数值分析.(第5版).北京: 清华大学出版社, 2008. | |
| 李寅祺, 祝永新. 2009. 体内胶囊TDoA定位算法研究与仿真. 微计算机信息, 25(22): 134–135. | |
| 林峰, 李庶林, 薛云亮, 等. 2010. 基于不同初值的微震源定位方法. 岩石力学与工程学报, 29(5): 996–1002. | |
| 刘建国. 1999.矩阵条件数及病态改善[硕士论文].重庆:重庆大学. | |
| 马成业, 杨胜良, 黎锁平. 2010. 求解病态线性方程组的一个正则化方法. 甘肃科学学报, 22(4): 33–35. | |
| 逄焕东, 姜福兴, 张兴民. 2004. 微地震的线性方程定位求解及其病态处理. 岩土力学, 25(增刊): 60–62. | |
| 田玥, 陈晓非. 2002. 地震定位研究综述. 地球物理学进展, 17(1): 147–155. | |
| 王彦飞. 反演问题的计算方法及其应用.北京: 高等教育出版社, 2007. | |
| 肖庭延, 于慎根, 王彦飞. 反问题的数值解法.北京: 科学出版社, 2003. | |
| 叶根喜, 姜福兴, 杨淑华. 2008. 时窗能量特征法拾取微地震波初始到时的可行性研究. 地球物理学报, 51(5): 1574–1581. | |
| 曾小牛, 李夕海, 贾维敏, 等. 2015. 位场各阶垂向导数换算的新正则化方法. 地球物理学报, 58(4): 1400–1410. DOI:10.6038/cjg20150426 | |
 2016, Vol. 59
2016, Vol. 59


