2. 海底科学与探测技术教育部重点实验室, 青岛 266100
2. Key Lab of Submarine Geosciences and Prospecting Techniques of Ministry of Education, Ocean University of China, Qingdao 266100, China
海洋可控源电磁法(Controlled-Source Electro Magnetic method,CSEM)是探测海底天然气水合物和海底油气以及矿产资源的一种海洋地球物理勘探方法(Eidesmo et al.,2002; Constable,2010).频率域海洋CSEM方法通常使用拖曳在离海底上方几十米处的电偶极子作为发射源,并在被拖曳过程中向位于海底的电磁采集站发射低频电磁信号(0.1~10 Hz),采集站接收到的信号主要是来自海底地层的电磁感应信号,其振幅和相位依赖于海底介质的电阻率.海洋CSEM方法已被广泛地应用于洋中脊和大陆边缘地质构造研究以及海底油气资源和天然气水合物探测中.
众所周知,地下介质的电阻率常常表现为各向异性.实验室的观测和研究表明片麻岩和其他类型的岩石具有明显的电导率各向异性.在断层破碎带和裂隙发育带上,呈脉状或条带状分布的岩体常常呈现出强烈的宏观电导率各向异性(Li and Spitzer,2005).据估计,世界上大约30%的油气资源赋存于岩性裂隙地层和泥砂岩薄互层中,而这两种地层的宏观电阻率常常表现为各向异性.当岩性裂隙地层的裂隙部分被海水灌入后,就会在沿裂隙面方向相比于垂直裂隙面方向显示出更低的电阻率,沿泥砂岩薄互层层理方向的电阻率小于垂直层理方向的电阻率(Li and Dai,2011).在解释海洋可控源电磁资料时,常常假定海底介质的电阻率是各向同性的,而海底岩性裂隙地层和海底层状沉积序列可能形成宏观电阻率各向异性,电导率各向异性的影响不应该被忽略,否则可能会得到错误的海底地电模型(Tompkins,2005; Li and Dai,2011; Li et al.,2013).
电阻率各向异性介质可控源电磁场正演方法研究始于20世纪70年代(Kong,1973; Yin and Weidelt,1999).Løseth和Ursin(2007)推导出了一维层状电阻率任意各向异性介质可控源电磁场波数域计算公式.最近,我们实现了一维电阻率任意各向异性介质海洋CSEM正演计算,讨论了覆盖层和高阻层分别具有电阻率各向异性时海洋CSEM响应特征(罗鸣和李予国,2015).Li和Dai(2011)以及Li等(2013)提出了二维电阻率各向异性介质海洋CSEM自适应有限元数值模拟方法,模型计算表明电阻率各向异性能够对海洋CSEM响应产生严重的影响.陈桂波等(2009)提出了各向异性海底地层海洋CSEM响应三维积分方程数值模拟方法.殷长春等(2014)利用交错网格有限差分技术实现了三维任意各向异性介质海洋CSEM正演.
在过去几十年中,电磁资料反演方法研究取得了很大进展,也出现了一些频率域海洋CSEM资料反演方法(Abubakar et al.,2008; Sasaki,2013).但是,大多数反演方法以海底介质电阻率是各向同性的为假设前提,关于电阻率各向异性反演方法研究的文献不多.Pek和Santos(2006)实现了一维层状电阻率垂直各向异性介质大地电磁(MT)资料反演;Ramananjaona和MacGregor(2010),Ramananjaona(2011)利用Occam反演方法解释1D和2D电阻率各向异性海洋CSEM资料;Herwanger等(2004)实现了电阻率各向异性介质井间层析成像.
本文提出了一维垂直各向异性(Vertical Transversal Isotropy,VTI)介质倾斜偶极源频率域海洋可控源电磁(CSEM)资料反演方法.在各向异性介质水平偶极源和垂直偶极源海洋CSEM正演算法的基础上,实现了各向异性介质倾斜偶极源海洋CSEM正演算法.理论模型合成数据和实测资料反演算例表明,我们提出的反演方法该方法能够较准确的重构海底围岩和基岩的各向异性电阻率以及高阻薄层的埋藏深度、厚度和垂向电阻率.
2 正演模拟在模拟和解释海洋CSEM资料时,通常假定发射源为理想的水平电偶极源.然而,在实际的海洋可控电磁勘探作业中,由于受洋流、波浪、潮汐等海水运动的影响,发射源可能会发生旋转和倾斜等,故而海洋CSEM的发射源应是有限长倾斜偶极源,于是有必要模拟有限长倾斜偶极源产生的电磁场.
倾斜偶极源产生的电磁场可以看作为三个等效偶极源,即垂直偶极VED(Vertical Electric Dipole)、沿x轴水平偶极源x-HED(Horizontal Electric Dipole)和沿y轴水平偶极源y-HED)所产生电磁场的叠加(Xu et al.,2016),公式为
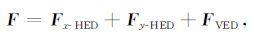
|
(1) |
其中, F 表示倾斜偶极源产生的电磁场, FVED 表示垂直电偶极源(VED)产生的电磁场, Fx-HED 和 Fy-HED 分别表示沿x轴和y轴取向水平电偶极源产生的电磁场.一维层状电阻率各向异性介质水平偶极源和垂直偶极源产生的频率域电磁场可以采用数字滤波法计算得到(罗鸣和李予国,2015).
一维层状垂直各向异性(VTI)介质中的电阻率张量表达式为

|
(2) |
本文用二维傅里叶变换将空间域电磁场转换到波数域中,通过计算波数域中地层界面的反射矩阵和透射矩阵,再依据发射源与接收站的位置计算模量场矩阵,从而得到任意姿态发射源激发、在任意接收点处波数域电磁场响应.在VTI介质中,电磁场能够分解为TE极化场和TM极化场(在电阻率任意各向异性介质中电磁场微分方程是耦合在一起的,不能分解为TE极化场和TM极化场),正因为如此,在模拟VTI介质的电磁场响应时,可通过数字滤波汉克尔变换实现由波数域到空间域的转换(Anderson,1982).
3 反演方法 3.1 目标函数本文利用高斯-牛顿反演方法求取观测数据与模型正演响应之差的极小值问题,并利用正则化约束稳定海洋CSEM一维电阻率各向异性反演过程(Tikhonov and Arsenin,1977).所采用的目标函数为
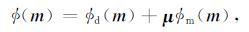
|
(3) |
其中,模型参数向量m包含了反演模型中各地层横向电阻率 ρh 和垂向电阻率 ρv 的对数,即 m=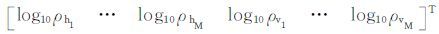
ød和øm 分别为观测数据与理论模型响应的拟合差和模型约束泛函. μ 为正则化因子,用于平衡拟合差 ød 与模型约束 øm 之间的权重,其维度与模型参数向量 m 的维度相同.
观测数据与理论模型响应的拟合差 ød 为
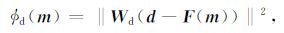
|
(4) |
其中 ‖·‖ 为标准差, d=[d1d2…dN]T为观测数据向量(维度为N), F(m) 表示模型 m 的正演响应, Wd 为数据加权矩阵(维度为N),公式为
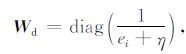
|
(5) |
其中η为与数据本底噪声有关的极小量,该极小量能够预防电磁数据振幅过小的情况(Pidlisecky et al.,2007);ei为第i个数据的估计误差,公式为
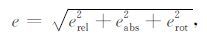
|
(6) |
其中erel为场强振幅的相对误差,这是由仪器的计量误差以及采集系统的测量误差引起的,通常假定相对误差为振幅的5%;eabs为激发-接收系统的本底噪声,设定电场 E 的本底噪声为10-15V·Am-2,磁场 B 的本底噪声为10-18T·Am-1;erot为由海底电磁采集站电场测量臂或磁场传感器方向的不确定性引起的误差.
模型约束泛函 øm 为

|
(7) |
其中 Δm 为模型参数向量的梯度, Wm 为模型加权矩阵(维度为2M),本文采用最小梯度支撑约束(MGS:Minimum Gradient Support)(Zhdanov,2002).
3.2 目标函数的极小值本文利用高斯-牛顿方法求解电阻率各向异性反演目标函数的极小值问题.高斯-牛顿方法在雅各比矩阵满秩或梯度矩阵非零情况下依然能够得到合适的搜索方向(Nocedal and Wright,2006).
在高斯-牛顿迭代中,通过求取目标函数的极小值可以得到搜索方向,下一次迭代的模型参量mi+1可表示为

|
(8) |
其中 Hi 为海森矩阵(Hessian), gi 为目标函数的梯度且表达式为
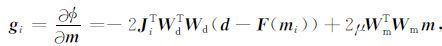
|
(9) |
其中 Ji 为维度 N×N 的雅各比矩阵,公式为

|
(10) |
如果将电阻率张量 e 理解为反演模型横向电阻率 ρh 和垂向电阻率 ρv 的函数,即 e=f(ρh,ρv), 当地下介质呈现电阻率各向同性时, e=ρiso. 电阻率各向同性情形和电阻率各向异性情形下,雅各比矩阵有如下关系为
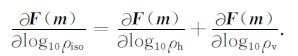
|
(11) |
忽略二阶导数项和非对称项,海森矩阵 Hi 可简化为

|
(12) |
在反演迭代过程中,反演迭代模型逐步收敛于真实模型,其目标函数拟合差ψ(Misfit)逐渐收敛于1.0,公式为
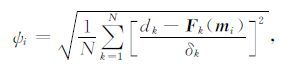
|
(13) |
其中 δk 为第 k 个数据的标准差.
3.3 自适应正则化因子正则化因子 μ 的选择方式是能否获得合理反演结果的关键.在地球物理反演研究中,出现了许多正则化因子选择方法(Constable et al.,1987; Hansen,1992; Haber and Oldenburg,2000).本文将矩阵乘积 [(WdJ)T(WdJ)] 中各行总和的最大值作为正则化因子的基数(Newman and Alumbaugh,1997),再结合当前反演模型横向电阻率(ρh)与垂向电阻率(ρv)的关系调节不同反演参数的正则化因子大小,从而实现正则化因子的自适应选择.
在第 i 个高斯-牛顿迭代中,正则化因子 μi 可写为
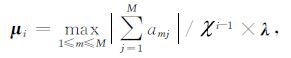
|
(14) |
其中 amj 为矩阵乘积 [(WdJ)T(WdJ)] 的元素,为正则化衰减因子(通常设为一个常数), λ 为与反演模型横向电阻率ρh与垂向电阻率ρv有关的加权因子,它由两个部分组成:横向电阻率部分(λh=1)和垂向电阻率部分(λv=上一次反演模型各层各向异性率),公式为
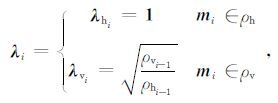
|
(15) |
其中 mi 为反演模型参数,权重向量的初始值 λ1 为单位向量.当反演模型地层中存在电阻率各向异性时,正则化因子可根据电阻率各向异性率自适应地进行调节,从而调节拟合差ød与模型约束øm之间的权重达到自适应调节反演过程的目的.
4 合成数据反演为了验证反演算法的有效性以及测试不同反演数据对电阻率各向异性反演的影响,以图 1所示一维电阻率各向异性模型为例,采用与Key(2009)中电阻率各向同性反演方法算例分析相类似的思路,分别使用不同频率、不同电磁场分量及混合观测模式(轴向观测模式和赤道观测模式)的合成数据进行电阻率各向异性反演.假设深度为1 km的海水层是电阻率各向同性的,其电阻率为0.3 Ωm.厚度为100 m的垂直各向异性高阻薄层的埋深为1 km,横向电阻率为ρh=50 Ωm,垂向电阻率为ρv=100 Ωm.覆盖层和基岩电阻率也具有垂直各向异性,覆盖层的横向电阻率和垂向电阻率分别为ρh=1 Ωm和ρv=3 Ωm,基岩的横向电阻率和垂向电阻率分别为ρh=2 Ωm和ρv=4 Ωm.假设测线与y轴重合,26个发射源等间距地布置于测线500~13000 m范围内,且均位于海底正上方50 m处;海底面上单个接收站的坐标为(x=0 m,y=0 m,z=1000 m).设定发射电流为1安培.反演数据由电磁场各分量的实部和虚部组成,各数据加入了2%的随机高斯噪声.在反演算例中,反演初始模型为空气、海水和电阻率为1 Ωm的均匀半空间,海水电阻率和深度固定.

|
图 1 一维电阻率各向异性模型 Fig. 1 One-dimensional resistivity model with anisotropic surrounding sediments |
在解释海洋电磁资料时,电阻率各向异性的影响可能会导致得到错误的海底地电模型.为了探讨电阻率各向异性对反演结果的影响,我们模拟图 1所示模型的海洋可控源电磁响应,并利用电磁场单分量响应合成的反演数据进行电阻率各向同性反演和电阻率各向异性反演.假定发射频率为0.125 Hz、0.25 Hz、1.0 Hz.
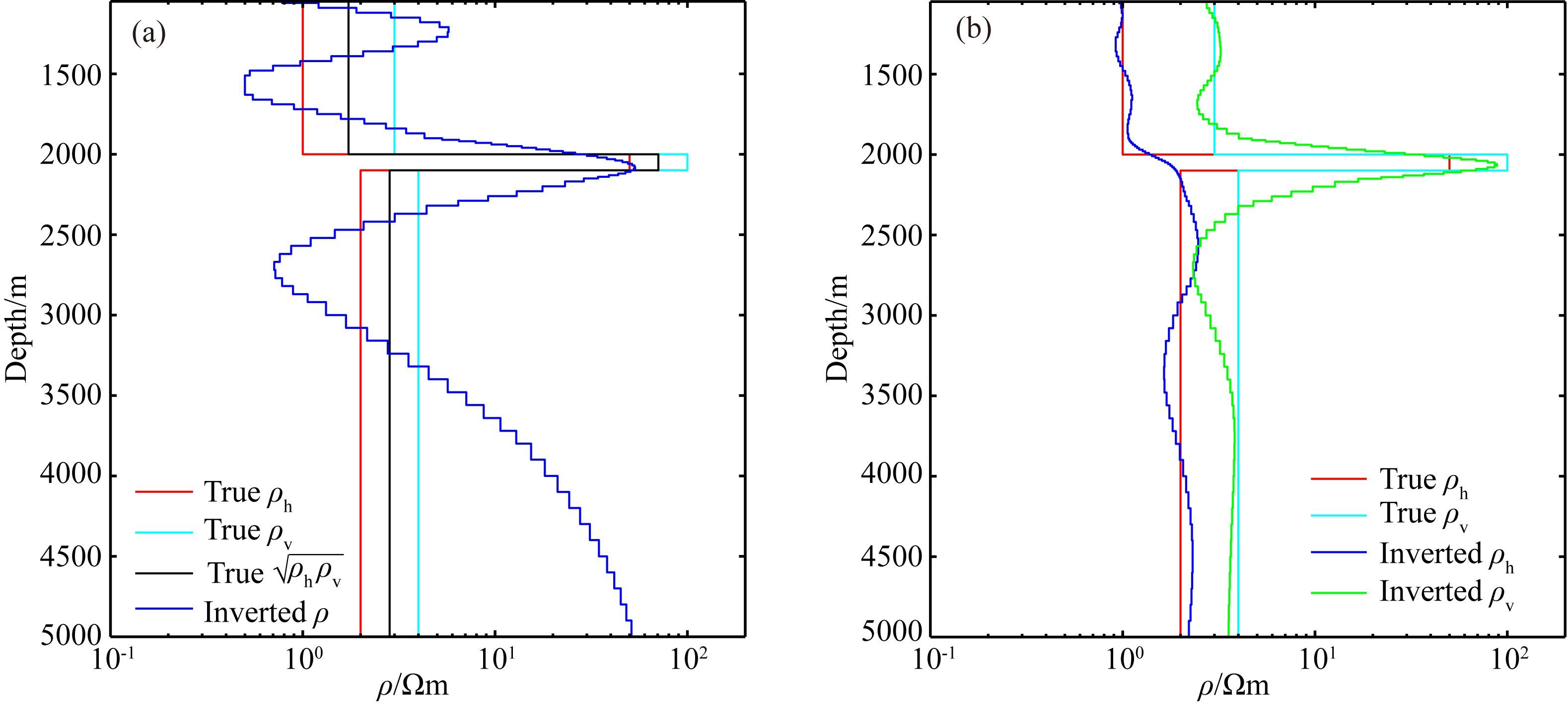
图 2a和图 2b分别为电阻率各向异性模型(图 1)可控源电磁响应的电阻率各向同性反演结果和电阻率各向异性反演结果(数据拟合差ψ接近于1.0).由图 2a可见,当用电阻率各向同性反演解释各向异性模型的电磁资料时,重构的覆盖层和基岩的电阻率与真实模型的其平均电阻率不相符合,覆盖层电阻率值震荡严重,基岩电阻率值明显高于其平均电阻率的真实值.重构的高阻薄层埋深与真实模型相符,但电阻率值偏低且厚度大于真实值.当采用电阻率各向异性反演时,反演结果有了明显的改善(图 2b),高阻薄层的埋深、厚度和电阻率值都非常接近于真实值,围岩和基岩的各向异性电阻率也与真实模型相吻合.
|
图 2 电阻率各向异性模型反演结果 (a)各向同性反演;(b)各向异性反演. Fig. 2 Inversion results of anisotropic resistivity model (a)Isotropic inversion;(b)Anisotropic inversion. |
我们首先进行不同发射频率电磁场响应电阻率各向异性反演.在轴向观测模式下,一个y取向的水平电偶极源产生一个水平磁场分量和两个电场分量:一个水平电场分量Ey和一个垂直电场分量Ez,将这三个电磁场分量的实部和虚部作为合成模型反演数据.图 3为不同频率合成数据的电阻率各向异性反演结果(数据拟合差ψ都非常接近于1.0).由图 3可见,当只用一个频率(0.25 Hz)合成数据进行电阻率各向异性反演时(图 3a),可以反演出高阻薄层,但其深度偏大,且不能准确反演出电阻率各向异性基岩;当使用两个频率(0.25 Hz,1.0 Hz)合成数据进行电阻率各向异性反演时(图 3b),重构的覆盖层呈现出与真实模型相符的各向异性电阻率值,高阻薄层的轮廓也被粗略地反演出来了,但其垂向电阻率较真实值偏低;当使用三个频率(0.125 Hz,0.25 Hz,1.0 Hz)和四个频率(0.125 Hz,0.25 Hz,1.0 Hz,3.0 Hz)合成数据进行电阻率各向异性反演时,反演结果有了明显的改善(图 3c、3d),高阻薄层的埋深、厚度以及垂向电阻率值都非常接近于真实值,围岩和基岩的各向异性电阻率也与真实模型相吻合.由于高阻薄层横向电阻率变化对海洋CSEM电磁响应的影响非常小(罗鸣和李予国,2015),各电磁场分量关于高阻薄层横向电阻率的灵敏度低,故而很难重构出高阻薄层的横向电阻率值.总之,采用多频率电磁场数据能够提高电阻率各向异性反演效果.

|
图 3 不同频率合成数据电阻率各向异性反演结果 (a)单一频率(0.25 Hz);(b)两个频率(0.25 Hz,1.0 Hz);(c)三个频率(0.125 Hz,0.25 Hz,1.0 Hz); (d)四个频率(0.125 Hz,0.25 Hz,1.0 Hz,3.0 Hz). Fig. 3 Inversion of multi-frequency EM data for the 1D anisotropic model (a)One frequency(0.25 Hz);(b)Two frequencies(0.25 Hz and 1.0 Hz);(c)Three frequencies(0.125 Hz,0.25 Hz and 1.0 Hz);(d)Four frequencies(0.125 Hz,0.25 Hz,1.0 Hz and 3.0 Hz). |
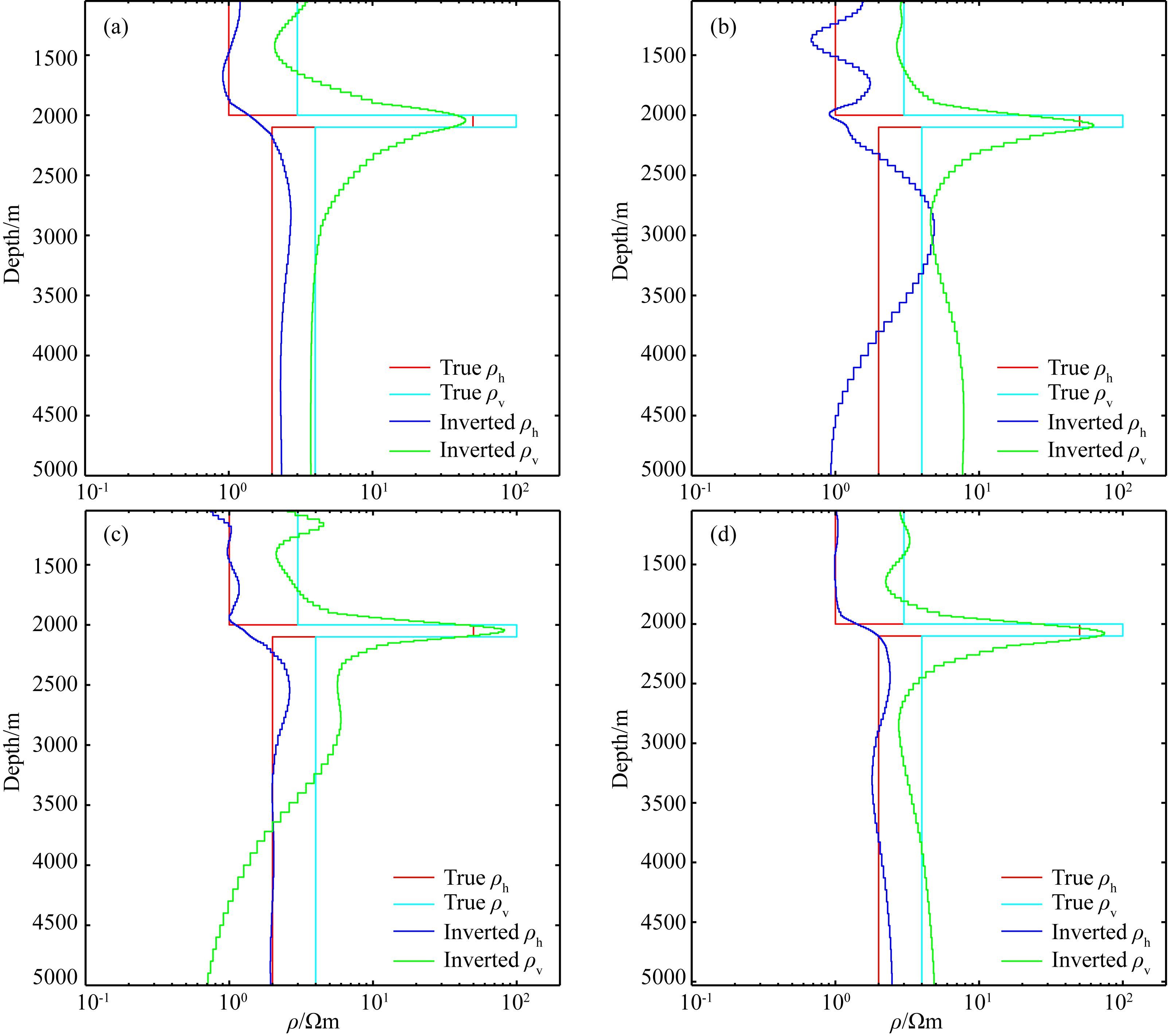
由上一节的反演结果可知,三个及其以上频率电磁场三分量合成数据的反演能够重构一维层状电阻率各向异性模型.下面,我们设定在三个不同发射频率(0.125 Hz、0.25 Hz和1.0 Hz)的情况下,比较单个电磁场分量数据和多个电磁场分量数据电阻率各向异性反演效果.图 4为只用Ey分量(图 4a),Ez分量(图 4b),Bx分量(图 4c)和联合三个电磁场分量(图 4d)实部和虚部资料时得到的反演结果,这四个反演结果的数据拟合差ψ都接近于1.0.由图 4可见,当只用一个电磁场分量数据进行电阻率各向异性反演时,能够粗略地反演出高阻薄层的轮廓,但不能恢复其真实的电阻率值.当分别使用Bx分量和Ez分量进行反演时,得到的高阻薄层垂向电阻率值偏低,基岩的电阻率值与真实模型差异较大.当联合三个电磁场分量进行电阻率各向异性反演时,反演结果有了明显的改善(图 4d),高阻薄层的埋藏深度、厚度和垂向电阻率都接近其真实值,围岩和基岩的电阻率也与真实模型比较接近.由此可见,多分量电磁场数据反演能够明显地改善反演效果.
|
图 4 不同电磁场分量电阻率各向异性反演结果 (a)Ey反演;(b)Ez反演;(c)Bx反演;(d)Ey、Ez、Bx三分量反演. Fig. 4 Inversions of various EM components for the 1D anisotropic model (a)Ey;(b)Ez;(c)Bx;(d)Ey,Bx and Ez. |
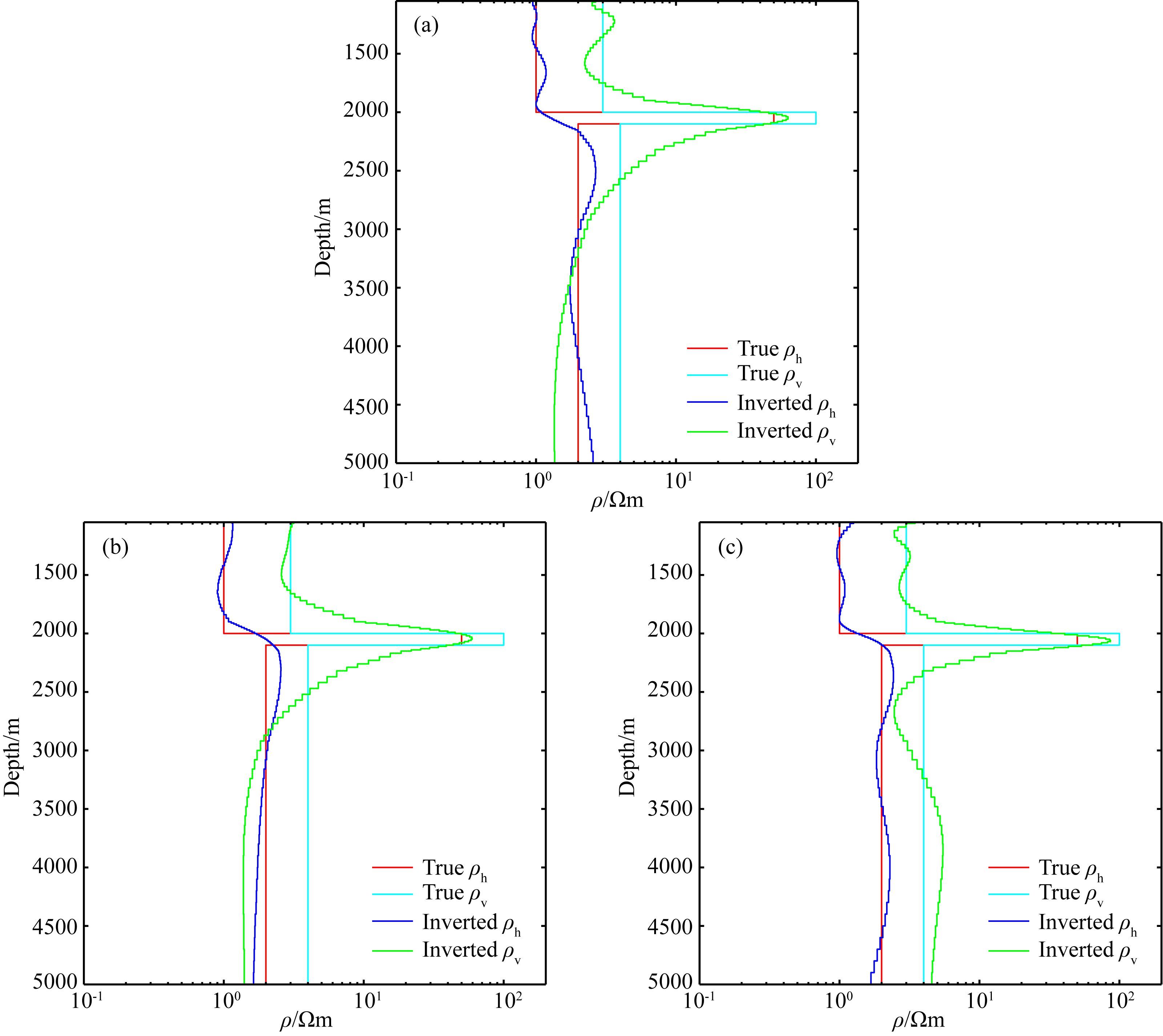
下面,我们测试单一观测模式合成数据和混合观测模式合成数据电阻率各向异性反演的效果.在测试中,三个发射频率(0.125 Hz、0.25 Hz和1.0 Hz)的所有电磁场分量参与反演,且所有合成数据添加了3%的随机高斯噪声.在单一观测模式合成数据反演中,轴向观测模式电磁场分量Ey、Ez和Bx参与反演;赤道观测模式电磁场分量Ex、By和Bz参与反演;混合观测模式6个电磁场分量均参与反演.图 5为轴向观测模式(图 5a)和赤道观测模式(图 5b)以及混合观测模式(图 5c)合成数据电阻率各向异性反演结果.当只有单一观测模式合成数据进行电阻率各向异性反演时,反演得到的覆盖层电阻率接近于真实值,但反演得到的高阻薄层垂向电阻率值偏低,且基岩电阻率值与其真实值相差较大.当联合轴向观测模式和赤道观测模式数据进行反演时,围岩和基岩的横向电阻率和垂向电阻率以及高阻薄层的埋深和垂向电阻率都能够得到很好地重构.由此可见,进行混合观测模式电磁场数据反演能够提高高阻薄层埋深和基岩各向异性电阻率的分辨能力.
|
图 5 单一观测模式数据和混合观测模式合成数据的电阻率各向异性反演结果 Fig. 5 Inversion of multi-geometry EM data for the 1D anisotropic model (a)Inline-geometry data;(b)Broadside-geometry data;(c)Combined inline and broadside geometry data. |
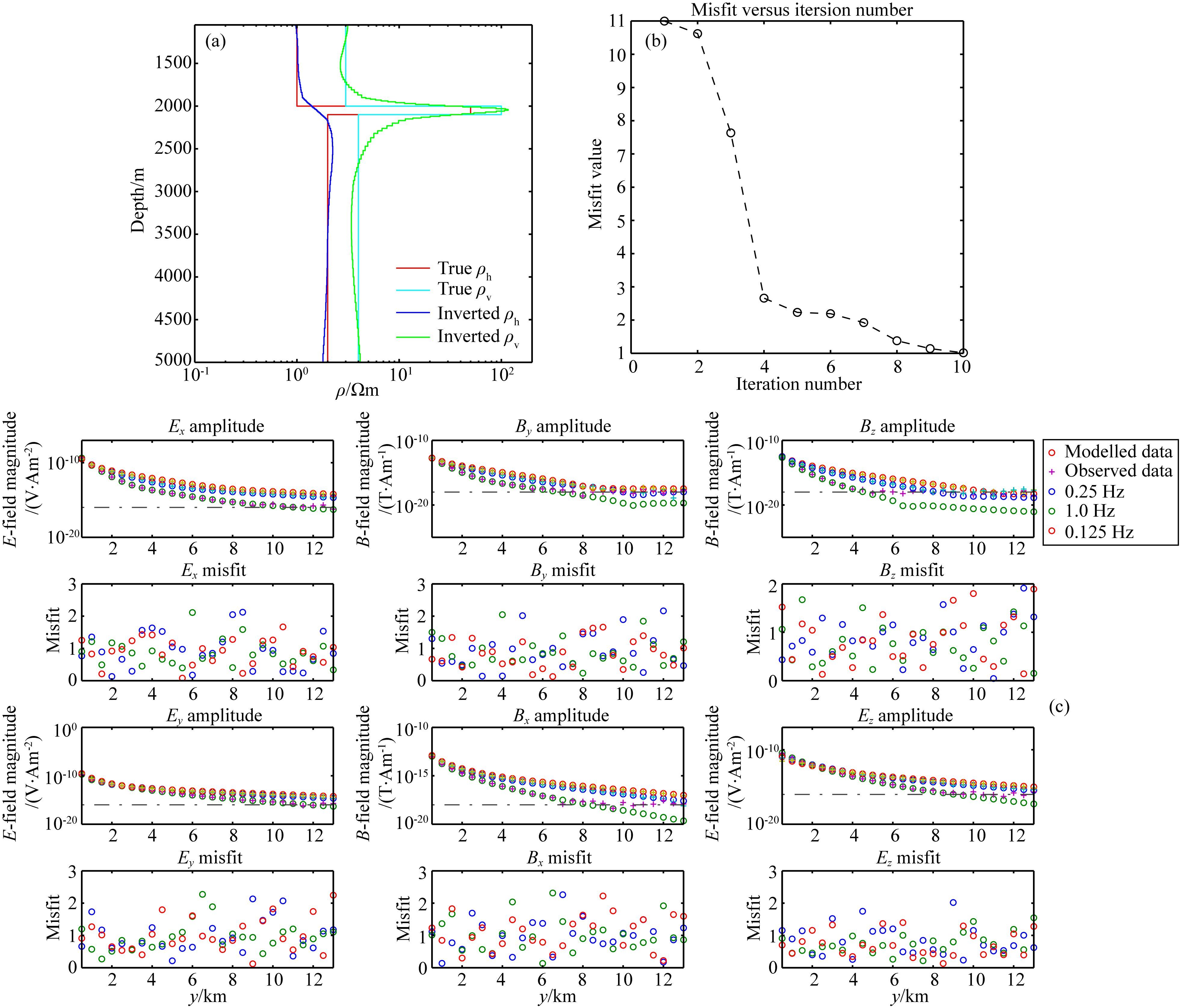
在模拟和解释海洋可控源资料时,通常假设发射源为一个理想的水平电偶极源,且其在设计的测线上拖曳.然而,实际海洋作业时,由于洋流等因素的影响,发射源会发生旋转或倾斜,并可能偏离设计的拖曳路径.下面,我们将倾斜电偶极源(假定沿y轴水平电偶极源向下倾斜了30°)产生的电磁场作为合成数据进行电阻率各向异性反演.设定3个发射频率分别为0.125 Hz、0.25 Hz和1.0 Hz .图 6为倾斜偶极源合成数据反演结果,从图 6b可见,在反演迭代的前期,数据拟合差下降迅速,随着反演次数增多,数据拟合差下降速度逐渐减慢,经过10次反演迭代后,数据拟合差最终收敛于1.01.
|
图 6 倾斜偶极源合成数据反演结果 (a)反演模型;(b)数据拟合差与反演迭代次数的变化曲线;(c)观测数据(“+”线)和反演模型正演响应(“o”线)的数据拟合情况(图 6c第一行和第三行),以及对应的数据拟合差(图 6c第二行和第四行). Fig. 6 Inversion of multi-component and multi-frequency data generated by a tilted dipole source (a)Inversion model;(b)Misfit versus iteration number;(c)Amplitude(first and third row)of three EM components(Ey,Ez,Bx)for the inversion model(‘o’)and observed data(‘+’). Dotted lines indicate the noise floor of corresponding EM components. Data misfits (second and forth row in c)are around 1.0. |
图 6c第一行和第三行为观测数据(“+”线)和反演模型正演响应(“o”线)对比,其下方的子图为各个收发距处观测数据与反演模型正演响应间的拟合差Dd,第i个数据的拟合差定义为
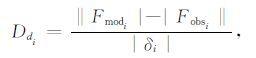
|
(16) |
其中 Fmod和Fobs 分别为反演模型正演响应和观测数据,δ为标准差.当反演模型与真实模型完全相同时,数据拟合差Dd等于1.0.从图 6c可见,除了在电磁场振幅小于本底噪声的数据以外,反演模型正演响应与观测数据都拟合得非常好,数据拟合差Dd均分布于1.0附近.
5 实测数据反演在本节中,我们将前面所述反演方法应用到挪威北海TWOP(Troll West Oil Province)地区海洋CSEM电磁资料反演中.测区水深约为330 m,总共46个发射源位于距离海底约30 m的海水中,9个接收站布置于海底剖面上,测线总长度约为9 km.勘探船拖曳着发射源沿着测线方向前行,但由于洋流等因素的影响,发射源出现了一定的旋转、倾斜,其位置偏离了设计的拖曳路径.发射频率为0.25 Hz,发射源的能量足以使海底接收站采集到三次谐波和五次谐波的有效信号,即接收到有效信号的频率为0.25 Hz、0.75 Hz和1.25 Hz.在电阻率各向异性反演中,选择其中一个接收站采集到的46个发射源水平轴向电场数据(在这次海试中,只有水平轴向电场分量是有效的)进行电阻率各向异性反演.反演初始模型由空气、海水和电阻率为1 Ωm均匀半空间构成,在反演迭代过程中海水电阻率和深度保持固定不变.
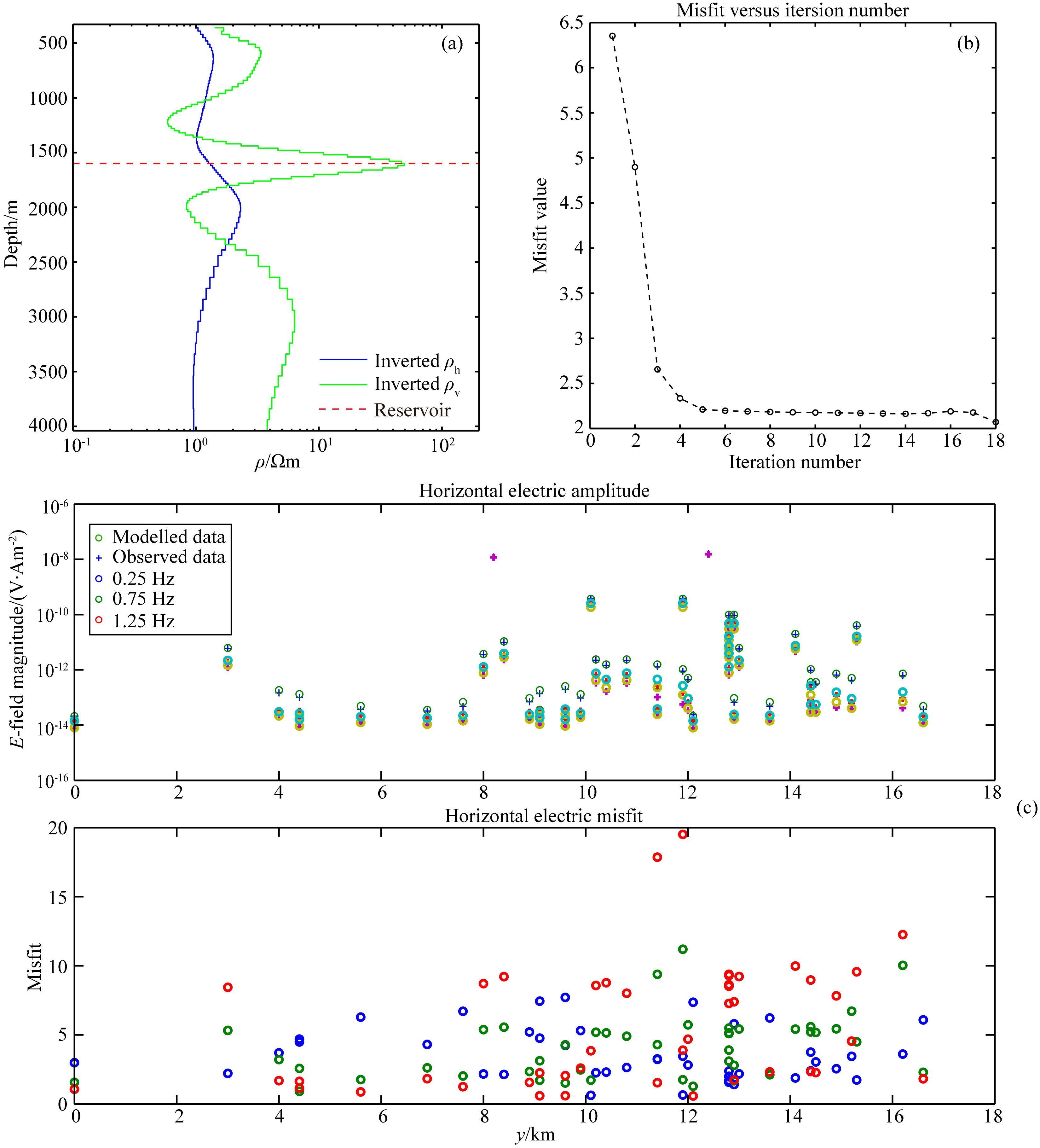
图 7为实测数据电阻率各向异性反演结果,根据地震资料分析结果,油气藏储层埋藏深度大约在1500~1600 m之间(图 7a红色虚线).由图 7a可知,在大约1600 m深度处存在垂向电阻率突然升高的高阻薄层,这与地震资料分析结果相一致,覆盖层和基岩层也呈现出了明显的电阻率各向异性.由图 7b可知,在反演迭代的前期,数据拟合差下降迅速,随着反演次数的增多数据拟合差下降速度减慢并趋于收敛,经过18次反演迭代后数据拟合差最终收敛于2.07.从水平电场拟合情况看(图 7c),除了频率0.25 Hz部分数据拟合差Dd较高外,不同收发距处反演模型电场响应与观测数据都拟合得比较好(在1.0附近).
|
图 7 实测数据反演结果 (a)反演模型;(b)数据拟合差(RMS)与反演迭代次数的变化曲线;(c)参与反演的电磁场分量的数据拟合情况. Fig. 7 Inversion results of real data (a)Inversion model;(b)Misfit versus iteration number;(c)Horizontal electric field amplitude and data misfit for each response. |
本文提出了一维电阻率垂直各向异性(VTI)介质倾斜偶极源激发频率域海洋可控源(CSEM)资料高斯-牛顿反演方法.我们将该反演方法应用于理论模型合成数据和实测资料反演中,验证了方法的有效性和重构电阻率各向异性层状地电模型的能力.我们的反演方法能够较准确的恢复围岩和基岩的各向异性电阻率以及高阻薄层的埋藏深度、厚度和垂向电阻率.多频率、多分量电磁场数据能够更好地重够电阻率各向异性地电模型;采用混合观测模式数据反演能够提高对高阻薄层埋深和基岩各向异性电阻率的分辨能力.
致谢感谢匿名审稿人对本文所提出的修改意见及建议,感谢Electromagnetic Geoservices(EMGS)公司提供TWOP海洋CSEM实测数据.
| Abubakar A, Habashy T M, Druskin V L, et al. 2008. 2.5d forward and inverse modeling for interpreting low-frequency electromagnetic measurements. Geophysics , 73 (4) : F165-177. DOI:10.1190/1.2937466 | |
| Alumbaugh D L, Newman G A. 1997. Three-dimensional massively parallel electromagnetic inversion-Ⅱ. Analysis of a crosswell electromagnetic experiment. Geophysical Journal International , 128 (2) : 355-363. | |
| Anderson W L. 1982. Fast Hankel transforms using related and lagged convolutions. ACM Transactions on Mathematical Software , 8 (4) : 344-368. DOI:10.1145/356012.356014 | |
| Chen G B, Wang H N, Yao J J, et al. 2009. Three-dimensional numerical modeling of marine controlled-source electromagnetic responses in a layered anisotropic seabed using integral equation method. Acta Physica Sinica (in Chinese) , 58 (6) : 3848-3857. | |
| Constable S. 2010. Ten years of marine CSEM for hydrocarbon exploration. Geophysics , 75 (5) : 75A67-75A81. DOI:10.1190/1.3483451 | |
| Constable S C, Parker R L, Constable C G. 1987. Occam's inversion:A practical algorithm for generating smooth models from electromagnetic sounding data. Geophysics , 52 (3) : 289-300. DOI:10.1190/1.1442303 | |
| Eidesmo T, Ellingsrud S, MacGregor L M, et al. 2002. Sea Bed Logging (SBL), a new method for remote and direct identification of hydrocarbon filled layers in deepwater areas. First Break , 20 (3) : 144-152. | |
| Haber E, Oldenburg D. 2000. A GCV based method for nonlinear ill-posed problems. Computational Geosciences , 4 (1) : 41-63. DOI:10.1023/A:1011599530422 | |
| Hansen P C. 1992. Analysis of discrete ill-posed problems by means of the l-curve. SIAM Review , 34 (4) : 561-580. DOI:10.1137/1034115 | |
| Herwanger J V, Pain C C, Binley A, et al. 2004. Anisotropic resistivity tomography. Geophysical Journal International , 158 (2) : 409-425. DOI:10.1111/gji.2004.158.issue-2 | |
| Key K. 2009. 1D inversion of multicomponent, multifrequency marine CSEM data:Methodology and synthetic studies for resolving thin resistive layers. Geophysics , 74 (2) : F9-F20. DOI:10.1190/1.3058434 | |
| Kong J A. 1972. Electromagnetic fields due to dipole antennas over stratified anisotropic media. Geophysics , 37 (6) : 985-996. DOI:10.1190/1.1440321 | |
| Li Y G, Dai S K. 2011. Finite element modelling of marine controlled-source electromagnetic responses in two-dimensional dipping anisotropic conductivity structures. Geophysical Journal International , 185 (2) : 622-636. DOI:10.1111/gji.2011.185.issue-2 | |
| Li Y G, Luo M, Pei J X. 2013. Adaptive finite element modeling of marine controlled-source electromagnetic fields in two-dimensional general anisotropic media. Journal of Ocean University of China , 12 (1) : 1-5. DOI:10.1007/s11802-013-2110-3 | |
| Li Y G, Spitzer K. 2005. Finite element resistivity modelling for three-dimensional structures with arbitrary anisotropy. Physics of the Earth & Planetary Interiors , 150 (1-3) : 15-27. | |
| Løseth L O, Ursin B. 2007. Electromagnetic fields in planarly layered anisotropic media. Geophysical Journal International , 170 (1) : 44-80. DOI:10.1111/gji.2007.170.issue-1 | |
| Luo M, Li Y G. 2015. Effects of the electric anisotropy on marine controlled-source electromagnetic responses. Chinese J. Geophys. (in Chinese) , 58 (8) : 2851-2861. DOI:10.6038/cjg20150819 | |
| Nocedal J, Wright S J. Numerical Optimization. New York: Springer, 2006 . | |
| Pek J, Santos F A M. 2006. Magnetotelluric inversion for anisotropic conductivities in layered media. Physics of the Earth and Planetary Interiors , 158 (2-4) : 139-158. DOI:10.1016/j.pepi.2006.03.023 | |
| Pidlisecky A, Haber E, Knight R. 2007. RESINVM3D:A 3D resistivity inversion package. Geophysics , 72 (2) : H1-H10. DOI:10.1190/1.2402499 | |
| Ramananjaona C, MacGregor L. 2010. 2.5d inversion of CSEM data in a vertically anisotropic earth. Journal of Physics:Conference Series , 255 (1) : 012004. | |
| Ramananjaona C, MacGregor L, Andréis D. 2011. Sensitivity and inversion of marine electromagnetic data in a vertically anisotropic stratified earth. Geophysical Prospecting , 59 (2) : 341-360. DOI:10.1111/gpr.2011.59.issue-2 | |
| Sasaki Y. 2013. 3d inversion of marine CSEM and MT data:An approach to shallow-water problem. Geophysics , 78 (1) . | |
| Tikhonov A N, Arsenin V Y. 1977. Solution of Ill-Posed Problems. Washington DC:W. H. Winston and Sons. | |
| Tompkins M J. 2005. The role of vertical anisotropy in interpreting marine controlled-source electromagnetic data.//SEG Technical Program Expanded Abstracts. SEG, 514-517. | |
| Xu Z H, Liu Y, Li Y G. 2016. Effects of uncertainties in the position and orientation of both the transmitter and receivers on marine controlled-source electromagnetic data. Journal of Ocean University of China , 15 (1) : 83-92. DOI:10.1007/s11802-016-2675-8 | |
| Yin C C, Ben F, Liu Y H, et al. 2014. MCSEM 3D modeling for arbitrarily anisotropic media. Chinese J. Geophys. (in Chinese) , 57 (12) : 4110-4122. DOI:10.6038/cjg20141222 | |
| Yin C C, Weidelt P. 1999. Geoelectrical fields in a layered earth with arbitrary anisotropy. Geophysics , 64 (2) : 426-434. DOI:10.1190/1.1444547 | |
| Zhdanov M S. 2002. Geophysical Inverse Theory and Regularization Problems. Amsterdam, The Netherlands:Elsevier. | |
| 陈桂波, 汪宏年, 姚敬金, 等. 2009. 各向异性海底地层海洋可控源电磁响应三维积分方程法数值模拟. 物理学报 , 58 (6) : 3848–3857. | |
| 罗鸣, 李予国. 2015. 一维电阻率各向异性对海洋可控源电磁响应的影响研究. 地球物理学报 , 58 (8) : 2851–2861. DOI:10.6038/cjg20150819 | |
| 殷长春, 贲放, 刘云鹤, 等. 2014. 三维任意各向异性介质中海洋可控源电磁法正演研究. 地球物理学报 , 57 (12) : 4110–4122. DOI:10.6038/cjg20141222 | |
 2016, Vol. 59
2016, Vol. 59


