2. 中国石油大学(北京)地球物理与信息工程学院, 北京 102249;
3. 莱斯大学 地球科学学院, 美国德克萨斯州休斯顿 77005
2. College of Geophysics and Information Engineering, China University of Petroleum, Beijing 102249, China;
3. Department of Earth Science, Rice University, Houston, TX 77005
随着地震勘探开发的深入,对地震波场正演模拟精度、地下成像结果分辨率等要求越来越高,基于波场延拓的逆时偏移成像(Etgen等,2007)、最小二乘逆时偏移(Dai等,2012;黄建平等,2013,2014)以及全波形反演(Virieux和Operto,2009)已经成为研究的热点,波场延拓的效率与精度直接影响后续成像和反演的效率和精度.有限差分法(Boore,1972; Levander,1988)兼顾计算效率与模拟精度,目前已经广泛应用于勘探地震的波场延拓中.有限差分法利用离散的差分算子逼近连续的偏导算子,在计算中通常存在数值频散,影响地震波波场模拟精度.传统的有限差分系数通常基于零波数处的泰勒展开求取,在低波数段能较精确地模拟地震波传播,但在高波数段会出现严重的数值频散(吴国忱和王华忠,2005).如何改进差分算子压制数值频散是有限差分正演模拟研究的重要领域.
针对数值频散问题,国内外许多研究人员开展了大量研究工作,常用的策略主要包括:(1)减小空间和时间采样间隔;(2)增加时间或者空间差分阶数;(3)通量传输校正法(FCT).这三种方法在一定程度上改善了数值频散,但都导致了计算量的增加.目前,计算量大仍然是制约三维高精度勘探、基于反演思想的最小二乘偏移、全波形反演、各向异性相关研究等推广应用的重要因素.无论是减少时空采样间隔,提高差分阶数,还是FCT校正(吴国忱和王华忠,2005),在理论方法实用化中优势和不足都较为明显.为此,许多学者转换思路,从优化差分系数入手,提出了一系列的改进方法以压制数值频散.下面简要介绍国内外正演差分算子优化的研究进展.
第一类方法主要是基于平面波原理,推导微分算子与差分算子在波数域中的滤波响应;并利用函数拟合算法使差分算子逼近微分算子.如Liu和Sen(2011,2013)提出的基于时空域频散关系的任意偶数阶差分格式;随后又基于最小二乘函数逼近算法给出了全局优化的差分系数并推广至三维声波正演模拟中(Liu,2013a,2013b;Cai et al.,2014),严红勇和刘洋(2013)将其应用到偏移成像中.在最小二乘函数逼近法使用过程中关键的一步是确定其积分上限,即优化的目标波数范围.梁文全等(2013)人依据震源、波速和网格间距划定目标波数范围,并在时空两个方面进行差分系数优化;考虑到差分系数求取中的稳定性,将正则化算子引入到基于二阶声波方程的交错网格差分系数求取过程(Wang等,2014).
第二类,大量数值实验表明,相比有限差分方法,谱方法具有更高的精度但傅里叶变换带来的大计算量制约了其在偏移成像中的应用.因而,一部分学者从这方面出发,在波数域将空间差分与谱分解相结合,改进差分算子减小计算误差,具有代表性的如Fomel等(2013)利用Lowrank分解算法对传播算子进行简化,选出具有代表性的特定波数值,计算差分系数使其在这些特定波数点满足传播算子.考虑到交错网格的对频散压制的优势,方刚等(2014)将Lowrank分解思想运用到标准交错网格正演与逆时偏移成像中;在此基础上,Wu和Alkhalifah(2014)分析正演过程中的稳定性与参数选择的关系,提出了在有效波数范围内进行差分系数优化,并将其拓展到各向异性介质正演与成像中.
第三类则是从网格节点方面改进有限差分计算精度.Tan等(2014a)使用了一种新的网格节点,在传统的网格节点上额外的增加一些特定角度的节点,研究表明额外节点的加入可以提高计算精度,尤其是在低频地震波走时方面的精度;Liu等(2014)在这种节点的基础上,使用余弦函数逼近,基于二阶声波方程推导了一种精确的显式时间递推格式(ETE),采用这种方法既可以达到压制数值频散,同时研究表明这种递推格式还可以提高地震波的走时精度.走时精度的提高对以波形匹配为目标函数的最小二乘逆时偏移与全波形反演具有重要的意义.
真实地下介质既存在速度变化也存在密度的变化,大量事实表明一阶压强-速度方程更加利于处理变密度介质.因此,一阶变密度声波方程在地震偏移成像中得到广泛的应用,针对其优化的方法目前成为正演频散压制的研究热点(Liu,2014; Tan和Huang,2014b;Ren和Liu,2015).本文以一阶声波方程组的数值模拟为研究对象,推导出一阶声波方程中的压强场与偏振速度场的解析表达式,据此给出了一种高精度的递推格式,并将匹配系数求取问题转化为最小二乘优化问题.考虑到系数求解的病态性,采用共轭梯度迭代算法确保稳定的求解优化的匹配系数.
2 交错网格差分算子优化原理 2.1 速度-压强方程组的平面波解首先考虑二维常密度与常速度情况下,一阶压强-速度偏微分方程组:
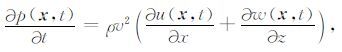
|
(1a) |
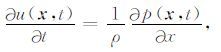
|
(1b) |
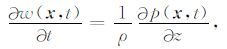
|
(1c) |
其中, p(x,t) 代表声波压强场, u(x,t)与w(x,t) 分别为质点x方向与z方向的质点偏振速度.v为介质速度,ρ为介质密度.t为时间, x=(x,z) 代表空间位置.
将方程(1b)与(1c)带入方程(1a)可得到二阶声波方程:
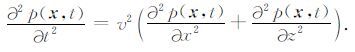
|
(2) |
在地震勘探中,通常可以将地震波分解为一系列简谐平面波.在这些简谐平面波中,不同的频率(波数)分量具有不同的振幅.即不同的谐波成分乘上振幅权重,再通过求和就合成了平面波.考虑二维简谐平面波,其表达式如下:
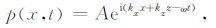
|
(3) |
其中,A为常数代表谐波的振幅,i=
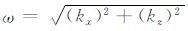
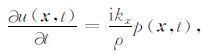
|
(4a) |
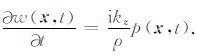
|
(4b) |
对(4)式做时间积分并省略常数项,得到简谐波偏振速度分量的通解如下:

|
(5a) |
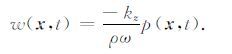
|
(5b) |
在此,偏振速度的解析表达式是通过压强场的解析解表达,基于偏振速度与压强场之间的解析关系,本文将给出一种高精确的显式交错时间递推格式,并通过共轭梯度优化算法求取时间递推匹配系数.因而,偏振速度与压强场的解析关系是本文方法的基础所在.
2.2 交错网格时间递推格式传统交错网格正演递推格式如下:

|
(6a) |
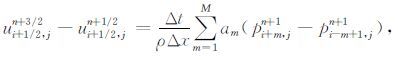
|
(6b) |
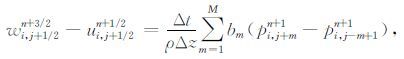
|
(6c) |
其中,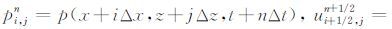
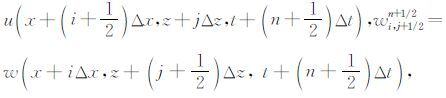
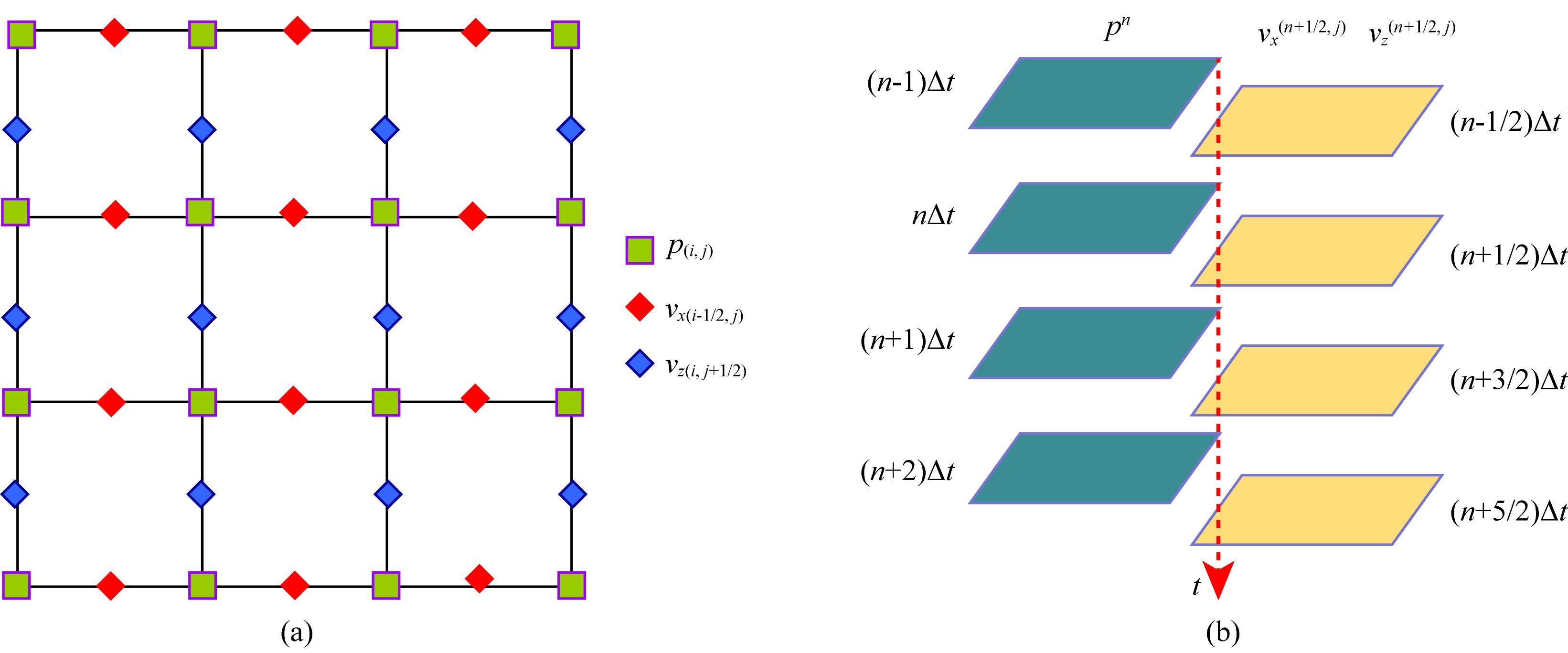
|
图 1 计算节点分布图 (a)空间网格节点分布;(b)交错时间递推示意图. Fig. 1 Compute diagram (a)Staggered space nodes distribution;(b)Staggered time evolution diagram. |
传统差分系数通过Taylor展开获得,本文将利用平面波解优化系数.偏导(或者差分)可以看作对地震波场的一种滤波作用.为了实现对时间差分与空间差分的同时优化,必须将空间差分算子与时间 差分算子对波场的滤波作用相结合.以(6a)式为例介绍如何联合时间差分与空间差分:
首先,利用平面波解(3)式的性质,得到时间差分的关系:
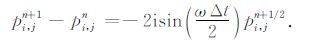
|
(7) |
随后,利用偏振速度与压强场的解析关系式(5a)和(5b),可以得到:
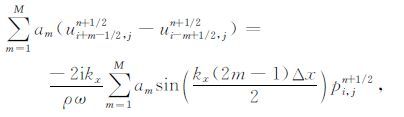
|
(8) |
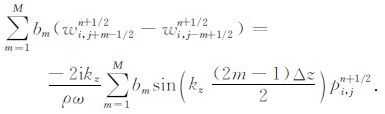
|
(9) |
注意到,(7)式与(8)、(9)式表示出了压强场递推格式(6a)中时间差分与空间差分与压强 pi,jn+1/2 的关系,式(6a)中的递推系数与(8)、(9)式中的系数是相同的.将(7)、(8)、(9)式代入式(6a)中,化简得到:
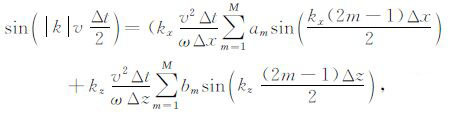
|
(10) |
其中, kx=kcos(θ),kz=ksin(θ),θ 代表传播方向.同样的,可以得到偏振速度递推格式的时间差分与空间差分关系如下:
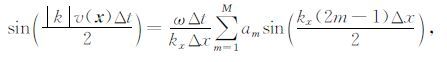
|
(11a) |
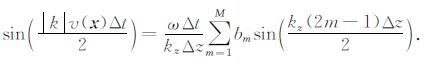
|
(11b) |
在(10)、(11a)和(11b)式中,如果等式的左边与右边完全相等,则表示没有频散.通过调整系数 am和bm, 使得等式右边尽可能逼近等式的左边.下面介绍如何使用最小二乘法求解匹配系数的具体步骤.
2.3 最小二乘迭代解以求取压强场的递推匹配系数为例,介绍最小二乘法迭代求解过程.首先,定义目标函数为
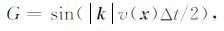
|
(12) |
另外,将等式(11)右边的函数组合表示为

|
(13) |
通过修改匹配系数向量 a,b,使得F(a,b) 尽可能的逼近精确时间递推算子G.
在此之前讨论的都是简谐平面波(单一波数),真实的地震波是由一系列的简谐波组合而成,因此必须在一定的波数范围内考虑优化,波数范围可根据子波的频谱与介质速度等决定(Wu and Alkhalifah,2014),地震波的有效波数范围可定义为 [0,2πfmax/v], 其中fmax为子波的最大频率,v为介质的速度.
研究表明通过优化 F(a,b) 与G的比值可以提高精度,对(12)式与(13)式进行等间隔离散采样,将系数的求取转换为最小二乘优化问题:
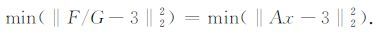
|
(14) |
对传播方向θ进行π/16的等间隔采样,考虑到对称性,范围选为[0,π/2].在定义的有效波数范围内进行等间隔采样,采样点数为Nk.A为一个9Nk行,2M列的矩阵,不同的列代表着不同的网格节点,每一列的元素随着波数值大小与角度大小变化;x为需要求取的匹配系数 [a1,…,aM,b1,…,bM]T. 需要指出的是上述(14)式中不包含密度项,数值频散优化涉及的主要计算参数为时间步长、空间步长、介质速度以及优化的波数范围.
一些学者指出,当波数范围较小、差分阶数M较大时,(14)式为一个病态的方程组,直接对其使用最小二乘求解可能会出现不稳定,本文采用共轭梯度迭代解法增加解的稳定性,流程如下:
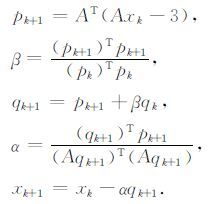
|
(15) |
考虑到传统的泰勒级数展开法(Chu and Stoffa,2012)获得的差分系数具有较高的稳定性,因此将其作为迭代的初值.即将 am=a′m与bm=b′m 作为迭代的初始值,其中, a′m与b′m 为传统差分系数,测试表明该初始值可以极大地增加计算稳定性.一般情况,只需要几次迭代就可以得到优化的系数.这里的迭代初始值也可以选用其他系数(Liu和Sen,2011)加快收敛速度,与传统系数作为初始值得到优化系数差异十分小.采用本文方法,不同速度对应着不同的系数,速度差异不大时,对应的优化系数基本相等.对于复杂模型我们首先以1 m·s-1为间隔对不同速度求取相应的差分系数,然后对速度场中每一个速度匹配相近速度值的系数,这样可以大大节省系数求取计算时间.
3 数值频散分析 3.1 一维频散分析有限差分正演模拟中,地震波的数值相速度不仅与介质速度有关,还与计算过程中的空间网格间距、时间步长、差分阶数等有关,我们定义压强场的模拟相速度相对误差为
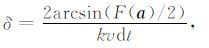
|
(16a) |
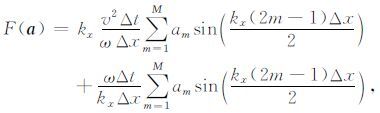
|
(16b) |
其中,v代表真实的介质速度,k为地震波的波数,ρ为介质密度,Δx为空间采样间隔,dt为时间采样间隔.分析可知:当δ为1时,表示计算中没有出现数值频散.在数值模拟中,地震波波数与子波频谱存在一定的联系,最大波数与最大频率具有下面的关系:
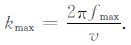
|
(17) |
正演过程中,需要重点关注地震信号零到最高频率之间的能量的模拟精度.相同的子波具有相同的频谱,在不同的介质中传播则有不同的波数范围,本文将其主要能量分布的波数范围称之为有效波数范围,优化的工作主要针对这部分波数范围展开.
不失一般性,首先考虑主要能量集中在0~60 Hz的地震波在低速介质v=1500 m·s-1中的传播,并对其在不同差分阶数下,传统的基于泰勒展开方法与本文优化方法频散分析结果对比如图 2a所示.接下来讨论在高速介质中考虑更大频率范围的数值频散,考虑0~110 Hz的地震波数值模拟频散(如图 2b所示),高速介质对应速度v=4500 m·s-1.在图 2中虚线代表传统的基于泰勒展开求取系数方法的频散曲线,实线为本文提出的新方法对应的频散曲线.从图 2可以看出,(1)在速度比较低时,所对应的波数范围比高速介质的波数范围大(公式(16));(2)传统方法将时间差分与空间差分相分离,介质速度较低时,有效波数范围内,传统方法的数值相速度既存在大于真实速度的部分,也存在数值相速度小于真实速度的部分,在高波数段表现为严重的数值相速度偏小,随着差分阶数的增加,传统方法一定程度上改善了高波数段相速度偏小的问题(通常说的空间频散);(3)低速介质中,采用最小二乘法优化方法的本文方法,在阶数较低时,频散误差波动较大,随着阶数的增加,对频散的改进显著提高.(4)在高速介质中,传统方法的频散误差主要体现在数值相速度大于真实速度上(通常说的时间频散),本文新方法可以将频散限制在一个较小的误差范围内.

|
图 2 不同速度两种方法在一维介质中不同差分阶数下的频散分析图 h=10 m,dt=1 ms,ρ=1 g·cm-3.(a)v=1500 m·s-1;(b)v=4500 m·s-1. Fig. 2 1D dispersion analysis for two methods with different velocity (a)v=1500 m·s-1;(b)v=4500 m·s-1 when h=10 m,dt=1 ms,ρ=1 g·cm-3. |
二维的压强场的频散误差定义为
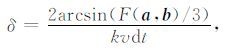
|
(18a) |
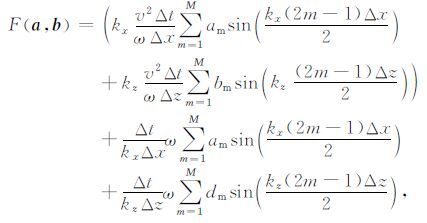
|
(18b) |
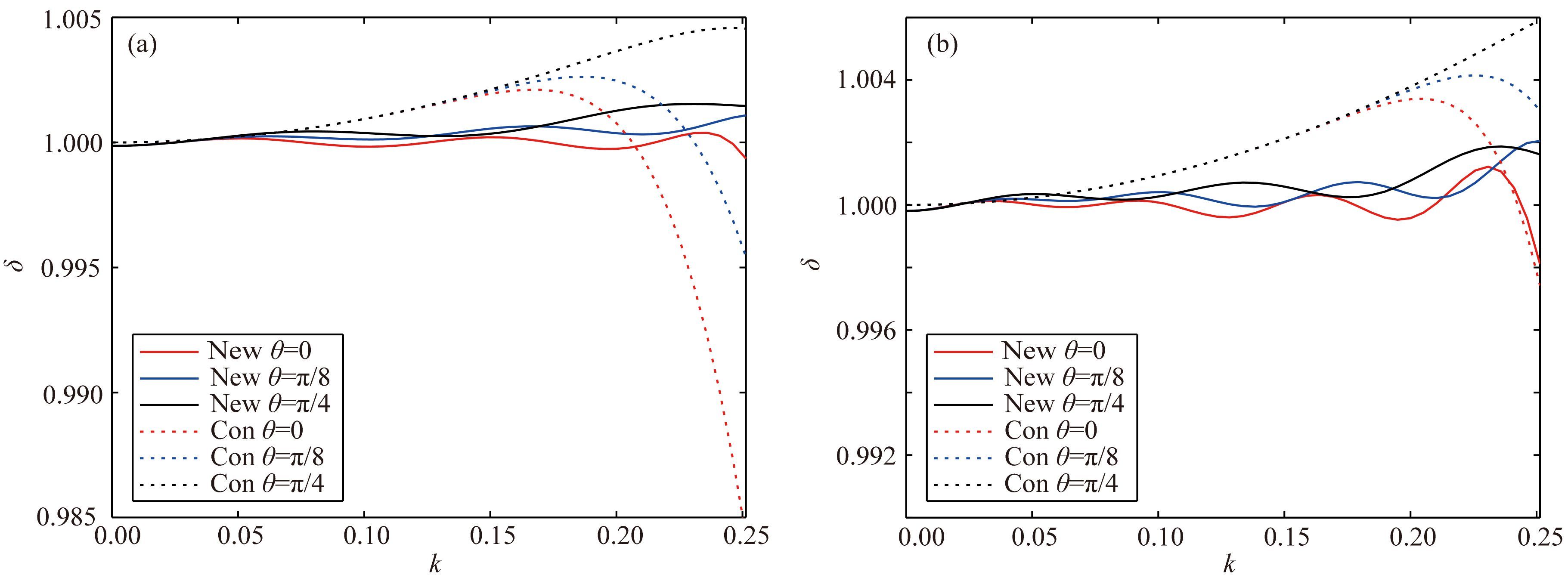
其中, kx=kcos(θ),kz=ksin(θ),θ 代表传播方向.当δ越接近1,则压强场的频散越小;当δ偏离1越大,则表示频散越严重.在二维情况下考虑地震波的频率范围为0~60 Hz.传统的基于泰勒展开方法与本文优化方法在不同的速度介质中的频散分析结果对比图如图 3与图 4所示.其中虚线代表传统的基于泰勒展开的方法的不同传播角度的频散,实线为本文提出的新方法对应的频散曲线.
|
图 3 两种方法在二维低速介质中不同阶差分阶数下的频散误差图 dx=dz=10 m,dt=1 ms,v=1500 m·s-1,ρ=1 g·cm-3.(a)M=6;(b)M=10. Fig. 3 2D dispersion analysis of for two methods with different SGFD order in low-velocity media (a)M=6,(b)M=10 when dx=dz=10 m,dt=1 ms,v=1500 m·s-1,ρ=1 g·cm-3. |
|
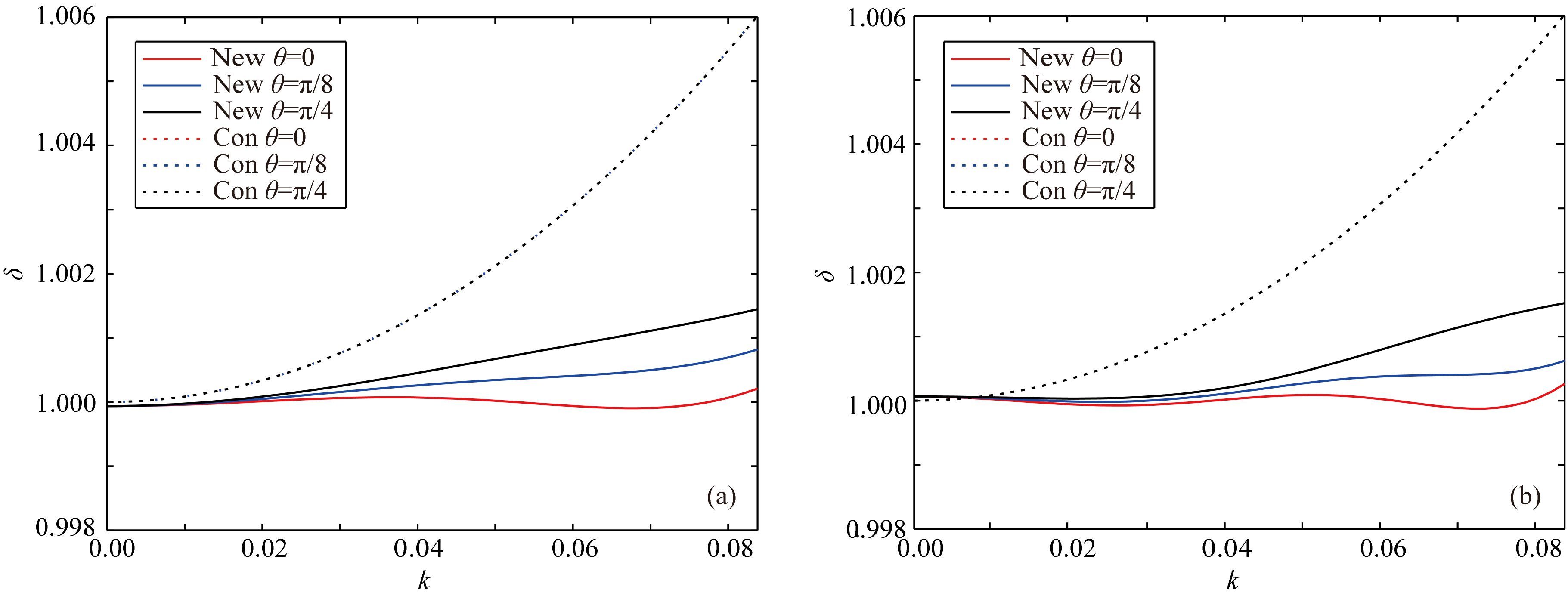
图 4 两种方法在二维高速介质中不同阶差分阶数下的频散误差图 dx=dz=10 m,dt=1 ms,v=4500 m·s-1,ρ=1 g·cm-3.(a)M=6;(b)M=10. Fig. 4 2D dispersion analysis of for two methods with different SGFD order in high-velocity media (a)M=6,(b)M=10 when v=4500 m·s-1,ρ=1 g·cm-3. dx=dz=10 m,dt=1 ms. |
图 3为低速介质中,不同阶数下两种方法的频散分析对比图.从图 3中可以看出:(1)在低速介质中,有效波数范围较大,其范围内传统方法既存在相速度大于真实速度也存在相速度低于真实速度的波数区间.(2)传统方法将时间差分与空间差分相分离,无论是在高阶数还是低阶数情况下,在高波数段不同传播方向频散差别较大.从图中看出,在45°传播方向上频散误差相对较小,在0°传播方向上频散最大.(3)本文优化的方法将时间差分与空间差分相统一,通过最小二乘算法在整体上减小了频散误差,同时实现了不同传播方向的优化.
图 4为高速介质中,两种方法不同阶数的频散分析对比图.从图中可以看出:(1)在高速介质中,传统方法对应的频散主要表现为相速度大于真实速度(时间频散);(2)在有效波数范围内,传统方法在不同角度频散趋于一致,随着波数增加误差不断增加,本文方法的结果在不同角度频散不一致,但在限制在一个较小误差范围内,正演模拟中精度更高;(3)当增加空间差分阶数对时间频散的改善不是很明显时,可以通过减小时间步长或者增加时间阶数压制频散.
4 模型试算结果考虑到优化的波数范围与模型参数的选取密切相关,本文对三个典型模型进行了正演模型测试.首先,使用均匀模型测试本文方法在压制时间频散的情况;其次,采用层状模型展示本文方法在空间频散压制方面的优势;最后,通过Marmousi2模型验证本文方法对复杂速度场的适应性.
4.1 均匀模型为了比较传统方法与本文方法在时间方面的模拟精度,取均匀模型,速度为2500 m·s-1,密度为1 g·cm-3计算区域为8000 m×8000 m,纵横向空间采样间隔Δx=Δz=20 m,时间步长Δt=4 ms,两种方法采用相同的差分阶数M=6.并采用主频为5 Hz的雷克子波作为震源,最高频率约为15 Hz,在模型中心处激发.一般来讲,传统方法高阶数差分正演结果,在总体上模拟精度高于低阶数正演结果,选择差分阶数M=10,时间步长Δt=0.1 ms的传统交错网格的正演结果作为参考结果.
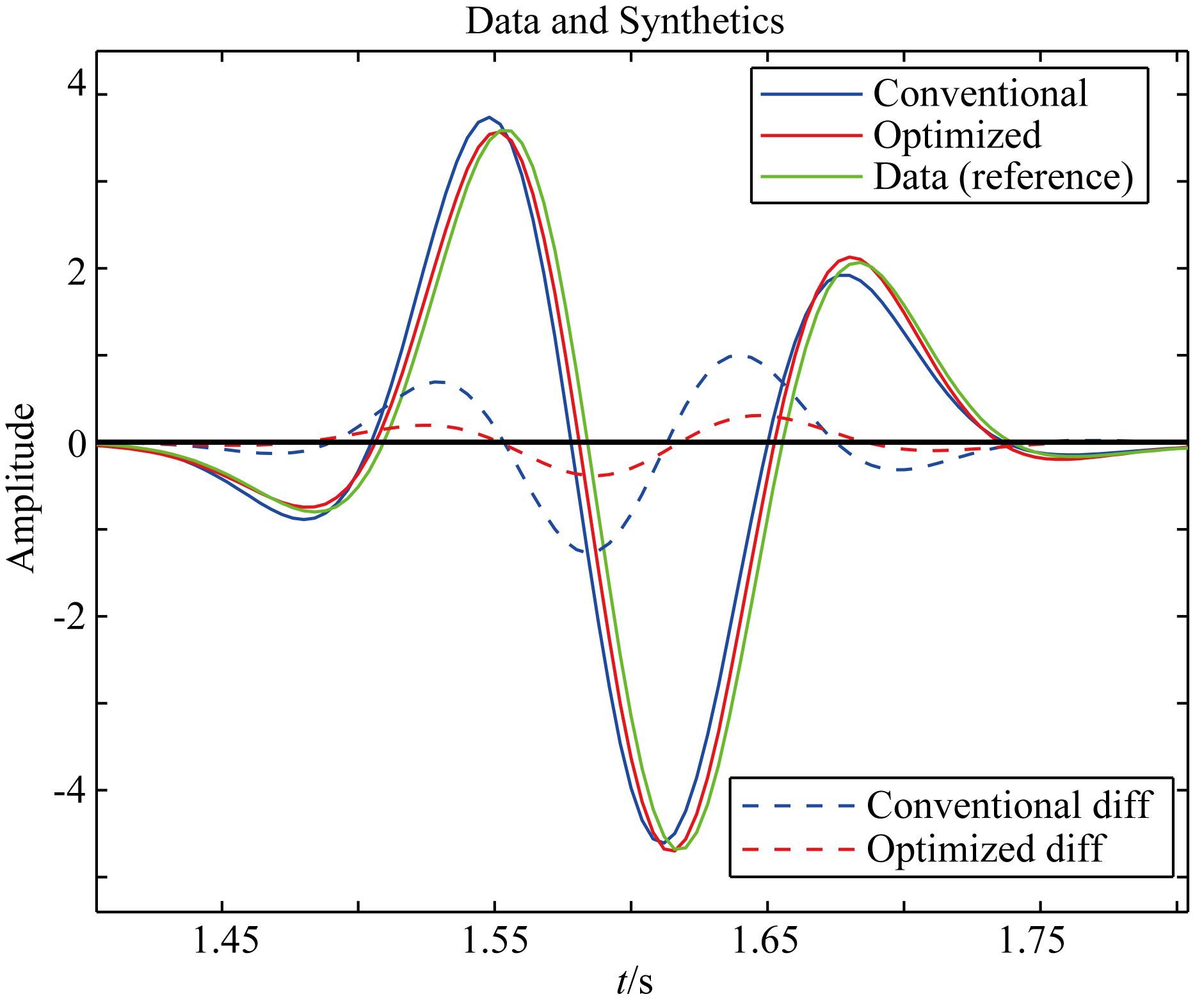
为了进一步给出两者模拟精度的差异,本文提取了三种情况下网格坐标为(51,201)的地震记录.其中蓝色实线为M=6,Δt=4 ms的传统方法得到的地震记录;红色实线为M=6,Δt=4 ms的本文方法的地震记录;绿色实线为参考结果.蓝色虚线、红色虚线分别代表传统方法、本文方法与参考结果的做差结果.
由图 5可以看到:M=6的传统方法在走时方面具有一定的“超前”(模拟的群速度大于真实速度);相比于传统方法,本文方法与参考结果吻合度更高,即基于精确时间递推格式的本文方法地震波走时计算精度优于传统方法.从图 5中还可以看到:M=6时传统方法与参考结果在波形形态上也存在一定的差异,而本文方法与参考结果在波形形态上更加一致,即本文方法较传统方法,在数值模拟波场特征保持方面具有一定的优势,从而验证了本文方法在时间频散处理和波场特征保持方面,相对于常规方法具有一定的优越性,这对于以波形匹配为目标函数的最小二乘逆时偏移与全波形反演具有重要的意义.事实上,如图 5所示的时间频散,主要是由于时间差分阶数低造成,增加空间差分阶数对其改善并不明显.在地震模拟中时间差分通常采用二阶,因而当固定时间差分阶数时,传统方法做法是减少时间步长,增加计算精度.通过本文方法在不改变时间步长条件下,通过优化系数减少时间频散.
|
图 5 走时精度比较 Fig. 5 Temporal accuracy comparison |
在研究了本文方法在时间频散压制和波场保持方面一定优越性基础上,进一步通过层状模型(方刚等,2014)对新方法与传统方法在空间频散方面进行比较.模型参数为:模型的上层速度为1.3 km·s-1,下层速度为3.2 km·s-1;上层密度为1.7 g·cm-3,下层密度为2.7 g·cm-3,网格大小为501×501,网格间距为Δx=Δz=10 m.计算参数为:采用主频为20 Hz的雷克子波作为震源,最高频率约为60 Hz,震源的网格坐标为(251,201),计算时间步长设定为1 ms.
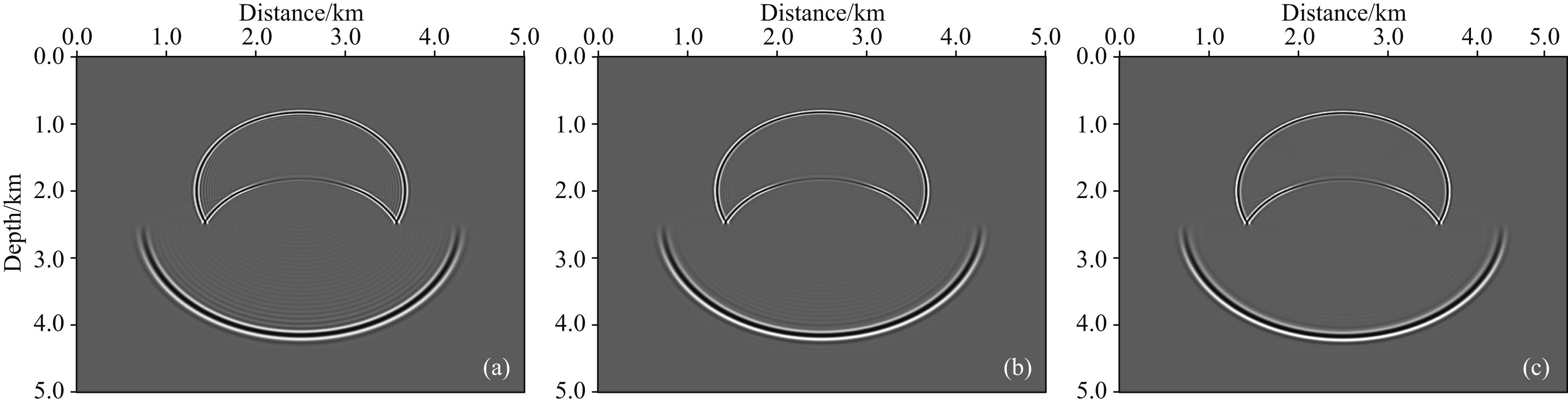
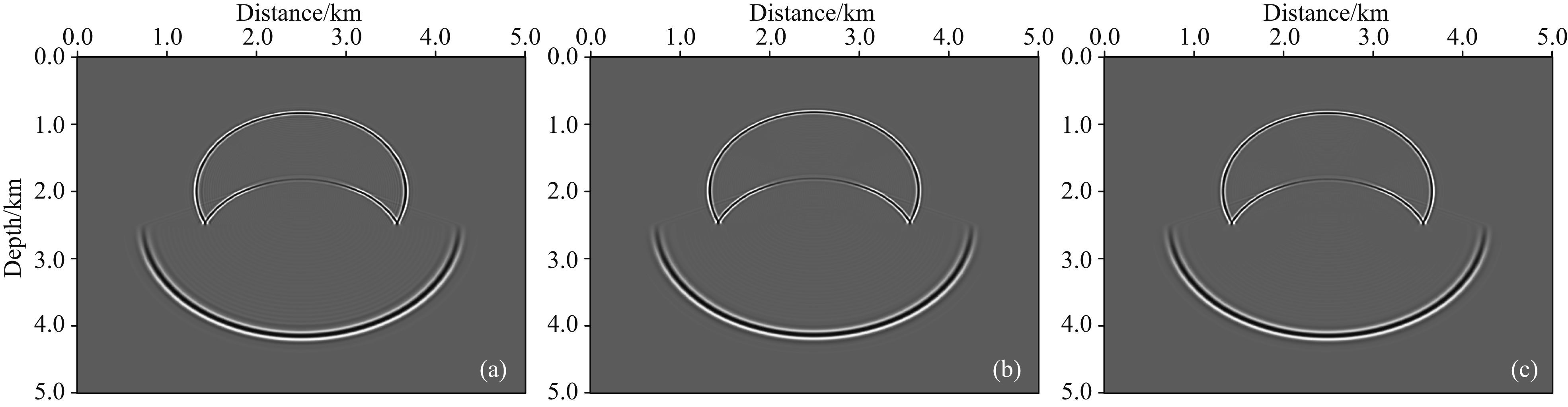
图 6为传统交错网格差分方法在不同阶数情况下t=1 s时刻的波场快照,图 7为本文优化后的交错网格差分方法使用不同阶数情况下t=1 s时刻的波场快照.对比图 6a与图 7a可以发现:在计算阶数较低时,传统方法空间频散现象严重,本文优化方法的频散相对较弱;从图 6b与图 7b中可以看出:在M=6时,传统的交错网格正演仍然存在较为严重的频散,使用本文方法频散压制效果较好;另外,从图 6c与图 7c也可以看出:采用阶数M=8的本文优化方法可以达到传统阶数M=10的正演效果.通过对层状模型的测试表明:有效波数范围内,通过最小二乘法优化差分算子改善压制频散取得不错效果.相同阶数下,本文方法相比传统方法在压制数值频散上具有明显的优势,随着差分阶数的增加,本文方法较传统方法可以更大的改善数值频散问题.
|
图 6 传统交错网格不同差分阶数正演波场快照 (a)M=4;(b)M=6;(c)M=10. Fig. 6 Snapshot of conventional SGFD with finite-difference order where M=4,6,10 |
|
图 7 本文优化交错网格不同差分阶数正演波场快照 (a)M=4;(b)M=6;(c)M=8. Fig. 7 Snapshot of optimized SGFD with different finite-difference order where M=4,6,8 |
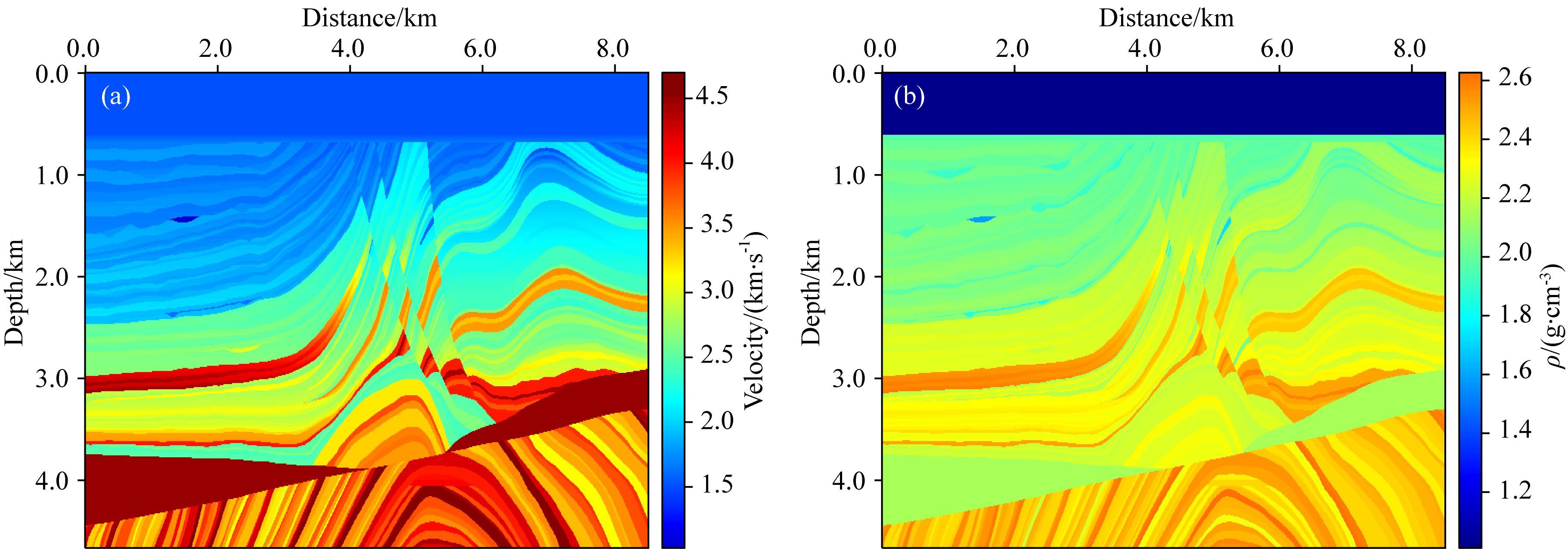
在验证了本文方法在时间频散与空间频散压制方面优势的基础上,进一步测试本文方法对复杂模型的适应性.为此,本文对SEG提供的国际标准Marmousi2模型进行正演模拟试处理.考虑到人工边界反射,我们使用了PML边界处理方法.不失一般性,同时为了提高计算效率,本文对模型进行了重采样(如图 8所示),采样后网格大小为851×467,空间采样间隔为Δx=Δz=10 m,模型速度变化范围为1428 m·s-1到4700 m·s-1,密度变化范围为1.01 g·cm-3到2.627 g·cm-3.计算参数为:采用主频为20 Hz的雷克子波作为震源,最高频率约为60 Hz,计算时间步长为Δt=1 ms,总共进行了5001次迭代,地震记录时长5 s.
|
图 8 Marmousi2模型 (a)速度模型;(b)密度模型. Fig. 8 Marmousi2 model (a)Velocity model;(b)Density model. |
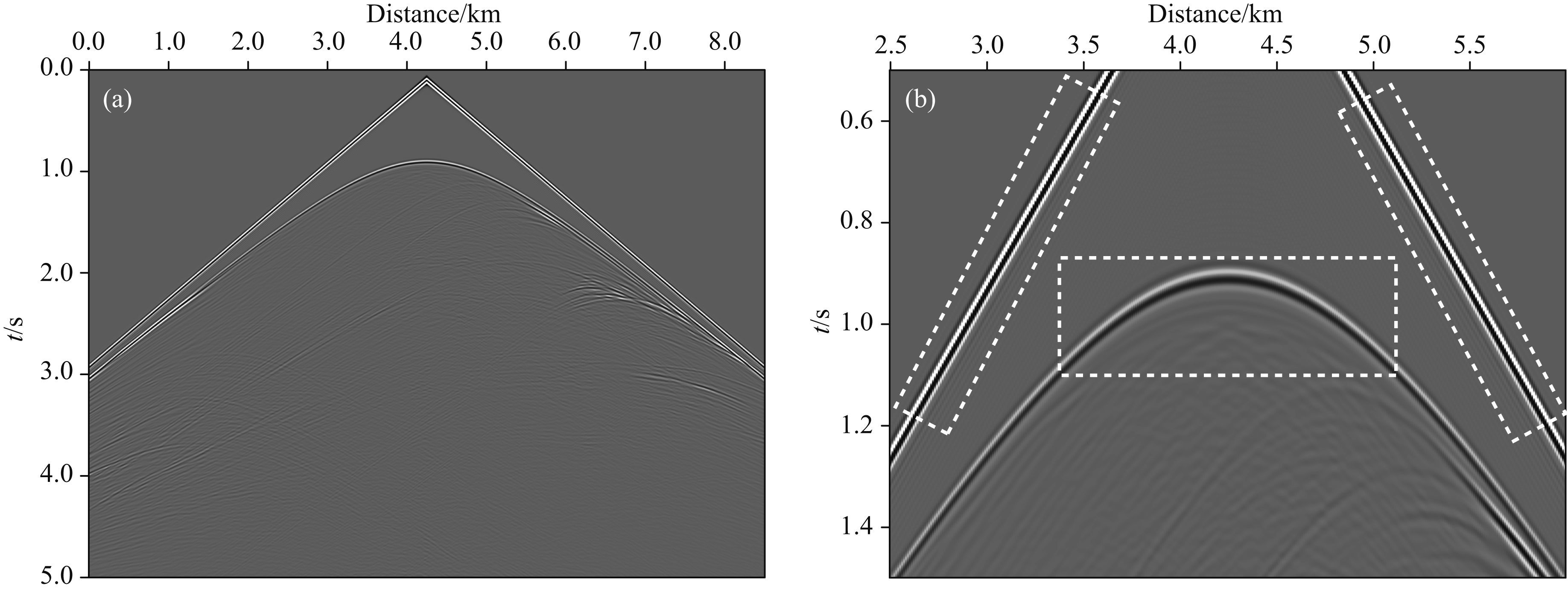
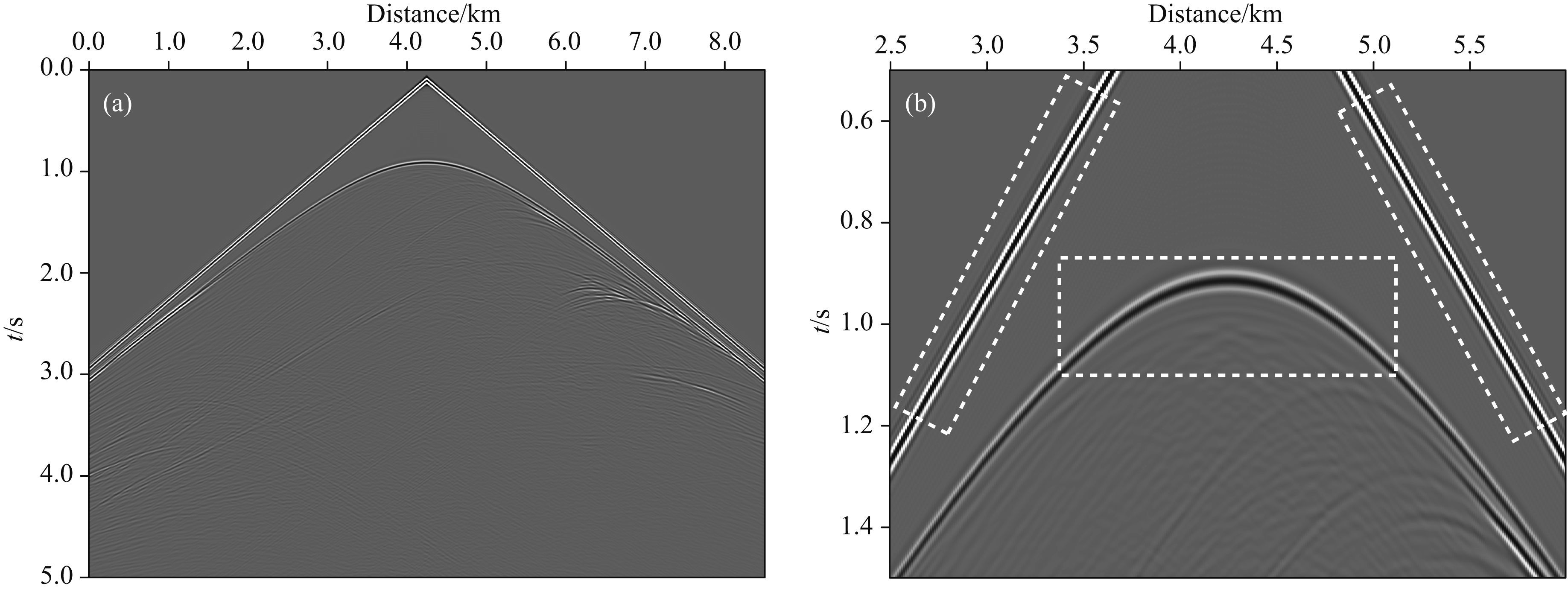
在正演模拟之前,先根据计算参数与速度值求取优化的差分系数(3373组),系数用时约6.25 s.然后利用得到的系数进行波场延拓,差分阶数M=4时,计算耗时约501.3 s;差分阶数M=6时,计算耗时约642.5 s.图 9a为传统方法采用差分阶数M=4得到的地震记录,其右侧(图 9b)为局部放大图,在虚线框中可以观察到明显的数值频散.增加差分阶数M=6,传统方法得到的地震记录如图 10a所示,为了便于比较,相应的局部放大图见图 10b;通过增加差分阶数,频散的得到了较好的压制.图 11a为本文方法M=4时对应的地震记录,其局部放大图见图 11b.对比局部放大图,采用本文方法M=4时得到的地震记录的精度与传统方法M=6时得到精度相当.本文方法时间(包括差分求取时间)约为传统方法所耗时间的0.78.

|
图 9 正演地震记录((a)传统方法M=4;(b)局部放大图) Fig. 9 Seismograms computed by(a)Conventional SGFD method M=4(b)Zoom of the seismograms |
|
图 10 正演地震记录((a)传统方法M=6;(b)局部放大图) Fig. 10 Seismograms computed by(a)Conventional SGFD method M=6(b)Zoom of the seismograms |
|
图 11 正演地震记录((a)本文优化方法M=4;(b)局部放大图) Fig. 11 Seismograms computed by(a)Optimized SGFD method M=4(b)Zoom of the seismograms |
本文在标准交错网格基础上,提出了一种新的时间递推匹配系数确定方法.该方法利用一阶声波偏微分方程组解析解将时间差分与空间差分相统一,并使用共轭梯度法在有效波数范围内对时间与空间差分算子进行同时优化.通过频散分析与三组典型模型试算得到以下两点认识:
(1) 本文给出的新的显式递推格式在有效波数区实现了对时间差分与空间差分的同时优化,相比传统方法,将时间频散与空间频散限制在更小的误差范围内.
(2) 模型试算表明本文方法,在低波数情况下对地震波的时间频散,与高波数情况下的空间频散都具有较为明显的改善.此外本文方法适用于复杂模型的正演模拟.
今后将着重于两个方面的研究,一是在交错网格时空优化的基础上,引入优化的网格节点同时将本文方法推广至三维地震波正演模拟;二是将优化的正演算法应用到逆时偏移成像、最小二乘偏移成像、全波形反演中,以提高地震偏移成像与反演的精度.
致谢感谢地震波传播与成像实验室(SWPI,http://swpi.upc.edu.cn/)提供的研究平台,感谢 Madagascar 软件(http://www.reproducibility.org)提供的绘图支持,特别感谢评审专家为本文完善提出的宝贵意见.
| Boore D. 1972. Finite difference methods for seismic wave propagation in heterogeneous materials.//Chang J ed. Methods in Computational Physics:Advances in Research and Applications. Amsterdam:Elsevier, 11:1-37. | |
| Cai X H, Liu Y, Wang J M, et al. 2014. 3D acoustic wave modelling with a globally optimal finite-difference scheme based on least squares.//76th EAGE Conference and Exhibition, Extended Abstracts. | |
| Chu C L, Stoffa P L. 2012. Determination of finite-difference weights using scaled binomial windows. Geophysics , 77 (3) : W17-W26. DOI:10.1190/geo2011-0336.1 | |
| Dai W, Fowler P, Schuster G T. 2012. Multi-source least-squares reverse time migration. Geophysical Prospecting , 60 (4) : 681-695. DOI:10.1111/gpr.2012.60.issue-4 | |
| Etgen J T, O'Brien M J. 2007. Computational methods for large-scale 3D acoustic finite-difference modeling:A tutorial. Geophysics , 72 (5) : SM223-SM230. DOI:10.1190/1.2753753 | |
| Fang G, Fomel S, Du Q Z. 2014. Lowrank finite difference on a staggered grid and its application on reverse time migration. Journal of China University of Petroleum (in Chinese) , 38 (2) : 44-51. | |
| Fomel S, Ying L X, Song X L. 2013. Seismic wave extrapolation using lowrank symbol approximation. Geophysical Prospecting , 61 (3) : 526-536. DOI:10.1111/gpr.2013.61.issue-3 | |
| Huang J P, Li Z C, Kong X, et al. 2013. A study of least-squares migration imaging method for fractured-type carbonate reservoir. Chinese J. Geophys. (in Chinese) , 56 (5) : 1716-1725. DOI:10.6038/cjg20130529 | |
| Huang J P, Cao X L, Li Z C, et al. 2014. Least square reverse time migration in high resolution imaging of near surface. Oil Geophysical Prospecting (in Chinese) , 49 (1) : 107-112. | |
| Levander A R. 1988. Fourth-order finite-difference P-SV seismograms. Geophysics , 53 (11) : 1425-1436. DOI:10.1190/1.1442422 | |
| Liang W Q, Yang C C, Wang Y F, et al. 2013. Acoustic wave equation modeling with new time-space domain finite difference operators. Chinese J.Geophys. (in Chinese) , 56 (10) : 3497-3506. DOI:10.6038/cjg20131024 | |
| Liu H F, Dai N X, Niu F L, et al. 2014. An explicit time evolution method for acoustic wave propagation. Geophysics , 79 (3) : T117-T124. DOI:10.1190/geo2013-0073.1 | |
| Liu Y, Sen M K. 2011. Scalar wave equation modeling with time-space domain dispersion-relation-based staggered-grid finite-difference schemes. Bulletin of the Seismological Society of America , 101 (1) : 141-159. DOI:10.1785/0120100041 | |
| Liu Y, Sen M K. 2013. Time-space domain dispersion-relation-based finite-difference method with arbitrary even-order accuracy for the 2D acoustic wave equation. Journal of Computational Physics , 232 (1) : 327-345. DOI:10.1016/j.jcp.2012.08.025 | |
| Liu Y. 2013a. An optimal finite-difference scheme based on least squares for acoustic modeling. //SEG Technical Program. Expanded Abstracts , 3537 : 3537-3542. | |
| Liu Y. 2013b. Globally optimal finite-difference schemes based on least squares. Geophysics , 78 (4) : T113-T132. DOI:10.1190/geo2012-0480.1 | |
| Liu Y. 2014. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling. Geophysical Journal International , 197 (2) : 1033-1047. DOI:10.1093/gji/ggu032 | |
| Ren Z M, Liu Y. 2015. Acoustic and elastic modeling by optimal time-space-domain staggered-grid finite-difference schemes. Geophysics , 80 (1) : T17-T40. DOI:10.1190/geo2014-0269.1 | |
| Tan S R, Huang L J. 2014a. An efficient finite-difference method with high-order accuracy in both time and space domains for modelling scalar-wave propagation. Geophysical Journal International , 197 (2) : 1250-1267. DOI:10.1093/gji/ggu077 | |
| Tan S R, Huang L J. 2014b. A staggered-grid finite-difference scheme optimized in the time-space domain for modeling scalar-wave propagation in geophysical problems. Journal of Computational Physics , 276 : 613-634. DOI:10.1016/j.jcp.2014.07.044 | |
| Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics. Geophysics , 74 (6) : WCC1-WCC26. DOI:10.1190/1.3238367 | |
| Wang Y F, Liang W Q, Nashed Z, et al. 2014. Seismic modeling by optimizing regularized staggered-grid finite-difference operators using a time-space-domain dispersion-relationship-preserving method. Geophysics , 79 (5) : T277-T285. DOI:10.1190/geo2014-0078.1 | |
| Wu G C, Wang H Z. 2005. Analysis of numerical dispersion in wave-field simulation. Progress in Geophysics (in Chinese) , 20 (1) : 58-65. DOI:10.3969/j.issn.1004-2903.2005.01.012 | |
| Wu Z D, Alkhalifah T. 2014. The optimized expansion based low-rank method for wavefield extrapolation. Geophysics , 79 (2) : T51-T60. DOI:10.1190/geo2013-0174.1 | |
| Yan H Y, Liu Y. 2013. Acoustic prestack reverse time migration using the adaptive high-order finite-difference method in time-space domain. Chinese J. Geophys. (in Chinese) , 56 (3) : 971-984. DOI:10.6038/cjg20130325 | |
| 方刚, FomelS, 杜启振. 2014. 交错网格Lowrank有限差分及其在逆时偏移中的应用. 中国石油大学学报(自然科学版) , 38 (2) : 44–51. | |
| 黄建平, 李振春, 孔雪, 等. 2013. 碳酸盐岩裂缝型储层最小二乘偏移成像方法研究. 地球物理学报 , 56 (5) : 1716–1725. DOI:10.6038/cjg20130529 | |
| 黄建平, 曹晓莉, 李振春, 等. 2014. 最小二乘逆时偏移在近地表高精度成像中的应用. 石油地球物理勘探 , 49 (1) : 107–112. | |
| 梁文全, 杨长春, 王彦飞, 等. 2013. 用于声波方程数值模拟的时间-空间域有限差分系数确定新方法. 地球物理学报 , 56 (10) : 3497–3506. DOI:10.6038/cjg20131024 | |
| 吴国忱, 王华忠. 2005. 波场模拟中的数值频散分析与校正策略. 地球物理学进展 , 20 (1) : 58–65. DOI:10.3969/j.issn.1004-2903.2005.01.012 | |
| 严红勇, 刘洋. 2013. 基于时空域自适应高阶有限差分的声波叠前逆时偏移. 地球物理学报 , 56 (3) : 971–984. DOI:10.6038/cjg20130325 | |
 2016, Vol. 59
2016, Vol. 59


