2. 中国石油勘探开发研究院西北分院, 兰州 730020
2. Research Institute of Petroleum Exploration & Development-Northwest, PetroChina, Lanzhou 730020, China
有限差分正演模拟方法具有计算效率高、内存占用小、简单易实现的优点,因而广泛应用于地震波正演模拟(Alterman and Karal, 1968; Alford et al., 1974; Kelly et al., 1976)、逆时偏移(Sun and McMechan, 2001; Sun et al., 2006; Jones, 2008; Etgen et al., 2009)和全波形反演(Gerhard et al., 1998; Virieux and Operto, 2009).然而,有限差分正演模拟中普遍存在的数值频散降低了模拟精度.数值频散是对空间和时间偏导数进行网格差分近似造成的,时间数值频散通常使相速度变大而出现“波至超前”,空间数值频散使相速度变小而出现“波至拖尾”,并且频率越大,数值频散误差越大(Dablain, 1986),严重影响了地震波高频成分的模拟精度.因此,压制数值频散一直是有限差分正演模拟的重要研究内容.
为了压制数值频散,高阶有限差分法、隐式有限差分法、低秩有限差分法相继被提出.隐式有限差分法需要求解大型线性方程组,内存占用大,计算效率低(Tian and Dai, 2007; Sherer and Scott, 2005; Nihei and Ishii, 2003);低秩有限差分法也需要大量的快速傅里叶变换,导致计算效率低(Fomel et al., 2013; Fang et al., 2014);高阶有限差分法被认为是一种兼顾效率和精度的有效方法,广泛应用于地震波正演模拟(Dablain, 1986; Levander, 1988; 刘洋等, 1998)和逆时偏移波场延拓(刘红伟等,2010a).
波动方程有限差分数值求解在时间域和空间域同时进行,而传统高阶有限差分法(本文称为传统2M阶有限差分法),仅基于空间域频散关系求取差分系数,本质上只有二阶空间精度.Liu和Sen(2009)提出了基于时空域频散关系的规则网格高阶有限差分法(本文称为时空域2M阶有限差分法),并证明该方法在二维正演模拟中沿8个方向达到2M阶空间精度,三维中沿48个方向达到2M阶空间精度.与传统2M阶有限差分方法相比,时空域2M阶有限差分法正演模拟精度明显提高.Liu和Sen(2011)进一步把基于时空域频散关系有限差分的思想推广到高阶交错网格,模拟精度也明显提高.严红勇和刘洋(2013)将时空域2M阶有限差分法推广到逆时偏移,通过自适应减小空间差分阶数而提高计算效率.传统2M阶和时空域2M阶有限差分正演,目前普遍采用十字交叉型规则网格或交错网格差分格式.
Saenger等(2000),Saenger和Bohlen(2004)针对弹性、黏弹性和各向异性介质提出了旋转交错网格有限差分法,避免对弹性参数求平均,提高了正演模拟精度.旋转交错网格有限差分正演模拟普遍应用于弹性、黏弹性和各向异性参数存在突变的介质(严红勇和刘洋, 2012).Liu和Sen(2013)改进时空域2M阶有限差分格式,由十字交叉网格推广到菱形网格,提出了二维声波方程菱形网格高阶有限差分方法,沿任意方向能够达到2M阶空间精度,进一步提高了正演模拟精度.但是,当差分阶数增大时计算量明显增大,而且较难推广到交错网格和三维正演.
频率-空间域,普遍采用旋转网格和常规网格混合的差分格式,并且有效地提高了正演模拟的精度和计算效率.Jo等(1996)提出9点混合网格有限差分格式,在增加少量计算量的情况下,有效提高了正演模拟精度.借鉴混合网格思想,Shin和Sohn(1998)提出25点混合网格有限差分格式,曹书红和陈景波(2012)提出17点有限差分格式,正演模拟精度进一步提高.这些方法仅适用于正方形网格,对于矩形网格,Chen(2012)对9点混合网格有限差分格式进行改进,提出了平均导数法9点混合网格有限差分格式,该方法实用性更强.平均导数法混合网格有限差分格式被广泛应用,并不断改进(刘璐等, 2013; Tang et al., 2015; 唐祥德等, 2015; 张衡等, 2015).
吸收边界是地震波数值模拟中为了消除人工边界反射而引入的.一阶应力速度声波方程正演模拟时,普遍采用分裂形式的PML吸收边界(Collino and Tsogka, 2001).二阶标量声波方程进行正演模拟时,采用CPML(Convolutional Perfectly Matched Layer)吸收边界(Komatitsch and Martin, 2007; Chen et al., 2014)和NPML(Nearly Perfectly Matched Layer)吸收边界(Hu et al., 2007; Chen, 2011).NPML吸收边界具有辅助变量少,易于实现的优点.本文提出的混合网格2M+N型有限差分法,基于二阶标量声波方程,因此采用NPML吸收边界.
本文将频率-空间域混合网格有限差分的思想引入到时空域,利用常规直角坐标系中M个拉普拉斯算子和旋转直角坐标系中N个拉普拉斯算子,构建声波方程混合网格2M+N型有限差分格式.借鉴Liu和Sen(2009, 2013)基于时空域频散关系计算差分系数的思路,推导出混合网格2M+N型有限差分格式的差分系数计算方法.在此基础上,进行频散分析、稳定性分析,并与传统2M阶、时空域2M阶有限差分方法进行比较,结果表明:当计算量基本相同时,混合网格2M+N型有限差分法能有效压制数值频散,模拟精度显著提高;混合网格有限差分法,相比传统2M阶有限差分法,稳定性增强,与时空域2M阶有限差分法稳定性基本相当.最后进一步将混合网格有限差分法应用于均匀介质、层状介质和盐丘模型的正演模拟及盐丘模型的逆时偏移,采用NPML吸收边界有效压制人工边界反射,正演模拟精度对比分析和逆时偏移成像质量,进一步证实了该方法的有效性和普遍适用性.
2 方法原理 2.1 声波方程混合网格2M+N型有限差分格式构建二维时间-空间域常密度标量声波方程可写为:
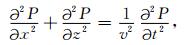
|
(1) |
其中P(x, z, t)为标量声波波场,v(x, z)为声波在介质中传播的速度,
对方程(1)进行有限差分法正演模拟时,由于时间高阶差分内存占用大、计算量大,并且稳定性降低(Chen, 2007),一般采用二阶时间精度、2M阶空间精度.时间二阶偏导数进行二阶有限差分离散近似,可以得到:
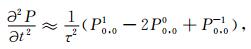
|
(2) |
其中,Pm, nj=P(x0+mh, z0+nh, t0+jτ),h为空间采样间隔(x和z方向空间采样间隔相等,均为h),τ为时间采样间隔,m, n, j分别为x, z, t方向的采样序列号.为了数学表述方便,设x0, z0, t0≡0.
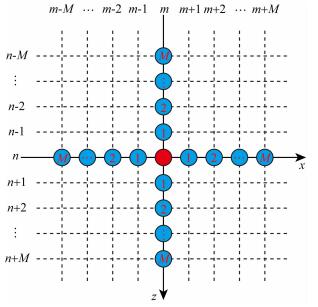
传统2M阶有限差分法(刘洋等, 1998)和时空域2M阶有限差分法(Liu and Sen, 2009)均采用图 1所示的十字交叉型差分格式,对方程(1)中的拉普拉斯算子进行2M阶有限差分离散近似,可以得到:
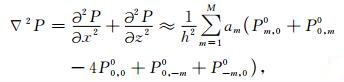
|
(3) |
|
图 1 传统2M阶和时空域2M阶有限差分格式 Fig. 1 Traditional 2Mth-order and time-space domain 2Mth-order finite-difference scheme |
其中,am为差分系数,每一项(Pm, 00+P0, m0-4P0, 00+P0, -m0+P-m, 00)/h2都可以用来近似拉普拉斯算子,因此,式(3)本质上是将拉普拉斯算子表示为M个拉普拉斯算子的加权平均,am为权系数.
将式(2)和(3)代入式(1),可以得到:
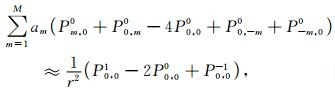
|
(4) |
其中,r=vτ/h,r为Courant稳定性条件数.
方程(4)是传统2M阶和时空域2M阶声波方程有限差分法的离散化方程,但两种方法求取差分系数的方法不同.传统2M阶有限差分法仅基于空间域频散关系计算差分系数,而时空域2M阶有限差分法则基于时空域频散关系计算差分系数.
我们将频率-空间域混合网格有限差分的思想引入到时空域,提出了时空域混合网格2M+N型有限差分法,M表示常规直角坐标系中的M个拉普拉斯算子,N表示旋转直角坐标系中的N个拉普拉斯算子.图 2a—2f给出了6种混合网格2M+N型有限差分格式的示意图.利用相同的方法,N取更大的数值,会得到更为丰富的混合网格2M+N型有限差分格式.
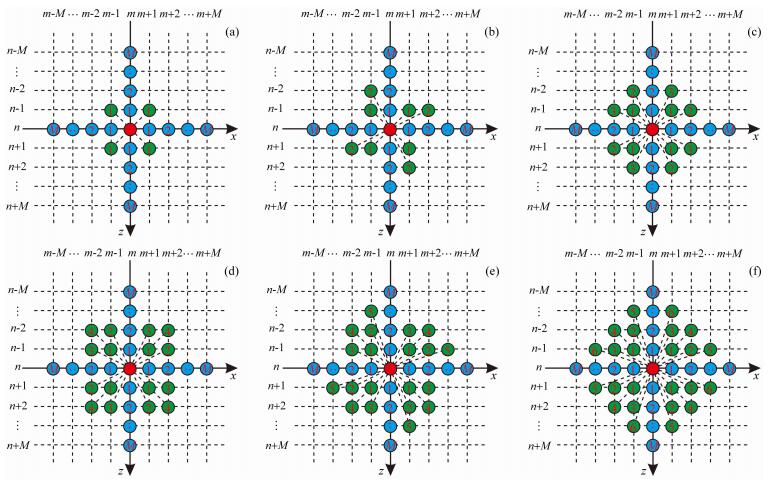
|
图 2 混合网格2M+N型有限差分格式 (a)—(f)分别为混合网格2M+N(N=1, 2, …, 6)型. Fig. 2 Mixed-grid 2M+N style finite-difference schemes (a)—(f) represent mixed-grid 2M+N (N=1, 2, …, 6), respectively. |
此外,与Liu和Sen(2013)给出的菱形网格有限差分法进行对比可以发现,菱形网格是混合网格中M和N取特定值的特殊格式,而混合网格是菱形网格的扩展,更具一般性和灵活性.例如,混合网格2M+N(M=4, N=6)型与四阶菱形有限差分格式完全等价.
下面以混合网格2M+1型有限差分格式为例,给出声波方程(1)的有限差分离散形式.按照图 2a所示的差分格式,对拉普拉斯算子进行有限差分离散近似,可以得到:
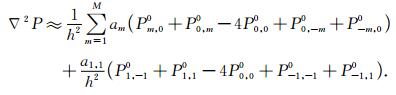
|
(5) |
式(5)表示,在混合网格2M+1型有限差分格式中,拉普拉斯算子可以表示为常规直角坐标系中M个拉普拉斯算子和旋转直角坐标系中1个拉普拉斯算子的加权平均,其中a1, a2, …, am; a1, 1为对应的差分系数.
将式(5)和(2)代入声波方程(1),可以得到:
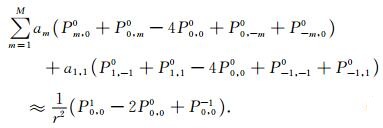
|
(6) |
方程(6)给出了混合网格2M+1型有限差分格式进行声波方程正演模拟的离散形式.利用相同的方法,可以推导出混合网格2M+N型有限差分格式的离散形式.
在模型网格化参数给定的情况下,拉普拉斯算子长度(网格点数)决定了有限差分正演模拟的计算量.拉普拉斯算子越长,计算量越大.表 1给出了传统2M阶,时空域2M阶,混合网格2M+N型(N=1, 2, …, 6)有限差分格式的拉普拉斯算子长度.本文用拉普拉斯算子长度来表述不同差分格式的计算效率.
|
|
表 1 传统2M阶,时空域2M阶和混合网格2M+N(N=1, 2, …, 6)型有限差分格式的拉普拉斯算子长度 Table 1 Laplace operator length of traditional 2M th-order, time-space domain 2M th-order, and mixed-grid 2M+N (N=1, 2, …, 6) style finite-difference schemes |
方程(6)中差分系数a1, a2, …, am; a1, 1的求解是混合网格2M+N型有限差分法的关键环节.我们以混合网格2M+1型有限差分格式为例,阐述混合网格2M+N型差分系数的计算方法.
方程(1)的平面波解的离散形式为:

|
(7) |

|
(8) |
其中,k为波数,kx、kz分别为水平波数和垂直波数,ω为圆频率,θ表示平面波传播方向与x轴正半轴的夹角,i2=-1.
将平面波解(7)代入式(6),可以得到:
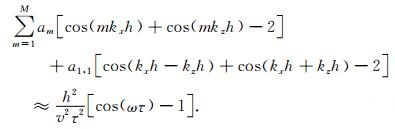
|
(9) |
对式(9)中的余弦函数进行泰勒级数展开,ωτ=kvτ=khr,可以得到:
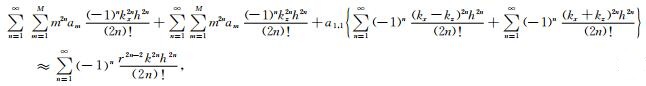
|
(10) |
其中k2=kx2+kz2.
使方程(10)左右两边kx2kz2h4的系数对应相等,可以得到:

|
(11) |
其中C42和C21表示组合数.式(11)是旋转网格坐标系中的差分系数求取方程,采用组合数表述,是为了更便利地将此差分系数计算方法推广到混合网格2M+N型差分格式.
使方程(10)左右两边kx2nh2n的系数对应相等,可以得到:

|
(12) |
方程(11)和方程(12)共有M+1个方程,刚好可以求解出M+1个差分系数a1, a2, …, am; a1, 1.
从式(11)和式(12)可以看出,混合网格差分系数不仅与M有关,还与N、r有关.而时空域2M阶有限差分格式的差分系数仅与M和r有关,传统2M阶有限差分格式的差分系数只与M有关.附录A给出了混合网格2M+2型有限差分格式的差分系数计算方法.利用同样的方法可以推导出其他混合网格2M+N型有限差分格式的差分系数.
表 2给出了M=5, v=3000 m·s-1, τ=0.001 s, h=10 m时的8种差分格式的差分系数.
|
|
表 2 传统2M阶,时空域2M阶和混合网格2M+N型有限差分格式的差分系数 Table 2 Finite difference coefficients for traditional 2M th-order, time-space domain 2M th-order, and mixed-grid 2M+N style finite-difference schemes |
地震波在非耗散介质中传播时,不会产生频散现象,即不同频率成分的地震波速度相同.然而,利用有限差分法求解波动方程时,对波动方程进行差分离散会导致地震波不同频率成分的地震波传播速度不再相等,即出现数值频散现象.数值频散是利用有限差分法求解波动方程时固有的本质特征,无法避免,只能减小.通常用数值频散的大小来衡量有限差分正演模拟的精度.因此可以定义归一化相速度δ来描述有限差分格式的数值频散:

|
(13) |
其中vph为相速度,v为地震波在介质中的真实速度.
结合相速度的定义vph=ω/k和方程(9)可以得出混合网格2M+1型有限差分格式的频散关系式为:
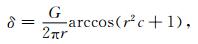
|
(14) |
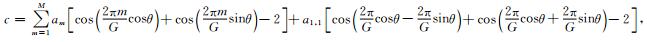
|
(15) |
其中G=λ/h,λ为波长,则G表示单位波长内网格点的个数.
δ的值与1越接近,表明数值频散误差越小;δ > 1表示存在时间数值频散,δ < 1表示存在空间数值频散.根据同样的方法可以计算出传统2M阶、时空域2M阶和其他混合网格2M+N型有限差分格式的频散关系.
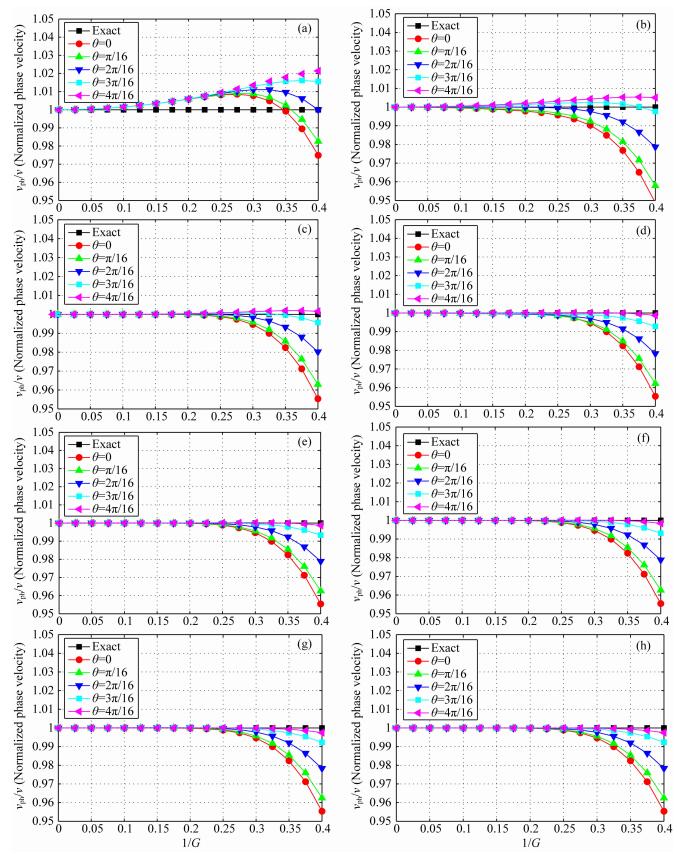
图 3给出了传统2M(M=5)阶,时空域2M(M=5)阶和混合网格2M+N型(M=5;N=1, 2, …, 6)有限差分格式的频散曲线;计算参数均为M=5, v=3000 m·s-1, τ=0.001 s, h=10 m.通过频散曲线分析和对比可以看出:
|
图 3 频散关系曲线 (a)传统2M阶;(b)时空域2M阶;(c)—(h)混合网格2M+N(N=1, 2, …, 6)型. Fig. 3 Dispersion curves (a) Traditional 2Mth-order; (b) Time-space domain 2Mth-order; (c)—(h) Mixed-grid 2M+N (N=1, 2, …, 6) style. |
① 传统2M阶(M=5)有限差分格式,空间频散最小,但是时间频散最大,相速度与真实速度之比约等于1时对应1/G的区间范围很小,大致为(0, 0.075).
② 时空域2M阶(M=5)有限差分格式,与传统2M阶(M=5)有限差分格式相比,时间频散减小,但空间频散增大,频散曲线仍比较发散,相速度与真实速度之比约等于1时对应1/G的区间范围略有增大,大致为(0, 0.125).因此,时空域2M阶有限差分格式比传统2M阶有限差分格式更能有效地压制数值频散,模拟精度更高.
③ 混合网格2M+N型(M=5;N=1, 2, …,6)有限差分格式,与传统2M阶(M=5)和时空域2M阶(M=5)有限差分格式相比,频散曲线较收敛,时间频散和空间频散都减小,相速度与真实速度之比约等于1时对应1/G的区间范围增大,大致为(0, 0.25),这一区间是时空域2M阶(M=5)有限差分格式的2倍,为传统2M阶(M=5)有限差分格式的5倍,因此,混合网格2M+N型有限差分格式能够更为有效地压制数值频散,模拟精度更高.
④ 混合网格2M+N型(M=5;N=1, 2, …,6)有限差分格式,数值频散曲线特征基本相同,模拟精度基本相当,但增大N的取值会增大正演模拟的计算量,降低效率.因此,在M取值不是足够大的情况下,建议采用混合网格2M+1型有限差分格式,这样既可以提高模拟精度,又可以保证模拟效率.
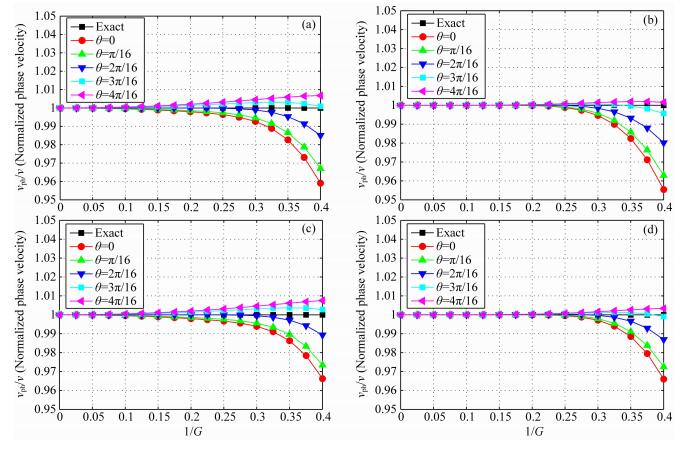
图 4a、4c分别给出了时空域2M(M=6, 7)阶有限差分格式的频散曲线,这两种差分格式的Laplace算子长度分别为25点和29点.图 4b、4d分别给出了混合网格2M+1(M=5, 6)型有限差分格式的频散曲线,这两种差分格式的Laplace算子长度分别为25点和29点.即混合网格2M+1(M=5, 6)型分别与时空域2M(M=6, 7)阶有限差分格式具有基本相同的计算量.计算频散曲线时选取的参数均为v=3000 m·s-1, τ=0.001 s, h=10 m.
|
图 4 时空域2M阶和混合网格2M+1型有限差分格式频散曲线 (a)、(c)分别为时空域2M阶(M=6, 7);(b)、(d)分别为混合网格2M+1型(M=5, 6). Fig. 4 Dispersion curves for time-space domain 2Mth-order and mixed-grid 2M+1 style finite-difference methods (a) and (c) are for time-space domain 2Mth-order (M=6, 7); (b) and (d) are for mixed-grid 2M+1 (M=5, 6) style. |
对比图 4a与4b、图 4c与4d,可以看出,混合网格2M+1(M=5, 6)型分别比时空域2M(M=6, 7)阶有限差分格式数值频散更小.因此,在计算量相同的情况下,混合网格2M+1型比时空域2M阶有限差分格式更能有效地压制数值频散.
图 5a、5c分别给出了混合网格2M+6型(M=4, 5)有限差分格式的频散曲线,这两种差分格式的Laplace算子长度分别为41点和45点;混合网格2M+6型(M=4)有限差分格式等价于四阶菱形网格差分格式(Liu and Sen, 2013).图 5b、5d分别给出了混合网格2M+1(M=5, 6)型有限差分格式的频散曲线,这两种差分格式的Laplace算子长度分别为25点和29点.因此,混合网格2M+1(M=5, 6)型分别比混合网格2M+6(M=4, 5)型有限差分格式计算量更小,正演模拟效率更高.

|
图 5 混合网格2M+6型和2M+1型有限差分格式频散曲线 (a)、(c)分别为混合网格2M+6(M=4, 5)型;(b)、(d)分别为混合网格2M+1(M=5, 6)型. Fig. 5 Dispersion curves for mixed-grid 2M+6 style and 2M+1 style finite-difference methods (a) and (c) are for mixed-grid 2M+6 (M=4, 5) style; (b) and (d) are for mixed-grid 2M+1 (M=5, 6) style. |
对比图 5b与5a、图 5d与5c,可以看出,混合网格2M+1(M=5, 6)型分别比混合网格2M+6(M=4, 5)型有限差分格式数值频散更小,正演模拟精度更高.因此,与混合网格2M+6型有限差分格式相比,混合网格2M+1型有限差分格式通过取相对较大的M值,可以达到计算效率高,同时数值频散小、模拟精度高的效果.图 5再次表明,在M值不是足够大的情况下,应该采用混合网格2M+1型有限差分格式;菱形网格不是最佳差分格式.
3.2 稳定性分析时间空间域有限差分法是以差分方程的解代替波动偏微分方程的解,只有离散后的差分方程的解收敛和稳定,这种替代才是合理的.稳定性条件描述了空间采样间隔和时间采样间隔与差分阶数、差分系数之间必需满足的条件关系,也称为Courant稳定性条件或CFL条件(Courant-Friedrichs-Lewy condition).
采用基于特征值的稳定性分析方法(Liu and Sen, 2009, 2013),得出混合网格2M+1型有限差分格式的稳定性条件为:

|
(16) |
其中,S为稳定性因子,M1=
利用相同的方法,可以给出传统2M阶、时空域2M阶以及其他混合网格2M+N型有限差分格式的稳定性条件和稳定性因子S的表达式.
进一步分析可知,混合网格2M+2型和2M+3型具有相同的稳定性条件;同样,混合网格2M+5型与2M+6型稳定性条件相同.在进行稳定性分析时,具有相同稳定性条件的混合网格2M+N型有限差分格式只给出其中一种.
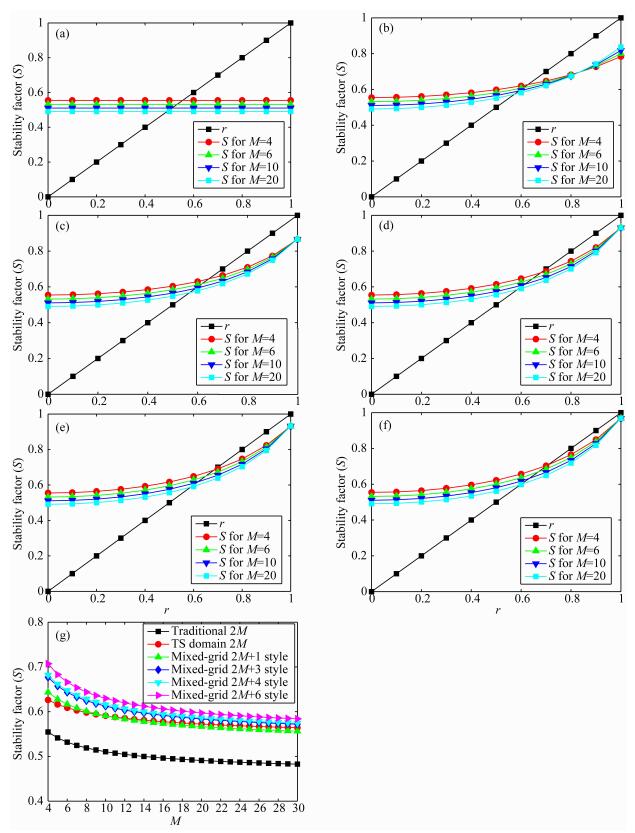
图 6a—6F分别给出了传统2M阶、时空域2M阶、混合网格2M+N(N=1, 3, 4, 6)型有限差分格式稳定性因子S随r的变化曲线.根据式(16)可知,稳定性条件要求r≤S,因此,稳定性因子S随r的变化曲线与直线r的交点为该有限差分格式的稳定性条件.图 6g给出了传统2M阶,时空域2M阶,混合网格2M+N(N=1, 3, 4, 6)型有限差分格式的稳定性条件.
|
图 6 稳定性曲线 (a)传统2M阶;(b)时空域2M阶;(c)—(f)混合网格2M+N (N=1, 3, 4, 6)型;(g)上述各种有限差分格式稳定性曲线对比图. Fig. 6 Stability curves (a) Traditional 2Mth-order; (b) Time-space domain 2Mth-order; (c)—(f) Mixed-grid 2M+N (N=1, 3, 4, 6) style; (g) Stability curves for all above finite-difference methods. |
对比可以看出,传统2M阶有限差分格式,稳定性最弱;时空域2M阶和混合网格2M+1型有限差分格式稳定性基本相当;混合网格2M+3,2M+4,2M+6型有限差分格式,比时空域2M阶有限差分格式稳定性略强.因此,混合网格2M+N型有限差分格式,增大N的取值,会增强稳定性,但同时也会增大正演模拟的计算量.
4 数值模拟 4.1 均匀介质模型正演模拟为了对比传统2M阶,时空域2M阶和混合网格2M+1型有限差分法正演模拟的精度,设计了12 km×12 km的均匀介质模型,波速为3000 m·s-1,模型网格化参数为Δx=Δz=10 m.震源位于模型中心(x=6 km, z=6 km),震源子波为30 Hz的雷克子波,时间采样间隔dt=0.001 s.分别用传统2M(M=6)阶,时空域2M(M=6)阶和混合网格2M+1(M=5)型有限差分格式进行正演模拟,三种有限差分格式的拉普拉斯算子长度均为25点,即具有基本相同的计算效率.
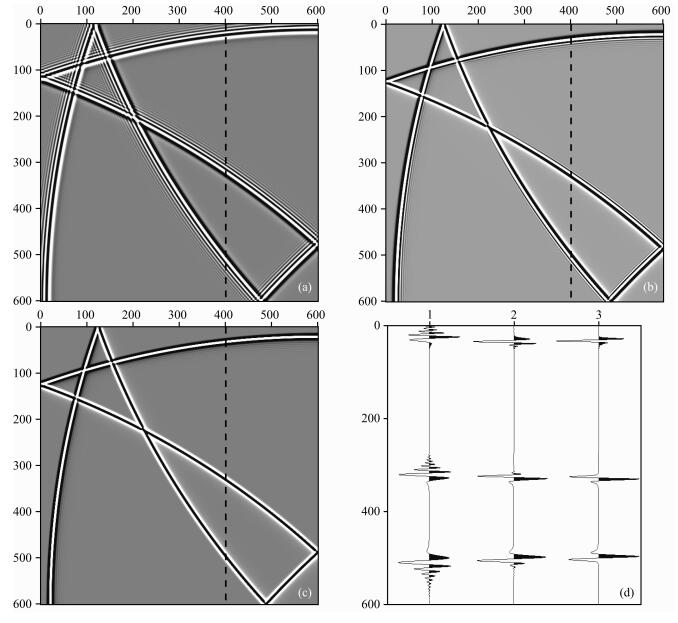
考虑到模型的对称性,绘制波场快照图时只画出左上角1/4部分.图 7a、7b、7C分别给出了传统2M(M=6)阶、时空域2M(M=6)阶、混合网格2M+1(M=5)型有限差分法在6 s时刻的波场快照.可以看出,传统2M(M=6)阶有限差分法存在严重的时间数值频散(“波至超前”,与图 3a频散曲线具有一致性),时空域2M(M=6)阶有限差分法仍然存在一定的数值频散(“波至超前”和“波至拖尾”,与图 3b频散曲线具有一致性),而混合网格2M+1(M=5)型有限差分法基本不存在数值频散,模拟精度显著提高.
|
图 7 正演模拟6s时刻波场快照及单道波形图 (a)传统2M (M=6)阶; (b)时空域2M (M=6)阶; (c)混合网格2M+1 (M=5)型; (d)黑线位置处波形图. Fig. 7 Forward modeling wavefield snap at 6s and single trace waveform (a) Traditional 2Mth-order (M=6); (b) Time-space domain 2Mth-order (M=6); (c) Mixed-grid 2M+1 (M=5) style; (d) Single trace waveform at the black dashed line indicated station. |
图 7d是分别将图 7a、7b、7c中虚线位置处的波场进行波形显示.可以看出,传统2M(M=6)阶有限差分法存在严重的数值频散,波形发生严重畸变;时空域2M(M=6)阶有限差分法存在一定程度的数值频散,波形发生一定程度的畸变;混合网格2M+1(M=5)型有限差分法基本不存在数值频散,波形未发生畸变.
因此,在计算效率基本相等的情况下,与传统2M阶和时空域2M阶有限差分法相比,混合网格2M+1型有限差分法更能有效地压制数值频散,提高正演模拟精度,这与频散分析的结果一致.
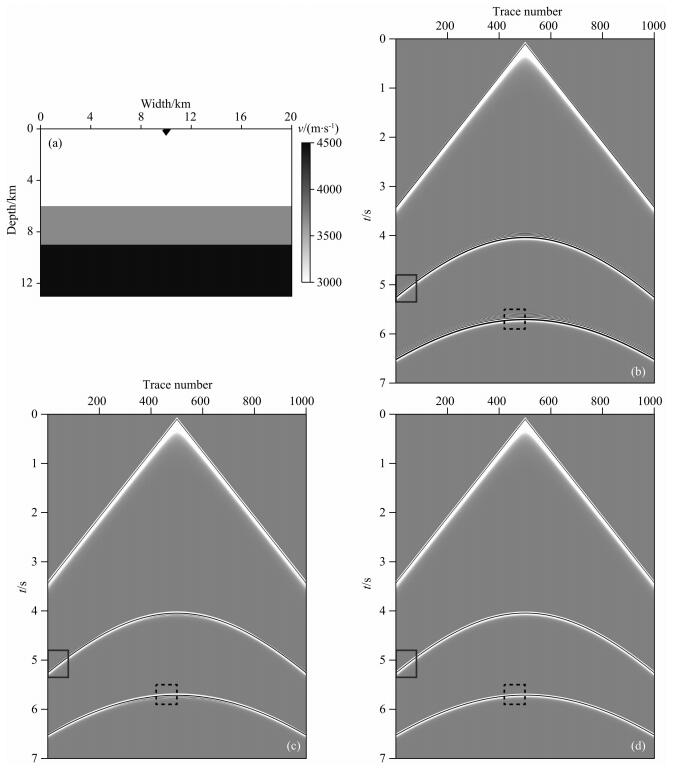
4.2 层状介质模型正演模拟图 8a是一个13 km×20 km的三层层状介质模型:h1=6 km, v1=3000 m·s-1;h2=3 km, v2=3600 m·s-1; h3=4 km, v3=4300 m·s-1;模型网格化参数为:Δx=Δz=10 m.震源位于z=100 m, x=11000 m处,震源子波为30 Hz的雷克子波,时间采样间隔为dt=0.001 s.
|
图 8 层状介质模型及正演炮集 (a)传统2M (M=6)阶;(b)时空域2M (M=6)阶;(c)混合网格2M+1 (M=5)型. Fig. 8 Layering model and forward modeling shot gather (a) Traditional 2Mth-order (M=6); (b) Time-space domain 2Mth-order (M=6); (c) Mixed-grid 2M+1(M=5) style. |
分别用传统2M(M=6)阶, 时空域2M(M=6)阶和混合网格2M+1(M=5)型有限差分格式进行正演模拟.三种有限差分格式的拉普拉斯算子长度均为25点.
图 8b、8c、8d分别给出了传统2M(M=6)阶,时空域2M(M=6)阶和混合网格2M+1型(M=5)有限差分法正演模拟的单炮记录.正演模拟过程中,均采用NPML吸收边界消除人工边界反射,从单炮记录可以看出,NPML吸收边界有效地吸收了边界反射能量.
图 9a、9b、9c分别是图 8b、8c、8d中实线方框部分的放大显示.可以看出,传统2M(M=6)阶有限差分法,由于存在较强的时间数值频散引起波形严重畸变;时空域2M(M=6)阶有限差分法,由于存在时间数值频散波形发生畸变;混合网格2M+1(M=5)型有限差分法,波形基本未发生畸变,数值频散最小.

|
图 9 波形放大显示图 8b—8d中实线和虚线方框部分 (a)—(c)分别对应图 8b—8d中实线方框部分;(d)—(f)分别对应图 8b—8d中虚线方框部分. Fig. 9 Waveforms show the part in the solid and dashed frames in Figs. 8b—8d (a)—(c) Waveforms show part in the solid frames in Figs. 8b—8d, respectively. (d)—(f) Waveforms show part in the dashed frames in Figs. 8b—8d, respectively. |
图 9d、9e、9f分别对图 8b、8c、8d中虚线方框部分进行放大显示,可以看出,传统2M(M=6)阶有限差分法,波形存在严重畸变(时间数值频散引起);时空域2M(M=6)阶有限差分法,波形也存在较严重的畸变(空间数值频散引起);混合网格2M+1(M=5)型有限差分法,波形基本未发生畸变,数值频散最小.
层状介质模型数值模拟试验表明,传统2M阶有限差分法数值频散最严重,而且以时间频散为主,正演模拟精度最低;时空域2M阶有限差分法存在一定程度的时间数值频散和空间数值频散,正演模拟精度相对较高;混合网格2M+1型有限差分法能够进一步减小时间频散和空间频散,正演模拟精度最高.
4.3 二维盐丘模型正演模拟及逆时偏移为了进一步验证本文提出的混合网格2M+N有限差分格式对于复杂介质模型的适用性,利用(SEG/EAGE)盐丘模型进行正演模拟,模拟过程中对实际的盐丘模型进行了适当的改造,将盐丘的速度变为原来的1.2倍,模型其他部分的速度变为原来的2倍.这种改造主要是考虑到,原始的盐丘模型速度较小,要想观测出混合网格2M+1型相比时空域2M型有限差分格式在压制数值频散,提高正演模拟精度方面的优势,需要将模型设计得非常大,正演模拟时间很长;盐丘部分速度变为原来的1.2倍(而不是将整个速度模型变为原来的2倍)主要是为了兼顾有限差分正演模拟的稳定性.
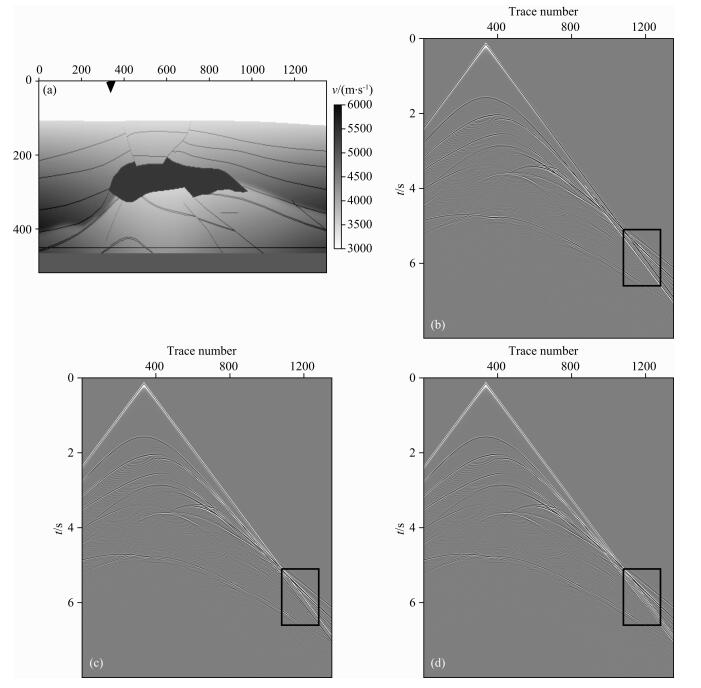
图 10a给出了盐丘速度模型,模型网格化参数为nz×nx=419×1351,Δx=Δz=20 m;正演模拟震源位于z=60 m, x=6740 m处,震源子波为主频25 Hz的雷克子波,时间采样间隔dt=0.0015 s.
|
图 10 二维盐丘模型及正演炮集 (a)二维盐丘模型;(b)传统2M (M=12)阶;(c)时空域2M (M=12)阶;(d)混合网格2M+1 (M=11)型. Fig. 10 2D salt model and forward modeling shot gathers (a) 2D salt model; (b) Traditional 2Mth-order (M=12); (c) Time-space domain 2Mth-order (M=12);(d) Mixed-grid 2M+1 (M=11) style. |
分别用传统2M(M=12)阶, 时空域2M(M=12)阶和混合网格2M+1(M=11)型有限差分格式进行正演模拟.三种有限差分格式的拉普拉斯算子长度均为49点,因此这三种有限差分格式的计算量基本相同.正演模拟和逆时偏移中,均采用NPML吸收边界.
图 10b、10c、10d分别给出了传统2M(M=12)阶,时空域2M(M=12)阶和混合网格2M+1型(M=11)有限差分法正演模拟的单炮记录.图 11b、11c、11d分别是图 10b、10c、10d中黑色方框部分的放大显示.可以看出:传统2M(M=12)阶有限差分法,存在严重的数值频散(主要为时间数值频散);时空域2M(M=12)阶有限差分法,也存在一定的数值频散(主要为空间数值频散);混合网格2M+1(M=11)型有限差分法,无明显数值频散.

|
图 11 (a)—(c)分别放大显示图 10b—10d中黑色方框部分 Fig. 11 (a)—(c) Zoom images of the part in the black frames in Figs. 10b—10d, respectively |
盐丘模型的数值模拟试验进一步验证了前面数值频散分析和均匀介质、层状介质模型数值模拟得出的结论:传统2M阶有限差分法数值频散最大,正演模拟精度最低;时空域2M阶有限差分法存在一定的数值频散,模拟精度中等;混合网格2M+1型有限差分法无明显数值频散,模拟精度最高.
进一步将混合网格2M+1(M=11)型有限差分法推广应用于逆时偏移,正演模拟参数与上面给出的参数相同.总共正演225炮,每炮1351道,炮间距120 m,道间距20 m.为了压制逆时偏移中的低频噪声同时保护成像的振幅和相位信息,首先对成像前模拟数据在时间域积分,然后对成像结果进行拉普拉斯滤波(刘红伟等,2010b; 严红勇和刘洋, 2013).图 12给出了逆时偏移成像结果,成像精度较高.

|
图 12 二维盐丘模型基于混合网格2M+1 (M=11)型有限差分法逆时偏移结果 Fig. 12 2D salt model RTM result based on mixed 2M+1 (M=11) style FD method |
本文将频率-空间域混合网格有限差分正演模拟的思想引入到时空域,提出时空域混合网格2M+N型有限差分格式,并导出了基于时空域频散关系的差分系数计算方法.在此基础上进行频散分析,稳定性分析,正演模拟和逆时偏移,结果表明:
(1) 计算量基本相等时,传统2M阶有限差分格式数值频散严重,主要为时间频散,正演模拟精度最低;时空域2M阶有限差分格式存在一定程度的时间频散和空间频散,正演模拟精度相对较高;混合网格2M+N型有限差分格式数值频散最小,正演模拟精度最高.
(2) 混合网格2M+N型有限差分格式,M取值不是足够大时,增大N的取值,对改善频散特性,提高正演模拟精度效果微弱,但会增大计算量,降低正演模拟效率.因此,我们建议采用混合网格2M+1型有限差分格式;菱形网格是混合网格2M+N型(N取值较大)的特殊形式,所以菱形网格有限差分格式并不是最优选择.
(3) 混合网格2M+N型有限差分格式,比传统2M阶有限差分格式稳定性强,与时空域2M阶有限差分格式具有基本相同的稳定性,增大N的取值,可以在一定程度上增强其稳定性,但计算量也会相应增大.
(4) 均匀介质、层状介质和复杂盐丘模型正演模拟结果,验证了混合网格2M+N型有限差分格式能有效压制数值频散,提高正演模拟精度.盐丘模型逆时偏移进一步验证了混合网格2M+N型有限差分格式具有普遍适用性.
本文提出的混合网格2M+N型有限差分格式能够有效地提高正演模拟精度,但仍存在一定的局限性:(1)混合网格2M+N型有限差分格式只适用于空间采样Δx=Δz的情况,对Δx≠Δz情况需要进一步研究.(2)混合网格2M+N型有限差分格式从声波方程导出,但对各向异性、弹性波方程的适用性未加研究.上述问题也是下一步的研究方向.
附录A 混合网格2M+2型有限差分格式及其差分系数求解方法按照图 2b给出的混合网格2M+2型有限差分格式对拉普拉斯算子进行差分离散近似,可以得到:
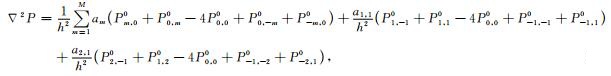
|
(A1) |
将式(A1)和(2)代入声波方程(1),可以得到:
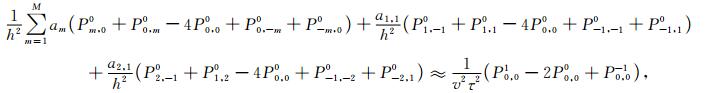
|
(A2) |
将平面波解式(7)代入式(A2),可以得到:
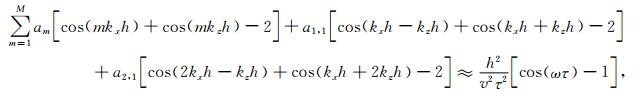
|
(A3) |
对式(A3)中的余弦函数进行泰勒展开,可以得到:
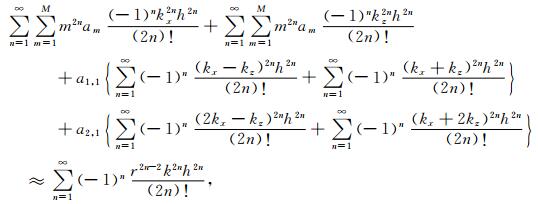
|
(A4) |
使方程(A4)左右两边kx2kz2h4和kx4kz2h6的系数对应相等,可以得到:
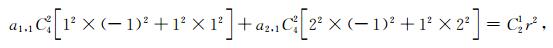
|
(A5) |
其中C42, C21, C64和C32均表示组合数.
使方程(A4)左右两边kx2nh2n的系数对应相等,可以得到:
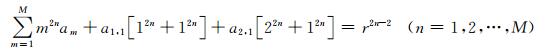
|
(A7) |
方程(A5)(A6)和(A7)总共M+2个方程,刚好可以求解出M+2个差分系数a1, a2, …, am; a1, 1, a2, 1.
| Alford R M, Kelly K R, Boore D M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics , 39 (6) : 834-842. DOI:10.1190/1.1440470 | |
| Alterman Z, Karal F C. 1968. Propagation of elastic waves in layered media by finite difference methods. Bulletin of the Seismological Society of America , 58 (1) : 367-398. | |
| Cao S H, Chen J B. 2012. A 17-point scheme and its numerical implementation for high-accuracy modeling of frequency-domain acoustic equation. Chinese J. Geophys. , 55 (10) : 3440-3449. DOI:10.6038/j.issn.0001-5733.2012.10.027 | |
| Chen H M, Zhou H, Li Y Q. 2014. Application of unsplit convolutional perfectly matched layer for scalar arbitrarily wide-angle wave equation. Geophysics , 79 (6) : T313-T321. DOI:10.1190/geo2014-0103.1 | |
| Chen J B. 2007. High-order time discretizations in seismic modeling. Geophysics , 72 (5) : SM115-SM122. DOI:10.1190/1.2750424 | |
| Chen J Y. 2011. Application of the nearly perfectly matched layer for seismic wave propagation in 2D homogeneous isotropic media. Geophysical Prospecting , 59 (4) : 662-672. DOI:10.1111/j.1365-2478.2011.00949.x | |
| Chen J B. 2012. An average-derivative optimal scheme for frequency-domain scalar wave equation. Geophysics , 77 (6) : T201-T210. DOI:10.1190/geo2011-0389.1 | |
| Collino F, Tsogka C. 2001. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media. Geophysics , 66 (1) : 294-307. DOI:10.1190/1.1444908 | |
| Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics , 51 (1) : 54-66. DOI:10.1190/1.1442040 | |
| Etgen J, Gray S H, Zhang Y. 2009. An overview of depth imaging in exploration geophysics. Geophysics , 74 (6) : WCA5-WCA17. DOI:10.1190/1.3223188 | |
| Fang G, Fomel S, Du Q Z, et al. 2014. Lowrank seismic-wave extrapolation on a staggered grid. Geophysics , 79 (3) : T157-T168. DOI:10.1190/geo2013-0290.1 | |
| Fomel S, Ying L X, Song X L. 2013. Seismic wave extrapolation using lowrank symbol approximation. Geophysical Prospecting , 61 (3) : 526-536. DOI:10.1111/j.1365-2478.2012.01064.x | |
| Gerhard P, Shin C, Hicks. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophysical Journal International , 133 (2) : 341-362. DOI:10.1046/j.1365-246X.1998.00498.x | |
| Hu W Y, Abubakar A, Habashy T M. 2007. Application of the nearly perfectly matched layer in acoustic wave modeling. Geophysics , 72 (5) : SM169-SM175. DOI:10.1190/1.2738553 | |
| Jo C H, Shin C, Suh J H. 1996. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator. Geophysics , 61 (2) : 529-537. DOI:10.1190/1.1443979 | |
| Jones I F. 2008. A modeling study of preprocessing considerations for reverse-time migration. Geophysics , 73 (6) : T99-T106. DOI:10.1190/1.2981183 | |
| Kelly K R, Ward R W, Treitel S, et al. 1976. Synthetic seismograms:a finite-difference approach. Geophysics , 41 (1) : 2-27. DOI:10.1190/1.1440605 | |
| Komatitsch D, Martin R. 2007. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics , 72 (5) : SM155-SM167. DOI:10.1190/1.2757586 | |
| Levander A R. 1988. Fourth-order finite-difference P-SV seismograms. Geophysics , 53 (11) : 1425-1436. DOI:10.1190/1.1442422 | |
| Liu H W, Li B, Liu H, et al. 2010a. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation. Chinese J. Geophys. , 53 (7) : 1725-1733. DOI:10.3969/j.issn.0001-5733.2010.07.024 | |
| Liu H W, Liu H, Zou Z. 2010b. The problems of denoise and storage in seismic reverse time migration. Chinese J. Geophys. , 53 (9) : 2171-2180. DOI:10.3969/j.issn.0001-5733.2010.09.017 | |
| Liu L, Liu H, Liu H W. 2013. Optimal 15-point finite difference forward modeling in frequency-space domain. Chinese J. Geophys. , 56 (2) : 644-652. DOI:10.6038/cjg20130228 | |
| Liu Y, Li C C, Mou Y G. 1998. Finite-difference numerical modeling of any even-order accuracy. Oil Geophysical Prospecting , 33 (1) : 1-10. | |
| Liu Y, Sen M K. 2009. A new time-space domain high-order finite-difference method for the acoustic wave equation. Journal of Computational Physics , 228 (23) : 8779-8806. DOI:10.1016/j.jcp.2009.08.027 | |
| Liu Y, Sen M K. 2011. Scalar wave equation modeling with time-space domain dispersion-relation-based staggered-grid finite-difference schemes. Bulletin of the Seismological Society of America , 101 (1) : 141-159. DOI:10.1785/0120100041 | |
| Liu Y, Sen M K. 2013. Time-space domain dispersion-relation-based finite-difference method with arbitrary even-order accuracy for the 2D acoustic wave equation. Journal of Computational Physics , 232 (1) : 327-345. DOI:10.1016/j.jcp.2012.08.025 | |
| Nihei T, Ishii K. 2003. A fast solver of the shallow water equations on a sphere using a combined compact difference scheme. Journal of Computational Physics , 187 (2) : 639-659. DOI:10.1016/S0021-9991(03)00152-9 | |
| Saenger E H, Gold N, Shapiro S A. 2000. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion , 31 (1) : 77-92. DOI:10.1016/S0165-2125(99)00023-2 | |
| Saenger E H, Bohlen T. 2004. Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid. Geophysics , 69 (2) : 583-591. DOI:10.1190/1.1707078 | |
| Sherer S E, Scott J N. 2005. High-order compact finite-difference methods on general overset grids. Journal of Computational Physics , 210 (2) : 459-496. DOI:10.1016/j.jcp.2005.04.017 | |
| Shin C, Sohn H. 1998. A frequency-space 2-D scalar wave extrapolator using extended 25-point finite-difference operator. Geophysics , 63 (1) : 289-296. DOI:10.1190/1.1444323 | |
| Sun R, McMechan G A. 2001. Scalar reverse-time depth migration of prestack elastic seismic data. Geophysics , 66 (5) : 1519-1527. DOI:10.1190/1.1487098 | |
| Sun R, McMechan G A, Lee C S, et al. 2006. Prestack scalar reverse-time depth migration of 3D elastic seismic data. Geophysics , 71 (5) : S199-S207. DOI:10.1190/1.2227519 | |
| Tang X D, Liu H, Zhang H. 2015. Frequency-space domain acoustic modeling based on an average-derivative and GPU implementation. Chinese J. Geophys. , 58 (4) : 1341-1354. DOI:10.6038/cjg20150421 | |
| Tang X D, Liu H, Zhang H, et al. 2015. An adaptable 17-point scheme for high-accuracy frequency-domain acoustic wave modeling in 2D constant density media. Geophysics , 80 (6) : T211-T221. DOI:10.1190/geo2014-0124.1 | |
| Tian Z F, Dai S Q. 2007. High-order compact exponential finite difference methods for convection-diffusion type problems. Journal of Computational Physics , 220 (2) : 952-974. DOI:10.1016/j.jcp.2006.06.001 | |
| Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics. Geophysics , 74 (6) : WCC1-WCC26. DOI:10.1190/1.3238367 | |
| Yan H Y, Liu Y. 2012. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media. Chinese J. Geophys. , 55 (4) : 1354-1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 | |
| Yan H Y, Liu Y. 2013. Acoustic prestack reverse time migration using the adaptive high-order finite-difference method in time-space domain. Chinese J. Geophys. , 56 (3) : 971-984. DOI:10.6038/cjg20130325 | |
| Zhang H, Liu H, Tang X D, et al. 2015. Forward modeling of VTI media in the frequency-space domain based on an average-derivative optimal method. Chinese J. Geophys. , 58 (9) : 3306-3316. DOI:10.6038/cjg20150924 | |
| 曹书红, 陈景波. 2012. 声波方程频率域高精度正演的17点格式及数值实现. 地球物理学报 , 55 (10) : 3440–3449. DOI:10.6038/j.issn.0001-5733.2012.10.027 | |
| 刘红伟, 李博, 刘洪, 等. 2010a. 地震叠前逆时偏移高阶有限差分算法及GPU实现. 地球物理学报 , 53 (7) : 1725–1733. DOI:10.3969/j.issn.0001-5733.2010.07.02 | |
| 刘红伟, 刘洪, 邹振, 等. 2010b. 地震叠前逆时偏移中的去噪与存储. 地球物理学报 , 53 (9) : 2171–2180. DOI:10.3969/j.issn.0001-5733.2010.09.017 | |
| 刘璐, 刘洪, 刘红伟. 2013. 优化15点频率-空间域有限差分正演模拟. 地球物理学报 , 56 (2) : 644–652. DOI:10.6038/cjg20130228 | |
| 刘洋, 李承楚, 牟永光. 1998. 任意偶数阶精度有限差分法数值模拟. 石油地球物理勘探 , 33 (1) : 1–10. | |
| 唐祥德, 刘洪, 张衡. 2015. 基于加权平均导数的频率-空间域正演模拟及GPU实现. 地球物理学报 , 58 (4) : 1341–1354. DOI:10.6038/cjg20150421 | |
| 严红勇, 刘洋. 2012. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟. 地球物理学报 , 55 (4) : 1354–1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 | |
| 严红勇, 刘洋. 2013. 基于时空域自适应高阶有限差分的声波叠前逆时偏移. 地球物理学报 , 56 (3) : 971–984. DOI:10.6038/cjg20130325 | |
| 张衡, 刘洪, 唐祥德, 等. 2015. 基于平均导数优化方法的VTI介质频率空间域正演. 地球物理学报 , 58 (9) : 3306–3316. DOI:10.6038/cjg20150924 | |
 2016, Vol. 59
2016, Vol. 59

