地震走时层析的目的是找到一个使理论合成走时与观测走时之差在某种意义下达到极小的“最佳”模型(Woodward et al., 2008; Zhu et al., 1992).目前基于线性反演思想的方法主要有两种实现方式.第一种是传统的求解层析方程组的方法.这种方法求解的方程组系数矩阵规模庞大,且非常稀疏,病态严重,需要采用正则化保证反演的正确性与稳定性(崔岩和王彦飞,2015),因此反演精度严重依赖于方程组的求解方法.第二种是基于局部最优化思想,通过对目标函数的局部线性化近似获得速度的修改方向,然后通过迭代实现该非线性反演问题的线性化求解.但无论哪种实现方式,线性反演方法的主要缺点是对初始模型依赖性强,当初始模型选择不合适时,很容易过早陷入局部极值.尽管如此,这些方法在实际应用中仍可以取得不错的效果.
在第二种方法中,每一次迭代中速度修改方向的计算是关键.利用伴随状态法(Li et al., 2013; 谢春等, 2014)或散射积分法(Chen et al., 2007)可以获得速度的修改方向.前者利用地震波的一次正传和数据残差的一次反传即可获得目标函数的梯度,无需存储大型矩阵,但其预条件在射线走时层析成像中不易实现.后者通过显式地计算核函数,并与走时残差向量相乘实现梯度的计算.但与传统的层析成像方法一样,散射积分法面临内存占用大的问题,特别是在利用Hessian矩阵时问题更加突出.
Hessian矩阵的利用在局部最优化反演中对提高反演精度与多参数解耦有非常重要的作用.核函数表达的Hessian矩阵包含两项,利用准确的Hessian矩阵构造的方向称为牛顿方向(Pratt et al., 1998),只保留Hessian第一项的矩阵称为近似Hessian矩阵,相对应的方向为高斯-牛顿方向(Ma and Hale, 2012).实际应用中,无论是牛顿方向还是高斯-牛顿方向都涉及到Hessian矩阵求逆的操作,因此往往难以准确构造(Métivier et al., 2013).更通常的做法是利用近似Hessian矩阵的对角阵来构造Hessian矩阵的逆,所对应的方向是拟牛顿方向的一种(Shin et al., 2001).由于Hessian矩阵的逆是直接作用在梯度上面,因此这种做法又称为梯度方向的预条件.正文中会展示,预条件的实施与否对层析有很大的影响.
Liu等(2015)在波形反演研究中提出了一种改进的散射积分算法.该方法将大规模的核函数-向量乘运算表示为具有明确物理含义的向量-标量乘的累加运算,因此避免了大规模矩阵的存储,使得传统散射积分法波形反演更加实用化.同时,该方法可以方便地实现Hessian矩阵主对角线元素的计算,进而可以方便实现梯度的预条件.本文将这种在波形反演中提出的改进的散射积分算法应用于初至波走时层析成像中,避免了传统层析成像中的大规模矩阵的存储和预条件实现不方便的问题,进而实现了带预条件的最速下降法地震走时层析成像.
2 方法原理 2.1 散射积分法初至波走时层析方法原理建立如下最小二乘目标函数:

|
(1) |
其中,t表示在当前模型下计算出的初至波理论走时,t0表示实际观测到的走时,s表示介质的慢度.在高频射线假设下,地震波走时t可以表示为
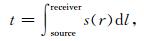
|
(2) |
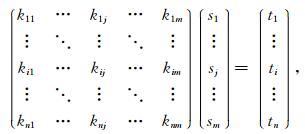
其中,积分上下限表示沿着射线路径的曲线积分,s(r)表示空间位置r处的慢度,dl表示射线路径上的微元.假设共有n个初至波走时数据,m个空间未知数,那么公式(2)离散化后得到方程组为
|
(3) |
其中,sj表示模型空间中某一点的慢度,ti表示某一炮检对所对应的初至波到达时.kij表示第i条射线在第j个模型网格内的长度,即系数矩阵中的每一行表示一条射线路径.公式(3)用矩阵符号表示为
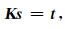
|
(4) |
这里,K即为走时层析中的敏感核函数(Fréchet导数矩阵),其规模为n×m.模型参数的修改量可以表示为修改方向p与步长α的乘积.通过对目标函数(1)式进行二阶泰勒级数展开,可以求得慢度修改方向p :
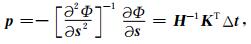
|
(5) |
这里,Δ t表示实际观测走时与当前模型下理论合成走时之差,H表示准确的Hessian矩阵,是目标函数对慢度参数的二阶导数,对于它的不同近似,可以得到不同的修改方向.步长α可以用下式求得
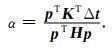
|
(6) |
根据先验信息给定初始模型s0,对于第l次迭代,可利用公式(5)求得模型参数修改方向,用公式(6)计算出步长,然后利用下式对模型进行更新:
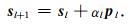
|
(7) |
高斯-牛顿方向(用符号Ha表示, H≈Ha=KKK)可以用矩阵表示为

|
(8) |
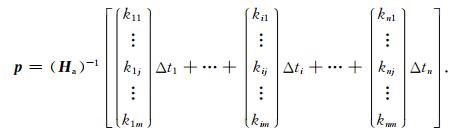
(8)式中矩阵K T规模庞大,不易存储,利用Liu等(2015)的改进算法,(8)式右端的大型核函数-向量乘可以表示为如下多个向量-标量乘的累加运算:
|
(9) |
根据前面的分析可知,公式(9)中等式右端每一个列向量(ki1 … kij … kim)T即为某一炮检对所对应的射线路径.因此,不必再存储完整的矩阵KT,仅需要存储单一炮检对所对应的射线路径即可实现梯度的计算,大大减少了内存的占用.
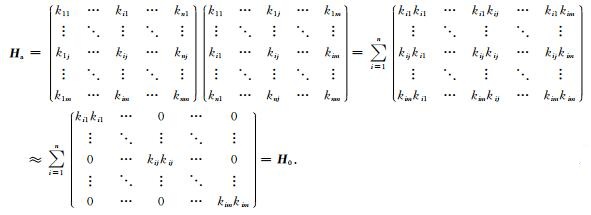
公式(9)中逆矩阵(Ha)-1难以准确求得,考虑到Ha矩阵通常为主对角线占优矩阵(尤其在高频情况下),本文利用它的对角阵(H0)的逆H0-1来近似Ha-1,利用上述相同的思路,根据公式(10)实现最速下降方向的预条件.
|
(10) |
这样就避免了存储大型矩阵K T和K,仅需将单炮检对核函数中的每一个元素平方,再对所有的炮检对累加求和即可.为了避免由于H0对角元素中存在很小的数而产生计算的不稳定,需要引入正则化项,所以预条件后的最速下降方向为
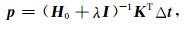
|
(11) |
其中,I表示单位矩阵,λ表示一个较小的数.将式(11)代入式(7),即可实现预条件最速下降法初至波走时层析.
3 数值实验为了验证本文方法的有效性,选取了一个二维简单模型和一个二维复杂起伏地表模型进行理论模型测试.观测方式分别为全方位观测和地表观测.基于相同的走时正演方法(刘洪等,1995),同一组“观测数据”,利用改进的散射积分法与传统解方程组的方法分别进行初至波走时层析(为方便,后文分别将二者称为散射积分法层析与传统层析).需要注意的是,为了提高计算效率与减少内存占用量,本文传统层析中大型病态方程组的求解采用的是SIRT法,且没有进行任何正则化处理(刘玉柱和董良国, 2007;刘玉柱等,2007).
3.1 全方位观测情况下的简单模型实验二维简单模型(图 1a)是一个包含101×101个离散网格的正方形模型,空间离散间隔为10 m×10 m.背景速度为1000 m·s-1,中间有一个半径为100 m的圆形高速异常体,速度为1160 m·s-1.在模型每一边均匀放置50个炮点,共计200个炮点.检波器均匀放置在模型四周,每一边50个,共200个.基于真实模型的高精度射线追踪得到的走时作为观测走时,初始模型为均匀背景模型,经过20次迭代后,反演结果如图 1所示.

|
图 1 二维简单模型反演结果对比图 (a)真实模型;(b)散射积分法层析第一次迭代时的梯度;(c)散射积分法层析20次迭代后的反演结果;(d)传统层析20次迭代后的反演结果. Fig. 1 Comparisons of the inversion results of a 2D simple model (a) True model; (b) Gradient of the first round computed by SI method; (c) The inversion result using SI method after 20 iterations; (d) The inversion result using the traditional method after 20 iterations. |
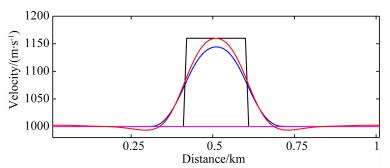
可以看出,散射积分法层析第一次迭代的梯度(图 1b)主要聚焦在速度异常附近,在速度无异常处梯度尽管不为0(这是照明角度不均匀造成的),但是相对较弱.为了更好地对比两种反演方法的精度,抽取地下500 m处的速度曲线(图 2).可以看出,散射积分法层析与传统层析的反演精度基本相当.表 1为两种方法的计算时间与内存占用量对比,可以看出,散射积分法层析内存占用仅为传统层析的4.6%,计算效率也比传统层析高.
|
图 2 地表下500 m处速度曲线对比 初始模型(粉色)、真实模型(黑色)、散射积分法层析反演结果(红色)、传统层析反演结果(蓝色). Fig. 2 Profile comparisons of the results using SI method and traditional method at depth 500 m Starting model (pink); True model (black); Result using SI method (red) and the result using traditional method (blue). |
|
|
表 1 二维简单模型不同方法内存占用量与一次迭代所需时间对比 Table 1 Comparisons of the memory requirements and computation time between different methods |
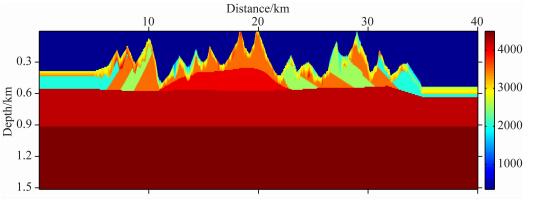
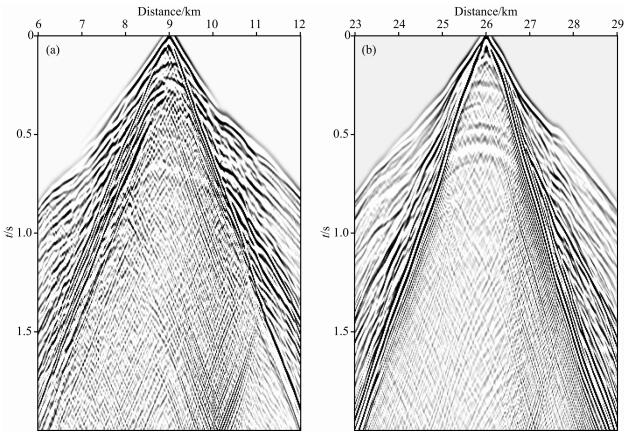
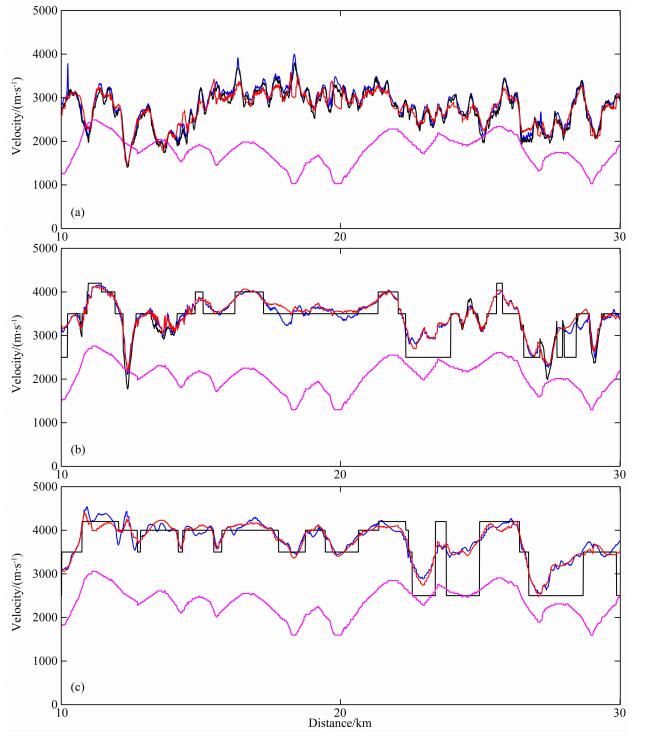
为了进一步验证该方法的反演能力,本文针对二维复杂起伏地表模型进行实验(图 3).该模型地表起伏落差达450 m,近地表速度横向变化剧烈.模型被离散为4001×151个网格,空间离散间隔为10 m×10 m.利用弹性波方程模拟地表地震记录,并拾取Z分量记录初至波走时作为观测数据.共模拟了619炮数据,第一炮位于5 km处,炮点间隔40 m.检波器均匀、对称地分布在炮点两端,水平间隔为20 m.每炮201个检波器,最小炮检距为0 m,最大炮检距为2.0 km.水平位置9 km和26 km处的两个Z分量炮记录如图 4所示.由于初至波走时层析仅能反演得到近地表的速度结构,因此为了更好地对比反演结果,下文仅显示0~0.7 km深度范围内的速度结构.该范围的真实模型如图 5a所示,初始模型如图 5b所示,散射积分法层析与传统层析经过40次迭代后的反演结果分别如图 5c、5d所示.为了定量地对比不同方法的反演结果,抽取了地下10 m、100 m、200 m处的速度曲线(图 6).由于模型左右两端并没有炮点覆盖,无法得到正确结果,因此仅显示了水平方向10~30 km的速度模型.对比不同深度的速度曲线可知,散射积分法层析可以获得与传统层析精度相当的反演结果.表 2为两种方法的内存占用量与计算效率对比.可以看出,散射积分法层析的内存占用量仅为传统层析的8.2%,计算效率也略高.
|
图 3 真实模型(深度范围0~1.5 km) Fig. 3 True model (0~1.5 km in depth) |
|
图 4 弹性波模拟地表Z分量观测记录((a)9 km处;(b)26 km处) Fig. 4 Z component records of the elastic wave simulation at (a) 9 km and (b) 26 km |

|
图 5 0.7 km深度范围内的(a)真实模型、(b)初始模型、(c)散射积分法层析40次迭代反演结果与(d)传统层析40次迭代反演结果 Fig. 5 Zoomed views of the (a) true model, (b) starting model and inversion results using (c) SI method and (d) traditional method after 40th iterations, from 0 to 0.7 km in depth |
|
图 6 地表下(a)10 m、(b)100 m、(c)200 m深度处的速度曲线对比 初始模型(粉色)、真实模型(黑色)、散射积分法层析反演结果(红色)、传统层析反演结果(蓝色). Fig. 6 Comparisons of the horizontal profiles of the inversion results using SI method and traditional method at depths of (a) 10 m, (b) 100 m and (c) 200 m Starting model (pink); True model (black); Results using SI method (red) and traditional method (blue). |
|
|
表 2 二维复杂起伏地表模型不同层析方法内存占用量与一次迭代所需时间对比 Table 2 Comparisons of the memory requirements and computation time between different methods |
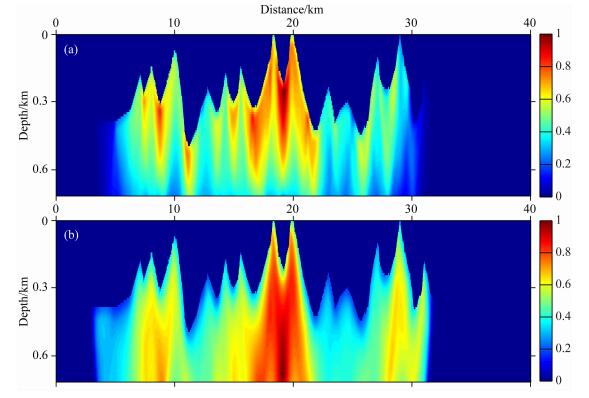
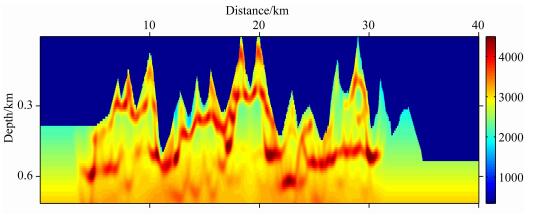
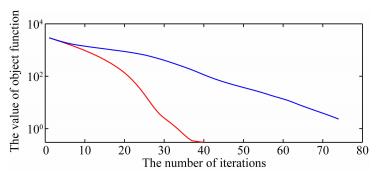
公式(11)采用预条件是该方法可以取得与传统方法相当的反演精度(图 6)的关键.在走时层析中,预条件的实现去除了射线密度的影响,起到了“照明补偿”的效果.因此,与无预条件的梯度(图 7a)相比,预条件(图 7b)使得梯度修改范围更深,速度修改方向更加合理,反演精度更高.如图 8所示,在不实施预条件的情况下,即使迭代次数达到74次依旧无法得到预条件情况下40次的反演精度.目标函数(自然对数值)的收敛情况(图 9)也有力地说明了预条件对于初至波走时层析的重要性.与无预条件的最速下降法相比,实施预条件可以使得目标函数收敛更快,并且避免过早陷入局部极值.
|
图 7 预条件对梯度的影响 第一次迭代时的(a)无预条件最速下降方向与(b)预条件最速下降方向. Fig. 7 Influence of preconditioning on gradient The gradients of the first iteration (a) without preconditioning and (b) with preconditioning. |
|
图 8 0.7 km深度范围内的最速下降法74次迭代后的结果 Fig. 8 Zoomed views of the inversion results using the SI method without preconditioning after 74th iterations, above 0.7 km |
|
图 9 不同方法目标函数(自然对数值)变化曲线 不实施预条件(蓝色)、实施预条件(红色)情况下的目标函数. Fig. 9 Comparisons of the object function Without preconditioning (blue) and with preconditioning (red). |
本文介绍的散射积分法层析对H0的实现有天然的优势(公式10).在计算梯度的同时便可以获得H0,几乎不需要增加额外的计算量.该思路可以直接推广到三维层析中,为大规模三维近地表速度建模提供了一种简单易行的方法.
5 结论本文将改进的散射积分算法应用于地震走时层析成像中,将庞大的核函数-向量乘运算表示为具有明确物理含义的向量-标量乘的累加运算.该方法同时方便地实现了Hessian对角元素的累加运算,进而实现了预条件的最速下降法初至波走时层析.二维简单模型和二维复杂起伏地表理论模型测试表明,该方法可以获得与传统解方程组的地震层析成像方法精度相当的反演结果,但内存占用量大大降低.同时,该方法还具有计算效率高、物理意义明确、反演稳定、易于并行等优点.这为以后大规模野外观测数据,尤其是三维地震层析成像处理提供了一条新的思路.
| Chen P, Jordan T H, Zhao L. 2007. Full three-dimensional tomography:a comparison between the scattering-integral and adjoint-wavefield methods. Geophysical Journal International , 170 (1) : 175-181. DOI:10.1111/gji.2007.170.issue-1 | |
| Cui Y, Wang Y F. 2015. Tikhonov regularization and gradient descent algorithms for tomography using first-arrival seismic traveltimes. Chinese J. Geophys. , 58 (4) : 1367-1377. DOI:10.6038/cjg20150423 | |
| Li S W, Vladimirsky A, Fomel S. 2013. First-break traveltime tomography with the double-square-root eikonal equation. Geophysics , 78 (6) : U89-U101. DOI:10.1190/geo2013-0058.1 | |
| Liu H, Meng F L, Li Y M. 1995. The interface grid method for seeking global minimum travel-time and the correspondent raypath. Chinese J. Geophys. , 38 (6) : 823-832. | |
| Liu Y Z, Dong L G. 2007. Analysis of influence factor of first-breaks tomography. Oil Geophysical Prospecting , 42 (5) : 544-553. | |
| Liu Y Z, Dong L G, Xia J J. 2007. Normalized approach in tomographic imaging of first breaks travel time. Oil Geophysical Prospecting , 42 (6) : 682-685. | |
| Liu Y Z, Yang J Z, Chi B X, et al. 2015. An improved scattering-integral approach for frequency-domain full waveform inversion. Geophysical Journal International , 202 (3) : 1827-1842. DOI:10.1093/gji/ggv254 | |
| Ma Y, Hale D. 2012. Quasi-Newton full-waveform inversion with a projected Hessian matrix. Geophysics , 77 (5) : R207-R216. DOI:10.1190/geo2011-0519.1 | |
| Métivier L, Brossier R, Virieux J, et al. 2013. Full waveform inversion and the truncated newton method. SIAM Journal on Scientific Computing , 35 (2) : B401-B437. DOI:10.1137/120877854 | |
| Pratt G, Shin C, Hicks. 1998. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophysical Journal International , 133 (2) : 341-362. DOI:10.1046/j.1365-246X.1998.00498.x | |
| Shin C, Jang S, Min D J. 2001. Improved amplitude preservation for prestack depth migration by inverse scattering theory. Geophysical Prospecting , 49 (5) : 592-606. DOI:10.1046/j.1365-2478.2001.00279.x | |
| WoodwardM J, NicholsD, ZdravevaO, 等. 2008. A decade of tomography. Geophysics , 73 (5) : VE5–VE11. | |
| XieC, LiuY Z, DongL G, 等. 2014. First arrival traveltime tomography based on the adjoint state method. Oil Geophysical Prospecting , 49 (5) : 877–883. | |
| Zhu X H, Sixta D P, Angstman B G. 1992. Tomostatics:turning-ray tomography+static corrections. The Leading Edge , 11 (12) : 15-23. DOI:10.1190/1.1436864 | |
| 崔岩, 王彦飞. 2015. 基于初至波走时层析成像的Tikhonov正则化与梯度优化算法. 地球物理学报 , 58 (4) : 1367–1377. DOI:10.6038/cjg20150423 | |
| 刘洪, 孟凡林, 李幼铭. 1995. 计算最小走时和射线路径的界面网全局方法. 地球物理学报 , 38 (6) : 823–832. | |
| 刘玉柱, 董良国. 2007. 初至波层析影响因素分析. 石油地球物理勘探 , 42 (5) : 544–553. | |
| 刘玉柱, 董良国, 夏建军. 2007. 初至波走时层析成像中的正则化方法. 石油地球物理勘探 , 42 (6) : 682–685. | |
| 谢春, 刘玉柱, 董良国, 等. 2014. 伴随状态法初至波走时层析. 石油地球物理勘探 , 49 (5) : 877–883. | |
 2016, Vol. 59
2016, Vol. 59


