2. 香港理工大学土地测量与地理资讯学系, 香港九龙;
3. 中南大学地球科学与信息物理工程学院, 长沙 410083
2. Dept. of Land Surveying & Geo-Informatics, The Hong Kong Polytechnic University, Hong Kong, China;
3. School of Geoscience and Info-Physics and Geomatics Engineering, Central South University, Changsha 410083, China
作为雷达遥感领域的重要分支,合成孔径雷达干涉测量(InSAR)已广泛应用于地球科学领域,成为地表参数反演不可或缺的对地观测手段之一(张红等, 2009; 郭华东等, 2000).其中,InSAR的衍生技术,差分干涉测量(D-InSAR),可用于监测地表微小形变,理论上可以达到毫米级的监测精度(Bamler and Hartl, 1998).虽然D-InSAR技术在理论上趋于成熟,也不乏成功的科学应用案例,但在解决实际工程应用问题中,要达到毫米级精度的形变检测水平,该技术仍然需要解决大气效应和时空失相关等误差源的影响(Li et al., 2006; 田馨和廖明生, 2013; 占文俊等, 2015; Zebker and Villasenor, 1992).
为了克服上述困难,在过去的数年中对于时间序列InSAR数据的点目标之后向散射特性的研究成为实现地表微小形变检测的突破口(Ferretti et al., 2001; 张红等, 2009).在这些研究成果之中,永久散射体干涉测量技术(PS-InSAR)是行之有效的方法之一.它的基本原理是利用多景同一地区雷达影像,通过相位和幅度信息,查找不受时间、空间去相关影响的点目标(例如,人工建筑物、裸露的岩石等).在统计分析基础之上,PS-InSAR能够减轻点目标的大气等误差的影响,从而估算出每个PS点上的移动速率或时序位移.然而,这一技术也存在一些限制.其中最主要的问题是在非人工地表区域,可用的永久散射体(Persistent Scatterer, PS)数目十分有限,导致观测结果不能客观反映研究区域的整体变化.从技术角度而言,低密度的空间点目标在构网之后可能给相位解缠和形变解算带来困难.为提高点密度,改善时序形变估计的质量,以小基线技术(SBAS-InSAR)和PS变种技术(如SqueeSAR,StaMPS)为代表的时序方法备受瞩目(Berardino et al., 2002; Ferretti et al., 2011; Goel and Adam, 2012; Hooper et al., 2007; Wang et al., 2011).除了PS点之外,这些方法还探究分布式目标点(distributed scatterer, DS)的相位信息.DS点目标机制的特点涉及分辨率单元内所有较小散射体的相干累加,这些散射体中没有一个的散射特性是占据统治地位的(Lee and Pottier, 2009).虽然上述技术都是通过探索DS点(或PS与DS结合)为目标,但是方法原理却不同.例如,SBAS技术通过选取短时空基线像对减小时空去相关的影响.另外,这一方法还需要通过常规多视或多重空间滤波处理处理增加散射体的信噪比.因此,SBAS应该是一种通过牺牲影像分辨率换取估计精度的方法.当影像细节变得丰富或空间形变信号复杂时,该方法容易损失许多细节,并伴随形变非形变区域的误读.相反地,以SqueeSAR为代表的技术仍然采用了单一主影像的策略(主要优点是减轻主影像大气误差和估计纯随机噪声),通过分析时间栈样本的相似程度,以假设检验为手段(例如基于两个样本的Kolmogorov-Smirnov检验(Ferretti et al., 2011),自适应检验(Jiang et al., 2013),Anderson-Darling检验(Goel and Adam, 2012; Parizzi and Brcic, 2011)),选取与目标像素具有相同统计属性的点并进行自适应多视.这一方法的理论假设前提是同质点都具有相同的散射特性和相位历史.之后,再采用常规PS数据处理链,联合PS和DS点进行形变反演.SqueeSAR技术的优点是保持空间分布特征,因而很好的弥补了SBAS技术的缺点.但是,假设检验步骤却十分耗时,甚至无法应用于大数据集.当影像数较少时(一般要大于25景),假设检验功效也很低,这导致偏向零假设的情况出现,即错误的接受两个样本是相似的(Jiang et al., 2013)结果,许多异质点都包含在同质点之中,造成平均后的影像分辨率的损失(Jiang et al., 2013).另外,目前的DS点选取方案多采用对相干性进行经验阈值设定.考虑到样本相干性自身的随机特征,使用经验阈值易选取低质量的DS点或删除高质量的点目标.
基于上述问题,本文将提出一种分布式目标雷达干涉数据处理框架(命名为FaSHPS-InSAR).FaSHPS-InSAR技术首先采用快速同质选点策略对每个DS目标点进行自适应多视(Jiang et al., 2015);然后,在空间相干性精确估计的条件下,采用无偏相干值和统计分析对DS点进行进一步筛选;最后,以稳健参数估计为手段,恢复研究区形变历史.为减小解缠误差对时序变形的影响,将使用重新加权的最小二乘策略.根据FaSHPS-InSAR技术,本文以美国加州Lost Hills油田区为例,采用27景RadarSAT-1雷达数据对实验区进行了地表变形反演,并与STAMPS PS-InSAR处理结果对比分析.研究结果揭示了该区域受油田开采影响的时序形变历史,为反演因孔隙流体萃取和孔隙压力降低引起的储层变形提供数据支撑.
2 分布式目标干涉数据处理核心算法 2.1 FaSHPS算法快速同质点选取的核心是在高斯假设的背景下,将假设检验问题转换为置信区间估计的一种方法.由于假设检验需要逐个比较参考点与候选点的时间样本,计算P值与比较分布特征需要很大开销(Jiang et al., 2015).而置信区间一旦确立,所有候选点只需通过简单的逻辑运算就可以判定与参考点的相似性,因而大大提高运算效率.此外,由于模型确定,即便影像数较小,同质点选择产生的不确定性也小于传统非参数假设检验方法.这两点成为这一技术的主要优势.
对于一个待估DS点p,它的N个时间强度样本可以写为{A1, A2, …, AN}.p的期望μ(p)的样本点估计可以写为A(p)=(A1(p)+A2(p)+…+AN(p))/N.若求得μ(p)的区间估计,则要首先确定A(p)的分布,根据中心极限定理,A(p)随着样本数N的增加逐渐靠近高斯分布.假设N足够大,高斯假设成立,可以获得A(p)的区间估计:

|
(1) |
其中P{·}表示概率,z1-α/2为标准正态分布的1-α/2分位点,Var(A(p))表示p点的真实方差.根据分布式目标SAR图像统计理论,在匀质区域,单视强度影像服从瑞利分布(Lee and Pottier, 2009).其数字特征,即变异系数CV是恒量:

|
(2) |
这里E(·)表示期望,在本文表示为μ(p).当后向散射特性在时间上变化不是十分剧烈的时候,可以假设时间上的样本是匀质的.因此,式(1)可以转换为一个只包含了μ(p)的区间:

|
(3) |
当μ(p)已知,式(3)就是一个确定的区间.在实际处理中,假定参考像元为pk,且待测像元数为K,算法首先将A(pk)作为pk的真值,即μ(pk)≈A(pk).接着,估计K-1个像素的样本均值A(pi), i=1, …, k-1, k+1, …, K,将它们逐个与式(3)比较.所有样本均值落入区间的点都被初步视为同质点,并不考虑像元的连接性.由于时间样本数N较小,获得的μ(pk)存在较大不确定性,算法应设置α=50%以便减小分布尾部产生的估计偏差.若将这个集合记为Ωinit,则平均集合内像素的所有时空样本重新估计μ(pk).最后,再以重新估计的μ(pk)作为参考点的真实均值,迭代执行上述步骤并重置α以便扩大区间.在获得新的集合Ω后,对所有点执行邻接性评估,只保留那些直接或间接与参考点相连的点.
当N较小时正态性很难维持,这直接影响着区间估计(3)式的有效性.根据经典统计文献(Papoulis, 1991),当概率分布平滑时(例如服从Rayleigh分布的单视强度序列),N=5就足够靠近高斯假设.
2.2 DS候选点选取相干性是InSAR数据处理中最重要的参数之一,它贯穿了整个数据处理流程(Jiang et al., 2013; Jiang et al., 2014a).在点目标选取中,常规方法是采用经验阈值设定,即选取高于相干性阈值的那些点作为DS候选点.由于干涉图噪声分布特征不同,每个带估点真实相干性不同,则估计的样本相干性偏差不同(Abdelfattah and Nicolas, 2006; Seymour and Cumming, 1994).因此,在低相干区域,设置较小的相干性阈值有可能小于高估系统偏差,使得那些原本干涉信号弱的点目标被选取为DS点.在高相干区域,高相干阈值又容易损失DS点.根据每个像素的参数空间(视数,样本相干性等)自适应的选择阈值判断DS点便成为本文的主要目标.这主要由精确相干性估计和阈值估计两个部分构成.
首先相干性观测可以由以下估计量获得(Jiang et al., 2013; Touzi et al., 1999):

|
(4) |
其中s1(·)代表s2(·)用于干涉的两景SLC,L代表集合Ω中同质点数量.为获得精确的估值,需要去除三类误差: (1)采用同质点,因影像质地引起的估计偏差能够直接去除;(2)采用条纹率估计方法或DEM模拟的地形相位去除因干涉相位引起的偏差(Jiang et al., 2013; Zebker and Chen, 2005);(3)采用计算加强技术去除估计量的有偏估计获得无偏相干值.这里采用的方法是非参数化的Bootstrap方法(Efron and Tibshirani, 1993).传统非参数Bootstrap只用于实数相关性的讨论,而SAR数据具有复数特征.因此,这一方法需要将实数域向复数域推广.在本文的例子中集合Ω的每一个点,可视为由一对复值观测构成xi=(s1i, s2i).因此集合中所有点可以表示为X=(x1, x2, …, xL).一个bootstrap样本X*=(x1*, x2*, …, xL*)就是从原始观测X中有放回的抽样L次.在进行反复抽样R次后,可以得到一组样本X1*, X2*, …, XR*.对每一个样本用式(4)进行估计后可以得到总共R个bootstrap复制γ1*, γ2*, …, γR*.偏差纠正是采用这些复制和原始估计的γ求得近似无偏估计

|
(5) |
一般地,考虑到计算效率和估计精度,R=200是一个折衷的选择.
假设真实相干性阈值为γTinit (暗示高于该阈值的点为DS),则自适应阈值应该表示为

|
(6) |
其中k是常数,代表倍数关系,在本文的研究中k=1;σγ表示无偏相干性的Cramer-Rao下界标准偏差(Touzi et al., 1999):

|
(7) |
对于空间上的任意待估点,将时间上的所有相干性样本与(6)式进行逐个比较,若

|
|
表 1 用于Lost Hills数据集的FaSHPS-InSAR数据处理参数 Table 1 The parameters used in FaSHPS-InSAR algorithm over Lost Hills area |
流程图 1为FaSHPS-InSAR的整体技术框架.其基本数据处理步骤如下:

|
图 1 FaSHPS-InSAR数据处理链流程图(SLCs表示单视复数影像集合) Fig. 1 The framework of FaSHPS-InSAR method |
假设所有时序单视复数影像(SLC)已被采样至公共主影像,第一步,将所有影像取模获得强度序列,采用差分振幅离差指数初步选择候选点,再采用2.1节提出的FaSHPS算法为每个待估点选取同质像元;
第二步,根据每个同质点集合Ω进行自适应多视得到差分干涉图序列IFGs;
第三步,根据2.2节的方法对初选点进行提炼获取DS候选点;
第四步,采用最新发展的自适应Goldstein滤波技术最大化去除噪声的同时保留影像细节(Jiang et al., 2014b).由于滤波需要在栅格中完成,选取的点目标应当采样至规则格网.这样做的好处有两点:(1)只对感兴趣的候选点进行滤波,节省开销;(2)将无数据的像元上设置为0值,从而避免那些无意义的点对频谱产生的贡献.在采样过程中,需要设定像元分辨率.这就意味着同一个像元格内可能落入多个点目标.本文的方法是将这些点目标进行加权平均,权的大小由1/(1-
第五步,采用3D相位解缠算法解算滤波后的DS点;
在估计DEM误差、轨道误差和主影像大气后,对原始差分观测进行分离并进行时空滤波,在分离时间非相关误差后得到时序变形.基于篇幅限制,上述相位分量分离步骤已在众多经典文献中讨论,此处不再赘述.值得注意的是,在进行DS点时序反演时,应考虑采用重新迭代加权最小二乘策略(ILRS)减小解缠误差的影响.文中权值大小由1/(1-
Lost Hills油田位于美国加州圣华金河谷Kern郡.Kern郡以石油业和农业为主要经济体,其石油储备在加州位居第6,等价于11亿桶原油产量(California Department of Conservation, 1991—2004).在圣华金河谷的局部区域,与油气藏开采有关的储层压实与沉降作用已经持续近60年,而LostHillls地区自20世纪50年代早期便观测到地表沉降.随着更多生产井的投入使用,该地区观测到的沉降在80年代末期呈加速趋势(Bruno and Bovberg, 1992).根据美国石油、天然气和地热资源加州分部数据统计,该区域数十年来原油年产量稳固提升,从1981年的近6×106桶(约950000 m3)增至2007年的1.2×107桶(约1940000 m3).
油气藏压实作用与沉降源于岩石孔隙压力和有效应力的孔隙塑性力学特性.当石油等流体运移出储层时,上覆岩层的重量未减小,而孔隙压力减小使得作用于固体基质上的垂向有效应力增加,导致压实.储层压实作用传播到地面引起地表沉降.而压实程度又取决于地层岩石属性.以Lost Hills油田区为例,1995年冬季累计沉降达到15 cm(Xu, 2002),沉降量远大于地理位置相邻的且油产量更大的Belridge油区.产生这一现象的主要原因归咎于Lost Hills地区绝大部分属硅藻岩油藏.相比Belridge更硬的砂岩,其储层更浅(91 m)、生产层更厚(300 m)、渗透度更高(0.1~2 μm2)、黏度更低(0.096 Pa·s)(California Department of Conservation, 1991—2004).被压实地层造成的井筒和设施损坏不仅无益于生产,而且对沿海地面的影响广泛.
本文采用RadarSAT-1卫星2002年2月至2004年2月获取的27景SAR影像作为数据源.波长约为5.6 cm,中心入射角38.4°.图 2为实验区概况和成像覆盖范围.油藏区地处中央谷地平原的南部,地势平坦,属地中海型气候.南部降雨少,较干燥,这里本是半沙漠地带.加州水道系统的兴建,此处成为农业的重要产地.在西北至东南沿线,主要地表类型为人工建筑(其中以生产井和平台为主)和裸土.沿线两侧分布着野生植被和农作物,FaSHPS-InSAR和STAMPS PS-InSAR技术将同时用于获取该地区的形变历史.

|
图 2 加州Lost Hills油田区地貌特征和RadarSAT-1影像覆盖图(红色边框) Fig. 2 The surface features and the coverage of RadarSAT-1 over Lost Hills area |
两种数据处理方法的干涉组合策略不同,PS-InSAR方法是以一景影像为主影像,其他影像为辅影像形成的星状图,如图 3b所示.其中每个点代表获取的单视复数影像(SLC),线段表示干涉图.FaSHPS-InSAR则采用多基线策略,尽可能地形成相干性高的干涉组合以便增加观测的质量和数量, 如图 3a所示.在连接SLC过程中,应确保没有子集出现以便增加解的可靠性.在本文的研究中,两种方法均配准至2003年4月4日的影像参考几何.

|
图 3 不同时序分析技术干涉组合策略图 (a) FaSHPS-InSAR干涉组合,色带表示干涉图DS候选点平均空间相干性;(b) PS-InSAR技术干涉组合图. Fig. 3 The configuration of different time series InSAR techniques (a) FaSHPS-InSAR, the colorbar denotes the mean coherence of DS candidates in a interferogram; (b) PS. |
在数据配准之后根据干涉组合和外部SRTM DEM在单视下形成差分干涉图.PS-InSAR以传统数据处理链进行处理(Ferretti et al., 2001; Hooper et al., 2007),此处不再赘述.其中振幅离差指数初始值设置为0.3.其他可用参数均与FaSHPS-InSAR保持一致(详见表 1).在FaSHPS-InSAR处理中,首先采用FaSHPS算法对像元逐个选取同质点并确保点的连通性.本例中原始窗口大小为19×13.图 4展示了FaSHPS方法和传统规则窗选点的比较结果.对于质地显著的区域,FaSHPS能够避免与中心像素反射强度不同的散射体.

|
图 4 FaSHPS算法与传统规则窗口同质点选择方法(红色点表示参考中心像元,绿色表示同质点) Fig. 4 Homogeneous pixel selection using FaSHPS and conventional boxcar; the reference pixel is shown in red, and its brother neighbors are shown in green |
接着,根据选取的同质点进行相干性估计.在相干性偏差纠正计算中,Bootstrap复制设置为R=200.图 5给出了其中一景干涉对的相干性估计结果,并与传统7×7规则窗的估计结果进行对照.整体上由于偏差存在,传统估计的对比度差在快速去相干的农业用地区域出现明显的高估.即便采用的是7×7窗口,空间分辨率仍然较低.从图 5椭圆标识放大的子区域,可以看出两种算法的差异.本文方法估计的相干性在田埂处仍然保证了分辨率,与周边农田的低相干性形成对比.

|
图 5 FaSHPS算法与传统规则窗口相干性估计结果对比图(红色点表示图 4中参考像元位置) Fig. 5 The coherence estimation using FaSHPS and conventional boxcar respectively(the red point corresponds to the reference pixel in Fig. 4) |
在自适应多视之后,采用自适应阈值策略对DS点进行提炼.本文设置的无偏相干阈值为γTinit=0.28,经过式(6)获得每个空间坐标的相干性阈值.对于一个时序序列,如果其相干性中有85%的点大于相干阈值,则保留并视为DS候选点.在自适应滤波之前,将所有DS点进行重采样至40 m间隔的规则格网.考虑到一个分辨率单元内可能有多个点落入,采用估计的相干性对这些点进行加权平均.在滤波之后采用STAMPS的3D解缠算法对格网进行解缠.最后,对解缠序列进行ILRS分离DEM误差并得到每个DS点的形变历史.实验中所用到的关键参数列于表 1.
图 6展示了基于常规最小二乘(L2)和ILRS(L1)的匀速率估计图.选择区域为图 7中左下角的农田区域.对于有解缠误差存在的干涉序列(解缠图(a)和(b)存在明显的2pi跳变),常规估计方法(图 6d)中出现了空间非相关性误差并伴随与解缠误差相关的匀速率误差,这在(图 6c)中并不显著.

|
图 6 解缠误差对匀速率估计的影响 (a)和(b)表示包含了解缠误差的相位图;(c)基于ILRS估计的匀速率图;(d)基于常规最小二乘估计的匀速率图. Fig. 6 The impact of unwrapping errors on the deformation rate estimation (a) and (b) show the interferograms including unwrapping errors; Deformation rate estimatedby ILRS (a) and conventional least square method (d). |

|
图 7 DS目标点和PS目标点上获取的年平均沉降量 Fig. 7 The deformation rate obtained from (a) DS and (b) PS targets. |
在FaSHPS-InSAR和PS-InSAR分别对DS和PS目标点进行解算之后,可以获得各自的年平均形变速率图.从图 7的结果来看,两种方法都获得了相似的沉降轮廓与形变分布.然而,FaSHPS-InSAR估计的匀速率在空间密度上有明显优势,例如位于影像中心区域的沉降盆以及左边区域的散射目标.在自然地表区域,缺少人工目标或强反射散射体成为PS-InSAR低空间密度的主要原因.在增加点密度的情况下最小化分辨率的损失成为FaSHS-InSAR的主要优点.本例中,在120 km2范围内得到的DS点为148508个,PS点为10911个.
图 8展示了FaSHPS-InSAR和PS-InSAR处理同名点的时间序列位移情况.从结果来看,在相干性差的区域(如图 8(a,b)),PS点的强度保持稳定,但是相位观测仍具有不确定性,即随机相位噪声.考虑到PS点周围的点密度更为稀疏,在STAMPS滤波时很难找到邻域样本进行平滑.在执行3D相位解缠时,存在的噪声与稀疏的点密度使得传统方法无法正确恢复每个干涉图相位的整周数.反演的时序离散度大.特别是点“2”,该目标已经远离生产井(见图 9),位于农田区域,持续的变形和振幅说明误差的存在.相比之下,在FaSHPS-InSAR处理中,由于引入了更多的DS点,空间平均和增强的点密度可以改善时空平滑度,从而使得解缠错误的概率减小.对于影像中心区域的点目标“3”和“4”(图 8(c,d)),由于生产井增加了PS点的密度和点的质量,两种方法因而获得相近的结果,这可以从两个序列的均方根(RMS)得以验证.

|
图 8 FaSHPS-InSAR和PS-InSAR同名点时间序列图 1, 2, 3, 4点位置对应于图 9;4个目标点形变RMS值分别为10.56、20.93、1.95、3.12 mm Fig. 8 The pattern of displacement time series from FaSHPS-InSAR and PS-InSAR The positions of the points 1, 2, 3, 4 are shown in Fig. 9; the RMS value for four selected pointsis 10.56 mm, 20.93 mm, 1.95 mm, 3.12 mm respectively. |

|
图 9 FaSHPS-InSAR的DS目标点残差标准偏差图 Fig. 9 The STD of the residuals of DS points |
最后,图 10展示了由FaSHPS-InSAR技术估计的2002—2004年油田区累计沉降二维时间序列,其中最大沉降量>16 cm.

|
图 10 基于FaSHPS-InSAR的DS目标点二维时间序列 为更清晰地显示沉降盆构架,本文将27景序列进行时间间隔采样至14景沉降图. Fig. 10 The displacement time series estimated from FaSHPS-InSAR For exhibition purpose, the series are under-sampled from 27 to 14. |
以上交互验证能够说明FaSHPS-InSAR在增加点密度和保持处理精度上的能力.由于缺少外部实测GPS和水准测量数据,验证工作主要依靠现有的地质资料和已取得的研究成果.图 11给出了美国Chevron公司公布的Lost Hills地区油井分布图(Xu, 2002).从中可以看出井的空间分布与图 7获取的沉降位置十分吻合,即形变从西北向东南方向延伸,两个沉降中心均与生产井密度最高的位置相对应.

|
图 11 Lost Hills油田区生产井分布图(Xu, 2002)(其中黑色点状目标代表生产井) Fig. 11 The distribution of producing well shown in black over Lost Hills area (Xu, 2002). |
由孔隙流体萃取和孔隙压力降低引起的地表变形是一个非常复杂的孔隙弹塑性过程.若要深入理解油藏区沉降还需要了解压实地层和岩石属性,以及油气田生产资料.一般地,沉降盆比压实区域范围广,传播幅度取决于上覆岩层的物理属性和压实地层的深度.在沉降盆中心,很少涉及水平运动,主要是垂向运动.盆中心的视线向形变被投影至垂直向.
文献(Xu, 2002)中获得的Lost Hills区域1995年冬季的最大沉降量为15 cm/105 days,等价于51.14 cm·a-1.相比于本文最大匀速率21.23 cm·a-1,形变速率的减小应该与生产历史相关.为此我们统计了油年产量、年注水量、生产井数量和沉降率的关系.从图 12中可以看出,油产量在1995年前后有较大波动,1994年的产量高达近1.4×107桶,而注水量仅为1.6×107桶,逆差2×106桶.在1992年达到注采平衡之前,注水量小于开采量.这些成为高沉降率的主要原因.1995年之后注水量仍在提升.特别是1996—1997年之间,注水量增加了近一倍,而油产量降低了5×106桶.持续不断的注水缓解了沉降率,我们推断这是获得较低观测结果的主要原因.值得注意的是,注水作用不会立刻发生.位于北海的Ekofisk油田就是典型的案例之一.根据测量历史和岩石属性,沉降速率的减小在注采平衡后4—5年才发生(Nagel, 2001; Thomas et al., 1987).这也间接说明了在1997年大幅度注水对后续缓解形变的影响是显著的.
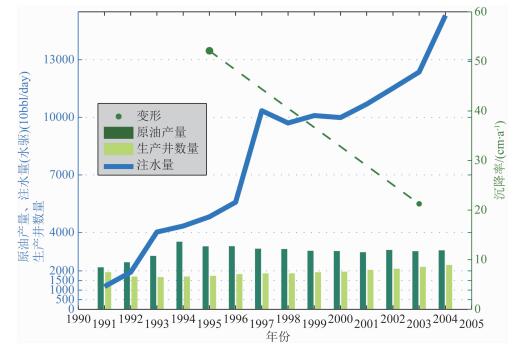
|
图 12 Lost Hills油田的生产历史 左坐标轴表示油产量、注水量以及生产井数量;右坐标轴表示沉降速率;柱状图表示油产量和井数量,蓝色曲线表示注水情况,墨绿色的点和虚线表示沉降率变化. Fig. 12 The history of oil production over Lost Hills The axis in left denotes the oil production, injection (waterflood) and the number of producing well; the bars show the oil and producing well; the curve in blue denotes the injection; the points and the dot line in green denote the change of the subsidence rate. |
本文提出了一种基于快速分布式目标探测的时序雷达干涉数据处理方法.该方法由两个核心部分构成: (1)采用快速选点方案对初始点进行同质点选取;(2)以真实相干性为阈值,根据统计推断结果自适应获得样本相干性阈值;另外,数据处理流程还融合了最新的滤波方法和稳健估计手段.在构建的FaSHPS-InSAR技术框架之下,本文采用27景美国加州Lost Hills油田区数据反演了当地的地表沉降情况,并与PS-InSAR进行了对比分析.实例结果表明,FaSHPS-InSAR在抗差、保留影像分辨率和增加空间观测密度上具有明显优势,这将有利于非人工地表的对地监测.根据研究结果和当地生产历史,本文还揭示了油藏生产井密度与地表形变的关系.相比1995年的高沉降率,2002—2004年缓解的沉降量应归因于持续的回灌水量增加.然而沉降还在继续,表明压实作用依然存在.这将对地表基础设施如井故障或套管损坏产生深远的影响.
除了上述特点之外,运算效率是需要重点关注的问题.就同质点选择而言,对于80万个初始点目标,FaSHPS-InSAR方法在Linux MATLAB 2011b Intel i7 2.80 GHz CPU平台上的运算效率仅为约5 min.对于相同数量的点,SqueeSAR耗时将超过7 h.这表明FaSHPS-InSAR更适用于处理大数据集和宽幅影像序列.因此,高效运算成为FaSHPS-InSAR的主要技术优势.
| Abdelfattah R, Nicolas J M. 2006. Interferometric SAR coherence magnitude estimation using second kind statistics. IEEE Transactions on Geoscience and Remote Sensing , 44 (7) : 1942-1953. DOI:10.1109/TGRS.2006.870440 | |
| Bamler R, Hartl P. 1998. Synthetic aperture radar interferometry. Inverse Problems , 14 (4) : R1. DOI:10.1088/0266-5611/14/4/001 | |
| Berardino P, Fornaro G, Lanari R, et al. 2002. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Transactions on Geoscience and Remote Sensing , 40 (11) : 2375-2383. DOI:10.1109/TGRS.2002.803792 | |
| Bruno M, Bovberg C A. 1992. Reservoir compaction and surface subsidence above the Lost Hills Field, California.//The 33th US Symposium on Rock Mechanics (USRMS). Santa Fe, New Mexico, USA:American Rock Mechanics Association. | |
| California Department of Conservation. 1991-2004. Oil and gas statistics, annual report. California:California Department of oil, Gas and Geothermal Resources. http://www.conservation.ca.gov/dog/pubs_stats/annual_reports/Pages/annual_reports.aspx | |
| Efron B, Tibshirani R J. An Introduction to the Bootstrap. New York: CRC Press, 1994 . | |
| Ferretti A, Prati C, Rocca F. 2001. Permanent scatterers in SAR interferometry. IEEE Transactions on Geoscience and Remote Sensing , 39 (1) : 8-20. DOI:10.1109/36.898661 | |
| Ferretti A, Fumagalli A, Novali F, et al. 2011. A new algorithm for processing interferometric data-stacks:SqueeSAR. IEEE Transactions on Geoscience and Remote Sensing , 49 (9) : 3460-3470. DOI:10.1109/TGRS.2011.2124465 | |
| Goel K, Adam N. 2012. An advanced algorithm for deformation estimation in non-urban areas. ISPRS Journal of Photogrammetry and Remote Sensing , 73 : 100-110. DOI:10.1016/j.isprsjprs.2012.06.001 | |
| Guo H D, Shao Y, Wang C L. Theory and Application of Radar Earth Observation. (in Chinese) Beijing: Science Press, 2000 . | |
| Hooper A, Segall P, Zebker H. 2007. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. Journal of Geophysical Research:Solid Earth (1978-2012) , 112 (B7) . DOI:10.1029/2006JB004763 | |
| Jiang M, Ding X L, Li Z W. 2014. Hybrid approach for unbiased coherence estimation for multitemporal InSAR. IEEE Transactions on Geoscience and Remote Sensing , 52 (5) : 2459-2473. DOI:10.1109/TGRS.2013.2261996 | |
| Jiang M, Ding X L, Li Z W, et al. 2014a. The improvement for baran phase filter derived from unbiased InSAR coherence. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 7 (7) : 3002-3010. DOI:10.1109/JSTARS.2013.2296322 | |
| Jiang M, Ding X L, Tian X, et al. 2014b. A hybrid method for optimization of the adaptive Goldstein filter. ISPRS Journal of Photogrammetry and Remote Sensing , 98 : 29-43. DOI:10.1016/j.isprsjprs.2014.09.012 | |
| Jiang M, Ding X L, Hanssen R F, et al. 2015. Fast statistically homogeneous pixel selection for covariance matrix estimation for multitemporal InSAR. IEEE Transactions on Geoscience and Remote Sensing , 53 (3) : 1213-1224. DOI:10.1109/TGRS.2014.2336237 | |
| Lee J S, Pottier E. Polarimetric Radar Imaging:From Basics to Applications. Boca Raton: CRC Press, 2009 . | |
| Li Z H, Fielding E J, Cross P, et al. 2006. Interferometric synthetic aperture radar atmospheric correction:GPS topography-dependent turbulence model. Journal of Geophysical Research:Solid Earth (1978-2012) , 111 (B2) . DOI:10.1029/2005JB003711 | |
| Nagel N B. 2001. Compaction and subsidence issues within the petroleum industry:from wilmington to ekofisk and beyond. Physics and Chemistry of the Earth, Part A:Solid Earth and Geodesy , 26 (1-2) : 3-14. DOI:10.1016/S1464-1895(01)00015-1 | |
| Papoulis A. Probability, Random Variables, and Stochastic Processes. New York: McGraw-Hill Book Company, 1991 . | |
| Parizzi A, Brcic R. 2011. Adaptive InSAR stack multilooking exploiting amplitude statistics:a comparison between different techniques and practical results. IEEE Geoscience and Remote Sensing Letters , 8 (3) : 441-445. DOI:10.1109/LGRS.2010.2083631 | |
| Seymour M S, Cumming I G. 1994. Maximum likelihood estimation for SAR interferometry.//Proceedings of the Surface and Atmospheric Remote Sensing:Technologies, Data Analysis and Interpretation, International Geoscience and Remote Sensing Symposium. Pasadena: IEEE, 2272-2275. | |
| Thomas L K, Dixon T N, Evans C E, et al. 1987. Ekofisk waterflood pilot. Journal of Petroleum Technology , 39 (2) : 221-232. DOI:10.2118/13120-PA | |
| Tian X, Liao M S. 2013. The analysis of conditions for InSAR in the field of deformation monitoring. Chinese J. Geophys. , 56 (3) : 812-823. DOI:10.6038/cjg20130310 | |
| Touzi R, Lopes A, Bruniquel J, et al. 1999. Coherence estimation for SAR imagery. IEEE Transactions on Geoscience and Remote Sensing , 37 (1) : 135-149. DOI:10.1109/36.739146 | |
| Wang T, Perissin D, Rocca F, et al. 2011. Three Gorges Dam stability monitoring with time-series InSAR image analysis. Science China Earth Sciences , 54 (5) : 720-732. DOI:10.1007/s11430-010-4101-1 | |
| Xu H B. Production induced reservoir compaction and surface subsidence, with applications to four-dimensional seismic[Ph. D. thesis]. Stanford: Stanford University, 2002 . | |
| Zebker H A, Villasenor J. 1992. Decorrelation in interferometric radar echoes. IEEE Transactions on Geoscience and Remote Sensing , 30 (5) : 950-959. DOI:10.1109/36.175330 | |
| Zebker H A, Chen K. 2005. Accurate estimation of correlation in InSAR observations. IEEE Geoscience and Remote Sensing Letters , 2 (2) : 124-127. DOI:10.1109/LGRS.2004.842375 | |
| Zhan W J, Li Z W, Wei J C, et al. 2015. A strategy for modeling and estimating atmospheric phase of SAR interferogram. Chinese Journal of Geophysics (in Chinese) , 58 (7) : 2320-2329. DOI:10.6038/cjg20150710 | |
| Zhang H, Wang C, Wu T, et al. The Study of DINSAR Technique Based on the Coherent Targets. (in Chinese) Beijing: Science Press, 2009 . | |
| 郭华东, 邵芸, 王长林. 雷达对地观测理论与应用. 北京: 科学出版社, 2000 . | |
| 田馨, 廖明生. 2013. InSAR技术在监测形变中的干涉条件分析. 地球物理学报 , 56 (3) : 812–823. DOI:10.6038/cjg20130310 | |
| 占文俊, 李志伟, 韦建超, 等. 2015. 一种InSAR大气相位建模与估计方法. 地球物理学报 , 58 (7) : 2320–2329. DOI:10.6038/cjg20150710 | |
| 张红, 王超, 吴涛, 等. 基于相干目标的DInSAR方法研究. 北京: 科学出版社, 2009 . | |
 2016, Vol. 59
2016, Vol. 59

