2. 中国国土资源航空物探遥感中心, 北京 100083
2. China Aero Geophysical Survey and Remote Sensing Center for Land and Resources, Beijing 100083, China
位场(重力场或地磁场)向下延拓可以从数学上拉近观测平面与场源间的距离,增强地质信息(改善信噪比),不仅在地球物理勘探中具有重要作用,还是利用重力场或地磁场特征进行导航的一项关键技术(胡小平等,2013),向下延拓技术在未爆军火探测等领域也有重要应用.位场向下延拓是经典的不适定问题(Blakely,1996;管志宁,2005),常规频率域位场下延强烈的表现出对数据高频部分的振荡,因而难于实际应用.尽管众多学者对位场向下延拓进行了大量细致的研究,但由于天然位场的频带之宽,各种向下延拓方法对不同资料适应性的差异很大.此外,几乎所有涉及频率域位场转换的研究中都假设输入的位场数据是纯粹的数学矩阵或向量,既要数据无空白,又要满足快速傅里叶变换(FFT)对数据长度的要求.实测位场资料很难满足上述条件,必须对资料空白部分进行填充、对数据进行扩充(扩边),这将直接关系到位场向下延拓的精度(王万银等,2009).数据的填充与扩充是实际位场资料延拓研究中难以回避的问题,需要加以解决.
正则化方法是求解不适定问题较完备且行之有效的方法.针对位场向下延拓的不适定性,我们以位场最小曲率作为约束条件求解稳定的下延位场,同时将位场数据的填充、扩充问题与向下延拓问题统筹考虑,提出一种将多种需求一并处理的向下延拓技术.具体研究中我们将位场向下延拓问题视为向上延拓的反问题,首先从二维位场剖面的向下延拓问题出发,将频率域向上延拓表达式用傅里叶变换矩阵的形式表示;利用矩阵乘法形式给出空间域向上延拓表达式的基础上,推导出向下延拓的频率域表达式及位场向下延拓的迭代解.同时,通过对下延位场引入最小曲率约束,给出了空间域向下延拓的最小曲率解,并最终通过正交变换给出更简洁的频率域解.随后,利用Kronecker积将上述结果拓展至三维位场,并给出了频率域三维位场向下延拓的最小曲率解.最后,我们讨论了频率域延拓中遇到的扩充数据、填补数据空白区等实际问题,给出了一种无须预扩充数据、填补数据空白的位场向下延拓技术,这对解决实际位场资料延拓问题具有重要意义.
2 向下延拓技术方法 2.1 二维位场延拓位场解析延拓是典型的狄利克莱问题,根据重磁勘探教科书(如Blakely,1996;管志宁,2005;等),两个高度层的剖面二维位场满足
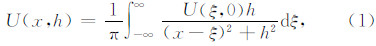


 1)/N)
1)/N)

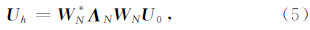
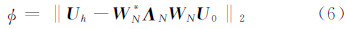


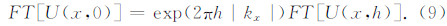
(9)式就是位场向下延拓的频率域表达式.(6)式的极小化问题也可采用数值方法求解,如采用超松弛迭代法,有




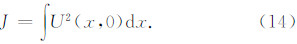
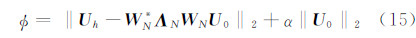
在处理位场资料插值或网格化问题时,Briggs(1974)引入了约束
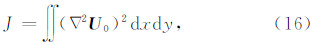
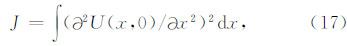


为了减少频率域位场转换中Gibbs效应,D N算子采用了周期性边界条件.因此,在最小曲率条件约束下,求解下延位场的目标函数可表示为

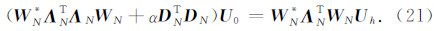

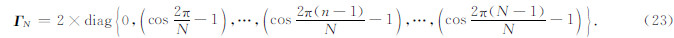




类似的,重磁勘探教科书(Blakely,1996;管志宁,2005;等)也给了不同高度层间三维位场的关系,有
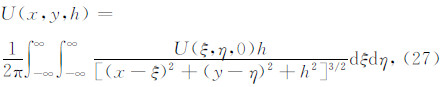

设二维矩阵 f ={fmn∈ f | 1≤m≤M,1≤n≤N},经二维傅里叶变换得到的矩阵为 F ={Fmn∈ F | 1≤m≤M,1≤n≤N},将其表示为列向量形式,有
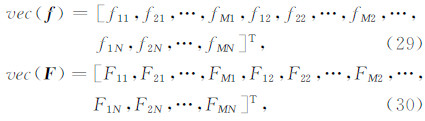

 表示Kronecker积,有
表示Kronecker积,有 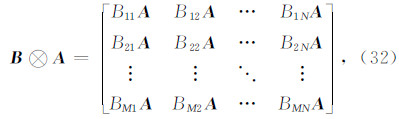
 W M是(M·N)阶酉阵,于是二维离散傅里叶变换逆变换的矩阵表达为
W M是(M·N)阶酉阵,于是二维离散傅里叶变换逆变换的矩阵表达为 
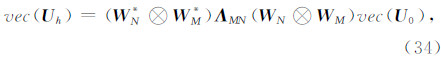

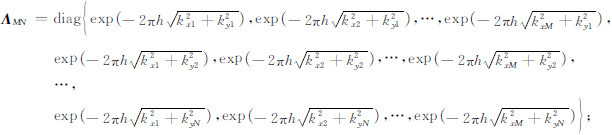

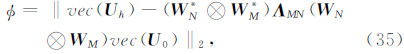
其最小化的解为
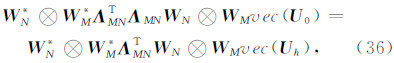


 D M+ D N
D M+ D N I M)vec( U 0),因此在最小曲率条件约束下求解下延位场的目标函数为
I M)vec( U 0),因此在最小曲率条件约束下求解下延位场的目标函数为 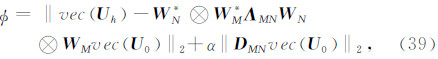


由于 I N= WN* I N W N且 D M= W *M Γ M W M,根据Kronecker积的性质,有

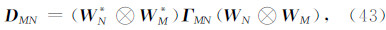
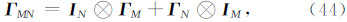
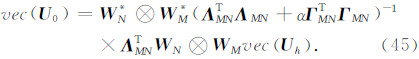

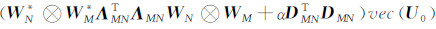


前面提出的基于最小曲率的位场向下延拓方法本质上属于正则化反演,正则参数的选择强烈地影响着向下延拓的结果,以往许多文献(栾文贵,1983;梁锦文,1989;Cooper,2004;陈生昌和肖鹏飞,2007)并没有专门对此进行讨论,其正则参数的选取多属经验性的.无论是二维位场还是三维位场其解析延拓都可表达为

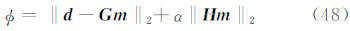
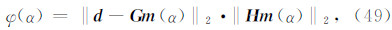
 为
为 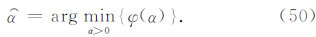


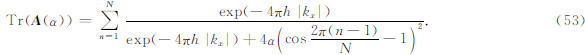


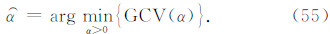
目前几乎所有的频率域位场转换都借助快速傅里叶变换(FFT)实现,而FFT对数据长度是有一定要求的,通常要求剖面数据的点数或网格数据的行、列数为合数,一般要求为以2为基(即2的自然数次幂).插值后的剖面位场或网格化后的位场通常难以满足上述要求,这就要求将剖面数据或网格数据向外扩充至FFT所要求的数据长度,即位场数据的扩充(扩边)问题.我们以FFT中最常见的2n为例,如果位场剖面的长度为1666个点,进行位场转换时就需要将剖面两端各扩充191个数据点,即扩充后数据长度为2048即211;再如位场网格的节点数为365×666,进行位场转换时就需要将网格首、末行的两端分别向外扩充73行和74行,再将扩充后网格的首、末列两端向外各扩充179列,扩充后的网格大小为512×1024即29×210.此外,由于多种因素某些区域缺乏实测位场数据,经过网格化后这些区域也无法形成相应的内插数据进而存在空白,位场转换中还要求将上述空白用合理的数据(称该数据为“假值”)进行填充(替代).填充与扩充中的间断现象将引起Gibbs效应,但许多理论研究者却并没有高度重视该问题.实际上,位场数据中空白值在航空磁测或航空重力测量中广泛存在却是不争的事实.测量中测线方向通常并非南北向或东西向,而是垂直于主地质构造走向,如果采用正网格(网格列方向为南北向)方式进行网格化势必产生大量数据空值(Zhang et al.,2012),即使采用斜网格(网格列方向为测线方向)方式进行网格化,也会因测区形状的不规则而产生一定数量的空值,有时还因特殊原因造成测区的部分数据缺失,部分历史航磁资料曾出现测区中间空白的情况.在航磁编图中数据空值问题更加突出,例如全国航磁编图中的位场转换中一个极重要的问题就是如何对网格空值进行假值填充处理,航磁编图数据在国境以外存在大量网格空值,即使利用国外磁测资料进行填充,但由于中国藏南地区、中国台湾海峡等尚存的航空磁测空白区,网格空值问题近乎无法避免!
除位场转换处理本身,数据填充与扩充处理是直接影响位场转换精度的重要因素,例如曾小牛等(2011)利用改进的积分迭代法处理重力资料时边界处的误差显著增大,明显是数据扩边不理想所致.由于某些位场转换研究本身就极富挑战性,很难再将填充与扩充处理统筹考虑,多数位场转换研究中仅讨论位场转换本身的精度,对数据空值填充或扩边的问题鲜有涉猎.姚长利等(2003)在低纬度化极时曾指出数据扩充对计算造成的影响不能忽视,但没给出进一步措施.张辉等(2009)结合正则化方法和维纳滤波方法研究波数域延拓算法时曾指出其算法存在边界效应问题,需引入扩边处理,但未对扩边算法进行研究.王万银等(2009)提出了用最小曲率方式对位场转换数据进行空值填补与扩边,其研究表明利用最小曲率方式进行数据扩充优于余弦方法,适于对位场数据扩充和填补空白.我们在前面的讨论中并没有涉及到数据填充与扩充处理,这就需要预先对位场数据中空值进行填补和扩充.似乎这样便解决位场下延中遇到的实际问题,但仔细考虑却存在矛盾,因为本文提出的向下延拓方法本身即基于最小曲率方式,而最小曲率方法却多用于对未知位场的插值处理(Briggs,1974;Smith and Wessel,1990),这似乎表明没有必要单独对数据进行填充和扩充处理.
基于解决位场数据存在假值与扩边问题的实际需求,结合最小曲率方法的特性,我们将前面所述的位场向下延拓方法进一步扩展.这里我们借鉴了Garcia(2010)对数据空值估计的思想,提出下延处理中对非空数据直接使用,而空白部分则利用上一次下延位场(估计)的上延值代替并进行迭代,具体的计算格式为
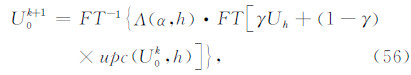
其中U0k表示第k次迭代的下延位场;FT[·]表示傅里叶变换,FT-1{·}表示其逆变换,upc(·,h)表示将位场上延h高度的操作;Λ(α,h)表示下延距离为h正则化参数为α的频率域算子,即(26)式或(46)式中的频率域下延因子;γ是权重因子,当观测位场在该节点处空白时取0,否则取1.(56)式的直观解释是下延位场在最小曲率条件约束下满足观测位场延拓关系的同时,保证空白区的上延估计同观测位场连续.具体迭代计算中,下延位场的初始值选零,并满足FFT对位场扩充的数据长度要求.若位场转换中要求边界趋于零,可令待求解位场最佳估计或最佳上延估计在数据边界取零.同时,为了保证在迭代过程中能有效地对数据空值和扩充区域进行估计,要求正则参数在迭代初期要适当大,以充分保证空白处位场的光滑,随着迭代次数的增加要逐步缩小正则参数,直至正则参数接近广义交叉验证(GCV)或L曲线方法对正则参数的预估计,迭代次数以能最佳恢复出观测位场为宜.
3 理论模型计算为了验证提出的位场下延方法,我们分别就二维位场和三维位场进行理论模型计算.由于剖面位场向下延拓实际应用较少,我们仅展示对(26)式中频率域位场下延算子的理论模型计算部分.选取Pateka等(2012)使用的剖面位场模型数据进行检验,该模型为埋深5000 m、半径500 m的无限延伸水平圆柱产生的重力异常.图 1a和图 1b分别给出了z=0 m(地面)和z=-4000 m(向下为负)处的重力异常理论曲线,图 1c给出使用REGCONT代 码(Pateka et al.,2012)向下延拓得到z=-4000 m 的重力异常曲线.为了检验我们给出的下延算子,我们直接将REGCONT代码中的下延算子修改为(26)式中频率域下延算子,其他不做任何修改(包括正则参数选取的C-norm准则),图 1d给出了最小曲率方式的向下延拓结果.通过对图 1d和图 1b及图 1c比较,可以看出最小曲率方式能获得较理想的下延结果,但同Tikhonov正则化下延结果相比振荡略显增大,这主要是由于C-norm准则选取的是位场模型最小的情况下的正则参数而非位场曲率最小,C-norm判据下的正则参数仅为8.5×10-10(图 1d),相比而言极小,故图 1d较图 1c表现出的振荡情况略明显,但图 1d的下延结果可以确认(26)式中频率域下延算子的有效性.
 | 图 1 二维重力模型及其向下延拓结果对比Fig. 1 Comparison of synthetic gravitational field and its downward continuation |
我们重点讨论对三维位场的理论模型计算,因为二维位场仅是三维情况的特例.这里采用郭志宏等(2004)给出三维磁性模型作为标准模型,高玉文等(2012)曾利用该模型进行向下延拓检验.该模型为长方体,长宽高分别为8 km、4 km、4 km,中心埋深3 km,磁化强度1 A·m-1,磁化方向为偏角30°倾角50°,地磁场偏角10°倾角60°.我们利用长方体磁场无解析奇点表达式(骆遥和姚长利,2007)计算距离地面1 km高空处的ΔT场作为延拓数据,下延1 km(10倍网格距)计算地面处的磁异常,并以地面处的磁异常正演结果作为评价标准进行检验.图 2a和图 2b分别给出地面处和1 km高空处磁异常的正演结果.利用(46)式计算将图 2b下延至地面处,其中扩边方式直接采用Cooper等编写的taper2d函数,该扩边方式曾在变磁倾角化极(Cooper and Cowan,2005)和Potensoft位场数据处理软件(Arisoy and Dikmen,2011)中应用.正则参数则分别采用改进L曲线方式和GCV方式确定,图 3a给出了GCV曲线和改进的L曲线,从图 3a可知两种方式确定的正则参数曲线形态一致仅幅度不同,确定最优正则参数均为 =0.102,这反映了GCV方式和L曲线方式在正则参数确定中的一致性.图 3b是最优正则参数下的向下延拓结果,可以看出图 3b给出的下延结果同图 2a的理论结果非常一致,二者差值均方差为0.6 nT,仅在0 nT等值线的边缘略有畸变,说明了向下延拓的可靠性.
=0.102,这反映了GCV方式和L曲线方式在正则参数确定中的一致性.图 3b是最优正则参数下的向下延拓结果,可以看出图 3b给出的下延结果同图 2a的理论结果非常一致,二者差值均方差为0.6 nT,仅在0 nT等值线的边缘略有畸变,说明了向下延拓的可靠性.
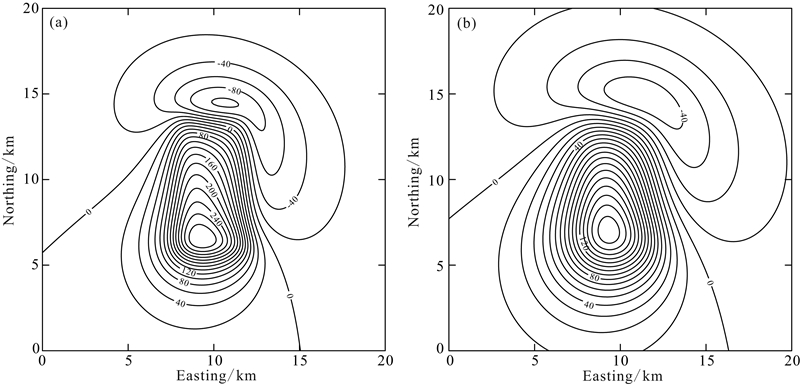 | 图 2 地面(h=0 km)和高空(h=1 km)处的模型磁异常Fig. 2 Total field anomalies of synthetic model at different observation planes |
 | 图 3 正则参数曲线(a)与向下延拓结果(b)Fig. 3 The regularization parameter curves (a) and corresponding evaluated regularized solution of downward continuation (b) |
为了进一步检验对数据填充与扩充的处理效果,我们将图 2b中“挖去”三处数据作为模型数据(图 4),图 4中三处空白分别选取在正异常梯度带 处、正负异常交接处及边部异常平缓处,具有一定的型性.利用(56)式将图 4数据向下延拓1 km,图 5a给出了下延至地面的ΔT等值线(图 5没有将数据空白处或扩充处的下延估计值去掉,故数据范围扩大),此外将下延后的磁异常重新上延回h=1 km的原平面(图 5b),进一步比较数据恢复误差.向下延拓时正则参数从2等速率下降至最佳估计 =0.102后保持恒定,图 6 给出了该过程使用的正则参数.同时,图 6也给出了迭代过程中恢复观测磁异常的误差变化情况,以说明计算的收敛性.为了进一步说明向下延拓的精度,无论是图 5a向下延拓结果还是图 5b恢复的观测数据都叠加了相应模型数据等值线的彩色填充以供对比.可以看出,图 5a的等值线与理论模型的等值线彩色填充区块叠合严密,仅-80 nT和-60 nT等值线的最南部边缘与色块区域略有错动,将下延结果上延回原平面恢复得到 的磁异常等值线(图 5b)与理论模型的等值线彩色填充区块相叠合则严丝合缝,进一步说明了向下延拓同数据填充、扩充结合所取得的明显试验效果.
=0.102后保持恒定,图 6 给出了该过程使用的正则参数.同时,图 6也给出了迭代过程中恢复观测磁异常的误差变化情况,以说明计算的收敛性.为了进一步说明向下延拓的精度,无论是图 5a向下延拓结果还是图 5b恢复的观测数据都叠加了相应模型数据等值线的彩色填充以供对比.可以看出,图 5a的等值线与理论模型的等值线彩色填充区块叠合严密,仅-80 nT和-60 nT等值线的最南部边缘与色块区域略有错动,将下延结果上延回原平面恢复得到 的磁异常等值线(图 5b)与理论模型的等值线彩色填充区块相叠合则严丝合缝,进一步说明了向下延拓同数据填充、扩充结合所取得的明显试验效果.
 | 图 4 高空(h=1 km)处的模型磁异常(白色区域为三处数据空白区)Fig. 4 Synthetic magnetic anomalies with missing values |
 | 图 5 向下延拓结果(a)及其上延恢复的观测异常(b) 其中(a)和(b)对应的理论模型异常数据以等值线的彩色填充形式叠加作为比照.Fig. 5 The downward continuation field (a) and the restored result (b) by continuing (a) to original elevation All the calculated contour maps added the image layers of corresponding synthetic data in colors. |
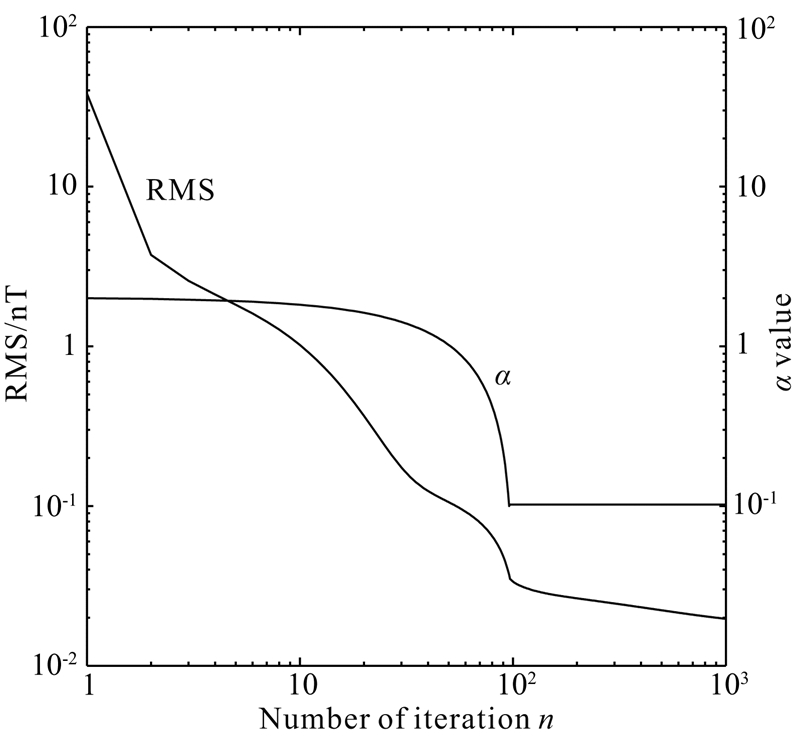 | 图 6 迭代过程使用的正则参数及相应迭代步的均方误差Fig. 6 The regularization parameter used in each steps and the corresponding RMS error |
为了检验位场最小曲率向下延拓方法在实际数据处理中的实用性,我们采用美国地质勘探局(USGS)2006年在阿富汗实测的航空重力资料进行数据处理检验.该航空重力测量数据经各项处理并最终归算至离地7000 m的高度,形成网格距为1 km的布格重力异常.图 7给出了布格重力异常图(等值线间隔10 mGal),其中角图中蓝色区块为航空重力测量覆盖范围,红点为1966—1967年地面重力测量点.由图 7可知该测区极不规则且不同区块测线方向不同(测线间距也有所不同),这些特 征是航空物探作业中的典型特点,但多数向下延拓文献却刻意回避这些特点,而是将类似情况的数据裁剪成特殊的无空值矩形网格进行处理,以避免数据填充或扩充(扩边)问题.我们将图 7的布格重力异常延拓至地面(下延距离7000 m),由于图 7的网格含有(大量)空白数据,这里采用(56)式给出的迭代格式进行求解(迭代过程中正则参数逐渐缩小并最终等于预估值α=0.65),图 8给出了最终下延至地面的布格重力异常(等值线间隔10 mGal).可以看出,向下延拓7000 m后得到的重力异常(图 8)没有出现虚假的振荡,在保持原始异常变化趋势的同时增强了局部异常.我们将图 8的布格重力异常同地面布格重力异常进行比较,二者的外符合精度(郭志宏等,2008)为7.5 mGal,反映二者差异较大,但却难以反映延拓处理的精度.USGS为了编图的需要将地面布格异常归算至距地面7000 m的高空,归算后的布格异常同航空重力异常比较,二者的外符合精度也仅为6.4 mGal,可见该地区的地面重力资料和航空重力资料本身符合的就不甚理想,这也是向下延拓至地面的布格异常同地面实测结果相差较大的原因.如果忽略二者间资料本身的差异,向下延拓引起的误差可近视为两种外符合精度之差即1.1 mGal,相对于下延7000 m(7倍网格距)而言,延拓精度是相当可观的.此外,我们将图 8的布格异常上延恢复至原高度比较其与图 7的差异,二者相差小于0.36 mGal的网格点占99%,其差值的均方差仅0.1 mGal,也进一步证明了向下延拓的数值精度.
 | 图 7 航空布格重力异常数据(归算离地高度7 km)Fig. 7 Airborne Bouguer gravity anomaly map at 7 km above ground |
 | 图 8 向下延拓至地面的航空布格重力异常Fig. 8 Airborne Bouguer gravity anomaly map continued to the ground |
我们将位场向下延拓视为向上延拓处理的反问题,并以位场最小曲率条件为正则化约束,反演位场数据向下延拓的最小曲率解.由于使用了傅里叶变换矩阵,我们提出的向下延拓方法既可以在空间域求解,也可在频率域通过快速傅里叶变换直接求解.此外,我们讨论了频率域延拓中遇到的扩充数据、填补数据空白区两项实际问题,给出了无须预扩充数据、填补数据空白的位场向下延拓算法.针对我们提出的频率域向下延拓的最小曲率解,我们分别利用二维重力模型和三维磁异常模型进行了检验,并特别针对三维位场数据中含数据空白的情况进行了专门的检验,无论是向下延拓的数值精度还是对空白区的恢复都取得了良好的理论模型效果.同时,我们选取实测的航空重力资料进行向下延拓处理.该测区极不规则,并含有大块的数据空白区域,甚至个别数据仅由单条测线网格化而来.在未对该资料进行填充、扩充等预处理情况下直接将其向下延拓至地面,处理结果表明该方法具有较高的向下延拓精度,可在实际位场资料处理应用中发挥积极作用.
致谢 图 7使用了美国地质勘探局(USGS)公布的航空重力数据和地面重力数据,在此表示感谢.| [1] | Arisoy M Ö, Dikmen Ü. 2011. Potensoft:MATLAB-based software for potential field data processing, modeling and mapping. Computers & Geosciences, 37(7):935-942, doi:10.1016/j.cageo.2011.02.008. |
| [2] | Blakely R J. 1996. Potential Theory in Gravity and Magnetic Applications. New York:Cambridge University Press. |
| [3] | Briggs I C. 1974. Machine contouring using minimum curvature. Geophysics, 39(1):39-48, doi:10.1190/1.1440410. |
| [4] | Chen S C, Xiao P F. 2007. Wavenumber domain generalized inverse algorithm for potential field downward continuation. Chinese J. Geophys.(in Chinese), 50(6):1816-1822. |
| [5] | Cooper G. 2004. The stable downward continuation of potential field data. Exploration Geophysics, 35(4):260-265, doi:10.1071/EG04260. |
| [6] | Cooper G R J, Cowan D R. 2005. Differential reduction to the pole. Computers & Geosciences, 31(8):989-999, doi:10.1016/j.cageo.2005.02.005. |
| [7] | Foks N L, Krahenbuhl R, Li Y G. 2013. Adaptive sampling of potential-field data:A direct approach to compressive inversion. Geophysics, 79(1):IM1-IM9, doi:10.1190/GEO2013-0087.1. |
| [8] | Gao Y W, Luo Y, Wen W. 2012. The compensation method for downward continuation of potential field from horizontal plane and its application. Chinese J. Geophys.(in Chinese), 55(8):2747-2756, doi:10.6038/j.issn.0001-5733.2012.08.026. |
| [9] | Garcia D. 2010. Robust smoothing of gridded data in one and higher dimensions with missing values. Computational Statistics & Data Analysis, 54(4):1167-1178, doi:10.1016/j.csda.2009.09.020. |
| [10] | Golub G H, Heath M, Wahba G. 1979. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics, 21(2):215-223, doi:10.1080/00401706.1979.10489751. |
| [11] | Guan Z N. 2005. Magnetic Field and Magnetic Exploration(in Chinese). Beijing:Geological Publishing House. |
| [12] | Guo Z H, Guan Z N, Xiong S Q. 2004. Cuboid ΔT and its gradient forward theoretical expressions without analytic odd points. Chinese J. Geophys.(in Chinese), 47(6):1131-1138. |
| [13] | Guo Z H, Xiong S Q, Zhou J X, et al. 2008. The research on quality evaluation method of test repeat lines in airborne gravity survey. Chinese J. Geophys.(in Chinese), 51(5):1538-1543. |
| [14] | Hu X P, Wu M P, Mu H, et al. 2013. Technologies on Underwater Geomagnetic Field Navigation(in Chinese). Beijing:National Defense Industry Press. |
| [15] | Liang J W. 1989. Downward continuation of regularization methods for potential fields. Chinese J. Geophys.(Acta Geophysica Sinica)(in Chinese), 32(5):600-608. |
| [16] | Liu D J, Hong T Q, Jia Z H, et al. 2009. Wave number domain iteration method for downward continuation of potential fields and its convergence. Chinese J. Geophys.(in Chinese), 52(6):1599-1605, doi:10.3969/j.issn.0001-5733.2009.06.022. |
| [17] | Luan W G. 1983. The stabilized algorithm of the analytic continuation for the potential field. Chinese J. Geophys.(Acta Geophysica Sinica)(in Chinese), 26(3):263-274. |
| [18] | Luo Y, Yao C L. 2007. Theoretical study on cuboid magnetic field and its gradient expression without analytic singular point. Oil Geophysical Prospecting(in Chinese), 42(6):714-719. |
| [19] | Pateka R, Karcol R, Kunirák D, et al. 2012. REGCONT:A Matlab based program for stable downward continuation of geophysical potential fields using Tikhonov regularization. Computers & Geosciences, 49:278-289, doi:10.1016/j.cageo.2012.06.010. |
| [20] | Smith W H F, Wessel P. 1990. Gridding with continuous curvature splines in tension. Geophysics, 55(3):293-305, doi:10.1190/1.1442837. |
| [21] | Strang G. 1999. The discrete cosine transform. SIAM Review, 41(1):135-147, doi:10.1137/S0036144598336745. |
| [22] | Wang W Y, Qiu Z Y, Liu J L, et al. 2009. The research to the extending edge and interpolation based on the minimum curvature method in potential field data processing. Progress in Geophys.(in Chinese), 24(4):1327-1338, doi:10.3969/j.issn.1004-2903.2009.04.022. |
| [23] | Xiong S Q, Zhou F H, Yao Z X, et al. 2001. Aeromagnetic Survey in Central and Western Qinghai-Tibet Plateau(in Chinese). Beijing:Geological Publishing House. |
| [24] | Xu S Z, Yang J Y, Yang C F, et al. 2007. The iteration method for downward continuation of a potential field from a horizontal plane. Geophysical Prospecting, 55(6):883-889, doi:10.1111/j.1365-2478.2007.00634.x. |
| [25] | Yao C L, Guan Z N, Gao D Z, et al. 2003. Reduction-to-the-pole of magnetic anomalies at low latitude with suppression filter. Chinese J. Geophys.(in Chinese), 46(5):690-696. |
| [26] | Yao C L, Li H W, Zheng Y M, et al. 2012. Research on iteration method using in potential field transformations. Chinese J. Geophys.(in Chinese), 55(6):2062-2078, doi:10.6038/j.issn.0001-5733.2012.06.028. |
| [27] | Zhang C, Yao C L, Xie Y M, et al. 2012. Reduction of distortion and improvement of efficiency for gridding of scattered gravity and magnetic data. Applied Geophysics, 9(4):378-390, doi:10.1007/s11770-012-0349-x. |
| [28] | Zhang H, Chen L W, Ren Z X, et al. 2009. Analysis on convergence of iteration method for potential fields downward continuation and research on robust downward continuation method. Chinese J. Geophys.(in Chinese), 52(4):1107-1113, doi:10.3969/j.issn.0001-5733.2009.04.028. |
| [29] | Zheng X N, Li X H, Liu D Z, et al. 2001. Regularization analysis of integral iteration method and the choice of its optimal step-length. Chinese J. Geophys.(in Chinese), 54(11):2943-2950, doi:10.3969/j.issn.0001-5733.2011.11.024. |
| [30] | 陈生昌, 肖鹏飞. 2007. 位场向下延拓的波数域广义逆算法. 地球物理学, 50(6):1816-1822. |
| [31] | 高玉文, 骆遥, 文武. 2012. 补偿向下延拓方法研究及应用. 地球物理学报, 55(8):2747-2756, doi:10.6038/j.issn.0001-5733.2012.08.026. |
| [32] | 管志宁. 2005. 地磁场与磁力勘探. 北京:地质出版社. |
| [33] | 郭志宏, 管志宁, 熊盛青. 2004. 长方体ΔT场及其梯度场无解析奇点理论表达式. 地球物理学报, 47(6):1131-1138. |
| [34] | 郭志宏, 熊盛青, 周坚鑫等. 2008. 航空重力重复线测试数据质量评价方法研究. 地球物理学报, 51(5):1538-1543. |
| [35] | 胡小平, 吴美平, 穆华等. 2013. 水下地磁导航技术. 北京:国防工业出版社. |
| [36] | 梁锦文. 1989. 位场向下延拓的正则化方法. 地球物理学报, 32(5):600-608. |
| [37] | 刘东甲, 洪天求, 贾志海等. 2009. 位场向下延拓的波数域迭代法及其收敛性. 地球物理学报, 52(6):1599-1605, doi:10.3969/j.issn.0001-5733.2009.06.022. |
| [38] | 栾文贵. 1983. 场位解析延拓的稳定化算法. 地球物理学报, 26(3):263-274. |
| [39] | 骆遥, 姚长利. 2007. 长方体磁场及其梯度无解析奇点表达式理论研究. 石油地球物理勘探, 42(6):714-719. |
| [40] | 王万银, 邱之云, 刘金兰等. 2009. 位场数据处理中的最小曲率扩边和补空方法研究. 地球物理学进展, 24(4):1327-1338, doi:10.3969/j.issn.1004-2903.2009.04.022. |
| [41] | 熊盛青, 周伏洪, 姚正煦等. 2001. 青藏高原中西部航磁调查. 北京:地质出版社. |
| [42] | 姚长利, 管志宁, 高德章等. 2003. 低纬度磁异常化极方法--压制因子法. 地球物理学报, 46(5):690-696. |
| [43] | 姚长利, 李宏伟, 郑元满等. 2012. 重磁位场转换计算中迭代法的综合分析与研究. 地球物理学报, 55(6):2062-2078, doi:10.6038/j.issn.0001-5733.2012.06.028. |
| [44] | 张辉, 陈龙伟, 任治新等. 2009. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究. 地球物理学报, 52(4):1107-1113, doi:10.3969/j.issn.0001-5733.2009.04.028. |
| [45] | 曾小牛, 李夕海, 刘代志等. 2011. 积分迭代法的正则性分析及其最优步长的选择. 地球物理学报, 54(11):2943-2950, doi:10.3969/j.issn.0001-5733.2011.11.024. |
 2016, Vol. 59
2016, Vol. 59

