地球物理学报  2015, Vol. 58 Issue (7): 2508-2524   PDF    
引用本文
王洋, 刘洪, 张衡, 王之洋, 唐祥德. 2015. 一种全局优化的隐式交错网格有限差分算法及其在弹性波数值模拟中的应用. 地球物理学报, 58(7): 2508-2524, doi: 10.6038/cjg20150726   
WANG Yang, LIU Hong, ZHANG Heng, WANG Zhi-Yang, TANG Xiang-De. 2015. A global optimized implicit staggered-grid finite-difference scheme for elastic wave modeling. Chinese J. Geophys. (in Chinese), 58(7): 2508-2524, doi: 10.6038/cjg20150726   
一种全局优化的隐式交错网格有限差分算法及其在弹性波数值模拟中的应用
王洋1,2, 刘洪1, 张衡3, 王之洋1,2, 唐祥德1,2    
1. 中国科学院地质与地球物理研究所 中国科学院油气资源研究重点实验室, 北京 100029;
2. 中国科学院大学, 北京 100049;
3. 国土资源部海底矿产资源重点实验室 广州海洋地质调查局, 广州 510075
投稿时间:2014-06-11    最后修改时间: 2015-05-16 .
基金项目：国家高技术研究发展计划(863计划)项目(2012AA061202),国家油气重大专项(2011ZX05008-006-50),国家油气重大专项(2011ZX05003-003),国家科技重大专项(2011ZX05023-005-002)联合资助.
作者简介：王洋,女,1989年生,中国科学院地质与地球物理研究所在读博士研究生,主要从事地震波成像方法的研究. E-mail: wangyang2010@mail.iggcas.ac.cn
通讯作者：刘洪,男,1959年生,研究员,主要从事油储地球物理研究.E-mail: liuhong@mail.iggcas.ac.cn
摘要：在数值模拟中,隐式有限差分具有较高的精度和稳定性.然而,传统隐式有限差分算法大多由于需要求解大型矩阵方程而存在计算效率偏低的局限性.本文针对一阶速度-应力弹性波方程,构建了一种优化隐式交错网格有限差分格式,然后将改进格式由时间-空间域转换为时间-波数域,利用二范数原理建立目标函数,再利用模拟退火法求取优化系数.通过对均匀模型以及复杂介质模型进行一阶速度-应力弹性波方程数值模拟所得单炮记录、波场快照分析表明:这种优化隐式交错网格差分算法与传统的几种显式和隐式交错网格有限差分算法相比不但降低了计算量,而且能有效的压制网格频散,使弹性波数值模拟的精度得到有效的提高.
关键词： 隐式有限差分     数值模拟     交错网格     弹性波方程     模拟退火    
A global optimized implicit staggered-grid finite-difference scheme for elastic wave modeling
WANG Yang1,2, LIU Hong1, ZHANG Heng3, WANG Zhi-Yang1,2, TANG Xiang-De1,2    
1. Key Laboratory of Petroleum Resources Research, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. MLR Key Laboratory of Marine Mineral Resources, Guangzhou Marine Geological Survey, Guangzhou 510075, China
Abstract: The advanced algorithms, such as reverse time migration (RTM) and full waveform inversion (FWI), require iterative calculation of the wave field. Its wave propagation part is highly sensitive to computational accuracy and stability. Therefore, how to find a way to obtain a finite-difference scheme that can consider the both aspects is absolutely critical. Here we propose a global optimized implicit staggered-grid finite-difference scheme that inherits the merit of high stability from the implicit finite-difference scheme and improves the computational efficiency remarkably.
The conventional implicit finite-difference operators generally have to obtain the high accuracy solutions from the inversion of either pentadiagonal or more diagonals matrices using the LU decomposition method, which greatly reduce the computation efficiency. Therefore, we first perform a global optimized implicit staggered-grid finite-difference (OISFD) scheme for first-order derivatives, which only needs to solve twice tridiagonal matrix inversion using the chasing method. In this way, it avoids the requirement of solving the large-scale matrix equation. Then we transform the new scheme from the time-space domain into the time-wavenumber domain, and develop the objective function by means of the two-norm theory. Different from traditional global optimized methods, we select the simulated annealing algorithm to get the optimized coefficients. And finally, after introducing the coefficients to the operator we establish the global optimized implicit staggered-grid finite-difference scheme.
We use independent tests to show that for same size matrix inversion, the average CPU time of the chasing method occupies 0.0019~0.0058 times that of the LU decomposition method. And this comparison becomes the theoretical basis of improving the computational efficiency. From the accuracy curves of approximation between the conventional explicit staggered-grid finite-difference method (ESFDM) and implicit staggered-grid finite-difference method (ISFDM), we can indicate that the OISFD operators have wider frequency coverage and smaller accuracy error fluctuation than those of the conventional ESFD operators and ISFD operators when using the same order spatial difference operator. In order to demonstrate the effect in elastic wave modeling, we perform first-order velocity-stress elastic wave equation numerical simulations on a homogeneous model and the modified Sigsbee2A model. The resulting shot records and wave field snapshots indicate that the OISFDM is more effective in suppressing the numerical dispersion, which is fully consistent with the theoretical accuracy curve comparison. What's more, the least CPU time cost in numerical simulation further confirms that the OISFD scheme reduces calculating amount while keeping high accuracy numerical simulation performance.
We have presented an implicit optimized scheme with any order of accuracy for calculating first spatial derivatives on a staggered-grid. The operator is designed by fitting the response in the wavenumber domain using the simulated annealing algorithm. The method is based on applying optimized operators to each of the spatial coordinates in elastic wave equation. It could utilize smaller stencils to achieve more accurate results than the corresponding explicit operator without adding significantly higher computational cost to conventional implicit finite-difference methods. The dispersion relation analysis and the numerical results demonstrate that the OISFD operators can achieve higher accuracy compared with those using the conventional ESFD operators and ISFD operators. This means we can greatly save the memory and computational cost required when using our optimized OISFD methods.
Key words: Implicit finite-difference     Numerical simulations     Staggered-grid     Elastic wave equation     Simulated annealing algorithm    


1 引言

有限差分算法凭借其高计算效率以及易于编程实现等优点，在地震波正演(Virieux，1984，1986; 裴正林，2005；严红勇和刘洋，2012)、逆时偏 移(Baysal et al.，1983; McMechan，1983; Yan and Liu，2013)和全波形反演(Virieux and Operto，2009;Warner et al.，2013)等领域已经得到了广泛使用.尤其是交错网格有限差分，因具有更高的精度和更好的稳定性而广受欢迎.目前，通常使用的有限差分算法主要分为显式和隐式两种.传统的波动方程显式有限差分系数通常由泰勒级数展开或优化算法而得到(刘洋等，1998；董良国等，2000； Liu et al.，2014)，为了得到高精度的数值解，通常需要采用较长的差分算子.Kosloff等(2010)认为高阶显式差分算子存在“饱和效应”，并且指出尽管高阶显式差分算法提高了精度，但精度提高的增量随差分算子阶数的增加而降低，经验表明最经济的差分阶数存在于四阶到八阶之间.相比之下隐式差分一般能以较短的差分算子长度得到较高的数值解精度，所以隐式差分备受关注.

与显式差分不同，隐式差分算子是由有理展开得到的，它不但比级数展开收敛更快(Fornberg，1998)，而且减小了高阶差分算子的长度.尽管隐式差分算子已经在许多领域中广泛应用(Lele，1992; Ekaterinaris，1999; Shang，1999)，但近年来才被引入解决地震波传播问题(Liu and Sen，2009a，2009b; Kosloff et al.，2010; Chu and Stoffa，2010，2012). Kosloff等(2008)将隐式差分算法引入到针对常密度时间域声波方程空间二阶导数的求取中.并随后在2010年，在声波方程空间隐式二阶导数的基础上，推导出隐式一阶导数交错网格有限差分算子，并将正演结果应用于逆时偏移中，证明了该算子能够有效的减少数值频散.Chu和Stoffa(2010)提出了频率域二阶声波方程空间导数的隐式算法，之后在2012年给出了由二阶隐式分裂时间积分和二阶空间导数隐式差分相结合的声波方程数值模拟方法.前面这些隐式算法，为了满足高精度模拟的需求通常需要通过LU分解的方法完成五或更多对角矩阵求逆，极大的降低了算法的计算效率.Zhang等(2007)将空间导数算子分为x、y、z三个方向，推导了空间二阶导数的分裂隐式差分格式，这种方法能够给出精确的点源响应并且能够应用于速度横向变化的情况.在适当参数的选择下，这种算法是无条件稳定的.Zhou和Zhang(2011)提出了预分解的策略，将隐式算法中原始的对角矩阵分解成两个独立的上三角矩阵和下三角矩阵，也就是使用L+U的预分解方法，替代了传统的LU分解方法.并利用Taylor级数展开与最小二乘相结合的思想求取隐式算法优化系数，极大的提高了模拟精度.然而，前述两种方法只适用于二阶声波方程，无法将其推广应用于一阶弹性波波动方程求解中.Liu和Sen(2009a，b)在Claerbout(1985)基础上，先后提出了针对一阶、二阶空间导数的规则网格和交错网格隐式有限差分新算法，并分别实现了该隐式算法来求解声波方程和一阶弹性波方程，从而进行了数值模拟分析；之后，Liu(2014)还在此隐式差分格式的基础上，提出利用最小二乘方法来优化该差分格式的差分系数，较大的提高了差分算子的计算精度和效率.

本文受Claerbout(1985)和Liu和Sen(2009b)思想的启发，构建出一种新的空间隐式差分格式，并采用非线性优化法来计算交错网格有限差分的空间差分系数.在差分系数优化过程中，先使用二范数建立目标函数，然后再用模拟退火法来求解优化的系数.最后，用此新隐式差分法来求解一阶速度-应力弹性波方程，并通过均匀介质和复杂模型测试来验证新差分法的计算精度和计算效率，同时与传统的显式交错网格有限差分算法(Explicit Staggered-grid Finite-Difference Method，简称ESFDM)和隐式交错网格有限差分算法(Implicit Staggered-grid Finite-Difference Method，简称ISFDM)进行了对比.

2 一阶弹性波速度—应力方程及高阶交错网格有限差分 2.1 一阶空间导数交错网格隐式有限差分格式

函数u(x)的空间一阶导数(2M+2N)阶ISFDM(其中由函数项提供2M阶精度，由函数导数 项提供2N阶精度)可以表示为(Chu，2009; Kosloff et al.，2010)

其中，其中M、N为正整数，am、bn为相应的差分系数，h为横向网格间距.

由平面波理论，令

其中，u0为常数，为波数.将式(2)代入式(1)，且令β=kh/2可以得到：

将式(3)中的余弦与正弦项进行泰勒级数展开，由左右系数对应相等可以通过矩阵求逆的方法直接求取系数，见表 1.

表 1 传统交错网格隐式有限差分系数 Table 1 Coefficients of the conventional implicit staggered-grid finite-difference formulas
2.2 一阶空间导数交错网格优化隐式有限差分格式

由上面推导的ISFDM可以看出，在使用隐式方法求取空间导数需要进行1D线性方程矩阵求逆，公式为

即：
其中矩阵 B x，A x分别由公式(1)中的am，bn，m=1，…M，n=1，2，…，N 确定，矩阵大小为(NX-1)×(NX-1)或(NX-2)×(NX-2)，视交错网格中参数的定义情况而定，NX为横向采样点个数.

为了达到高精度模拟的需求，公式(1)通常需要满足N＞1的条件.当N=1时，有

此时 B x为三对角矩阵，可以通过追赶法或LU分解法进行矩阵求逆.当N=2时，有
此时 B x为五对角矩阵，追赶法已经不适用，必须通过LU分解法进行矩阵求逆.

由以上分析看出，当N≥2时，求解每一个空间导数的过程中进行五或更多对角矩阵求逆，此时已经不能应用追赶法快速求解，LU分解成为此时的最优选择.

表 2 不同矩阵求逆方法平均CPU计算时间 Table 2 Average CPU time of different algorithms for matrix inversion

隐式差分正演中，在求解每一个空间导数的过程中均需进行一次对角矩阵求逆，因此，矩阵求逆的计算效率成为了整个算法效率至关重要影响因素.通过对追赶法和LU分解法计算时间对比测试可以看出，追赶法的求解速度明显优于LU分解.因此构造一种新的可以由追赶法计算的隐式差分格式成为了提高隐式差分计算效率的有效途径.

根据Claerbout(1985)以及Liu和Sen(2009b)的观点，函数u(x)的二阶有限差分算子可以通过增加一个高阶项的方法来提高FD算子的精度，通常为了易于编程实现，它是以下面的形式出现的(Claerbout，1985)，其中b为一个常量，表达式为

Liu和Sen(2009b)在此基础上提出了交错网格隐式差分格式，通过增加三阶导数项来提高精度，公式为

受他们的思想启发，本文构建出一种一阶导数的优化隐式交错网格有限差分算法(Optimized Implicit Staggered-grid Finite-Difference Method，简称OISFDM)，表达式为

即：
其中a，c为可调常量，h为横向网格间距.简单起见，令


当需要高阶精度时可以将(12)写成2M阶差分形式：

将公式(10)写成矩阵形式可以表示为
即：
其中

Cx和Ax矩阵大小均为(NX-1)×(NX-1)或(NX-2)×(NX-2)，视交错网格中参数的定义 情况而定.同理，在z向时矩阵大小(NZ-1)×(NZ-1)或(NZ-2)×(NZ-2).NX和NZ分别表示数值模拟中横向和纵向的网格点个数.可以看出，公式(16)通过两次三对角矩阵求逆来得到优化ISFD算子，避免使用LU分解，提高了计算效率.

2.3 隐式算法中三对角矩阵的计算策略

由于在公式(16)中每求解一个空间导数都要进行两次三对角矩阵求逆.因此可以将一些重复的求逆过程提前计算出来，提高隐式算法的计算效率(Liu and Sen，2009 a，b).通过对(17a)和(17b)三对角矩阵的观察可以发现这两个矩阵都只含有一个参数c或a.在每条对角线上，元素的值都是相等的，并且上下相对的两条对角线的值也是相等的.在这种情况下，可以不需要真正的建立矩阵 C x和A x，而是在追赶算法中将它们对应的参数直接赋值，并且将追赶法求逆矩阵分解为LU两个矩阵的过程在时间迭代前计算出来，这样在节省内存空间的同时降低了计算量.

3 模拟退火法求取交错网格优化隐式有限差分系数

将u(x)=u0eikx，β=kh/2，(13)和(14)带入公式(10)可得：

由此，本文中采用二范数原理建立2M阶所对应的目标函数为
其中
本文选择目标函数积分上下限分别为βl=0，βr=0.58π.

通过公式(11)可以看出，由于算子中存在系数相乘项，为非线性FD算子，不能通过常规的线性矩阵求逆的方法得到差分系数.常用的非线性全局优化方法有共轭梯度法、高斯牛顿法、模拟退火法等，模拟退火法因其能克服优化过程陷入局部极小、克服初值依赖性、目标函数灵活等优点被广泛认可.因此，本文对公式(19)选用模拟退火法求解优化系数.

模拟退火算法最早的思想由Metropolis等(1953)提出，图 1展示了模拟退火法求解目标函数的流程图，该算法试图在给定容差限Tolerance下寻找一组最佳的优化系数.图中函数obj由公式(19)(20)定义，算法初值设定: MARKOV链长 度N=1000，初始温度T=1000，终止温度T0=100，步长因子Stepfactor=0.02，容差Tolerance=5×10-8，最大搜索值XMAX=[1；1]，PreX=XMAX×rand ，PreBestX=PreX，BestX=-XMAX×rand . 随机选取下一点NextX=PreX+ Stepfactor ×XMAX×(rand -0.5)．

图 1 模拟退火法求解OISFD算子流程 Fig. 1 Flow chart of the ISFD scheme using the simulated annealing algorithm

根据热力学的原理，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为P(dE)=exp〖－dE/(KT)〗，(21)其中dE=obj(NextX)-obj(PreX).(22)K是物理学中的波尔兹曼常数；exp表示自然指数，且dE>0.温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小.本质上讲，温度T控制解的扰动范围.对于高温度，更有可能使它达到一个更广的范围(Zhang and Yao，2013).由于-dE/KT<0，所以P(dE)的函数取值范围是(0，1).事实上，在给定的容差限Tolerance下将得到许多不同组解而不是像其他优化方法所得到的唯一组解.因此可以进一步通过一些精确的波数范围和误差之间权衡来选择一组最优的解(Zhang and Yao，2013).

本文在离散化的假设下，利用优化一阶算子逼近真正的波数，进而得到系数数组X=[a； c].通过以上计算流程，得到数组 X=[ 0.09737101； -0.05866972]，即a=0.09737101，c= -0.05866972，此时M=1.当选取高阶差分时系数可见表 3.事实上，由于模拟退火法求解的灵活性，也可以使用最大范数或者相对误差等方式设定目标函数(Zhang and Yao，2013).

表 3 优化隐式交错网格有限差分系数 Table 3 Coefficients of the optimized implicit staggered-grid finite-difference formulas
4 隐式显式方法精度对比

传统ESFDM精度分析表达式为(Liu and Sen，2009b)

其中N为正整数，cn为相应的差分系数，取值见Liu和Sen(2009b)中表 1.

由公式(1)可以得到传统ISFDM精度分析表达式为<

其中M、N为正整数，am、bn为相应的差分系数，取值见表 1.

Liu和Sen(2009b)提出的ISFDM可表示为

其中，N为正整数，cn为相应的差分系数，b为一个常量，取值见Liu和Sen(2009b)中表 2.Liu(2014)采用ISFDM同公式(25)，在系数求取时采用最小二乘方法，取值见Liu(2014)中表 9.

OISFDM精度分析表达式为

其中a和c为常量，cm为相应的差分系数，见表 3.

由图 2—图 5中对比OISFD算子与其他差分算子的精度分析对比可以看出:(2+4)阶OISFD算子的精度明显高于传统6阶、8阶ESFD算子甚至能达到10阶ESFD算子精度.在与传统ISFD算子精度的对比中，(2+4)阶OISFD算子介于传统ISFD(4+2)阶与ISFD(6+2)阶算子之间.(2+4)阶OISFD算子精度高于Liu和Sen(2009b)的(4+2)阶算子，低于Liu和Sen(2009b)的(6+2)阶算子，与Liu(2014)的(4+2)阶算子的精度接近.随着差分阶数的提高，OISFD算子的精度得到了明显的改进.

图 2 一阶导数传统ESFD算子和OISFD算子精度对比 Fig. 2 Accuracy comparison between the conventional ESFD operators and OISFD operators for the first-order derivative

图 3 一阶导数传统ISFD算子和OISFD算子精度对比 Fig. 3 Accuracy comparison between the conventional ISFD operators and OISFD operators for the first-order derivative

图 4 一阶导数Liu 和 Sen(2009b)的 ISFD算子和OISFD算子精度对比 Fig. 4 Accuracy comparison between Liu and Sen (2009b)′s ISFD operators and OISFD operators for the first-order derivative

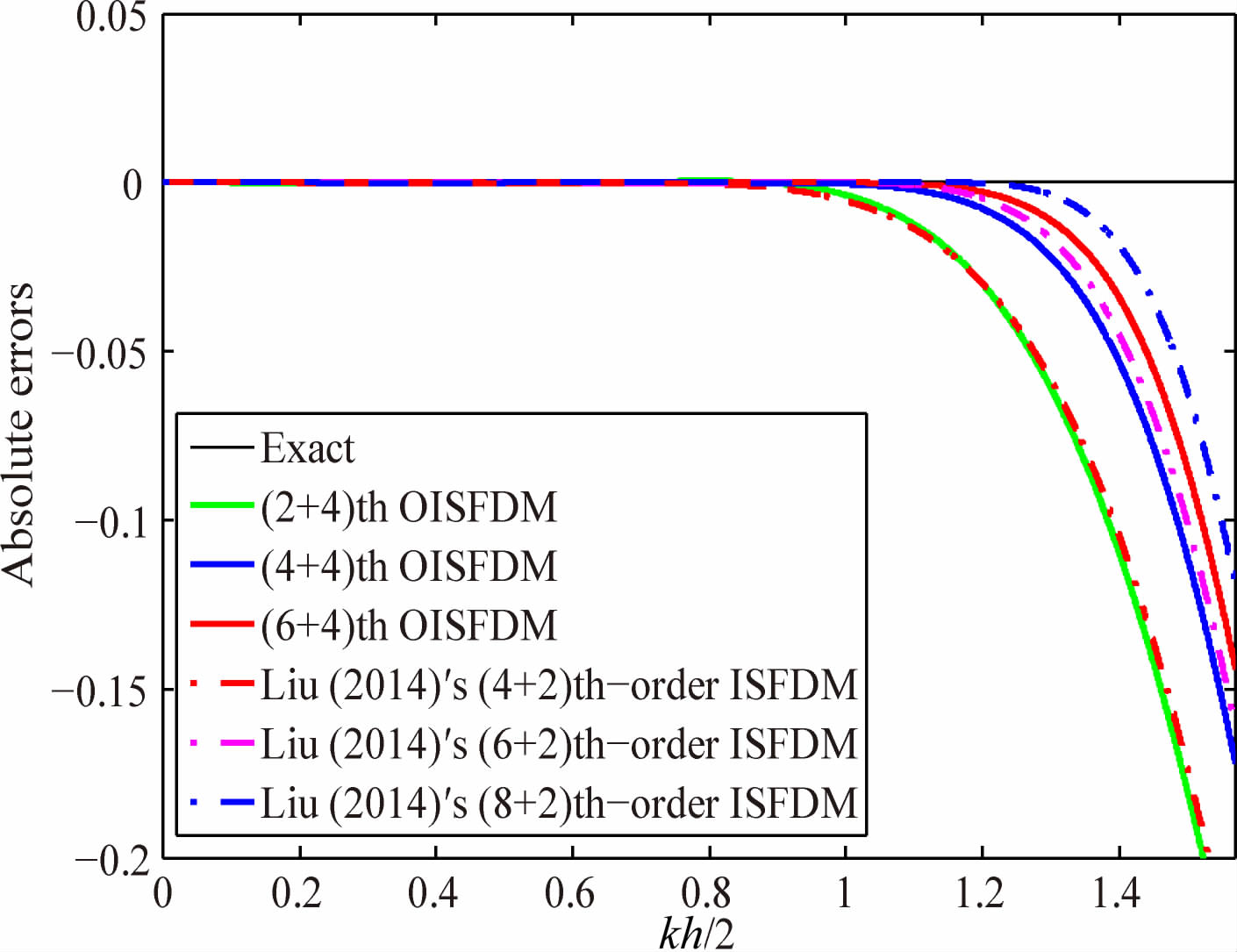图 5 一阶导数Liu(2014)的 ISFD算子和OISFD算子精度对比 Fig. 5 Accuracy comparison between Liu (2014)′s ISFD operators and OISFD operators and for the first-order derivative
5 数值模拟与分析

2D一阶弹性波速度-应力方程可以表示为(Virieux，1986)

其中t为时间，x和z为坐标方向，(vx，vz)为质点的振动速度，(τxx，τzz，τxz)为应力的三个分量，λ和μ为拉梅常数，ρ为密度.

6 数值模拟实例 6.1 均匀介质模型数值模拟

为了验证弹性介质中OISFDM数值模拟的结果，本文首先设计了均匀模型，模型参数参见表 4，分别采用传统ESFDM、传统ISFDM、Liu和Sen(2009b)的ISFDM和OISFDM进行数值模拟.

表 4 均匀介质模型正演模拟参数 Table 4 Parameters of a homogeneous model for forward modeling

图 6为不同差分算法在计算时间为0.55 s处的波场快照，从图中可以看到，各差分算法随着差分阶数的提高，频散减弱，即模拟精度越高.通过快照对比可以发现传统6阶ESFDM会产生严重的波场 畸变，在相同模拟参数条件下，由(2+4)阶OISFDM 引起的频散则非常的微弱，可以得到与传统10阶 ESFDM相当或更高的模拟精度；(2+4)阶OISFDM 模拟结果与传统(4+2)阶 ISFDM相比波形保持得 比较好，频散相对较弱，与传统(4+4)阶ISFDM模拟精度相近，介于Liu和Sen(2009b)的(4+2)阶ISFDM与Liu和Sen(2009b)的(6+2)阶ISFDM之间.

图 6 均匀模型0.55 s波场快照(左侧为水平分量，右侧为垂直分量) (a)(2+4)阶OISFDM；(b)传统6阶 ESFDM；(c)传统10阶 ESFDM；(d)传统(4+2)阶ISFDM；(e)传统(4+4)阶ISFDM．(f)Liu和Sen(2009b)的(4+2)阶ISFDM；(g)Liu和Sen(2009b)的(6+2)阶ISFDM． Fig. 6 Homogeneous model sanpshots at 0.55 s(Left:horizontal component. Right: vertical component) (a)(2+4)th-order OISFDM；(b)Conventional 6th-order ESFDM；(c)Conventional 10th-order ESFDM;(d)Conventional(4+2)th-order ISFDM；(e)Conventional(4+4)th-order ISFDM;(f)Liu and Sen(2009b)′s(4+2)th-order ISFDM；(g)Liu and Sen(2009b)′s(6+2)th-order ISFDM．
6.2 复杂介质模型数值模拟

为了测试本文优化隐式差分格式在复杂介质波场模拟中的适应能力，我们对修改的Sigsbee2A模型(如图 7)进行数值模拟，模型参数见表 5.

表 5 复杂介质模型正演模拟参数 Table 5 Parameters of a complex medium model for forward modeling

图 8分别给出了不同差分算法水平分量单炮记录.图 10分别给出了不同差分算法垂直分量单炮记录.为了对不同算法数值模拟的结果进行比较，对图 8和图 10虚线框部分分别进行局部放大得到图 9和图 11.从图 9和图 11中可以看到传统6阶ESFDM、传统(4+2)阶 ISFDM存在较为明显的数值频散.并且(2+4)阶OISFDM可以得到与传统(4+4)阶ISFDM相当有时甚至更佳的计算精度，介于Liu和Sen(2009b)的(4+2)阶 ISFD算法(6+2)阶 ISFD算法之间.

图 12分别给出了时间为0.92 s不同差分算法的波场快照.通过对比炮记录和波场快照，可以看到(2+4)阶OISFDM能够较为有效的压制数值频散.将传统10阶ESFDM与(2+4)阶OISFDM进行对比时，它们的数值模拟精度几乎是一样的；传统(4+2)阶ISFDM会产生比(2+4)阶OISFDM严重的数值频散，当将(2+4)阶OISFDM与传统(4+4)阶ISFDM进行对比时，(2+4)阶OISFDM可以得到较高的精度；Liu和Sen(2009b)的(4+2)阶 ISFDM会产生严重的数值频散.然而，(2+4)阶OISFDM精度介于Liu和Sen(2009b)的(4+2)阶 ISFDM与(6+2)阶 ISFDM之间.

图 7 复杂介质速度模型 Fig. 7 Velocity model in complex medium

图 8 复杂介质水平分量单炮记录  其他说明同图 6. Fig. 8 Horizontal component in seismograms for complex medium  Other the same as the Fig. 6

图 9 复杂介质水平分量炮记录局部放大 其他说明同图 6. Fig. 9 Zoom of horizontal component in seismograms for complex medium  Other the same as the Fig. 6

图 10 复杂介质垂直分量单炮记录 其他说明同图 6. Fig. 10 Vertical component in seismograms for complex medium Other the same as the Fig. 6

图 11 垂直分量单炮记录局部放大 其他说明同图 6. Fig. 11 Zoom of vertical component in seismograms for complex medium  Other the same as the Fig. 6

图 12 0.92s波场快照（左侧为水平分量，右侧为垂直分量） 其他说明同图 6. Fig. 12 Snapshots at 0.92 s（Left:horizontal component. Right: vertical component） Other the same as the Fig. 6

同时，通过图 13中4000个时间步长的计算时间对比，可以得出：(2+4)阶OISFDM所需的CPU计算时间较少，具有更高的计算效率.此外，由公式(1)中N值更高的传统ISFDM，在相同M值的情况下所带来的精度提升空间有限，并不能显著提升计算精度，反而因为求逆矩阵带宽增加会明显增加计算成本，降低计算效率.

图 13 测试时间对比 （a） OISFDM与传统ESFDM对比； （b） OISFDM与传统ISFDM对比; （c） OISFDM与Liu 和 Sen（2009b）的ISFDM对比． Fig. 13 Comparison of computing costs （a） Comparison between OISFDM and conventional ESFDM; （b） Comparison between OISFDM and conventional ISFDM; （c） Comparison of between OISFDM and Liu and Sen (2009b)′s ISFDM．
7 结论

本文建立了一种空间OISFD格式，并在此基础上应用二范数原理建立绝对误差的目标函数；然后通过模拟退火法对目标函数进行多参数的优化，以求取优化系数；最后采用该优化差分法对弹性波场进行了数值模拟与分析，还与传统的几种交错网格差分方法进行了对比.在均匀介质以及复杂介质中，对传统ESFDM、传统ISFDM、Liu和Sen(2009b)的ISFDM和OISFDM进行数值模拟，通过单炮记录、波场快照、计算效率等角度分析可以看出：在相同模拟参数的前提下，(2+4)阶OISFDM可以比传统6阶 ESFDM更为有效的压制数值频散并且能达到传统10阶ESFDM的精度；在与传统ISFDM的对比中可以看出，(2+4)阶OISFDM较传统(4+2)阶ISFDM能够更好的压制频散，可以得到比传统(4+4)阶ISFDM略高的精度；在与Liu和Sen(2009b)的ISFDM的对比中，(2+4)阶OISFDM可以达到介于Liu和Sen(2009b)的(4+2)阶ISFDM与(6+2)阶ISFDM之间的模拟精度.在高精度的数值模拟中可以应用高阶的OISFDM来达到更佳的模拟效果.因此，OISFDM具有更高的精度和计算效率，为弹性波正演模拟提供了一种新的数值算法.

此外，当将OISFDM应用于3D复杂介质时，计算量和内存需求也急剧增大，成为影响数值模拟计算效率的瓶颈.因此可以考虑引入GPU/CPU协同并行架构，将模型在慢维方向分块并行，在每块中通过GPU实现每个时间步的波场数值计算，然而这一思想仍需要在下一步的研究中详细讨论实现.
致谢 感谢严红勇博士对本论文工作的建议和帮助.

参考文献
[1] Baysal E, Kosloff D, Sherwood W C. 1983. Reverse time migration. Geophysics, 48(11): 1514-1524.
[2] Chu C. 2009. Seismic modeling and imaging with the fourier method: numerical analyses and parallel implementation strategies[Ph. D. thesis]. Univ. of Texas.
[3] Chu C L, Stoffa P L. 2010. Frequency domain modeling using implicit spatial finite difference operators. // SEG Technical Program Expanded Abstracts, 3076-3080, doi: 10.1190/1.3513485.
[4] Chu C L, Stoffa P L. 2012. Implicit finite-difference simulations of seismic wave propagation. Geophysics, 77(2): T57-T67, doi: 10.1190/geo2011-0180. 1.
[5] Claerbout J F. 1985. The craft of wavefield extrapolation. // Imaging the Earth's Interior, 260-265, Oxford: Blackwell Scientific Publications.
[6] Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese), 43(3): 411-419.
[7] Ekaterinaris J A. 1999. Implicit, high-resolution, compact schemes for gas dynamics and aero acoustics. Journal of Computational Physics, 156(2): 272-299, doi: 10.1006/jcph.1999.6360.
[8] Fornberg B. 1998. Calculation of weights in finite difference formulas. SIAM Review, 40(3): 685-691, doi: 10.1137/S0036144596322507.
[9] Kosloff D, Pestana R, Tal-Ezer H. 2008. Numerical solution of the constant density acoustic wave equation by implicit spatial derivative operators. // 78th Annual International Meeting, SEG Expanded Abstracts, 2057-2061.
[10] Kosloff D, Pestana R, Tal-Ezer H. 2010. Acoustic and elastic numerical wave simulations by recursive spatial derivative operators. Geophysics, 75(1): T167-T174, doi: 10.1190/1.348521.
[11] Lele S K. 1992. Compact finite difference schemes with spectral-like resolution. Journal of Computational Physics, 103(1): 16-42, doi: 10.1016/0021-9991(92)90324-R.
[12] Liu Y, Sen M K. 2009a. A practical implicit finite-difference method: examples from seismic modeling. Journal of Geophysics and Engineering, 6(3): 231-249, doi: 10.1088/1742-2132/6/3/003.
[13] Liu Y, Sen M K. 2009b. An implicit staggered-grid finite-difference method for seismic modeling. Geophysical Journal International, 179(1): 459-474, doi: 10.1111/j.1365-246X. 2009.04305.x.
[14] Liu Y. 2014. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling. Geophysical Journal International, 197(2): 1033-1047, doi: 10. 1093/gji/ggu032.
[15] Liu Y, Li C C, Mou Y G. 1998. Finite-difference numerical modeling of any even-order accuracy. Oil Geophysical Prospecting, 33(1): 1-10.
[16] Liu Y, Yan H Y, Liu H. 2014. Least squares staggered-grid finite-difference for elastic wave modelling. Exploration Geophysics, 45(4): 255-260. doi: 10.1071/EG13087.
[17] McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting, 31(3): 413-420, doi: 10.1190/geo2012-0338.1.
[18] Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. 1953. Equation of state calculations by fast computing machines. Journal of Chemical Physics, 21(6): 1087-1092.
[19] Pei Z L. 2005. Numerical simulation of elastic wave equation in 3-D isotropic media with staggered-grid high-order difference method. Geophysical Prospecting for Petroleum, 44(4): 308-315.
[20] Shang J S. 1999. High-order compact-difference schemes for time dependent Maxwell equations. Journal of Computational Physics, 153(2): 312-333, doi: 10.1006/jcph.1999. 6279.
[21] Virieux J. 1984. SH-wave propagation in heterogeneous media: velocity stress finite-difference method. Geophysics, 49(11): 1933-1957.
[22] Virieux J. 1986. P-SV wave propagation in heterogeneous media: velocity stress finite difference method. Geophysics, 51(4): 889-901.
[23] Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics. Geophysics, 74(6): WCC1-WCC26.
[24] Warner M, Ratclife A, Nangoo T, et al. 2013. Anisotropic 3D full-waveform inversion. Geophysics, 78(2): R59-R80, doi: 10.1190/geo2012-0338.1.
[25] Yan H Y, Liu Y. 2012. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media. Chinese J. Geophys. (in Chinese), 55(4): 1354-1365, doi: 10.6038/j. issn. 0001-5733.2012.04.031.
[26] Yan H Y, Liu Y. 2013. Visco-acoustic pre-stack reverse-time migration based on the time-space domain adaptive high-order finite-difference method. Geophysical Prospecting, 61(5): 941-954, doi: 10.1111/1365-2478.12046.
[27] Zhang H, Zhang Y, Sun J. 2007. Implicit splitting finite difference scheme for multi-dimensional wave simulation. // SEG Technical Program Expanded Abstracts, 2011-2015, doi: 10.1190/1.2792885.
[28] Zhang J H, Yao Z X. 2013. Optimized explicit finite-difference schemes for spatial derivatives using maximum norm. Journal of Computational Physics, 250: 511-526, doi: 10.1016/j. jcp. 2013.04.029.
[29] Zhou H B, Zhang G Q. 2011. Prefactored optimized compact finite difference schemes for second spatial derivatives. Geophysics, 76(5): WB87-WB95, doi: 10.1190/geo2011-0048.1.
[1] 董良国, 马在田, 曹景忠等. 2000. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报, 43(3): 411\419.
[2] 刘洋, 李承楚, 牟永光. 1998. 任意偶数阶精度有限差分法数值模拟. 石油地球物理勘探, 33(1): 1\10.
[3] 裴正林. 2005. 三维各向同性介质弹性波方程交错网格高阶有限差分法模拟. 石油物探, 44(4): 308\315.
[4] 严红勇, 刘洋. 2012. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟. 地球物理学报, 55(4): 1354\1365, doi: 10.6038/j.issn.0001\5733.2012.04.031.