2. 北京应用气象研究所, 北京 100029
2. Beijing Institute of Applied Meteorology, Beijing 100029, China
The WRF model is used to reconstruct the Typhoon "Muifa" (2011). The gravity wave parameters including horizontal wavelengths, vertical wavelengths and periods are estimated by the three-dimensional FFT wave spectrum analysis. The AIRS observations data is used to analyze the stratospheric gravity wave features and validate the model outputs.
The vertical velocity field from model outputs shows that the typhoon has the energy to induce gravity waves nearly in all directions of the troposphere, while in the stratosphere the waves are only concentrated in the east of the typhoon center, and the range can reach 1000 km when the gravity waves propagate to the stratosphere. In addition, the stratospheric gravity waves and the spiral rain bands have some similarities in the pattern, location and scale. Furthermore, the wind analysis indicates that the differences of gravity waves at different heights mainly result from the modulation of westward background wind and wind shear, which happens in the process of vertical propagation. It reveals that the gravity waves mainly propagate against the background wind field. Then the FFT wave spectral analysis reveals that the gravity wave has the horizontal wavelengths of approximately 1000 km, the periods of 15~25 h, and the vertical wavelengths of 8~12 km at 25 km height. At last, AIRS observations show semicircular arc waves at 30~40 km height, which are similar to those shown at lower heights in the WRF model.
This study indicates that the WRF model can reasonably reproduce the stratospheric gravity waves in terms of pattern, propagation and scope. It also reveals that the data from different techniques are complementary for stratospheric gravity wave analysis. Finally, the AIRS observations show great application potential in stratospheric gravity waves analysis.
大气重力波是中高层大气的主要波动之一,是影响中高层大气的热力学结构和环流结构的重要动力学因素.重力波的发生和传播与强对流活动、背景风场、地形以及行星波都具有十分密切的联系.特别是,台风这类强对流作为一种重要的重力波激发源,拥有完整的组织结构,其激发的重力波不仅对平流层和对流层物质交换产生十分显著的影响,造成大气成分和动量的输送(Pfister et al.,1993;Vincent and Joan Alexander,2000),甚至对电离层总电子含量(TEC)也具有重要的影响(毛田等,2009).但目前我们对台风这种强对流诱发平流层重力波的源及其产生机制还未完全认识.因此,台风诱发平流层重力波的研究一直是大气科学领域的热点问题之一.
目前,平流层重力波的研究主要是采用数值模拟以及基于探空气球、雷达、火箭等探测资料的分析.由于数值模拟可以给出大量的高时空分辨率的输出结果,利用中尺度数值模式开展台风激发重力波的研究被越来越多的学者所采用.Kim等(2005)采用27 km的水平分辨率对台风Rusa进行模拟,其结果揭示台风诱发的平流层重力波的纬向波长能够达到300~600 km.Kuester等(2008)利用3 km的高水平分辨率对台风Humberto进行了数值模拟,得到的重力波水平波长为15~300 km.可见,不同个例及模式分辨率的选择对于利用数值模式研究重力波结果也存在着一定的差异,这也说明了重力 波具有较宽的波谱范围.另外,Chane-Ming等(2002)通过风廓线仪探测数据发现,下平流层存在近1000 km 水平尺度的重力波,对于这种和台风对流本体尺度相当的重力波的诱发机制目前还没有完全认识清楚.随着遥感技术的发展,卫星观测数据在平流层重力波分析中也得到广泛应用.Wu等(2006)通过研究基于不同探测技术的卫星资料,发现这些资料都能够探测到很强的重力波活动.Choi等(2012)对卫星AIRS观测的重力波进行了个例分析.Yue等(2013)由地基气辉成像仪和卫星AIRS观测资料同时观测到了对流激发的重力波.
东亚区域是全球热带气旋最活跃的区域,其激发的平流层重力波波动的数值模拟分析研究是进一步认识这一类波动发生发展机制的基础.陈丹等(2011)开展了台风激发平流层重力波数值模拟的个例分析.陈丹等(2013)指出,台风诱发的重力波波动 能量在上传的过程中对于驱动QBO(Quasi-Biennial Oscillation,准两年周期振荡)现象具有不可忽视的作用.姚志刚等(2015)利用AIRS观测资料分析了东亚夏季平流层的重力波的分布特征并给出了多种波动形态,其结果表明,该区域的平流层半圆弧状的波动与对流层深对流存在时空相关性,但需要进一步利用其他手段对AIRS观测的这种平流层波动进行验证.显然,基于数值模拟与卫星观测的台风诱发平流层重力波的综合分析,不仅有助于以上两种结果的相互对比验证,也有助于更全面地认识重力波的波动特征.
为了深入分析台风诱发平流层重力波的特征以及验证不同手段得到的平流层重力波的分析结果,本文重点针对2011年7—8月超强台风“梅花”,开展了时效为6天的数值模拟,利用模式输出结果,分析了台风诱发重力波在平流层的上传过程以及形态、波长、周期等特征,并与AIRS观测得到的平流层重力波的波动特征进行了对比.
2 台风“梅花”及其数值模拟方案 2.1 基本情况2011年第9号超强台风“梅花”于7月28日14时在菲律宾以东洋面上生成,29日后期向偏北方向移动,从8月2号转向西北方向移动,3号开始又向偏西方向运行,4日23时转向西北方向,6日开始转向西北偏北方向移动,7日再向偏北方向移动,最终于8月8日18时30分在朝鲜西北部沿海登陆.“梅花”的移动速度比较慢,导致该台风维持时间较长,生命史共12天,约为一般台风的2.5倍.该台风强度强,两次增强为超级台风后又减弱,中心附近最大 风速达到近50 m·s-1,最低海平面气压达到930 hPa. 在向北移动的过程中,路径多次发生偏折(曹晓岗等,2013).
图 1为AIRS在台风发生时段内812.16 cm-1通道获得的亮温图.由图可见,在该时段内,台风云系十分密集,组织结构完整,处于成熟期,云系尺度达到上千公里.此外,在台风成熟阶段存在很高的对 流云,且在台风眼壁周围,有着许多活跃的带状云. 靠近台风眼区附近的云顶温度达到了200 K甚至更低,这意味着台风中心附近云系已经渗透到了上对流层.
 |
图 1 2011年8月2日16时(a)和8月6日17时(b)AIRS在812.16 cm-1通道观测的亮温 Fig. 1 AIRS brightness temperature at 812.16 cm-1 at 1600UTC Aug 2(a) and 1700UTC Aug 6(b),2011 |
本文主要利用美国环境预报中心提供的FNL资料作为模式的初始场和边界场.该资料目前被广泛应用于WRF模式作为初始场和边界场,数据包括了水平风速、温度、位势高度、涡度、相对湿度等一系列气象变量场.资料的水平分辨率为1°×1°,时间间隔为6 h,垂直方向分为26个气压层,覆盖由 地面(1000 hPa)至平流层中低层(10 hPa)的高度范围.
模式模拟区域采用了Mercator投影,东西和南 北方向格点数为187×187,中心设置为(20°N,130°E),时间积分步长为30 s.模式垂直分辨率由地面至模式层顶逐渐变粗,共86层,其中在10~25 km高度上约为等高度500 m,顶层设为10 hPa.为了防止波动的反射,上边界采用了阻尼层方案,阻尼层高度为5 km.
此次模拟过程采用的物理方案主要包括:WSM6微物理方案、RRTM长波辐射方案(Mlawer et al.,1997)、Dudhia短波辐射方案(Dudhia,1989)、 Monin-Obukhov近地面层方案、热量扩散方案以及Kain-Fritsch积云参数化方案(Kain,2004),行星边界层主要采用了YSU方案(Hong et al.,2006).模拟时间为2011年8月01日00时—8月7日00时,主要基于该段时间内台风发展十分成熟,便于我们更好地进行其诱发平流层重力波的研究.
3 数值模拟结果分析 3.1 路径和强度图 2a显示了为期6天的模拟路径与日本气象厅(JMA)提供的最佳路径对比图.其中,模拟路径主要通过模式输出的每隔6 h最低海平面气压所在的位置表征.在该段时间内,“梅花”整体上表现为向西北移动的趋势,并且发生了偏折.从模拟效果来看,尽管在路径偏折模拟与实际存在一些小的纬度上的偏差,但是总体上模拟的台风路径与最佳路径之间具有较好的一致性,并且模拟出了台风路径的转折趋势.台风的强度演变主要利用最低海平面气压来表征,从图 2b中可以看出,在模拟时段内,台风“梅花”仍处于一个十分成熟的阶段,海平面气压基本维持在945 hPa附近,只是在模拟后期强度逐渐减弱,且模式模拟的台风强度以及变化趋势与JMA给出的事后分析结果十分接近.可见,台风“梅花”的路径和强度都得到了很好的再现,故可利用模式输出结果开展其诱发平流层重力波的研究.
 |
图 2 2011年8月1日00时到8月7日00时WRF模拟的和日本气象厅提供的台风“梅花”路径(a)以及近地面最低海平面气压(b)对比图 Fig. 2 Typhoon Muifa′s track(a) and minimum sea level pressure(b)from WRF simulations and JMA observations from 0000UTC Aug 1 to 0000UTC Aug 7,2011 |
这里主要利用模式输出的不同高度的垂直速度场分析平流层重力波特征.由图 3a可以看出,在对流层12 km高度上,垂直速度场的分布主要为伴随台风中心的圆形对称结构,这种很强的垂直振动能量主要和台风眼墙和对流带有着密切的关系,并且 随着时间的增长,台风中心附近波动能量分布越来越对称(未展示).虽然台风在对流层各个方向上都具备诱发出重力波的能量,但到了平流层高度上,波动主要位于台风中心以东,不同高度上的波动形态也存在着一定的差异,且在25 km高度上(图 3c)的波动幅度要强于20 km(图 3b).根据重力波上传理论(Lindzen,1981),重力波在上传的过程中,其扰动量正比于ρ-1/2,即在其上传中波振幅必然是随高度不断增加的.因此,这里的模拟结果和以上理论是一致的.
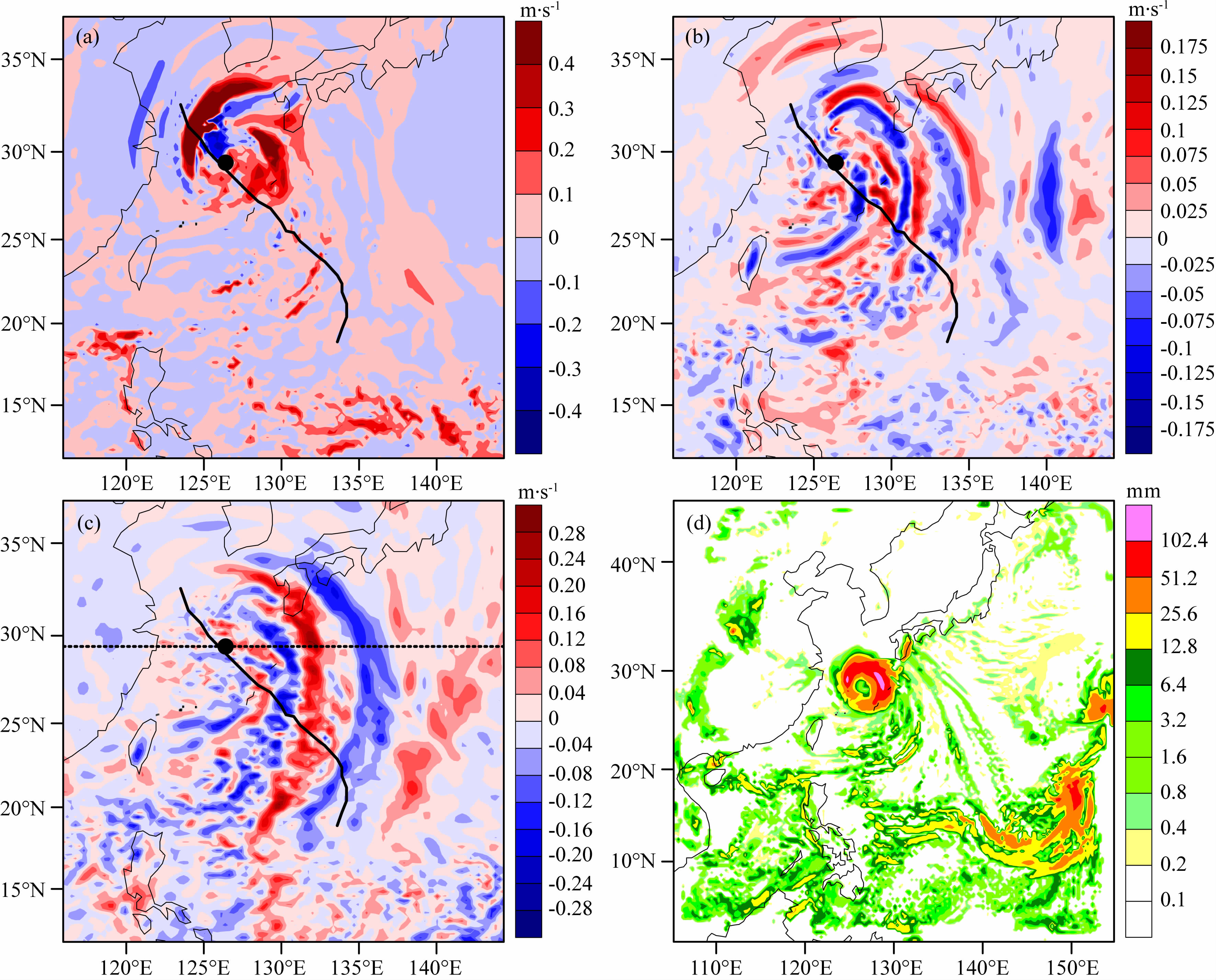 |
图 3 2011年8月6日00时12 km(a)、20 km(b)、25 km(c)高度上垂直速度场(图中黑色实心圆圈代表该时刻台风中心位置,黑色实线为模拟的台风路径)以及累计6 h降水量(d) Fig. 3 Vertical velocity at 12 km(a),20 km(b),25 km(c)(the black solid circle denotes the typhoon center,and the black solid line represents the simulated typhoon track) and 6 h precipitation(d)at 0000UTC Aug 6,2011 |
此外,从图 3d累计6 h降水量可以看出,台风产生的螺旋雨带也主要集中于台风中心以东.对照图 3c可见,这种雨带与平流层重力波在尺度、位置以及形态上具有一定的相似性.这一结果表明,对流层雨带可能是平流层重力波特征的一个指示.Tepper(1958)首先指出,热带气旋在眼壁附近产生重力波,并向外传播成为螺旋雨带.Anthes(1972)、Kurihara和Tuleya(1974)、Kurihara(1976)的数值模拟分析工作也指出,台风内部的螺旋雨带是正压不稳定引起的旋转不稳定,以重力波向四周频散能 量.徐祥德等(2004)研究指出台风系统存在涡旋螺旋波动力特征,这种重力波列传播可能与台风涡旋基本态波流及其能量频散动力效应相关.可见,台风诱发的平流 层重力波可能与产生的螺旋雨带上的深对流云相关.
图 4为沿图 3c中黑色虚线的高度-经度剖面图.由图可见,在对流层中台风中心附近存在着很强的上升气流,这就为波动的上传提供了动力.台风中心附近这种强的垂直气流运动,造成了等位温线也出现了很强的扰动.由该图也可见,波动在平流层上传过程中,主导波列主要集中在台风中心以东,并逆着背景流向东倾斜,波动在上传中随着高度增加,传播距离也越来越远,在平流层高度上甚至传到千公里以外的区域.此外,随着高度的增加波动幅度也逐渐增大,这也说明了台风“梅花”诱发的重力波在平流层30 km高度上未饱和破碎,波动仍会继续上传,即台风这类组织结构完整的强对流诱发的重力波能够传播到上平流层.
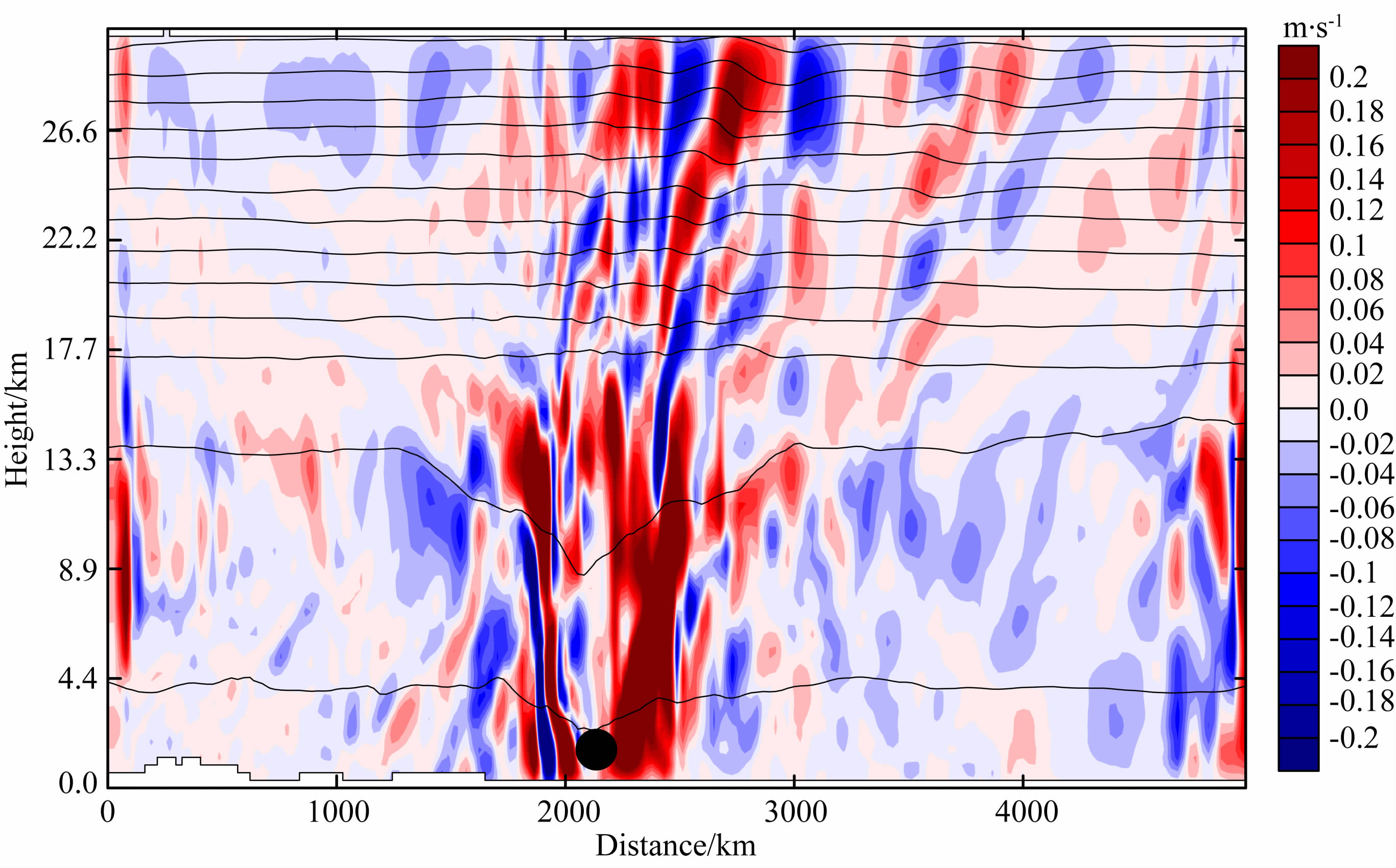 |
图 4 数值模式输出的8月6日00时沿29°N垂直速度剖面图(图片底端的黑色实心圆圈代表该时刻台风中心的位置,实线为等位温线,横轴为沿着29°N纬线转换的距离) Fig. 4 The profile of vertical velocity along the 29°N at 0000UTC,Aug 6 from WRF(the black solid circle denotes the typhoon center,and black solid line denotes the potential temperature,the horizontal axis represents the transform distance along the line of latitude 29°N) |
刘晓和徐寄遥(2006)的理论研究认为,反向背景风场将拉伸重力波的垂直波长,加速重力波的上传;同向背景风场会延迟重力波发生不稳定的时间,缩短垂直波长,对重力波的上传有抑制作用.为了进一步分析重力波传播与背景风场之间的关联性,这里对台风的风场进行分析.图 5为模式输出的台风 影响区域内(10°N—30°N、125°E—145°E)在0~30 km 高度上的平均风场.由图可见,在平流层高度上存在着很强的东风气流,最大风速达到-30 m·s-1,并且纬向方向的风速随高度的增量显著地比经向方向大,但经向方向背景风场对于波动的上传也会起到一定的作用.此外,纬向风场在0~30 km高度上存在着多次的风切变,经向风场主要在15 km高度处存在着一个大的风切变,而这些风切变区也会影响到波动上传(Beres et al.,2002).以上这些风场因素导致台风在对流层激发的重力波在上传的过程中向西传的波动逐渐被背景风场过滤掉,这种传播方式表明了重力波逆着背景流向上传播.因此,这里的结果进一步揭示了平流层中的背景风场对于对流层中的重力波上传起着重要的过滤调制作用.
 |
图 5 模式输出的2011年8月2日06时—8月3日22时0~30 km纬向(a)和经向(b)台风影响区域内(10°N—30°N,125°E—145°E)的平均风场(U正值表示西风,V正值表示南风) Fig. 5 The zonal(a) and warp(b)direction mean wind speed at 0~30 km in the region influenced by typhoon(10°N—30°N,125°E—145°E)by model output from 0600UTC Aug 2 to 2200UTC Aug 3,2011(positive U represents west wind,and positive V represents south wind) |
重力波参数化问题在全球大气模式中(GCMs)还未完全得到解决(Beres et al.,2004;Chun and Baik,1998;Song and Chun,2005),因此分析台风诱发的重力波参数特征对参数化方案具有一定的指导意义.为了定量地分析台风诱发的平流层重力波特征,本文对波动波谱结构进行了分析.
分析数据主要采用模拟时段内8月2日06时—8月3日22时连续41个小时的垂直风场w,时间分辨率为30 min,空间范围为选择时段内每个 时刻台风中心相邻的111×111(2997 km×2997 km)格点区域.这样就可以得到一个以台风移动的坐标系下的谱参数.在计算过程中,首先将垂直风场减去该变量在整个时空范围内的平均值,得到垂直风场的扰动值w′.随后,利用该扰动数据进行三维傅里叶变换(FFT)得到功率谱密度(Beres et al.,2002;陈丹等,2013).
对于速度扰动场w′=(x,y,z,t),对某一高度z的数据利用三维傅里叶变换获得关于纬向波数(k)、经向波数(l)以及频率(ω)的FFT谱,计算公式为:
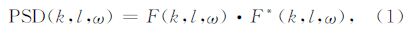
其中,F*为F的共轭复数.
为了直观地展示波动参数信息,参照Kim等(2009)以及陈丹等(2013)的工作,将(k,l)的笛卡儿坐标转换成方位角坐标,即
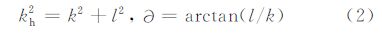
其中,kh表示沿着∂方向的水平波数,∂表示从正东方向逆时针旋转角度.这样,功率谱密度就表示为水平波数kh、方向∂以及频率ω的函数.这里重点选取了具有代表性的0°(正东)、45°(东北)、90°(正北)以及-45°(东南)4个方向进行分析.其中,负值角度表示沿着∂+180°方向.图 6即为选取的时间段内,垂直速度扰动场经三维FFT变换获得的25 km高度上四个不同方向的垂直速度扰动场的功率谱密度.
 |
图 6 25 km高度上四个不同方向垂直速度扰动场功率谱密度(单位:m2·s-2) Fig. 6 w′ in four different directions at 25 km height(units: m2·s-2) |
由图 6可见,在分析的四个方向上,能量主要集中于正水平波数的一侧,也即台风中心的东侧,而负水平波数一侧能量普遍很小,这种不对称能量分布也表明了重力波在上传过程中逆着背景流向东传播.在分析的四个剖面中,0°和45°方向能量相对较大,其中0°方向最强,而-45°和90°方向能量相对很弱.由此可见,波动在25 km高度上的优势传播方向为正东以及东北方向.从谱结构可以看出,在该高 度上分析的波动能量主要在0.001 km-1波数(1000 km 波长)以及0.04~0.06 h-1频率(15~25 h周期)附近.
此外,根据重力波的色散关系式(3),即
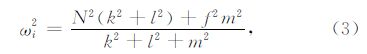
其中ωi=ω-u-v,可进一步计算得到垂直波数m,ωi为固有频率,ω为相对于地面的频率,和分别为分析高度上谱分析时段内纬向平均风速和经向平均风速,f为科氏参数,N为Brunt-Valsala频率,以上均为已知量.图 6中红色曲线即为计算得到等垂直波长线.由图可见,在25 km高度四个方向上波动的主要垂直波长在8~12 km.
本文研究的台风“梅花”诱发的平流层重力波特征虽与陈丹等人(2013)使用27 km分辨率对台风“Matsa”分析出的1000 km水平波长,12~18 h周期,8~12 km垂直波长的单峰窄谱结构水平尺度相似,均达到了1000 km,但其波动的最优传播方向为 东北方向.Kuester等(2001)利用3 km水平分辨率 获得的台风“Humberto”诱发的下平流层重力波水平波长为15~300 km.可见,不同的台风以及模式水平分辨率分析出的波动参数都会具有一定的差异,这就需要我们今后进行更多的个例分析,总结不同类型的台风诱发的平流层重力波特征,为重力波参数化方案的研究提供一定的依据.
4 AIRS观测结果由于NCEP(National Centers for Environmental Prediction,美国国家环境预报中心)资料高度的限制,这里的数值模拟无法得到30 km以上高度的重力波特征.AIRS观测资料可以用于识别20~65 km高度范围内垂直波长大于15 km、水平波长在50~ 1000 km范围内的平行波动(Hoffmann and Alexander,2010). 为了分析更高高度上的平流层重力波特征,这里采用权重函数在30~40 km高度范围内的AIRS通道的观测开展分析.理论上,更高高度上的重力波应由其下方的重力波向上传播所致,因而这里的AIRS观测分析在一定程度上也可以进一步验证数值模式得到的平流层重力波特征.
这里选取了AIRS权重函数在30~40 km高度上的42个通道的数据来进行分析(姚志刚等,2015).图 7(a1,a2)分别为8月2日16时以及8月6日17时AIRS对应于30~40 km观测的亮温扰动值.图 7(b1,b2)分别为8月2日12时以及8月6日15时模式输出的25 km高度上的温度扰动.首先,由两种资料的对比可以看出,在120°E—150°E,15°N—35°N范围内(台风影响区域),均存在明显的半圆弧状波动,这与图 2所示的模式输出结果也具有较好的一致性.尽管目前不能进行同一高度上的对比,但卫星观测结果与模式输出结果在波动形态和波动极值区域上具有较好的一致性,而这些特征在所用的NCEP资料结果(图略)中则没有体现出来.这在一定程度是说明了WRF较好地模拟出了这个台风诱发的平流层重力波特征,同时也说明了AIRS观测的平流层重力波主要由该台风的深对流诱发.其次,由WRF输出的谱分析得到的该时刻25 km高度的 垂直波长为8~12 km,而利用AIRS权重函数在25 km 附近的敏感探测通道也确实未能观测到大气波动,但当波动上传到30~40 km高度范围内时则在AIRS观测数据中存在明显的波动特征.根据理论分析,AIRS的敏感探测波长为15 km以上.因此,两种资料的综合结果不仅表明了在较低平流层高度上的结果是一致的,也表明了30~40 km高度的重力波的垂直波长应大于25 km高度上的垂直波长,这与上文提到的波长随高度增长的理论也是一致的.第三,AIRS观测的30~40 km高度范围内的重力波波列相对于WRF在25 km高度的波列存在向东的位移,这与重力波逆着背景流向东向上传播的特性是一致的.第四,需要注意的是,AIRS观测的是一定高度范围内大气温度的积分量以亮温的形式给出,而WRF输出的是某一高度上的温度场,故亮温扰动强度的量值显著地小于大气温度的扰动值.但从前后两个时刻的扰动强度的变化上看,卫星观测的后一时刻的扰动强度的极正值和极负值约为前一时刻的1.7和1.3倍,而WRF得到的扰动强度的比值为1.6和1.4倍.因此,从重力波扰动强度的变化上看,数值模拟结果与卫星观测结果具有极好的一致性.此外,从AIRS结果中也揭示了台风激发的重力波可传至水平方向上距台风中心1000 km以外的平流层,并且由于AIRS资料具有较高的水平分辨率,可以探测出很多细致的波动.因此,AIRS观测资料可以很好地弥补数值模式输出高度不足这一缺陷,两者之间具有一定的互补性.当然,最佳的融合两种资料去分析提取重力波特征是未来的一项十分重要而困难的研究工作.
 |
图 7 AIRS在2011年8月2日16时(a1)、8月6日17时(a2)30~40 km亮温扰动图以及WRF输出的2011年8月2日12时(b1)、8月6日15时(b2)在25 km高度的温度扰动图 Fig. 7 AIRS brightness temperature perturbation at 30~40 km height at 1600UTC Aug 2(a1) and 1700UTC Aug 6(a2) and WRF temperature perturbation at 25 km height at 1200UTC Aug 2(b1) and 1500UTC Aug 6(b2),2011 |
本文利用新一代中尺度预报模式WRF-ARW(V3.5),对2011年第9号超强台风“梅花”进行了时效为6天的数值模拟,并结合卫星AIRS观测资料对其波动特征进行了分析.主要结果包括:
(1)通过对WRF模式输出的不同高度上的垂直速度场的分析表明,虽然台风在对流层各个方向上都具有诱发重力波的能量,但是在平流层高度上波动呈现出集中于台风中心以东的半圆弧状.此外,平流层波动与对流层雨带在形态、位置以及尺度上具有一定的相似性;
(2)针对对流层与平流层波动形态的差异,进一步对台风影响区域内的风场分析结果表明,平流层向西传的背景风场以及风切变对于重力波垂直上传起到了十分重要的调制作用,使得向西传的波动在上传过程中逐渐被过滤掉,从而揭示了重力波逆着背景流垂直上传的特征;
(3)基于三维傅里叶变换的平流层25 km高度上波动参数特征的分析表明,台风“梅花”在平流层诱发的重力波水平波长中心值达到了1000 km,周期在15~25 h,垂直波长主要在8~12 km,能量传播最强方向为正东方向;
(4)基于AIRS资料的分析结果表明,台风“梅花”在30~40 km高度上也出现了与数值模拟结果一致的半圆弧状扰动,并且可以传播到上千公里以外的平流层,较高的水平分辨率使得其可以探测出一些更细致的波动.此外,两者之间的一致结果也说明了WRF模式能够较好地模拟台风这类强对流诱发平流层重力波的形态、波长、影响范围、强度变化等特征.
最近,Zou等(2015)的研究表明,进一步增加WRF模式的层顶高度并同化平流层卫星探测通道可显著改进热带气旋路径和强度的预报精度.目前,关于台风诱发重力波的机制尚未完全清楚,进一步提高模式分辨率和顶层高度并同化平流层卫星观测资料,对于研究这类重力波的发生、发展和传播机理具有重要的意义.特别是,不同台风诱发的平流层重力波特征具有较大的差异,这种差异可能与背景风场、台风的位置以及发展阶段相关,且一种探测资料只能获取具有一定波长范围的重力波特征.因此,在未来的工作中,我们需要利用数值预报模式并结合不同的卫星观测资料综合分析不同台风的重力波特征及其对台风发生发展的反馈作用.
此外,本文的研究也展示了卫星高光谱红外大气遥感资料在平流层重力波观测上的优势特点及其在重力波研究上的应用潜力.我国风云系列卫星也将装载类似于AIRS的卫星高光谱红外大气垂直探测器.因此,利用AIRS观测资料研究东亚区域的平流层重力波特征也为进一步利用我国自主的风云系列卫星类似载荷开展平流层重力波活动的监测与研究提供启发和借鉴.
致谢 衷心感谢南京信息工程大学陈丹博士在重力波波谱分析方面给予的帮助.感谢两位审稿专家提出的宝贵修改意见.
| [1] | Anthes R A. 1972. Development of asymmetries in a three-dimensional numerical model of the tropical cyclone. Mon. Wea. Rev., 100(6): 461-476. |
| [2] | Beres H J, Joan Alexander M, Holton J R. 2002. Effects of tropospheric wind shear on the spectrum of convectively generated gravity waves. J. Atmos. Sci., 59(11): 1805-1824. |
| [3] | Beres J H, Alexander M J, Holton J R. 2004. A method of specifying the gravity wave spectrum above convection based on latent heating properties and background wind. J. Atmos. Sci., 61(3): 324-337. |
| [4] | Cao X G, Wang H, Liu X B. 2013. Analysis on the turning and forecast of super typhoon Muifa. Torrential Rain and Disasters (in Chinese), 32(2): 151-157. |
| [5] | Chane-Ming F, Roff G, Robert L, et al. 2002. Gravity wave characteristics over Tromelin Island during the passage of cyclone Hudah. Geophys. Res. Lett., 29(6): 18-1-18-4, doi: 10.1029/2001GL013286. |
| [6] | Chen D, Chen Z Y, Lü D R. 2012. Simulation of the stratospheric gravity waves generated by the Typhoon Masta in 2005. Science China Earth Sciences, 55(4): 602-610, doi: 10.1007/s11430-011-4303-1. |
| [7] | Chen D, Chen Z Y, Lü D R. 2013. Spatiotemporal spectrum and momentum flux of the stratospheric gravity waves generated by a typhoon. Science China: Earth Sciences, 56(1): 54-62, doi: 10.1007/s11430-012-4502-4. |
| [8] | Choi H J, Chun H Y, Gong J, et al. 2012. Comparison of gravity wave temperature variances from ray-based spectral parameterization of convective gravity wave drag with AIRS observations. J. Geophys. Res., 117: D05115, doi: 10.1029/2011JD016900. |
| [9] | Chun H Y, Baik J J. 1998. Momentum flux by thermally induced internal gravity waves and its approximation for large-scale models. J. Atmos. Sci., 55(21): 3299-3310. |
| [10] | Dudhia J. 1989. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimension model. J. Atmos. Sci., 46(20): 3077-3107. |
| [11] | Hoffmann L, Alexander M J. 2010. Occurrence frequency of convective gravity waves during the North American thunderstorm season. J. Geophys. Res., 115: D20111, doi: 10.1029/2010JD014401. |
| [12] | Hong S Y, Noh Y, Dudhia J. 2006. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Wea. Rev., 134(9): 2318-2341. |
| [13] | Kain J S. 2004. The Kain-Fritsch convective parameterization: An update. J. Appl. Meteor., 43(1): 170-181. |
| [14] | Kim S Y, Chun H Y, Baik J J. 2005. A numerical study of gravity waves induced by convection associated with Typhoon Rusa. Geophys. Res. Lett., 32: L24816, doi: 10.1029/2005GL024662. |
| [15] | Kim S Y, Chun H Y, Wu D L. 2009. A study on stratospheric gravity waves generated by Typhoon Ewiniar: Numerical simulations and satellite observations. J. Geophys. Res., 114: D22104, doi: 10./2009JD011971. |
| [16] | Kuester M A, Alexander M J, Ray E A. 2008. A model study of gravity waves over Hurricane Humberto (2001). J. Atmos. Sci., 65(10): 3231-3246. |
| [17] | Kurihara Y, Tuleya R E. 1974. Structure of a tropical cyclone developed in a three-dimensional numerical simulation model. J. Atmos. Sci., 31(4): 893-919. |
| [18] | Kurihara Y. 1976. On the development of spiral bands in a tropical cyclone. J. Atmos. Sci., 33(6): 940-958. |
| [19] | Lindzen R S. 1981. Turbulence and stress owing to gravity wave and tidal breakdown. J. Geophys. Res., 86(C10): 9707-9714. |
| [20] | Liu X, Xu J Y. 2006. The nonlinearity interactions of gravity waves and different background winds. Progress in Natural Science (in Chinese), 16(11): 1436-1441. |
| [21] | Mao T, Wang J S, Yang G L, et al. 2010. Effects of typhoon Matsa on ionospheric TEC. Chinese Science Bulletin, 55(8): 712-717. |
| [22] | Mlawer E J, Taubman S J, Brown P D, et al. 1997. Radiative transfer for inhomogeneous atmosphere: RRRTM, a validated correlated-k model for the longwave. J. Geophys. Res., 102 (D14): 16663-16682. |
| [23] | Pfister L, Scott S, Loewenstein M, et al. 1993. Mesoscale disturbances in the tropical stratosphere excited by convection: observations and effects on the stratospheric momentum budget. J. Atmos. Sci., 50(8): 1058-1075. |
| [24] | Song I S, Chun H Y. 2005. Momentum flux spectrum of convectively forced internal gravity waves and its application to gravity wave drag parameterization. PartⅠ: Theory. J. Atmos. Sci., 62(1): 107-124. |
| [25] | Tepper M. 1958. A theoretical model for hurricane radar bands. //Preprints of 7th Weather Radar Conference. Miami. Amer. Meteor. Soc., 56-65. |
| [26] | Vincent R A, Joan Alexander M. 2000. Gravity waves in the tropical lower stratosphere: An observational study of seasonal and interannual variability. J. Geophys. Res., 105(D14): 17971-17982. |
| [27] | Wu D L, Preusse P, Eckermann S D, et al. 2006. Remote sounding of atmospheric gravity waves with satellite limb and nadir techniques. Advances in Space Research, 37(12): 2269-2277. |
| [28] | Xu X D, Zhang S J, Chen L S, et al. 2004. Dynamic characteristics of typhoon vortex spiral wave and its translation: a diagnostic analyses. Chinese J. Geophys. (in Chinese), 47(1): 33-41, doi: 10.3321/j.issn:0001-5733.2004.01.006. |
| [29] | Yao Z G, Zhao Z L, Han Z G. 2015. Stratospheric gravity waves during summer over East Asia derived from AIRS observations. Chinese J. Geophys. (in Chinese), 58(4): 1121-1134, doi: 10.6038/cjg20150403. |
| [30] | Yue J, Hoffmann L, Joan Alexander M. 2013. Simultaneous observations of convective gravity waves from a ground-based airglow imager and the AIRS satellite experiment. J. Geophys. Res., 118(8): 3178-3191, doi: 10.1002/jgrd.50341. |
| [31] | Zou X L, Weng F Z, Tallapragada V, et al. 2015. Satellite data assimilation of upper-level sounding channels in HWRF with two different model tops. J. Meteor. Res., 29(1): 001-027, doi: 10.1007/s13351-015-4108-9. |
| [32] | 曹晓岗, 王慧, 刘晓波. 2013. 超强台风“梅花” (1109号) 的转向原因与预报分析. 暴雨灾害, 32(2): 151-157. |
| [33] | 陈丹, 陈泽宇, 吕达仁. 2011. 台风“麦莎”(Matsa)诱发平流层重力波的数值模拟. 中国科学: 地球科学, 41(1): 1-9. |
| [34] | 陈丹, 陈泽宇, 吕达仁. 2013. 台风重力波的谱结构和动量通量特征分析. 中国科学: 地球科学, 43(5): 874-882. |
| [35] | 刘晓, 徐寄遥. 2006. 重力波与不同背景风场之间的非线性相互作用. 自然科学进展, 16(11): 1436-1441. |
| [36] | 毛田, 王劲松, 杨光林等. 2009. 台风“麦莎”对电离层TEC的影响. 科学通报, 54(24): 3858-3863. |
| [37] | 徐祥德, 张胜军, 陈联寿等. 2004. 台风涡旋螺旋波及其波列传播动力学特征: 诊断分析. 地球物理学报, 47(1): 33-41, doi:10.3321/j.issn:0001-5733.2004.01.006. |
| [38] | 姚志刚, 赵增亮, 韩志刚. 2015. AIRS观测的东亚夏季平流层重力波特征. 地球物理学报, 58(4): 1121-1134, doi: 10.6038/cjg20150403. |
 2015, Vol. 58
2015, Vol. 58


