2. 湖南涉外经济学院信息科学与工程学院, 长沙 410205
2. College of Information Science and Engineering, Hunan International Economics University, Changsha 410205, China
We proposed a new adaptive bidirectional MSD (Mean Square Deviation) threshold method to detect and eliminate gross errors in raw data of EM prospecting. This method sorts raw sample data set at first, and then adopts an iterative or recursive way to separately calculate two MSD values repeatedly for the front and rear part of the sample data set which is separated at the array midpoint. Afterwards, it picks the larger one of the two calculated MSDs to compare with the MSD threshold value. If the picked one is larger than the threshold, then we delete the very one data point at endpoint in corresponding part, otherwise the algorithm finished. In addition, if the size of data sample is less than 3 after deletion, the algorithm finished as well. To test and verify this method, we used lots of real raw data of prospecting sites from two industrial projects; one from a shale gas prospecting project, the other from an oil-gas prospecting project. We try various values as the MSD threshold to obtain satisfactory handled results. Consequently the value between 30 and 90 shows pretty good. Based on experimental data, we compare our method with some traditional methods such as Pauta, Grubbs and Dixon criteria, and Robust Estimation and Median Filtering methods.
In the first experiment case, bad data quality causes the tail part (below 0.03125 Hz) of full 40 frequencies curve to exhibit a sharp peak shape. After handling gross errors by our new method and Pauta, Grubbs and Dixon criteria, the results show that the new method smoothes the sharp peak shape segment well and keeps the rest of the curve almost unchanged, while the Pauta and Dixon criterion methods have no effect to the sharp peak shape segment, actually producing no change for the whole curve. While the Grubbs criterion method smoothes the sharp peak shape of the curve, but also deletes the most of samples (include most of credible samples) while only 2 samples left for every frequency point after processing. So this result is not good for subsequent procedures such as further data processing and interpretation. To go deep into details, compared the raw sample data set of some frequencies below 0.03125 Hz with handled results of our method, we find that the apparent gross error sample points are eliminated correctly and the most credible samples are preserved. In the same case, we tried 4 typical MSD threshold values as 90, 60, 30 and 15, respectively. The results show that the smaller threshold value cannot make the result obviously better below 30, but more suspected sample points are removed. It means the value 30 is pretty good. In the second experiment case, we compare our method with the classical Robust Estimation method. The result shows that the two methods are quite consistent above 0.03125 Hz, both smooth the sharp peak at 48 Hz and keep the rest curve shape almost no change, but apparent difference appears at the tail part below 0.03125 Hz, in which our method is better than the Robust Estimation. Furthermore, if the sample size is small (less than 20) and the proportion of gross error samples is not small or the value of gross error samples is very big, especially those frequencies below 0.03125 Hz, the Robust Estimation method cannot obtain satisfactory results. At the same time, both the Robust Estimation and our method work pretty well at 48 Hz. In the third experiment case, we adopt the two same experiment data samples used at the first and the second cases and use the SMF (Standard Median Filtering) method to handle these data samples and compared the results with our method. The results show that in first example the SMF has no effect on the peak shape at 0.023438 Hz. The reason is that there are three big outliers just at the position of rear endpoint of the sample and SMF can not handle outliers at this point (either head or tail) as an inherent limitation. The second example is better than the first, but not better than our method. Finally, we analyze differences between Median Filtering and our method at the end of section in this case. Besides these three experiment cases, lots of experiments illustrate that our method can eliminate reliably gross errors mixed in EM data, and keep the most credible data as much as possible. By choosing an appropriate MSD threshold value between 30 and 90, we can achieve satisfactory results.
This work suggested a novel method based on the statistical theory. It has some good features such as adaptive optimization, threshold parameterization adaptive for small sample data size and large proportion of gross error sample, being easy to program implementation and low computation cost, high efficiency. The MSD value between 30 and 90 is determined by mass of practice data handling, which be proved appropriate for handling EM prospecting data. Theoretical analysis and experiments show this method has better adaptability and handling results than the classical methods as Pauta, Grubbs and Dixon criteria. Furthermore, in conditions of small sample data size (less than 20), large proportion of gross error and huge values of gross errors, our method is better in method adaptability and can obtain more satisfactory results than Robust Estimation. In other conditions, the handling results of our method and Robust Estimation are quite consistent. Based on experiments and theoretical analysis, in the suitability of the application field, inherent limitation of algorithm and the consistency of parameters of algorithm, our method is also superior to the Median Filtering method.
在电磁法勘探中,接收机接收的电场信号中除了有效信号之外,同时还包含大量干扰信号,有效信号幅值往往在微伏级或毫伏级,而干扰信号特别是工业用电所造成的干扰信号幅度却很大,往往在毫伏级甚至达到伏特级,干扰信号的频率范围也非常宽,从直流到几十赫兹甚至上百兆赫兹范围内都存在(蒋奇云,2010),因此,采集到的电磁勘探原始电场数据中往往混有一些偏离均值较大的粗大误差数据.一般采用在每个测点的各个频率点都进行冗余采集,再将剔除粗大误差后的均值作为测量结果的方法来提高采集数据的可靠性和可信度.与传统的精密测量(如机械工件尺寸测量等)不同,电磁勘探采集到的原始数据值的分布范围要比精密测量大得多;尤其在采集低频信号时(0.1 Hz以下),由于信号周期长,野外勘探采集到的原始数据样本集规模(即样本数量)较小;在某些干扰源较多、干扰频率范围较宽以及干扰信号较强的工区勘探时,数据样本 中常常混有较大比例且偏离度较大的粗大误差数据点.
目前,常见的粗大误差处理方法从原理上大致可分为三类:基于统计学的方法;基于灰度理论的方法;基于其他理论的方法(如小波理论等).其中以基于统计学的方法较多,有经典的粗大误差判别准则(莱伊达准则、格拉布斯准则、狄克逊准则等)的方法(马宏和王金波,2009),也有基于RUBOST估计的稳健统计方法(赵黎明,1992),以及基于其他统计量的判别方法.如刘宗宝等(2012)采用结合莱伊达准则和滑动窗口方法实现粗大误差剔除和数据平滑处理,熊艳艳和吴先球(2010)对比了四种常用粗大误差判别准则,耿素军和余剑(2005)应用格拉布斯准则在智能系统中处理粗大误差,刘志平(2009)应用格拉布斯和狄克逊准则在检测仪表中处理粗大误差,梁暄(2006)和余剑(2003)采用统计估值理论处理粗大误差等.在小样本数据中,王广林和李云峰(2005)、高宁等(2012)采用灰度系统理论进行粗大误差的处理.其他理论方面,高用竹和蔡冬曼(2011)、李登辉和李智(2009)采用基于信息熵的方法判别粗大误差,吴维勇和王英惠(2005)采用小波变换方法去除粗大误差,刘振宇等(2013)采用基于数据拓扑距离的方法进行粗大误差处理.在国外,Carvalho和Bretas(2013)在电力系统控制中采用最大标准化残差健壮性分析来处理加权最小二乘法状态估计中的粗大误差,Bretas等(2011)提出采用一个“创新指数”指标来处理电力系统状态估计中的测量粗大误差,Manescu(2006)在电力系统状态估计中采用修改的松弛方法检测粗大误差,Sproule等(2006)在澳大利亚陆地重力数据库中采用DEM-9S和经局部插值精化处理的布格重力异常进行交叉验证的方法检测粗大误差,Nyrnes等(2005)在油井产量可靠性分析中,采用了一种基于统计测试的方法检测井眼定向测量中的粗大误差,Badria等(2012)采用统计质量控制方法来检测和处理测量数据中的粗大误差.以上方法中,传统的基于统计学的粗大误差处理方法主要适用于测量样本量较大,基本呈正态分布,测量样本值分布范围集中,粗大误差比例小等情况,如传统的静态精密测量,包括机件尺寸等静态物理量状态测量等.由于电磁勘探数据具有数值分布范围较大,测量样本量可能较小(低频段),数据分布不一定呈正态分布等特点.经试验,在采用传统统计方法处理时,数据点被剔除的比例过大,处理结果不理想.
中值滤波作为一种具有稳健特性的非线性滤波方法,在信号处理领域一直以来有着广泛的应用,尤其是在数字图像处理领域有着非常多的基于中值滤波的方法研究和应用(刘丽梅等,2004;索俊祺,2010;王欢和王修晖,2011).在地球物理勘探数据预处理阶段,也经常采用一维中值滤波进行信号去噪(地震法中应用非常广泛).自20世纪90年代起,李承楚(1986)在垂直地震剖面法(VSP)的资料处理中,为了分离上行波和下行波,采用中值滤波方法,并对其理论进行了完整的分析和阐述;刘道安(1989)研究了矢量中值滤波方法,以提高传统中值滤波的处理效率,并在零偏移距VSP资料处理中进行了应用并取得良好效果;在地震资料叠前处理剔除野值和提高信噪比中,徐常练(1992)利用了中值滤波的特点,使计算效率大为提高,数据试验表明,叠前中值滤波在自动剔除野值和不正常道、提高叠前资料的信噪比以及消除面波干扰三个方面都有较好的效果.刘财等(2005)将二维多级中值滤波技术应用于地震数据随机噪声消除,不仅能有效地压制随机噪声,而且在一定程度上削弱了浅层折射干扰.王典(2006)在其博士学位论文中详细研究了中值滤波在地震勘探数字信号处理中的应用.
上述文献中的各种方法一般也是针对其自身领域数据特点所提出,在一定范围内能够获得较好的效果.作者在综合方法原理和电磁勘探数据特点的基础上,提出一种自适应的双向均方差阈值方法实现电磁勘探数据粗大误差处理,经实验验证,此方法能取得良好的处理效果.
2 自适应双向均方差阈值法依据测量理论,测量结果中可能存在系统误差、随机误差和粗大误差(马宏和王金波,2009).对于电磁勘探来说,数据采集设备在使用前需通过一致性标定,因而系统误差基本可控制在能接受的范围内;勘探生产中存在的测量随机误差,一般采用冗余采集并计算均值方式可使其降低到能接受的范围内;而由各种不可预测的地电强干扰等因素造成的粗大误差数据(简称粗差),则必须采取有效的方法进行判别和剔除.
2.1 方法原理勘探采集到的原始数据样本,在干扰较少的情况下,样本分布一般接近正态分布(理论上应服从正态分布),而在干扰源较多,干扰较强的情况下,分布形态往往不规则,不呈近似正态分布.
在将测点原始数据样本排序后,一般靠近两端点位置的数据点偏离均值较大,而位于中点附近的数据点则更接近均值(中位值原理),当数据中存在粗大误差时,一般位于两端位置(极大或极小).
由于干扰因素不同,从几何意义上分析排序后样本从中点分成前后两段的数据分布形态,一般有三种情况(如图 1):中心点对称形态;右侧陡峭形态;左侧陡峭形态.从统计指标量来看,形态较平缓则均方差较小,形态较陡峭则均方差较大;反之,均方差较小则形态较平缓,均方差较大则形态较陡峭. 因此,若要采用迭代的方式判别并剔除样本中的粗 大误差,则每次均应从形态较陡峭一侧进行判别,若符合剔除条件,则删除端点处数据点.遵循上述原则,一般情况下每次迭代剔除的是整个样本中偏离度最大的数据点.在不断迭代处理的过程中,中间点的位置也不断变化,样本分布逐渐向中心点对称形态收敛(自适应优化).进一步地,在样本数量较少的情况下,此方法在统计学原理上仍成立,因此适应于小样本数据处理.使用本方法时,应根据可信样本值分布范围选取一个合适的均方差作为粗大误差的判别阈值(对于电磁勘探数据,阈值范围可在1到90之间,一般情况下取经验值30),阈值越大判别条件越宽松(允许更大的样本离散度),反之则越严格.
 | 图 1 数据样本典型分布形态 (a)中心点对称形态;(b)右侧陡峭形态;(c) 左侧陡峭形态. Fig. 1Typical distribution shape of sample data (a) Center point symmetry shape; (b) Right steep shape; (c) Left steep shape. |
本文提出的自适应双向均方差阈值法先对原始数据样本排序,然后采用迭代(或递归)方式,每次均以中点为界分别计算前后两段数据的均方差,判断并剔除均方差大于阈值的较大一端的端点数据点,在前后两段的均方差值都小于阈值或样本数量小于3时算法结束.算法描述如下:
(1)将含N个数据点的样本数据由小到大排序.
(2)计算样本数据前段末元素位置m1和后段首元素位置m2(公式(1)).为使前后两段具有相关性,需在中点位置相互重叠(N为奇数时重叠一个数据点,为偶数时重叠两个数据点),即m1≥m2.
(3)采用贝塞尔公式(公式(2))分别计算前段[1,m1]和后段[m2,N]的均方差σfront和σrear.
(4)比较得到σlarger=Max(σfront,σrear),将σlarger与均方差阈值σthreshold比较.
(5)若σlarger≤σthreshold,则算法结束;否则转到步骤(6).
(6)若σlarger=σfront 则删除样本的第一个数据点P1,否则删除最后一个数据点PN;样本数量N=N-1.
(7)若样本数量N<3,则算法结束;否则转到步骤(2).
中间点位置计算公式如下:
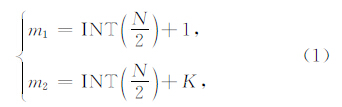
均方差采用贝塞尔公式计算,公式如下:
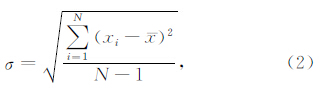

根据前述分析,本算法具有以下特点.
(1)自适应优化
算法在处理过程中每次迭代都只删除位于端点处的一个数据点,删除后样本数量减1,在接下来的一次迭代中,中点位置计算将自动调整前后两段分界点(公式(1)).在循环迭代处理中,算法不断趋向样本数据中分布最集中的一部分(即最可信的部分),样本数据的分布形态也不断趋向中心点对称形态,使得算法具有自适应优化的特点.
(2)阈值参数化控制
算法在处理过程中粗大误差的判断依据是均方差阈值,此阈值是算法从外部接收的控制参数,用于控制判断粗大误差的宽严程度.在实际应用时,根据样本数据值的分布范围选取宽严条件不同的阈值,以获得较好的处理效果.(3)适用于小样本数据
本算法基于统计学原理,因此样本数量越大,处理结果越接近真值.同时,根据均方差计算公式和算法中前后段的分段方式,在仅有3个样本数据点的情况下,仍可分成前后两段计算均方差并进行比较和剔除,最后保留两个数据样本,理论上适用于小样本数据.
(4)适用于误差比例较大样本
根据算法原理和实验验证,本方法在样本中的误差比率较大的情况下,仍能有效地判别和剔除粗大误差数据,而相比较的其他方法均已失效或效果较差.
(5)算法实现简单,处理效率高
算法中采用贝塞尔公式(公式(2))计算均方差,每次迭代时只计算两个均方差值,计算代价较小、效率较高;同时,算法的过程较为简单,容易实现,适用于各种计算能力一般的计算设备.
2.4 阈值选取方法均方差作为一个统计指标量,其大小表示的是样本数据集的离散程度,值越大表明样本数据越分散,越小则越集中,对于测量数据来说,数据分布越集中其质量相对越好.本文算法中使用的均方差阈值作为一个参数传递给算法,其大小直接影响最终的处理结果,是一个关键参数,在使用时须给定一个具体数值,如何确定这个给定的阈值,目前没有通用的计算公式,而是根据应用中样本数据的分布范围由试验得出.
电磁勘探采集到的有效信号幅值往往在微伏级或毫伏级(蒋奇云,2010),反映在数值上为几十到几千之间(实际情况一般为10至3000之间),在此范围之外的数据值一般为干扰信号,实际上,一个勘探测点的某一个频率点的测量样本数据值分布一般会比上述范围更小.经过反复试验,采用按90,75,60,45,30,15,10,5逐步收紧(数值减小)的方式可选取出适合电磁勘探数据预处理的均方差阈值,大多数情况下在30至90范围内总可以选取到适合的阈值(经验值).在实际应用时,一般选取阈值为30进行处理,若处理结果不理想,导致多数频率点的样本数据点剔除比例过大,则可按相反顺序逐步放宽阈值(数值加大)进行试验,反之则可逐步收紧.
2.5 数据质量评价一般情况下,电磁勘探采集到的原始数据均由仪器设备采集,从信号感应到采样量化等过程无人工干预.为保证原始数据的真实性,在进行数据预处理时,只是剔除粗大误差数据点,而不对样本数据值进行任何修改.数据质量的好坏,可从两个方面综合评价.一是按传统的统计学方法,根据各频点数据样本的相对均方误差大小评价.相对均方误差为均方差与算术均值之比的百分比值(公式(4)),一般而言在10%及以下可以接受,5%及以下为良好.二是在对数坐标系中观察测点的频率数值曲线的形态,一般频率曲线形态变化平缓(即曲线较为平滑)表明数据质量相对较好,如图 2中0.03125 Hz及以上频率,反之,若曲线在某些频点位置有明显波折、上下尖峰或呈锯齿状,则相应频点的数据质量不良,如图 2中0.03125 Hz以下频率.
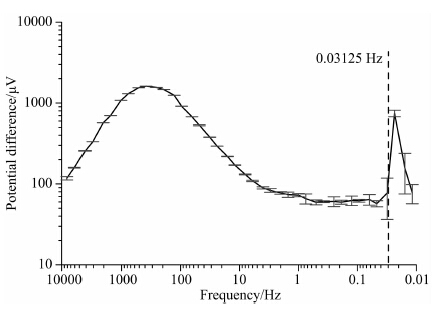 | 图 2 原始数据频率曲线图 Fig. 2 Frequency curve of raw data |
为直观了解数据相对均误差,本文中大部分图中在频率曲线的频率点位置一般绘有一条垂直的浅灰色线条,此线条代表相应频点样本数据的相对均方误差,通常称为误差棒(见图 2),误差棒越长表示 相对均方误差越大,数据质量相对越差,反之则越好.
相对均方误差计算公式如下:

本算法的研究目的,主要为解决电磁勘探生产项目中的数据处理的实际问题,限于篇幅,选取两个项目的两个测点数据进行实验与分析.为简化文字,在本文的余下部分均以“本文方法”指代本文提出的自适应双向均方差域值法.
3.1 本文方法与经典粗大误差处理方法实例处理对比与分析以某页岩气电磁勘探项目中某个测点数据为例进行本文方法与经典粗大误差处理方法的处理结果分析对比研究.
图 2为本实例原始数据的频率曲线图.如图所示,此测点0.03125 Hz以上频段频率曲线较为平滑,且相对均方误差小(多数5%以下,部分10%以下),表明此频段数据质量较好;而0.03125 Hz及以下低频部分曲线呈现明显尖峰形态(尖峰出现在0.023438 Hz频率点处),且各频点相对均方误差较大(见误差棒),数据质量较差.对0.03125 Hz及以下各频率点(共4个)原始样本数据分布情况进行对比分析,如图 3所示,各频率点样本数量范围为8~24个,分布形态为非近似正态分布.
 | 图片说明(本图及以下所有数据样本分布图均参照此说明):1) 各坐标图中左上部均直方图为数据样本分布直方图(样本数量小于5个时无分布直方图);2) 由于各频率点样本数据数量和样本数据值范围可能不同,为了完整显示样本数据,各频率样本坐标系中的X和Y 坐标刻度单位和范围不一定相同. 图 3 0.03125 Hz及以下频率点原始样本分布图(a) 0.03125 Hz;(b) 0.023438 Hz;(c) 0.015625 Hz;(d) 0.0117 Hz. Fig. 3 Raw sample data distribution and histogram of frequencies below 0.03125 Hz |
在实验中,对此测点的所有频点样本数据分别用本文方法和三种经典的基于统计准则的粗差处理方法,即莱伊达、格拉布斯以及狄克逊准则方法,进行处理结果的对比分析.对于三种经典准则方法,莱伊达准则是以测量样本充分大为前提(N10时适用),在样本较小时可靠性不高;当样本较小时格拉布斯准则可靠性最高(当20<N<50时判别效果较 好),最适用于样本中仅混入一个异常值的情况;狄 克逊准则适用于剔除多个异常值,对粗大误差的判别速度快(马宏和王金波,2009).此三种经典准则方法主要适用于传统精密测量数据处理,而应用于电磁勘探数据,则存在许多不适用的情况.首先,电磁勘探数据值的分布范围远远大于精密测量数值范围,若不加以控制,则各频率点的原始样本数据在进行处理时绝大部分样本数据被认为是粗大误差而剔除,处理结果仅能保留很少几个样本点;其次,电磁勘探数据从高频到低频,各个频率范围的数据样本大小不同,一般在高频区间样本大小可到200个,而在最低频的区间,样本大小往往小于10个;其三,勘探数据中粗大误差的比例无法估计,在无干扰或干扰较小的情况下,粗大误差样本比例较小,而在相反的情况下,粗大误差样本比例有时相对较高;最后,电磁勘探数据因强干扰等原因产生的粗大误差数据值可能非常大,正常信号值与误差值可能相差几个数量级.
采用本文方法(阈值=30)和三种经典准则方法处理结果对比如图 4所示,四种方法对0.03125 Hz及以上数据质量较好部分的频率曲线形态基本没有影响,而在0.03125 Hz以下的低频部分,本文方法明显消除了频率曲线的尖峰形态,使频率曲线呈平缓变化形态,同时明显降低了各频点的相对均方误差;莱伊达和狄克逊准则方法基本上对尖峰形态无效,且对相关频率点相对均方误差无改善;从频率曲线形态观察,格拉布斯准则有效地消除了尖峰,同时所有频点(全部40个频率点)的相对均方误差都变得非常小,看似处理效果很好,但从剔除的样本点数量和比例来分析,见表 1,格拉布斯准则处理后每个频率点均只保留了两个数据样本(表 1 未列出的其余各个频率点也都仅只保留了两个数据样本),其余均认为是粗大误差而进行了剔除,而实际情况并非如此,如图 3所示,此例中0.03125 Hz及以下频率范围的每个频率点的有效样本均不止两个,因此格拉布斯准则的条件对电磁勘探数据来说过于严格,导致了样本数据的过度剔除,其结果将影响后续的勘探数据处理和解释.此例中三种经典准则方法的适用前提条件、判别准则条件等是其不能适用于电磁勘探数据处理的根本原因.
 | 图 4 4种方法处理结果对比 (a)本文方法处理结果(阈值=30);(b)莱伊达准则粗大误差处理结果;(c)格拉布斯准则粗大误差处理结果;(d)狄克逊准则粗大误差处理结果. Fig. 4 Results comparison of the 4 methods (a) Our method result (threshold=30);(b) Pauta criterion result; (c) Grubbs criterion result; (d) Dixon criterion result. |
|
|
进一步分析本文方法处理后0.03125 Hz及以下各频点的样本数据,如图 5所示,处理后原始数据样本中离群较大的粗大误差数据点均已有效剔除,结果数据样本分布形态已近似正态分布.
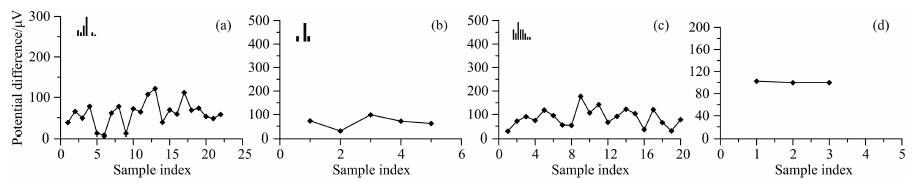 | 图 5 0.03125 Hz及以下频率点样本本文方法处理后数据分布图
(a) 0.03125 Hz;(b) 0.023438 Hz;(c) 0.015625 Hz;(d) 0.0117 Hz. Fig. 5 Result distribution and histogram comparison of frequencies below 0.03125 Hz handled by our method |
为了能够在平滑频率曲线和降低各频率点相对均方误差的情况下尽可能多地保留可信的样本数据,可选取不同宽严程度的均方差阈值进行进一步处理,并对结果进行比较和分析.下面是选取90、60、30和15四个不同的阈值时本文方法处理结果的对比,见图 6,随着阈值的逐步减小,各个频率点的相对均方误差相应变小(相对均方误差与均方差直接相关),频率曲线的整体平滑形态变化不大,在此例中选取阈值为30时即可取得满意的效果,并尽可能多地保留了各频率点的样本数据.
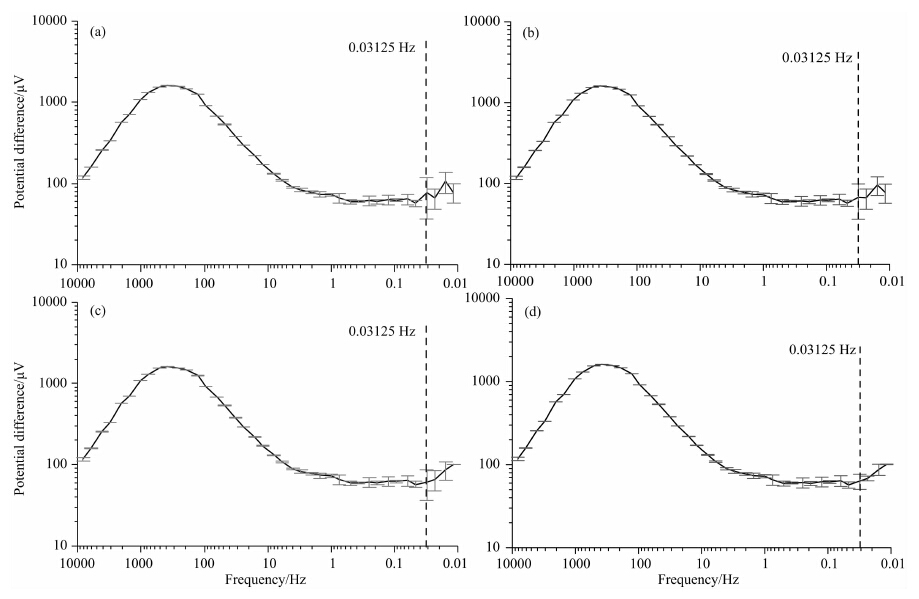 | 图 6 4种不同阈值处理结果曲线形态对比图 (a) 阈值=90;(b) 阈值=60;(c) 阈值=30;(d) 阈值=15. Fig. 6 Results curve shapes comparison of 4 different threshold values (a) Threshold=90;(b) Threshold=60;(c) Threshold=30;(d) Threshold=15. |
以某油气资源电磁法勘探项目中某个测点数据为例,对比原始数据、Robust估计结果以及本文方法的处理结果并进行分析.
图 7a为本测点原始数据采用算术均值计算的频率曲线,由图可见,此测点采集到的数据质量不佳,反映在频率曲线上,除48 Hz的工频干扰形成一个尖峰突起外,0.03125 Hz以下频率由于干扰较大(相对均方误差很大)、样本数量小,频率曲线形态也呈现出明显的尖峰突起.图 7b为原始数据采用Robust估计后的曲线形态,与原始数据对比,首先,消除了48 Hz频率点处由粗大误差造成的尖峰,其次,0.03125 Hz以下频率估计后的曲线形态较原始数据也明显改善,但粗大误差的影响仍未完全消除,仍有较明显的小尖峰存在,处理结果的相对均方误差也明显降低.图 7c为本文方法处理结果数据(采用算术均值计算)的频率曲线形态,除了完全消除 48 Hz频率点处的尖峰外,0.03125 Hz以下频段曲线形态也较Robust估计结果好,完全消除了粗大误差造成的影响,曲线形态更加平滑,能够正确地反映实际信号变化趋势,同时相对均方误差也明显降低.表 2中列出了部分频点的处理结果对比数据,并在图 8和图 9中分别显示了相应频点样本处理前后的数据分布图.
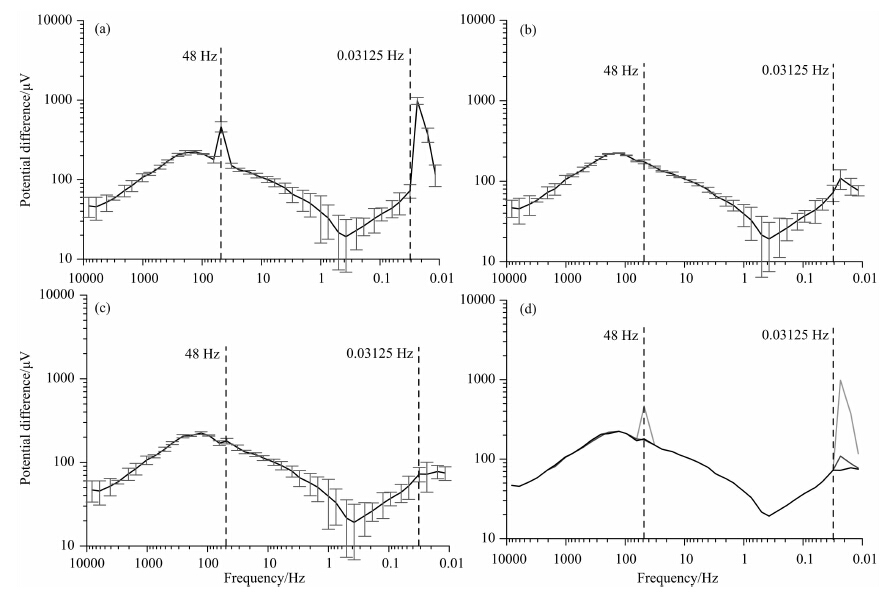 | 图 7 本文方法与Robust估计处理结果对比图 (a) 原始数据算术均值频率曲线;(b) 原始数据Robust估计均值频率曲线;(c) 本文方法处理结果算术均值曲线;(d) 曲线对比(浅灰:原始,深灰:Robust估计,黑:本文方法). Fig. 7 Results comparison of our method and Robust Estimation (a) Raw data frequency curve of arithmetic mean;(b) Raw data frequency curve of Robust Estimation mean;(c) Result data frequency curve of arithmetic mean handled by our method;(d) Curves comparison (light gray: raw, dark gray: Robust Estimation, black: our method). |
|
|
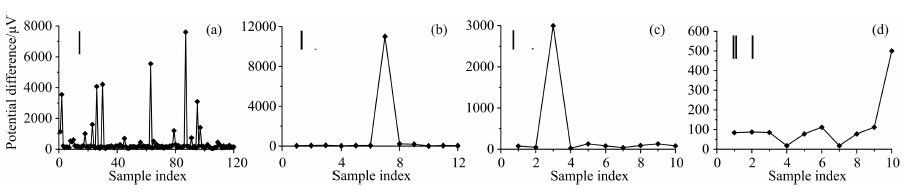 | 图 8 部分频点样本处理前数据分布图 (a) 48 Hz;(b) 0.023438 Hz;(c) 0.015625 Hz;(d) 0.0117 Hz. Fig. 8 Pictures of sample data distribution and histogram of some frequencies of raw data |
 | 图 9 部分频点样本处理后数据分布图 (a) 48 Hz; (b) 0.023438 Hz; (c) 0.015625 Hz; (d) 0.0117 Hz. Fig. 9 Pictures of sample data distribution and histogram comparison of some frequencies handled by our method |
总体而言,在本例中Robust估计和本文方法均较好地改善了原始数据中数据质量较差的大部分频点,只在0.03125 Hz以下频率范围内两种方法的效果有所区别.根据图 8、图 9和表 2分析,首先,全部频率点的数据样本数量分为两类:以48 Hz为代表的频率点,其样本数量较大,一般都有100个以上;以0.03125 Hz以下频率为代表的频率点,样本数量较小,不超过20个.其次,观察处理前后的样本分布直方图(见图 8、图 9),处理后的样本分布形态较原始形态更趋向正态分布.
根据表 2分析,在样本数量较大的频率区间,两种方法处理结果比较接近,处理效果都比较好.而在0.03125 Hz以下频率范围,在样本数量较小,粗大误差数值较大的情况下本文方法的处理结果明显比Robust估计效果更好.
图 10是3.1节实验用例采用本文方法和Robust估计结果的对比图.由图可见,0.023438 Hz频率处的尖峰突起在Robust估计中无法有效消除,据图 3、图 5和表 1分析,0.023438 Hz频率点的样本小(8个),粗大误差比例高(37.5%)且粗大误差数值较大,是Robust估计方法无效的原因.
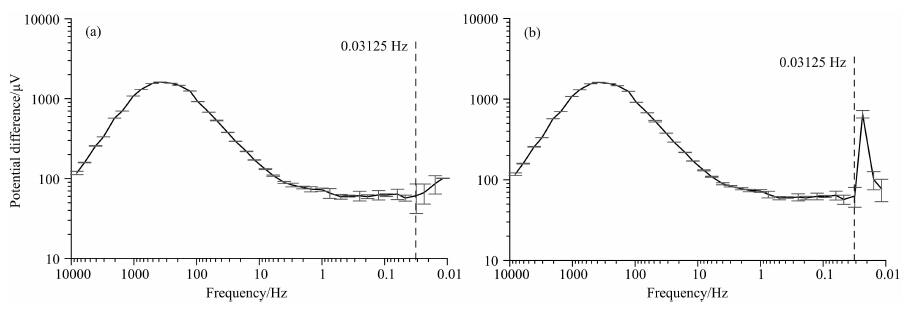 | 图 10 本文方法与Robust估计处理结果对比 (a) 本文方法处理结果曲线;(b) Robust估计结果曲线. Fig. 10 Results comparison of our method and Robust Estimation (a) Our method result curve;(b) Robust Estimation result curve. |
据实验结果和分析,本文方法在数据样本较大,粗大误差较小的情况下与Robust估计的结果比较一致,均有较好的处理效果;在样本数量较小,粗大误差比例较高或误差数值很大等情况下,Robust估计往往无法消除粗大误差的影响,而本文方法仍能取得较好的处理效果,较Robust估计有更好的适应性.
3.3 本文方法与中值滤波方法实例处理对比与分析中值滤波作为一种非线性滤波方法,广泛应用于信号处理领域,是一种有效的经典滤波抑噪方法.为使本文方法能够更全面地与各种传统经典方法进 行对比,本节采用标准中值滤波方法(SMF,St and ard Median Filtering)对3.1和3.2节的实例数据进行处理,并将结果与本文方法进行对比分析.
图 11是3.1节实验用例采用标准中值滤波方法设置窗口大小为3、5、7和9的处理结果.
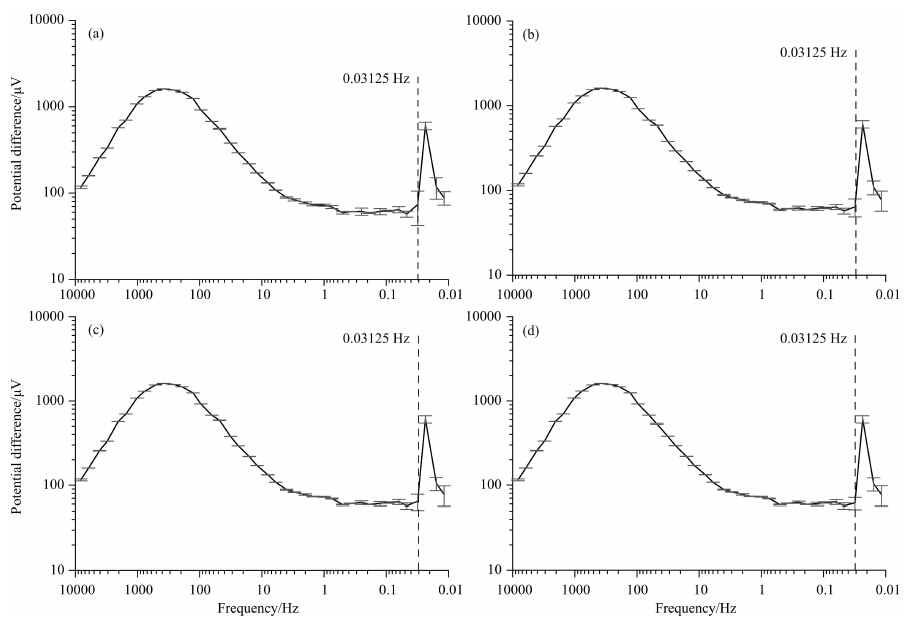 | 图 11 采用4种不同滤波窗口大小结果对比 (a) 滤波窗口大小=3;(b) 滤波窗口大小=5;(c) 滤波窗口大小=7;(d) 滤波窗口大小=9. Fig. 11 Results comparison with 4 different filter window size (a) Filter window size =3;(b) Filter window size =5;(c) Filter window size =7;(d) Filter window size =9. |
如图所示,4种不同大小的滤波窗口不能消除 0.03125 Hz以下频率段曲线的尖峰(位于0.023438 Hz 频率点位置),对0.03125 Hz以上频率的正常曲线形态基本无影响.实际实验时进行多次迭代滤波或是选择更大的滤波窗口效果也没有改善(未附图).进一步查看不同滤波窗口大小处理后0.03125 Hz及以下各个频率点的样本数据分布情况,如图 12(WS表示滤滤窗口大小,即Window Size的缩写).
图 12与原始数据样本分布图(图 3)对比.首先,位于样本中非端点位置出现的异常离群值,SMF方法能够在不同大小的窗口条件下有效抑制,如图 12中的子图(e)、(g)、(i)、(k)、(m)、(o),在窗口大小为5、7、9时,均能有效抑制0.03125 Hz和0.015625 Hz频率点中的异常离群值.其次,对于0.023438 Hz频率点,其样本分布中有多个连续异常值(3个异常大值)位于样本末端,此时受到SMF方法自身特性约束(刘道安,1987),即使改变滤波窗口大小也无法有效消除异常,如图 12中的子图(b)、(f)、(j)、(n);同样地,对于0.0117 Hz频率点,样本中有一个异常值(异常小值)位于样本末端,在不同大小滤波窗口条件下也无法有效消除,如图 12中的子图(d)、(h)、(l)、(p).图 12与本文方法处理结果样本数据分布图(图 5)对比,本文方法能够在不修改样本数据值的情况下,有效判别并剔除离群异常值,保留分布最为集中的可信的样本结果.
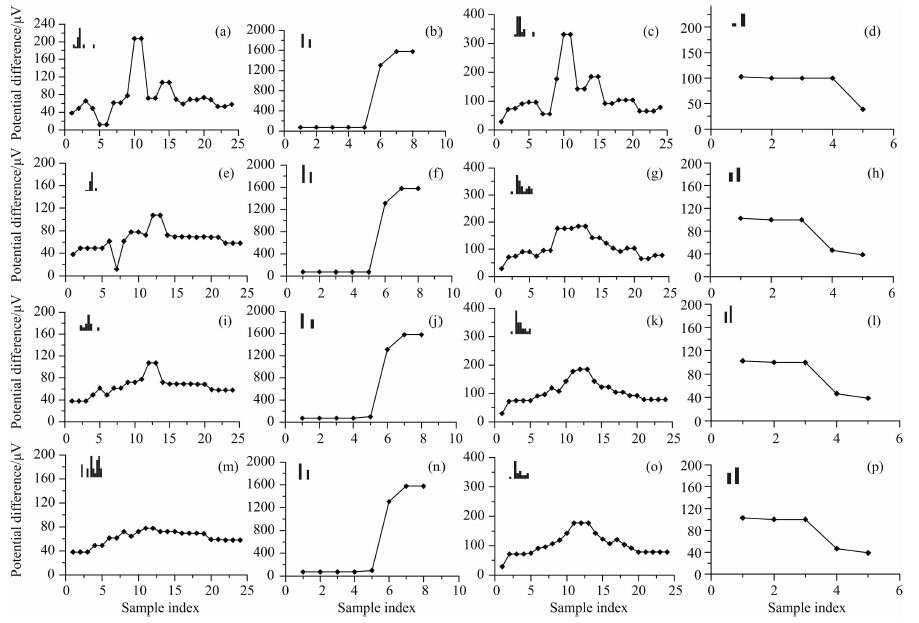 | 图 12 0.03125 Hz及以下频率点样本标准中值滤波处理后数据分布图 (a) 0.03125 Hz, WS=3; (b) 0.023438 Hz, WS=3; (c) 0.015625 Hz, WS=3; (d) 0.0117 Hz, WS=3; (e) 0.03125 Hz, WS=5; (f) 0.023438 Hz, WS=5; (g) 0.015625 Hz, WS=5; (h) 0.0117 Hz, WS=5; (i) 0.03125 Hz, WS=7; (j) 0.023438 Hz, WS=7; (k) 0.015625 Hz, WS=7; (l) 0.0117 Hz, WS=7; (m) 0.03125 Hz, WS=9; (n) 0.023438 Hz, WS=9; (o) 0.015625 Hz, WS=9; (p) 0.0117 Hz, WS=9. Fig. 12 Result distribution and histogram comparison of frequencies below 0.03125 Hz handled by SMF |
图 13是3.2节实验用例采用标准中值滤波方法设置窗口大小为3、5、7和9的处理结果.
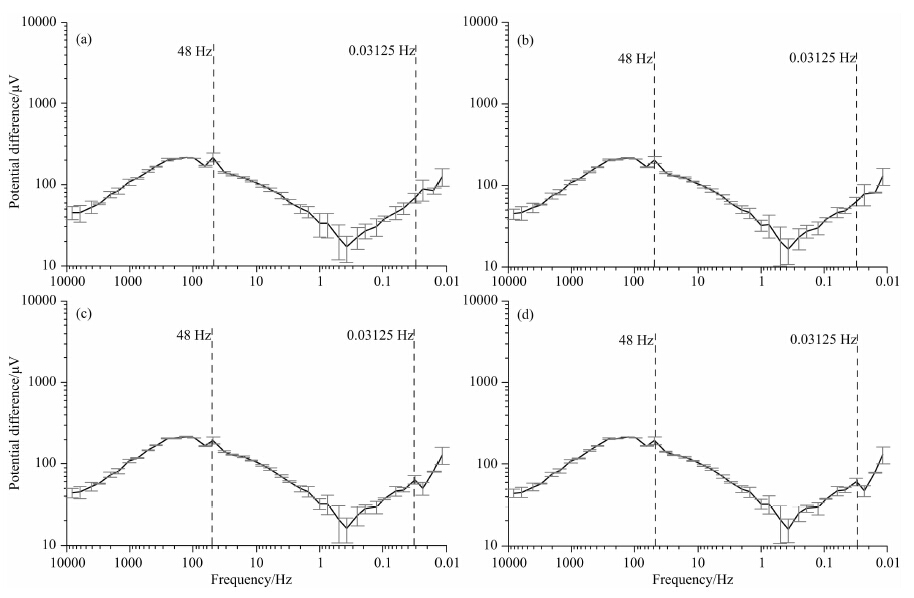 | 图 13 采用4种不同滤波窗口大小结果对比 (a) 滤波窗口大小=3;(b) 滤波窗口大小=5;(c) 滤波窗口大小=7;(d) 滤波窗口大小=9. Fig. 13 Results comparison with 4 different filter window size (a) Filter window size =3;(b) Filter window size =5;(c) Filter window size =7;(d) Filter window size =9. |
与图 7a对比.首先,位于48 Hz处的曲线尖峰形态已明显抑制(尚未完全消除),且随滤波窗口的加大而更趋平滑;其次,位于0.03125 Hz以下频率段的尖峰形态也明显抑制,其中,0.023438 Hz频率 点随着滤波窗口的变大,其值越来越小,而0.0117 Hz 频率点对窗口大小变化无反应,进而造成0.023438 Hz频率点处的曲线形态随滤波窗口变大而逐渐向下突出.进一步查看不同滤波窗口大小处理后上述频率点样本数据分布情况,如图 14.
图 14与原始数据样本分布图(图 8)对比,同图 12类似,位于样本中非端点位置出现的异常离群 值,SMF方法能够在不同大小的窗口条件下有效抑制,且随滤波窗口变大,可滤除的脉冲干扰宽度相应增大,但对于样本中有异常值位于样本两端时,无法有效消除,如图 14中的子图(d)、(h)、(l)、(p).图 14与本文方法处理结果样本数据分布图(图 9)对比,本文方法能够在不修改样本数据值的情况下,有效判别并剔除离群异常值,保留分布最为集中的可信的样本结果.
 | 图 14 部分频点样本处理后数据分布图 (a) 48 Hz, WS=3; (b) 0.023438 Hz, WS=3; (c) 0.015625 Hz, WS=3; (d) 0.0117 Hz, WS=3; (e) 48 Hz, WS=5; (f)0.023438 Hz, WS=5; (g)0.015625 Hz, WS=5; (h)0.0117 Hz, WS=7; (i)48 Hz, WS=7; (j)0.023438 Hz, WS=7; (k)0.015625 Hz, WS=7; (l) 0.0117 Hz, WS=7;(m) 48 Hz, WS=9;(n) 0.023438 Hz, WS=9; (o) 0.015625 Hz, WS=9; (p) 0.0117 Hz, WS=9. Fig. 14 Sample data distribution and histogram comparison of some frequencies handled by SMF |
图 15为3.1和3.2节的SMF滤波处理结果与本文方法处理结果的频率曲线形态对比.如图所示,本文方法处理结果的曲线形态在此两例中要比SMF滤波结果更好.
 | 图 15 两个样例处理结果频率曲线对比(黑:本文方法,灰:SMF中值滤波) (a) 样例1处理结果对比;(b) 样例2处理结果对比. Fig. 15 Results comparison of the 2 examples (Black: our method, Gray: SMF method) (a) Comparison of example 1 results; (b) Comparison of example 2 results. |
从方法理论基础和上述实验分析处理结果来看,本文方法与中值滤波方法的主要区别在于:
(1)方法原理和应用领域不同:中值滤波方法是一种非线性低通滤波方法,在处理过程中,除能够抑制和消除随机噪声、脉冲干扰外,对正常信号的值也会产生影响,即除修改异常值外,也会修改一些正常的样本值,常常用于时间域(一维信号滤波)或空间域(二维空间信号滤波,如数字图像处理)连续采样信号的滤波处理;本文方法是一种基于统计原理,对多次观测得到的测量值样本进行粗大误差的判别与剔除方法,一般用于随机变量样本中判别并剔除离群异常值,而对正常样本点不做任何修改,一般不用于时间域或空间域的连续采样信号处理(剔除异常点后会造成连续采样信号间断缺失).
(2)算法局限性:标准中值滤波算法(SMF)自身存在一个局限,即对于首末任意一端出现异常值(一个或多个)时无法对其进行有效处理(由算法定义决定);本文方法不存在此局限性,即方法与样本异常数据点的位置无关.
(3)算法参数确定:中值滤波窗口大小的选择要根据信号中连续异常值的宽度(即干扰脉冲宽度)确定,一般需要根据人工观察数据来确定选用的窗口大小以获得满意的处理结果,可滤除的脉冲宽度应小于L/2(L为滤波窗口大小)(刘道安,1989);本文方法由均方差阈值决定对离群值的容忍度,可由试验了解应用领域的测量数值分布范围,从而在相同应用领域中可确定较为通用和一致的阈值.
(4)迭代处理:中值滤波处理在不改变窗口大小的情况下可多次迭代处理;本文方法在不缩小阈值的情况下迭代操作无效,即一次处理的结果和N次迭代处理的结果一样.
4 结论(1)本文以统计学理论为基础,提出了一种粗大误差处理的新方法,其具有自适应优化、参数化控制、适应小样本及大误差比例数据以及算法实现简单和处理效率高等特点.
(2)根据电磁勘探采集到的电场数据的特点,提出均方差阈值选取方法,并由试验得出:在30至90范围内选取均方差阈值(经验值),在作者所处理的电磁勘探频率范围为0.01 Hz至8192 Hz的电场数据时取得较为满意的效果.
(3)经理论分析和实验验证,在电磁勘探数据的处理应用中,在经典的粗误差判别准则方法,包括莱伊达、格拉布斯和狄克逊准则,不适用的情况下,本 文方法具有更好的适应性,并能取得满意的处理效果.
(4)经实例数据对比实验分析,在数据样本数量较大(大于100)时,本文方法与Robust估计方法的结果非常一致,但在样本数量较小(小于20),粗差比例较大或误差数值很大的情况下,本文方法的适应性要比Robust估计更强一些,能够取得更好的处理结果.
(5)经实例数据对比实验分析,在应用领域的合理性、算法自身局限性、算法参数通用性等方面,本文方法比中值滤波更显合理,得到的处理结果也更令人满意.
5 建议与展望均方差是衡量数据样本集分散程度的一个常用统计指标.实际上,数据样本集的分散程度指标还可通过其他方式计算和表达,如绝对残差和、线性拟合直线斜率等.本方法选取均方差作为计算和判别指标主要是考虑到此指标的常用性和通用性,在将来的应用中,也可考虑选择其他的统计指标替代均方差,以获得更好的计算效率或适应更多的应用场合.
此方法的原理具有一般性,理论上具备在其他领域推广应用的基础.若在其他领域应用时,需根据测量数据可信值的分布范围,经试验后选取与之匹配的阈值,可期待取得良好的处理效果.此方法目前主要应用于数据采集后的预处理阶段,若要在采集过程中应用此方法实时检测和剔除粗大误差,也可通过软件编程方式进行实验和实现.此方法处理时首先需要对原始数据集进行排序,处理完成后结果数据已非原序,若需要在处理完成后恢复为原序,作者已通过程序数据结构设计的方法予以了解决(另有文章发表).
致谢 本文在撰写过程中,得到了导师何继善院士的指导,何老师以杖朝之年在百忙之中仔细审阅初稿,并指出了文章中一些不够严谨的地方,经作者多次修改最终完成了本文的撰写工作,在此非常感谢何老师对学生的指导.同时,李帝铨老师在论文的修改过程给予了帮助,在此表示感谢.
| [1] | Bretas N G, Bretas A S, Piereti S A. 2011. Innovation concept for measurement gross error detection and identification in power system state estimation. IET Generation, Transmission & Distribution, 5(6): 603-608. |
| [2] | Carvalho B, Bretas N. 2013. Analysis of the largest normalized residual test robustness for measurements gross errors processing in the WLS state estimator. Systemics, Cybernetics and Informatics, 11(7): 1-6. |
| [3] | Elgazooli B A G, Ibrahim A M. 2012. Multiple gross errors detection in surveying measurements using statistical quality control. Journal of Science and Technology, 13: 36-47. |
| [4] | Gao N, Cui X M, Gao C Y. 2012. Grey envelope detection method for multidimensional gross error of deformation data. Journal of Geodesy and Geodynamics (in Chinese), 32(6): 99-102. |
| [5] | Gao Y Z, Cai D M. 2011. Non-statistics judging method for gross error in measurement. Science & Technology Information (in Chinese), (30): 59, doi: 10.3969/j.issn.1672-3791.2011.30.047. |
| [6] | Geng S J, Yu J. 2005. Gross error processing in intelligent measuring system. Journal of Electrical & Electronic Education (in Chinese), 27(3): 37-39, doi: 10.3969/j.issn.1008-0686.2005.03.010. |
| [7] | Jiang Q Y. 2010. Study on the key technology of wide field electromagnetic sounding instrument [Ph. D. thesis] (in Chinese). Changsha: Central South University. |
| [8] | Li C C. 1986. The basic theory of median filtering. Oil Geophysical Prospecting (in Chinese), 21(4): 372-379. |
| [9] | Li D H, Li Z. 2009. Processing of gross error in small samples based on measurement information theory. Mechanical Engineering & Automation (in Chinese), (6): 115-117. |
| [10] | Liang X. 2006. A processing method of gross error in intelligent electronic measuring system. Journal of Shanxi Normal University (Natural Science Edition) (in Chinese), 20(4): 46-49, doi: 10.3969/j.issn.1009-4490.2006.04.012. |
| [11] | Liu C, Wang D, Liu Y, et al. 2005. Preliminary application study on of using 2D multi-level median filtering technology on eliminating random noise. Oil Geophysical Prospecting (in Chinese), 40(2): 163-167. |
| [12] | Liu D A. 1989. Vector median filtering and its application. Oil Geophysical Prospecting (in Chinese), 24(4): 460-468. |
| [13] | Liu L M, Sun Y R, Li L. 2004. Research of median filter technology. Journal of Yunnan Normal University (in Chinese), 24(1): 23-27. |
| [14] | Liu Z B, Gao S Q, Du J Q. 2012. An algorithm for measurement data eliminating gross error and smoothing (in Chinese). // Proceedings of the 31st Chinese Control Conference.7582-7587. |
| [15] | Liu Z P. 2009. Treatment analysis of rough error about measurement instrument. Electronic Measurement Technology (in Chinese), 32(11): 55-57, doi: 10.3969/j.issn.1002-7300.2009.11.016. |
| [16] | Liu Z Y, Zhou S H, Tan J R, et al. 2013. Multiple parameters correlation analysis and prediction method of product performance based on multi-criteria modification. Journal of Mechanical Engineering (in Chinese), 49(15): 105-114. |
| [17] | Ma H, Wang J B. 2009. Instrument Precision Theory (in Chinese). Beijing: Beihang University Press, 80-87. |
| [18] | Manescu L G. 2006. Detection of gross error by modified relaxation state estimation in power system. Annals of the University of Craiova, Electrical Engineering Series, 30: 275-281. |
| [19] | Nyrnes E, Torkildsen T, Nahavandchi H. 2005. Detection of gross errors in wellbore directional surveying for petroleum production with emphasis on reliability analyses. Kart Og Plan, 65(2): 1-19. |
| [20] | Sproule D M, Featherstone W E, Kirby J F. 2006. Localised gross-error detection in the Australian land gravity database. Exploration Geophysics, 37(2): 175-179. |
| [21] | Suo J Q. 2010. A new improved filtering algorithm based on median filter algorithm [Master's thesis] (in Chinese). Beijing: Beijing University of Posts and Telecommunications. |
| [22] | Wang D. 2006. Several new digital techniques and its application in seismic prospecting [Ph. D. thesis] (in Chinese). Changchun: Jilin University. |
| [23] | Wang G L, Li Y F. 2005. An effective method for distinguishing the gross error. Journal of Computation and Measurement Technology (in Chinese), 25(6): 15-17, doi: 10.3969/j.issn.1674-5795.2005.06.005. |
| [24] | Wang H, Wang X H. 2011. An improved adaptive median filter based on noise detection. Journal of China University of Metrology (in Chinese), 22(4): 382-385. |
| [25] | Wu W Y, Wang Y H. 2005. Method for eliminating the measured bulky errors based on wavelet transformation. Journal of Machine Design (in Chinese), 22(6): 61-62, doi: 10.3969/j.issn.1001-2354.2005.06.023. |
| [26] | Xiong Y Y, Wu X Q. 2010. The generalizing application of four judging criterions for gross errors. Physical Experiment of College (in Chinese), 23(1): 66-68, doi: 10.3969/j.issn.1007-2934.2010.01.022. |
| [27] | Xu C L. 1992. Prestack mid-value filtering. Oil Geophysical Prospecting (in Chinese), 27(3): 387-396. |
| [28] | Yu J. 2003. Gross error processing technology in intelligence measuring system with high precision. Journal of Test and Measurement Technology (in Chinese), 17(3): 258-261, doi: 10.3969/j.issn.1671-7449.2003.03.017. |
| [29] | Zhao L M. 1992. Robust statistics method applied in sample mixed with outliers. Environment Surveillance Management and Technology (in Chinese), 4(4): 58-59. |
| [30] | 高宁, 崔希民, 高彩云. 2012. 变形数据多维粗差的灰包络线探测方法. 大地测量与地球动力学, 32(6): 99-102. |
| [31] | 高用竹, 蔡冬曼. 2011. 测量中粗大误差的非统计判定方法. 科技资讯, (30): 59, doi: 10.3969/j.issn.1672-3791.2011.30.047. |
| [32] | 蒋奇云. 2010. 广域电磁测深仪关键技术研究[博士论文]. 长沙: 中南大学. |
| [33] | 李承楚. 1986. 关于中值滤波的理论基础. 石油地球物理勘探, 21(4): 372-379. |
| [34] | 李登辉, 李智. 2009. 基于测量信息论的小样本粗大误差处理研究. 机械工程与自动化, (6): 115-117. |
| [35] | 梁暄. 2006. 一种智能电子测量系统中粗大误差的处理方法. 山西师范大学学报(自然科学版), 20(4): 46-49, doi: 10.3969/j.issn.1009-4490.2006.04.012. |
| [36] | 刘财, 王典, 刘洋等. 2005. 二维多级中值滤波技术在随机噪声消除中的应用初探. 石油地球物理勘探, 40(2): 163-167. |
| [37] | 刘道安. 1989. 矢量中值滤波及其应用. 石油地球物理勘探, 24(4): 460-468. |
| [38] | 刘丽梅, 孙玉荣, 李莉. 2004. 中值滤波技术发展研究. 云南师范大学学报, 24(1): 23-27. |
| [39] | 刘宗宝, 高世桥, 杜井庆. 2012. 测量数据剔除粗大误差与平滑处理的一种算法. // 第三十一届中国控制会议论文集. 7582-7587. |
| [40] | 刘志平. 2009. 检测仪表中粗大误差的剔除分析. 电子测量技术, 32(11): 55-57, doi: 10.3969/j.issn.1002-7300.2009.11.016. |
| [41] | 刘振宇, 周思杭, 谭建荣等. 2013. 基于多准则修正的产品性能多参数关联分析与预测方法. 机械工程学报, 49(15): 105-114. |
| [42] | 马宏, 王金波. 2009. 仪器精度理论. 北京: 北京航空航天大学出版社, 80-87. |
| [43] | 索俊祺. 2010. 一种新的基于中值滤波的优化滤波算法[硕士论文]. 北京: 北京邮电大学. |
| [44] | 王典. 2006. 地震勘探几种数字新技术及其应用[博士论文]. 长春: 吉林大学. |
| [45] | 王广林, 李云峰. 2005. 一种有效的粗大误差判别方法. 计测技术, 25(6): 15-17, doi: 10.3969/j.issn.1674-5795.2005.06.005. |
| [46] | 王欢, 王修晖. 2011. 基于阈值判断的自适应中值滤波算法. 中国计量学院学报, 22(4): 382-385. |
| [47] | 吴维勇, 王英惠. 2005. 基于小波变换的粗大误差去除算法. 机械 设计, 22(6): 61-62, doi: 10.3969/j.issn.1001-2354.2005.06.023. |
| [48] | 熊艳艳, 吴先球. 2010. 粗大误差四种判别准则的比较和应用. 大学物理实验, 23(1): 66-68, doi: 10.3969/j.issn.1007-2934.2010.01.022. |
| [49] | 耿素军, 余剑. 2005. 智能测量系统中粗大误差的处理. 电气电子教学学报, 27(3): 37-39, doi: 10.3969/j.issn.1008-0686.2005.03.010. |
| [50] | 徐常练. 1992. 叠前中值滤波. 石油地球物理勘探, 27(3): 387-396. |
| [51] | 余剑. 2003. 高精度智能测量系统中粗大误差的处理技术. 测试技术学报, 17(3): 258-261, doi: 10.3969/j.issn.1671-7449.2003.03.017. |
| [52] | 赵黎明. 1992. 稳健统计法在含离群值样本中的应用. 环境监测管理与技术, 4(4): 58-59. |
 2015, Vol. 58
2015, Vol. 58


