2. 国土资源部应用地球物理综合解释理论开放实验室—波动理论与成像技术实验室, 长春 130026;
3. 东方地球物理公司物探技术研究中心, 河北涿州 072751;
4. 重庆市地质矿产勘查开发局208水文地质工程地质队, 重庆 408300
2. Laboratory for Integrated Geophysical Interpretation Theory of the Ministry for Land and Resources of China-Laboratory for Wave Theory and Imaging Technology, Changchun 130026, China;
3. Research Center of BGP, Zhuozhou Hebei 072751, China;
4. Chongqing Bureau of Geology and Minerals Exploration 208 Hydrogeological & Engineering Geology Brigade, Chongqing 408300, China
地震波走时是描述地震波运动学特征的一个很重要的物理参数,其刻画了地震波由震源点激发后到达地下介质空间中各个位置坐标点所需耗消的走时,而该走时和地下介质的速度参数的分布情况密切相关,所以地震波走时计算方法常常被应用于走时反演、层析成像、偏移成像、速度分析等一些重要的地震数据处理技术中.地震波走时计算的精度、效率、稳定性等性质直接影响着这些地震数据处理的效果和效率(Sun,1998,1999,2000,2004;井西利等,2007;瞿辰等,2007),同时考虑到三维地震勘探正在全面大范围展开的大背景,所以对三维地震波走时计算进行研究具有很重要的理论意义和实际价值.
在走时计算方面,目前采用的主要方法有两点射线追踪法(Julian and Gubbins,1977)、最短路径射线追踪法(Moser,1991;张美根等,2006)、波前构建法(Vinje et al.,1993)、走时插值法(Asakawa and Kawanaka,1993;Wang and Ma,1999)、有限差分法(Vidale,1988;Sethian and Popovici,1999;Sun et al.,2011)、辛几何算法(秦孟兆和陈景波,2000;高亮等,2000)等.其中,两点射线追踪法在早期天然地震数据处理中起着非常重要的作用,但在现代三维地震数据处理中其计算效率相对较低.最短路径射线追踪法具有不错的走时计算精度,但由于其需要设置很多网格线上的计算节点,所以在求解三维问题时其需要耗费相对更大的计算和存储成本.波前构建法能同时计算走时和射线路径,并且其计算精度也相对不错,不过在三维算法时,其中的网格定位、插值问题等都相对非常复杂.实际上,走时插值法和有限差分法是目前被广泛采用的三维走时算法,其中有限差分法具有计算效率高、局部走时算法简洁等优势,但其计算精度有限,而具有更高计算精度的高阶有限差分需要花费相对更多的计算成本.走时插值法具有不错的计算精度,但是其算法的整体实现策略的效率相对有限差分法低很多.因此,本文将采用走时插值法作为局部走时算法,而在整体实现策略上采用有限差分算法中的快速算法.
目前,三维走时插值法主要采用B样条插值法(张东等,2013)、双线性插值法(李培明等,2013;刘锋等,2012;梅胜全等,2010;张东等,2009)等算法.在双线插值法中,有两方面关键算法.一方面是局部走时算法,其包括计算公式和局部计算策略等技术环节;另一方面是算法的整体实现策略,也即算法的整体实现步骤.在局部走时算法方面,目前普遍认为双线性插值法求解极小值的方程为一个超越方程,无法求出解析解(其可能解分布在一条双曲线上),所以一些学者分别采用网格界面剖分法(张东等,2009)、快速插值法(李培明等,2013;梅胜全等,2010)、最速下降法(刘锋等,2012)来获得一个约束条件下接近于真实解的一个近似解.而在走时计算的整体实现步骤方面,目前普遍采用“向前处理”的按行列扫描计算(张东等,2009)、最短路径射线追踪算法的实现步骤(李培明等,2013;梅胜全等,2010)等.针对以上两个方面的关键技术,笔者充分利用平面波双线性假设的结论,推导出了双线性法求解极小值超越方程的解析计算公式,同时构造性地证明了该解析计算公式的正确性和相对应的地震波传播的物理规律.此外,笔者还借鉴快速推进法中的迎风差分格式的构建思想,提出了迎风双线性插值的局部走时计算的实现策略,并以快速推进法中的窄带技术(这是一种满足地震波传播基本规律的、计算效率高且灵活的波前扩展算法)作为算法的整体实现策略.最后的精度分析和计算实例表明了本文算法的正确性和在面对复杂介质时的稳定性和有效性.
2 算法的描述为了获得一种精度高且兼顾效率的三维走时计算方法,本文将提出一种快速推进迎风双线性插值法的三维地震波走时算法.如图 1所示,这是一种网格算法,和以往基于网格的双线插值法、有限差分法、最短路径追踪法等类似,该算法主要包括三个方面的核心内容:局部计算公式、局部实现策略以及整体实现策略.
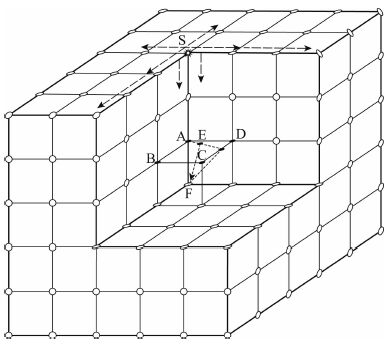 | 图 1 算法的描述 Fig. 1 The description of the algorithm |
如图 1所示,局部计算公式的建立可描述为如下问题:在计算的某一个时刻一个平面上的点A、B、C、D的走时值已知,且该平面内的走时值为双线性分布,则如何构建计算与该平面邻近的网格节点F的走时值的计算公式;局部实现策略则可以描述为如下问题:在计算过程中,与走时值待求的F点相邻近的、类似于平面ABCD的、走时值已知且分布满足双线性分布的平面可能会有很多种情况,而在不同情况时应该分别采用怎样对应的不同的处理方法;最后,整体实现策略可以描述为如下问题:从源点S处给定的初始条件出发,应该采用怎样的实现步骤或过程来逐次地计算整个计算空间内所有网格节点的走时值.
与如上描述的三个问题相对应,这实际上涉及到算法的局部计算公式、算法的局部实现策略、算法的整体实现策略,所以接下来本文将分别详细阐述这三方面问题.最后,还将通过算法的精度分析和计算实例来验证算法的精度、正确性和有效性.
3 算法的局部计算公式:双线性插值解析公式为了计算三维地震波走时,首先需要推导建立局部走时计算公式.如上所述,局部走时计算公式的推导可描述为:如图 2所示,设点A、B、C、D的走时值已知,分别为: tA、tB、tC、tD; 正方体网格的网格间距为h;假设平面ABCD上的走时值为双线性分布;求F点的走时值 tF 的计算公式.
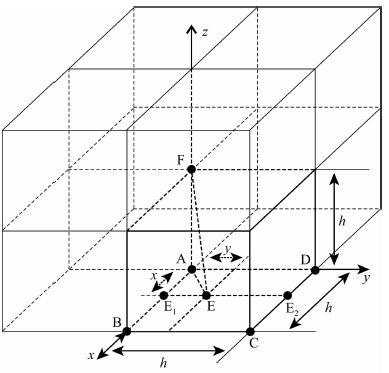 | 图 2 算法的局部计算公式:双线性插值公式 Fig. 2 The local computation formulas of algorithm: the bilinear interpolation formulas |
为了推导计算 tF的公式,首先以点A为坐标原点,向量AB方向为 x 轴正方向,向量AD方向为 y 轴正方向,向量AF方向为 z 轴正方向,建立局部笛卡尔坐标系,则有点A、B、C、D、F的坐标分别为A(0,0,0),B(h,0,0),C(h,h,0),D(0,h,0),F(0,0,h);其次,假定到达F点的射线经过了走时值分布为已知的平面ABCD内的任意一点E,设E点的坐标为 E(x,y,0),因为E点被限定位于平面ABCD内,则有 0≤x≤h,0≤y≤h. 过E点作平行于 y 轴的直线,该直线与线段AB、CD分别相交于E1和E2点,则点E1、E2的坐标分别为 E1(x,0,0)、E2(x,h,0).
根据平面ABCD上的走时值为双线性分布的假设,线段AB、CD及E1E2上的走时值均为线性分布,则有
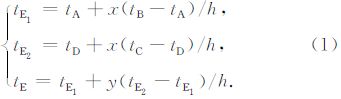
对上述(1)式进行整理可得

其中
k1=(tB-tA)/h,k2=(tD-tA)/h,
k3=(tA+tC-tB-tC)/h2.
设在局部正方体网格单元内地震波传播速度为均匀,并基于上述到达F点的射线经过平面ABCD内的 E(x,y,0)点的假定,可得

其中 s 为当前正方体网格单元内的地震波传播速度的倒数(即慢度).将式(2)代入(3)中,则有
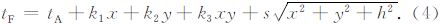
根据Fermat原理,只要确定能使得(4)式取最小值的 E(x,y,0)点的位置,即可获得计算 tF 的公式,所以对(4)式 tF 分别关于变量 x,y 求偏导数,并令该偏导数为零,即

分析方程组(5)可知:只要求出该方程组的解,即可获得 E(x,y,0)点的位置坐标,然后再将其带回到(4)式即可获得计算 tF 的公式.但是,一些研究已表明方程组(5)实际上是一个超越方程组,无法求出相应的解析解(其可能解分布在一条双曲线上),所以一些学者分别采用网格界面剖分法(张东等,2009)、快速插值法(李培明等,2013;梅胜全等,2010)、最速下降法(刘锋等,2012)来获得一个约束条件下接近于真实解的一个近似解.
与以往的双线插值法的近似处理不同,在此笔者将充分利用双线性假设的结论,来获取方程组(5)的精确解析解,并构造性地证明计算 tF 的公式的正确性以及其背后满足的地震波传播波的物理事实.根据走时插值法的提出者Asakawa的线性假设(Asakawa and Kawanaka,1993),实际上即是平面波的假设,其阐述的是如果当前传播的为平面波,则该波传播经过的二维空间中的走时分布在二维空间中的任意一条网格线上均为线性,而在三维空间中的一个平面上的走时分布则均为双线性.同样基于平面波的假设,并假定在局部的相对较小的一个网格单元内地震波的传播速度为匀速.如图 3所示,则无论从那个方向(假定箭头方向为平面波的任意一个传播方向)途经平面ABCD均有 tD-tA=tC-tB,因为如图 3所示,设该平面波与平面ABCD相交于如图 3所示的一系列平行的虚线,其中经过点A、B、C、D的虚线分别位于平面波 tA、tB、tC、tD 时刻的波前上,因为这些波前是相互平行的,并且网格四边形ABCD为一正方形,所以必有 tA 时刻的波前传到 tD 时刻花费的走时等于 tB 时刻的波前传到 tC 时刻花费的走时,也即是 tD-tA=tC-tB.
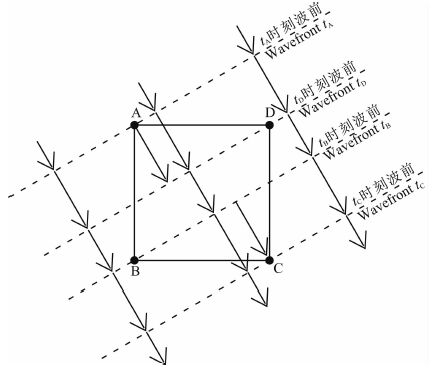 | 图 3 平面波假设分析 Fig. 3 The analysis of plane wave assumption |
基于上述双线性假设,即平面波假设的进一步结论 tD-tA=tC-tB,可以得出 k3=0. 将该结论带回到(5)式中,则(5)可简化为
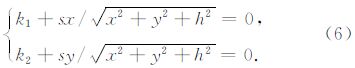
再分析(6)式,若在 k1、k2 均不为零的情况下,则用下式除以上式再整理有: y=k2x/k1,即方程组(6)的解实际上是位于一条直线上(而并非一条双曲线上),并且将该直线代回方程组(6)中的任意一个方程,均可以获得解析的 x、y 的解.不过要获得各种情况下的方程组(6)的解,还得分情况讨论 k1、k2 取不同值时,方程组(6)的解的情况:
① k1=0且k2=0 时
此时,将 k1、k2 代回方程组(6)可得: x=y=0,再将该结论代回(4)式中可得计算 tF 的公式为

② k1=0 且 k2<0 时
在此种情况下,将 k1=0 代入方程组(6)可得 x=0,再将该结论代回方程组(6)中可将其简化为
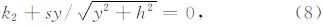
融入 0≤y≤h 的限定条件,求解(8)式可得

其中 Δt=tD-tA,且需满足: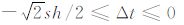 (此是基于 0≤y≤h 的限定条件).综合 x=0 的结论,可知E点的坐标为
(此是基于 0≤y≤h 的限定条件).综合 x=0 的结论,可知E点的坐标为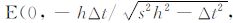 (,0),再 将其代入(4)式中即可获得此种情况下计算 tF 的公式:
(,0),再 将其代入(4)式中即可获得此种情况下计算 tF 的公式:
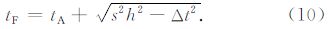
③ k2=0且k1<0 时
这种情况与情况②相似,不同之处仅在于交换了变量 x与y 的角色,所以同理情况②的推导过程可得:
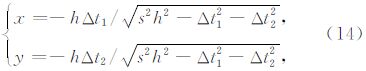
其中: Δt=tB-tA,且需满足: 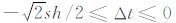 (此是基于 0≤x≤h 的限定条件).同时E点的坐 标为
(此是基于 0≤x≤h 的限定条件).同时E点的坐 标为 ,计算 tF 的公式为:
,计算 tF 的公式为:

④ k1<0且k2<0
这种情况下,直接求解方程组(6),即将上述结论

代入方程组(6)的上式,并融入 0≤x≤h、0≤y≤h 的限定条件,则可得方程(6)的解:
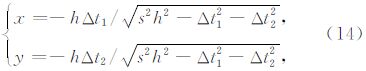
其中,Δt1=tB-tA、Δt2=tD-tA,且需满足: 0≤Δt 2 1+Δt 2 2≤2s2h2/3(此是基于 0≤x≤h、0≤y≤h 的限定条件).将(14)式代回(5)式中,即可获得计算 tF 的公式:

同时,此时E点的坐标为: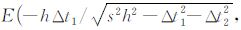
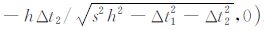 .
.
⑤ k1>0 或 k2>0
这种情况下,因为上述将E点限定于平面ABCD内的限定条件有 0≤x≤h、0≤y≤h,所以很容易分析出,此时方程组(6)无解.这种无解的情况表面上表明:上述计算公式可能出现不稳定的情况.不过,这种所谓的不稳定的情况,在将上述算法 融入一定的局部实现策略和算法的整体实现策略 后,是不可能出现的,关于该问题将在后续内容中阐述.
经过以上的推导,实际上已经获得了当 k1、k2 取不同值的情况时,点 E(x,y,0)的位置坐标和tF 的计算公式.如图 4所示,下面将构造性地证明这些公式的正确性,以及它们对应的不同情况下的地震波传播的物理事实.
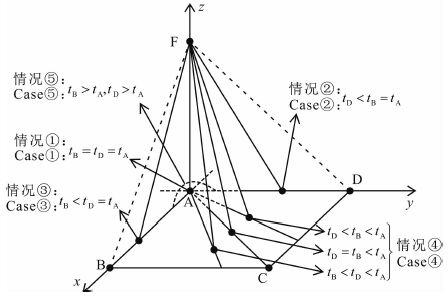 | 图 4 双线性插值公式的分析 Fig. 4 The analysis of bilinear interpolation formulas |
上述情况①:当 k1=0且k2=0 时,即有 tB=tA,tD=tA,也即tA=tB=tD,该式对应的物理事实为点A、B、D位于地震波传播过程中的同一个等时面上.此外,根据不在同一条直线上的三点确定一个平面的数学事实和上述基于的平面波假设,则有与A、B、D点位于同一平面上的C点也位于该等时面上,所以可以进一步得出 tA=tB=tC=tD,也即平面ABCD为平面波的一个等时面.同时,根据局部笛卡尔坐标系可知,直线AF与平面ABCD垂直,再根据射线路径和等时面相互垂直的物理规律,可以得出在这种情况下平面波沿着 z 轴正方向传播,而经过平面ABCD到达F点的射线与平面ABCD相交于A点,所以此时自然有: x=y=0,tF=tA+sh,也就是说上述情况①得的方程组(6)的解和tF 的计算公式符合在这种情况下平面波的传播规律,即是正确的.
上述情况②:当 k1=0 且 k2<0 时,即有 tB=tA,tD<tA,此时再根据双线性假设,因为 tB=tA,所以平面ABCD上的走时分布沿 x 方向没有变化,而仅沿着 y 方向有变化,所以此时的插值问题实际上已简化为二维插值问题,而E点则被固定到距F更近的线段AD上,即有 x=0. 此外,基于二维空 间中Asakawa提出的走时线性插值法同样可以获得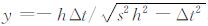 、
、 ,其中 Δt=tD-tA. 再分析 tF 的计算公式,实际上其可以变形为(tA-tF)/h 2+(tA-tD)/h 2=s2,该方程实际上是二维Eikonal方程
,其中 Δt=tD-tA. 再分析 tF 的计算公式,实际上其可以变形为(tA-tF)/h 2+(tA-tD)/h 2=s2,该方程实际上是二维Eikonal方程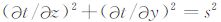 在网格上以A点为中心的差分离散方程,也就是说此处得到的 tF 的计算公式,在局部上满足Eikonal方程,所以其是正确的.同时上述
在网格上以A点为中心的差分离散方程,也就是说此处得到的 tF 的计算公式,在局部上满足Eikonal方程,所以其是正确的.同时上述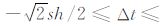 的限定条件还能保证 tF 的计算公式不会出现负数开平方的不稳定情况.
的限定条件还能保证 tF 的计算公式不会出现负数开平方的不稳定情况.
上述情况③:当 k2=0且k1<0 时,此时的情况与情况②是类似的,也可以简化为一个二维插值问题,不同之处仅在于坐标方向 x与y 交换了角色,所以在此不再重复阐述.
上述情况④:当 k1<0且k2<0 时,即有 tB<tA,tD<tA,在这种情况下插值问题才真真变为一个三维双线性插值问题,在此条件下方程组(6)有解.求解该方程组即可获得E点的坐标为 x=-hΔt1/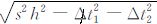 ,
,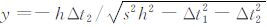 ,同时将它们代回(5)式得到 tF 的计算公式: tF=tA+
,同时将它们代回(5)式得到 tF 的计算公式: tF=tA+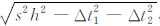 ,其中 Δt1=tB-tA、Δt2=tD-tA. 同样其可以变形为(tA-tF)/h 2+(tA-tD)/h 2+(tA-tB)/h 2=s2,该方程实际上是三维Eikonal方程
,其中 Δt1=tB-tA、Δt2=tD-tA. 同样其可以变形为(tA-tF)/h 2+(tA-tD)/h 2+(tA-tB)/h 2=s2,该方程实际上是三维Eikonal方程
 在网格上以A点为中心的差分离散方程,也就是说此处得出的 tF 的计算公式在局部上是满足Eikonal方程的,所以其是正确的.此外,再仔细分析E点的坐标可得: y=kx,其中 k=Δt2/Δt1,也就是说,实际上E点是位于坐标平面 xAy 内的一条直线上,该直线的斜率为 k.k 的取值实际上和已知条件 tA、tB、tD 的取值情况有关: k=Δt2/Δt1=(tD-tA)/(tB-tA). 如图 4所示,tD<tB时有k>1,此时直线途径ACD半区域,也即E点位于走时分布较小(因为双线假设和tD<tB)的区域.这实际上与Fermat原理和地震波传播的基本规律是相符合的,即地震波总是从走时值相对更小的区域传向下一个区域.而当 tB<tD 时有 k<1,此时有如上同样的结论.最后当 tB=tD 时,则 k=1,此时E点位于正方形ABCD的对角线AC上.综上 所述,在情况④下得出的E点的坐标位置是满足地震波的传播规律和Fermat原理的,tF 的计算公式在局部上满足Eikonal方程.同时 0≤Δt12+Δt22≤2s2h2/3 的限定条件,还能保证 tF 的计算公式不会出现负数开平方的不稳定情况.
在网格上以A点为中心的差分离散方程,也就是说此处得出的 tF 的计算公式在局部上是满足Eikonal方程的,所以其是正确的.此外,再仔细分析E点的坐标可得: y=kx,其中 k=Δt2/Δt1,也就是说,实际上E点是位于坐标平面 xAy 内的一条直线上,该直线的斜率为 k.k 的取值实际上和已知条件 tA、tB、tD 的取值情况有关: k=Δt2/Δt1=(tD-tA)/(tB-tA). 如图 4所示,tD<tB时有k>1,此时直线途径ACD半区域,也即E点位于走时分布较小(因为双线假设和tD<tB)的区域.这实际上与Fermat原理和地震波传播的基本规律是相符合的,即地震波总是从走时值相对更小的区域传向下一个区域.而当 tB<tD 时有 k<1,此时有如上同样的结论.最后当 tB=tD 时,则 k=1,此时E点位于正方形ABCD的对角线AC上.综上 所述,在情况④下得出的E点的坐标位置是满足地震波的传播规律和Fermat原理的,tF 的计算公式在局部上满足Eikonal方程.同时 0≤Δt12+Δt22≤2s2h2/3 的限定条件,还能保证 tF 的计算公式不会出现负数开平方的不稳定情况.
上述情况⑤:当 k1>0或k2>0 时,即有 tB>tA,tD>tA,此时上述的结论为无解.实际上,再回顾方程组(6),此时并非方程组(6)无解,只是解的情况为 x<0,y<0,即E点不在平面ABCD内.实际上,为了公式推导的方便和局部网格计算的限定,将E点限定于走时值已知的平面ABCD内,而在该限定条件下 x<0,y<0 的解不能满足该限定条件,所以致使方程组(6)无解.事实上,x<0,y<0 的解的情况说明:在这种情况下E点位于其他的邻近的网格单元内.同时 tA<tB、tA<tD,再加上双线性假设,暗含了其他相邻的网格单元上的分布的走时值会比网格单元ABCD上的更小.而根据Fermat原理,此时计算 tF 的公式则应该通过其他网格单元上推导获得,也即在计算时应该采用其他网格单元进行计算.该问题实际上引伸出了局部走时计算策略的问题:如图 5所示,在进行三维局部走时计算时,包围被算点F周围的类似于ABCD的网格单元实际上有24个,从几何的角度讲,到达F点的射线必与用于封闭F点的类似于ABCD的24个网格单元中的一个相交,而该交点正是我们上述需要求解的E点.当然要是在24个网格单元中逐次搜寻计算E点,必定是一种繁琐且计算效率低下的算法.为了解决该问题,此处借鉴迎风差分的思想,提出了一种非常简洁的迎风双线性插值的局部实现策略,下面将详细阐述该策略.
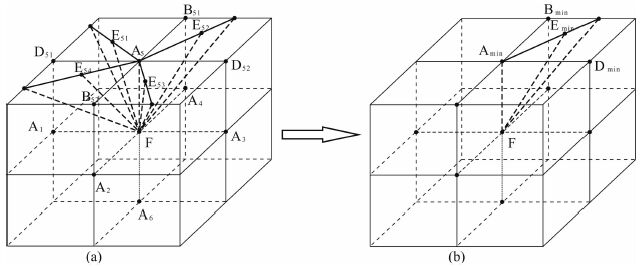 | 图 5 算法的局部实现策略:迎风双线性插值 Fig. 5 The local implementation strategy of algorithm: the upwind bilinear interpolation |
如图 5所示,在三维走时计算的某一时刻,当前需要计算的是点F的走时值 tF. 如图 2所示,上述推导了网格单元ABCD走时分布为已知的情况下点F的走时值 tF 的计算公式.但实际上,在被算点F周围的24个类似于ABCD的网格单元中,走时分布为已知的网格单元可能有很多个,那么究竟应该 采用那个网格单元作为已知条件是合理的和稳定的?
在此,引入迎风差分的基本思想(Sethian and Popovici,1999),该思想是指地震波总是从地震波走时值分布更小的区域向走时值未知的区域传播,而在局部数值计算实现时就应该迎着走时值分布更小的区域去做差分代替微分的近似.迎风差分格式的基本思想实际上是Huygens原理和Fermat原理的综合利用,主要体现在其隐含的将被算点周围的走时值最小的网格节点当作子震源点,也正因为此迎风差分格式具有无条件稳定性.同样借鉴该思想,在此提出迎风双线性插值法,该方法的核心借用迎风差分格式选取最小邻近走时点的方法,选取被算点周围的最小走时分布网格单元,然后再采用类似于图 2所示的推导的公式进行局部走时计算.总体上讲,实际就是要构建相应的迎风双线性插值公式.
如图 5a所示的局部正方体网格,以点F为中心的大正方体的六个面分别由以A1、A2、A3、A4、A5、A6为中心的4个类似于图 2中的ABCD的网格单元组成,这样就总共有24个类似于ABCD的网格单元.在当前计算点F的走时值 tF 的时刻,这24个网格单元上的26个网格节点的走时值可能为已知,可能为未知.由后续将阐述的算法的整体实现策略的初始化步骤(详见后续阐述内容的“算法的整体实现步骤:快速推进法”部分)可知,若网格节点的走时值为未知(即没有被计算出来),其值为固定的一个非常大的数(这个数为人为规定的,其值远大于所有网格节点最终可能算出的走时值),若网格节点的走时值被计算完成,其值即为最终的走时计算结果.在一般情况下,当前被算点F周围的26个网格节点的走时值为一部分被计算完成,一部分未开始计算(如图 6a所示).而在被计算完成的部分里面,先完成的走时值一定是小于后完成的走时值(该结论由后续内容的窄带技术的阐述可知),也就是说与点F邻近的26个网格节点均有一个走时值,而用于计算 tF 的网格单元的走时分布应为最小.具体挑选最小走时分布区域的方法为:①确定与点F直接相邻的6个网格节点的走时值最小的网格节点Amin,其中有 tAmin=min(tA1,tA2,tA3,tA4,tA5,tA6); ②在以Amin为中心的平面上分别确定其他两个方向上的最小走时网格节点Bmin,Dmin,若设Amin=A5则分别有 tBmin=min(tB51,tB52),tDmin=min(tD51,tD52); ③Amin,Bmin,Dmin所在的网格单元即为最终的类似于公式推导过程中的网格单元ABCD,与该网格单元相对应,tF 的计算公式相应地变为
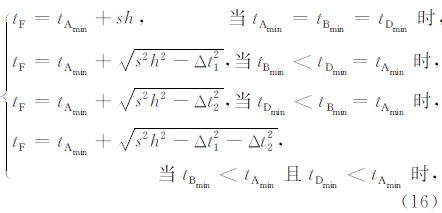
其中 Δt1=tBmin-tAmin,Δt2=tDmin-tAmin.
 | 图 6 算法的整体实现策略:窄带技术 Fig. 6 The global implementation strategy of algorithm: the narrow band technique |
公式(16)即为最终的迎风双线性插值公式,与常规的双线性插值公式相比,该公式实际上是一种优化的公式.该公式隐含着一个优化的局部实现策略,而该优化的局部实现策略将Huygens原理和Fermat原理融入到算法的局部计算过程中,使得算法是在满足地震波传播的基本规律的基础上实现的.与迎风差分格式类似,此处的迎风双线性插值法也具有无条件稳定性.
5 算法的整体实现策略:窄带技术上述内容分别建立了算法的局部走时计算公式和局部实现策略,实际上要想完成整个计算区域的地震波走时计算,还需要拟定一个算法的整体实现步骤,即算法的整体实现策略.算法的整体实现策略往往决定着算法的稳定性和计算效率.基于对计算效率、无条件稳定性、对迎风双线性插值的适应性等因素的综合考虑,在此引入快速推进法中的窄带技术(Sethian and Popovici,1999)作为算法的整体实现策略.
如图 6b所示,窄带技术的核心思想是采用一个包含当前所有波前点的窄带来近似模拟地震波前,通过窄带的扩展演化来模拟地震波前的传播过程,
其充分考虑了地震波前传播过程中的熵守恒理论,同时此处因为迎风差分思想的融入,所以窄带技术具有无条件稳定性.窄带技术在实现过程中将计算空间中的网格节点分为三种类型:完成点,其走时计算已经完成的点,在图 6b中用黑色填充的点表示;窄带点,当前窄带内的点,也即近似波前上的网格节点,在图 6b中用灰色填充的点表示;远离点,窄带扩展还未到达的点,也即还未进行走时计算的网格节点,在图 6b中用白色填充的点表示.
窄带技术的实现过程可以分为初始化和扩展计算两个部分.在初始化时,震源点为唯一的完成点,其走时值为零;与震源点直接相邻的正方体网格单元内的网格节点为初始窄带点,它们构成初始窄带,即初始波前,它们的走时值通过局部的解析公式求取;其它所有剩下的计算空间中的网格节点为远离点,其初始值设置为一个相对很大的数(远大于最终可能计算出来的最大的走时值即可,这主要是为了实现上述迎风双线性插值对最小走时分布区域的选定而设定的,这也是为什么此处的初始值不设为0的原因).
扩展计算的步骤为:①通过比较找出窄带内走 时值最小的窄带点作为子震源点,并将其类型由窄带点改为完成点;②对子震源直接邻近的6个网格节点的类型进行判断,如果其类型为远离点则采用公式(16)计算它的走时值,并将其类型由远离点改为窄带点;如果其类型为窄带点则再次计算它的走时值,并与其原来的走时值比较,较小者被保留;如果其类型为完成点则不对其作任何处理;③判断窄带内的窄带点是否还存在,是,则跳回步骤①重复循环计算,否则,计算结束.
上述窄带技术的实现过程,与常规快速推进法中的窄带技术的不同之处仅在于局部扩展计算采用的计算公式不一样,常规快速推进法采用的是有限差分公式,而此处采用的是双线性插值公式.由于将迎风差分的基本思想融入到了此处的双线性插值公式中,提出了迎风双线性插值法,所以此处的局部计算公式和整体实现策略的窄带技术是完全兼容的.不过此处的迎风线性插值法和有限差分法在计算精度和效率方面却有很大程度的差别,所以下面将对算法进行精度和效率分析.
6 算法的精度和效率分析 6.1 均匀介质模型为了验证本文算法的计算精度和效率,选用一阶精度有限差分法作对比分析.对比分析时,采用的模型为三维均匀介质模型,模型大小为1.0 km×1.0 km×1.0 km,计算时采用的网格间距分别为 20.0、10.0、5.0 m,震源点置于(0.5,0.5,0.0 km)点处.如图 7a所示,误差分析时分别提取三维模型的三个剖面:Z=0.0 km(图 7a的左图)、Y=0.5 km(图 7a 的中图)、X-Y=0.0 km(图 7a的右图)上的计算结果.
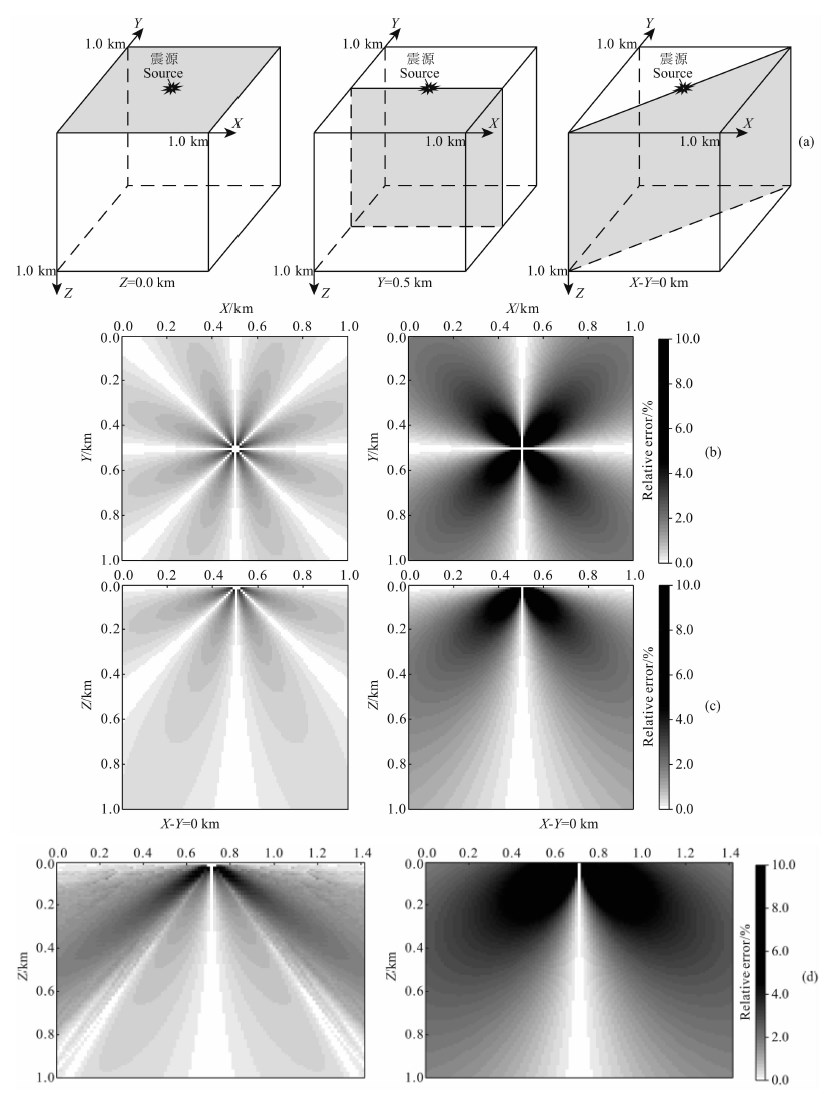 | 图 7
算法的精度和效率分析 (a)三维均匀介质模型的三个剖面:Z=0.0 km(左)、Y=0.5 km(中)、X-Y=0.0 km(右); (b)Z=0.0 km剖面上本文方法(左)与一阶精度有限差分法(右)的精度对比; (c)Y=0.5 km剖面上本文方法(左)与一阶精度有限差分法(右)的精度对比; (d)X-Y=0.0 km剖面上本文 方法(左)与一阶精度有限差分法(右)的精度对比. Fig. 7 The analysis of computational accuracy and efficiency for our method (a) The three sections of the 3D homogeneous model: Z=0.0 km (Left)、Y=0.5 km (Middle)、X-Y=0.0 km (Right); (b) The accuracy comparison between the method purposed in this paper (Left) and the 1st order finite-difference method (Right) in the section of Z=0.0 km; (c) The accuracy comparison between the method purposed in this paper (Left) and the 1st order finite-difference method (Right) in the section of Y=0.5 km; (d) The accuracy comparison between the method purposed in this paper (Left) and the 1st order finite-difference method (Right) in the section of X-Y=0.0 km. |
图 7b、图 7c、图 7d分别给出了当网格间距取 10.0 m时,剖面Z=0.0 km、Y=0.5 km、X-Y=0.0 km上,本文方法与一阶精度有限差分法的误差对比.分析这些误差分布图表明,在均匀介质中本文方法能获得正确的计算结果,并且本文方法具有很好的计算精度,其精度要远高于一阶精度有限差分法.
表 1给出了均匀介质中取不同网格间距时,一阶精度有限差分法和本文算法在剖面Z=0.0 km、Y=0.5 km、X-Y=0.0 km上计算结果的平均相对误差和整个模型计算的CPU耗时的对比,分析表 1可以发现:①两种方法的计算精度均受网格间距的影响,网格间距越小其计算精度越高;②当采用相同网格间距时,在所有剖面上本文的算法均有着比一阶精度有限差分法更高的计算精度;③本文算法比一阶精度有限差分法的计算效率高很多.通过仔细分析两种算法实现过程可得出促使本文算法计算效率更高的主要原因是:在进行第5节“算法的整体实现策略”中阐述的步骤②的各网格节点走时的更新迭代计算时,本文算法精度更高,其更易快速获取收敛于精确解附近的计算结果,所以其大幅度减少了更新重复计算的次数,进而大幅提高了计算效率.
|
|
表 1 均匀介质中本文方法与一阶精度有限差分法的精度和效率对比 Table 1 Comparing the accuracy and CPU time of our method with the 1st finite-difference method in homogeneous media |
为了分析地下速度不连续界面对走时计算的影响程度,将如图 7a所示的均匀介质模型改为一个两层的水平层状介质模型,其中分界面的深度为0.5 km,上下两层地震波传播速度分别为1500.0 m·s-1、1000.0 m·s-1,其他模型参数和计算参数与图 7a所示的均匀介质模型完全相同.表 2给出了层状介质中取不同网格间距时,一阶精度有限差分法和本 文算法在剖面Z=0.0 km、Y=0.5 km、X-Y=0.0 km 上计算结果的平均相对误差和整个模型计算的CPU耗时的对比,对比分析表 2和表 1可以发现,算法在如上采用的层状介质模型中的计算精度略高于均匀介质模型,而计算效率大体略低于均匀介质模型,但总体上两者只有细微的数值差别.该计算结果表明,无论采用一阶精度有限差分法,还是采用本文算法进行走时计算,地下速度不连续界面对走时计算的影响程度很小.此外,基于该结论,在此不再重复显示水平层状介质模型对应的与如 图 7b—d类似的剖面上的误差分布,因为它们基本上与图 7b—d相同,仅有极细微的差别.
|
|
表 2 层状介质中本文方法与一阶精度有限差分法的精度和效率对比 Table 2 Comparing the accuracy and CPU time of our method with the 1st finite-difference method in layered media |
为了验证本文算法在面对复杂介质时的稳定性和有效性,引入一个由二维Marmousi模型生成的三维模型,该模型地下介质分布非常复杂.如图 8a 所示,模型的尺度为3.83 km×3.83 km×1.21 km,计算时采用的网格间距为Δx=Δy=Δz=10.0 m,震源置于(0.0,0.0,0.0 km)处.图 8b—e分别给出了Z=0.0 km、Y=0.0 km、X=0.0 km、X-Y=0.0 km这4个剖面上的地震波走时值的等时线分布,从这4个图可以看出,本文算法在面对地下复杂介质分布时,能够有效地、无条件稳定地获得符合地震波传播规律的计算结果.
 | 图 8
三维复杂介质模型中地震波走时计算结果 (a)三维复杂介质速度模型; (b)Z=0.0 km剖面上的走时分布; (c)Y=0.0 km剖面上的走时分布; (d)X=0.0 km剖面上的走时分布; (e)X-Y=0.0 km剖面上的走时分布. Fig. 8 The traveltime computational results in the 3D complex model (a) The 3D complex velocity model; (b) The traveltime contours are superimposed on the section Z=0.0 km; (c) The traveltime contours are superimposed on the section Y=0.0 km; (d) The traveltime contours are superimposed on the section X=0.0 km; (e) The traveltime contours are superimposed on the section X-Y=0.0 km. |
在此需要特别提出的是,Z=0.0 km剖面上的计算结果.如图 8a和图 8b所示,Z=0.0 km剖面上的地震波传播速度的分布实际上是均匀的,即均匀介质.按照地震波传播规律,在均匀介质中地震波走时的等时线应该为一系列的同心圆弧,但是图 8b显示的计算结果并非如此,难道是本文算法在面对复杂介质时出现了不适应和错误吗?其实并非如此!实际上,其更能说明本文算法的有效性和正确性,因为本文采用的迎风双线性插值技术和窄带技术是严格以Fermat原理和Huygens原理为理论基础的,同时其计算出来的走时值为初至波走时值.也正因为此,Z=0.0 km剖面上,远离震源的区域开始接收到了来自下覆高速地层的首波,而这类型波的走时小于Z=0.0 km剖面上的直达波的走时,所以它们被作为最终计算结果.其实,这种现象的出现在折射波法勘探和三维地震观测系统设计方面有重要的指导意义,有利于分析接收数据的特征和指导有针对性勘探的观测系统设计.
8 结论与讨论为了获得简洁且精度高的三维地震波走时计算结果,笔者提出了一种新的快速推进迎风双线性插值法,该方法包括如下核心技术环节:①充分利用平面波双线插值的假设,采用分情况进行参数讨论的方式,推导出了不同已知条件下双线插值极小值方程的解析解,进而获得了解析的局部走时计算公式;②引入迎风差分思想提出了迎风双线插值的局部走时计算策略;③将上述局部走时计算公式和策略与常规快速推进法中的窄带技术相结合提出了算法的整体实现步骤.由于采用了上述核心技术,新算法具有如下特征:①通过构造性的证明,新推导的双线插值极小值方程的解析计算公式满足Fermat原理和Eikonal方程;②迎风双线插值的局部走时计算策略算法简洁、易于编程实现且无条件稳定;③在算法的整体实现过程中,因为引入了迎风差分的思想,所以迎风双线性插值的局部走时计算策略能够无条件稳定地与窄带技术兼容,进而有效地适应任意复杂介质.最后,算法的精度和效率分析验证了上述提出的双线插值极小值方程的解析公式是正确有效的,并且其计算结果具有比一阶精度有限差分法高很多的计算精度和效率;同时计算实例还表明新提出的三维地震波走时计算方法能够无条件稳定地适应复杂介质.
| [1] | Asakawa E, Kawanaka T. 1993. Seismic ray tracing using linear traveltime interpolation. Geophysical Prospecting, 41(1): 99-111. |
| [2] | Gao L, Li Y M, Chen X R, et al. 2000. An attempt to seismic ray tracing with symplectic algorithm. Chinese J. Geophys. (in Chinese), 43(3): 402-410, doi:10.3321/j.issn:0001-5733.2000.03.014. |
| [3] | Jing X L, Yang C C, Wang S Q. 2007. A improved seismic reflection tomographic method. Chinese J. Geophys. (in Chinese), 50(6): 1831-1836. |
| [4] | Julian B R, Gubbins D. 1977. Three-dimensional seismic ray tracing. J. Geophys., 43: 95-113. |
| [5] | Li P M, Mei S Q, Ma Q B. 2013. An improved bilinear interpolation travel-time ray tracing method. Oil Geophysical Prospecting (in Chinese), 48(4): 553-558. |
| [6] | Liu F, Zhang D, Yang Y, et al. 2012. A fast numerical solution to minimum equation in 3-D seismic LTI ray tracing. Journal of Wuhan University (Natural Science Edition) (in Chinese), 58(5): 395-400. |
| [7] | Mei S Q, Deng F, Zhong B S, et al. 2010. The 3D ray tracing method base on the improved bilinear traveltime interpolation. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 32(2): 152-157. |
| [8] | Moser T J. 1991. Shortest path calculation of seismic rays. Geophysics, 56(1): 59-67. |
| [9] | Qin M Z, Chen J B. 2000. Maslov asymptotic theory and symplectic algorithm. Chinese J. Geophys. (in Chinese), 43(4): 522-533, doi: 10.3321/j.issn:0001-5733.2000.04.013. |
| [10] | Qu C, Zhou H L, Zhao D P. 2007. Deep structure beneath the west margin of Philippine Sea Plate and South China Sea from P and S wave travel time tomography. Chinese J. Geophys. (in Chinese), 50(6): 1757-1768. |
| [11] | Sethian J A, Popovici A M. 1999. 3-D traveltime computation using the fast marching method. Geophysics, 64(2): 516-523. |
| [12] | Sun J G. 1998. On the limited aperture migration in two dimensions. Geophysics, 63(3): 984-994. |
| [13] | Sun J G. 1999. On the aperture effect in 3D Kirchhoff-type migration. Geophysical Prospecting, 47(6): 1045-1076. |
| [14] | Sun J G. 2000. Limited-aperture migration. Geophysics, 65(2): 584-595. |
| [15] | Sun J G. 2004. True-amplitude weight functions in 3D limited-aperture migration revisited. Geophysics, 69(4): 1025-1036. |
| [16] | Sun J G, Sun Z Q, Han F X. 2011. A finite difference scheme for solving the eikonal equation including surface topography. Geophysics, 76(4): T53-T63. |
| [17] | Vidale J E. 1988. Finite-difference calculation of traveltimes. Bull. Seism. Soc. Am., 78(6): 2062-2076. |
| [18] | Vinje V, Iversen E, Gjøystdal H. 1993. Traveltime and amplitude estimation using wavefront construction. Geophysics, 58(8): 1157-1166. |
| [19] | Wang H Z, Ma Z T. 1999. Traveltime calculation in 3D media with arbitrary velocity distribution. // 69th Annual International Meeting, SEG, Expanded Abstracts, 1778-1781. |
| [20] | Zhang D, Fu X R, Yang Y, et al. 2009. 3D seismic ray tracing algorithm based on LTI and partition of grid interface. Chinese J. Geophys. (in Chinese), 52(9): 2370-2376, doi: 10.3969/j.issn.0001-5733.2009.09.023. |
| [21] | Zhang D, Zhang T T, Qiao Y F, et al. 2013. A 3-D ray tracing method based on B-spline traveltime interpolation. Oil Geophysical Prospecting (in Chinese), 48(4): 559-566. |
| [22] | Zhang M G, Jia Y G, Wang M Y, et al. 2006. A global minimum traveltime ray tracing algorithm of wavefront expanding with interface points as secondary sources. Chinese J. Geophys. (in Chinese), 49(4): 1169-1175. |
| [23] | 高亮, 李幼铭, 陈旭荣等. 2000. 地震射线辛几何算法初探, 地球物理学报, 43(3): 402-410, doi:10.3321/j.issn:0001-5733.2000.03.014. |
| [24] | 井西利, 杨长春, 王世清. 2007. 一种改进的地震反射层析成像方法. 地球物理学报, 50(6): 1831-1836. |
| [25] | 李培明, 梅胜全, 马青坡. 2013. 一种改进的双线性插值射线追踪方法. 石油地球物理勘探, 48(4): 553-558. |
| [26] | 刘锋, 张东, 杨艳等. 2012. 三维LTI射线追踪极小值方程的快速数值解法. 武汉大学学报(理学版), 58(5): 395-400. |
| [27] | 梅胜全, 邓飞, 钟本善等. 2010. 基于改进的双线性走时插值的三维射线追踪. 物探化探计算技术, 32(2): 152-157. |
| [28] | 秦孟兆, 陈景波. 2000. Maslov渐近理论与辛几何算法. 地球物理学报, 43(4): 522-533, doi: 10.3321/j.issn:0001-5733.2000.04.013. |
| [29] | 瞿辰, 周蕙兰, 赵大鹏. 2007. 使用纵波和横波走时层析成像研究菲律宾海板块西边缘带和南海地区的深部结构. 地球物理学报, 50(6): 1757-1768. |
| [30] | 张东, 傅相如, 杨艳等. 2009. 基于LTI和网格界面剖分的三维地震射线追踪算法. 地球物理学报, 52(9): 2370-2376, doi: 10.3969/j.issn.0001-5733.2009.09.023. |
| [31] | 张东, 张婷婷, 乔友锋等. 2013. 三维走时场B样条插值射线追踪方法. 石油地球物理勘探, 48(4): 559-566. |
| [32] | 张美根, 贾豫葛, 王妙月等. 2006. 界面二次源波前扩展法全局最小走时射线追踪技术. 地球物理学报, 49(4): 1169-1175. |
 2015, Vol. 58
2015, Vol. 58


