地球物理学报  2015, Vol. 58 Issue (3): 748-755   PDF    
引用本文
于锦海, 曾艳艳, 朱永超, 孟祥超. 2015. 超高阶次Legendre函数的跨阶数递推算法. 地球物理学报, 58(3): 748-755, doi: 10.6038/cjg20150305   
YU Jin-Hai, ZENG Yan-Yan, ZHU Yong-Chao, MENG Xiang-Chao. 2015. A recursion arithmetic formula for Legendre functions of ultra-high degree and order on every other degree. Chinese J. Geophys. (in Chinese), 58(3): 748-755, doi: 10.6038/cjg20150305   
超高阶次Legendre函数的跨阶数递推算法
于锦海1,2, 曾艳艳1,2, 朱永超1,2, 孟祥超1,2    
1. 中国科学院计算地球动力学重点实验室, 北京 100049;
2. 中国科学院大学地球科学学院, 北京 100049
投稿时间:2014-04-28    最后修改时间: 2014-07-09 .
基金项目：国家高技术研究发展计划(863计划)项目(2013AA122502-2),国家自然科学基金项目(41274034)与CAS/CAFEA国际创新团队项目(KZZD-EW-TZ-19)联合资助.
作者简介：于锦海,男,1961年生,江苏盐城人,教授,理学博士,研究方向:大地测量学、地球重力学.E-mail:yujinhai@ucas.ac.cn
摘要：本文引入了Legendre函数的跨阶数递推算法,并利用该算法在双精度数范围内计算了按间隔为1°余纬从1°变化至89°对应的直到完整的20000阶次的归一化连带Legendre函数的值.为验证计算精度,通过多种途径对该算法的计算结果进行检验,结果表明:该算法算得的每个阶次连带Legendre函数的值至少具有10-10这样的绝对精度.此外还对该算法的计算用时进行了统计,结果为该算法的计算用时大约是Legendre函数计算中常用的按阶数递推算法用时的1.6倍.
关键词： Legendre函数     递推算法     双精度数    
A recursion arithmetic formula for Legendre functions of ultra-high degree and order on every other degree
YU Jin-Hai1,2, ZENG Yan-Yan1,2, ZHU Yong-Chao1,2, MENG Xiang-Chao1,2    
1. Key Laboratory of Computational Geodynamics, Chinese Academy of Sciences, Beijing 100049, China;
2. College of Earth Science, University of Chinese Academy of Sciences, Beijing 100049, China
Abstract: The most popular arithmetic for Legendre functions in the study of the gravity field is the increasing degree recursion method (IDR). Although IDR has a simple expression in mathematics, it is not suitable to compute Legendre functions of ultra-high degree and order. For example, when degree reaches 1800, IDR cannot be used to compute Legendre functions because of under-flow in the double floating-point range. Hence, some modified versions for IDR are discussed. A typical modification is to extend the double floating-point range, and the result is that the run-time in computation increases rapidly too. In order to solve the problem in computing Legendre functions of ultra-high degree and order, a recursion arithmetic approach on every other degree for Legendre functions is presented in this paper. Our aim is to illustrate that this approach can be not only used to compute Legendre functions, but the run-time of computation is also saved.
The main method is computation, that is, the values of Legendre functions are computed based on the recursion formulas of Legendre functions on every other degree, and then the computation accuracies and the run-time are assessed.
The values of the fully normalized associated Legendre functions up to complete degree and order 20000 are computed from colatitude 1° to 89° with 1° interval in the double floating-point range. The computation accuracies are estimated according to the properties of Legendre functions. From our computation results, it can be acclaimed that the computation accuracies of Legendre functions up to complete degree and order 20000 can reach 10-10 at least if the recursion arithmetic on every other degree is applied. The run-time for computation is listed. From the statistical results, the run-time of the arithmetic in this work is approximately 1.6 times that of IDR.
The computation of Legendre functions of ultra-high degree and order plays an important role in refining the gravity field. The recursion arithmetic on every other degree is suitable to compute Legendre functions of ultra-high degree and order. The arithmetic has two main advantages: it has enough accuracies and its run-time is also acceptable compared with IDR. In all, the recursion arithmetic on every other degree is an efficient approach to compute Legendre functions of ultra-high degree and order.
Key words: Legendre function     Recursion arithmetic     Double floating-point    
1 引言

超高阶次Legendre函数的计算是地球重力场以及相关领域中的重要研究课题，国内外有许多学 者(Colombo，1981; Fantino and Casotto， 2009; Fukushima，2012; Gleason，1985; Holmes and Featherstone， 2002; Jekeli et al., 2007; Wenzel，1998; Wittwer et al., 2008; 刘缵武等，2011; 彭富清和夏哲仁，2004; 王建国等，2009; 吴星和刘雁雨，2006; 张传定等，2004)都讨论过超高阶次Legendre函数的计算问题.从目前的研究成果来看，计算Legendre函数的主要途径仍然是利用Legendre函数的性质对其进行递推计算.若按使用的Legendre函数的递推公式来分类的话，则递推方法大致分为三类(刘缵武等，2011;王建国等，2009; 吴星和刘雁雨，2006)：第一是按阶(次)数递推方法，该方法的优点是计算方便和用时较少，但缺点是该方法会导致计算数据向下溢出，例如在双精度数范围内大致在计算至1900阶连带Legendre函数时就会产生数据向下溢出现象.第二是Belikov递推方法.第三是跨阶数递推方法.就这三种递推算法而言，吴星和刘雁雨(2006)、王建强等(2009)都曾进行过分析，特别是王建强等(2009)对阶数3060时计算了P3060，m(0.1)与P3060，m(0.9)的值，得出了跨阶数递推方法更适合用于超高阶次Legendre函数计算的结论.然而在目前对超高阶次Legendre函数计算的研究中大多算法仍然仅限于按阶(次)数递推方法的研究上.

事实上，目前关于超高阶次Legendre函数计算的研究主要还是集中在按阶(次)数递推的改进方法上，而改进的途径体现在两个方面：第一是在递推过程中分离出奇异因子sinmθ，从而在双精度数范围内增加递推计算Legendre函数的阶次数，例如Holmes和Featherstone(2002)利用该方法将Legendre函数计算至2700完整阶次；第二是采用扩充双精度数域的方法(Fukushima，2012; Jekeli et al., 2007; Wittwer et al., 2008)，例如可以将双精度数的存储空间扩充四倍从而使得数据下溢向后 推延，但这样做的结果是计算用时也相应地增大(大约增加50倍用时以上).这里要特别指出，Fukushima(2012)引入了X-数域的方法，该方法是将用两个双精度数来表示一个X-数，其中第一个双精度数表示某个双精度数的有效数字，而第二个双精度数则表示该数的指数，这样就构成了一个X-数，显然X-数表示数值的范围就扩大了很多，而且计算用时也比直接将双精度数扩充四倍的方法要节约许多.

此外还有许多关于Legendre函数性质的研究工作.例如Jekeli等(2007)证明了连带Legendre函数P n，m(cosθ)当m≥nsinθ+μ时可以近似地等于零，这里μ是一个正整数(例如：μ=15)，这样的简化并不会影响球谐级数的计算结果，从而就极大地减少了计算Legendre函数的用时.又如 Cheong等(2012)、Sneeuw和Bun(1996)、Swarztrauber(1993)还研究了连带Legendre函数的Fourier展 开式，特别是Cheong等(2012)给出了连带Legendre函数的 Fourier展开系数的算法，为Legendre函数的计算提供另一种途径.除了递推算法外，Yu等(2012)还研究了Legendre函数的积分表达式，给出了连带Legendre函数一种积分表达式，其中被积函数是有界的，这样可以在双精度数的范围内对任意阶次的Legendre函数进行计算.

以上简要地概括了关于超高阶次Legendre函数计算的一些主要结果，但这些结果存在着一些缺陷：例如，若采用扩充双精度数域的方法，则计算用时增加很多；若仍以双精度数作为基准，则计算过程中难以评价是否会因数据溢出而产生的发散等现象.本文的目的就是要基于跨阶数递推方法来讨论在双精度数范围内超高阶次连带Legendre函数的计算问题.在本文计算Legendre函数时将阶数取为20000，对P n，m(cosθ)以1°为间隔从θ=1°至θ=89°进行了计算，并通过多种途径对计算结果的准确性进行了验证. 2 Legendre函数的计算公式 2.1 关于Legendre函数的记号

记Pn(x)是n阶Legendre多项式，即：

并记Pn，m(x)是n阶m次连带Legendre函数，即：

从公式(1)和(2)易知，

对Pn，m(x)进行归一化处理，则有

这里P n，m(x)就是归一化的n阶m次连带Legendre 函数，以后简称为Legendre函数.由于本文只涉及Legendre函数的计算，而不讨论球谐函数的计算，故对Pn，m(x)归一化处理时并没有对m=0和m≠0进行区分.

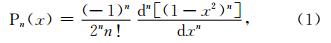
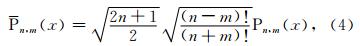
因为在球谐级数计算中总有x=cosθ，这里θ∈[0，π]是归化余纬，所以使用符号时不再区分P n，m(x)和P n，m(cosθ)，并记成P n，m.又因为连带Legendre函数P n，m(x)在区间[－1，+1]中当n－m是偶数时是偶函数，当n－m是奇数时是奇函数，因此下面计算时仅需讨论归化余纬θ∈[0，π/2]的情况. 2.2 按阶数递推算法

关于P n，m的按阶数递推算法的公式为(Fantino and Casotto， 2009; Fukushima，2012; Holmes and Featherstone， 2002; Jekeli et al., 2007)

其中

事实上，按阶数递推公式(5)是计算Legendre函数的基本算法，该算法在θ接近90°(即：赤道附近)具有很好的收敛性. 2.3 跨阶数递推公式

引入记号：当m>n时

则对m≥2，便有公式(Swarztrauber，1993; Cheong et al., 2012; 张传定等，2004)

其中

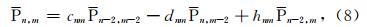
由于公式(8)是按跨阶数给出的，所以公式(8)被称为Legendre函数的跨阶数递推公式. 2.4 当m=0和m=1时P n，m的计算

因为公式(8)仅对m≥2成立，所以还需讨论m=0和m=1时P n，m的计算方法.事实上，此时P n，0和P n，1可由公式(5)给出，即：

2.5 使用跨阶数递推方法计算P n，m的步骤

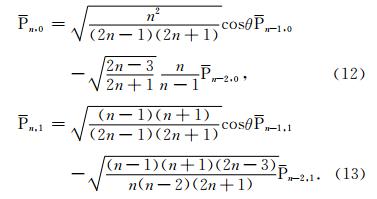
第一步，引入初始值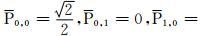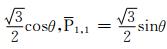，由此利用公式(12)与(13)便可计算P n，0与P n，1；第二步，再利用初始值P0，0，P1，0，P0，1，P1，1以及P n，0与P n，1，按公式(8)便可递推计算当n≥2和m≥2时P n，m的值.称上述递推计算P n，m的方法为跨阶数递推算法. 3 数值计算与精度分析

利用上述给出的跨阶数递推算法可以对P n，m(cosθ)在双精度数范围内进行计算，本文对P n，m(cosθ)的值计算至完整20000阶次，其中余纬以1°为间隔从θ=1°变换至θ=89°.为了与P n，m的理论值进行区分，下面使用P n，m(r)表示利用跨阶数递推算法计算得到的P n，m的值.为了分析P n，m(r)的计算精度，下面将用几种不同的检验途径.

例1 首先引入关于P n，m的恒等式如下

为此令

因为P n，m(r)是通过递推算法来计算的，所以仅需对最 后阶数的结果进行评估，即：η(θ)值的大小代 表了P n，m(r)(cosθ)的计算精度，显然η(θ)的值越小，P n，m(r)(cosθ)的计算精度就越高.文中计算了η(θ)的值，其分布由图 1给出.从图 1可知，当θ在1°与89°之间变化时η(θ)的值均小于10－12.
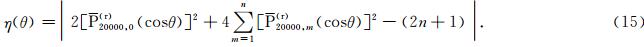
图 1 P n，m的平方和的精度 Fig.1 The accuracies for summation of square of P n，m

例2 例1中的η(θ)反映的是同一阶数内Legendre函数值的平方和的精度，该精度并不能用于评价某个特定阶次Legendre函数的计算精度.如何评价每个Legendre函数的计算精度呢？注意到P n，m(r)(cosθ)的值是经过递推计算的，因此只需评价P 20000，m(r)(cosθ)或 (r)19999，m(cosθ)的精度即可，这里0≤m≤20000.为此引入Legendre函数的积分公式如下(Yu et al., 2012)： 当n－m=2k是偶数时，则有

其中

因为 Pn(x)≤1，所以可在双精度数范围内通过公式(16)来计算P n，m(x).本文在计算公式(16)中 的积分时将积分区间[0，π/2]分割成40000等分，然后通过求和直接计算了当m是偶数时P 20000，m(cosθ)的值. 使用记号P 20000，m(r)(cosθ)表示P 20000，m(cosθ)的积分计算值，并令

这里m是偶数.显然δm(θ)可以作为P 20000，m(r)(cosθ)中每项的计算精度指标(m是偶数).文中分别对θ=3°、30°、60°、87°计算了δm(θ)的分布，其结果由图 2给出.
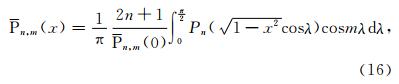
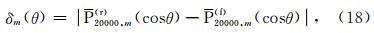
图 2 δm(θ)的分布 Fig. 2 The distributions of δm(θ)

对于 (r)19999，m(cosθ)而言(m是奇数)，同样能够给出类似图 2的计算结果，这里不再叙述.而对于m是奇数时可利用Legendre函数的性质(党诵诗，1988)

来计算P 20000，m(r)(cosθ)或 (f)19999，m(cosθ).

总之，图 2描述了P 20000，m(r)(cosθ)中每项的精度.由图 2可见，对于中高纬度的项来说P 20000，m(r)(cosθ)的计算精度均达到了10－10，但在赤道附近δm(θ)的值则要相应地大了一些.虽然如此，但在赤道附近P 20000，m(r)(cosθ)的计算精度均也能达到10-9，这样的精度对于超高阶次Legendre函数值的计算来说是能够满足要求的.

例3 是否在赤道附近P 20000，m(r)(cosθ)的计算精度就会差些呢？或者说，为何δm(θ)的值在赤道附近会比在中高纬度地区要大一个量级呢？事实上，产生这样情况的原因是利用积分方法计算的P 20000，m(r)(cosθ)值在赤道附近的精度较低而引起的.为证实这样的结论，下面在赤道附近使用按阶数递推算法来计算Legendre函数，理由是在赤道附近按阶数递推算法具有较好的收敛性.本文专门针对赤道附近(θ=87°、89.5°)利用按阶数递推公式(5)计算了P 20000，m(cosθ)的值，记为 (d)20000，m(cosθ)，并统计了 P 20000，m(r)(cosθ)－ (d)20000，m(cosθ)的值(m=0，1，…，20000)，结果由图 3给出.

图 3 |P 20000，m(r)(cosθ)－P 20000，m(d)(cosθ)|的分布 Fig. 3 The distributions of |P 20000，m(r)(cosθ)－P 20000，m(d)(cosθ)|

从图 3可以断言，在赤道附近P 20000，m(r)(cosθ)每项的计算精度均可达到10-11.总之，结合例2与例3可知，跨阶数递推算法计算的P n，m(cosθ)的绝对精度要优于10-10.

例4 本文在双精度数范围内研究了超高阶次Legendre函数的计算问题，并针对阶数为20000时对余纬θ以1°为间隔从θ=1°至θ=89°计算了Legendre函数的值.通常情况下，20000阶次的Legendre函数在纬度方向上对应的分辨率为 180/20000 ×1°=32.4″，而在θ接近于0°时P n，m(cosθ)的值极易产生向下溢出，从而在计算过程中容易导致P n，m(cosθ)会出现不稳定的现象.是否本文使用的Legendre函数的跨阶次算法在计算至20000阶时也会出现这种不稳定现象呢？为此本文专门针对θ=30″与θ=60″使用跨阶次算法计算了P n，m(cosθ)的值，并统计了相应δm(θ)的分布，结果由图 4给出.

图 4 θ=30″与θ=60″时δm(θ)的分布 Fig. 4 The distributions of δm(θ) when θ=30″ and θ=60″

从图 4可见，在两极附近使用跨阶次算法计算了P n，m(cosθ)至20000阶次时在分辨率范围内该算法是稳定的，而且Legendre函数计算值的绝对精度至少优于10-10量级. 4 球谐级数合成的精度分析

本节讨论球谐级数合成的精度.假设地球引力位的球谐级数展开式为

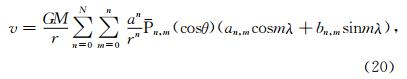
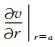这里a是赤道半径，N是引力场模型的最高阶数(本文中N=20000).下面以计算赤道处引力的径向分量的值(即：)来研究球谐级数合成的精度.经计算可得

这里 可近似地看成是赤道处的引力值.

若采用跨阶数递推算法去计算完整到20000阶次的Legendre函数，则使用公式(21)的实际计算值为

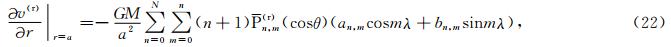
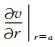记每个P n，m(r)(cosθ)的计算精度为ε，即： P n，m(r)(cosθ)－P n，m(cosθ)≤ε，(例如：例2给出了ε≤10－9)，那么可得 的计算精度的估计如下：

引入关于位系数的Kaula假设(Kaula， 1966，2000)，即：

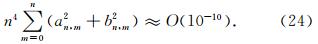
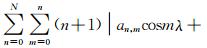由此可见，式(23)中的级数bn，msinmλ | 是平方和收敛的，因此在平方和意义下，恒有

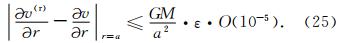
如果P n，m(r)(cosθ)的计算精度ε满足：ε≤10－9，则利用跨阶数递推算法计算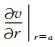的精度便可达到 ·O(10－14).由于×10－9约为1 μGal，因此可得结论：利用跨阶数递推算法从球谐展开式计算引力的精度可达到10-5 μGal的量级.显然，这样的精度足以满足重力观测的精度要求. 5 计算时间

由于按阶数递推是计算Legendre函数的常用方法，所以本文需要去比较跨阶数递推算法与按阶数递推算法的计算用时.表 1给出了在同一台计算机上用跨阶数递推算法与按阶数递推算法计算不同阶数Legendre函数从θ=1°到89°的时间.由于按阶 数递推算法会遇到数值向下溢出的情况，所以在出现数据向下溢出时总是对溢出变量赋予了一个小数以便能够统计出按阶数递推算法的计算用时.

表 1 计算用时比较 Table 1 The comparison of run-times

从表 1可见，跨阶数递推算法的计算用时大约是按阶数递推算法的1.6倍.其原因是按阶数递推算法公式(5)是从两个变量去推算下一个变量，而跨阶数递推算法公式(8)则是从三个变量去推算下一个变量，因此跨阶数递推算法的用时应该大约是按阶数递推算法的1.6倍左右.

与扩充双精度数域来计算Legendre函数算法的计算用时进行比较的话，明显可以看出，跨阶数递推算法的计算用时是完全可以接受的. 6 结论

本文基于Legendre函数的跨阶数递推公式研究了相应的计算Legendre函数的方法，使用该算法在双精度数范围将Legendre函数计算至完整20000阶次，实现了在双精度数范围内快速计算超高阶次Legendre函数的方法.

使用多种方法检验了使用跨阶数递推算法计算Legendre函数的精度，得出了该算法计算的每个Legendre函数的绝对精度都优于10-10的结论.

统计了跨阶数递推算法计算Legendre函数的用时，相对于常用的按阶数递推算法而言，跨阶数递推算法的计算用时大约是按阶数递推算法的1.6倍.

在计算Legendre函数的绝对精度是10-9的前提下，借助于Kaula准则证明了在进行球谐级数合成时其精度大致可以达到计算量的10-14左右.例如，若使用球谐级数去计算引力值，则引力值的计算精度将会达到10-5 μGal左右.

最后说明一下，Legendre函数的跨阶数递推公式(8)并非本文首次给出，跟踪的国外最早文献是Swarztrauber(1993)，而国内则由张传定等(2004)最早给出，但将该公式用于超高阶次Legendre函数的计算，并对计算结果的精度进行检验与验证则是本文首次实现的.根据检验与验证的结果，可以得出结论：跨阶数递推算法不仅可以在双精度数范围内用于超高阶次Legendre函数的计算，而且计算结果准确、计算用时还完全可以接受.总之，本文提出的算法完全满足超高阶次Legendre函数的要求.

参考文献
[1] Cheong H B, Park J R, Kang H G. 2012. Fourier-series representation and projection of spherical harmonic functions. J. Geod., 86(11): 975-990.
[2] Colombo O L. 1981. Numerical methods for harmonic analysis on the sphere. OSU Rep 310. Columbus, Ohio: The Ohio State University.
[3] Dang S S. 1988. Mathematical Basement in Physical Geodesy (in Chinese). Beijing: Surveying and Mapping Press.
[4] Fantino E, Casotto S. 2009. Methods of harmonic synthesis for global geopotential models and their first-, second- and third-order gradients. J. Geod., 83(7): 595-619.
[5] Fukushima T. 2012. Numerical computation of spherical harmonics of arbitrary degree and order by extending exponent of floating point numbers. J. Geod., 86(4): 271-285.
[6] Gleason D M. 1985. Partial sums of Legendre series via Clenshaw summation. Manu. Geod., 10: 115-130.
[7] Holmes S A, Featherstone W E. 2002. A unified approach to the Clenshaw summation and the recursive computation of very high degree and order normalised associated Legendre functions. J. Geod., 76(5): 279-299.
[8] Jekeli C, Lee J K, Kwon J H. 2007. On the computation and approximation of ultra-high-degree spherical harmonic series. J. Geod., 81(9): 603-615.
[9] Kaula W M. 1966. Theory of Satellite Geodesy. London: Blaisdell Publishing Company.
[10] Kaula W M. 2000. Theory of Satellite Geodesy: Applications of Satellites to Geodesy. Mineola: Dover.
[11] Liu Z W, Liu S H, Huang O. 2011. Scale factors in recursion of ultra-high degree and order Legendre functions and Horner's scheme of summation. Acta Geodaetica et Cartographica Sinica (in Chinese), 40(4): 454-458.
[12] Peng F Q, Xia Z R. 2004. Algorithms for computing ultra-high-degree disturbing geopotential elements. Chinese J. Geophys. (in Chinese), 47(6): 1023-1028.
[13] Sneeuw N, Bun R. 1996. Global spherical harmonic computation by two-dimensional Fourier methods. J. Geod., 70(4): 224-232.
[14] Swarztrauber P N. 1993. The vector harmonic transform method for solving partial differential equations in spherical geometry. Mon. Wea. Rev., 121(12): 3415-3437.
[15] Wang J G, Zhao G Q, Zhu G B. 2009. Contrastive analysis of common computing methods of ultra-high degree and order fully normalized associated Legendre function. J. Geod. Geodyn. (in Chinese), 29(2): 126-130.
[16] Wenzel G. 1998. Ultra-high degree geopotential models GPM98A, B, and C to degree 1800. Paper to the joint meeting of the International Gravity Commission and International Geoid Commission, 7-12 September, Trieste.
[17] Wittwer T, Klees R, Seitz K, et al. 2008. Ultra-high degree spherical harmonic analysis and synthesis using extended-range arithmetic. J. Geod., 82(4-5): 223-229.
[18] Wu X, Liu Y Y. 2006. Comparison of computing methods of the ultra-high degree and order. Journal of Zhengzhou Institute of Surveying and Mapping, 23(3): 188-191.
[19] Yu J H, Wan X Y, Zeng Y Y. 2012. The integral formulas of the associated Legendre functions. J. Geod., 86(6): 467-473.
[20] Zhang C D, Xu H Z, Wu X. 2004. Tyros problem in harmonic analysis of the gravity field (in Chinese). // Proc. Geod. and Geodyn. Hubei: Science and Technology Press, 302-314.
[21] 党诵诗. 1988. 物理大地测量的数学基础. 北京: 测绘出版社.
[22] 刘缵武, 刘世晗, 黄欧. 2011. 超高阶次勒让德函数递推计算中的压缩因子和Horner求和技术. 测绘学报, 40(4): 454-458.
[23] 彭富清, 夏哲仁. 2004. 超高阶扰动场元的计算方法. 地球物理学报, 47(6): 1023-1028.
[24] 王建国, 赵国强, 朱广彬. 2009. 常用超高阶次缔合勒让德函数计算方法对比分析. 大地测量与地球动力学, 29(2): 126-130.
[25] 吴星, 刘雁雨. 2006. 多种超高阶次缔合勒让德函数计算方法的比较. 测绘科学技术学报, 23(3): 188-191.
[26] 张传定, 许厚泽, 吴星. 2004. 地球重力场调和分析中的“轮胎”问题. // 大地测量与地球动力学进展. 湖北: 科学技术出版社, 302-314.