2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
The truncated window function method is used to get optimized finite-difference operators. Firstly, we analyze the influence on the accuracy of finite-difference operators caused by the properties of main lobe and side lobe in the amplitude response of truncated window functions. Secondly, based on the methods of auto-convolution and weighted combination, a window function which has narrower main lobe and larger attenuation of side lobe is designed,correspondingly bringing higher accuracy of finite-difference approximation. Finally, we use the window function to get optimized finite-difference operators.
From the analysis of window functions, the factors that affect the accuracy of finite-difference approximation can be summarized in two aspects: (1) The width of main lobe of window functions. (2) The attenuation of side lobe of window functions.The window functions which have narrower main lobe and larger attenuation of side lobe can yield higher accuracy of finite-difference approximation. The Chebyshev window function has appropriate width of main lobe and attenuation of side lobe to get better stability of accuracy error on the premise of maintaining the appropriate wave number coverage range. Furthermore, the auto-convolution method will increase the attenuation of side lobe, however, widen the main lobe.Weighted combination can remedy the defect, choose different weight coefficients to reduce the width of main lobe. Combining the two methods, a specific window function named Chebyshev auto-convolution combined window is designed. Compared with the accuracy curves of approximation between the finite-difference operators truncated by Chebyshev auto-convolution combined window and the conventional operators, the former lead to great accuracy in a bigger frequency region. Tests on a homogeneous model and the Marmousi model show that the dispersion caused by the operators based on the Chebyshev auto-convolution combined window is quite weak under the same order of the conventional operators. Further comparison with the finite-difference operators truncated by improved binomial window, our operators still have a bigger frequency coverage range and smaller fluctuation of accuracy error.
The finite-different operators based on the Chebyshev auto-convolution combined window have higher accuracy than that of the conventional operators and operators based on the improved binomial window. Our optimized eighth-order and twelfth-order operators can respectively reach, even exceed the accuracy of the conventional twelfth-order and twenty-fourth-order finite-difference operators, and the maximum deviation of absolute error is within [0, 0.0004]. For higher-order operators, the accuracy increase becomes more obvious.The results of elastic wavefield numerical modeling demonstrate that the operators based on the Chebyshev auto-convolution combined window can efficiently suppress the numerical dispersion and has greater modeling accuracy under the same discretizations without extra computing costs.In addition,through adjusting parameters of the auto-convolution combined window, we can adjust the accuracy of finite-difference approximation as required, visually and intuitively.
随着我国对产油区的勘探深度不断加深,对更高精度的成像和反演的需求也越来越迫切,而作为成像和反演方法基础的地震波场数值模拟技术也变得尤为重要.常用的数值模拟方法分为三大类:几何射线法、积分方程法和波动方程法,波动方程法的模拟结果因为包含了波场的运动学与动力学特征,是最常用的(程冰洁等,2008).而使用较多的波动方程数值模拟方法则是有限差分方法(Alterman and Karal, 1968; Kelly et al., 1976;Dablain,1986;Igel et al., 1995)和伪谱法(Gazdag,1981;Kosloff and Baysal, 1982;Carcione et al., 1992).有限差分数值模拟技术起源于20世纪60年代末,Alterman和Karal(1968)首次使用显式有限差分技术来模拟层状介质中二阶弹性波波场. Kelly等(1976)提出和发展了适合非均匀介质的二阶弹性波方程有限差分数值模拟方法.Dablain(1986)实现了声波方程高阶有限差分的数值模拟.刘洋等(1998)从Taylor级数展开出发,推导出了任意偶数阶导数的任意偶数精度的有限差分算子.董良国等(2000)实现了弹性波方程有限差分在时间和空间上任意高阶精度的差分解法.裴正林和牟永光(2003)推导了一阶空间导数交错网格的任意偶数阶精度差分系数.Liu和Sen(2009a,2010)提出了一种基于时空域频散关系的有限差分法,该差分法能有效地改善波动方程数值解精度.而后,Yan和Liu(2013a,2013b)将该时空域有限差分法推广发展到黏滞声波和各向异性声波方程的数值模拟与逆时偏移中.
数值频散问题是有限差分数值模拟不可避免的一个问题,会直接影响模拟的精度.数值频散的产生是由于使用差分算子来逼近微分算子,截断之后导致了误差;为了降低数值频散,可以采用更细的网格或者降低子波主频.但是更细的网格意味着海量的计算量,降低了计算效率,且对存储和计算性能都提出了挑战;降低子波主频则会损失高频成分,影响分辨率.前人在研究如何降低数值频散方面做了许多工作,其一是利用通量校正技术(FCT)来压制数值频散,Boris和Book(1973)提出利用FCT技术来压制数值频散.杨顶辉和腾吉文(1997)将FCT技术应用到各向异性介质中的三分量地震数值模拟.其二是通过最优化方法来压制数值频散,Holberg(1987)和Robertsson等(1994)利用最优化方法,最小化频散误差,计算优化的有限差分系数.Zhang和Yao(2013)通过优选设定误差的容许范围,利用模拟退火法得到优化算子,其拥有更高的频谱覆盖范围和较小的误差限.Liu(2013)基于最小二乘方法,得到一种全局优化的有限差分算子.Yang等(2014)基于数值频散关系和最小二乘理论推导了适合求解空间一阶导数的交错网格优化差分系数,并实现了弹性波数值模拟.其三是优选窗函数压制数值频散,Fornberg(1987)证明了有限差分方法随着阶数的增加,逼近伪谱法.伪谱法因为采用了所有的点,解决了数值频散的问题,换句话说,在空间域,可以采用不同的截断窗函数去截断伪谱法的空间褶积序列推导出有限差分算子.Zhou和Greenhalgh(1992)使用了广义加权的Hanning窗截断得到了有限差分算子.Igel等(1995)使用了高斯窗截断得到了有限差分算子.Chu和Stoffa(2012)使用了二项式窗统一了有限差分方法和伪谱法,使用二项式窗截断不仅可以推导出常规的有限差分算子系数,而且稍加改进,就可以设计出一种优化的有限差分算子,Chu和Stoffa(2012)认为,这种改进的二项式窗截断方案与Liu和Sen(2009b)提出的一种截断的有限差分方法本质上是相同的.
在空间域,将伪谱法的空间褶积序列截断就得到了有限差分法,如果从信号处理层面来讲,截断相当于加了一个窗函数.截断会产生边缘效应,造成频谱泄露.为了压制数值频散,选择合适形状的有限长的窗函数使数据逐渐截断;不同的窗函数会产生不同的结果,具体来讲,窗函数相当于有限长的滤波器,不同的窗函数,其幅值响应拥有不同的主瓣和旁瓣形状,主瓣的形状控制着过渡带的范围,也就是频谱覆盖范围;旁瓣的形状决定了有限差分算子逼近微分算子的偏差程度.如果有种窗函数的幅值响应主瓣窄,旁瓣衰减大,由该种窗函数截断的有限差分算子的精度误差谱覆盖范围大,误差稳定性高.谱覆盖范围大,意味着采用低阶窗函数截断得到的有限差分算子就可以达到高阶常规有限差分算子的精度;精度误差稳定性高意味着逼近精度不会出现大幅波动;满足这两者,表明有限差分算子逼近微分算子的程度就越好,数值频散越小.本文就是从窗函数的性质出发,设计一种窗函数,截断伪谱法的空间褶积序列得到优化的有限差分算子,抑制数值频散.
Zhou和Greenhalgh(1992)提出的广义加权的Hanning窗,其本质是三角函数类窗,三角函数类窗函数的幅值响应有相对较窄的主瓣,但是旁瓣衰减程度不够高,使用该三角函数类窗函数截断逼近的有限差分算子,其截断逼近的精度误差波动相对较大,即使有较大的谱覆盖范围,但是精度误差的波动对逼近的效果的影响还是很大(Zhang and Yao, 2013).Chu和Stoffa(2012)的改进的二项式窗是一个可调节的窗函数,但是其主瓣还是过宽,导致过渡带过长,使用该改进的二项式窗函数截断逼近的有限差分算子,其精度误差谱覆盖范围较小,且对于低阶有限差分算子,其精度误差存在较大波动,特别是12阶以下的差分算子.本文分析了窗函数幅值响应的主旁瓣属性对有限差分算子逼近微分算子的精度的影响,研究了自褶积组合的效应,设计了一种基于Chebyshev自褶积组合的窗函数,该窗函数的幅值响应在维持较窄主瓣的前提下,可以获得更好的旁瓣衰减,从而进一步提高了窗函数截断逼近的有限差分算子的精度误差稳定性,并且可以通过只改变三个参数,更直观和可视化地调节主瓣和旁瓣的形状,进而控制有限差分算子逼近微分算子的精度,保持了较大的灵活性.
2 窗函数截断的逼近误差分析 2.1 常规有限差分算子我们使用sinc函数插值理论推导出有限差分算子,根据离散信号的采样理论(Diniz et al., 2012),一个带限的连续信号 f(x)可以被以一个均匀采样的信号 fn 通过sinc函数插值重建:

 为截止波数.
为截止波数.如果对公式(1)左右两边分别求一阶导数和二阶导数,并取 x=0 处的导数值,可以得到:
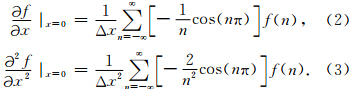
Chu和Stoffa(2012)认为存在一个长度为N+1点的窗函数,N为偶数,去截断公式(2)和公式(3),得到常规有限差分算子.

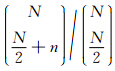 ,对于 组合数,有
,对于 组合数,有 =
= ,Chu和Stoffa(2012)称此类窗为二项式窗.并且认为,只要在该二项式窗上稍加改动,定义一个改进的二项式窗 wnN+M,就可以得到更好的频散效应. M 是一个正偶数,对于常规有限差分算子,M=0.
2.2 窗函数对逼近效果的影响
,Chu和Stoffa(2012)称此类窗为二项式窗.并且认为,只要在该二项式窗上稍加改动,定义一个改进的二项式窗 wnN+M,就可以得到更好的频散效应. M 是一个正偶数,对于常规有限差分算子,M=0.
2.2 窗函数对逼近效果的影响 前人做了很多的工作去选择不同的截断窗函数,Zhou和Greenhalgh(1992)提出了广义加权的Hanning窗,Igel等(1995)使用了高斯窗,Chu和Stoffa(2012)提出了改进的二项式窗.Zhou和Greenhalgh(1992)提出的广义加权的Hanning窗本质上是一类三角函数窗.本文比较四种窗函数,分 别是Hanning窗,改进的二项式窗(Chu and Stoffa, 2012),Kaiser和Chebyshev窗,分析窗函数幅值响应的主旁瓣属性对有限差分算子逼近微分算子的精度的影响.
图 1是窗函数长度为N+1=25时的系数分布,图 2展示了对应窗函数幅值响应.从图中可以看出,图 1中窗函数系数分布越细长,在图 2中,其幅值响应,主瓣越宽.Diniz等(2012)指出较宽的主瓣意味着加窗处理后会出现较宽的过渡带,随着过渡带的增宽,频谱覆盖范围会变小,对高波数部分的逼近精度就越低,出现较为严重的频散效应;相比于其他窗函数,改进的二项式窗拥有最宽的主瓣,这表明该改进的二项式窗频谱范围没有其余三个窗大,对高波数部分逼近精度不够;另外改进的二项式窗拥有衰减最大的旁瓣,旁瓣衰减越大,证明其逼近的稳定性越高,逼近精度不会出现较大的波动.Hanning窗虽然拥有较小的主瓣,旁瓣衰减也是最快的,但是其前面几个频率点的旁瓣衰减幅度较小,逼近精度会出现较大的波动.相对而言,Kasier窗和Chebyshev窗是比较自由的窗函数,通过调节 β和r,可以拥有不同的幅值响应.这里选择r=60,Chebyshev窗的旁瓣衰减固定在-60 dB,拥有较窄的主瓣.而Kasier窗和Hanning类似,选择Kaiser窗的参数β=5,由图 2可知,在前面几个频率点旁瓣衰减幅度较小,低波数时会出现逼近精度的波动.
 | 图 1 四种窗函数对比,N=24Fig. 1 Comparison of window functions,N=24 |
 | 图 2 四种窗函数的幅值响应,频率点M=512Fig. 2 Amplitude response of four window functions,frequency points M=512 |
为了进一步确认可调参数的Kasier窗和Chebyshev 窗的幅值响应,图 3分别示意β=2,5,9 的Kasier窗的幅值响应和r=35,60,95的Chebyshev窗的幅值响应. 窗函数长度N+1=25.
 | 图 3 改变β和r,两种窗函数幅值响应,频率点M=512 (a)Kaiser窗;(b)Chebyshev窗.Fig. 3 Amplitude response of two window functions,different β and r,frequency points M=512 (a)Kaiser window;(b)Chebyshev window. |
图 3表明,当固定窗函数长度时,对于Kaiser窗,随着β增大,其幅值响应的变化表现为:主瓣宽度增加,旁瓣衰减增大. 而对于Chebyshev窗,随着r的增大,其幅值响应的主旁瓣也有相同的变化;对于这两种窗函数来说,Chebyshev窗拥有衰减更大的旁瓣,逼近精度相对来说更加稳定.
本文以二阶导数为例,说明不同窗函数截断逼近的精度误差.
因为n=0是公式(2)和公式(3)的一个奇异点,根据Lee和Seo(2002),公式(2)和公式(3)可以表示为:

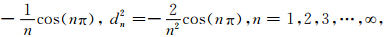
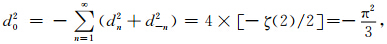 这里ζ 代表黎曼 ζ 函数,加窗 w(n)截断后就有:
这里ζ 代表黎曼 ζ 函数,加窗 w(n)截断后就有:


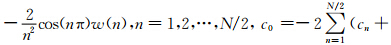 c-n). 对公式(8)和公式(9)分别进行傅里叶变换,可得:
c-n). 对公式(8)和公式(9)分别进行傅里叶变换,可得:

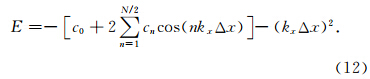
图 4a表明,Hanning窗和Kaise窗截断逼近的有限差分算子拥有更大的谱范围;改进的二项式窗截断逼近的有限差分算子谱覆盖范围较小,Chebyshev窗截断逼近的有限差分算子谱覆盖范围介于它们之间,但更接近Hanning窗和Kaise窗截断逼近的有限差分算子的谱覆盖范围.图 4b是将图 4a的精度误差 放大1000倍的示意图,从图 4b中可以发现Hanning 窗和Kaiser窗截断的有限差分算子的逼近精度误差曲线围绕零点波动得比较大,而Chebyshev窗和改进的二项式窗截断逼近的有限差分算子的精度误差曲线波动最小.这也与前面的分析相符,旁瓣衰减越大,逼近精度误差出现波动越小,结果越准确.综上,在上述提到的四种窗函数里,折中主瓣宽度和旁瓣衰减,Chebyshev窗是一个较优的选择.
 | 图 4 四种窗函数截断逼近的有限差分算子的精度误差曲线(二阶导数)(N=24) (a)精度误差;(b)精度误差放大1000倍.Fig. 4 Accuracy errorfor second derivative of four window truncated finite-difference operators(N=24) (a)Accuracy error;(b)Magnified 1000 times. |
N是偶数,将一个长度为N+1的Chebyshev窗函数作自褶积运算,可以得到长度为2N+1的Chebyshev自褶积窗函数,同理,将L个相同长度为N+1的Chebyshev窗函数作L-1次自褶积,即可得到L阶Chebyshev自褶积窗函数.
对Chebyshev窗函数应用傅里叶变换,并令 ω=kxΔx,即可得其幅值响应函数为:
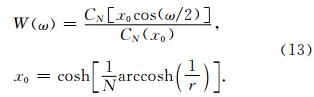
图 5是不同褶积阶数的Chebyshev自褶积窗幅值响应,频率点M=512.展示了经过自褶积之后,窗函数的幅值响应的变化.进行自褶积的Chebyshev窗长度N+1=5,r=60,将此Chebyshev窗分别作1-5次的自褶积运算,构建长度N+1分别为9,13,17,21,25的Chebyshev自褶积窗;在对Chebyshev窗进行自褶积之后,调整Chebyshev自褶积窗的系数为 cL(n)=wcL(n)/wcL(0),这样可以使
cL(n)=wcL(n)/wcL(0),这样可以使 cL(0)=1,且对于不同的n,wc(n)之间的距离也随之增加. 定义1次褶积运算L=2,依次类推,图中L最大为6.
cL(0)=1,且对于不同的n,wc(n)之间的距离也随之增加. 定义1次褶积运算L=2,依次类推,图中L最大为6.
 | 图 5 Chebyshev自褶积窗函数幅值响应(N=4),L=1,2,3,4,5,6Fig. 5 Amplitude response ofChebyshev auto-convolution window function(N=4),L=1,2,3,4,5,6 |
随着褶积次数的增大,自褶积之后Chebyshev窗函数的旁瓣衰减得很快,主瓣越来越窄.图 5中绿色线为Chebyshev窗函数的幅值响应,其旁瓣衰减位于-60 dB,经过一次自褶积后,观察图 5中青色线,其旁瓣衰减位于-120 dB,可见自褶积拥有很好的压制旁瓣的效果.
如果固定窗函数的长度N+1为一个常数,对于不同的褶积阶数,窗函数的幅值响应见图 6,固定窗函数长度为N+1=25,绿色线为未褶积前长度为25点Chebyshev窗的幅值响应曲线,红色线和青色线分别为自褶积1次的L=2的Chebyshev自褶 积窗和自褶积3次的L=4的Chebyshev自褶积 窗.由褶积原理可知,L=2的Chebyshev自褶积窗是长度为13的Chebyshev窗自褶积1次生成;L=4的Chebyshev自褶积窗是长度为7的Chebyshev窗自褶积3次生成.从图 6可以看到,固定窗函数长度,主瓣宽度取决于自褶积阶数,成一个正比的关系,阶数越高,主瓣越宽.而随着自褶积阶数的提高,旁瓣衰减迅速增大,自褶积阶数越高,旁瓣衰减越大,更有效抑制频谱泄露.
 | 图 6 Chebyshev自褶积窗函数幅值响应(固定N=24),L=2,4Fig. 6 Amplitude response of Chebyshev auto-convolution window function(Fix N=24),L=2,4 |
仍以二阶导数为例,使用公式(12)计算图 6所示三种窗函数截断逼近的有限差分算子的精度误差,这时N=24.
图 7所示不同自褶积次数的Chebyshev自褶积窗截断逼近的有限差分算子精度误差曲线,图 7a是三种窗函数截断逼近的精度误差曲线,图 7b是将图 7a放大1000倍之后的精度误差曲线.其中绿色线是Chebyshev窗函数截断逼近的有限差分算子的精度误差曲线,其拥有更高的谱覆盖范围,青色线是自褶积4次的Chebyshev窗函数截断逼近的有限差分算子的精度误差曲线,其谱覆盖范围很低;红色线代表自褶积2次的Chebyshev窗函数截断逼近的有限差分算子的精度误差曲线,其谱覆盖范围介于前两者之间.图 7a中无法看出逼近精度误差曲线的稳定性;图 7b展示了三种窗函数截断逼近的有限差分算子精度误差曲线的稳定性,可以观察到绿色线Chebyshev窗截断逼近的有限差分算子的精度误差曲线波动相对较大,红色线和青色线波动较小.由此,对窗函数自褶积之后再去截断伪谱法的空间褶积序列得到的有限差分算子的逼近精度误差稳定性更高,对压制频谱泄露有更好的效果.综合截断窗函数的幅值响应的主瓣和旁瓣的性能及不同窗函数截断逼近的有限差分算子的精度误差的比较,折中谱覆盖范围和逼近精度误差稳定性,窗函数自褶积2次,可以得到幅值响应属性更优的窗函数.
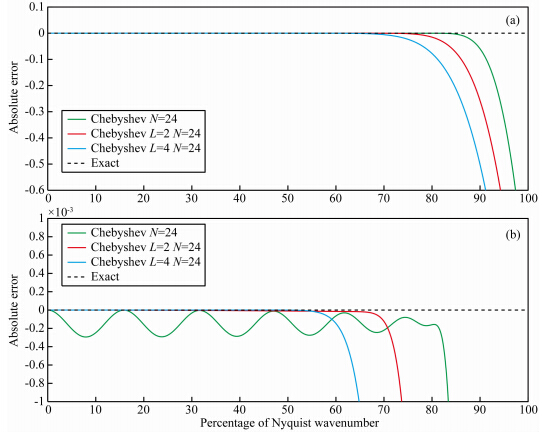 | 图 7 自褶积窗函数截断逼近的有限差分算子精度误差曲线(二阶导数)(N=24,L=2,4) (a)精度误差曲线;(b)精度误差曲线放大1000倍.Fig. 7 Accuracy errorfor second derivative of auto-convolution window truncated finite-difference operators(N=24,L=2,4) (a)Accuracy error;(b)Magnified 1000 times. |
但是,由图 7可知,自褶积2次的Chebyshev窗函数截断逼近的有限差分算子的精度误差虽然有较高的稳定性,但是其谱覆盖范围小于Chebyshev窗函数截断逼近的有限差分算子的谱覆盖范围.基于前面的分析,本文的目的是为了设计一种窗函数,使截断得到的有限差分算子在合适的谱覆盖范围的前提下,获得更好的精度误差稳定性.因此,考虑使用加权函数,对两种窗函数做一个加权组合.本文选用一个简单的线性加权函数.
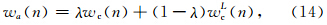
本文提出的基于Chebyshev窗函数自褶积组合窗,仅需要三个参数,就可以直观地优选窗函数去截断逼近伪谱法的空间褶积序列得到优化的有限差分算子;第一个参数是Chebyshev窗函数的纹波率 r; 第二个参数是窗函数自褶积的次数 L; 第三个参数是线性组合的加权系数 λ. 本文选择λ=0.89,r=60,L=2,图 8展示了不同阶的自褶积组合窗函数截断逼近的有限差分算子的精度误差曲线(二阶导数).观察图 8a,很明显,8阶的自褶积组合窗函数截断逼近的有限差分算子相比常规8阶的有限算子,拥有更高的精度,达到了常规12阶的精度,其精度误差曲线基本重合.而12阶的自褶积组合窗函数截断逼近的有限差分算子的准确度远远高于常规12阶有限差分算子的精度,甚至超过了常规24阶的精度.图 8b是将图 8a放大1000倍之后的精度误差曲线,相比常规有限差分算子的精度误差曲线,自褶积组合窗函数截断逼近的有限差分算子的精度误差都有波动,但是,其精度误差控制在0.0004之内,拥有较高的精度误差稳定性.
 | 图 8 不同N的自褶积组合窗函数截断逼近的有限差分算子精度误差曲线(二阶导数) (a)精度误差曲线;(b)精度误差曲线放大1000倍.Fig. 8 Accuracy errorfor second derivative of auto-convolution window truncated finite-difference operators with different N(different order) (a)Accuracy error;(b)Magnified 1000 times. |
将该自褶积组合窗函数截断逼近的有限差分算子与改进的二项式窗函数截断逼近的有限差分算子(Chu and Stoffa, 2012)的精度误差曲线相比较,对比结果见图 9.图 9a说明8阶的自褶积组合窗函数截断逼近的有限差分算子精度误差曲线的谱覆盖范围不如8阶的改进的二项式窗函数截断逼近的有限差分算子精度误差曲线,但是其精度误差稳定性大大提高,8阶的改进的二项式窗函数截断逼近的有限差分算子精度误差曲线围绕零点出现巨大的波动.对于16阶和24阶的情况,自褶积组合窗函数截断逼近的有限差分算子精度误差曲线谱覆盖范围要大于改进的二项式窗函数截断逼近的有限差分算子精度误差曲线;16阶的自褶积组合窗函数截断逼近的有限差分算子精度高于24阶的改进的二项式窗函数截断逼近的有限差分算子精度;图 9b是将图 9a放大1000倍之后的精度误差曲线,自褶积组合窗函数截断逼近的有限差分算子在低波数时的精度误差曲线波动要小于同条件的改进的二项式窗函数截断逼近的有限差分算子的精度误差曲线.
 | 图 9 不同N的自褶积组合窗函数截断逼近的有限差分算子与改进的二项式窗函数截断逼近的有限差分算子的精度误差比较(二阶导数) (a)精度误差曲线;(b)精度误差曲线放大1000倍.Fig. 9 Comparison of accuracy error for second derivative between auto-convolution window truncated finite-difference operators and improved Binomial window truncated finite-difference operators with different N(different order) (a)Accuracy error;(b)Magnified 1000 times. |
表 1列出了该自褶积组合窗函数截断逼近的有限差分算子系数(二阶导数).
| 表 1 自褶积组合窗函数截断逼近的有限差分算子系数(二阶导数)Table 1 Auto-convolution window truncated finite-difference operates coefficients for the second derivative |
对于一阶导数的情况,引入误差函数:
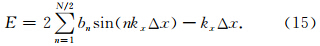
图 10展示了该自褶积组合窗函数截断逼近的有限差分算子在不同阶数时的精度误差曲线(一阶导数).对于一阶导数,自褶积组合窗函数截断逼近的有限差分算子的精度误差曲线在频谱覆盖范围和误差稳定性方面相比于常规有限差分算子也有较好的结果.
 | 图 10 不同N的自褶积组合窗函数截断逼近的有限差分算子精度误差曲线(一阶导数) (a)精度误差曲线;(b)精度误差曲线放大1000倍.Fig. 10 Accuracy error for first derivative of auto-convolution window truncated finite-difference operators with different N(different order) (a)Accuracy error;(b)Magnified 1000 times |
表 2列出了该自褶积组合窗函数截断逼近的有限差分算子系数(一阶导数).
| 表 2 自褶积组合窗函数截断逼近的有限差分算子系数(一阶导数)Table 2 Auto-convolution window truncated finite-difference operates coefficients for the first derivative |
线性弹性理论的假设下,可以建立应变张量和位移之间的联系,可得:
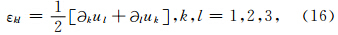

从应力表示的动力学平衡方程出发,不考虑体积力的影响,得到弹性动力学方程:

在这个部分,我们做一个脉冲响应的数值模拟,比较8阶Chebyshev自褶积组合窗截断逼近的优化有限差分算子和常规8阶,12阶有限差分算子数值模拟的效果.定义二维各向同性介质,网格大小为 255×300,网格间距为5 m,纵波速度为2000 m·s-1,横波速度为1500 m·s-1,ρ=1000 kg·m-3.点源 在中间激发,采用主频为50 Hz的Ricker子波,Δt=0.5 ms,nt=3000.
图 11是250 ms的波场快照.从波场快照上可以清晰地看出,图 11a的X和Z分量都存在较明显的数值频散,图 11b采用我们的优化有限差分算子,能够有效地压制数值频散,相比图 11c采用常规12阶有限差分算子的数值模拟结果,我们的优化8阶有限差分算子有更好的效果.
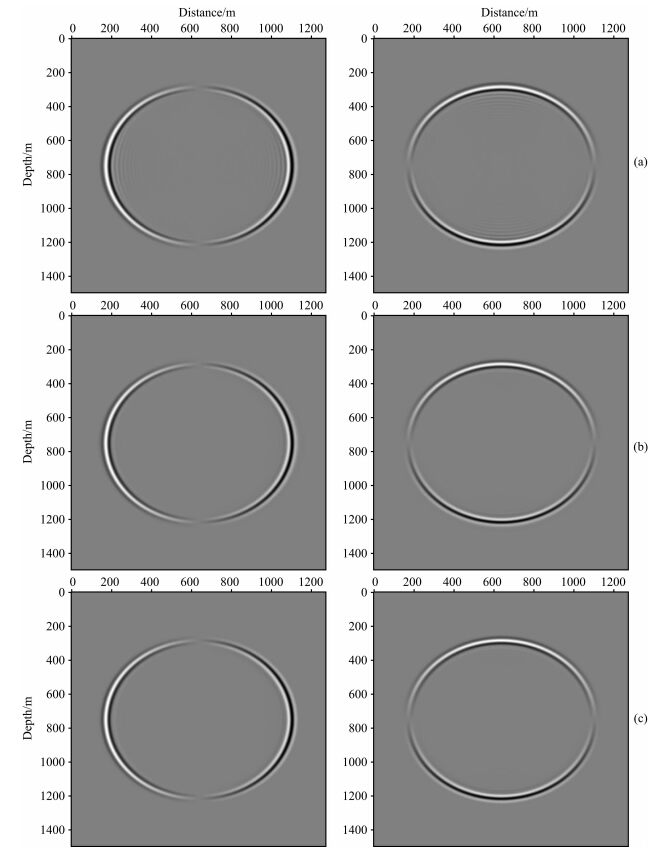 | 图 11 Chebyshev自褶积组合窗优化有限差分算子和常规有限分算子脉冲响应波场快照对比(250 ms) (a)采用常规8阶算子;(b)采用优化8阶算子;(c)采用常规12阶算子.左图为X分量,右图为Z分量.Fig. 11 Comparison of snapshot of impulse responses before and after using our optimized operators(250 ms) (a)Using the 8th conventional operator;(b)Using the 8th optimized operator;(c)Using the 12th conventional operator. left is X component,right is Z component. |
脉冲响应的数值模拟证明,Chebyshev自褶积组合窗截断逼近的优化有限差分算子在压制频散上较常规方法更有优势.
3.2 Marmousi模型为了进一步检测我们的优化的有限差分算子,对复杂的Marmousi模型进行数值模拟测试.速度模型大小为737×750,横向采样间隔为12.5 m,纵向采样间隔为4 m. vS=vP/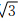 ,ρ=1000 kg·m-3.采用主频为30 Hz的Ricker子波,震源位置在表面,Δt=0.5 ms,nt=10000.图 12是Marmousi速度模型.
,ρ=1000 kg·m-3.采用主频为30 Hz的Ricker子波,震源位置在表面,Δt=0.5 ms,nt=10000.图 12是Marmousi速度模型.
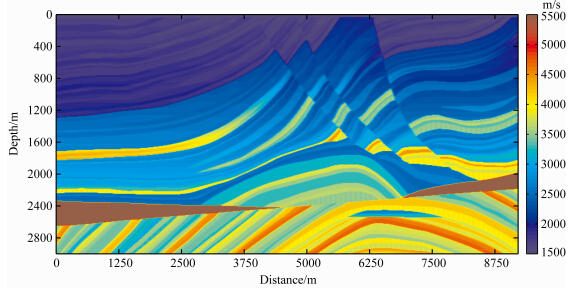 | 图 12 Marmousi速度模型Fig. 12 Marmousi velocity model |
采用的GPU型号是GTX 550TI,有192个计算核心和1 GB的显存,CUDA版 本是4.2,CPU型号是Intel(R)Core i5 2300 @2.8 GHz,配有8 GB内存.分别应用8阶,12阶,16阶,24阶的常规和优化的有限差分算子进行计算效率对比测试,并且选择5个不同的炮点位置,炮点1对应x=0.0 m,炮点2对应x=2303.1 m,炮点3对应x= 4606.3 m,炮点4对应x=6909.4 m,炮点5对应x=9212.5 m.
表 3和表 4分别列出了不同阶数的优化和常规的有限差分算子在Marmousi模型上的测试时间.
| 表 3 不同阶数的优化有限差分算子在Marmousi模型上的计算时间对比Table 3 Comparison of computation cost using different orders auto-convolution window truncated finite-difference operators |
| 表 4 不同阶数的常规有限差分算子在Marmousi模型上的计算时间对比Table 4 Comparison of computation cost using different orders conventional finite-difference operators |
图 13显示了常规8阶,12阶有限差分算子和8阶Chebyshev自褶积组合窗截断逼近的有限差分算子的炮记录的Z分量,炮点在中间位置.
 | 图 13 Chebyshev自褶积组合窗优化的有限差分算子和常规有限差分算子模拟炮记录对比(Z分量) (a)单炮记录(左侧图采用常规8阶算子,中间图采用优化8阶算子,右侧图采用常规12阶算子);(b)区块1放大炮记录;(c)区块2放大炮记录;(d)区块3放大炮记录.Fig. 13 Comparison of a shot record for the Marmousi model computed by the conventional finite-difference operators and auto-convolution window truncated finite-difference operators(Z component) (a)One shot record(left using the 8th conventional operator,middle using the 8th optimized operator,right using the 12th conventional operator);(b)Zoomed in view of a shot record(Block 1);(c)Zoomed in view of a shot record(Block 2);(d)Zoomed in view of a shot record(Block 3). |
如果将图 13a整体放大,可以观察到图 13a左侧图有明显的数值频散,中间图采用我们的优化算子,数值频散得到较大的压制,相比右侧图采用常规12阶算子有更好的数值模拟结果.现将图 13a中频散较明显的三个区块放大,绘制图 13b,13c,13d.图 13b是图 13a中区块1的放大,可以清晰地观察到,左侧图存在比较明显的频散现象;而中间图数值频散得到了较好的压制,且要略优于右侧采用常规12阶算子的数值模拟结果.图 13c是图 13a中区块2的放大,比较图 13c的左中右三图,可以发现采用8阶Chebyshev自褶积组合窗截断逼近的优化有限差分算子压制数值频散效果更明显.图 13d是图 13a中区块3的放大,图 13d左侧图采用常规8阶有限差分算子模拟,可以发现同相轴存在较为明显的频散现象,即出现较长的“拖尾”,中间图采用8阶Chebyshev自褶积组合窗截断逼近的优化有限差分算子模拟,很大程度地抑制了数值频散,压制效果是图 13d三图中最好的.
Marmousi模型的数值模拟也证明,Chebyshev 自褶积组合窗截断逼近的优化有限差分算子在压制频散上较常规方法更有优势.
4 结论本文分析了改进二项式窗函数和三角函数类窗函数的优缺点,提出了一种基于Chebyshev自褶积组合窗函数截断逼近的有限差分算子优化方法.在空间域,有限差分法可看作是伪谱法空间褶积序列的截断.截断窗函数对有限差分算子逼近微分算子精度的影响,从本质上来讲,是由其幅值响应的主瓣和旁瓣属性所决定的;其主瓣越窄,旁瓣衰减越大,逼近的效果越好,数值频散压制得更彻底.基于Chebyshev自褶积组合窗函数拥有较好的主旁瓣属性,与改进的二项式窗相比较,该窗函数截断逼近的有限差分算子的精度误差曲线拥有更大的谱范围,另外,有比三角函数类窗函数截断逼近的有限差分算子更大的精度误差稳定性,且可只调节三个参数,直观可视化地控制主瓣和旁瓣的形状,进而调整有限差分算子逼近微分算子的精度,这也是窗函数截断逼近优化的一个优点.
本文提出的优化有限差分算子比常规有限差分算子有更高的精度.本文定义了自褶积窗函数的三个参数为λ=0.89,r=60,L=2,得到8阶的Chebyshev自褶积组合窗截断逼近的有限差分算子的精度超过了12阶常规有限差分算子;12阶的Chebyshev自褶积组合窗截断逼近的有限差分算子的精度超过了24阶常规有限差分算子;另外,通过该自褶积组合窗截断逼近的有限差分算子的精度误差在0.0004之内;在脉冲响应和Marmousi模型上的测试,都证实了该方案在压制数值频散的有效性.也可以通过选择不同的窗函数参数,调节加权组合系数和自褶积次数,达到谱覆盖范围和稳定性的一个优选.
| [1] | Alterman Z, Karal F C Jr. 1968. Propagation of elastic waves in layered media by finite difference methods. Bulletin of Seismological Society of America, 58(1): 367-398. |
| [2] | Boris J P, Book D L. 1973. Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works. Journal of Computational Physics, 11(1): 38-69. |
| [3] | Carcione J M, Kosloff D, Behle A, et al. 1992. A spectral scheme for wave propagation simulation in 3-D elastic-anisotropic media. Geophysics, 57(12): 1593-1607, doi: 10.1190/1.1443227. |
| [4] | Cheng B J, Li X F, Long G H. 2008. Seismic waves modeling by convolutional Forsyte polynomial differentiator method. Chinese J. Geophys. (in Chinese), 51(2): 531-537. |
| [5] | Chu C L, Stoffa P L. 2012. Determination of finite-difference weights using scaled binomial windows. Geophysics, 77(3): W17-W26, doi: 10.1190/GEO2011-0336.1. |
| [6] | Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66, doi: 10.1190/1.1442040. |
| [7] | Diniz P S R, da Silva E A B, Netto S L. 2012. Digital Signal Processing System Analysis and Design. Beijing: China Machine Press. |
| [8] | Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation. Chinese J. Geophys. (in Chinese), 43(3): 411-419. |
| [9] | Fornberg B. 1987. The pseudospectral method: Comparisons with finite differences for the elastic wave equation. Geophysics, 52(4): 483-501, doi: 10.1190/1.1442319. |
| [10] | Gazdag J. 1981. Modeling of the acoustic wave equation with transform methods. Geophysics, 46(6): 854-859, doi: 10.1190/1.1441223. |
| [11] | Holberg O. 1987. Computational aspects of the choice of operator and sampling interval for numerical differentiation in large-scale simulation of wave phenomena. Geophysical Prospecting, 35(6): 629-655, doi: 10.1111/j.1365-2478.1987.tb00841.x. |
| [12] | Igel H, Mora P, Riollet B. 1995. Anisotropic wave propagation through finite-difference grids. Geophysics, 60(4): 1203-1216, doi: 10.1190/1.1443849. |
| [13] | Kelly K R, Ward R W, Treitel S, et al. 1976. Synthetic seismograms: A finite-difference approach. Geophysics, 41(1): 2-27, doi: 10.1190/1.1440605. |
| [14] | Kosloff D D, Baysal E. 1982. Forward modeling by a Fourier method. Geophysics, 47(10): 1402-1412, doi: 10.1190/1.1441288. |
| [15] | Lee C, Seo Y. 2002. A new compact spectral scheme for turbulence simulations. Journal of Computational Physics, 183(2): 438-469, doi: 10.1006/jcph.2002.7201. |
| [16] | Liu Y, Li C C, Mou Y G. 1998. Finite-difference numerical modeling of any even-order accuracy. OGP (in Chinese), 33(1): 1-10. |
| [17] | Liu Y, Sen M K. 2009a. A new time-space domain high-order finite-different method for the acoustic wave equation. Journal of Computational Physics, 228(23): 8779-8806, doi: 10.1016/j.jcp.2009.08.027. |
| [18] | Liu Y, Sen M K. 2009b. Numerical modeling of wave equation by a truncated high-order finite-difference method. Earthquake Science, 22(2): 205-213, doi: 10.1007/s11589-009-0205-0. |
| [19] | Liu Y, Sen M K. 2010. Acoustic VTI modeling with a time-space domain dispersion-relation-based finite-difference scheme. Geophysics, 75(3): A11-A17, doi: 10.1190/1.3374477. |
| [20] | Liu Y. 2013. Globally optimal finite-difference schemes based on least squares. Geophysics, 78(4): T113-T132, doi: 10.1190/geo2012-0480.1. |
| [21] | Pei Z L, Mou L G. 2003. A staggered-grid high-order difference method for modeling seismic wave propagation in inhomogeneous media. Journal of China University of Petroleum (Edition of Natural Science) (in Chinese), 27(6): 17-27. |
| [22] | Robertsson J O A, Blanch J O, Symes WW, et al. 1994. Galerkin-wavelet modeling of wave propagation: Optimal finite-difference stencil design. Mathematical and Computer Modelling, 19(1): 31-38, doi: 10.1016/0895-7177(94)90113-9. |
| [23] | Yan H Y, Liu Y. 2013a. Visco-acoustic prestack reverse-time migration based on the time-space domain adaptive high-order finite-difference method. Geophysical Prospecting, 61(5): 941-954, doi: 10.1111/1365-2478.12046. |
| [24] | Yan H Y, Liu Y. 2013b. Pre-stack reverse-time migration based on the time-space domain adaptive high-order finite-difference method in acoustic VTI medium. Journal of Geophysics and Engineering, 10(1): 015010, doi: 10.1088/1742-2132/10/1/015010. |
| [25] | Yang D H, Teng J W. 1997. FCT finite difference modeling of three-component seismic records in anisotropic medium. OGP (in Chinese), 32(2): 181-190. |
| [26] | Yang L, Yan H Y, Liu H. 2014. Least squares staggered-grid finite-difference for elastic wave modelling. Exploration Geophysics, 45(4): 255-260, doi: 10.1071/EG13087. |
| [27] | Zhang J H, Yao Z X. 2013. Optimized finite-difference operator for broadband seismic wave modeling. Geophysics, 78(1): A13-A18, doi: 10.1190/GEO2012-0277.1. |
| [28] | Zhou B, Greenhalgh S A. 1992. Seismic scalar wave equation modeling by a convolutional differentiator. Bulletin of the Seismological Society of America, 82(1): 289-303. |
| [29] | 程冰洁, 李小凡, 龙桂华. 2008. 基于广义正交多项式褶积微分算子的地震波场数值模拟方法. 地球物理学报, 51(2): 531-537. |
| [30] | 董良国, 马在田, 曹景忠等. 2000. 一阶弹性波方程交错网格高阶差分解法. 地球物理学报, 43(3): 411-419. |
| [31] | 刘洋, 李承楚, 牟永光. 1998. 任意偶数阶精度有限差分法数值模拟. 石油地球物理勘探, 33(1): 1-10. |
| [32] | 裴正林, 牟永光. 2003. 非均匀介质地震波传播交错网格高阶有限差分法模拟. 石油大学学报(自然科学版), 27(6): 17-27. |
| [33] | 杨顶辉, 腾吉文. 1997. 各向异性介质中三分量地震记录的FCT有限差分模拟. 石油地球物理勘探, 32(2): 181-190. |
 2015, Vol. 58
2015, Vol. 58


