Taking statistical property of seismic random noise into account, we propose a Shapiro-Wilk (SW) statistic based adaptive time-frequency peak filtering (S-TFPF) to suppress seismic random noise in seismic data at low SNR. The SW test, a statistical method for the measurement of Gaussianity of time series, is introduced into TFPF method. Based on the assumption that seismic random noise usually is white Gaussian noise and seismic signals are non-Gaussian, the SW statistics of seismic random noise are different from those of seismic signals. Therefore, the seismic signals in seismic data can be identified by means of the SW statistics. Furthermore, Gaussianization of seismic data is done by applying a band-pass filter to seismic data, which makes complex seismic random noise Gaussian and keep seismic signals. As a result, the accuracy of identification of valid signals under complex seismic random noise is improved based on SW statistics. Then, adaptively adjusting window length of S-TFPF is implemented based on the SW statistics. In this algorithm, the window length of S-TFPF in the signal-dominant segment are set according to the frequencies of signals to preserve signals, whereas the window length of S-TFPF for noise-dominant segment increases with the variance of noise increasing, so as to completely eliminate seismic random noise.
The Gaussianity of seismic noise data is investigated by SW test and the performance of new method is analyzed on synthetic data and field data. The SW test result show that most seismic random noise are non-Gaussian noise and their SW statistics are lower than but close to the SW statistic of ideal Gaussian noise. The significant difference of the SW statistics exists between random noise and seismic signals. However, the difference of SW statistic of noisy seismic data decreases, because signals are contaminated by seismic random noise and properties of seismic random noise are complex. After preprocessing seismic data by means of Gaussianization, the SW statistics of seismic random noise becomes closer to 1 and the SW statistics of seismic signals slightly decrease, which leads to an accurate segmenting of seismic signal and seismic random noise. Then the adaptive window length of the S-TFPF is obtained based on the SW statistics and apply to processing synthetic and field seismic data. The results show that the S-TFPF method better keeps the amplitude and frequency component of filtered seismic signals than the TFPF. Furthermore, the filtered seismic data obtained by the S-TFPF has higher SNR and lower mean square error comparing with the TFPF. Application to the field data shows that the filtered seismic data by using S-TFPF has less background noise and more continuous seismic events.
The proposed method improves the adaptability of window length of the TFPF using SW statistics of seismic data. In the new method, the window length can be adapted at different segments of seismic data according to characteristics of seismic signals and statistical property of seismic random noise, respectively, thus reducing the bias of seismic signal estimation and improving denoising performance of the TFPF. The results of synthetic and field data demonstrate the practicability and effectiveness of the S-TFPF method.
随着国民经济对矿产资源需求的增长,利用地震勘探方法探查矿产资源逐步向深部矿床发展(Tang et al.,2013;梁锋等,2014;祁光等,2014;肖晓等,2014),所获得的地震勘探记录信噪比低,且噪声性质复杂,严重干扰了地震勘探记录中有效信号的辨识及后续处理.因此,压制低信噪比地震勘探记录中的复杂随机噪声、提取有效信号,在地震勘探信号处理中尤为重要(徐明才等,2004).近年来,人们先后发展了多种金属矿区地震勘探噪声压制方法.韩佳君等(2010)基于波动方程理论对散射噪声进行压制,并取得了很好的噪声压制效果.王权峰等(2012)将小波方法和盲分离JADE算法结合压制金属矿原始记录中的强噪声.针对金属矿区地震数据噪声种类多的特点,李阳等(2012)联合F-K滤波,Radon变换方法和Curvelet变换对金属矿区地震数据进行降噪处理,噪声压制效果显著.然而,传统噪声压制方法对低信噪比地震勘探记录中随机噪声压制和有效信号保持效果不理想.
时频峰值滤波(TFPF)方法是一种适合于低信噪比记录的信号增强方法(Boashash and Mesbah,2004).近年来,TFPF应用于地震勘探随机噪声压制,在处理低信噪比地震勘探记录方面具有一定的优势(林红波等,2011;Li et al.,2013; Lin et al.,2013).时频峰值滤波方法无失真地恢复信号的条件是噪声为高斯白噪声,信号接近线性.然而,实际地震资料无法完全满足信号线性的假设,导致TFPF估计强非线性地震勘探信号时存在偏差.传统时频峰值滤波方法通过减小时窗长度,使信号局部线性化,从而降低地震信号估计偏差.但较短的窗长弱化了噪声的高斯白性质,导致时频峰值滤波方法去噪能力降低.因此,为了在压制随机噪声同时有效保持信号,时频峰值滤波方法采用时变窗长滤波方案.时变窗长TFPF方法的总体思想是,利用地震信号特征将地震记录划分为信号区和噪声区,在信号集中部分采用较小时窗参数,满足信号无偏估计的线性条件;在噪声区采用较大的时窗参数,更好地压制噪声,其中噪声和信号的精确划分至关重要(Lin et al.,2014,2015; Zhang et al.,2015).但在强复杂噪声背景下,仅考虑信号特征而不考虑噪声特性,很难准确辨识低信噪比地震勘探记录中的有效信号,导致时变窗长时频峰值滤波去噪效果不理想.
本文结合随机噪声统计特性,提出了基于Shapiro-Wilk(SW)统计量的自适应时频峰值滤波方法(S-TFPF).Shapiro-Wilk算法是对时间序列高斯性检验的有效方法,利用统计学中的SW高斯性检验对地震记录测量可知,SW统计量值陡然变低部分对应于地震反射信号.因此,可根据SW统计量划分地震勘探记录中的有效信号和随机噪声,分区域调整时频峰值滤波时窗参数,在噪声集中区采用较长时窗,而在信号集中部分选择有利于信号无偏估计的较短时窗,提高时频峰值滤波方法压制随机噪声且无失真恢复有效信号的能力.
本文结构安排如下,首先简述时频峰值滤波算法原理;然后根据SW检验分析地震勘探随机噪声性质,并在此基础上提出S-TFPF方法;最后,通过合成数据和实际资料处理对该方法进行了验证.
2 时频峰值滤波原理地震勘探记录可以表示为反射信号与随机噪声的叠加,公式为

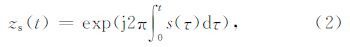
然后,TFPF通过求取解析信号的伪维格纳-威力分布(PWVD)的峰值,获得有效信号的估计为

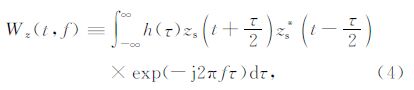
分析TFPF原理可知,TFPF方法通过频率调制过程,将有效信号编码为解析信号zs(t)的瞬时频率,再通过求解解析信号时频分布的峰值频率估计瞬时频率.若有效信号x(t)是关于时间的线性函数,且噪声为高斯白噪声,TFPF可以获得有效信号的无偏估计.然而,地震勘探信号为时间的非线性函数,且随机噪声性质复杂,TFPF处理实际地震勘探数据时难以完全满足信号无偏估计条件.在实际应用中,TFPF通过减小时窗长度,使解析信号的瞬时频率在时窗内近似线性,从而降低信号估计的偏差,更好地恢复有效地震信号.但较短的时窗长度降低TFPF去噪效果.因此,采用固定窗长的时频峰值滤 波方法难以同时改善随机噪声压制和信号保持效果.
为了在压制复杂随机噪声过程中有效保持信号,TFPF方法应根据信号和噪声特性自适应调整时窗参数,这就需要在滤波前划分出地震勘探记录中的有效信号和噪声区域.在地震勘探信号处理中,通常假设地震勘探随机噪声服从高斯分布,而地震反射信号为非高斯信号,他们的高斯统计特性存在较大差异.本文引入SW高斯性检验方法,借助地震勘探随机噪声和有效信号SW统计量的差异,辨识地震勘探记录中的有效信号.
3 基于SW统计量的自适应TFPF 3.1 SW检验SW检验算法是检验随机序列非高斯性的统计学方法(Shapiro and Wilk,1965).其基本思想是在数据服从正态分布的假设下,利用线性回归计算SW检验统计量,度量待测数据顺序统计量与标准高斯分布顺序统计量的相关程度.相关程度越高,待 测数据越近似服从正态分布.SW检验统计量定义为

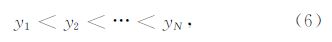
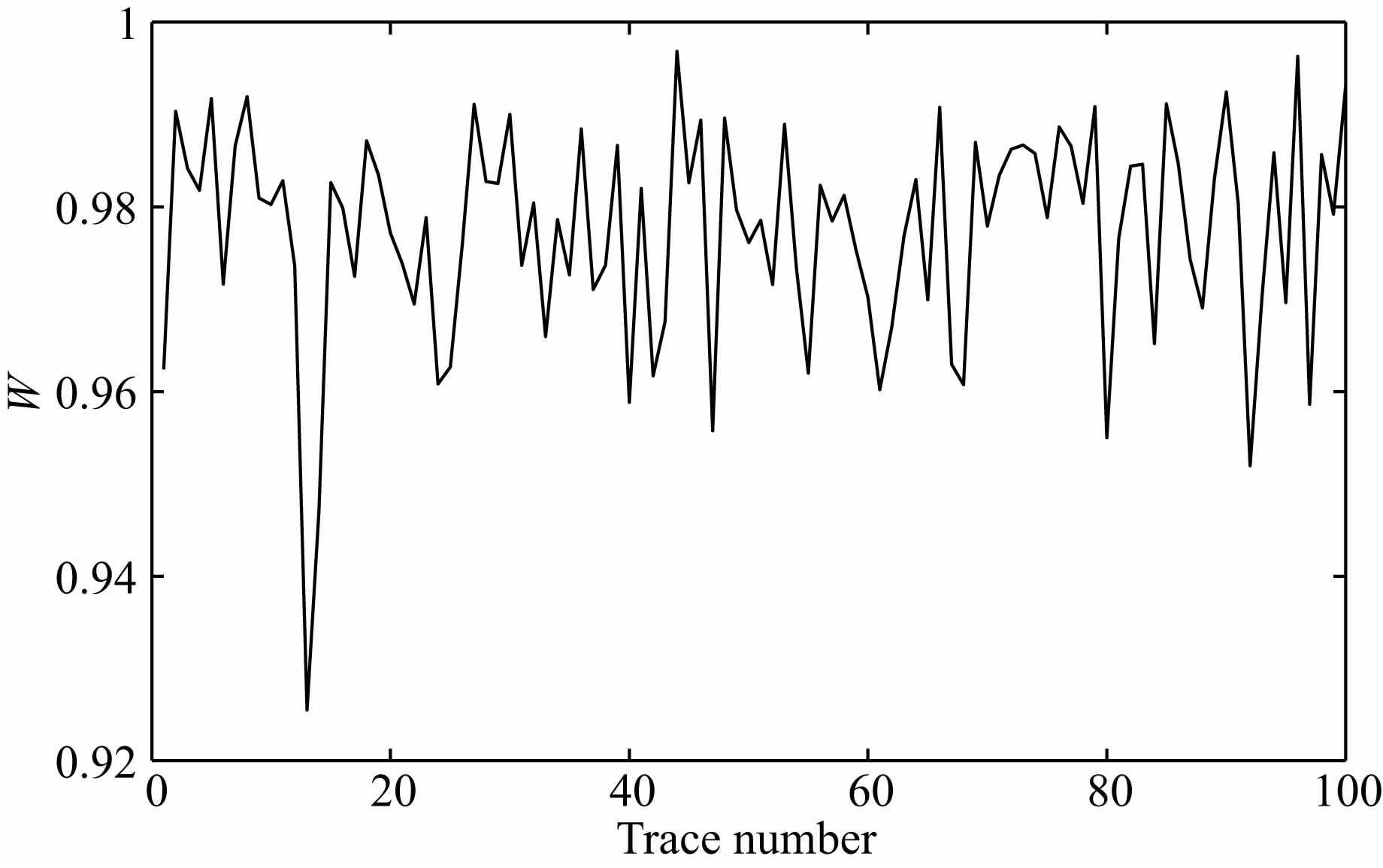
利用SW检验算法,我们分析了沙漠某矿区100道地震勘探随机噪声记录,如图 1所示.我们首先对该随机噪声记录进行SW检验,SW检验结果如图 2所示.对SW检验结果进行统计可知,在5%的置信区间下,97%的噪声记录的SW检验结果低于高斯判决门限(横线),被判定为非高斯噪声.由此可知,地震勘探随机噪声不满足理想高斯分布假设,具有非高斯性.我们进一步计算随机噪声记录的SW统计量W,并与理想高斯白噪声和模拟地震信号的SW统计量进行比较.随机噪声的SW统计量 值在0.926到0.997之间变化(图 3),平均值为0.985(表 1). 与之相比,理想高斯白噪声的SW统计量的平均值为0.998,接近1;而由Ricker子波构建的模拟地震 信号的SW统计量W的值仅为0.297,接近0(表 1). 对比分析上述结果表明,地震勘探随机噪声记录非高斯性较弱,其SW统计量与理想高斯噪声接近,与有效信号相比差异较大.

|
图 1 地震勘探随机噪声记录 Fig. 1 Seismic random noise data |

|
图 2 地震勘探噪声高斯性检验结果 Fig. 2 The result of Gaussianity test of seismic random noise |
|
图 3 地震勘探噪声高斯性检验统计量 Fig. 3 The statistic of Gaussianity test for seismic random noise |
|
|
表 1 噪声和信号的高斯性统计量值对比 Table 1 Comparison of W between signal and noise |
我们进一步分析含噪记录的SW统计量.在处理实际金属矿地震勘探记录时,由于随机噪声性质较为复杂,随机噪声的SW统计量的值会有所降低.另一方面,由于有效信号受到随机噪声的干扰,含噪有效信号的SW统计量与无噪情况下相比有所提高.因此地震勘探记录的信号部分与噪声部分的SW统计量差异变小,不利于区分随机噪声和有效信号.此外,TFPF获得无偏估计的条件为噪声服从高斯分布,复杂的非高斯噪声不利于TFPF对有效信号进行保真恢复.因此,我们引入高斯化方法对地震勘探记录预处理,增强随机噪声的高斯性,并尽可能地保持有效信号不变,进而扩大有效信号和随机噪声SW统计量的差异,提高基于SW统计量划分有效信号和噪声的精准度.
高斯化的理论基础为,若系统输入为非高斯分布的平稳随机过程,且输入过程的等效噪声带宽远大于系统的通频带,则可得到接近高斯分布的随机过程(张坚等,2011).基于高斯化思想,本文设计等波纹带通滤波器预处理地震勘探记录,并使其通频带范围与有效信号带宽一致.由于非高斯地震勘探随机噪声为平稳随机过程,其带宽远大于等波纹带通滤波器的通频带,因此利用该等波纹带通滤波器预处理地震勘探记录,可以将地震勘探随机噪声高斯化,且保持地震勘探信号不变.
我们以加入实际勘探噪声的模拟地震信号(图 4a)为例分析高斯化前后SW统计量的变化.采用以当前点为中心,窗长为100采样点的矩形滑动窗截取样本序列,分别计算样本序列的SW统计量和高斯化SW统计量.含噪记录中有效信号区的SW统计量W的值低于地震勘探噪声集中区的W值(图 4b中虚线),但对应于反射信号的W值与噪声的W值差异不大;经高斯化处理后(黑线),信号的W值降低,而随机噪声高斯化SW统计量的值增加到1附近,高斯化处理加大了噪声和信号SW统计量的差异.上述结果表明,高斯化SW统计量值陡然下降对应于有效地震信号,能更好地辨识地震勘探记录中有效信号.

|
图 4 含噪信号高斯检验统计量 (a)含实际噪声的合成记录;(b)含噪记录高斯性统计量W. Fig. 4 SW statistic of noisy signal (a)Ricker wavelet with field seismic noise;(b)Values of SW statistic of noisy signal. |
本文将SW统计量引入TFPF方法,利用地震 勘探随机噪声和有效信号SW统计量的差异,提出基 于SW统计量的TFPF时窗长度的自适应调整方案.
基于SW的自适应时频峰值滤波(S-TFPF)方法首先对地震勘探记录高斯化预处理,然后对每道高斯化的地震数据,以第j个样本点为中心,采用滑动窗获取L个样本观测值,利用公式(5)计算SW统计量,记做第j个样本的SW统计量Wj.
自适应TFPF根据SW统计量的值计算窗长度系数为
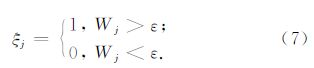
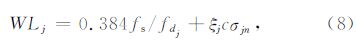
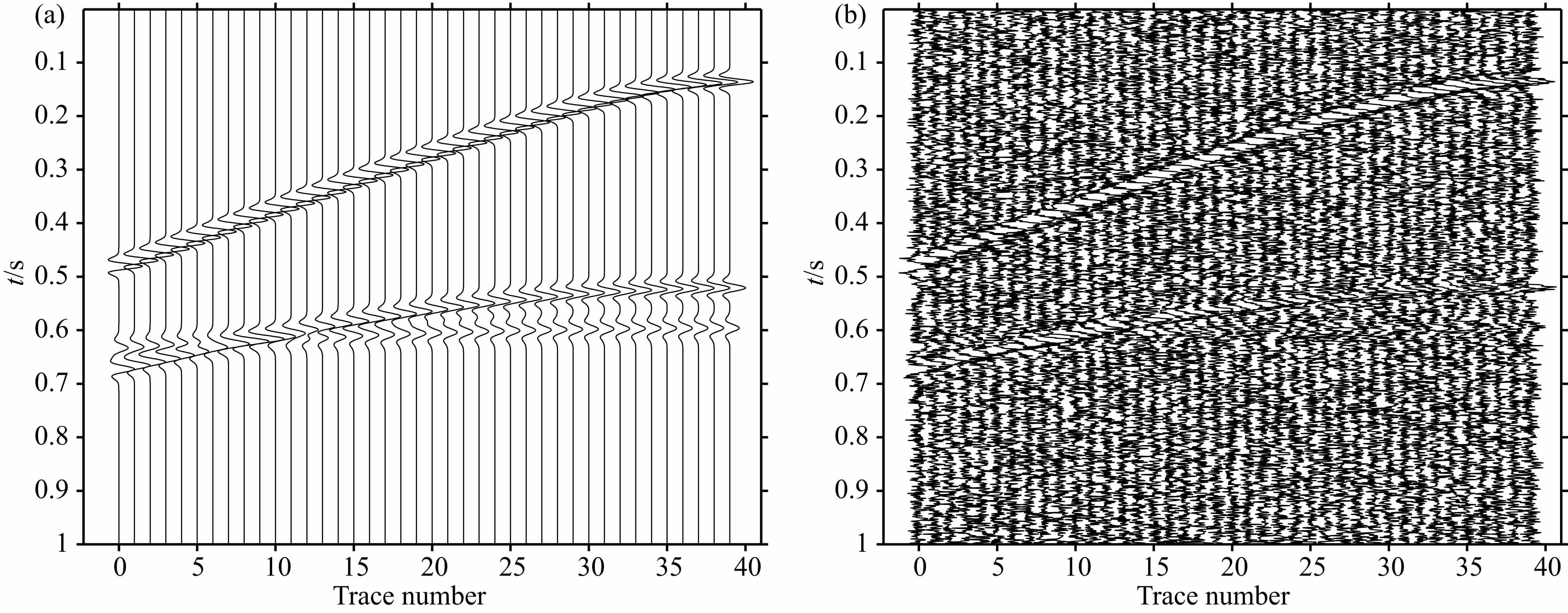
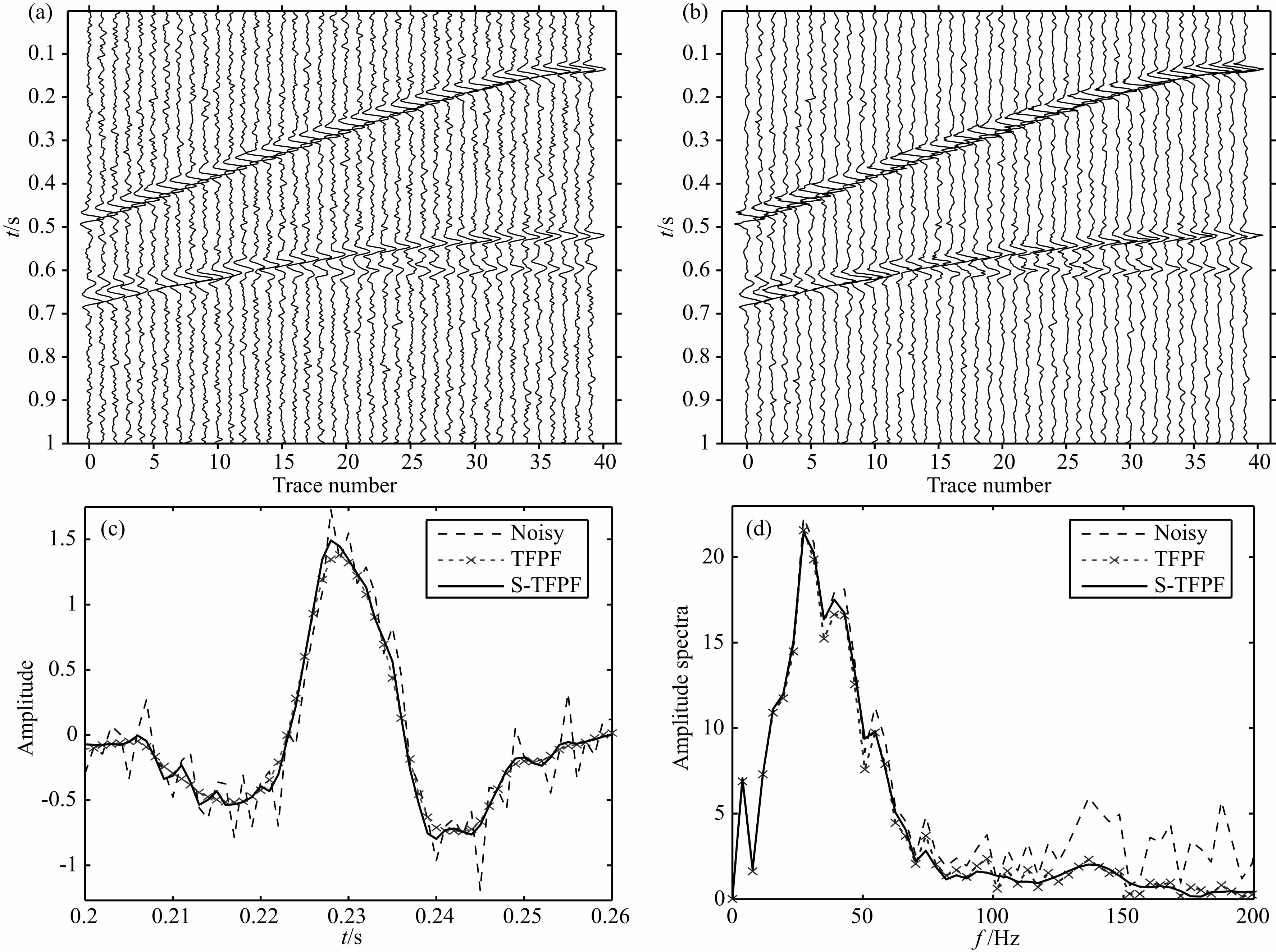
为了验证S-TFPF方法的有效性,本文将其应用于合成地震勘探记录.图 5a为采用Ricker子波构建的40道合成记录,包含三个同相轴,视主频分别为45 Hz、30 Hz和25 Hz,采样间隔为1 ms.图 5b所示的含噪合成记录存在较强随机噪声,信噪比 为-5 dB.对含噪声地震记录分别采取固定窗长为13样本点的TFPF和S-TFPF方法降噪处理.与TFPF滤波结果(图 6a)相比,S-TFPF 滤波结果的背景更干净,同相轴更清晰、连续(图 6b).可见,S-TFPF在噪声压制和信号保持方面较TFPF方法得到改善.为进一步分析S-TFPF滤波效果,任取一道滤波结果进行时域波形对比和频谱分析.从图 6c可以看出,与TFPF滤波结果(虚线)相比,S-TFPF滤波信号(实线)的幅度保持得更好,图 6d中频谱对比也可见,S-TFPF方法对信号能量保持更好.上述结果表 明,自适应窗长的S-TFPF具有更好地信号保持效果.
|
图 5 含噪合成记录
(a)合成记录;(b)含噪记录. Fig. 5 Noisy synthetic seismic data (a)Synthetic data;(b)Noisy data. |
|
图 6 含噪合成记录降噪结果
(a)TFPF结果;(b)S-TFPF降噪结果;(c)第25道滤波结果波形对比;(d)第25道滤波结果幅度谱对比. Fig. 6 Filtering result of noisy synthetic data (a)Result of TFPF;(b)Result of S-TFPF;(c)Comparison of waveforms of the 25th filtered trace;(d)Comparison of spectra of the 25th filtered trace. |
为了定量地描述滤波效果,分别对TFPF和S-TFPF滤波结果的信噪比(SNR)和均方误差(MSE)进行比较(表 2),SNR和MSE分别表示为

|
|
表 2 信噪比和均方误差比较 Table 2 Comparison of SNRs and MSEs |
实际资料处理时采用某矿区168道共炮点记录,道间距为30 m,采样间隔为1 ms(图 7).该记录中可见大量随机噪声存在,同相轴被随机噪声中断而不易辨识.
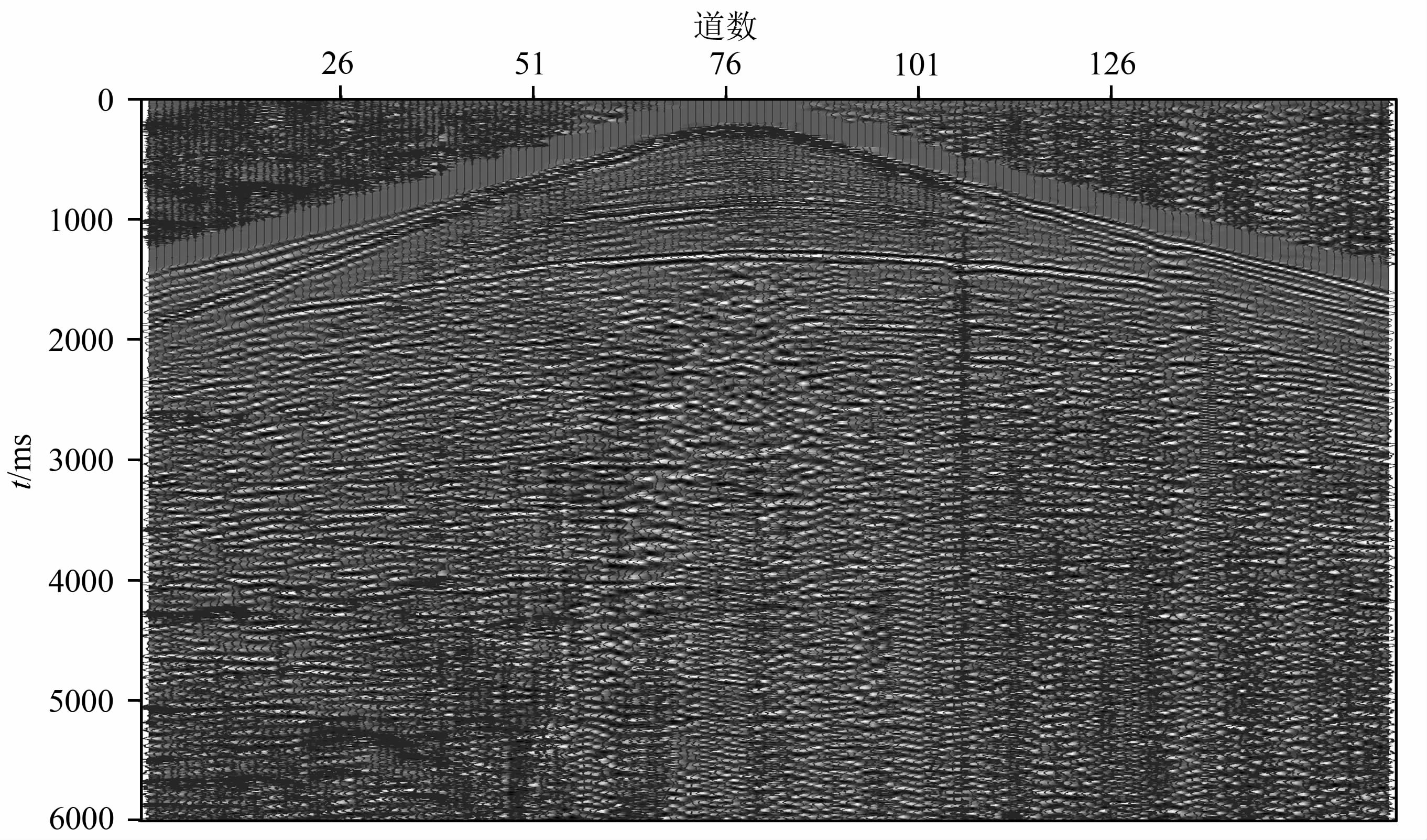
|
图 7 某矿区实际记录 Fig. 7 Field data from some area |
分别采用TFPF和S-TFPF方法处理共炮点记 录,TFPF窗长为13采样点.从图 8a可见,经TFPF处理后,地震勘探记录质量有较大改善,大部分随机噪声都已消除,但对方框区域深层噪声压制不彻底.采用S-TFPF方法处理结果如图 8b所示,S-TFPF方法在噪声较强区域增加了窗长,有效压制了强噪声,TFPF滤波结果中的残留噪声在S-TFPF处理结果中得到有效压制;与此同时,S-TFPF对有效信号降低窗长,处理后的同相轴更加连续.

|
图 8 实际地震勘探记录滤波结果
(a)时频峰值滤波结果;(b)本文方法的滤波结果. Fig. 8 Filtering data of field seismic data (a)Result of using TFPF;(b)Result of using S-TFPF. |
分析上述结果表明:(1)S-TFPF方法基于SW统计量可精确地划分地震记录中的有效信号和随机噪声;(2)S-TFPF方法能够自适应调节时窗长度,在消减复杂随机噪声过程中有效保持地震信号幅度.
5 结论本文针对时频峰值滤波时窗参数选择问题,利用地震勘探噪声高斯统计特性,结合SW统计量建立自适应时频峰值滤波方法(S-TFPF),并应用于地震勘探复杂随机噪声压制.本文提出的S-TFPF方法利用高斯化SW统计量,提高分离地震勘探记录中复杂随机噪声和有效信号的精准度,从而实现地震勘探记录不同区域的时窗长度自适应调节,解决了传统固定窗长TFPF对随机噪声压制不彻底和信号幅度衰减问题.仿真实验和实际地震勘探记录处理结果表明,与传统TFPF相比,S-TFPF方法在压制复杂地震勘探随机噪声同时,更好地保持了地震勘探信号信息,在低信噪比地震勘探记录随机噪声压制方面具有一定的优势.
| [1] | Boashash B, Mesbah M. 2004. Signal enhancement by time-frequency peak filtering. IEEE Transactions on Signal Processing, 52(4): 929-937. |
| [2] | Donoho D L. 1995. De-noising by soft-thresholding. IEEE Trans. Information Theory, 41(3): 613-627. |
| [3] | Han J J, Han L G, Gong X B, et al. 2010. Attenuation of near-surface scattering noise based on wave theory. Global Geology (in Chinese), 29(2): 310-313. |
| [4] | Li Y, Lü Q T, Han L G, et al. 2012. Application of serial de-noise method in seismic exploration of metal mine. Global Geology (in Chinese), 31(2): 406-411. |
| [5] | Li Y, Yang B J, Lin H B, et al. 2013. Suppression of strong random noise in seismic data by using time-frequency peak filtering. Science China Earth Sciences, 56(7): 1200-1208. |
| [6] | Liang F, Lü QT, Yan J Y, et al. 2014. Deep structure of Ningwu volcanic basin in the Middle and Lower reaches of Yangtze River: Insights from reflection seismic data. Acta Petrologica Sinica (in Chinese), 30(4): 941-956. |
| [7] | Lin H B, Li Y, Ma H T, et al. 2015. Matching-pursuit-based Spatial-trace time-frequency peak filtering for seismic random noise attenuation. IEEE Geoscience and Remote Sensing Letters, 12(2): 394-398. |
| [8] | Lin H B, Li Y, Xu X C. 2011. Segmenting time-frequency peak filtering method to attenuation of seismic random noise. Chinese J. Geophys. (in Chinese), 54(5): 1358-1366, doi: 10.3969/j.issn.0001-5733.2011.05.025. |
| [9] | Lin H B, Li Y, Yang B J, et al. 2013. Random denoising and signal nonlinearity approach by time-frequency peak filtering using weighted frequency reassignment. Geophysics, 78(6): V229-V237. |
| [10] | Lin H B, Li Y, Yang B J, et al. 2014. Seismic random noise elimination by adaptive time-frequency peak filtering. IEEE Geoscience and Remote Sensing Letters, 11(1): 337-341. |
| [11] | Qi G, Lü Q T, Yan J A, et al. 2014. 3D Geological modeling of Luzong Ore district based on priori information constrained. Acta Geologica Sinica (in Chinese), 88(4): 466-477. |
| [12] | Shapiro S S, Wilk M B. 1965. An analysis of variance test for normality (complete samples). Biometrika, 52(3-4): 591-611. |
| [13] | Tang J T, Zhou C, Wang X Y, et al. 2013. Deep electrical structure and geological significance of Tongling ore district. Tectonophysics, 606: 78-96. |
| [14] | Wang Q F, Xu D P, Zhan Z D, et al. 2012. Research on seismic data noise reduction in metallic ore based on wavelet domain blind source separation JADE algorithm. Scientific and Technological Management of Land and Resources (in Chinese), 29(6): 106-110. |
| [15] | Xiao X, Wang X Y, Tang J T, et al. 2014. Conductivity structure of the Lujiang-Zongyang Ore concentrated Area, Anhui Province: Constraints from Magnetotelluric Data. Acta Geologica Sinica (in Chinese), 88(4): 478-495. |
| [16] | Xu M C, Gao J H, Rong L X, et al. 2004. Application prospects of the seismic method as discussed from the experimental effects of the method for metal exploration. Geology in China (in Chinese), 31(1): 108-112. |
| [17] | Zhang C, Li Y, Lin H B, et al. 2015. Seismic random noise attenuation and signal-preserving by multiple directional time-frequency peak filtering. Comptes Rendus Geoscience, 347(1): 2-12. |
| [18] | Zhang J, Lin C S, Deng P, et al. 2011. Detection of weak magnetic anomaly signal in non-Gaussian noise background. Journal of Naval University of Engineering (in Chinese), 23(4): 22-26. |
| [19] | 韩佳君, 韩立国, 巩向博等. 2010. 基于波动理论的近地表散射噪音衰减. 世界地质, 29(2): 310-313. |
| [20] | 李阳, 吕庆田, 韩立国等. 2012. 串联去噪技术在金属矿地震勘探中的应用. 世界地质, 31(2): 406-411. |
| [21] | 梁锋, 吕庆田, 严加永等. 2014. 长江中下游宁芜火山岩盆地深部结构特征——来自反射地震的认识. 岩石学报, 30(4): 941-956. |
| [22] | 林红波, 李月, 徐学纯. 2011. 压制地震勘探随机噪声的分段时频峰值滤波方法. 地球物理学报, 54(5): 1358-1366, doi: 10.3969/j.issn.0001-5733.2011.05.025. |
| [23] | 祁光, 吕庆田, 严加永等. 2014. 基于先验信息约束的三维地质建模: 以庐枞矿集区为例. 地质学报, 88(4): 466-477. |
| [24] | 王权峰, 胥德平, 詹泽东等. 2012. 金属矿地震数据降噪研究—基于小波域盲分离JADE算法. 国土资源科技管理, 29(6): 106-110. |
| [25] | 肖晓, 王显莹, 汤井田等. 2014. 安徽庐枞矿集区大地电磁探测与电性结构分析. 地质学报, 88(4): 478-495. |
| [26] | 徐明才, 髙景华, 荣立新等. 2004. 从金属矿地震方法的试验效果探讨其应用前景. 中国地质, 31(1): 108-112. |
| [27] | 张坚, 林春生, 邓鹏等. 2011. 非高斯背景噪声下的微弱磁异常信号检测算法. 海军工程大学学报, 23(4): 22-26. |
 2015, Vol. 58
2015, Vol. 58


