2. 中国海洋大学海底科学与探测技术教育部重点实验室, 青岛 266100
2. Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education, Qingdao 266100, China
We analyze each term in imaging conditions of reverse time migration of multiples and draw the following conclusions: only the correlation of the Nth (N≥0) order multiples (primaries are regarded as the 0th-order multiples) and the (N+1)th order multiples can image the interfaces correctly. The correlation of the Nth order multiples and the (N+i)th (i>1) order multiples will generate crosstalk artifacts and the correlation of the Mth (M≥1) order multiples and the Lth (1≤L≤M) order multiples will generate background noises. Based on the above conclusions, we propose a strategy of reverse time migration of divided-order multiples. Firstly, the primaries are acquired with multiples attenuation in the original record using the surface related multiples elimination (SRME) method. Secondly, based on the primaries, the first-order multiples are forecasted with the feedback loop theory, and then each order of multiples is forecasted in turn. Finally, each pair of the Nth order multiples and the (N+1)th order multiples are used to image, respectively.
The test on a horizontal layered model shows that the real interfaces can be imaged accurately with each order multiples based on the strategy of RTM of divided-order multiples, which can effectively suppress crosstalk of unrelated multiples from the same interface. The test on the Sigsbee2B model also shows that the crosstalk can be suppressed effectively in the imaging sections of each order multiples when the strategy of RTM of divided-order multiples is used. Among all the sections of each order multiples, the section of the first-order multiples has the highest imaging precision and its imaging quality is obviously superior to that of the common RTM of multiples in the deep structures.
Both of the theoretical analysis and the model tests confirm that the crosstalk can be suppressed and the imaging precision can be improved by the strategy of RTM of divided-order multiples, which shows its application prospect in industry. However, the imaging quality of high order multiples is not high enough and the strategy is only suitable for suppressing the crosstalk of unrelated multiples from the same interface, so developing high precision methods of multiples prediction and imaging technology to suppress the crosstalk and improve the imaging quality of each order multiples (especially high order multiples) further will be the focus of future work.
常规地震勘探是基于一次反射波进行成像,而将多次波视为干扰加以剔除,但基于一次波的成像在一次波照明度较低的区域或一次波无法到达的阴影区遇到困难.事实上,多次波同样是来自地下反射界面的反射波,其也包含能够反映地下地质构造的有效信息,并且相比于一次反射波,多次波传播路径更长,覆盖范围更广,地下照明度更加均衡,因此近年来地球物理学家们针对多次波偏移成像技术开展了诸多卓有成效的研究工作.
Reiter等(1991)应用Kirchhoff积分叠前偏移方法实现了深水多次波成像,Sheng(2001)以及Yu和Schuster(2002)提出了基于互相关偏移的多次波成像方法.Guitton(2002)于SEG年会上提出了基于炮-剖面的多次波偏移,其将包含多次波的原始地震记录作为震源下行波,多次波记录作为上行波,分别对上、下行波延拓后作互相关成像,最后将所有炮的偏移结果叠加得到最终的成像剖面.随后Muijs等(2005)将多次波与一次反射波分解为上、下行波后分别进行波场延拓,然后利用二维反褶积成像条件成像.Jiang等(2005,2007)、He等(2007)和Vasconcelos等(2008)成功地将多次波成像应用于VSP(VerticalSeismic Profile,垂直地震剖面)数据中,Brown和Guitton(2005)以及Zhang和Schuster(2014)又成功地应用最小平方偏移方法实现了多次波成像.
2005、2006年的SEG年会上,Verschuur和Berkhout(2005),Berkhout和Verschuur(2006)分别提出了基于“准一次波”(应用互相关算法将多次波进行转化,得到的类似于一次波的地震波)进行成像的思路;单国健(2007)基于该思路实现了准一次波的逆时偏移,其模型实验结果显示准一次波可有效弥补偏移时远、近炮检距数据的缺失;郭书娟等(2012)也基于将多次波转化为准一次波的思路,应用扩展的分步傅里叶算法实现了准一次波成像.
Liu和Chang(2011),Liu等(2011)将含多次波的原始地震记录作为正时波场扰动,以基于自由界面多次波衰减(SRME)方法预测得到的多次波记录作为逆时波场扰动实现了自由界面多次波的逆时偏移,并且其在Sigsbee2B模型的成像实验中取得成功.随后,郭书娟等(2011)和Wang等(2014)以脉冲震源与含多次波的原始地震记录之和作为正时波场扰动,以含多次波的原始地震记录作为逆时波场扰动,对两个时间方向上的波场进行延拓后应用2D反褶积成像条件实现了多次波逆时偏移成像.叶月明等(2014)又基于单程波算子实现了多次波的叠前深度偏移以及多次波成像结果与一次波偏移结果的匹配叠加.针对多次波逆时偏移的低计算效率问题,朱博等(2015)实现了基于多卡GPU加速的多次波逆时偏移,显著提高了其计算效率.Liu等(2015)则基于南海实际地震资料实现了实际地震数据的多次波偏移成像.
以原始地震记录作为正时波场扰动,以多次波记录作为逆时波场扰动的自由界面多次波逆时偏移(以下简称多次波逆时偏移)能够充分利用多次波传播路径长、照明度均衡等优势,能较好地保持偏移剖面的动力学特征,因此其被视为能够提高一次波低照明度区域和一次波无法到达的阴影区域成像质量的重要方法;但当前的多次波逆时偏移算法分别以原始地震记录(包含一次波和各阶多次波)和基于原始地震记录预测得到的包含各阶多次波的炮集记录(以下简称全多次波记录)作为正时扰动和逆时扰动,“不匹配”的多次波记录在互相关成像过程中会产生严重的串扰假象,大大降低了多次波逆时偏移的成像质量和可信度.
本文深入分析了多次波逆时偏移成像原理和串扰假象产生机制,提出了多次波分阶逆时偏移策略以压制多次波逆时偏移的串扰假象.水平层状模型和Sigsbee2B模型实验结果表明,多次波分阶逆时偏移能够有效压制串扰假象,并可显著提高深层的成像质量,显示出其具有良好的工业应用前景.
2 多次波逆时偏移原理及成像条件分析2.1 多次波逆时偏移原理多次波逆时偏移成像原理与常规逆时偏移相似,都是先进行正时、逆时波场的延拓,再基于成像条件提取深度成像值;不同点是多次波逆时偏移分别以原始地震记录和基于原始地震记录预测得到的多次波记录作为正时、逆时的扰动波场(多次波逆时偏移成像原理示意如图 1所示).
 | 图 1 多次波逆时偏移成像示意图Fig. 1 Illustration of RTM of multiples |
图 1中,射线SRPPRM1M1RM2M2表示某一地震波的传播路径,其中S为震源点,P、M1和M2分别为一次波记录、一阶多次波记录和二阶多次波记录接收点,RP、RM1和RM2分别为一次波、一阶多次波和二阶多次波在地下地层的反射点.一阶多次波逆时偏移是以P点处的一次波记录作为正向扰动进行正演模拟获得正时波场,同时以M1点处的一阶多次波记录作为逆向扰动进行波场逆时延拓得到逆时波场,然后即可根据成像条件实现一阶多次波记录对RM1点的成像;同理以M1点处的一阶多次波记录作为正向扰动并以M2点处的二阶多次波记录作为逆向扰动可实现二阶多次波记录对RM2点的成像.
2.2 多次波逆时偏移成像条件分析通常情况下,多次波逆时偏移的成像条件可表示为:



下面对式(4)中的各相加项进行详细分析:
(1)第一项各部分依次为N(N≥0)阶多次波正时波场(这里将一次波视为零阶多次波,以下同)与N+1阶多次波逆时波场的互相关成像值,由2.1节分析可知其计算结果为多次波逆时偏移中的正确成像部分.
(2)第二项各行依次为N阶多次波正时波场与N+i(i>1)阶多次波逆时波场的互相关成像值,现选取其第一行的第一项进行分析.
第一行的第一项为一次波正时波场与二阶多次波逆时波场互相关成像值,其多次波成像示意如图 2所示.图 2中,射线SRPPRM1M1RM2M2RM3M3表示某一地震波的传播路径,其中S为震源点,P、M1、M2和M3分别为一次波、一阶多次波、二阶多次波和三阶多次波接收点,RP、RM1、RM2和RM3分别为一次波、一阶多次波、二阶多次波和三阶多次波在地下地层的反射点.P点处的一次波记录作为正向扰动进行正演模拟时部分能量会以透射波的形式进入下层介质,M2点处的二阶多次波记录作为逆向扰动进行波场逆时延拓时同样会有部分能量以透射波的形式进入下层介质,两个时间方向上的透射波场将根据成像条件在O点成像(O点位置与模型有关),但事实上此处并无反射界面,故O点所成的像即为串扰假象;同理,第一行中的一次波正时波场与其余N+j(j>2)阶多次波逆时波场的互相关均可产生串扰假象.以此类推,第二项中的其余行均可形成串扰假象.
 | 图 2 一次波与二阶多次波成像示意图Fig. 2 Illustration of the imaging of the primaries and the second-order multiples |
(3)第三项各行依次为I(I≥1)阶多次波正时波场与L(1≤L≤I)阶多次波逆时波场的互相关成像值.首先选取其第一行的第一项进行分析.
第一行第一项表示一阶多次波正时波场与一阶多次波逆时波场互相关计算结果,其多次波传播路径如图 3所示.图 3中,S为震源点,P、M分别是作为正时波场和逆时波场扰动的一阶多次波记录接收点.假设炮检距SP、SM距离分别为x1、x2,其接收到的一阶多次波走时分别为t1、t2,此时分两种情况讨论:
 | 图 3 一阶多次波传播路径示意图Fig. 3 Illustration of propagation path of the first-order multiples |
①若P、M点重合,有x1=x2、t1=t2,此时正时波场和逆时波场的扰动来源于同一接收道.当正时波场延拓时,直到t1时刻才加入一阶多次波扰动,也就是说正时波场中只有在t>t1时才有与一阶多次波记录相关的波场值;当波场逆向延拓时,直到t2时刻才加入一阶多次波扰动,也就是说逆时波场中只有在t<t2时才有与一阶多次波记录相关的波场值,由此可知,当P、M点重合时,一阶多次波正时波场与一阶多次波逆时波场在时间轴上“不相遇”,此时一阶多次波正时波场与一阶多次波逆时波场不成像.
②若P、M点不重合,对于复杂构造的多次波,如倾斜界面或绕射点产生的多次波,可能出现t1>t2的情况,但显然该情况下一阶多次波正时波场与一阶多次波逆时波场在时间轴上“不相遇”,即此时一阶多次波正时波场与一阶多次波逆时波场不成像.而当t1<t2时,P处的一阶多次波正时波场MF1与M处的一阶多次波逆时波场MB1可以在时间轴相遇,并且当速度模型合适时,来自P点的正时波场和来自M点的逆时波场完全有可能在t2-t1时间段“相遇”于空间某点,因此此时来自P点的正时波场和来自M点的逆时波场能够具备成像的条件,但是由于P点的正时波场和来自M点的逆时波场的成像值与其余接收点的成像值以及与其他炮的接收点的成像值不具有相关性,因此一阶多次波正时波场与一阶多次波逆时波场的成像结果难以显现于最终剖面上,更多地表现为背景干扰.
第三项其余各行依次为K(K≥2)阶多次波正时波场与G(1≤G≤K)阶多次波逆时波场的互相关值,同理可知这些项也可能具备成像的条件,但其成像值也更多地表现为背景干扰.
此外,值得注意的一点是,以上的分析均是针对来自同一反射界面的一次波及其多次波,而实际上来自不同界面的一次波和多次波同样有形成串扰的可能,但其最终是否形成串扰与实际模型有关,这里不展开讨论.
3 多次波分阶逆时偏移根据第2节的分析可知:只有地震记录中的N阶多次波和N+1阶多次波互相关才可正确成像,因此本文提出多次波分阶逆时偏移策略以压制串扰假象,其具体实现步骤为:
(1)基于原始炮集记录,应用SRME方法剔除多次波,得到一次波记录;
(2)基于一次波记录,应用反馈循环理论预测得到一阶多次波记录,然后应用一阶多次波记录预测得到二阶多次波记录,以此类推,预测得出N阶多次波记录;
(3)以零阶多次波和一阶多次波分别作为正时波场扰动和逆时波场扰动进行逆时偏移计算,得到一阶多次波逆时偏移成像剖面;
(4)分别以k-1(2≤k≤N)阶多次波和k阶多次波替代零阶多次波和一阶多次波,重复步骤(3),直到k=N,即可得到各阶多次波成像剖面(多次波分阶逆时偏移处理流程详见图 4).
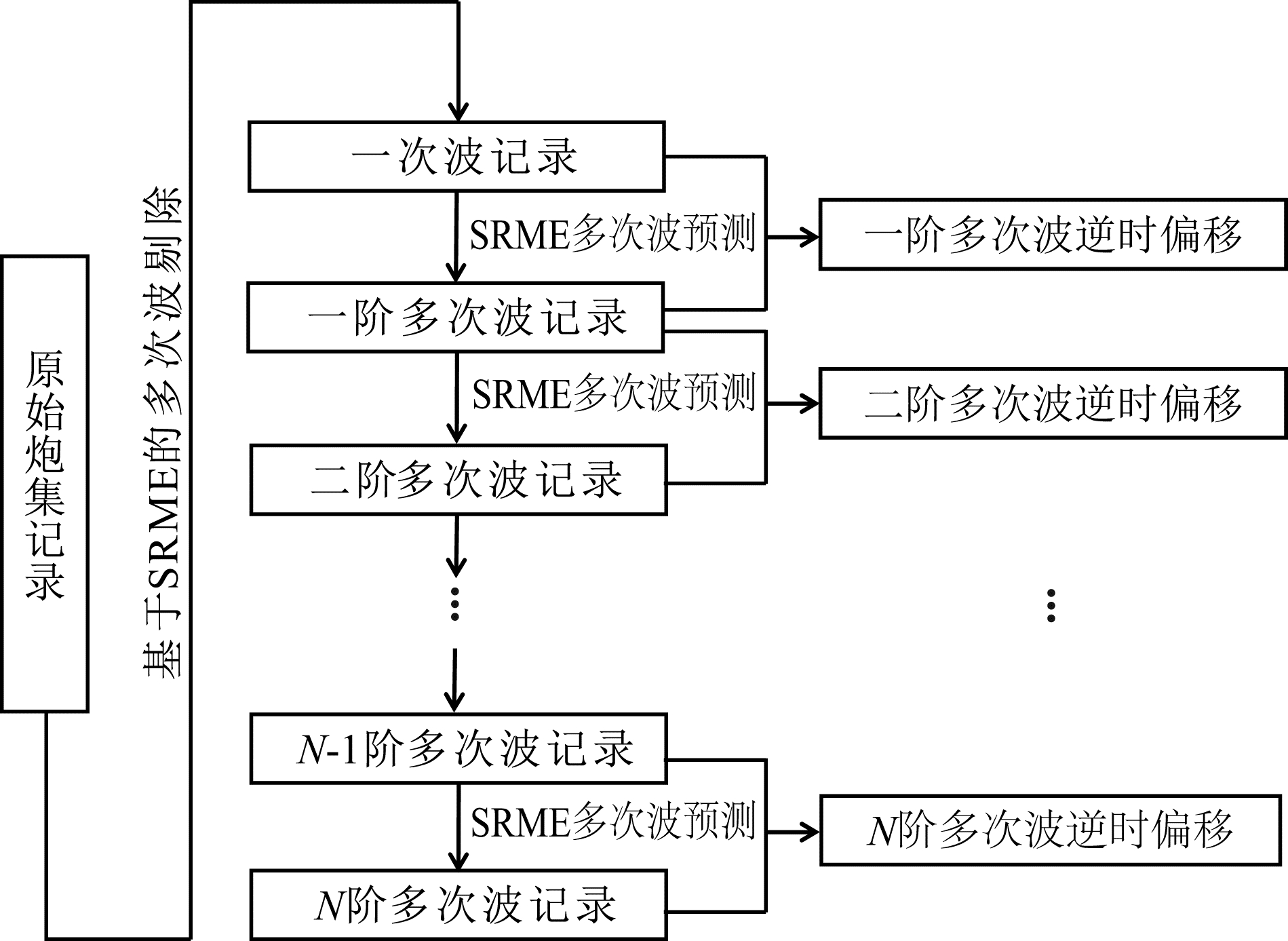 | 图 4 多次波分阶逆时偏移处理流程Fig. 4 The flow chart of reverse time migration of divided-order multiples |
多次波分阶逆时偏移策略其各阶多次波的成像条件可表示为:

建立如图 5所示的水平层状模型,该模型共两层,第一层速度为1800 m·s-1,深度为500 m,第二层速度为2500 m·s-1.模型横向总长度为4000 m,总深度为3000 m.对该模型应用右边放炮,左边接收的单边观测系统,共501炮,每炮301道接收,炮间隔和道间隔均为5 m,检波点深度为5 m.
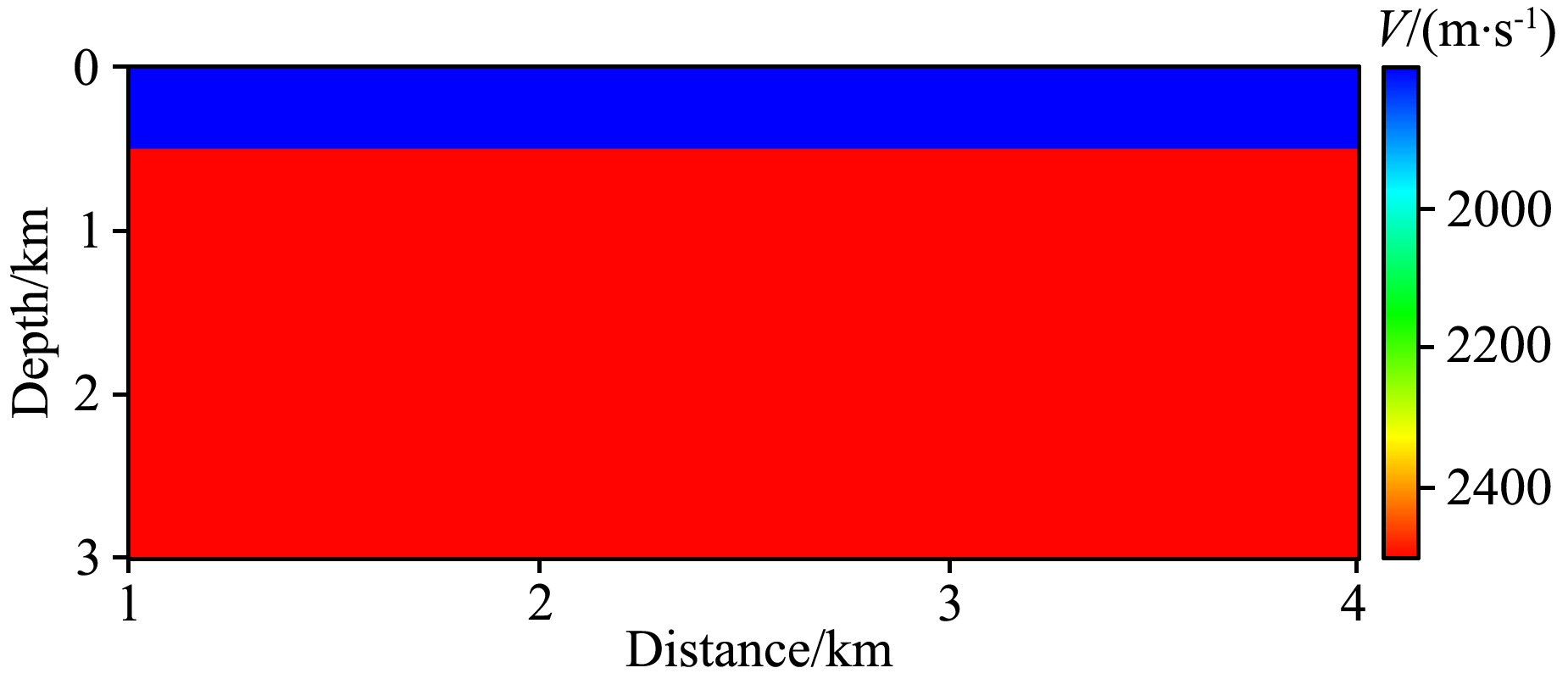 | 图 5 水平层状速度模型Fig. 5 The horizontal layer velocity model |
本文首先基于该模型模拟一套原始炮集数据(包含一次波和各阶多次波),并基于原始炮集应用SRME方法预测获得全多次波记录;为实现多次波分阶逆时偏移,本文又基于该原始炮集数据,应用SRME方法剔除多次波得到一次波记录(第301炮 的原始炮集记录、全多次波记录以及一次波记录见 图 6),然后基于该一次波记录依次预测得到一阶、二阶、三阶和四阶多次波炮集记录(第301炮的各阶多次波炮集记录见图 7).
 | 图 6 第301炮记录 (a)包含一次波和多次波的原始记录; (b)全多次波记录; (c)一次波记录.Fig. 6 The 301st shot records(a) Original record including the primaries and multiples; (b) Whole multiples record; (c) Primaries record. |
 | 图 7 第301炮多次波记录(a)一阶多次波记录;(b)二阶多次波记录;(c)三阶多次波记录;(d)四阶多次波记录. Fig. 7 The 301st multiples records(a) First-order multiples record; (b) Second-order multiples record; (c) Third-order multiples record; (d) Fourth-order multiples record. |
基于水平层状模型的多次波逆时偏移成像结果如图 8所示.图 8中,除真实的成像界面外,还形成了三层由于串扰噪声导致的串扰假象(如图 8中标注所示),经分析可知,串扰假象1来源于以零阶多次波(一次波)作为正时扰动且以二阶多次波作为逆时扰动的成像结果,以一阶多次波作为正时扰动且以三阶多次波作为逆时扰动的成像结果,以及以二阶多次波作为正时扰动且以四阶多次波作为逆时扰动的成像结果的叠加;串扰假象2来源于以零阶多次波(一次波)作为正时扰动且以三阶多次波作为逆时扰动的成像结果,以及以一阶多次波作为正时扰动且以四阶多次波作为逆时扰动的成像结果的叠加;而串扰假象3则为以零阶多次波(一次波)作为 正时扰动且以四阶多次波作为逆时扰动的成像结果.
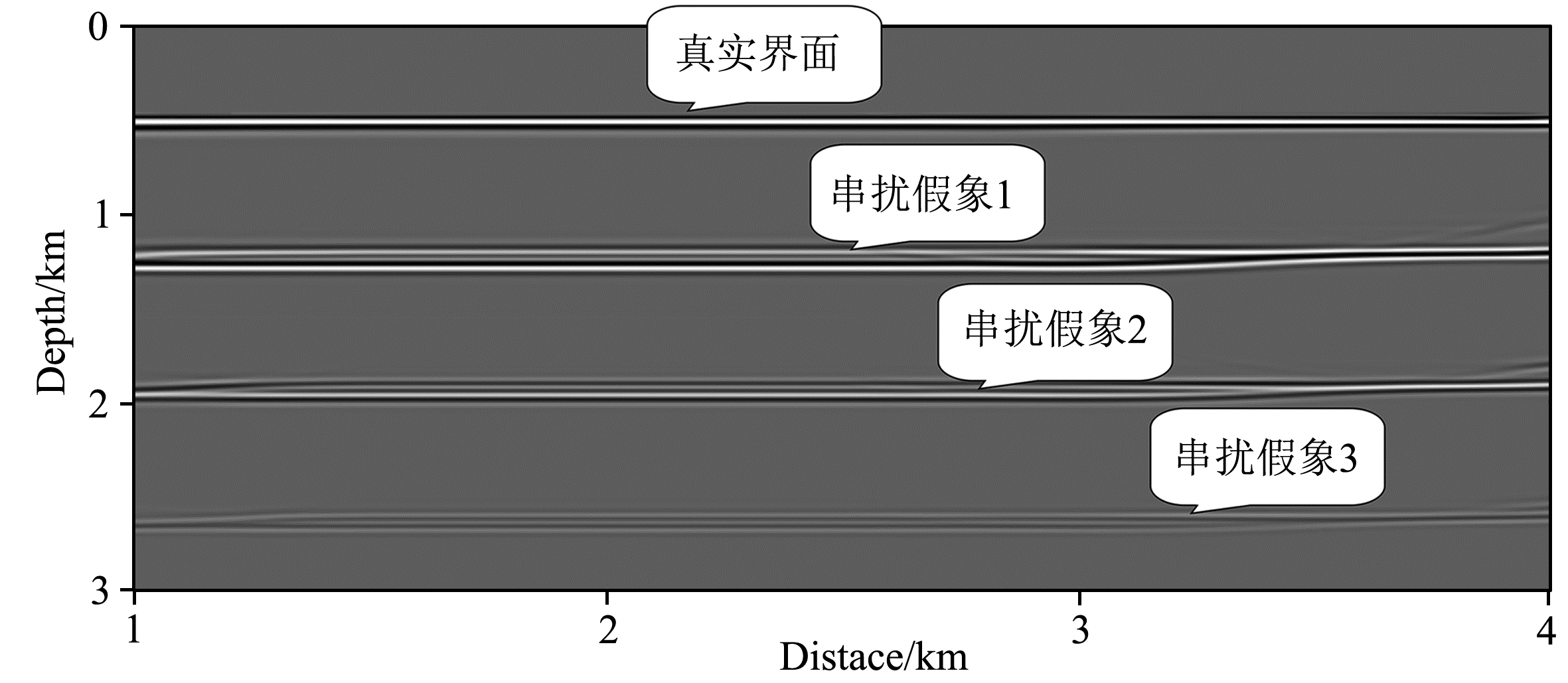 | 图 8 多次波逆时偏移成像剖面Fig. 8 The section of RTM of multiples |
多次波分阶逆时偏移的成像结果见图 9.对比图 8和图 9可知,多次波分阶逆时偏移中的各阶多次波成像剖面均能够正确反映界面信息,证明了多次波分阶逆时偏移策略能够有效消除来自同一反射界面的一次波和多次波产生的串扰.
 | 图 9 注释多次波分阶逆时偏移成像剖面(a)一阶多次波成像剖面;(b)二阶多次波成像剖面;(c)三阶多次波成像剖面;(d)四阶多次波成像剖面.Fig. 9 The section of RTM of divided-order multiples(a) Imaging section of the first-order multiples; (b) Imaging section of the second-order multiples; (c) Imaging section of the third-order multiples; (d) Imaging section of the fourth-order multiples. |
Sigsbee2B模型是国际上用于地震多次波数据处理的标准模型(图 10),模型横向长度为24386 m、 纵向深度为9144 m,横向和纵向网格步长均是7.62 m,模型中含有一个起伏海底界面和高陡盐丘构造.
 | 图 10 Sigsbee2B速度模型Fig. 10 The Sigsbee2B velocity model |
Sigsbee2B模型数据中包含496炮,炮间隔为45.72 m,每炮接收道不同,最大道数为348道,道间隔为22.86 m,记录长度为12 s,时间采样率为8 ms.本文以包含一次波和多次波的模型数据为原始炮集记录,基于该原始记录应用SRME方法剔除多次波得到一次波记录(第226炮的原始炮集记录和一次波炮集记录见图 11),然后基于原始炮集记录预测得到全多次波记录(包含各阶多次波),并基于一次波炮集记录依次预测得到一阶多次波和二阶多次波记录(第226炮的全多次波、一阶多次波以及二阶多次波记录见图 12,其中全多次波和一阶多次波记录实际预测到24 s,这里仅显示到16 s;二阶多次波记录实际预测到36 s,这里仅显示到18 s).
 | 图 11 第226炮记录 (a)包含一次波和多次波的原始记录; (b)一次波记录.Fig. 11 The 226th shot records(a) Original shot record including the primaries and multiples; (b) Primaries record. |
 | 图 12 第226炮多次波记录(a)全多次波记录;(b)一阶多次波记录;(c)二阶多次波记录.Fig. 12 The 226th multiples records (a) Whole multiples record; (b) First-order multiples record; (c) Second-order multiples record. |
由图 11可知,经SRME多次波剔除处理后的原始炮集中的多次波(如图 11a中箭头所示)得到了有效压制;由图 12可知,基于一次波记录预测得到的多次波记录中主要为一阶多次波信息,而基于原始炮集预测得到的全多次波炮集记录中有较为明显的二阶和三阶多次波信息(如图 12a中箭头所示),因此基于全多次波记录的多次波逆时偏移会产生较强的串扰假象.
以原始炮集记录为正时扰动,并以全多次波记录为逆时扰动的常规多次波逆时偏移成像剖面以及基于多次波分阶逆时偏移策略所得的一阶多次波逆时偏移成像剖面和二阶多次波逆时偏移成像剖面如图 13所示.
 | 图 13 多次波逆时偏移成像剖面 (a)常规多次波逆时偏移剖面;(b)一阶多次波成像剖面;(c)二阶多次波成像剖面. Fig. 13 The sections of RTM of multiples (a) Imaging section of common RTM of multiples; (b) Imaging section of the first-order multiples; (c) Imaging section of the second-order multiples. |
由图 13可知,常规多次波成像剖面中存在明显的串扰假象(如图 13a中箭头所示),大大降低了成像剖面的精度和可信度,而基于多次波分阶逆时偏移成像策略的一阶多次波和二阶多次波成像剖面中无明显的串扰噪声.为进一步分析各剖面的成像精度,对图 13中窗口内区域的成像剖面进行放大对比,窗口所对应的速度模型局部放大图见图 14,各剖面的局部放大图见图 15.
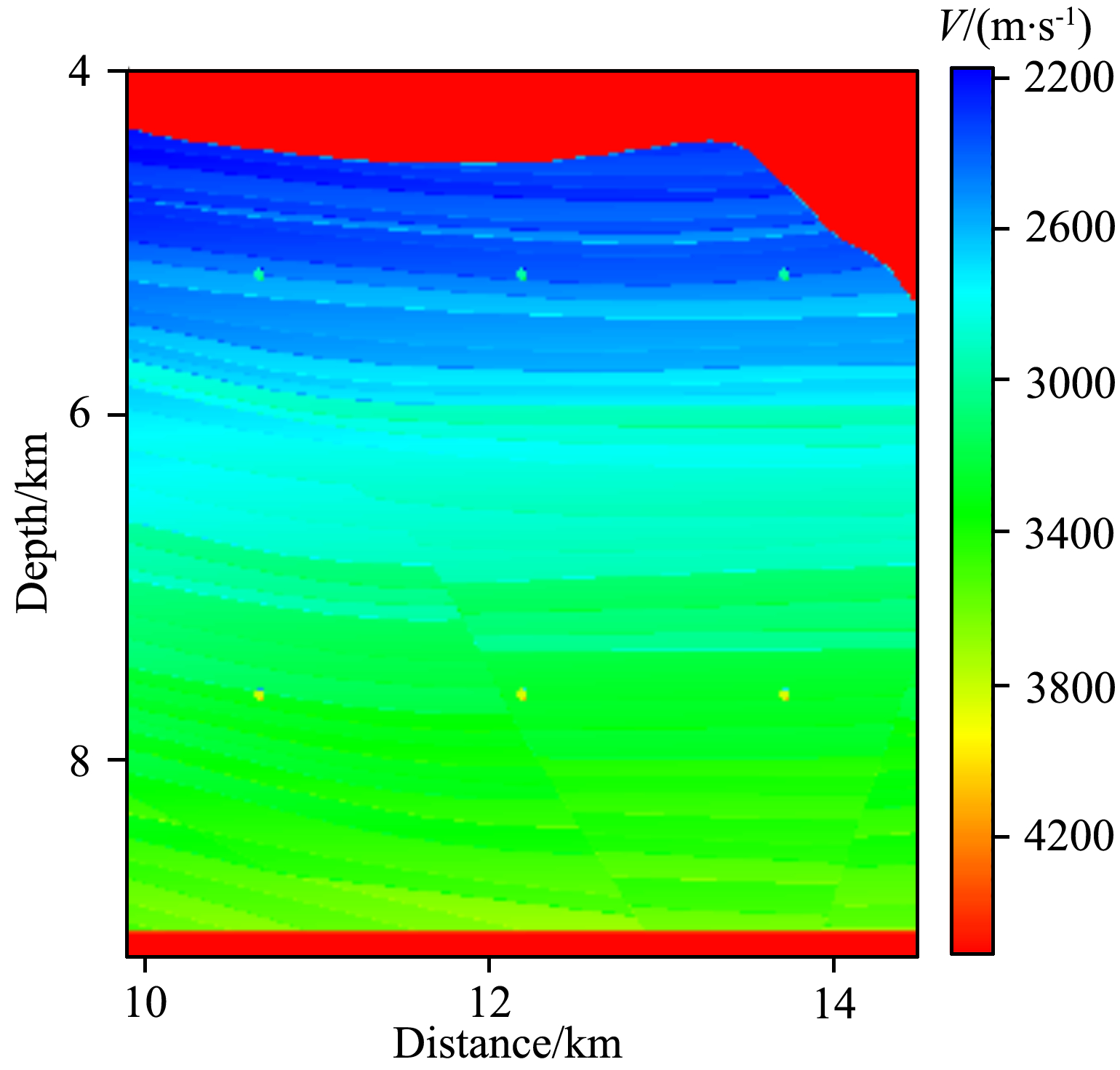 | 图 14 窗口区域速度模型的放大图Fig. 14 Magnified view of the velocity model in the rectangular window |
 | 图 15 窗口区域成像剖面的放大图(a)多次波逆时偏移剖面; (b)一阶多次波成像剖面; (c)二阶多次波成像剖面. Fig. 15 Magnified views of the sections in the rectangular window(a) Section of the common RTM of multiples; (b) Section of the first-order multiples; (c) Section of the second-order multiples. |
由图 15可知,常规多次波逆时偏移成像剖面其深层构造模糊,成像精度低,而基于多次波分阶逆时偏移成像策略的一阶多次波成像结果其深层成像精度明显高于常规多次波逆时偏移成像,这充分证明了基于多次波分阶成像策略对于串扰压制的有效性,但同时我们也注意到二阶多次波逆时偏移成像剖面其深层的成像精度也不高,其原因是一次波记录中尚有部分残余多次波,并且在多次波剔除过程中一次波也会受到一定程度的损伤,受其影响,多次波的阶数越高其预测精度越低,同时由于高阶多次波的传播路径通常也长于一阶多次波,因此二阶多次波的预测精度和能量都要弱于一阶多次波,由此导致二阶多次波逆时偏移的成像精度低于一阶多次波逆时偏移.
5 结论与展望本文在深入分析多次波成像原理及串扰产生机制的基础上,提出并实现了多次波分阶逆时偏移成像策略,模型实验结果表明:各阶多次波成像剖面均可对真实反射界面进行成像,且能有效避免来自同一界面的不相关多次波的串扰,而对于复杂构造模型,基于多次波分阶逆时偏移成像策略的一阶多次波的逆时偏移剖面能够显著降低串扰假象干扰,大大提高多次波逆时偏移的深层成像质量,显示出了多次波分阶逆时偏移成像的良好应用前景.
当然,本文所提出的多次波分阶逆时偏移策略还面临着计算效率低下和高阶多次波成像精度低等诸多问题,并且该策略仅适应于来自同一反射界面的多次波成像的串扰压制.当前随着GPU集群在地球物理界的广泛应用,借助于GPU集群的高性能并行计算能力,多次波逆时偏移的计算效率可得到大幅度提升.本文基于四个型号为Tesla K20的GPU卡的多次波逆时偏移实验显示,Sigsbee2B模型的多次波逆时偏移的计算时间仅约为3 h,而随着大型GPU集群的逐渐普及,基于实际数据的多次波逆时偏移处理已成为可能,因此发展高精度的多次波预测方法和多次波成像技术,进一步压制多次波成像的串扰,全面提高各阶多次波(尤其是高阶多次波)的成像精度将是下一步的工作重点.
致谢 衷心感谢两位匿名审稿专家所提出的宝贵修改意见和建议.
| [1] | Berkhout A J, Verschuur D J. 2006. Imaging of multiple reflections. Geophysics, 71(4): SI209-SI220, doi: 10.1190/1.2215359. |
| [2] | Brown M P, Guitton A. 2005. Least-squares joint imaging of multiples and primaries. Geophysics, 70(5): S79-S89, doi: 10.1190/1.2052471. |
| [3] | Guitton A. 2002. Shot-profile migration of multiple reflections.//SEG Technical Program Expanded Abstracts. SEG, 1296-1299, doi: 10.1190/1.1816892. |
| [4] | Guo S J, Li Z C, Tong Z Q, et al. 2011. Joint imaging of primaries and surface-related multiples based on generalized shot-profile migration. Chinese Journal of Geophysics (in Chinese), 54(4): 1098-1105, doi: 10.3969/j.issn.0001-5733.2011.04.025. |
| [5] | Guo S J, Li Z C, Tong Z Q, et al. 2012. Method and technique for imaging of surface-related multiples. Progress in Geophysics (in Chinese), 27(6): 2570-2576, doi: 10.6038/j.issn.1004-2903.2012.06.034. |
| [6] | He R Q, Hornby B, Schuster G T, et al. 2007. 3D wave-equation interferometric migration of VSP free-surface multiples. Geophysics, 72(5): S195-S203, doi: 10.1190/1.2743375. |
| [7] | Jiang Z Y, Yu J H, Schuster G T, et al. 2005. Migration of multiples. The Leading Edge, 24(3): 315-318, doi: 10.1190/1.1895318. |
| [8] | Jiang Z Y, Sheng J M, Yu J H, et al. 2007. Migration methods for imaging different-order multiples. Geophysical Prospecting, 55(1): 1-19, doi: 10.1111/j.1365-2478.2006.00598.x. |
| [9] | Liu Y K, Chang X. 2011. Reverse time migration of multiples.//81st Ann. Internat. Mtg., Soc. Expl. Geophys. Expanded Abstracts. San Antonio, 3326-3331. |
| [10] | Liu Y K, Chang X, Jin D G, et al. 2011. Reverse time migration of multiples for subsalt imaging. Geophysics, 76(5): WB209-WB216, doi: 10.1190/geo2010-0312.1. |
| [11] | Liu Y K, Zhu W L, Mi L J, et al. 2015. Migration of multiples from the South China Sea. Science China Earth Sciences, 58(3): 482-490. |
| [12] | Muijs R, Robertsson A J O, Holliger K. 2005. Prestack depth migration of primary and surface-related multiple reflections: Part I—Imaging. Geophysics, 72(2): S59-S69, doi: 10.1190/1.2422796. |
| [13] | Reiter E C, Toksöz M N, Keho T H, et al. 1991. Imaging with deep-water multiples. Geophysics, 56(7): 1081-1086, doi: 10.1190/1.1443119. |
| [14] | Shan G J. 2007. Surface-related multiple migration. Geophysical Prospecting for Petroleum (in Chinese), 46(6): 604-610. |
| [15] | Sheng J M. 2001. Migrating multiples and primaries in CDP data by crosscorrelation migration.//71st Ann. Internat. Mtg., SEG Technical Program Expanded Abstracts. SEG, 1297-1300, doi: 10.1190/1.1816333. |
| [16] | Vasconcelos I, Snieder R, Hornby B. 2008. Imaging internal multiples from subsalt VSP data—Examples of target-oriented interferometry. Geophysics, 73(4): S157-S168, doi: 10.1190/1.2944168. |
| [17] | Verschuur D J, Berkhout A J. 2005. Transforming multiples into primaries: Experience with field data.//Expanded Abstracts of the 75th Annual Meeting of the Society of Exploration Geophysicists. 2103-2106, doi: 10.1190/1.2148127. |
| [18] | Wang Y B, Chang X, Hu H. 2014. Simultaneous reverse time migration of primaries and free-surface related multiples without multiple prediction. Geophysics, 79(1): S1-S9, doi: 10.1190/geo2012-0450.1. |
| [19] | Ye Y M, Zhao C L, Zhuang X J, et al. 2014. Migration of surface correlated multiples based on one-way wave equation. Chinese Journal of Geophysics (in Chinese), 57(4): 1241-1250, doi: 10.6038/cjg20140421. |
| [20] | Yu J H, Schuster G T. 2002. Joint migration of primary and multiple reflections in RVSP data.//72nd Ann. Internat. Mtg, Soc. Expl. Geophys., Expanded Abstracts. 2373-2376, doi: 10.1190/1.1817193. |
| [21] | Zhang D L, Schuster G T. 2014. Least-squares reverse time migration of multiples. Geophysics, 79(1): S11-S21, doi: 10.1190/geo2013-0156.1. |
| [22] | Zhu B, Song P, Li J S, et al. 2015. Reverse time migration of multiples based on the acceleration of multi-card GPU. Petroleum Geology and Recovery Efficiency (in Chinese), 22(2): 60-65. |
| [23] | 郭书娟, 李振春, 仝兆岐等. 2011. 基于广义的炮偏移方法实现地表多次波和一次波联合成像. 地球物理学报, 54(4): 1098-1105, doi: 10.3969/j.issn.0001-5733.2011.04.025. |
| [24] | 郭书娟, 李振春, 仝兆岐等. 2012. 表层多次波成像方法技术研究. 地球物理学进展, 27(6): 2570-2576, doi: 10.6038/j.issn.1004-2903.2012.06.034. |
| [25] | 单国健. 2007. 地表多次波应用研究. 石油物探, 46(6): 604-610. |
| [26] | 叶月明, 赵昌垒, 庄锡进等. 2014. 基于单程波偏移算子的地表相关多次波成像. 地球物理学报, 57(4): 1241-1250, doi: 10.6038/cjg20140421. |
| [27] | 朱博, 宋鹏, 李金山等. 2015. 基于多卡GPU集群的多次波逆时偏移成像技术. 油气地质与采收率, 22(2): 60-65. |
 2015, Vol. 58
2015, Vol. 58


