近场波动的数值模拟需引入人工边界将无限域截断成有限的计算区,并设置人工边界条件(Artificial Boundary Condition,ABC)模拟外行波穿过边界进入外部无限域.关于ABC的研究已有半个世纪的历史,研究思路主要建立在单向波概念之上,即ABC应保证计算区内的外行波在人工边界上无反射,由此建立了众多ABC.建立ABC的方法主要有两类:其一由满足场方程的外行波假定导出,如粘性ABC(Lysmer and Kulemeyer,1969),黏弹性 ABC( Deeks and Randolph,1994; 刘晶波等,2005;杜修力等,2006),高阶弹簧-阻尼-质量ABC(Du and Zhao,2010),Clayton-Engquist ABC(Clayton and Engquist,1977),Higdon ABC(Higdon,1986; 1990),辅助变量实现的Higdon ABC(Givoli and Neta,2003; Hagstrom and Warburton,2004; Baffet et al.,2012).其二在人工边界外设置吸收层,通过在吸收层内设置场方程,衰减掉进入层内的外行波,以消除人工边界的反射.代表性工作为完美匹配层(Bérenger,1994; Chew and Weedon,1994; Xie et al.,2014).
以上ABC的建立均遵循传统的研究思路:ABC具有与场方程相匹配的连续形式,然后离散化实现数值模拟.Liao等(1984a,1984b)提出了可描述体波、面波和导波的单向波形式表达式,以离散形式直接模拟外行波穿过边界,由此建立的ABC称为 多次透射公式(Multi-Transmitting Formula,MTF). MTF与前述ABC的区别如下:第一,MTF与内域场方程无关,可直接用于各种场方程,而PML则需针对特定场方程建立相应的ABC;第二,MTF由单向波形式表达式导出,可适用于人工边界上的各节点,如角点和分层界面点,而应用辅助变量实现的Higdon ABC则较难处理;第三,MTF是一维表达式,其数值实现方式灵活、易于实现且计算量低;第四,MTF的精度阶含义明确且可控,易与内域离散格式的精度阶一致.但是,在数值模拟中MTF存在数值稳定问题.文献(Liao et al.,1984a; 廖振鹏等,2002)中的算例清晰地显示了MTF的潜在应用前景,但更仔细的数值实验结果表明延长计算时间仍将发生失稳.已有的MTF失稳机理研究结果可归 纳为两类:计算区内外行波的多次反射放大(Liao and Liu,1992)和局部区域的耦合失稳(李小军和廖振鹏,1996; 周正华和廖振鹏,2001; 景立平等,2002).前者是人工边界对高频行波的反射放大,及在有限计算区内反复放大所致.后者则为ABC与相邻内域离散格式的耦合所致,可由GKS定理(Gustafsson et al.,1972)的群速度解释(Trefethen,1983)加以阐明,即模型(人工边界与内域离散格式)支持群速度指向内域的外行平面谐波,从而波动能量将自发地从边界进入内域,导致失稳.由于前者可通过保证反射系数小于1避免(Xie and Liao,2008),下面概述消除局部耦合失稳的研究结果.
就MTF与相邻内域离散格式的耦合所造成的局部失稳而言,可通过消除失稳耦合达到(廖振鹏和谢志南,2011),即改变内域离散格式,或MTF,或两者.局部耦合失稳的形态可区分为高频失稳(景立平等,2002)和零频飘移失稳(李小军和廖振鹏,1996; 周正华和廖振鹏,2001),飘移失稳可采用加小量修改MTF(周正华和廖振鹏,2001)或內域离散格式(李小军和杨宇,2012)来消除.高频失稳常出现在对近场波动数值模拟无意义的高频段,曾采用阻尼滤波来消除(廖振鹏等,2002),但阻尼大小的选取无确定准则,过小仍可能失稳,过大则影响计算精度.谢志南和廖振鹏(2012)针对波导的有限元数值模拟,通过调整长方形单元的长宽比来改变内域离散格式的频散关系,使之不再支持群速度指向内域的外行平面谐波,稳定实现了MTF.但对于半空间或全空间模型,此法失效.
由上述讨论可知,高频耦合失稳目前仍无有效的消除方法,这是本文的论题.本文的研究思路是通过改变内域离散格式来消除失稳耦合,达到稳定实现MTF的目的.关于改变内域离散格式的工作应提及Yue和Guddati(2005)针对标量波动的数值模拟提出了一种修改的数值积分方法,即对质量和刚度矩阵积分表达式进行数值积分时,通过对频散误差的控制来选取积分点,使正方形单元频散误差由原来 的二阶精度提高到四阶精度.Idesman和Pham(2014)则将这一方法推广到弹性波情形.我们将进一步研究这一改变内域离散格式的方法,达到消除高频耦合失稳,同时保证内域离散格式的精度不低于原有格式的精度.
本文第二节给出SH波动数值模拟的有限元离散格式.第三节分析离散格式的频散关系,进而阐明MTF高频耦合失稳的机理,并分析刚度阵对有限元频散的影响.第四节基于修改的数值积分方法来修改刚度,提出一个稳定实现MTF的集中质量有限元格式.第五节利用数值实验验证本文措施的有效性.最后,对本文工作做了小结.
2 有限元离散格式各向同性、均匀、线弹性SH波动方程为
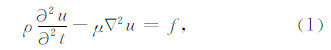
其中 u 为位移,f 为荷载,ρ 为密度,μ 为弹性模量,Δ 2 为拉普拉斯算子.连续模型的解由满足初始和边界条件的波动方程(1)给出.
采用线性有限元(廖振鹏,2002)离散上述连续模型可得

其中 U 为节点位移矢量,Ü 为其二阶时间导数.系统矩阵 M,K 分别由单元矩阵 M e,K e 组装而成,系统荷载向量 F 由单元荷载矩阵 f e 组装而成.
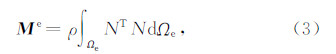
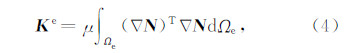

其中 N 是线性形函数矩阵,Ωe 代表单元所在空间区域.
用中心差分对时间离散,可得全离散格式
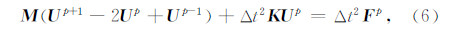
其中 Δt 为时间步距,U p和F p为pΔt 时刻的位移和荷载向量.
全离散格式(6)可以写成与节点(m,n)相关的局部节点系格式,即四个相邻单元组成的9节点系(如图 1),即
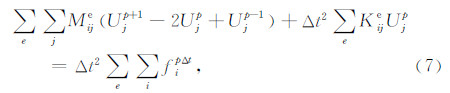
其中 Mije和Kije 分别表示单元质量阵和刚度阵元素,Upj 表示节点 j 在 pΔt 时刻的位移,fpΔti 表示节点 i 在 pΔt 时刻的荷载.
 | 图 1 长方形单元节点编号和二维局部节点系Fig. 1 Node number and 2D local grid system for rectangle element |
采用长方形单元(如图 1),其边长为 Δx和Δy,则由(3)和(4)可得单元质量和刚度矩阵

其中,q=Δy/Δx. 一致质量矩阵元素
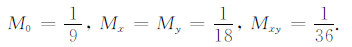
对一致质量矩阵作行和集中得到集中质量矩阵,其元素
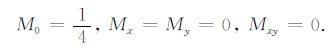
刚度矩阵元素
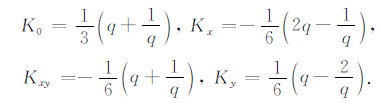
ABC采用MTF(Liao et al.,1984a),

其中二项式系数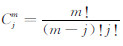 ,ujp为沿边界法 线距人工边界 jΔx 处的节点在 pΔt 时刻的位移.为简化分析,本文假定MTF的计算点和离散网格节点重合.
,ujp为沿边界法 线距人工边界 jΔx 处的节点在 pΔt 时刻的位移.为简化分析,本文假定MTF的计算点和离散网格节点重合.
GKS定理的群速度解释表明,若内域离散格式和人工边界支持群速度指向内域的外行平面谐波,则将导致失稳.内域离散格式支持的平面谐波由频散分析可知,而对于人工边界支持的平面谐波,可将人工边界进行无限延拓当成内域离散格式进行频散分析,本文将无限延拓的MTF称之为MTF格式.因此,若内域与人工边界格式频散曲线的交点对应群速度向内的外行平面谐波,则导致耦合失稳.
首先对连续模型、一致质量有限元、集中质量有限元和MTF格式作频散分析,利用GKS定理的群速度解释来揭示MTF高频耦合失稳的机理.
考虑平面谐波
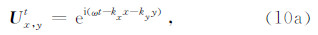
其时空离散形式为

其中 ω 为圆频率,沿 x和y 轴正向的视波数分别为 kx=k cosθ,ky=ksinθ,k 为波数,θ 为平面谐波入射方向与 x 轴正向的夹角.
作频散分析时,可忽略荷载项,将平面谐波(10a)代入(1)式,可得连续模型的频散关系
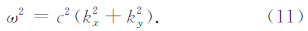
将平面谐波(10b)代入局部节点系格式(7),可得一致质量有限元的频散关系
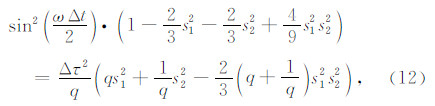
以及集中质量有限元的频散关系

其中 Δτ= ,波速
,波速 s2=
s2=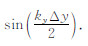 .
.
将平面谐波(10b)代入(9),当人工边界垂直 x 方向时,可得MTF格式的频散关系

同理,当人工边界垂直 y 方向时,可得MTF格式的频散关系

由于频散关系的对称性,可只考虑第一象限,即 ωΔt∈[0,π],kxΔx∈[0,π],kyΔy∈[0,π].
图 2给出 q=1,Δτ=0.4 时,连续模型和离散格式在第一象限的频散,其中连续模型的频散关系式(11)改写为
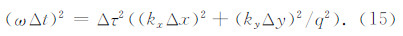
 | 图 2 q=1,Δτ=0.4时,连续模型和离散格式在第一象限的频散 (a)连续模型;(b)一致质量有限元;(c)集中质量有限元;(d)人工边界垂直 x 方向时的MTF格式.Fig. 2 The dispersion of continuous model and discrete schemes at the first quadrant when q=1,Δτ=0.4. (a)Continuous model;(b)Consistent mass FEM;(c)Lumped mass FEM;(d)MTF scheme when ABC is perpendicular to x-axis. |
图 3给出 q=1,Δτ=0.4 时,在给定不同取值 kyΔy 下,离散格式在第一象限的频散曲线.
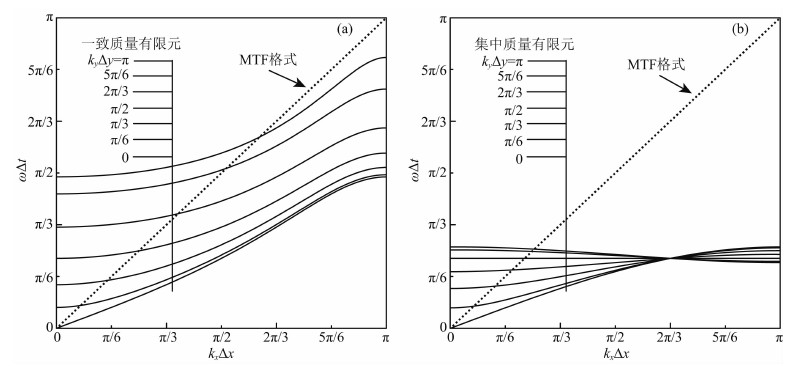 | 图 3 q=1,Δτ=0.4时,在给定 kyΔy 不同取值下,离散格式在第一象限的频散曲线 (a)一致质量有限元(实线)与人工边界垂直 x 方向时的MTF格式(虚线)的频散曲线 (b)集中质量有限元(实线)与人工边界垂直 x 方向时的MTF格式(虚线)的频散曲线.Fig. 3 The dispersion curves of discrete schemes at the first quadrant under the given different value of kyΔy when q=1,Δτ=0.4 (a)The dispersion curves of consistent mass FEM(solid lines) and MTF scheme(dash line)when ABC is perpendicular to x-axis; (b)The dispersion curves of lumped mass FEM(solid lines) and MTF scheme(dash line)when ABC is perpendicular to x-axis. |
主要说明两点:第一,从图 3(a、b)可以看出一致质量有限元与MTF格式频散曲线的交点斜率均为正,而集中质量有限元与MTF格式频散曲线的交点斜率在高频段为负(高频指 ωΔt 接近内域离散格式的截止频率).由此可知,一致质量有限元结合MTF不会导致高频耦合失稳,而集中质量有限元结合MTF将导致高频耦合失稳.
第二,由连续模型的频散式(15),即图 2a可知,其 x和y 方向频散曲线的割线和切线斜率均为正,表明第一象限的波动相速度和群速度均为正.一致质量有限元的频散图 2b或图 3a也表明其具有相同性质,而从集中质量有限元频散图 2c或图 3b可知,其 x和y 方向频散曲线在高频段的割线斜率为正,而切线斜率为负,表明这类高频波动相速度为正,而群速度为负.因此,集中质量有限元在高频段出现了有别于连续模型和一致质量有限元的异常频散.这异常频散对应的平面谐波就是集中质量 有限元允许的群速度向内的外行高频平面谐波.可见,消除集中质量有限元的异常频散可稳定实现MTF.
虽然一致质量有限元与MTF结合不会导致高频耦合失稳,但一致质量有限元空间耦联,计算量大.因此,对于大型波动数值模拟有必要采用集中质量有限元.
本文不探讨零频飘移失稳,但同样可以采用GKS定理的群速度解释,即内域和边界支持群速度向内的外行零频平面谐波,可参看文献(周正华和廖振鹏,2001).本文的数值实验采用该文献提出的小量处理MTF来消除零频飘移失稳.
以上简化分析表明,有限元质量集中造成其异常频散,进而导致MTF高频耦合失稳.由于有限元的频散由其质量和刚度阵决定,而集中质量可以极大地提高计算效率,因此可修改刚度阵以消除有限元与MTF共同支持的群速度向内的外行平面谐波.下面在一般情形下分析刚度对有限元频散的影响,进一步论证MTF的失稳机理.
将平面谐波(10b)代入局部节点系格式(7),把刚度当成未知量,仅利用关系
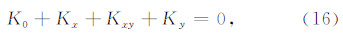
并代入集中质量,由此可得集中质量有限元的频散关系
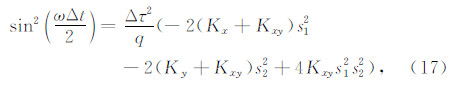
式(17)中的各项对 kxΔx 求偏导,可得
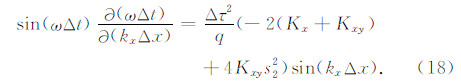
由于在第一象限内,故 sin(ωΔt)≥0,sin(kxΔx)≥0. 对于一定的 kyΔy,s2 是常数,则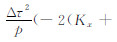
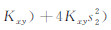 也为常数,所以
也为常数,所以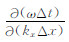 保持≤0或保持≥0. 也就是说,对于 kyΔy 一定取值的频散曲线,其 x 方向具有单调性.同理易知,对于 kxΔx 一定取值的频散曲线,其 y 方向也具有单调性.
保持≤0或保持≥0. 也就是说,对于 kyΔy 一定取值的频散曲线,其 x 方向具有单调性.同理易知,对于 kxΔx 一定取值的频散曲线,其 y 方向也具有单调性.
考虑到MTF格式的频散关系(14a)和(14b),其为三维斜面,分布在频率 [0,π]和波数 [0,π] 内,必然与有限元的 x和y 方向上任意一条频散曲线相交.因此,为保证集中质量有限元和MTF格式的频散曲线交点斜率为正,就要要求有限元的频散曲线单调递增.
由式(18)可得有限元 x 方向频散曲线单调递增的条件:

同理可得有限元 y 方向频散曲线单调递增的条件:

式(19)是保证集中质量有限元不存在异常频散,与MTF结合不会导致高频耦合失稳的条件.
由此可知,对于正方形单元,Kx=Ky=-1/6,Kxy=-1/3,不满足式(19).因此,垂直 x或y 方向的人工边界MTF均会导致高频耦合失稳.
对于长方形单元,稳定实现垂直 x 方向的人工边界MTF可依据式(19a)得 q≥ √2,稳定实现垂直 y 方向的人工边界MTF可依据式(19b)得 q≤√2/2. 对于波导模型,仅需设置垂直 x或y 一方向上的人工边界,选取合适的单元长宽比,MTF可以稳定实现(谢志南和廖振鹏,2012).但对于半空间或全空间模型,需设置垂直 x和y 两方向上的人工边界,MTF结合集中质量有限元无法稳定实现.
4 修正的集中质量有限元由上节可知,修改刚度可消除集中质量有限元的异常频散,能稳定实现MTF.因此,对单元刚度的积分计算式(4),不采用精确积分或是常用的Gauss数值积分,而采用修改的数值积分方法(Yue and Guddati,2005),即
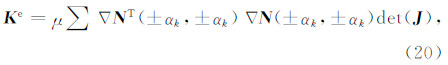
其中积分点 αk∈[0,1],det(J)为Jacobi行列式,对于长方形单元,det(J)=Δx·Δy/4.
利用数值积分(20)式,可得修正刚度
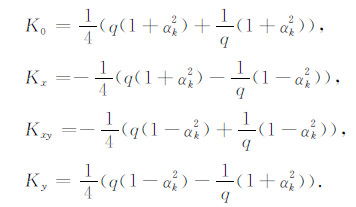
当 αk=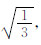 ,对应的有限元为之前讨论的集中质量有限元.以示区别,将之前讨论的称为传统的集中质量有限元,此处引入的称为修正的集中质量有限元.
,对应的有限元为之前讨论的集中质量有限元.以示区别,将之前讨论的称为传统的集中质量有限元,此处引入的称为修正的集中质量有限元.
将修正刚度代入式(19a),可得稳定实现垂直 x 方向的人工边界MTF的条件
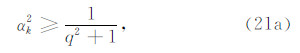
同理,将修正刚度代入式(19b),可得稳定实现垂直 y 方向的人工边界MTF的条件
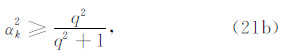
令 qr 为长方形单元长边与短边的比值,则稳定实现垂直 x和y 方向的人工边界MTF的条件为
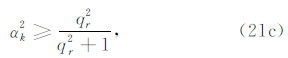
式(21)表明选取合适的数值积分点 αk 可以稳定实现MTF.对于积分点 αk 的取值,将依据格式精度和稳定性来确定.
格式精度可用截断误差来衡量.对式(7)中的各项在 Ujp处作Tayloy展开,忽略荷载项,代入集中质量和修正刚度,可得其截断误差为
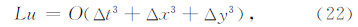
可知无论 αk 取何值,该格式具有二阶精度,但也无法找到合适的 αk 来提高格式的精度.对于波动数值模拟,格式的频散误差与精度阶一样能衡量格式精度.本文同文献(Yue and Guddati,2005; Idesman and Pham,2014)一样采用频散误差进一步衡量格式精度,以其截断系数确定较优的 αk 取值以保证修正有限元的精度不低于传统有限元的精度.
对修正有限元的频散式(17)引入余量
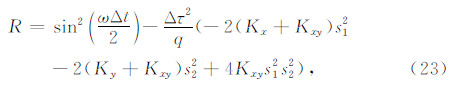
对 R 中的各项作Taylor展开(ωΔt,kxΔx,kyΔy«1),并代入连续模型的频散式(15),则余量 R 可衡量有限元格式的频散误差.由此可得
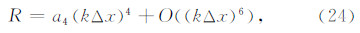
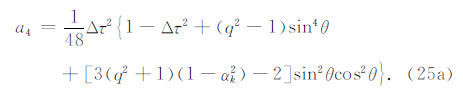
对于传统有限元,有
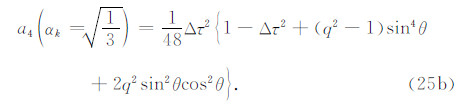
当 q≥1 时,并由下文稳定性条件(30)式可知 Δτ≤1,故式(25a)和(25b)的共同项 1-Δτ2+(q2-1)sin4θ≥0. 若对于两式中的 sin2θcos2θ 项系数有
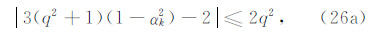
则该条件下的 αk 能保证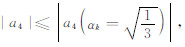 即
即
修正有限元的精度不低于传统有限元的精度,即
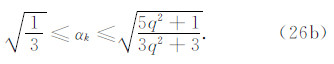
由 q≥1可知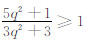 ,又有αk∈[0,1],故
,又有αk∈[0,1],故
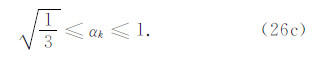
当 q<1 时,先利用(sin2θ+cos2θ)2=1 改写式(25a),即

对于传统有限元,
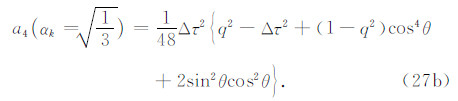
由下文稳定性条件(30)式可知 Δτ≤q,故式(27a)和(27b)中的 q2-Δτ2+(1-q2)cos4θ≥0. 同理可得
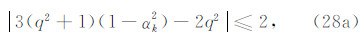
即

由 q≤1 可知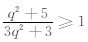 ,又有αk∈[0,1],故
,又有αk∈[0,1],故
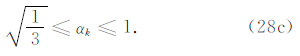
可以发现(26c)和(28c)是一样的,故无论q取何值,满足式(28c)的 αk 能保证修正有限元的精度不低于传统有限元的精度.
下面给出几个满足式(28c)和MTF稳定实现条件式(21c)的 αk 取值,可取
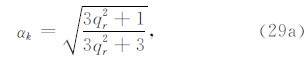
此时(25a)和(27a)中的 sin2θcos2θ 项系数为0.
或取

这是满足式(21c)的最小取值.在有限元稳定条件方面,由下文的稳定性条件(30)容易验证(29b)取值优于(29a)取值.
或取

此时数值积分(20)式即为两点Gauss-Lobatto积分,修正有限元格式等同中心差分格式.
内域离散格式的稳定性可由Von-Neumann稳定性分析得到,即要求波数 kx和ky 为实数的平面谐波(10b)式不能随时间无限增长.由格式的频散关系(17)式可知,kx和ky 为实数时,ω 必为实数,故 sin2(ωΔt)≤1,进而由(17)式可得修正有限元的稳定性条件
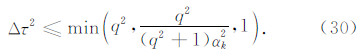
Liao等(1984a)中的算例由于计算时间不长,未出现MTF与传统有限元耦合所致的高频失稳.为了揭示MTF的高频数值失稳现象,以及验证MTF结合修正有限元可以稳定实现,本文数值实验采用Liao等(1984a)的均匀弹性半空间模型.
模型的几何关系如图 4所示,剪切波速c=1 m·s-1. 波源为在自由表面处沿 z 方向作用的暂态荷载:
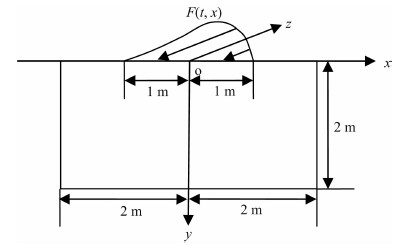 | 图 4 弹性半空间SH波动模型Fig. 4 Elastic half-space model of SH wave motion |
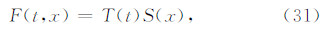
其中输入时间函数为三角形脉冲:

荷载空间分布函数 S(x)由下式给出:
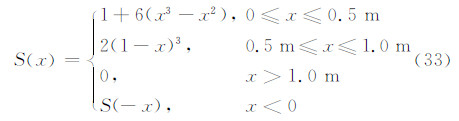
其余三边设置人工边界MTF,观测点设置在自由地表(1,0)处.
本文的人工边界稳定性分析是针对透射公式(9),首先用数值实验验证其稳定性.
图 5中的(a)和(b)分别为采用传统和修正有限元结合MTF(N=1,2,3)计算的观测点位移时程.离散 方案为 Δx=0.05 m,Δy=0.025 m,Δt=0.02 s,即 Δτ=0.4.对于修正有限元,积分点 αk=√13/15 . 明显可见,传统有限元结合MTF存在高频失稳和飘移失稳.高频失稳出现时间随MTF阶数提高而提前.而修正有限元结合MTF未出现高频失稳,图中只显示1500步的计算结果,实际计算100万步.其中采用小量处理MTF来消除飘移失稳,小量取为0.005,其取值并无确定准则,根据实际计算调整.
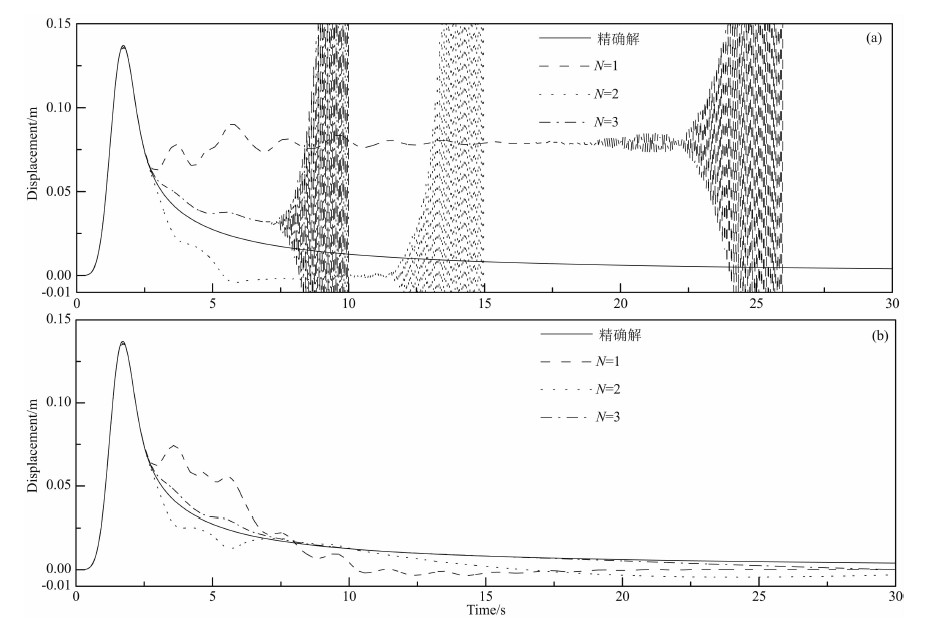 | 图 5(a)和(b)分别为采用传统有限元和修正有限元结合MTF(式(9),N=1,2,3)计算的观测点(1,0)位移时程离散方案为Δx=0.05 m,Δy=0.025 m,Δt=0.02 sFig. 5(a) and (b)are the displacement time history of the observation point(1,0)computed by classic FEM and modified FEM with MTF(formula(9),N=1,2,3)separately. The discretization mesh is Δx=0.05 m,Δy=0.025 m,Δt=0.02 s |
对于MTF的计算点和离散网格节点不重合 时,MTF的计算点采用空间内插(Liao et al.,1984a),因为内域格式已消除异常频散,故不会导致高频耦合失稳.下面也通过数值实验验证.
图 6中的(a)和(b)分别为采用传统和修正有限元结合MTF(N=1,2,3)计算的观测点位移时程. 离散方案为Δx=Δy=0.05 m,Δt=0.025 s,即Δτ=0.5. 对于空间内插形式的MTF,取人工波速 ca=c. 对于修正有限元,积分点 αk=√2/3.明显可见,传统有限元结合MTF存在高频失稳和飘移失稳.而修正有限元结合MTF未出现高频失稳,图中只显示6400步的计算结果,实际计算100万步.同样采 用小量处理MTF来消除飘移失稳,小量取为0.002.
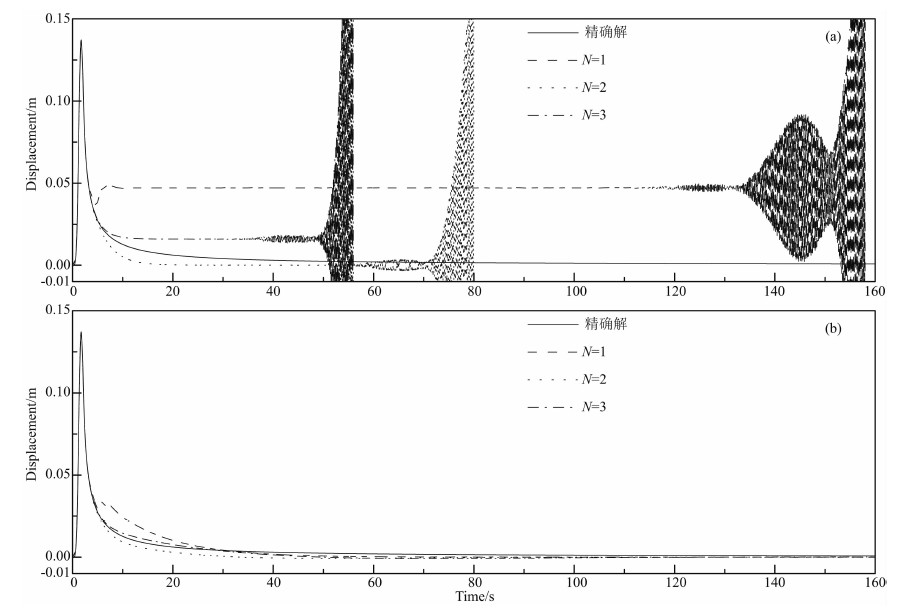 | 图 6(a)和(b)分别为采用传统有限元和修正有限元结合MTF(空间内插公式,人工波速 ca=c,N=1,2,3)
计算的观测点(1,0)位移时程,离散方案为Δx=Δy=0.05 m,Δt=0.025 s Fig. 6(a) and (b)are the displacement time history of the observation point(1,0)computed by classic FEM and modified FEM with MTF(spatial interpolation formula with artificial wave velocity ca=c,N=1,2,3)separately. The discretization mesh is Δx=Δy=0.05 m,Δt=0.025 s |
对于大型近场波动数值模拟,建立高精度、低计算量、稳定的人工边界是一个尚未圆满解决的问题.MTF具有高精度、低计算量,但其存在稳定问题.本文针对SH波动集中质量有限元模拟,阐明了MTF高频耦合失稳机理,稳定实现了MTF.本文的研究结果对于地球物理中的波动正反演问题具有应用前景.依据作者已获得的研究结果,对于其他内域离散格式(如差分、谱元等),只要其不出现异常频散,均不会导致MTF的高频耦合失稳.本文的研究工作是针对SH波动进行的,但其研究思路适用于更广类型波动数值模拟中人工边界的稳定问题.关于在P-SV和三维弹性波数值模拟中MTF的稳定实现,将在后续报告中提出.
| [1] | Baffet D,Bielak J,Givoli D,et al. 2012. Long-time stable high-order absorbing boundary conditions for elastodynamics. Computer Methods in Applied Mechanics and Engineering,241-244: 20-37. |
| [2] | Bérenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics,114(2): 185-200. |
| [3] | Chew W C,Weedon W H. 1994. A 3-D perfectly matched medium from modified Maxwell's equations with stretched coordinates. Microwave Opt. Technol. Lett.,7(13): 599-604. |
| [4] | Clayton R,Engquist B. 1977. Absorbing boundary conditions for acoustic and elastic wave equations. Bull. Seism. Soc. Am.,67(6): 1529-1540. |
| [5] | Deeks A J,Randolph M F. 1994. Axisymmetric time-domain transmitting boundaries. Journal of Engineering Mechanics,120(1): 25-42. |
| [6] | Du X L,Zhao M,Wang J T. 2006. A stress artificial boundary in FEA for near-field wave problem. Chinese Journal of Theoretical and Applied Mechanics (in Chinese),38(1): 49-56. |
| [7] | Du X L,Zhao M. 2010. A local time-domain transmitting boundary for simulating cylindrical elastic wave propagation in infinite media. Soil Dynamics and Earthquake Engineering,30(10): 937-946. |
| [8] | Givoli D,Neta B. 2003. High-order non-reflecting boundary scheme for time dependent waves. J. Comput. Phys.,186(1): 24-46. |
| [9] | Gustafsson B,Kreiss H O,Sundström A. 1972. Stability theory of difference approximations for mixed initial boundary value problems II. Mathematics of Computation,26(119): 649-686. |
| [10] | Hagstrom T,Warburton T. 2004. A new auxiliary variable formulation of high-order local radiation boundary conditions: corner compatibility conditions and extensions to first order systems. Wave Motion,39(4): 327-338. |
| [11] | Higdon R L. 1986. Absorbing boundary conditions for difference approximations to the multi-dimensional wave equation. Mathematics of Computation,47(176): 437-459. |
| [12] | Higdon R L. 1990. Radiation boundary conditions for elastic wave propagation. SIAM Journal on Numerical Analysis,27(4): 831-869. |
| [13] | Idesman A,Pham D. 2014. Finite element modeling of linear elastodynamics problems with explicit time-integration methods and linear elements with the reduced dispersion error. Computer Methods in Applied Mechanics and Engineering,271: 86-108. |
| [14] | Jing L P,Liao Z P,Zou J X. 2002. A high-frequency instability mechanism in numerical realization of multi-transmitting formula. Earthquake Engineering and Engineering Vibration (in Chinese),22(1): 7-13. |
| [15] | Liao Z P,Wong H L,Yang B P,et al. 1984a. A transmitting boundary for transient wave analyses. Scientia Sinica (Series A),27(10): 1063-1076. |
| [16] | Liao Z P,Wong H L. 1984b. A transmitting boundary for the numerical simulation of elastic wave propagation. International Journal of Soil Dynamics and Earthquake Engineering,3(4): 174-183. |
| [17] | Liao Z P,Liu J B. 1992. Numerical instabilities of a local transmitting boundary. Earthquake Engineering and Structural Dynamics,21(1): 65-77. |
| [18] | Liao Z P,Xie Z N. 2011. Stability of numerical simulation of wave motion. Journal of Harbin Engineering University (in Chinese),32(9): 1254-1261. |
| [19] | Liao Z P. 2002. Introduction to Wave Motion Theories in Engineering (Second edition) (in Chinese). Beijing: Science Press. |
| [20] | Liao Z P,Zhou Z H,Zhang Y H. 2002. Stable implementation of transmitting boundary in numerical simulation of wave motion. Chinese Journal of Geophysics (in Chinese),45(4): 554-568,doi: 10.3321/j.issn:0001-5733.2002.04.011. |
| [21] | Li X J,Liao Z P. 1996. The drift instability of local transmitting boundary in time domain. Acta Mechanica Sinica (in Chinese),28(5): 627-632. |
| [22] | Li X J,Yang Y. 2012. Measures for stability control of transmitting boundary. Chinese Journal of Geotechnical Engineering (in Chinese),34(4): 641-645. |
| [23] | Liu J B,Wang Z Y,Du X L,et al. 2005. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems. Engineering Mechanics (in Chinese),22(6): 46-51. |
| [24] | Lysmer J,Kulemeyer R L. 1969. Finite dynamic model for infinite media. Journal of Engineering Mechanics Division,95(4): 859-878. |
| [25] | Trefethen L N. 1983. Group velocity interpretation of the stability theory of Gustafsson Kreiss and Sundström. Journal of Computational Physics,49(2): 199-217. |
| [26] | Xie Z N,Komatitsch D,Martin R,et al. 2014. Improved forward wave propagation and adjoint-based sensitivity kernel calculations using a numerically stable finite-element PML. Geophys. J. Int.,198(3): 1714-1747. |
| [27] | Xie Z N,Liao Z P. 2008. A note for the mechanism of high-frequency oscillation instability resulted from absorbing boundary conditions. Acta Seismologica Sinica,21(3): 306-310. |
| [28] | Xie Z N,Liao Z P. 2012. Mechanism of high frequency instability caused by transmitting boundary and method of its elimination—SH wave. Chinese Journal of Theoretical and Applied Mechanics (in Chinese),44(4): 745-752. |
| [29] | Yue B,Guddati M N. 2005. Dispersion-reducing finite elements for transient acoustics. J. Acoust. Soc. Am.,118(4): 2132-2141. |
| [30] | Zhou Z H,Liao Z P. 2001. A measure for eliminating drift instability of the multi-transmitting formula. Acta Mechanica Sinica (in Chinese),33(4): 550-554. |
| [31] | 杜修力,赵密,王进廷. 2006. 近场波动模拟的人工应力边界条件. 力学学报,38(1): 49-56. |
| [32] | 景立平,廖振鹏,邹经湘. 2002. 多次透射公式的一种高频失稳机制. 地震工程与工程振动,22(1): 7-13. |
| [33] | 廖振鹏. 2002. 工程波动理论导论(第二版). 北京: 科学出版社. |
| [34] | 廖振鹏,周正华,张艳红. 2002. 波动数值模拟中透射边界的稳定实现. 地球物理学报,45(4): 554-568,doi: 10.3321/j.issn:0001-5733.2002.04.011. |
| [35] | 廖振鹏,谢志南. 2011. 波动数值模拟的稳定性. 哈尔滨工程大学学报,32(9): 1254-1261. |
| [36] | 李小军,廖振鹏. 1996. 时域局部透射边界的计算飘移失稳. 力学学报,28(5): 627-632. |
| [37] | 李小军,杨宇. 2012. 透射边界稳定性控制措施探讨. 岩土工程学报,34(4): 641-645. |
| [38] | 刘晶波,王振宇,杜修力等. 2005. 波动问题中的三维时域粘弹性人工边界. 工程力学,22(6): 46-51. |
| [39] | 谢志南,廖振鹏. 2012. 透射边界高频失稳机理及其消除方法–SH波动. 力学学报,44(4): 745-752. |
| [40] | 周正华,廖振鹏. 2001. 消除多次透射公式飘移失稳的措施. 力学学报,33(4): 550-554. |
 2015, Vol. 58
2015, Vol. 58

