随着勘探开发水平的提高,人们对地下介质的认识逐渐深入,针对各向异性介质的地震资料处理技术及正反演方法成为研究的重点(滕吉文等,2000;徐善辉等,2012;李振春等,2013),而作为地震勘探的基础,各向异性正演方法的精度和效率直接影响到后续处理解释的正确性及可行性.由于TTI、单斜等各向异性的对称性较低,现有的正演模拟方法拓展到此类介质时需要做一些特殊处理,导致计算量增加或引入不必要的误差.为了更加精确的描述波在TTI介质中的传播规律,本文针对有限差分正演模拟方法的三个关键问题分别作了改进(李国平等,2011):(1)网格定义方式;(2)差分系数求取;(3)边界条件优化.
(1)针对各向异性的网格定义方式:Virieux(1986)首次采用标准交错网格(Standard Staggered Grid,SSG)有限差分方法模拟了非均匀介质中P-SV波的传播.随后,该方法因其易实现、高效率、高精度等特点被广泛应用于各向同性介质的波场模拟中(Levander, 1988).由于TTI介质或一般各向异性介质的刚度矩阵中非零弹性参数较多,求解波动方程时同一变量在不同方向上的偏导项同时存在,而标准交错网格每个变量的不同分量都是交错定义的,需要对某些点上没有定义的波场变量插值,进而引入数值误差,降低了模拟精度(Igel et al, 1995).
为了克服这一缺陷,近几年提出了两种新的网格定义机制:一个是Saenger等,2000的旋转交错网格(Rotated Staggered Grid, RSG),其将同一变量的不同分量定义在相同位置,速度变量分布在应力的对角线上,先计算沿对角线方向的空间导数,然后通过线性组合得到坐标轴方向的偏导值;另一个 则是Lisitsa et al,2010, 2012的Lebedev 网格(Lebedev Grid,LG), 该网格机制同样将速度、应力的不同分量定义在同一网格点上,但两个变量交错分布,相当于在SSG机制中增加了需要插值的分量,这样变量在每个方向的导数都可以直接计算,无需插值.相较于RSG,LG方法具有更宽松的频散条件,可以允许较大的空间采样间隔,降低了对内存的需求,尤其在模拟大尺度模型时,LG所需的计算内存是RSG的1/3或2/3(Lisitsa et al, 2010);同时,LG不存在变量插值,比SSG方法具有更高的模拟精度,通过上述对比分析,本文选用LG算法开展各向异性介质波场特征的研究,并有针对性的对该算法做进一步的优化.
(2)差分系数求取:网格频散是有限差分方法离散化求解波动方程产生的固有本质特征,频散会降低模拟结果的分辨率,而差分系数是影响频散效果的重要因素.目前,应用较为广泛的是Taylor系数, 此外,Tam et al,1993引入最小二乘思想得到同位 网格下线性欧拉方程的DRP(Dispersion-relation-preserving) 差分系数;沿用Tam等的思路,Ye et al,2005推导了非均匀网格二阶偏导的DRP系数并将其应用到声波数值模拟中;McGarry等(2011)提出交错网格一阶微分的DRC(Dispersion-reducing-coefficients)系数,改善了频散现象.在前人的基础上,本文将Taylor级数展开方法与最小二乘思想结合得到新的频散改进差分系数,降低了Taylor系数对空间间距的依赖,使得在大网格间距下仍然具有较高的模拟精度,从而节约了内存和计算量,并且模型数据越大,该算子的优势越明显.
(3)边界条件优化:边界反射是正演模拟需要解决的又一个关键问题.Bérenger,1994在电磁波模 拟中提出了完全匹配层(PML)吸收边界条件,研 究表明通常情况下,PML边界条件较旁轴近似(Clayton et al, 1980)、指数衰减等阻尼衰减方法(Cerjan et al, 1985; Kosloff R et al, 1986)具有更好的边界吸收效果,但也存在不足(Chew et al, 1994; Chen et al, 1997).<Bécache et al,2003)从理论上证明了在某些各向异性介质中传统PML边界条件具有指数增长解,由此产生不稳定现象;Meza-Fajardo et al,2008提出M-PML边界条件,并利用特征值灵敏度分析法证实了Bécache等的结论,指出当介质的Christoffel方程存在多重实部为零的特征解时PML边界条件就会引起不稳定,而M-PML边界条件在几个正交方向上同时引入衰减因子,通过调整衰减因子的比例系数使结果满足渐近稳定性.
本文将优化的频散改进差分系数及M-PML吸收边界条件引入到Lebedev网格有限差分方法中,通过对TTI介质的模型试算验证了改进算法的模拟精度和频散改善效果,并在保证较好的边界吸收效果的同时解决了某些各向异性介质中边界条件不稳定的问题.
二维TTI介质的一阶速度-应力方程可以表示为

其中,
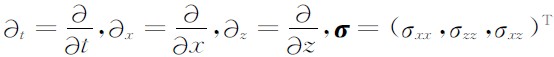 为应力张量,
为应力张量,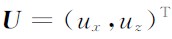 为速度张量,I为二阶单 位矩阵,P为介质密度,A1, A2 矩阵的具体表达形式为
为速度张量,I为二阶单 位矩阵,P为介质密度,A1, A2 矩阵的具体表达形式为
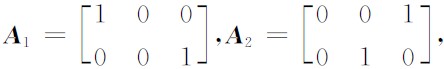
S为TTI介质的弱度矩阵,
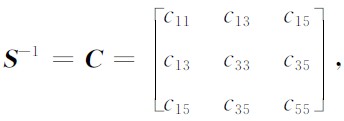
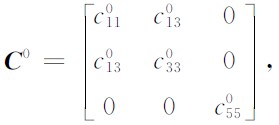
C由VTI介质弹性参数矩阵
通过坐标变换矩阵
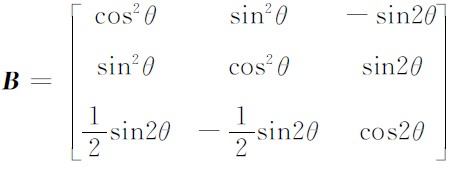
得到:C=BC0BT,θ为极化角(VTI介质主对称轴与z轴的夹角).
如图1 所示,Lebedev网格机制的主要思想就是将速度(图1中矩形)和应力(图1中圆圈)的不同分量交错定义在同一网格点上,(i, j)为空间网格坐标,根据网格定义特点,可将二维坐标集合分为四类:
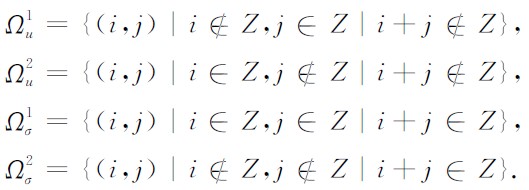
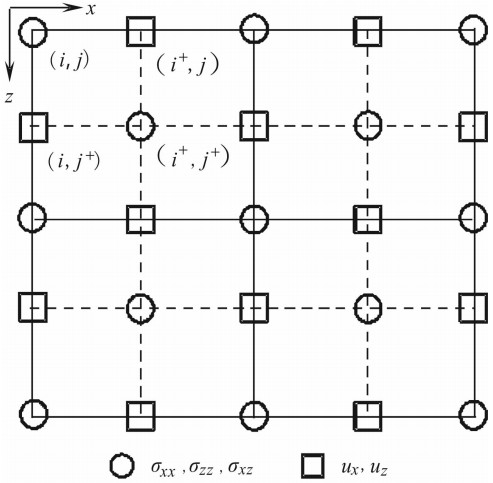 | 图1 Lebedev网格示意图(i+=i+1/2 ,j+=j+1/2表示半网格点) Fig.1 Grids for Lebedev Scheme (i+=i+1/2 is the half-grid point and the same to j+) |
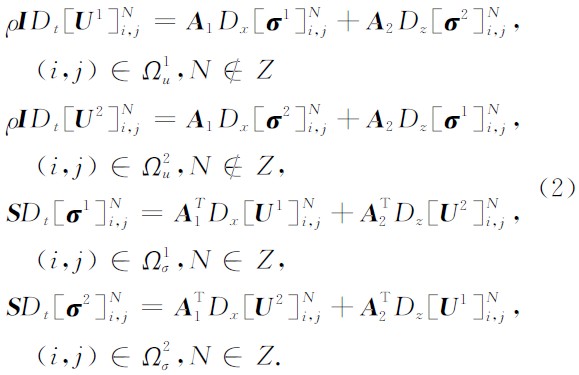
其中,N为离散时间点(整数点和半整数点两类),Dt,Dx,Dz为中心差分算子,表示形式如下:
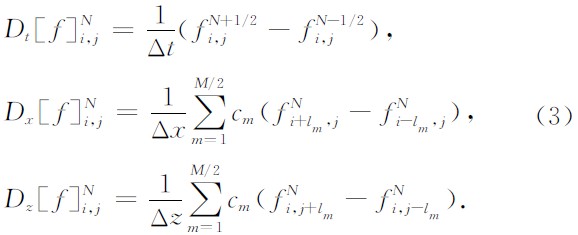
M为空间差分精度,cm为交错网格M阶精度的有限差分系数,lm=(2m-1)/2.
有限差分正演模拟的基本思想就是用(3)式的M阶差分算子代替波动方程(1)中的偏微分,通过求取波动方程差分形式的数值解来近似偏微分方程的解析解,偏微分的M阶差分形式可以表示为
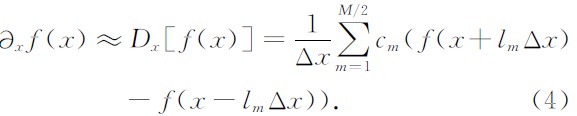
可以看出,当差分精度M固定时,(4)式的近似精度取决于差分系数cm及空间间隔Δx.现在广泛采用的是Taylor差分系数,首先对(4)式进行傅立叶变换,由欧拉公式得到一个关于波数与Δx的近似式为
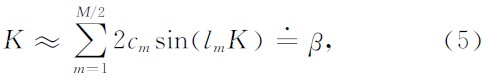
式中,K=kΔx,k为波数,将(5)式中的正弦函数展成Taylor 级数,截取前M/2项,根据等式两端对应项系数相等,可得到计算Taylor系数的线性方程组(6)为
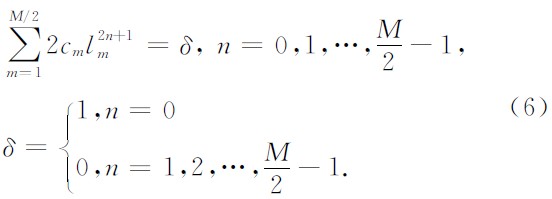
由Taylor级数的性质可知,采用Taylor差分系数时(5)式的精度随Δx的减小而提高,但是单纯的依靠减小空间间隔来提高精度会使内存和计算量成倍增加,不利于大规模数据的处理.为了提高方法的计算效率,本文引入最小二乘思想,寻找使得(5)式对所有Δx∈(0,Δxmax)的误差平方和最小的差分系数(Δxmax为采样定理允许的最大间距),这样每个采样间隔对应的偏差都很小,近似精度不会因为Δx的增大而降低,数值模拟时便可选取较大的采样间隔,从而降低存储内存与计算量.最小二乘方法的误差目标函数方程为
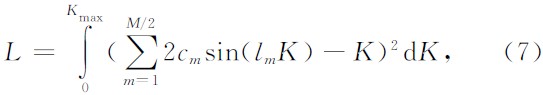
根据K与Δx的关系及Nyquist 频率得到Kmax=
 (N为单位波长内的采样点数,本文中N=3).此外,(7)式的误差目标函数中直接选用正弦函数,避免了先前方法中Taylor级数截断带来的误差,提高了(5)式的精度.使(7)式最小的差分系数可以通过方程组(8)得到
(N为单位波长内的采样点数,本文中N=3).此外,(7)式的误差目标函数中直接选用正弦函数,避免了先前方法中Taylor级数截断带来的误差,提高了(5)式的精度.使(7)式最小的差分系数可以通过方程组(8)得到

虽然(8)式得到的差分系数可以允许较大的采样间隔,但由于求取准则是误差平方和最小,而平方和内各项的误差大小不确定,这可能会使小采样间隔下的误差增大,导致频散甚至不稳定现象(McGarry et al, 2011);因此,本文将最小二乘思想与Taylor方法结合:利用最小二乘方法降低对大空间采样的限制,同时,通过Taylor展开关系保证小采样间距下的模拟精度.经过多次试验,由(6)式的第一个与(8)式的前M/2-1个(m=1,2,…,M/2-1)构建的新方程组能够得到最优的差分系数(DIC).
为了测试效果,将本文推导的差分系数与Taylor系数,DRP系数(联立(6)式前M/2-1个及(8)式中的任意一个得到)及DRC系数(结合(6)式前两个(n=0,1)及(8)式前M/2-2个方程得到)进行对比,图2为10阶差分精度(M=10)下,分别采用上述四种差分系数得到的(5)式的频散曲线(已将β归一化),可以看出:在大空间网格间距下,本文提出的DIC算子与真实值K最接近,能更好的压制网格频散现象.
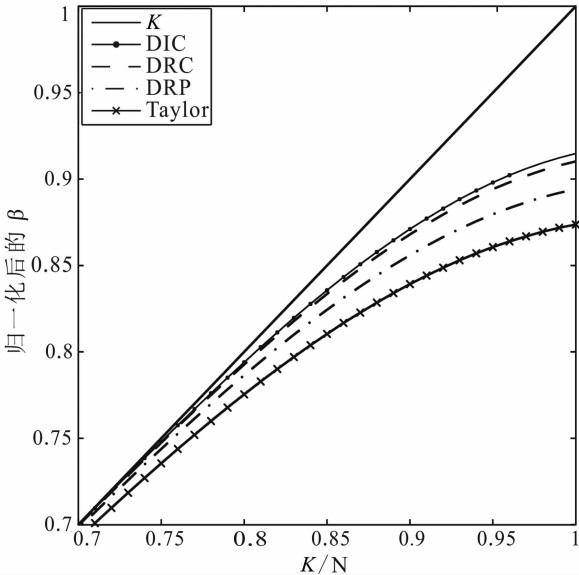 | 图2 四种有限差分系对应的频散曲线(M=10) Fig.2 Dispersion curves of the four kinds of FD coefficients with order M=10 |
传统PML边界条件通过分裂变量并沿偏导方向引入衰减因子d来实现边界内的波场衰减.以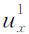 为例,将其分裂为垂直于边界的
为例,将其分裂为垂直于边界的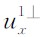 和平行于边界的
和平行于边界的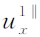 两项,即
两项,即

为使波在垂直于x轴的匹配层内呈指数衰减,波动方程(1)变为
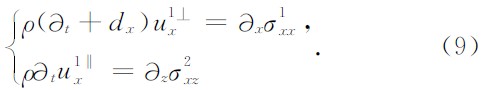
其中dx为沿x方向的衰减因子.M-PML对传统PML边界条件进行了扩展,在分裂的两个正交方向上同时引入衰减因子
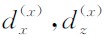 ,则(9)式变为
,则(9)式变为
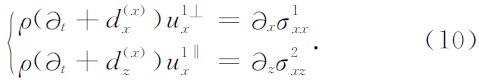
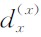 与传统PML中的dx取法一致,
与传统PML中的dx取法一致,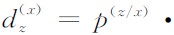 ·dx;类似地,在垂直于z轴的匹配层内引入衰减因子
·dx;类似地,在垂直于z轴的匹配层内引入衰减因子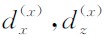 ,其中,
,其中,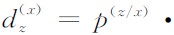 .系数
.系数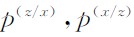 称为稳定性因子,正演模拟时通过调整两个因子达到稳定的目的;稳定性因子根据经验获得,不同介质模型对应的稳定性因子可能不同.当稳定性因子为零时,M-PML退化为传统的PML边界条件.
称为稳定性因子,正演模拟时通过调整两个因子达到稳定的目的;稳定性因子根据经验获得,不同介质模型对应的稳定性因子可能不同.当稳定性因子为零时,M-PML退化为传统的PML边界条件.
为了验证优化后的LG正演模拟算法的正确性与普适性,分别对两组均匀TTI介质进行测试;随后,根据Meza-Fajardoet al,2008)提出的判别标准,选取了一种特殊的TI介质(Ⅲ)来说明M-PML边界的渐近稳定性.模拟过程中均采用爆炸震源,模型参数见表1.
|
|
表1 模型参数 Table 1 The model parameters |
首先,通过介质Ⅰ验证本文LG算法的正确性与有效性,设计参数如下:301*301的网格区域,网格间距8 m,主频25 Hz,时间采样间隔0.4 ms.图3为分别采用LG与SSG算法得到的0.44 s的z分 量波场快照(a,b)及黑色虚线方框区域的局部放大图(c,d),并通过群速度曲线(黑色实线)分析两种算法的模拟精度.
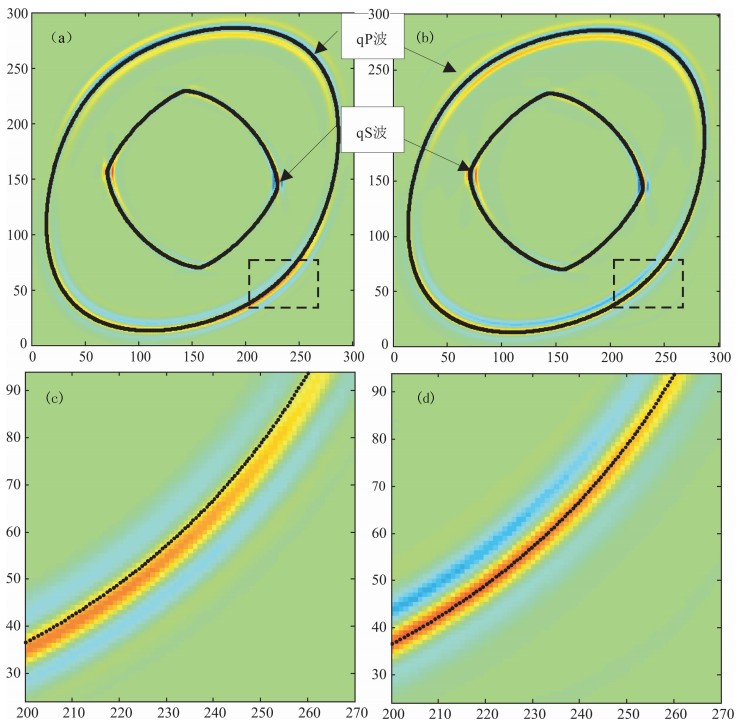 | 图3 z分量波场快照(t=0.44 s) (a)SSG方法波场快照;(b)LG方法波场快照;(c)图(a)黑色虚线方框内的放大图;(d) 图(b)黑色虚线方框内的放大图;黑色实线为群速度曲线. Fig.3 z-component snapshots at 0.44 s (a) Snapshot computed by SSG; (b) Snapshot computed by LG; (c) Close-up image of the black dotted box in (a); (d) Close-up image of the black dotted box in (b);The black solid line is the group velocity. |
对比图3中两个局部放大部分可知,LG算法得到的qP与qSV波波前能量最强区域与理论群速度曲线吻合的较好,而SSG方法经波场插值后的波前能量发生了偏离,说明LG机制能有效地减少插值带来的数值误差,更准确的模拟波在各向异性介质中的传播特征,这对后续各向异性介质群速度、相速度的正确提取以及高精度偏移成像都有着重要的意义(郝重涛等,2006).
进一步,为了说明本文提出的DIC差分系数在网格频散方面的改进效果,分别采用10阶精度的DIC与Taylor差分系数对介质Ⅱ进行模拟,计算中的具体参数如下:网格间距8 m,主频25 Hz,时间采样间隔1.0 ms.模拟结果如图4所示,图(a)为采用Taylor差分系数的结果,图(b)为DIC的结果,图(c,d)为对应黑色方框区域qSV波三叉区的局部放大图,对比左右图可见:改进的DIC差分系数能够显著的降低空间网格频散(如图中白色箭头位置所示).为了达到与DIC系数相同的效果,采用Taylor系数模拟时需要将网格间距减小到6 m,导致内存增加约77.8%,计算量也随之增大,不利于大规模数据的正演处理,体现了DIC算子在内存与计算效率方面的优势.
 | 图4 z分量波场快照(t=0.8 s) (a) 采用Taylor差分系数的波场快照; (b) 采用DIC系数的波场快照;(c) 图(a)黑色方框区域的放大图; (d) 图(b)黑色方框区域的放大图. Fig.4 z-component snapshots at 0.8 s (a) Snapshot computed with Taylor coefficients; (b) Snapshot computed with DIC; (c) Close-up image of the black box in (a); (d) Close-up image of the black box in (b). |
本节最后通过模型III对比分析传统PML与M-PML边界条件的稳定性,计算参数如下:网格区域为321×321(含匹配层),网格间距0.05 m,震源点距上边界和左边界均为0.15 m,主频0.9 Hz,时间采样间隔2.0 ms.不同时刻x分量波场快照如图 5所示:左边一列为采用传统PML边界条件的结果,右边为M-PML的结果(稳定性因子p(z/x)=0.2,p(x/z)=0.4),每列从上至下提取的时刻依次是2.8 s、3.8 s、5.0 s、7.2 s.
 | 图5 不同时刻x分量场快照(左:PML,右:M-PML) (a)t=2.8 s;(b)t=3.8 s;(c)t=5.0 s;(d)t=7.2 s. Fig.5 x-component snapshots at different time (left: PML, right: M-PML) |
由图5可知:波场传播到匹配层后(3.8 s),传统PML边界在右上方开始出现不稳定(如图5b中箭头位置所示);随着时间步长的增加,不稳定性逐渐增强(图5c),在7.2 s时(图5d)不稳定能量已将原波场信息全部淹没,而采用M-PML的模拟结果(右边一列)一直都是稳定的,并且具有较好的边界吸收效果.
针对TTI介质,本文实现了LG有限差分数值模拟算法,并从差分系数和边界条件两个方面对算法做了优化,通过对比分析不同TTI介质的模拟结果,得到如下几点认识:
(1)LG方法无需波场插值,具有较高的模拟精度,适用于各种对称系统的各向异性介质,是人们真实了解地下地质构造的有力工具(吴永国等,2008),但该算法占用内存较大,是SSG方法的两倍.
(2)基于Taylor级数展开,本文结合最小二乘思想,推导出一种新的频散改进系数(DIC),对比Taylor系数发现,DIC能更好的改善空间网格频散,节约内存,提高计算效率.
(3)针对传统PML在某些各向异性介质中由于具有指数增长解而产生的不稳定,将M-PML边界条件引入到本文算法中,实现了解的渐近稳定性;但该边界条件基于分裂的波动方程,计算中会增加内存.
从上述认识中不难发现计算内存是LG算法的局限,但也应该看到,本文给出的DIC差分系数能够允许更大的空间网格间距,可以缓解对内存与计算量的需求;此外,当介质为对称性较高的VTI或正交各向异性介质时,LG体系可以解耦成两个独立的子体系,内存减少1/2,与SSG体系等效;在此基础上,我们还将进一步研究不分裂且稳定的边界条件以减少内存,提高本文方法的适应性.
致 谢 作者感谢两位匿名审稿专家的宝贵意见,感谢国家973项目(2011CB202402),国家自然科学基金(41104069,41274124),山东省自然科学基金(ZR2011DQ016)及中央高校基本科研业务经费专项资金资助(R1401005A)联合资助支持.| [1] | Bécache E, Fauqueux S, Joly P. 2003. Stability of perfectly matched layers, group velocities and anisotropic waves. J. Comput. Phys., 188(2): 399-433, doi: 10. 1016/S0021-9991(03)00184-0. |
| [2] | Bérenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys., 114(2):185-200, doi: 10.1006/jcph.1994.1159. |
| [3] | Cerjan C, Kosloff D, Kosloff R, et al. 1985. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics, 50(4): 705-708, doi: 10.1190/1.1441945. |
| [4] | Chen Y H, Chew W C, Oristaglio M L. 1997. Application of perfectly matched layers to the transient modeling of subsurface EM problems. Geophysics, 62(6):1730-1736, doi: 10.1190/1.1444273. |
| [5] | Chew W C, Weedon W H. 1994. A 3-D perfectly matched medium from modified Maxwell′s equations with stretched coordinates. Microwave and Optical Technology Letters, 7(13): 599-604, doi: 10.1002/mop.4650071304. |
| [6] | Clayton R, Engquist B. 1980. Absorbing boundary conditions for wave-equation migration. Geophysics, 45(5): 895-904, doi: 10.1190/1.1441094. |
| [7] | Hao C T, Yao C, Wang X. 2006. The characteristics of velocities with azimuth variation for arbitrary spatial orientation TI media. Progress in Geophysics (in Chinese), 21(2): 524-530, doi: 10.3969/j.issn.1004-2903.2006.02.029. |
| [8] | Igel H, Mora P, Riollet B. 1995. Anisotropic wave propagation through finite-difference grids. Geophysics, 60(4): 1203-1216, doi: 10.1190/1.1443849. |
| [9] | Kosloff R, Kosloff D. 1986. Absorbing boundaries for wave propagation problems. J. Comput. Phys., 63(2): 363-376, doi: 10. 1016/0021-9991(86)90199-3. |
| [10] | Levander A R. 1988. Fourth-order finite-difference P-SV seismograms. Geophysics, 53(11): 1425-1436, doi: 10.1190/1.1442422. |
| [11] | Li G P, Yao F C, Shi Y M, et al. 2011. Several key issues of finite-difference seismic wave numerical simulation. Progress in Geophysics (in Chinese), 26(2): 469-476, doi: 10.3969/j.issn.1004-2903.2011.02.011. |
| [12] | Li Z C, Li N, Huang J P, et al. 2013. The Quantity study of the factors that influence the Shear-wave splitting time in Fracture Media. Progress in Geophysics (in Chinese), 28(1): 240-249, doi: 10.6038/pg20130125. |
| [13] | Lisitsa V, Vishnevskiy D. 2010. Lebedev scheme for the numerical simulation of wave propagation in 3D anisotropic elasticity. Geophysical Prospecting, 58(4): 619-635, doi: 10.1111/j.1365-2478.2009.00862.x. |
| [14] | Lisitsa V, Tcheverda V. 2012. Numerical simulation of seismic waves in models with anisotropic formations: coupling Virieux and Lebedev finite-difference schemes. Comput. Geosci., 16(4):1135-1152, doi: 10. 1007/s10596-012-9308-0. |
| [15] | McGarry R, Pasalic D, Ong C. 2011. Anisotropic elastic modeling on a Lebedev grid: Dispersion reduction and grid decoupling. 81th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2829-2833. |
| [16] | Meza-Fajardo K C, Papageorgiou A S. 2008. A non-convolutional split-field, perfectly matched layer for wave propagation in isotropic and anisotropic elastic media: stability analysis. Bulletin of the Seismological Society of America, 98(4): 1811-1836, doi: 10. 1785/0120070223. |
| [17] | Saenger E H, Gold N, Shapiro S A. 2000. Modeling the propagation of elastic waves using a modified finite-difference grid. Wave Motion, 31(1): 77-92, doi: 10. 1016/S0165-2125(99)00023-2. |
| [18] | Tam C K W, Webb J C. 1993. Dispersion-relation-preserving finite difference schemes for computational acoustics. J. Comput. Phys., 107(2): 262-281, doi: 10.1006/jcph.1993.1142. |
| [19] | Teng J W, Zhang Z J, Wang G J, et al. 2000. The seismic anisotropy and geodynamics of earth′s interior media. Progress in Geophysics (in Chinese), 15(1): 1-35. |
| [20] | Virieux J. 1986. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics, 51(4): 889-901, doi: 10.1190/1.1442147. |
| [21] | Wu Y G, He Z H, Huang D J. 2008. Wave equation forward modeling and migration for beads-shaped corroded cave model. Progress in Geophysics (in Chinese), 23(2): 539-544. |
| [22] |
Xu S H, Han L G, Guo J. 2012. Multiwave inversion of anistropic parameter and PS wave AVO analysis in TTI media. Chinese J. Geophys. (in Chinese), 55(2): 569-576, doi: 10.6038/j.issn.0001-5733.2012.02.019. |
| [23] | Ye F, Chu C. 2005. Dispersion-relation-preserving finite difference operators: derivation and application. 75th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 1783-1786. |
| [24] | 郝重涛, 姚陈, 王迅. 2006. 任意空间取向TI介质中速度随方位变化特征. 地球物理学进展, 21(2): 524-530, doi: 10.3969/j.issn.1004-2903.2006.02.029. |
| [25] | 李国平, 姚逢昌, 石玉梅等. 2011. 有限差分法地震波数值模拟的几个关键问题. 地球物理学进展, 26(2): 469-476, doi: 10.3969/j.issn.1004-2903.2011.02.011. |
| [26] | 李振春, 李娜, 黄建平等. 2013. 裂缝介质横波分裂时差影响因素定量研究. 地球物理学进展, 28(1): 240-249, doi: 10. 6038/pg20130125. |
| [27] | 滕吉文, 张中杰, 王光杰等. 2000. 地球内部各圈层介质的地震各向异性与地球动力学. 地球物理学进展, 15(1): 1-35. |
| [28] | 吴永国, 贺振华, 黄德济. 2008. 串珠状溶洞模型介质波动方程正演与偏移. 地球物理学进展, 23(2): 539-544. |
| [29] | 徐善辉, 韩立国, 郭建. 2012. TTI介质各向异性参数多波反演与PS波AVO分析. 地球物理学报, 55(2): 569-576, doi: 10.6038/j.issn.0001-5733.2012.02.019. |
 2014, Vol. 57
2014, Vol. 57


