2. 中国科学院大学, 北京 100049
2. Graduate University, Chinese Academy of Sciences, Beijing 100049, China
由于野外采集条件的限制,实际采集往往无法获得完整且规则的地震数据,而数据的完整性和规则性对后期资料处理及解释工作至关重要.因此不完整、不规则数据的规则化处理是地震数据处理中的一项关键技术.
在过去的半个世纪里,Nyquist采样定理在传统的信号的采样、存储、传输及处理等环节中起到了非常重要的作用.该采样定理认为:如果信号是带限的,而且采样频率高于信号带宽的一倍,那么原来的连续信号可以从采样样本中完全重建出来,否则将产生混叠效应,信号将不能被完整恢复.因此,高分辨率的图像或信号处理中,这种采样生成的数据需要庞大的存储空间,或者只能保留重要的部分,丢弃其余数据,造成极大的资源浪费.近年由David Donoho、Emmanuel Candès、 Terence Tao、Romberg 等提出的压缩感知(Compressed Sensing)理论(Donoho et al., 2006;Candès et al., 2006a,c,d),打破了传统采样的理念.压缩感知理论指出:当信号具有稀疏性或者在某个变换域可以稀疏表示时,通过设计一个与稀疏变换基不相关的测量矩阵观测该信号,将高维信号投影到低维空间上,得到少量观测值,利用稀疏促进算法求解最优化问题实现数据的高概率重构.稀疏约束最优化问题可以追溯到90年代,Mallat等在1993年提出了基于稀疏约束的贪婪算法-匹配追踪(Matching Pursuit,MP)(Mallat and Zhang, 1993),该方法主要通过迭代算法在变换域找出与原始信号匹配最佳的基函数,即每次迭代时在变换域找出与原始信号内积最大的基函数.该算法绝对收敛,稳定可靠.但是由于每次迭代需在变换基函数大集合中找出最佳匹配的基函数,因此计算量较大.另一方面,作为贪婪算法,其后面迭代过程有可能一直纠正前面迭代结果中产生的误差,最终只能得到稀疏性差的解.随后发展出 其正交形式的算法,即Orthogonal Matching Pursuit(Pati et al,,1993).该算法与MP不同点在于每次迭代得到近似解后,其余部分与该解正交,也就是说同一个基函数不可能在不同迭代中被选择两次,从而最终得到更准确的解,相应地计算量也加大.1994年提出的基追踪(Basis Pursuit)方法(Chen et al., 1994),采用L1范数表示信号稀疏性的度量,通过最小化L1范数将信号稀疏问题转化为一类有约束条件的极值问题,从而转化为线性规划问题求解问题.BP方法是一种全局优化的原则,计算复杂度要高于MP类方法,算法形式不受限制.虽然理论结果表明这些算法可以恢复稀疏解,但是测量类型以及规模是次优的,后来在压缩感知理论得到了显著地提高.2004年,Emmanuel Candès,Terence Tao,David Donoho发现了重要的结果,在数据不满足Nyquist-Shannon采样定理时重构数据所需要的最小个数.该理论提出之后,带动了基于该理论的稀疏促进算法方面的研究.迭代阈值法(Daubechies et al., 2004)因其算法简单、计算复杂度低而得到了广泛的研究,近几年研究人员又进一步提出了新的迭代阈值算法,如CRSI(Curvelet Recovery by Sparsity- promoting Inversion)方法(Herrmann and Hennenfent, 2008)、 Bregman快速迭代方法(Yin,2010;Ma,2011)等.CRSI方法将Daubechies等人提出的迭代阈值法应用到不完整地震资料在Curvelet域的恢复研究中,通过冷却阈值办法不断迭代得到较满意的恢复结果,但是收敛速度慢,一般进行相对较多的迭代会得到较好的结果.Bregman快速迭代算法由于每次迭代“吸收”阈值之前的所有恢复量,因此表现出了快速的收敛速度,仅若干次迭代就能恢复出大部分有效信号,恢复速度比CRSI快得多,然而到了迭代后期,阈值逐渐减小过程中,由于将小于阈值的非有效信息也加进结果中,导致恢复结果渐渐变差.
在图像处理或科学计算中经常使用的变换域有Fourier变换域(Bochner and Ch and rasekharan, 1949)、小波变换域(Chui,1992)、Radon变换域(Deans,1983)、Curvelet变换域(Candès and Donoho, 2005a,b;Candès et al., 2006b)等.选择合适的稀疏变换域,对信号的恢复结果有很大的影响.Curvelet是局部的、带有方向的、在切向上光滑而在垂向上震荡的“小型平面波”,对于含二次可微的曲线奇异函数有接近最优的逼近性能.地震数据体是地表接收的地震波场在空间、时间方向上采样的数字信号,地震同相轴作为有效信号,绝大部分都是光滑的曲线,因此在Curvelet域可以探测到各个方向上的地震同相轴并且可以以高压缩比表达地震信号.Herrmann等人将Curvelet应用到了基于压缩 感知的数据重建(Herrmann and Hennenfent, 2008)、 去除面波(Yarham et al., 2006)和去除多次波(Herrmann et al., 2007)等处理中.由于Curvelet变换对曲线、边界等对象具有稀疏表示的优势,因此也有大量的研究将Curvelet变换应用到图像处理、地震资料处理、医学成像、遥感工作中,并取得了良好的效果(Starck et al., 2003;Ali et al., 2008;Ma,2011).
本文首先阐述了压缩感知理论以及DCT(Discrete Curvelet Transform)的基本内容和原理,介绍了CRSI方法和Bregman算法分析,结合CRSI方法和Bregman方法的优缺点,进一步提出了结合两种方法的联合迭代算法,并进一步对简单模型数据和实际数据做了数据重建试验,得到了满意的结果.
2 压缩感知理论压缩感知(Compressive Sensing,CS),也称作压缩采样和稀疏采样,是一种寻找欠定线性系统的稀疏解的技术,由David Donoho、Emmanuel Candès、 Terence Tao、 J. Romberg等人于2004年提出(Donoho,2006;Candès et al., 2006a,c,d).压缩感知理论的成立有两个重要的前提条件:信号的稀疏性和测量矩阵与稀疏变换域的不相关性.
2.1 稀疏表示(Sparse Representation)现具体考虑一个实值离散信号 f ∈ R N,假设 f 在 Ψ 变换域可以稀疏表示,用矩阵形式表示为


根据压缩感知理论,如果信号具有稀疏性,那么即使信号缺失得较多,也可通过合适的测量矩阵和稀疏促进恢复算法得到一个准确度很高的重构结果.
2.2 测量矩阵(Measurement Matrix)测量是完整信号 f ∈ R N到不完整信号 y ∈ R M(M≤N)的映射,M为测量个数,用矩阵形式表示为


A 是一个m×p矩阵,s是满足1≤s≤p的一个整数.如果存在一个常数δs,对 A 的每个m×s的子矩阵以及每一个向量 y 满足:

RIP可以描述近似正交矩阵的非正交程度,满足RIP的矩阵有随机观测的高斯随机矩阵、伯努利矩阵以及可以确定性观测的Chirp测量矩阵(Applebaum et al., 2009)等.随机高斯矩阵与大多数正交基构成的矩阵不相关,以高概率满足RIP,因此常常选择其作为压缩感知测量矩阵.
2.3 稀疏促进算法(Sparsity Promoting Algorithm)RIP从理论上保证s-稀疏信号能由M个测量值 y 重构出长度为N的信号 f .(4)式中,测量得到的原始高维信号在低维空间上的投影即为测量值 y,这是一个典型的欠定方程,是一个多解问题.压缩感知理论通过稀疏约束,求出该方程具有高概率准确度的唯一解(Candès et al., 2006a;Mallat,2008;Herrmann and Hennenfent, 2008).式(4)的最稀疏解可描述为如下问题的解:
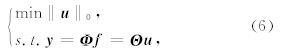
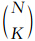 个非零元素的组合,属于一个经典的NP-hard非凸优化问题.目前求解该类问题办法主要有三类:第一类是利用线性规划求解稀疏恢复问题的基追踪(Basis Pursuit,BP)算法(Chen et al., 1994),基本思想是用l1范数来代替l0“范数”:
个非零元素的组合,属于一个经典的NP-hard非凸优化问题.目前求解该类问题办法主要有三类:第一类是利用线性规划求解稀疏恢复问题的基追踪(Basis Pursuit,BP)算法(Chen et al., 1994),基本思想是用l1范数来代替l0“范数”:
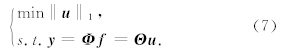
当服从独立同分布的高斯测量值的个数M≥cKlog(N/K)时,就可以以高概率重构K-稀疏信号.从而问题变成了凸优化问题,可以通过线性规划 问题来求解.该算法具有全局最优的优点,但计算复杂度高;另一类是采用基于贪婪算法(Greedy Algorithm)(Leiserson C E et al., 2001)的方法,如匹配追踪算法(Matching Pursuit,MP)(Mallat and Zhang, 1993),正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)(Pati et al., 1993),阶段 式正交匹配追踪算法(Stagewise Orthogonal Matching Pursuit,StOMP)(Donoho et al,2012).这类方法中大多数需要的采样点数为M=O(clogN),贪婪算法以多于BP算法需要的采样数目换取计算复杂度 的降低,计算速度相对第一类方法较快,但是缺乏稳 定性;也有一类算法为迭代阈值法(Iterative Thresholding Method)(Daubechies et al., 2004),该类算法结构简单,计算量小,稳定,故经常用来解决上述问题.文章的第4节将详细研究迭代阈值算法,分析和比较了几种迭代阈值类方法的优缺点,并提出了一种新的联合迭代阈值方法.
3 曲波变换理论考虑二维情况下的曲波变换(Curvelet Transform),设有空间域变量为x,频率域变量为ω,用r和θ表达频率域极坐 标.那么曲波正变换表达式为(Candès et al., 2005a,b;Candès et al., 2006b)
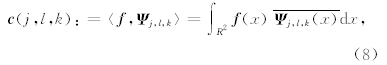
根据Plancherel定理(Plancherel,1910),上式在频率域表示为
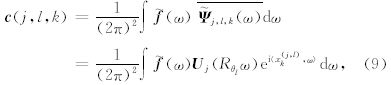
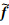 (ω)是 f 的频率域表示,
(ω)是 f 的频率域表示,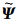 j,l,k(ω)是 Ψ j,l,k(x)的傅里叶变换,U j(Rθlω)是频率域极坐标下与尺度、角度相关的扇形窗函数,x(j,l)k为Curvelet域位置坐标.
j,l,k(ω)是 Ψ j,l,k(x)的傅里叶变换,U j(Rθlω)是频率域极坐标下与尺度、角度相关的扇形窗函数,x(j,l)k为Curvelet域位置坐标.
另外,最内尺度低通窗W0满足条件有
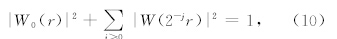
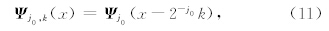
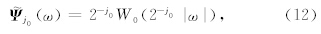
Curvelet具有多尺度、多方向以及空间域、频率域的局部特性.只要地震数据体可以表示成二次可微的曲线奇异函数,Curvelet就可以探测到地震波同相轴并且可以稀疏表达此类有效信号.
4 稀疏促进算法设计及理论模型实验 4.1 算法对比及设计压缩感知的关键技术之一是设计稀疏促进算法(Bregman,1967;Daubechies et al., 2004;Herrmann and Hennenfent, 2008; Yin,2010; Ma,2011).稀疏促进问题可以表示为(Donoho,2006)
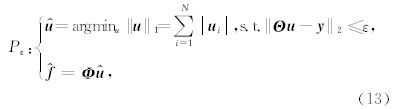
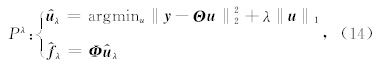
拉格朗日乘子λ决定了l1项和l2项之间的权重,Pλ问题求解过程即通过不断调节λ直到满足:
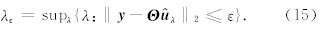
在Pλ问题求解过程中,通常先强调稀疏促进的l1项,即选取较大的λ值求得稀疏逼近解,再放松λ 使其递减,即增加l2项相对权重,不断迭代得到真实逼近解.通常采用基于L and weber下降法(L and weber, 1951)发展的冷却阈值迭代方法(Pati et al., 1993; Mallat,2008;Herrmann and Hennenfent, 2008)求解上述问题.CRSI方法即在Curvelet域实现冷却阈值迭代,其具体算法如下:
输入:不完整数据 y,测量矩阵 Θ ;
初始化:阈值参数‖ Θy ‖∞>λ1>λ2>…>λk,变换域系数 J 0=0,i=0;
输出: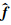 = ΘJ ;
= ΘJ ;
迭代:while ‖ y - ΘJ i‖>ε and i≤K,do
for l=1 to L,do
J i+1=Tλi(J i+ Θ T(y - ΘJ i))
end for
i=i+1;
end while
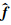 = ΘJ i,
其中,λi为第i次迭代的阈值,随着迭代增加逐渐减小,J i为第i次迭代得到的Curvelet域恢复结果,Tλ(J)= :sgn(J)·max(0,| J |-λ),为软阈值函数.每次迭代更新减小阈值,都会最小化Pλ中的二次方项,投影到l1球上.
= ΘJ i,
其中,λi为第i次迭代的阈值,随着迭代增加逐渐减小,J i为第i次迭代得到的Curvelet域恢复结果,Tλ(J)= :sgn(J)·max(0,| J |-λ),为软阈值函数.每次迭代更新减小阈值,都会最小化Pλ中的二次方项,投影到l1球上.
CRSI方法重构信噪比高,但收敛速度慢.为此,相继出现了加速改进算法,如Bregman迭代阈值法(Yin,2010;Ma,2011)等.其算法如下:
输入:(J 0,v 0)=(0,0),λ=λ0,i=0;
迭代:while 不满足迭代终止条件,do
(1)v i+1= v i+αi ΨΦ T(y - ΦΨ -1 J i);
(2)J i+1=δ·Tλ(v i+1);
(3)减少λ;
(4)i=i+1;
end while
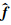 = Ψ -1 J i+1;
= Ψ -1 J i+1;
输出: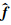 ,
,
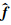 为对重建结果作反变换后的时空域信号,J i为第i次迭代后的Curvelet域结果,v i+1为 J i+1阈值前的值,αi为迭代步长,Tλ(ν)= :sgn(ν)·max(0,| ν |-λ)为软阈值函数,δ为阈值常数.由算法中的步骤(1)发现,与CRSI相比,主要区别在于该方法将右端第1项用第i次阈值前的迭代结果 v i代替第i次阈值后的结果 J i.每次迭代的校正量 v i相比 J i,加回了部分阈值前的有效信号部分,从而加快了收敛速度.但另一方面,该方法虽然在迭代初期收敛很快,到迭代后期由于在恢复有效信号的同时将小于阈值的非有效信号部分也吸收进来,导致信噪比降低.
为对重建结果作反变换后的时空域信号,J i为第i次迭代后的Curvelet域结果,v i+1为 J i+1阈值前的值,αi为迭代步长,Tλ(ν)= :sgn(ν)·max(0,| ν |-λ)为软阈值函数,δ为阈值常数.由算法中的步骤(1)发现,与CRSI相比,主要区别在于该方法将右端第1项用第i次阈值前的迭代结果 v i代替第i次阈值后的结果 J i.每次迭代的校正量 v i相比 J i,加回了部分阈值前的有效信号部分,从而加快了收敛速度.但另一方面,该方法虽然在迭代初期收敛很快,到迭代后期由于在恢复有效信号的同时将小于阈值的非有效信号部分也吸收进来,导致信噪比降低.
综合考虑到两者的优缺点,本文提出一种两者结合的迭代算法,如下:
输入:(J 0,v 0)=(0,0),λ=λ0,i=0,δ=δ0;
迭代:while 迭代终止条件不满足,do
(1)v i+1=(1-β(i))v i+β(i)J i
+αi ΨΦ T(y - ΦΨ -1 J i);(2)J i+1=δ·Tλ(v i+1);
(3)减少λ;
(4)i=i+1;
end while
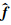 = Ψ -1 J i;
= Ψ -1 J i;
输出: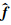 .
.
与前两种算法相比,该算法在Bregman迭代算法的步骤(1)中的等式右边多加了 J i项,并通过β调整其权重.在这里有
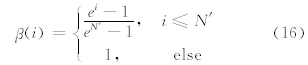
本文首先用一个模型做试验,模型如图 1a所示,炮点在模型最左端的地表激发,共341道接收,道间距为4 m,每道870个时间采样点,采样间隔2 ms,选择雷克子波作为震源子波,图 1b为其正演模拟地震记录.随后,随机抽空50%、70%的地震道,分别得到如图 1c和图 1g所示的不完整地震数据.接着分别用CRSI方法、Bregman方法以及本文提出的方法重建数据,得到了数据重建结果.可以看出,CRSI方法和本文提出的方法相比Bregman方法,都得到了更高信噪比结果,同相轴更加连续、光滑,连续缺失达8道的地方也恢复得很准确.在能量相对弱的底部,本文方法恢复得结果相比其他两个方法要好,除了极小部分有噪声之外,浅层强能量轴和底层较弱的能量轴都得到了较好的恢复.
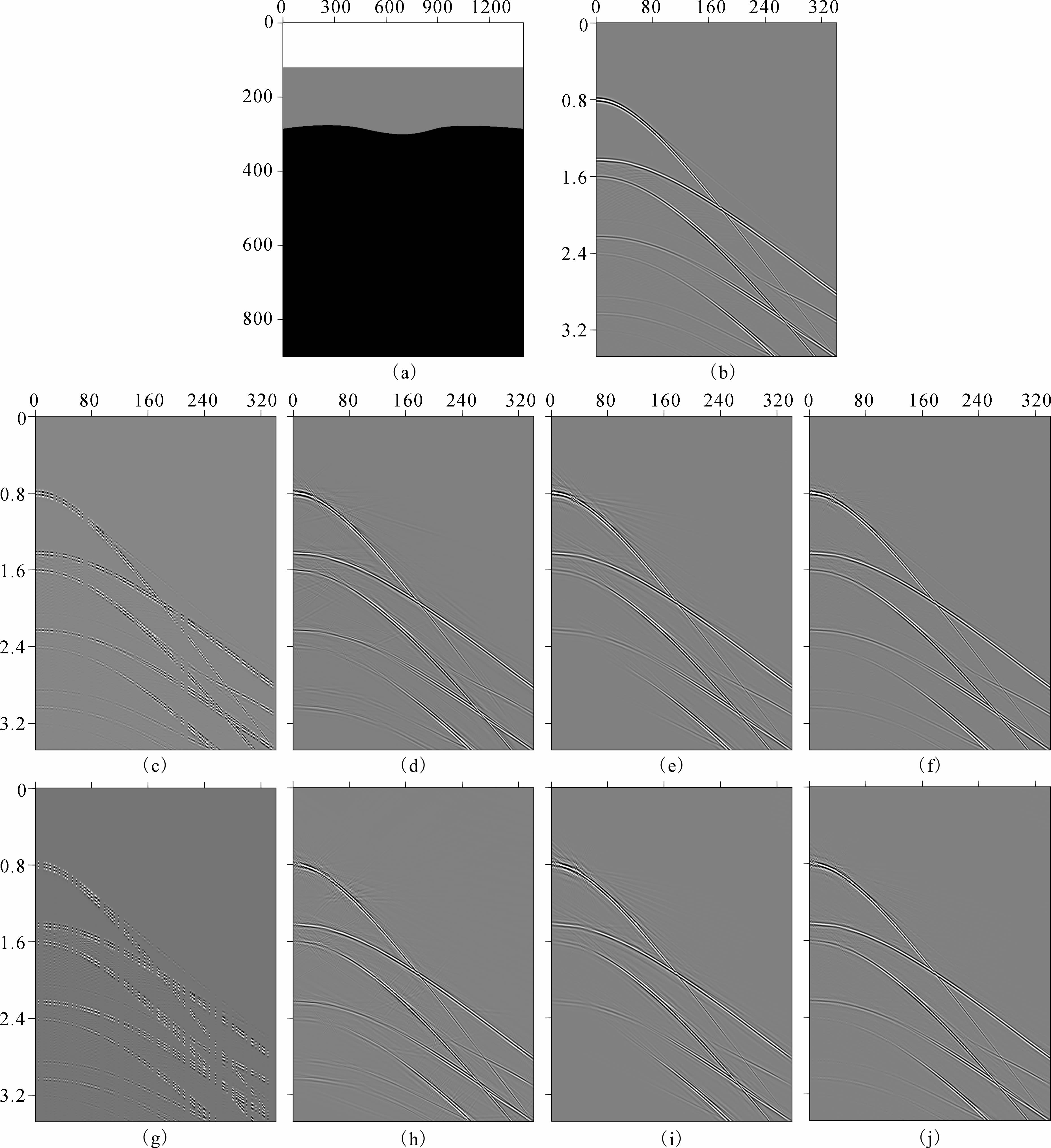 | 图 1 模拟数据试验结果(a)速度模型;(b)原始模型数据;(c)50%随机抽道后不完整数据;(d)50%随机抽道后Bregman迭代法恢复结果;(e)50%随机抽道后CRSI方法恢复结果;(f)50%随机抽道后本文方法恢复结果;(g)70%随机抽道后不完整数据;(h)70%随机抽道后Bregman迭代法恢复结果;(i)70%随机抽道后CRSI方法恢复结果;(j)70%随机抽道后本文方法恢复结果.Fig. 1 Synthetic data reconstructed result(a)Velocity model;(b)Original Complete data;(c)Incomplete data with 50% r and omly missing traces;(d)Reconstruction result of(c)by Bregman method;(e)Reconstruction result of(c)by CRSI;(f)Reconstruction result of(c)by the method of this paper;(g)Incomplete data with 70% r and omly missing traces;(h)Reconstruction result of(g)by Bregman method;(i)Reconstruction result of(g)by CRSI ;(j)Reconstruction result of(g)by our method. |
另外,图 2中绘出了误差曲线(用E表示)以及信噪比曲线(用SNR表示),其中E、SNR分别由下面两个等式得到:

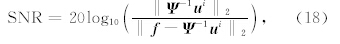
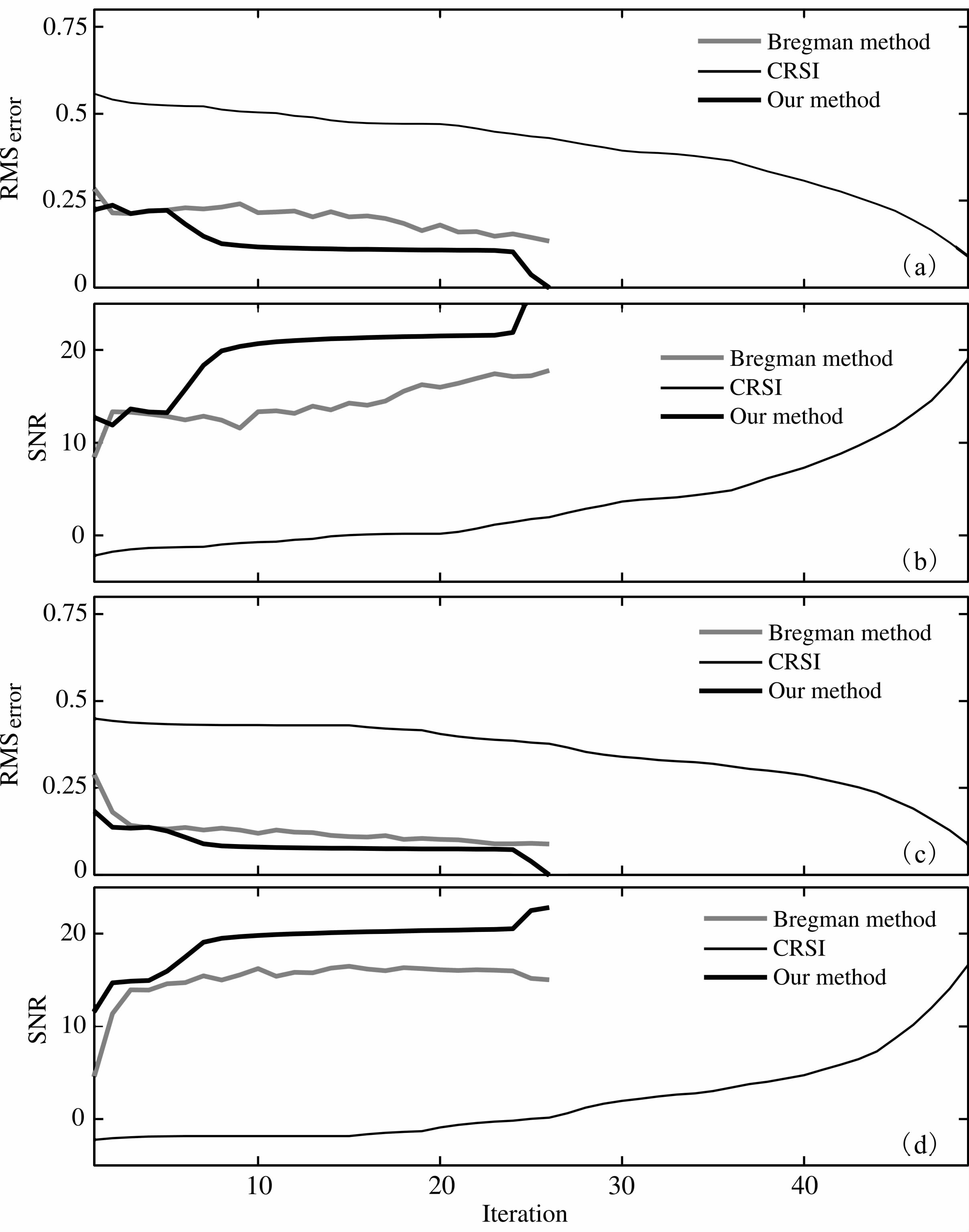 | 图 2 CRSI、Bregman方法和本文方法的重建信噪比及收敛速度对比图(a)50%随机采样时恢复误差随着迭代次数的变化图;(b)50%随机采样时信噪比随着迭代次数的变化图;(c)70%随机采样时恢复误差随着迭代次数的变化图;(d)70%随机采样时信噪比随着迭代次数的变化图.Fig. 2 Comparison of reconstruction SNR,convergence speed by CRSI,Bregman method and our proposed methodRecovery errors varying with iteration times for 50% r and om sampling;(b)SNR varying with iteration times for 50% r and om sampling;(c)Same as(a)but for 70% r and om sampling;(d)Same as(b)but for 70% r and om sampling. |
图 2中用三种不同的线条绘出了CRSI方法、Bregman方法和本文提出的方法得到的恢复结果对应的相对误差和信噪比.整体来说,三种方法虽然恢复70%缺失的数据的最终信噪比略低于恢复50%缺失的数据时的信噪比,但还是很好地恢复出了大部分确实数据.在信噪比方面,可以看到CRSI和本文方法得到的恢复结果的信噪比都相对Bregman方法要高,尤其是本文方法恢复出的数据信噪比明显高于其它两种方法.收敛速度方面,我们观察误差曲线发现,Bregman方法和本文方法收敛得要比CRSI快得 多.尤其是在迭代初期,虽用了相同的阈值,Bregman 方法和本文方法的误差水平远远低于CRSI方法,因为前两者会将阈值以下的有用信息部分保留下来,而不是做阈值处理.综合考虑信噪比、收敛速度等因素,本文提出的方法得到的效果最好,正演模型数据试验验证了本文提出的方法对恢复大比例随机缺失地震数据的有效性.
5 实际数据处理本文在正演模型试验的基础上对实际数据也做了处理.实际数据与模型数据相比复杂得多,不同的实际数据其复杂程度也大相径庭.本文选择的实际数据为某区叠后地震资料.该资料共661道,每道2001个时间采样点,采样间隔为2ms,如图 3a.可以看到,该数据即有强能量的、连续性好的同相轴,也有能量弱的、连续性差的信号以及部分噪声.图 3b 为抽空原始数据中40%的地震道后的缺失数据,采用本文方法得到的恢复结果见图 3c.可以看到经恢复后,各缺失道均得到了很好的恢复,地震同相轴光滑、连续,其中强振幅同相轴恢复效果最为明显.
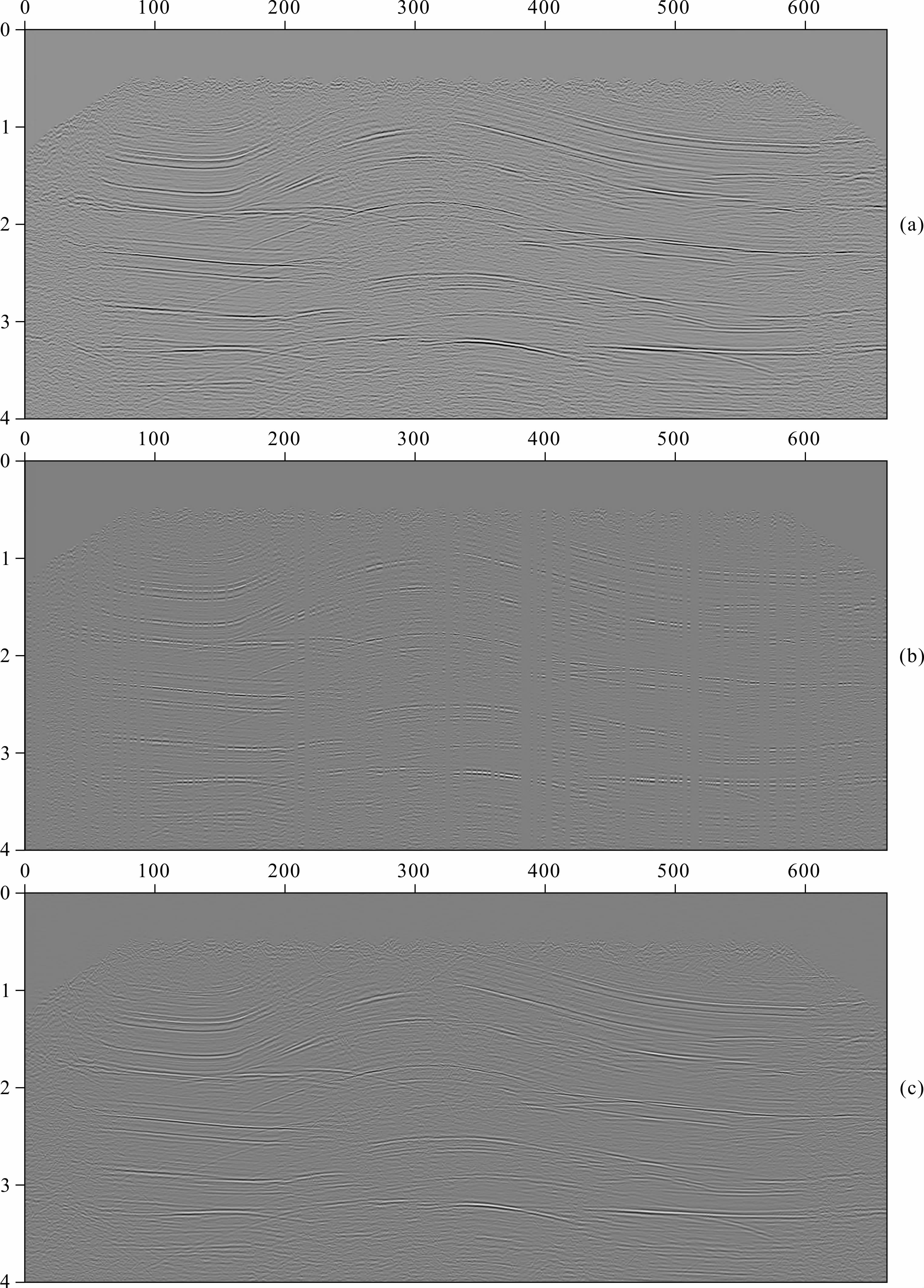 | 图 3 实际资料试验结果(a)原始地震数据;(b)40%随机抽空后的不完整数据;(c)恢复后数据.Fig. 3 Real data reconstructed result(a)Original real data;(b)Real data with 40% r and omly missing data;(c)Reconstructed data. |
本文提出的算法框架综合CRSI方法和Bregeman 方法的优缺点,通过比例因子调节两种方法得到的 恢复量的权重,使迭代结果在反演初期表现出Bregman 方法快速收敛的优点,在反演后期表现出CRSI高信噪比稳定重建的优点.文章详细比较了CRSI方法、Bregman方法和本文提出的方法在高比例缺失的合成数据中的重建表现,结果表明相比前两种算法,本文提出的方法同时具有收敛快、信噪比高的特点,反演结果稳定可靠的优势.最后的实际地震数据重建结果验证了本文方法在实际资料重建中的准确性和有效性.
| [1] | Ali F E, El-Dokany I M, Saad A A, et al. 2008. Curvelet fusion of MR and CT images. Progress in Electromagnetics Research C, 3: 215-224, doi: 10.2528/PIERC08041305. |
| [2] | Applebaum L, Howard S D, Searle S, et al. 2009. Chirp sensing codes: Deterministic compressed sensing measurements for fast recovery. Applied and Computational Harmonic Analysis, 26(2): 283-290, doi: 10.1016/j.acha.2008.08.002. |
| [3] | Bochner S, Chandrasekharan K. 1949. Fourier Transforms. Princeton: Princeton University Press. |
| [4] | Bregman L M. 1967. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Computational Mathematics and Mathematical Physics, 7(3): 200-217, doi: 10.1016/0041-5553(67)90040-7. |
| [5] | Candès E J, Donoho D L. 2005a. Continuous curvelet transform I: resolution of the Wavefront Set. Applied and Computational Harmonic Analysis, 19(2): 162-197, doi: 10.1016/j.acha.2005.02.003. |
| [6] | Candès E J, Donoho D L. 2005b. Continuous curvelet transform: II. discretization and frames. Applied and Computational Harmonic Analysis, 19(2):198-222, doi: 10.1016/j.acha.2005.02.004. |
| [7] | Candès E J, Tao T. 2006a. Near optimal signal recovery from random projections: universal encoding strategies. IEEE Transactions on Information Theory, 52(12): 5406-5425, doi: 10.1109/TIT.2006.885507. |
| [8] | Candès E J, Demanet L, Donoho D L, et al. 2006b. Fast discrete curvelet transforms. SIAM Multiscale Model. Simul., 5(3): 861-899, doi: 10.1137/05064182X. |
| [9] | Candès E J, Romberg J, Tao T. 2006c. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. on Information Theory, 52(2): 489-509, doi: 10.1109/TIT.2005.862083. |
| [10] | Candès E J, Romberg J K, Tao T. 2006d. Stable signal recovery from incomplete and inaccurate measurements. Communications on Pure and Applied Mathematics, 59(8): 1207-1223, doi: 10.1002/cpa.20124. |
| [11] | Candes E J. 2008. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Mathematique, 346(9-10): 589-592, doi: 10.1016/j.crma.2008.03.014. |
| [12] | Chen S B, Donoho D L, Saunders M A. 1994. Atomic decomposition by basis pursuit. SIAM Journal on Scientific Computing, 20(1): 33-61, doi: 10.1137/S003614450037906x. |
| [13] | Chui C K. 1992. An Introduction to Wavelets. San Diego: Academic Press. |
| [14] | Daubechies I, Defrise M, De Mol C. 2004. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics, 57(11): 1413-1457, doi: 10.1002/cpa.20042. |
| [15] | Deans S R. 1983. The Radon Transform and Some of Its Applications. New York: John Wiley & Sons. |
| [16] | Donoho D L. 2006. Compressed sensing. IEEE Transactions on Information Theory, 52(4): 1289-1306, doi: 10.1109/TIT.2006.871582. |
| [17] | Donoho D L, Tsaig Y, Drori I, et al. 2012. Sparse solution of underdetermined systems of linear equations by Stagewise Orthogonal Matching Pursuit. IEEE Trans. on information Theory, 58(2): 1094-1121, doi: 10.1109/TIT.2011.2173241. |
| [18] | Herrmann F J, Wang D, Hennenfent G. 2007. Multiple prediction from incomplete data with the focused Curvelet transform. Presented at the SEG International Exposition and 77th Annual Meeting. |
| [19] | Herrmann F J, Hennenfent G. 2008. Non-parametric seismic data recovery with Curvelet frames. Geophysical Journal of International, 173(1): 233-248, doi: 10.1111/j.1365-246X.2007.03698.x. |
| [20] | Landweber L. 1951. An iteration formula for Fredholm integral equations of the first kind. American Journal of Mathematics, 73(3): 615-624, doi: 10.2307/2372313. |
| [21] | Leiserson C E, Rivest R L, Stein C, et al. 2001. Introduction to Algorithms, Chapter 16 "Greedy Algorithms": The MIT Press. |
| [22] | Ma J W. 2011. Improved iterative Curvelet thresholding for compressed sensing. IEEE Transactions on Instrumentation and Measurement, 60(1): 126-136, doi: 10.1109/TIM.2010.2049221. |
| [23] | Mallat S. 2008. A Wavelet Tour of Signal Processing: The Sparse Way. San Diego: Academic Press. |
| [24] | Mallat S G, Zhang Z. 1993. Matching Pursuits with time-frequency dictionaries. IEEE Trans. Signal Process, 41(12): 3397-3415, doi: 10.1109/78.258082. |
| [25] | Pati Y C, Rezaiifar R, Krishnaprasad P S. 1993. Orthogonal Matching Pursuit: recursive function approximation with application to wavelet decomposition. In Asilomar Conf. on Signals, Systems and Computers in 1993. |
| [26] | Plancherel M. 1910. Contribution à l'étude de la représentation d'une fonction arbitraire par les integrals définies. Rendiconti del Circolo Matematico di Palermo, 30(1): 289-335, doi: 10.1007/BF03014877. |
| [27] | Starck J L, Murtagh F, Candès E J, et al. 2003. Gray and color image contrast enhancement by the Curvelet Transform. IEEE Transaction on Image Processing, 12(6): 706-717, doi: 10.1109/TIP.2003.813140. |
| [28] | Yarham C, Boeniger U, Herrmann F. 2006. Curvelet-based ground roll removal. 2006 SEG Annual Meeting. |
| [29] | Yin W T. 2010. Analysis and generalizations of the Linearized Bregman Method. SIAM J. Imaging Sci., 3(4): 856-877, doi: 10.1137/090760350. |
 2014, Vol. 57
2014, Vol. 57

