1 引言
分数维和分数阶微积分已经成了物理学的前沿,但是很少有人探究两者的物理意义及关系(陈文等,2012).对于复杂的湍流问题,间歇湍流是十分被关注的问题.它说明湍流由大涡串级成小涡的过程中,小涡并不充满空间,它只是占空间的一部分,这是客观的、现实的.因而相对于充满空间的整数维而言,引入分数维来描述间歇性湍流更自然,更有物理意义(Frisch,1995).正是因为串级过程中有跨好多量级尺度差别的涡旋存在,使得湍流涡旋的游动距离和等待时间也有跨量级尺度的差别(刘式达等,2013),这就造成了湍流运动的概率密度分布带有长尾巴的幂律分布.一方面造成涨落的平均值毫无意义(刘式达等,2008;胡非,1995),另一方面,大涨落事件的概率虽然小,但是,仍有相当大的概率(胡非,1995).同时涡旋串级或碰撞的过程中会给将来的速度涨落有延迟效应,这就造成了湍流的记忆性(刘式达等,2013).因而,必须引入有记忆核的分数阶微积分到描述湍流的Navier-Stokes(NS)方程中去(Uchaikin 2013).通过分析,我们将分数阶拉普拉斯算子的阶数和分数维联系起来.我们也将大小涨落引起的超扩散和分数维及分数阶导数的阶数联系起来.本文系统介绍了分数维、分数阶导数在间歇湍流中的意义,从而对分数维和分数阶导数有相当深入的了解.
2 间歇湍流的维数及其占居的概率为了描述方便,我们以二维间歇湍流为例.假设平面上有一个单位正方形的涡旋,它分成三个尺寸为1/2的小正方形涡旋,并空出一个,见图 1.
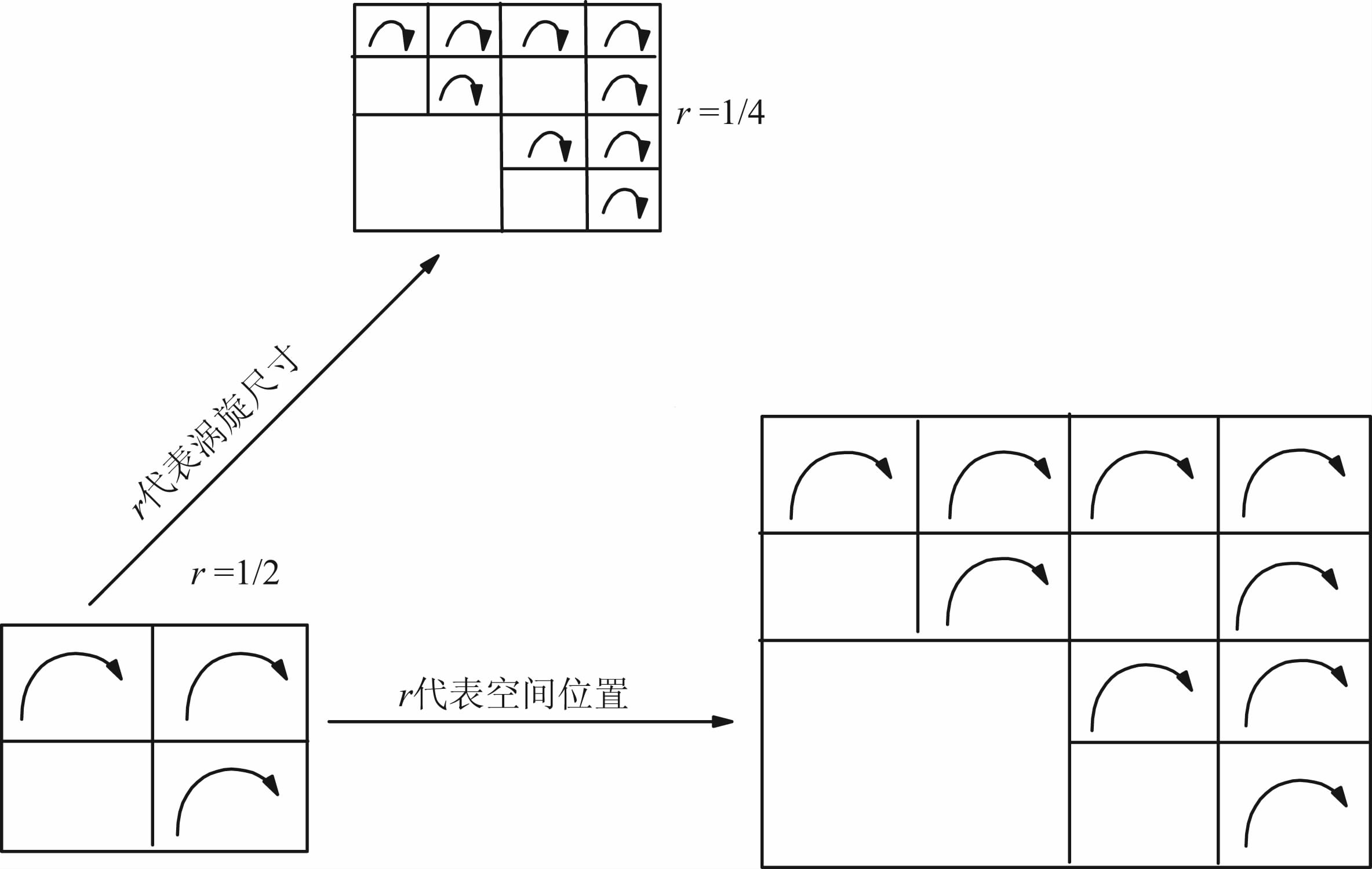 | 图 1 大涡旋分裂成小涡旋的串级过程(示意图) Fig. 1 Schematic plot for the process from the larger eddies cascade to smaller ones |
若以r表示涡旋的尺寸,这三个大涡旋又串级各自分成尺寸为r=1/4的三个小涡旋.若r表示空间位置,原来r=1的正方形涡旋扩大成r=2的正方形,相当于原有的r=1涡旋为种子,扩大成原来种子的三倍.
按照分数维的定义,以r为尺寸量出来的涡旋个数为N,则分数维为(刘式达等,2008;胡非,1995)

若r表示空间位置,图 1的尺寸放大2倍,图形是原来的3倍,即维数为
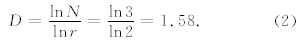
以上两种结果是一样的.它说明在平面上,间歇湍流的维数为1<D<2.将其推广到三维间歇湍流,那么间歇湍流的维数为

若r表示涡旋的尺寸,由图 1看出涡旋所占面积s(r)随着r的减小而减小,设s(r)为




1941年Kolmogorov均匀各向同性湍流是一种无间歇性的湍流,惯性区的功率谱为
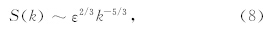
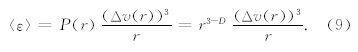
由此求得速度差Δv(r)为

同样,对于二阶结构函数(刘式达等2008)也只有活动涡旋那部分,即
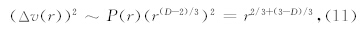

设惯性区的功率谱指数为β,即

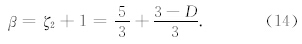
既然间歇湍流有大大小小的涡旋,其游动距离有长有短,等待下一步游动的时间也有长有短.所以,游动距离x和等待时间的概率可表示为(刘式达 等2013)
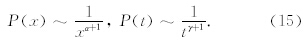
(15)式称为Levy分布(Chen 2006).显然若游动的距离x有长有短,且是好多量级,x的平均值就没有意义.
同时,随着游动距离的加大,扩散也加大.通常湍流扩散系数为二阶结构函数乘以时间,即


对于Kolmogorov湍流,二阶结构函〈(Δv(r))2〉~ε2/3r2/3,时间尺度为r/Δv,即t~ε-1/3r2/3,所以,由(16)式得到湍流扩散系数K为

由(17)式的两边量纲分析得到r2~Kt~ε1/3r4/3t,即方差为

将(19)式与布朗运动的扩散方差

而对于间歇性湍流,(16)式中的二阶结构函数加大了,所以扩散方差也要大.由(11)式得到
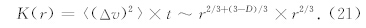
且由(17)式的量纲分析得到r2~Kt~r4/3+(3-D)/3t,故扩散方差为

由(22)式看出,当D=3时,就化为Richardson扩散定律(19).对于2
对于像图 1那样,每次串级过程,活动涡旋只占整个涡旋的一部分(3/4).这里3/4是固定的,称为β=3/4模式,它是均匀的间歇湍流.此时,只要用一个维数D来描述.此时,测度的q阶矩的标度指数(刘式达等,2008)为
而对于串级过程每次活动涡旋所占的比例并不是常数的非均匀间歇湍流,例如She(Frisch,1995;胡非,1995)模型:
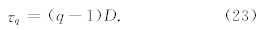

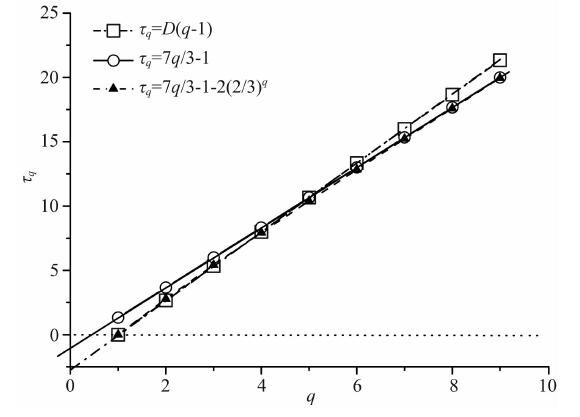
图 2 τq随q变化图
Fig. 2 Variation of τq with q
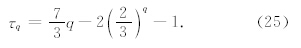
过去我们把流体作为一个连续介质,流体运动可以用Navier-Stokes(N-S)方程来描述(朗道与栗弗席兹,2013).对于间歇湍流,流体质点并不充满空间,这并不能看作连续介质.
按照(7)式,若体积元、面元和线元分别是dV,dS,dL,那么间歇湍流的分形介质,流体质点所占有的体积、面积和线段分别就是


Tarasov(Tarasov,2010)认为,若设密度ρ为常数,通过分数维积分出的流体质量为

那么间歇湍流的分形介质就可以看成是连续介质了.此时,相应的流体力学方程要作相应的修改.
假如连续介质的不可压缩流体的质量守恒定律修改为
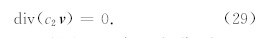
Navier-Stokes方程中的惯性力项就变成
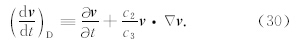
对于N-S方程中的分子黏性力项,有

以上修改仅仅是从分形介质中的流体质点只占一部分出发的.从未考虑到间歇湍流的长程相关性和记忆性.为此,Chen 等(Chen et al., 2004)指出间歇湍流的黏性项可以表示为

我们已经找出了α和间歇湍流维数D的关系为

若把间歇湍流串级过成看成是随机过程的话,布朗运动游动距离x和白噪声μ的关系为著名的Langevin方程:

若把(34)式改成分数阶导数,则有


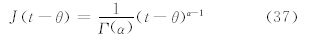
那么
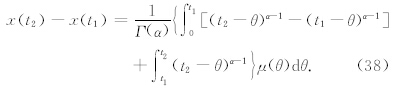
但是,当α=1时,(38)式右端的第一项积分为零,因此

从前面的分析可以看出,间歇湍流具有显著的分形特征,分数维和分数阶导数是刻画其分形特征的自然选择.
越来越多的研究表明自然界与自然科学遇到的很多现象与分形关系密切(陈文等,2012;Uchaikin,2013;Tarasov,2010;Chen et al., 2004;Chen et al., 2010).而且研究发现,用经典的方程或研究方法不能够完全正确地刻画这些现象.分形或分数阶导数建模(陈文等,2012;Uchaikin,2013)越来越多地被应用到这些复杂现象的研究中,取得了非常多 的重要成果(陈文等,2012;Uchaikin,2013;Tarasov,2010;Chen et al., 2004;Chen et al., 2010).同时,自然界中的很多过程的变化具有显著的记忆性,例如气温 变化(Feng et al., 2009)、降水变化(Feng et al., 2008)及灾害过程的演变等.从前一节的分析可以看出,分数阶导数的引入是刻画这些现象的自然选择,而这方面的研究尚未开展或需要更多深入的研究.
| [1] | Chen W, Holm S. 2004. Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency. J. Acoust. Soc. Am. , 115(4): 1424-1430. |
| [2] | Chen W, Sun H G, Zhang X D, et al. 2010. Anomalous diffusion modeling by fractal and fractional derivatives. Computers Math. Appl. , 59(5): 1754-1758. |
| [3] | Chen W, Sun H G, Li X C, et al. 2012. Fractional Derivative Modeling in Mechanical and Engineering Problems (in Chinese). Beijing: Science Press, 11-54. |
| [4] | Chen W. 2006. A speculative study of 2/3-order fractional Laplacian modeling of turbulence: Some thoughts and conjectures. Chaos, 16(2): 023126. |
| [5] | Feng G L, Gong Z Q, Zhi R, et al. 2008. Analysis of precipitation characteristics of south and north China based on the power-law tail exponents. Chinese Physics B, 17(7): 2745-2752. |
| [6] | Feng G L, Yang J, Wan S Q, et al. 2009. On the prediction of record-breaking daily temperature events. Acta Meteorologica Sinica, 67(1): 61-74. |
| [7] | Frisch U. 1995. Turbulence: The Legacy of Kolmogoroved A N. Cambridge: Cambridge University Press. |
| [8] | Hu F. 1995. Turbulence, Intermittency, Atmosphere Boundary Layer (in Chinese). Beijing: Science Press. |
| [9] | Landau L D, Lifshitz E M. 2013. Fluid Mechanics (5th edition)(in Chinese). Beijing: Higher Education Press. |
| [10] | Liu S D, Liang F M, Liu S K, et al. 2008. Atmospheric Turbulence (in Chinese). Beijing: Peking University Press. |
| [11] | Liu S D, Liu S K. 2013. Fractals in Physics (in Chinese). Beijing: Peking University Press. |
| [12] | Tarasov V E. 2010. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media. Beijing: Higher Education Press. |
| [13] | Uchaikin V V. 2013. Fractional Derivatives for Physicists and Engineers. Beijing: Higher Education Press. |
| [14] | 陈文, 孙洪广, 李西成等. 2012. 力学与工程问题的分数阶导数建模. 北京: 科学出版社, 11-54. |
| [15] | 胡非. 1995. 湍流、间歇性与大气边界层. 北京: 科学出版社. |
| [16] | 朗道L D, 栗弗席兹E M. 2013. 流体动力学(第五版). 北京: 高等教育出版社. |
| [17] | 刘式达, 梁福明, 刘式适等. 2008. 大气湍流. 北京: 北京大学出版社. |
| [18] | 刘式达, 刘式适. 2013. 物理学中的分形. 北京: 北京大学出版社. |
 2014, Vol. 57
2014, Vol. 57


