地磁变化场是地磁学和空间物理学等研究的重要内容，在很多应用研究领域都需要考虑变化磁场，比如空间天气的监测和预报(徐文耀，2009)，地震孕育过程中的地磁日变规律研究(彭纯一和陈兴东，2007)，地磁活动指数的计算(徐文耀，2005)，地磁测量数据的日变校正(边刚等，2007)，以及地磁导航技术(彭富清，2006)等.

地磁变化场起源于磁层和电离层电流体系，包含多种成分，主要有太阳静日变化、太阴日变化、磁暴、亚暴以及地磁脉动等，近几年的观测和研究结果表明，变化磁场是一个很复杂的不断有能量输入和输出的开放系统中的非线性动力学过程，与太阳、行星际空间、磁层、电离层乃至中低层大气中发生的一系列现象有密切关系(徐文耀，2009)，包括太阳耀斑爆发、日冕物质抛射、磁层大尺度对流、电离层骚扰、大气潮汐运动等，这些现象的相互作用形成了地磁变化场的复杂的非线性非平稳性特征，以及复杂的时间演化和空间分布特征. 这些特征都是复杂系统所具有的基本特征，即：复杂系统要求必须由多个子系统组成，它们之间以某种或多种方式发生复杂的非线性和非平稳的相互作用，而非线性和非平稳性是复杂性产生的主要根源，且复杂系统在时间和空间上通常呈现出各种复杂形式的相干结构.因此，地磁变化场是一个复杂系统.

近似熵(Approximate Entropy，简称ApEn)是 Pincus(1991)提出的一种度量时间序列复杂性的方法，但其有自身匹配的缺点，因此，Richman和Moorman(2000)提出了另一种时间序列复杂性的测度方法——样本熵(Sample Entropy，简称SampEn)，与近似熵相比其精度更高，且只需较少数据便可得到稳定数值，较适合于工程应用.但是，近似熵和样本熵只反映时间序列在单一尺度上的信息，Costa等(2002，2005)在样本熵的基础上，提出了另一种衡量时间序列复杂度的方法——多尺度熵(Multi-scale Entropy，简称MSE)，用来反映时间序列在不同尺度因子下的自相似性和复杂性程度.近似熵、样本熵和多尺度熵都是时间序列在维数变化时产生新模式概率大小的量度方法，时间序列的复杂性越大，其产生新模式的概率越大，熵值也越大.近年来，对各种复杂现象的研究已成为非线性科学的前沿课题之一，在地球物理科学(张增平和王启光，2008；何文平等，2011；黄宁波等，2012)、医学(Bornas et al., 2006；Norris et al., 2008)、生物生理学(刘慧等，2004；庄建军，2008)、故障诊断(赵海峰等，2010；郑近德等，2012)以及其他领域(何亮等，2008；王振亚等，2009)对复杂性进行了大量的研究.

地磁变化场时间序列是地球整体和其外部空间构成的复杂系统中的观测资料.目前关于地磁变化场演变周期性、混沌和分形特性方面研究较多(Voros et al., 1994；王赤等，1995；Hongre et al., 1999；Wei et al., 2004；Bolzan et al., 2009；Asimopolos et al., 2010；牛超等，2010)，而对地磁变化场时间序列从复杂系统层面上的研究相对较少，主要有：Gillet等(2007)应用最大熵谱理论分析了地磁场的长期变化，指出最大熵谱可以很好地表征地磁场长期变化的特征，并能找出一些反映太阳活动性和地磁活动本身随时间变化的周期成分；谢周敏(2009)结合信息熵和小波多尺度理论，提出了一种局部多尺度熵方法，可用于分析各种复杂的地球物理信号，以便深入挖掘更多的信号特征信息，但作者仅仅提出理论方法，并没有给出实际地球物理信号的具体应用；De Santis和Qamili(2010)亦应用信息论中的信息熵及Kolmogorov熵研究了地磁场7000年来的变化；杨建平(2010)运用小波熵复杂度对南极中山站的地磁观测数据进行了分析，指出其可以反演地球及其外围空间的动力学特征，但所用数据仅取自一个台站；齐玮等(2011)从信息科学的角度研究了地磁场K变化的信息熵，从定量的角度给出了K指数缺陷本质的认识，其研究对象为地磁活动指数.

对于复杂度及复杂系统的概念，不同的研究方向有着不同的理解.就地磁变化场而言，从军事地球物理需求出发，需要分析地磁扰动强度及演化特征，以便衡量地磁扰动大小，选择武器运载平台导航模式；通过定位地磁扰动时间段，选择武器系统运用窗口，特别是对于磁暴识别(磁暴类型、级别大小和持续时间等)，以及空间灾害性天气预警等都有一定的参考价值.有鉴于此，本文提出运用样本熵、多尺度熵及滑动窗样本熵方法对不同磁扰程度下的地磁变化场时间序列进行复杂度特征分析，得到了一些有用的结果，这对于更好地分析、理解以及充分利用地磁场信息，有重要的理论意义和军事应用价值.

样本熵(SampEn)是由Richman和Moorman(2000)提出的一种与近似熵类似但精度更高的时间序列复杂性的度量方法，刘慧等(2004)通过分析包含不同成分(确定性信号和随机信号)的混合信号对样本熵和近似熵的优缺点进行了仿真验证，结果表明样本熵精度更高，所以本文采用样本熵来计算地磁变化场时间序列的复杂度.其计算方法大致如下：

(1)假设原始数据为{x₁，x₂，…，x_N}，长度为N.预先给定嵌入维数m和相似容限r，依据原始信号重构一个m维向量为

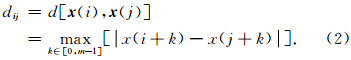
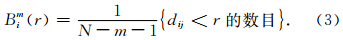
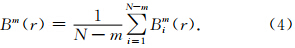
(6)理论上，原始序列的样本熵定义为

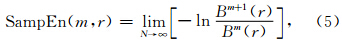
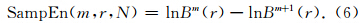
Costa等(2002，2005)在样本熵的定义中引入了尺度因子，提出了多尺度熵的概念，用以衡量时间序列在不同尺度因子下的复杂性，其计算方法如下：

(1)设原始数据为{x₁，x₂，…，x_N}，长度为N.预先给定嵌入维数m和相似容限r，建立新的粗粒向量(Coarse Grained Vector)为

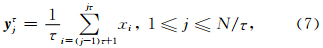
(2)对每一个粗粒序列求其样本熵，则得到τ个粗粒序列的样本熵值，并把熵值画成尺度因子的函数，称之为多尺度熵分析.这里对每段时间序列求样本熵时，相似容限r保持0.15SD(SD是原始数据的标准差，而不是每段粗粒序列的标准差).

样本熵是用来刻画时间序列在单一尺度上的自相似性和复杂性程度，熵值越大，序列越复杂；熵值越小，序列越简单，序列自身的相似性越高.多尺度熵定义为时间序列在不同尺度因子下的样本熵，因此，多尺度熵曲线反映的是时间序列在不同尺度因子下的自相似性、复杂性以及维数变化时序列产生新模式的能力.如果一个序列的熵值在大部分尺度上都比另一个序列的熵值大，那么就认为前者比后者复杂性更高.

滑动窗样本熵方法能够很好地对实际观测资料进行动力学结构突变检测，其计算方法描述如下：

对一个长度为N的时间序列，从资料的第一个数据开始，首先取一长度为L的窗口的数据，并计算窗口内数据的样本熵复杂度，然后将窗口向后滑动，滑动步长为M，得到下一组数据并计算其复杂度，重复上述步骤直至全部数据；每个窗口计算得到的复杂度赋值给窗口内最后一点，将各个窗口计算得到的复杂度依次连接，由此构建复杂度序列.基于不同动力学性质的数据其复杂度大小不同，而具有相同动力学性质的数据其复杂度差异不大这一特点，结合得到的复杂度序列判断突变点或突变区间.

选取混沌方程(Mackey-Glass方程、Rossler方程)、周期序列(sin函数)、噪声序列(高斯白噪声、1/f噪声)对样本熵及多尺度熵方法进行检验.

(1)混沌区域的Mackey-Glass方程

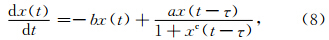
该方程为时滞微分方程(Delay Differential Equation，DDE)，是与普通微分方程(Ordinary Differential Equation，ODE)并列的一类非线性方程，具有广泛的应用领域，在物理、人口生物学、经济等领域中的许多现象都可以用DDE方程来描述.a，b，c为参数，τ为时滞参数，通常取b=0.1，c=10，a=0.2.Farmer(1982)对Mackey-Glass方程的行为特性作过深入研究，当τ=17时呈现混沌性，τ值越大，混沌程度越高，并具有分形维数近似为2.1的奇异吸引子.

这里选择Mackey-Glass混沌方程作为典型信号，是因为我们发现该时滞方程中x(t)的值随时间的演化呈现出与地磁场日变曲线非常相似的形态，如图 1所示.图 1为时滞参数τ=17时Mackey-Glass序列与某时间段地磁变化场日变曲线的比对图.地磁仪器所记录到的地磁变化场值是地球整体和其外部空间构成的复杂系统中的一个观测资料，由前述可知，地磁变化场起源于磁层—电离层电流体系，与磁层、电离层状态(电离层电子密度TEC)及太阳活动性(如太阳黑子数、太阳射电流量、太阳风等参数)有关.未来某一时刻的地磁变化场值，不仅与过去一定时间的地磁场观测值有关，显然也与上述影响制约因素有关，可以认为，在太阳风和行星际磁场的作用下，地磁变化场叠加了一定的变量，经过一系列复杂过程，形成了若干时间以后的地磁变化场值，具有较强的前后相关性(易世华等，2013).由此可知，地磁变化场应该具有时滞特性，且已证明，地磁变化场具有混沌特性(牛超等，2010)，故此，地磁变化场或许可用时滞混沌方程来表示.

图 1

Fig. 1

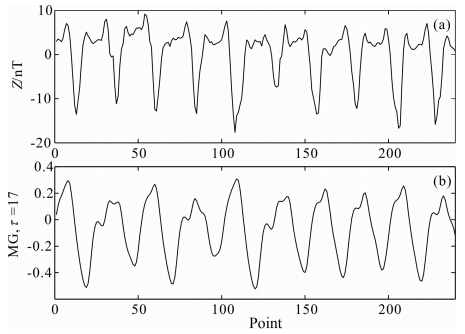图 1 地磁变化场时间序列与Mackey-Glass序列 (a)地磁变化场时间序列;(b)Mackey-Glass序列.Fig. 1 Geomagnetic variation time series and Mackey-Glass series (a)Geomagnetic variation time series;(b)Mackey-Glass series.

(2)Rossler方程

(3)正弦信号

(4)高斯白噪声序列

(5)1/f噪声

表 1为不同序列长度下的各种典型信号时间序列的样本熵，序列长度分别为500、1000、5000、10000、20000.由表 1可以看出，不同序列长度的各典型信号序列的样本熵仅有很小差异，说明样本熵在序列长度选择上的不敏感性.周期序列sin函数的样本熵最低，接近于0；其次为混沌函数，其熵值大概处在区间[0.4，0.5]，居中；噪声系统的样本熵最大.这与样本熵定义及实际情况相符.此外，发现三种混沌时间序列的样本熵值差别不大，难以区分，所以，可以考虑用多尺度熵进行分析.

表 1(Table 1)

表 1 各种典型信号时间序列样本熵(不同序列长度)Table 1 Sample entropy values of typical signal time series(series of different lengths) 500 1000 5000 10000 20000 MG(τ=17) 0.4343 0.4289 0.4219 0.4139 0.4203 MG(τ=30) 0.5009 0.4739 0.4671 0.4428 0.4440 Rossler 0.4443 0.4376 0.4295 0.4200 0.4208 White noise 2.4704 2.5100 2.4660 2.4695 2.4779 1/f noise 2.2244 2.1680 2.0430 2.0185 1.9731 sin 0.0207 0.0305 0.0278 0.0278 0.0278

表 1 各种典型信号时间序列样本熵(不同序列长度)Table 1 Sample entropy values of typical signal time series(series of different lengths)

表 2为Mackey-Glass方程时间序列(N=10000)取不同时滞参数τ时的样本熵.由前述可知，Mackey-Glass方程τ值越大，混沌程度越高.而由 表 2可以看出，随着时滞参数τ的增大，Mackey-Glass时间序列的样本熵值亦逐渐增大，说明其复杂程度逐渐增大，证明了样本熵可以表征和衡量不同时间序列的复杂度.

表 2(Table 2)

表 2 Mackey-Glass方程取不同时滞参数时的样本熵(N=10000)Table 2 Sample entropy values of Mackey-Glass equation with different time delay parameters(N=10000) 时滞τ 17 20 23 26 29 32 样本熵 0.4139 0.4212 0.4362 0.4412 0.4421 0.4481

表 2 Mackey-Glass方程取不同时滞参数时的样本熵(N=10000)Table 2 Sample entropy values of Mackey-Glass equation with different time delay parameters(N=10000)

图 2为不同序列长度下的各种典型信号时间序列的多尺度熵特征，序列产生条件如上述方程所述，长度分别为5000、10000、20000、30000.由图 2可以更直观地看出，不同序列长度的各典型信号序列的多尺度熵仅有很小差异，说明多尺度熵在序列长度选择上的不敏感性.此外，从图 2中可以看出，在尺度为1时(即原始长度的信号)，白噪声的熵值要比1/f噪声高，当尺度增加到4时，1/f噪声的熵值开始比白噪声高；随着尺度的增加，白噪声的熵值单调下降，而1/f噪声的熵值基本保持恒定，这与1/f噪声在各个尺度上都包含着复杂结构的特征相一致.sin信号的样本熵保持在较低熵值，且第8个尺度之后几乎保持不变，这一点与正弦信号具有周期性及规则性的特征是一致的.Mackey-Glass序列(τ=17，τ=30)和Rossler序列第一个尺度的样本熵非常接近，如果仅用样本熵就难以区分这三种序列，而用多尺度熵则可以看出三种序列存在明显差异，这也证明了多尺度熵方法在分析复杂时间序列上比样本熵方法更具有优势，它能从不同的时间尺度来展 现序列的细节特征.另外，从图 2可以看出，Mackey-Glass(τ=17)序列的样本熵在不同的尺度表现出不同的变化趋势，如在前5个尺度呈上升趋势，5至9尺度逐渐减小，之后在10至16尺度基本保持不变，而从17~20尺度其熵值又开始快速增大，由此可以看出，Mackey-Glass序列具有更高的复杂度.而且比较图 3中MG(τ=17)序列和MG(τ=30)序列，发现MG(τ=30)其各个尺度上的样本熵值都比MG(τ=17)序列大，这也直观地验证了表 2所述观点.综上所述，表明多尺度熵可用来表征不同时间序列在不同尺度上的复杂性，可作为分析复杂时间序列的工具.

图 2

Fig. 2

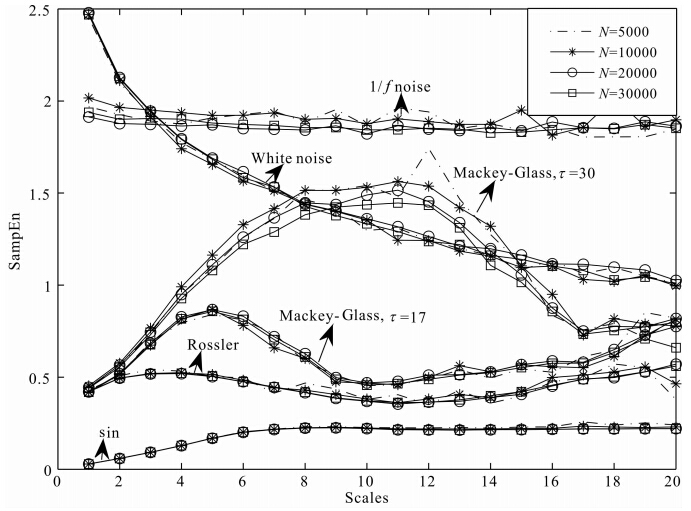图 2 不同序列长度下的各种典型信号时间序列多尺度熵Fig. 2 Multiscale entropy values of typical signal time series with different lengths

构造理想时间序列y(t)，序列y(t)长度为6000点，前2000点为Logistic混沌序列S1；中间2000点为sin函数周期序列S2，表达式为0.5 sin(0.2t)；后2000点为白噪声序列S3.

图 3a为该理想时间序列y(t)的演化曲线，图 3b为滑动窗样本熵曲线，窗口长度L=200，滑动步长M=1.由图 3可以看出，滑动窗样本熵曲线能够根据时间序列的复杂性很好地区分动力系统的异同.对于前2000点Logistic序列，其依次经历稳定不动点、不稳定不动点、周期、混沌四个不同的演化阶段时，样本熵复杂度呈现明显的依次变大趋势，且复杂度的变化与Logistic序列复杂程度的变化步调 一致；第2000点处是突变点，由混沌区域的Logistic 序列突变为sin函数周期序列，由图 3b可以看出，从对应点处的样本熵值开始，逐渐减小，并稳定在一个比较小的熵值，说明序列在由混沌方程变为周期方程后，其复杂度降低；第4000点处也是突变点，由sin函数周期序列突变为随机行为的白噪声序列，体现在图 3b滑动窗样本熵曲线上，其熵值在对应点处逐渐增大，说明后2000点的系统复杂度突然增大.由此可见，滑动窗样本熵可以鉴别出一个时间序列中不同的演化特征，当系统动力学结构发生改变时，对应的熵值会发生明显跃变，且动力学结构越复杂，熵值就越大.

图 3

Fig. 3

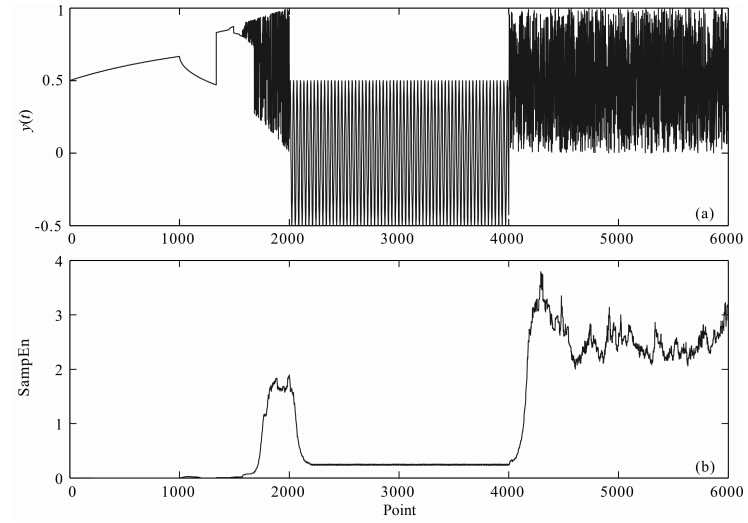图 3 理想时间序列突变检测示意图 (a)理想时间序列演化曲线;(b)理想时间序列的滑动窗样本熵曲线.Fig. 3 Sketch of mutation detection diagram for ideal time series (a)Evolution curve of ideal time series;(b)Sliding window SampEn curve of ideal time series.

本文对地磁变化场的复杂度分析主要从两方面展开，一是不同磁扰程度下的地磁变化场的样本熵分析及多尺度熵分析，二是地磁变化场的滑动窗样本熵分析.这里采用Ap指数，即行星性等效日幅度，作为全天地磁活动水平的量度.由于地磁扰动在H分量上表现得最为明显，所以，这里地磁数据取H分量.对于不同磁扰程度的地磁变化场，其复杂度(这里体现为熵值大小)应会有差异.

相应的地磁数据亦分为两部分，第一部分为不同Ap指数的地磁日变数据，这些数据取自中国大陆地区6个地磁台站观测的地磁场H分量分均值数据，各地磁台站名称及位置参数见表 3，所选取的不同Ap指数对应的日期见表 4.由表 3可知，这些地磁台站覆盖了很广的地域范围(南至琼中，北至满洲里，跨越了30.6个纬度；西到乌鲁木齐，东达崇明，横跨37.5个经度，覆盖了两个时区多)，因此具有广泛的代表性.

表 3(Table 3)

表 3 各地磁台站名称及位置信息Table 3 Names，locations and other information of geomagnetic stations 台站名称 IAGA代码 地理经度(°E) 地理纬度(°N) 海拔(m) 观测量 数据时间 乾陵 QIX 108.2 34.6 893 ZHD 2009 拉萨 LSA 91.0 29.6 3655 ZHD 2009 满洲里 MZL 117.4 49.6 682 ZHD 2009 琼中 QGZ 109.8 19.0 227 ZHD 2009 乌鲁木齐 WMQ 87.7 43.8 970 ZHD 2009 崇明 COM 121.6 31.6 8 ZHD 2009 注：Z为地磁垂直分量，H为地磁水平分量，D为地磁偏角.

表 3 各地磁台站名称及位置信息Table 3 Names，locations and other information of geomagnetic stations

表 4(Table 4)

表 4 不同Ap指数对应的日期Table 4 Ap indexes of varied dates Ap指数 0 3 6 12 20 24 日期 2009-02-08 2009-01-08 2009-01-14 2009-04-09 2009-08-30 2009-07-22

表 4 不同Ap指数对应的日期Table 4 Ap indexes of varied dates

第二部分数据取自北京地磁台所观测的地磁场H分量时均值数据，用于地磁变化场的滑动窗样本熵分析.由三部分构成，一是地磁扰动相对较小的数据，时段范围为1996年4月24日至1996年8月21日，数据个数为2880，由磁暴报告可知，在该段时间内没有发生磁暴，统计该时段的Ap指数，可知Ap 6的占了63.3%，而Ap 12的占了97.5%，说明在该时段内绝大部分时间变化磁场是非常平静的；二是地磁扰动相对较大的数据，时段范围为1995年2月11日至5月31日，由磁暴报告可知在该段时间内发生了三次磁暴(时间分别为1995年3月26日、1995年4月6日、1995年5月16日)，数据个数为2640，统计该时段的Ap指数，可知Ap>6的占了56.4%，说明在该时段内地磁扰动是比较大的；三是磁暴数据，这里收集了北京地磁台所记录的1990年发生的20个SC型磁暴，用作磁暴的滑动窗样本熵分析.

计算不同Ap指数下的地磁变化场H分量日变化时间序列的样本熵，所用地磁数据为分均值，数据点数为1440，结果如表 5所示.

表 5(Table 5)

表 5 不同Ap指数地磁变化场H分量日变化时间序列的样本熵Table 5 Sample entropy values of H component geomagnetic diurnal variation time series with different Ap indexes 乾陵(QIX) 拉萨(LSA) 满洲里(MZL) 琼中(QGZ) 乌鲁木齐(WMQ) 崇明(COM) Ap=0 0.3642 0.3349 2.1394 0.3614 0.3286 2.3933 Ap=3 0.5842 0.6949 0.6845 0.5614 0.6786 1.8933 Ap=6 0.6098 0.6700 0.7037 0.6092 0.6607 1.6807 Ap=12 0.9585 0.9243 0.9978 0.9983 0.9650 1.9280 Ap=20 1.2509 1.2811 1.2951 1.2192 1.2773 2.2727 Ap=24 1.3577 1.3487 1.3912 1.3719 1.3381 1.3583

表 5 不同Ap指数地磁变化场H分量日变化时间序列的样本熵Table 5 Sample entropy values of H component geomagnetic diurnal variation time series with different Ap indexes

由表 5中样本熵值可知，随着Ap指数的增大，即随着地磁扰动的增大，大部分台站的样本熵值呈现出逐渐增大的趋势，说明地磁时间序列随着地磁扰动的增大，其复杂性亦逐渐增大，可预测性变小，动力学结构越来越复杂，呈现出较强的不确定性.但崇明(COM)地磁台的样本熵值却没有表现出同样的规律，分析其原因：图 4为崇明(COM)地磁台2009-02-08(Ap=0)的H分量秒数据日变化曲线，从图中可以看出，日变化曲线上叠加了大量噪声，崇明台在2009-01-08(Ap=3)、2009-01-14(Ap=6)、2009-04-09(Ap=12)、2009-08-30(Ap=20)的日变曲线均是如此，这应是崇明台H分量日变化时间序列样本熵值出现异常的原因.满洲里(MZL)地磁台 在2009-02-08(Ap=0)的样本熵值异常亦是此原因.

图 4

Fig. 4

图 4 崇明(COM)地磁台的H分量秒数据日变化曲线(2009-02-08，Ap=0)Fig. 4 Curve of H component geomagnetic diurnal variation at COM geomagnetic station(2009-02-08，Ap=0)

以乾陵(QIX)地磁台为例，由表 4可以看出，当Ap=3和Ap=6时，其样本熵值非常接近，这里计算不同Ap指数时地磁变化场H分量日变化时间 序列的多尺度熵，所用地磁数据为10 s均值，数据点数为8640，图 5为不同Ap指数地磁变化场H分量日变化时间序列的多尺度熵曲线.

图 5

Fig. 5

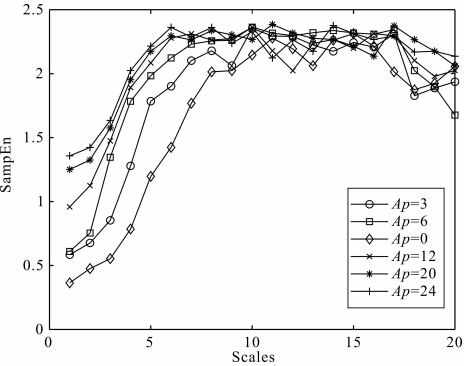图 5 不同Ap指数地磁变化场H分量日变化时间序列的多尺度熵Fig. 5 Multiscale entropy curves of H component geomagnetic diurnal variation time series with different Ap indexes

由图 5可以看出，不同Ap指数的地磁变化场多尺度熵特征呈现出比较相似的变化趋势，而且还发现，在第3和第4尺度，Ap=3与Ap=6的样本熵值表现出比较明显的差异，这进一步证明了多尺度熵在分析复杂时间序列时(比如不同地磁扰动条件下的地磁变化场)所具有的优越性，即它既能从整体上反映其共有的动力学特征，又能从细节上揭示其独特的演化特征.

对磁扰较小时间段以及磁扰较大时间段进行滑动窗样本熵分析，选择滑动窗口长度L=200，滑动步长M=1，结果如图 6所示.由图 6可以看出，磁扰较大时间段的滑动窗样本熵值整体上要比磁扰较小时间段偏大，且变化较为剧烈，说明了磁扰较大时间段地磁变化场的复杂性要强于磁扰较小时间段；仔细观察图 6c和6d，可以发现，在发生磁暴的时间段所对应的滑动窗样本熵值上下波动幅度较大，反映出地磁扰动较剧烈时地磁变化场具有较复杂的动力学结构.

图 6

Fig. 6

图 6 不同磁扰情况下的地磁变化场及其滑动窗样本熵曲线 (a)磁扰较小地磁变化场曲线;(b)磁扰较小地磁变化场滑动窗样本熵曲线;(c)磁扰较大地磁变化场曲线;(d)磁扰较大地磁变化场滑动窗样本熵曲线.Fig. 6 Sliding window SampEn curves of geomagnetic variation with different geomagnetic disturbance (a)Curve of low disturbance geomagnetic variation;(b)Sliding window SampEn curve of low disturbance geomagnetic variation;(c)Curve of high disturbance geomagnetic variation;(d)Sliding window SampEn curve of high disturbance geomagnetic variation.

对1990年发生的20个SC型磁暴进行滑动窗样本熵分析，滑动窗口长度L=200，滑动步长M=1.以1990年7月28日发生的磁暴为例，图 7a为包含该磁暴的一段较短时间长度(10天)地磁变化场H分量曲线示意图，起始时间为1990年7月21日至7月31日.图 7b为其滑动窗样本熵曲线示意图.由图 7可以看出，在地磁活动比较平静的时期(21日到27日)，其滑动窗样本熵值在很小的一个区间范围内波动，1990年7月28日发生磁暴，产生磁暴急始SC，此后，所计算的滑动窗样本熵值迅速增大，反映出地磁变化场的动力学结构发生突变，复杂性增强.同时还发现，滑动窗样本熵值开始增大的时间点要早于磁暴急始SC发生的时间，这对于磁暴识别及预报有一定的参考价值.

图 7

Fig. 7

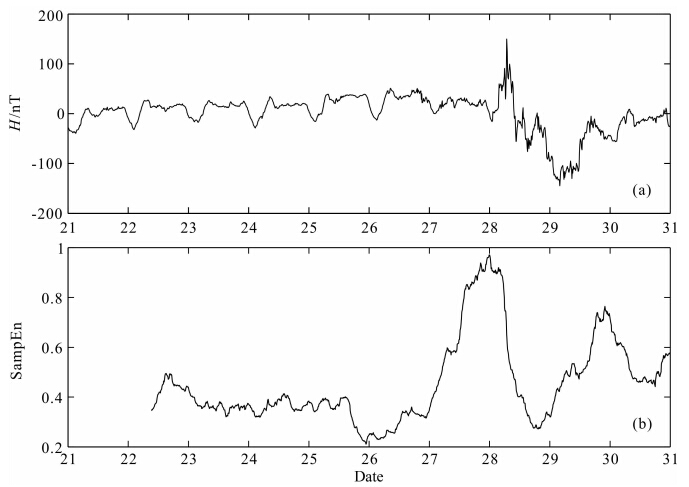图 7 1990-07-28日磁暴曲线(a)及其滑动窗样本熵曲线(b)示意图Fig. 7 Geomagnetic storm curve of 28 July 1990(a) and sliding window SampEn curve(b)

本文从复杂系统的角度提出运用样本熵、多尺度熵及滑动窗样本熵方法对不同磁扰程度下的地磁变化场时间序列进行复杂度分析，主要有以下结论：

(1)样本熵值能较好地表征地磁扰动的强度.

(2)不同Ap指数地磁变化场的多尺度熵特征曲线呈现出比较相似的变化趋势，且对于不同的尺度，不同Ap指数的样本熵值表现出明显的差异，表明了多尺度熵在分析不同地磁扰动条件下的地磁变化场所具有的优越性，即它既能从整体上反映其共有的动力学特征，又能从细节上揭示其独特的演化特征.

(3)地磁变化场的滑动窗样本熵分析结果表明，滑动窗样本熵既能很好地表征地磁扰动的强度，又能准确定位扰动时间段，而且对于磁暴识别及预报有一定的参考价值.

(4)地磁变化场具有混沌特性，而Mackey-Glass时滞混沌方程随时间的演化呈现出与地磁场日变曲线非常相似的形态，因此，地磁变化场或许可用时滞混沌方程来表示.

对于复杂度及复杂系统的概念，不同的研究方向有着不同的理解，就地磁变化场而言，本文对其从复杂系统层面上做了一些初步工作，得出了一些有用的结果，比如对于样本熵和多尺度熵能够很好地表征地磁扰动强度及演化特征这一特点，启发我们可设计一种新的“熵指数”来衡量表征地磁扰动大小；对于滑动窗样本熵理论应用于磁暴的分析结果，可以将其应用于在线观测的地磁场资料处理，利用处理信息研究地磁场的快速异常变化，及时地预测预报空间灾害性天气等；而对于Mackey-Glass时滞混沌方程表现出与地磁场日变曲线形态非常相似这一特点，我们将做深入研究，如能用确定性的时滞混沌系统方程来描述地磁变化场的演化特点，无疑是一个很好的发现，有可能应用于地磁变化场时间序列建模预测.总之，复杂性科学理论和方法提供了研究地磁变化场的一种新思路和新途径，尽管当前地磁变化场的复杂度分析研究尚处于初步探索阶段，但是，如若能够真正认识这些复杂性特征，那对于地磁变化场研究及地磁导航与寻的等军事工程应用，都将起到一定的推动作用.

致谢感谢中科院地质与地球物理研究所以及中国地震局提供的台站磁测资料.