2. 中国石油化工股份有限公司石油物探技术研究院, 南京 210014
2. SINOPEC Geophysical Research Institute, Nanjing 210014, China
随着计算机技术的迅速发展,使得区域以及全球尺度的地震波模拟成为可能(Komatitsch et al., 2002; Yan et al., 2009; 张怀等,2009; Komatitsch et al., 2010; 龙桂华等,2010). 由于地形起伏与物性界面的非规则性(Komatitsch and Tromp, 2002a,b),传统的有限差分法与伪谱法由于网格刻画能力不强(Fornberg,1987; Moczo,2000; Magnoni,2014),无法满足全球地震波模拟的需要. 经典的谱元法通过选取GLL(Gauss-Lobatto-Legendre)插值点,构造单元内的张量积形式的Lagrange型插值多项式,运用GLL积分得到对角的质量矩阵,避免了有限元法需要求解大型线性方程组等弊端(汪文帅等,2012),但经典的谱元法所使用的四边形(三维为六面体)网格单元无法对精细地表与地下复杂界面进行准确的刻画,虽然细分单元能加强网格刻画能力,但计算量和内存要求必然成几何量级增加. 三角网格谱元法虽然解决了网格刻画不灵活的缺点,但三角单元内构造的Koornwinder-Dubiner多项式精度往往不一致,且其所使用的数值积分精度较低难以获得精确的质量矩阵,为了获得一定的精度,需要选取更多插值节点(Pasquetti and Rapetti, 2004),巨大的计算量阻止了其在地震学中的广泛运用. 虽然在传统方法上发展起来的诸多优化方法,如Yang等(2003; 2014)发展的近似解析离散方法、Li等(2012)构造的褶积微分方法和Zhang等(2013)提出的优化系数方法等,这些方面虽然具有某些方面的优势,但依然面临着起伏地表不易处理或面波模拟精度不高等弊端.
经典的有限元法具有网格剖分的灵活性,但离散地震波方程后形成的质量(分布式质量)矩阵(CFEM)为非对角的,使得必需求解大规模稀疏线性方程组,这必然影响有限元法地震波模拟的效率. 通过质量集中技术,认为单元内加速度无明显变化,将惯性力集中在一个节点上,形成对角质量(集中质量)矩阵(LFEM)与CFEM的数值误差是同阶的,有效地避免了求解线性方程组等问题(Wu,2006; 刘有山等,2013),前提是此时网格边长应远小于地震波长,且具有足够的数值积分精度,否则LFEM将面临较大误差. Marfurt(1984)通过分布式质量与集中质量矩阵线性组合成新的质量(混合质量)矩阵(MFEM),通过频散关系分析了其精度,但混合质量矩阵不能避免求解方程组. 本文引入剩余质量矩阵,将逆矩阵进行Taylor展开,根据不同的精度需求选取有限项,可以有效地避免求解方程组以提高算法的计算效率.
有关三角网格有限元地震波模拟的频散分析在文献中较少见(Mullen,1982),关于有限元法的频散分析大多集中于正方形或矩形网格(Abboud and Pinsky, 1992; Mulder,1999; Zyserman and Gauzellino, 2005; De Basabe and Sen, 2007,2010; Zyserman and Santos, 2007; Seriani and Oliveira, 2008),三角网格谱元法格式构造困难,频散关系讨论更少见(Mazzieri and Rapetti, 2012; Liu et al., 2013). 我们有必要对不同类型质量矩阵的有限元在地震波模拟时的频散关系做定量讨论,选择适合于地震波模拟的质量矩阵类型,同时网格形状、单元插值阶数以及介质的波速比对频散亦有影响,需要对三角网格有限元做深入全面的评估.
线性四边形有限元法两个方向的插值基函数是可以解耦的,质量矩阵和刚度矩阵可以分解为一维质量矩阵和刚度矩阵的直接乘或并乘形式(王润秋,1993; 周辉等,1997),通过网格的周期性可得到二维频散与一维频散之间的关系(De Basabe and Sen, 2007,2010). 与四边形不同的是,三角网格有限元法由于两个面积坐标之和需满足一定等式,使其插值是非解耦的,故二维频散不可能由一维频散直接得到. 为此,本文构造二维情形下的一般特征值问题,通过分析二维情形下三角网格的周期性,将无穷阶矩阵转化为有限阶矩阵,分析三角网格有限元法地震波模拟的频散关系,对声波与弹性波模拟的频 散因素做了全面讨论,最后给出了方法的数值耗散性. 2 声波与弹性波方程有限元法离散 2.1 经典有限元法
实际地球介质是极其复杂的,为了理论分析的需要,地震波在地下介质中的传播,常常用声波或弹性波方程描述(马啸等,2010; Ma et al., 2011). 非均匀介质中声波方程可以表示为

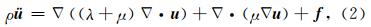
在频散分析之前需要对方程做一些假设,首先震源为0,其次介质为无限介质,最后介质为各向同性介质,在此假设下(1)式可以简化为

 为声速. 同样(2)式可以简化为
为声速. 同样(2)式可以简化为

 为P波速度,β=
为P波速度,β=  为S波速度.
为S波速度.对(3)式运用有限元法离散,用任意测试函数v乘(3)式,在空间域做积分,运用分部积分以及Green公式,可以得到(3)式对应的弱形式:



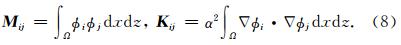
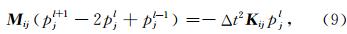
对弹性波方程(4)两端乘以测试向量函数 v =(vx,vz),在有限元空间域积分,同样运用分部积分和Green公式,可以得到弹性波方程的弱形式:
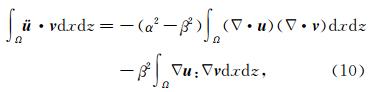
 ,A 与 B 为m阶张量.(10)式可以离散成如下形式:
,A 与 B 为m阶张量.(10)式可以离散成如下形式:

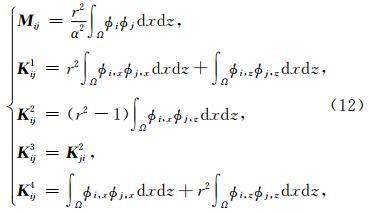
由(9)、(11)式可知,有限元法地震波模拟时需要求解线性方程组,为了减少计算量,常常需要将质量矩阵集中,认为单元内加速度无明显变化,将惯性 力集中在一个节点上,有限元基本理论可以证明这种近似处理方法与采用分布式质量矩阵的误差是同阶的,因此,通过此处理后解的收敛性并未改变(Fried and Malkus, 1975),但其精度有明显损失(Mullen and Belytschko, 1982). 集中质量矩阵表示为
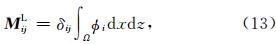

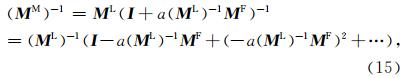
声波与弹性波传播的频散分析即是求解(17)式的一般特征值问题,该部分分析不同影响因素对三角网格有限元法地震波模拟频散的影响. 当空间插值为低阶时,可以给出频散关系的封闭形式;当空间插值阶数为高阶时,只能给出其数值解. 假设在有限元空间中传播的波为如下简谐平面波的形式,

将(16)式代入(9)式后,得到如下一般特征值问题:
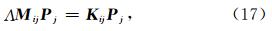
3.1 三种质量矩阵频散对比
将有限元空间剖分成如图 1所示的边长为h的等腰直角三角形网格,讨论(8)、(13)和(14)式中三种质量矩阵的频散关系. 网格中每一点都是周期出现的,每一点处的频散相同,任意第一点的频散即能代表整体的频散,即(17)式中Λ唯一,证明见附录A. 在空间为线性插值时,由(16)和(17)式得到三种质量矩阵对应的(9)式的声波模拟的频散关系:

 | 图 1 等腰直角三角形用于分析三种质量矩阵有限元法的数值频散 Fig. 1 Dispersion analysis of three types of mass matrix in isosceles right triangle mesh |
由(18)式可得CFEM、LFEM与MFEM的库朗数分别为0.408248、0.707107和0.577350. 其中,CFEM的库朗数最小,LFEM的库朗数最大,MFEM库朗数介于两者之间;从图 2可知,三种质量矩阵在沿坐标轴方向上频散最大,在45°方向频散最小,在所有方向上,CFEM的数值速度大于物理速度,LFEM和MFEM数值速度小于物理速度,就数值频散幅值而言,LFEM偏差最大,CFEM偏差其次,MFEM为两种质量矩阵误差相互抵消之后,偏差最小,一个波长内采样数大于5时数值频散 误差在1%以内. 从以上对比发现,相对而言MFEM是一种较好的地震波模拟方法. 在以下频散分析中均选用MFEM进一步对比分析.
 | 图 2 当p=0.2时三种质量矩阵有限元法声波模拟不同方向的数值频散对比;+:CFEM,▽:LFEM,○:MFEM Fig. 2 Numerical dispersion of three types of mass matrice in different directions; the stability parameter p is equal to 0.2; symbols +,▽ and ○ are corresponding to CFEM,LFEM and MFEM,respectively |
在地震波模拟时,我们需要了解MFEM的数 值频散对不同网格的敏感程度,在网格剖分时避免因网格畸变引起的严重数值频散或数值散射. 除图 1中所示的网格(T1)外,额外选取图 3所示的三种网格做测试,另外三种单元分别为等边三角形(T2)、顶角为30°的等腰三角形(T3)和顶角为120°的等腰三角形(T4). 与上节分析方法相似,当单元为线性插值时,它们的频散关系如图 4所示.
 | 图 3 不同三角形网格单元用于频散分析 (a)等边三角形;(b)顶角为30°等腰三角形;(c)顶角为120°的等腰三角形. Fig. 3 Triangle meshes of different shape are used for numerical dispersion analysis (a)Equilateral triangle;(b)Isosceles triangle with vertex angle being equal to 30°;(c)Isosceles triangle with vertex angle being equal to 120°. |
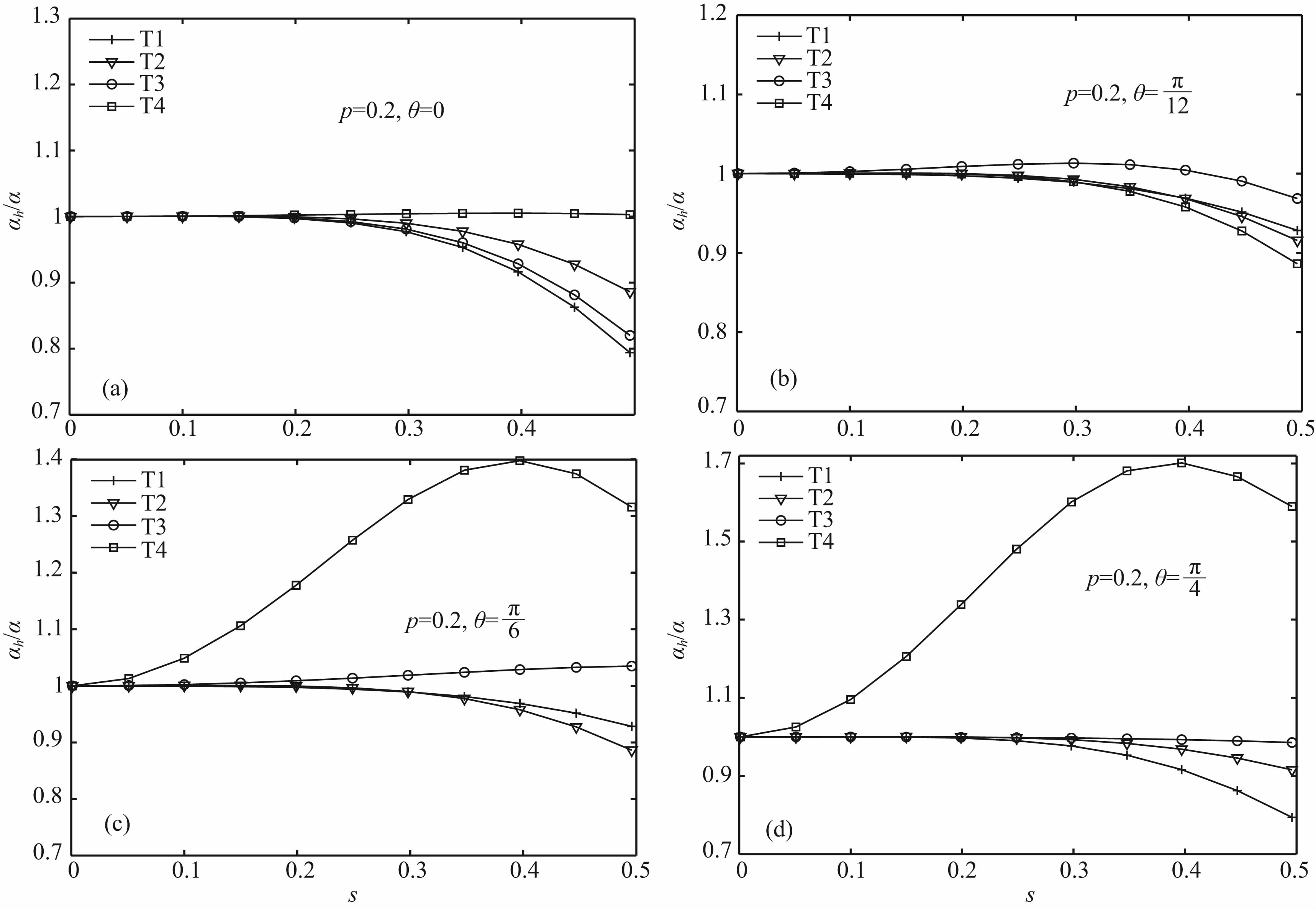 | 图 4 MFEM在不同网格中的数值频散方向各向异性 +:等腰直角三角形,▽:等边三角形,○:锐角三角形,□:钝角三角形. Fig. 4 Numerical dispersion of MFEM in four triangle meshes in different directions The four curves of +,▽,○ and □ are corresponding to T1,T2,T3 and T4,respectively. |
与上节相同,可得到T2、T3和T4的库朗数分别为0.645497、0.203597和0.268643,其中,T1与 T2稳定性较好,另外两种稳定性较差. 当波沿z轴传播时,T4频散最小,当传播方向略偏离z轴其频散迅速变大,角度为60°时其频散已经超过了40%,角度为90°时超过70%;T3频散随传播方向的波动也较大,特别是在s较小时,其频散明显;T1和T2频散随角度波动较小,频散幅度也较小. 从网格对比可知,在网格剖分时要尽量避免钝角三角形或较小内角的锐角三角形,由于直角三角形面积为等边三角形面积的2/ 3 倍,直角三角形剖分可以得到更少的单元,计算时节省了内存和计算时间,因此网格形状应尽量接近等腰直角三角形. 3.3 单元插值阶数对频散的影响
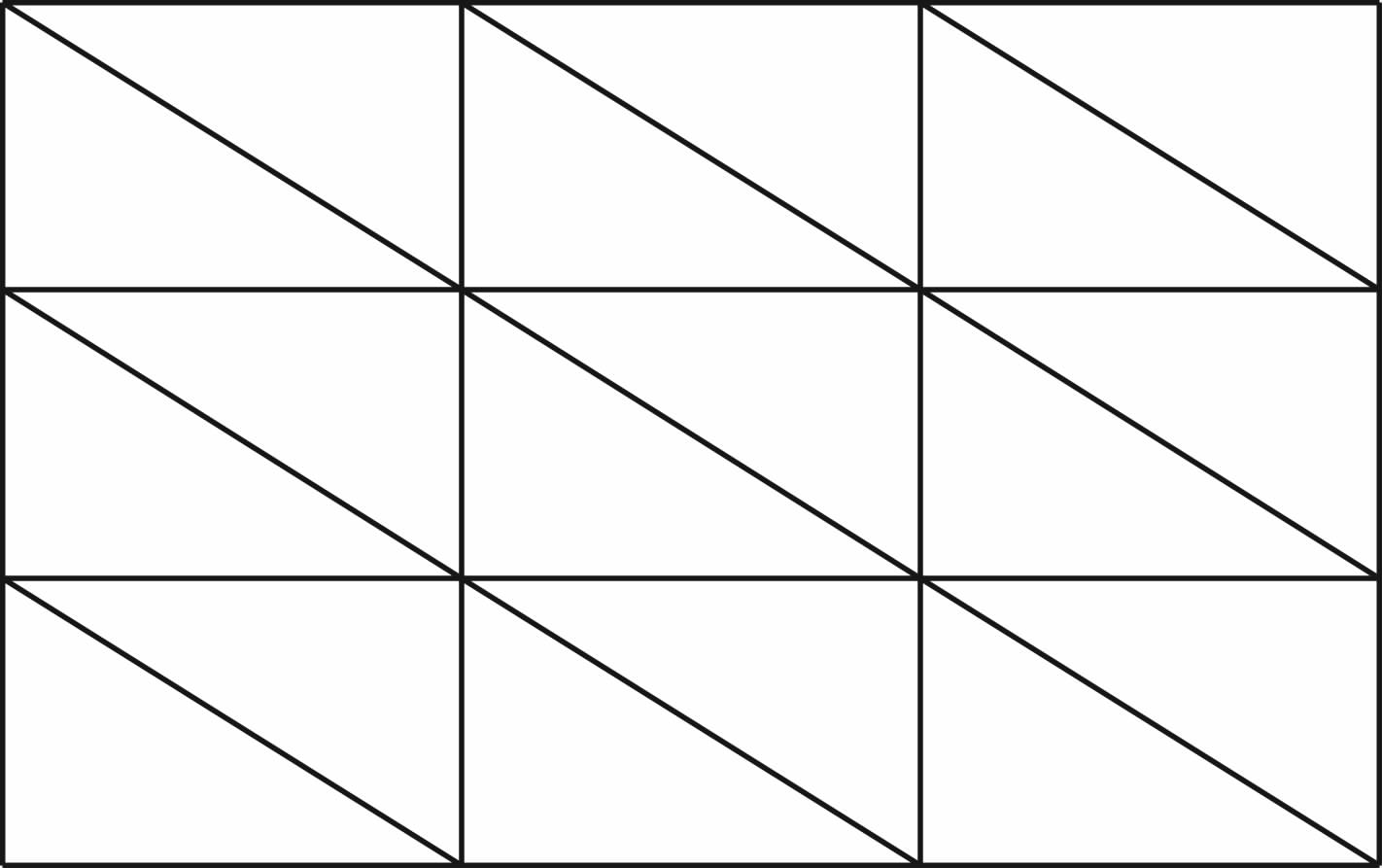
从3.1—3.2节可知,当单元采用线性插值时频散幅度和方向各向异性都较大,为了较好地压制频散,常常采用高阶插值,本节主要讨论T1单元中的二阶和三阶插值,网格中周期出现的节点如图 5所示,二阶插值时空间中周期出现的点数为4个,三阶插值时为9个. 以三阶为例讨论三阶插值的一般特征值问题,若空间的第A组9个点经过x方向的a次平移和z方向的b次平移得到第B组点,第A组和第B组点构成的一般特征值问题为
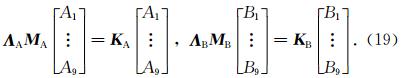
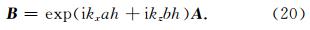

 | 图 5 二阶与三阶插值空间周期出现采样点的分布 实心圆代表二阶时的情况,空心圆代表三阶时的情况 Fig. 5 Four points(solid circle)periodically occur in the mesh when second-order interpolation is used in each cell. Nine points(empty circle)are corresponding to third-order interpolation. |
 | 图 6 单元插值阶数为二阶(a)和三阶(b)时的数值频散 +、▽、○和□对应于波传播的角度为0,π/12,π/6和π/4. Fig. 6 Numerical dispersion of MFEM with second-order(a) and third-order(b)interpolation in each element Four curves under +,▽,○ and □ are corresponding to propagation angles in the directions 0,π/12,π/6 and π/4,respectively. |
当插值阶数为二阶和三阶时频散迅速变小,每个波长内采样数大于3时,二阶频散误差在1%以内,三阶频散误差在0.6%以内;二阶的方向各向异性相比于线性插值已明显减弱,但仍表现出较小的方向各向异性,三阶的方向各向异性几乎可以忽略,数值频散主要受采样率控制,在实际地震波模拟时最好采用三阶插值以减小数值方向各向异性. 3.4 波速比对频散的影响
以上讨论均是针对声波方程的,在波速比一定的情况下,P波和S波的频散与声波相似,故未做讨论. 本节主要讨论空间插值为三阶时波速比(泊松比)对P波和S波频散的影响. 图 7给出了p=0.2,波沿z轴传播时P波和S波的频散.
图 7为空间为三阶插值时,波速比对频散的影响,可见,S波(图 7a)与P波(图 7b)数值频散都随波速比的增加而增大,S波的频散略大于P波的频散,在空间插值为三阶的情况下,波速比对频散影响较小,每个波长内采样数大于2时,S波频散在3.6%以内,P波频散在2.8%以内.
 | 图 7 三阶插值时波速比对S波(a)与P波(b)频散的影响 +、▽、○、□和右对应于波速比分别为1.7、2.0、4.0、6.0和8.0时的数值频散. Fig. 7 Numerical dispersion of S(a) and P(b)wave corresponds to five P to S wave speed ratios when third-order interpolation in each cell is used Five curves under +,▽,○,□ and right are corresponding to five wave speed ratios r=1.7,2.0,4.0,6.0 and 8.0,respectively. |
由(16)式可知,解一般特征值问题得到的特征频率如果是虚数,如ωh+iε,其中ωh表示数值频率. 得到的特征频率代入(16)式,出现的虚部iε,表现在数值耗散上,即每一个时间步相比于上一个时间步振幅衰减为e-εΔt. 本节罗列出当网格形状为T1,稳定性参数为p=0.2,波沿z轴传播,不同插值阶数和采样率时,声波与弹性波方程(r=1.7)MFEM离 散后的数值耗散性,即ε值,结果如表 1所示. 可以看出,空间插值一到三阶声波方程均未表现出数值耗散性,空间插值为一、二阶时弹性波方程也无数值耗散,当空间插值为三阶时,P波和S波(括号中所示)表现出很小的耗散,P波的数值耗散性要至少高出S波一个数量级,它们大致随s变大而变大,但它们都很小以至于可以忽略,说明地震波模拟时,数值误差主要由数值频散引起,而数值耗散性对数值误差的贡献甚微.
|
|
表 1 不同阶数和采样率下的声波与弹性波数值耗散性 Table 1 The ε values of MFEM under various sampling ratios and interpolation orders; the dissipation values of S wave are presented in the brackets |
本节用三组数值试验更加直观地说明三角网格 有限元法的数值频散特征. 第一组试验模型大小为 2000 m×2000 m,均匀介质的声速为2000 m·s-1,震源位于模型中心,时间函数均为20 Hz的Ricker子波,为了消除时间离散对频散的影响,时间步长均 为0.2 ms. 选用T1有限元网格,直角边边长为10 m,一阶的CFEM、LFEM和MFEM得到的0.4 s时的的波场快照如图 8所示. 在CFEM得到的快照中(图 8a),与竖直方向成45°的方向,有强烈的数值频散; LFEM得到的声波等时面的内部,出现了明显的数值频散,其数值频散要弱于CFEM; MFEM在45°方向,等时面之前表现出轻微的数值频散. 从第一组数值对比可知,MFEM数值频散压制能力强于CFEM和LFEM.
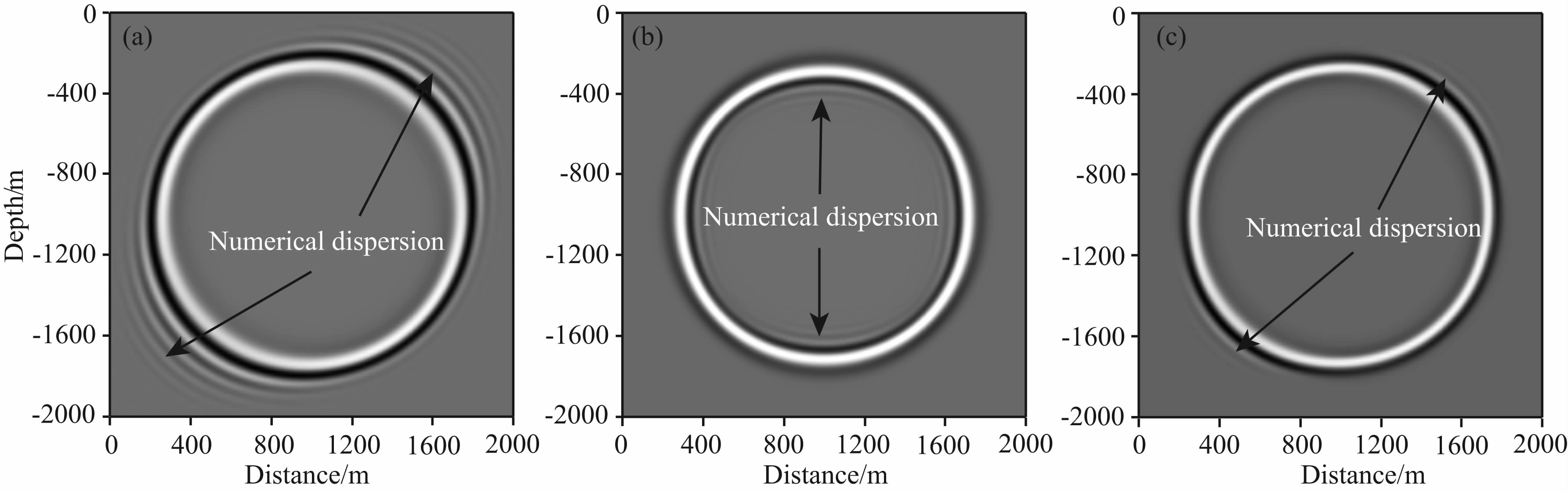 | 图 8 CFEM(a)、LFEM(b)和MFEM(c)三种质量有限元法模拟声波传播0.4 s时的波场快照; 箭头所指为数值频散 Fig. 8 Snapshots of acoustic wavefield at t=0.4 s modeled by three types of mass matrix.(a)CFEM,(b)LFEM, and (c)MFEM. Arrows point at numerical dispersion |
第二组试验的Ricker子波的主频为35 Hz,选用T2、T3和T4三种有限元网格,模型其他参数与第一组试验相同. 图 9为三种网格中MFEM模拟声波传播0.3 s时的波场快照. 图 9a无明显的数值频散; 图 9b在竖直方向等时面的内部表现出轻微的数值频散; 图 9c在水平方向上表现出强烈的数值频散. 第二组数值试验说明,虽然有限元法以其网格剖分的灵活性著称,但剖分时要避免内角过大或过小的网格单元.
 | 图 9 T2(a)、T3(b)和T4(c)三种有限元网格MFEM模拟声波传播得到的0.3 s时的波场快照 Fig. 9 Snapshots of acoustic wavefield at t=0.3 s modeled by MFEM with three types of FEM mesh:(a)T2,(b)T3, and (c)T4 |
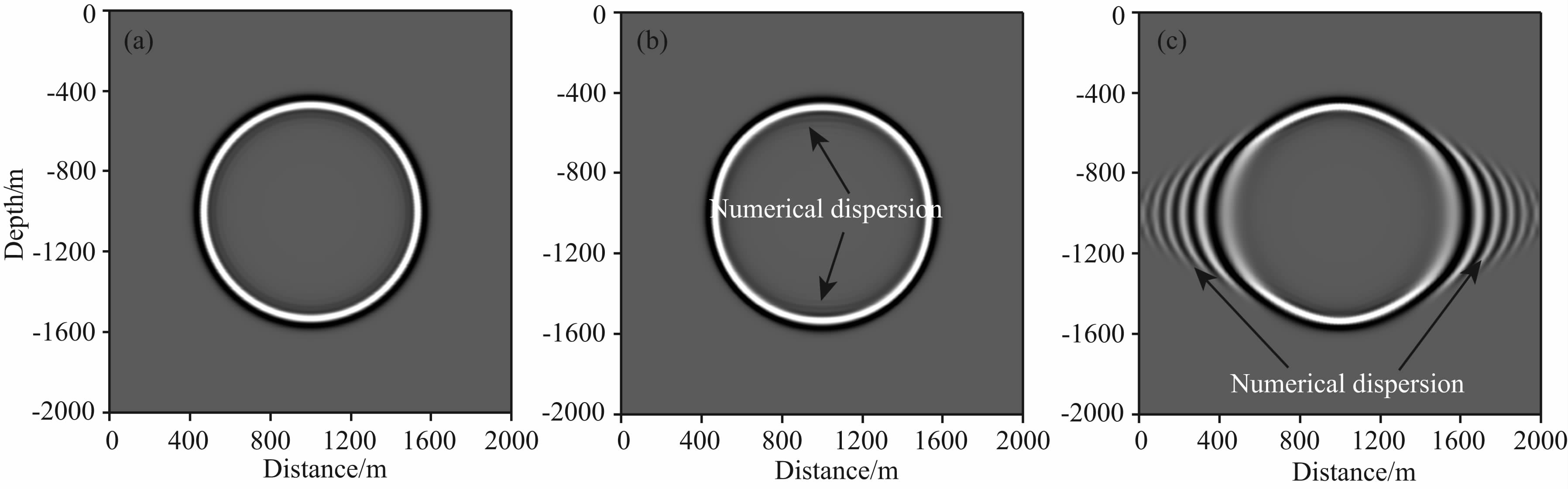
第三组试验为不同阶的MFEM模拟较大波数比弹性介质中P-SV波的传播. 模型大小1500 m× 1500 m,P波速度为3000 m·s-1,S波速度为1000 m·s-1,Ricker子波主频为20 Hz,选用T1有限元网格. 一阶、二阶和三阶的MFEM,单元的直角边分别为5 m、10 m和15 m,插值以后模型总的点数相同. 时间步长为0.2 ms. 0.2 s 时的波场快照如图 10所示,由于S波的最短波长大约为20 m,即一个波长内的最小采样点数为4,所以图 10a中S波等时面之前表现出很强的数值频散,且数值各向异性也很明显,以至于S波的等时面为椭圆. 二阶的MFEM(图 10b)在等时面之前表现出微弱的数值频散,无明显数值各向异性. 三阶的MFEM(图 10c)数值频散和各向异性得到了很好的压制. 此组试验说明,实际模拟时最好选用二阶、特别是三阶的MFEM.
 | 图 10 一到三阶MFEM模拟波速比为3的弹性介质中P-SV波0.2 s时的波场快照 (a)一阶MFEM;(b)二阶MFEM;(c)三阶MFEM. Fig. 10 Snapshots of P-SV wavefield modeled by first-,second-, and third-order MFEM in elastic media with wave speed ratio r=3 (a)First-order MFEM,(b)Second-order MFEM, and (c)Third-order MFEM. |
本文构造了一种地震波模拟的MFEM方法,与CFEM和LFEM比较,在数值频散角度说明了地震波传播MFEM模拟时的弱频散性. 分析了MFEM地震波模拟时数值频散的影响因素,在网格剖分时网格形状应尽量规则,应避免内角过小或过大的三角形;单元插值阶数的提高能有效减小数值频散以及其方向各向异性,空间为三阶插值时能兼顾计算精度与效率;弹性波频散随波速比增加而加大,但三阶插值时,其变化幅度并不大;并且MFEM的数值耗散性几乎可以忽略.
本文采用的单元是较为规则的周期单元,但实际地震波模拟时,在地表或地下界面起伏剧烈时剖分的单元形状较为复杂,我们很难得到一般网格中地震波的频散关系,而只能通过本文已有的结论推测一般情况下频散的变化趋势. 致谢 感谢中国科学院计算地球动力学重点实验室的张怀教授对本文提出的建设性意见. 感谢两位匿名审稿专家对本文提出的详细修改要求. 附录A
(9)式中离散时如果单元为线性插值,将物理单元上的积分映射至参考单元Ωe上的积分,单元分布式质量矩阵与刚度矩阵可表示为
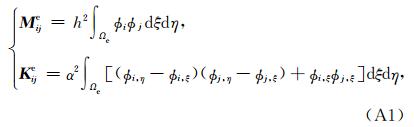

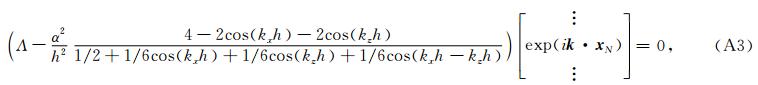
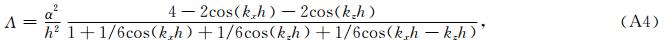
| [1] | Abboud N N, Pinsky P M. 1992. Finite element dispersion analysis for the three-dimensional second-order scalar wave equation. Int. J. Numer. Methods Eng. , 35(6): 1183-1218. |
| [2] | Chen J B. 2009. Lax-Wendroff and Nyström methods for seismic modelling. Geophysical Prospecting, 57(6): 931-941. |
| [3] | Chen S, Yang D H, Deng X Y. 2010. An improved algorithm of the fourth-order Runge-Kutta method and seismic wave-field simulation. Chinese J. Geophys. (in Chinese), 53(5): 1196-1206. |
| [4] | Dablain M A. 1986. The application of high-order differencing to the scalar wave equation. Geophysics, 51(1): 54-66. |
| [5] | De Basabe J D, Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equation. Geophysics, 72(6): T81-T95. |
| [6] | De Basabe J D, Sen M K. 2010. Stability of the high-order finite elements for acoustic or elastic wave propagation with high-order time stepping. Geophys. J. Int. , 181(1): 577-590. |
| [7] | Fornberg B. 1987. The pseudospectral method: Comparisons with finite differences for the elastic wave equation. Geophysics, 52(4): 483-501. |
| [8] | Fried I, Malkus D S. 1975. Finite element mass matrix lumping by numerical integration with no convergence rate loss. Int. J. Solid. Structures, 11(4): 461-466. |
| [9] | Komatitsch D, Tromp J. 2002a. Spectral-element simulations of global seismic wave propagation-Ⅰ. Validation. Geophys. J. Int. , 149(2): 390-412. |
| [10] | Komatitsch D, Tromp J. 2002b. Spectral-element simulations of global seismic wave propagation-Ⅱ. Three-dimensional models, oceans, rotation and self-gravitation. Geophys. J. Int. , 150(1): 303-318. |
| [11] | Komatitsch D, Ritsema R, Tromp J. 2002. The spectral-element method, Beowulf computing, and global seismology. Science, 298(5599): 1737-1742. |
| [12] | Komatitsch D, Erlebacher G, Göddeke D, et al. 2010. High-order finite-element seismic wave propagation modeling with MPI on a large GPU cluster. J. Comp. Phys. , 229(20): 7692-7714. |
| [13] | Li X F, Wang W S, Lu M W, et al. 2012. Structure-preserving modelling of elastic waves: a symplectic discrete singular convolution differentiator method. Geophys. J. Int. , 188(3): 1382-1392. |
| [14] | Liu S L, Li X F, Liu Y S, et al. 2013a. Symplectic RKN schemes for seismic scalar wave simulations. Chinese J. Geophys. (in Chinese), 56(12): 4197-4205. |
| [15] | Liu S L, Li X F, Wang W S, et al. 2013b. Optimal symplectic scheme and generalized discrete convolutional differentiator for seismic wave modeling. Chinese J. Geophys. (in Chinese), 56(7): 2452-2462. |
| [16] | Liu T, Sen M K, Hu T Y, et al. 2012. Dispersion analysis of the spectral element method using a triangular mesh. Wave Motion, 49(4): 474-483. |
| [17] | Liu Y S, Teng J W, Liu S L, et al. 2013. Explicit finite element method with triangle meshes stored by sparse format and its perfectly matched layers absorbing boundary condition. Chinese J. Geophys. (in Chinese), 56(9): 3085-3099. |
| [18] | Long G H, Li X F, Jiang D H. 2010. Accelerating seismic modeling with staggered-grid Fourier Pseudo-spectral differentiation matrix operator method on graphics processing unit. Chinese J. Geophys. (in Chinese), 53(12): 2964-2971. |
| [19] | Ma X, Yang D H, Zhang J H. 2010. Symplectic partitioned Runge-Kutta method for solving the acoustic wave equation. Chinese J. Geophys. (in Chinese), 53(8): 1993-2003. |
| [20] | Ma X, Yang D H, Liu F Q. 2011. A nearly analytic symplectically partitioned Runge-Kutta method for 2-D seismic wave equations. Geophys. J. Int. , 187(1): 480-496. |
| [21] | Magnoni F, Casarotti E, Michelini A, et al. 2014. Spectral-element simulations of seismic waves generated by the 2009 L'Aquila Earthquake. Bull. Seism. Soc. Am. , 104(1): 73-94. |
| [22] | Marfurt K J. 1984. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations. Geophysics, 49(5): 533-549. |
| [23] | Mazzieri I, Rapetti F. 2012. Dispersion analysis of triangle-based spectral element methods for elastic wave propagation. Numer. Algor. , 60(4): 631-650. |
| [24] | Moczo P, Kristek J, Halada L. 2000. 3D fourth-order staggered-grid finite-difference schemes: stability and grid dispersion. Bull. Seism. Soc. Am. , 90(3): 587-603. |
| [25] | Mulder W A. 1999. Spurious modes in finite-element discretizations of the wave equation may not be all that bad. Appl. Numer. Maths. , 30(4): 425-445. |
| [26] | Mullen R, Belytschko T. 1982. Dispersion analysis of finite element semidiscretizations of the two-dimensional wave equation. International Journal for Numerical Methods in Engineering, 18(1): 11-29. |
| [27] | Pasquetti R, Rapetti F. 2004. Spectral element methods on triangles and quadrilaterals: comparisons and applications. Journal of Computational Physics, 198(1): 349-362. |
| [28] | Seriani G, Oliveira S P. 2007. Optimal blended spectral-element operators for acoustic wave modeling. Geophysics, 72(5): SM95-SM106. |
| [29] | Seriani G, Oliveira S P. 2008. Dispersion analysis of spectral element methods for elastic wave propagation. Wave Motion, 45(6): 729-744. |
| [30] | Wang R Q. 1993. Stability analysis in wave equation migration using finite element method. OGP, 28(6): 657-665. |
| [31] | Wang W S, Li X F, Lu M W, et al. 2012. Structure-preserving modeling for seismic wavefields based upon a multisymplectic spectral element method. Chinese J. Geophys. (in Chinese), 55(10): 3427-3439. |
| [32] | Wu S R. 2006. Lumped mass matrix in explicit finite element method for transient dynamics of elasticity. Comput. Methods Appl. Engrg. , 195(44-47): 5983-5994. |
| [33] | Yan Z Z, Zhang H, Yang C C, et al. 2009. Spectral element analysis on the characteristics of seismic wave propagation triggered by Wenchuan Ms8.0 earthquake. Science in China Series D: Earth Sciences, 52(6): 764-773. |
| [34] | Yang D H, Teng J W, Zhang Z J, et al. 2003. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media. Bulletin of the Seismological Society of America, 93(2): 882-890. |
| [35] | Yang D H, Wang M X, Ma X. 2014. Symplectic stereomodelling method for solving elastic wave equations in porous media. Geophys. J. Int. , 196(1): 560-579. |
| [36] | Zhang H, Zhou Y Z, Wu Z L, et al. 2009. Finite element analysis of seismic wave propagation characteristics in Fuzhou basin. Chinese J. Geophys. (in Chinese), 52(5): 1270-1279. |
| [37] | Zhang J H, Yao Z X. 2013. Optimized finite-difference operator for broad-band seismic wave modeling. Geophysics, 78(1): A13-A18. |
| [38] | Zhou H, Xu S Z, Liu B, et al. 1997. Modeling of wave equations in anisotropic media using finite element method and its stability condition. Chinese J. Geophys. (in Chinese), 40(6): 833-841. |
| [39] | Zyserman F I, Gauzellino P M. 2005. Dispersion analysis of a nonconforming finite element method for the three-dimensional scalar and elastic wave equations. Finite Elements in Analysis and Design, 41(13): 1309-1326. |
| [40] | Zyserman F I, Santos J E. 2007. Analysis of the numerical dispersion of waves in saturated poroelastic media. Comput. Methods Appl. Mech. Engrg. , 196(45-48): 4644-4655. |
| [41] | 陈山, 杨顶辉, 邓小英. 2010. 四阶龙格—库塔方法的一种改进算法及地震波场模拟. 地球物理学报, 53(5): 1196-1206. |
| [42] | 刘少林, 李小凡, 刘有山等. 2013. 求解声波方程的辛RKN格式. 地球物理学报, 56(12): 4197-4205. |
| [43] | 刘少林, 李小凡, 汪文帅等. 2013. 最优化辛格式广义离散奇异核褶积微分算子地震波场模拟. 地球物理学报, 56(7): 2452-2462. |
| [44] | 刘有山, 滕吉文, 刘少林等. 2013. 稀疏存储的显式有限元三角网格地震波数值模拟及其PML吸收边界条件. 地球物理学报, 56(9): 3085-3099. |
| [45] | 龙桂华, 李小凡, 江东辉. 2010. 基于交错网格Fourier伪谱微分矩阵算子的地震波场模拟GPU加速方案. 地球物理学报, 53(12): 2964-2971. |
| [46] | 马啸, 杨顶辉, 张锦华. 2010. 求解声波方程的辛可分Runge-Kutta方法. 地球物理学报, 53(8): 1993-2003. |
| [47] | 王润秋. 1993. 有限元法解波动方程偏移过程中的稳定性分析. 石油地球物理勘探, 28(6): 657-665. |
| [48] | 汪文帅, 李小凡, 鲁明文等. 2012. 基于多辛结构谱元法的保结构地震波场模拟. 地球物理学报, 55(10): 3427-3439. |
| [49] | 张怀, 周元泽, 吴忠良等. 2009. 福州盆地强地面运动特征的有限元数值模拟. 地球物理学报, 52(5): 1270-1279. |
| [50] | 周辉, 徐世浙, 刘斌等. 1997. 各向异性介质中波动方程有限元法模拟及其稳定性. 地球物理学报, 40(6): 833-841. |
 2014, Vol. 57
2014, Vol. 57

