地球物理学报  2014, Vol. 57 Issue (7): 2244-2257   PDF    
引用本文
李娜, 任恒鑫, 黄清华, 陈晓非. 2014. 三维层状孔隙介质中弹性波的一种积分表达式II：正确性检验和数值模拟实验. 地球物理学报, 57(7): 2244-2257, doi: 10.6038/cjg20140719   
LI Na, REN Heng-Xin, HUANG Qing-Hua, CHEN Xiao-Fei. 2014. An integral expression of elastic waves in 3D stratified porous media II：Validation and numerical simulation experiments. Chinese J. Geophys. (in Chinese), 57(7): 2244-2257, doi: 10.6038/cjg20140719   
三维层状孔隙介质中弹性波的一种积分表达式II：正确性检验和数值模拟实验
李娜1,2, 任恒鑫1,3, 黄清华4, 陈晓非1,3    
1. 中国科学技术大学地球和空间科学学院, 合肥 230026;
2. 西方科奇, 斯伦贝谢中国分公司, 北京 100015;
3. 中国科学技术大学地震与地球内部物理实验室, 合肥 230026;
4. 北京大学地球与空间科学学院, 北京 100871
投稿时间:2013-12-6    最后修改时间: 2014-4-10 .
基金项目：国家自然科学基金面上项目（41274053，41274054），国家杰出青年基金项目（41025014）资助.
作者简介：李娜，女，1985年生，2012年毕业于中国科学技术大学并获博士学位，现就职于斯伦贝谢中国分公司.E-mail：angelinaer0922@gmail.com
通讯作者：任恒鑫，男，1982年生，中国科学技术大学特任副研究员，2009年毕业于北京大学并获博士学位，主要从事孔隙介质波动理论、地震电磁学方面的研究.E-mail：renhx@ustc.edu.cn
摘要：基于前一篇文章中得到的关于三维层状孔隙介质中弹性波场的积分形式半解析解，本文通过离散波数法开展了数值模拟.将全空间均匀孔隙介质中单力点源和爆炸点源作用下弹性波场的解析解和我们的数值模拟结果进行对比，发现两者是完全一致的.而在一个两层半空间模型下的数值模拟，验证了固相位移Green函数的9组空间互易性情况.通过以上两种对比检验，验证了半解析解理论公式、数值模拟方法以及相应程序代码的正确性和可靠性.随后利用敏感度分析研究了不同的介质参数变化对爆炸点源在界面上会产生的反射波场的影响.通过垂直地震剖面模型的数值模拟，发现弹性波场能很好地反映孔隙介质物理性质的变化，同时也讨论了动力协调这一孔隙介质中的特殊现象.我们发展的基于半解析解的数值模拟方法可以为三维层状孔隙介质中弹性波传播特征的研究提供一种可供选择的有效工具和手段.
关键词： 层状孔隙介质     弹性波     数值模拟     敏感度分析     垂直地震剖面    
An integral expression of elastic waves in 3D stratified porous media II：Validation and numerical simulation experiments
LI Na1,2, REN Heng-Xin1,3, HUANG Qing-Hua4, CHEN Xiao-Fei1,3    
1. School of Earth and Space Sciences, University of Science and Technology of China, Hefei 230026, China;
2. WesternGeco, Schlumberger China, Beijing 100015, China;
3. Laboratory of Seismology and Physics of Earth's Interior, University of Science and Technology of China, Hefei 230026, China;
4. School of Earth and Space Sciences, Peking University, Beijing 100871, China
Abstract: Based on the integral expression of half-analytical solution for elastic waves in three-dimensional (3D) stratified porous media derived in the companion paper, we carry out numerical simulations by using the discrete wave-number method in this study. Comparing the analytical solutions of the elastic waves generated by a point source of single-force or explosion in homogeneous full-space porous media with our numerical solutions, we find they are identical. We also confirm the special reciprocity of the solid displacement by the numerical simulation on a two-layer half-space model. Thus, we verify the validity and reliability of our half-analytical solution, the numerical simulation method and the program code used by us. Then we carry out sensitivity study to discuss the impact of the media parameter on the reflection waves induced by an explosion point source on the interface. In the numerical simulation of a model of vertical seismic profile, we find that solid displacement, seepage displacement and pore-fluid pressure all can reflect the variation of the media properties. Meanwhile, we also discuss the dynamic compatibility phenomenon in porous media. It can be concluded that the developed numerical simulation method based on our half-analytical solution provides an alternative and effective instrument for the study of elastic waves' propagation in 3D stratified porous media.
Key words: Stratified porous media     Elastic waves     Numerical simulation     Sensitivity study     Vertical seismic profile    

1 引言

在上一篇文章中，我们利用Luco-Apsel-Chen(LAC)广义反透射方法(Generalized Reflection and Transmission Method缩写为GRTM)(Luco and Apsel， 1983; Chen， 1993，2007; Martin and Thomson， 1997; Ge and Chen， 2008)给出了三维层状孔隙介质中点源激发的弹性波场的具体解，其形式为积分表达式，所以可称之为半解析解.我们可以很方便地通过数值方法计算其数值解，与有限差分和有限元方法相比，该半解析解无疑具有计算速度快的优势，而有限差分和有限元一类的方法具有可以计算复杂结构模型的优势.但是在地球物理勘探领域的实际应用中，油气水储层常常呈现层状分布，这使得我们的方法具有了实际应用的可能.

在本文中，将首先介绍积分形式半解析解的一种数值实现方法——离散波数法，接着利用傅里叶变换方法得到均匀全空间孔隙介质中单力点源和爆炸点源作用下的固相位移、渗流位移和孔隙流体压力在频率域的解析解，并和数值模拟结果进行对比.而理论分析表明单力点源作用下的固相位移Green函数具有空间互易性，我们将通过数值模拟对此进行验证.然后，将给出两个数值模拟实验的算例，其中一个是敏感度分析，在此我们将分析不同的介质参数变化对爆炸点源在界面上产生的反射波场的影 响；另一个是垂直地震剖面(Vertical Seismic Profile缩写为VSP)模型下的数值模拟，将在此讨论动力协调这一孔隙介质中的特殊现象. 2 积分表达式的数值计算

我们在前一篇文章中所给出的固相位移 u 、渗流位移 w和孔隙流体压力P的半解析解是一组关于波数k的积分表达式(李娜等，2014)，该积分可以利用离散波数法(Bouchon， 1979，1981)数值求解.利用离散波数法计算弹性波场时可以计算全波场，具有结果精准的优点.通过引入在空间上周期性分布的源，可以实现波数k的离散化.在柱坐标下，初始源位于r=0，离散化之后，将会引入无限多的附加源，这些附加源是初始源的复制体，它们位于以初始源为圆心且等间隔分布的一系列同心圆环之上，这些同心圆环的空间周期Lp(即两个相邻圆环的径向距离)决定了离散化后的波数间隔：

空间周期Lp必须取得足够大，使得所有附加源产生的波场到达接收点的时间大于我们所关心的时间窗tmax.例如，接收点位于xr=(r0，z0)，源位于xs=(0，zs)，则空间周期Lp需满足

其中，vmax是介质中的最大波速.

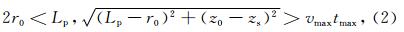
实现k积分之后即得到了空间-频率域的数值解，再利用离散傅里叶变化即可得到空间-时间域的解.在整个数值计算过程中，为了去除被积函数的奇点，我们采用了一种使用复数频率的方法，而引入虚频率所产生的衰减也可以在最后从频率域到时间域 的反傅里叶变换过程中去除，Bouchon在其工作(Bouchon，1979)中详细地介绍了该方法. 3 与解析解的对比

在本节，将通过与均匀全空间模型下点源解析解的对比来验证理论公式和数值计算方法的正确性.首先，要给出全空间模型下点源激发的弹性波场的频率域解析解. 3.1 点源解析解

从20世纪70年代开始，关于孔隙介质弹性波场Green函数的研究就取得了一系列的重要成果(Burridge and Vargas， 1979; Norris，1985; 丁伯阳等， 1999，2009).Pride和Haartsen(1996)利用傅里叶变换方法得到了孔隙介质中震电波场的Green函数在频率域的解析表达式，其形式简洁明了，物理意义清晰，而震电波场的控制方程是孔隙介质弹性波方程和Maxwell方程的耦合，所以我们完全可以遵循Pride和Haartsen(1996)的思路和方法求解孔隙介质弹性波场的Green函数.

根据Biot理论(Biot， 1956a，1956b，1962)，孔隙介质中弹性波方程在频率域可以写成如下 形式：

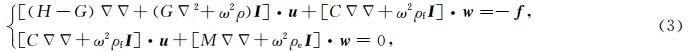
其中，ω为圆频率，u和w 分别为固相位移和渗流位移，f 表示作用在介质上的体力，I 表示单位矩阵，ρ=(1-φ)ρs+φρf表示介质平均密度，ρs和ρf分别代表介质的固相密度和孔隙流体密度，φ为孔隙度，ρe=iη/(κω)，为有效渗流密度，由它控制孔隙介质中流体和固体的相对运动情况，η为流体黏度，κ为动态渗透率，其具体公式由Johnson 等(1987)给出，G为固体骨架剪切模量，H、C和M为Biot定义的孔隙介质的弹性参数(Biot，1956b).

考虑点源的情况，则力源 f 可以表示为

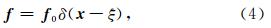
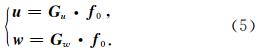
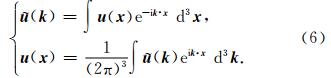
其中，δ为狄拉克函数，x和ξ 分别表示源和接收点的位置，为了便于下面的推导，可以将坐标原点取在源点位置(即令ξ=0).点源激发的固相位移 u和渗流位移 w 可以用Green函数张量表示如下

现在我们用傅里叶变换的方法来求解Green函数张量，采用如下形式的变换对，

通过傅里叶变换，(3)式可以写为

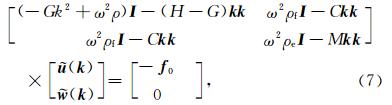
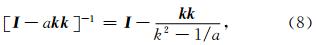
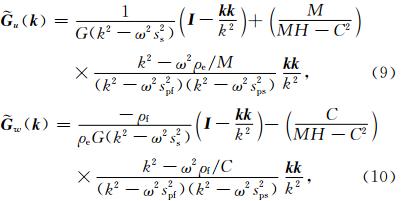
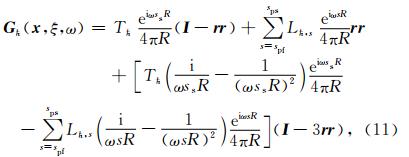
其中 I 为单位矩阵.通过等式

由式(7)可以得到波数域的Green函数：

再通过傅里叶反变换，从波数域变换回到空间域，用留数定理计算对k的积分，最终得到的Green函数形式如下：

其中，

h=u，w，代表弹性波场的类型，ss，spf和sps分别表示横波、快速纵波和慢速纵波的慢度，其具体表达式参见前一篇文章(李娜等，2014)，含有张量(I - rr)的项是横波，含有有张量 rr 的项是纵波，而含有张量(I -3 rr)的项是近场项，可以看成是由纵波和横波组合而成，当距离远远大于波长时(ωsR1)，近场项可以忽略.式中的横波振幅系数T和纵波振幅系数L的具体表达式如下:

如果点源 f 激发的孔隙流体压力P表示为

由等式－P=C Δ · u +M Δ · w 可以得到

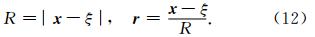
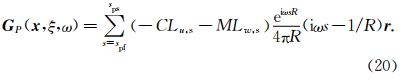
在地球物理勘探领域，常常用到爆炸点源，它是一种带有矩张量的源，可以表示为

其中，M 为其矩张量，对于爆炸源，它是对角矩阵，满足 M =M0 I .因此，爆炸点源产生的固相位移 u和渗流位移 w 可以用Green函数张量表示为

将公式(11)代入上式，可以得到

其中，h=u，w，代表弹性波场的类型，下标i代表各个分量，ri是单位矢量 r 的各个分量，不难看出，爆炸点源只产生纵波.而爆炸点源产生的孔隙流体压力P相应地可以表示为

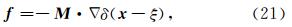
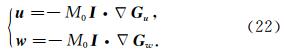
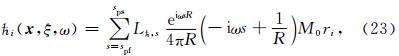
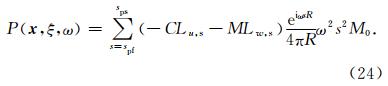
至此，我们得到了三维全空间孔隙介质中固相位移 u 、渗流位移 w和孔隙流体压力P的频率域Green函数以及对于爆炸点源的响应，其形式简洁明了，物理意义清晰.求出频率域的数值解之后，只要进行反傅里叶变换即可得到时间域的解.点源解析解可以帮助我们很好地了解和分析波场的传播、衰减特征，Green函数也是边界积分方法所必需的.上述的三维点源解析解还可以用来求二维问题的数值解，二维点源问题可以看成是三维空间中的点源沿着某一维度的无穷积分，这种积分可以通过数值方法快捷地求解.例如，我们可以在柱坐标下将无穷积分变换为θ在(-π/2，π/2)区间上的积分，然后利用高斯-勒让德公式即可轻松地得到数值解，二维点源问题的解可以为二维的数值模拟方法提供对比检验. 3.2 对比结果

现在，我们分别针对单力点源和爆炸点源，将数值计算结果和解析解进行对比.

首先考虑单力点源情况，所用的全空间模型由介质l1构成(本文中所用介质的物性参数见表 1)，源位于原点而接收点坐标为(2.5 km，0 km，1.6 km)，所施加的单力力源沿着z轴正方向，大小为1 N，所采用的震源时间函数是峰值频率为2.5 Hz、无相位偏移的Ricker子波.

表 1 本文所用介质的物性参数 Table 1 Properties of the used medium in this paper

通过我们的方法(LAC GRTM)计算得到相应的固相位移 u 、渗流位移 w和孔隙流体压力P，然后和解析解进行对比，结果如图 1所示.第一行显示了固相位移的 x分量和z 分量，显然，最先到达的是快速纵波，大约在0.5~1 s，然后是横波，大约在1~2 s，最后到达的是慢速纵波，大约在3.5~4 s，其中慢速纵波产生的固相位移的振幅远远小于快速纵波和横波，将其放大100倍之后才和前两者相当.第二行显示的是渗流位移的x分量和z分量，快速纵波、横波以及慢速纵波均能和固相位移的结果一一对应.最后一行是孔隙流体压力P，快速纵波和慢速纵波均能产生孔隙流体压力，而横波不会产生孔隙流体压力，这显然是合理的.固相位移和渗流位移的y分量均为零.对比图 1中的两种结果，发现它们是完全一致，无论是对于快速纵波、慢速纵波还是横波，均是如此.我们也分别测试了单力点源沿着x方向和y方向的情况，均发现我们的方法得到的结果和解析解完全吻合.

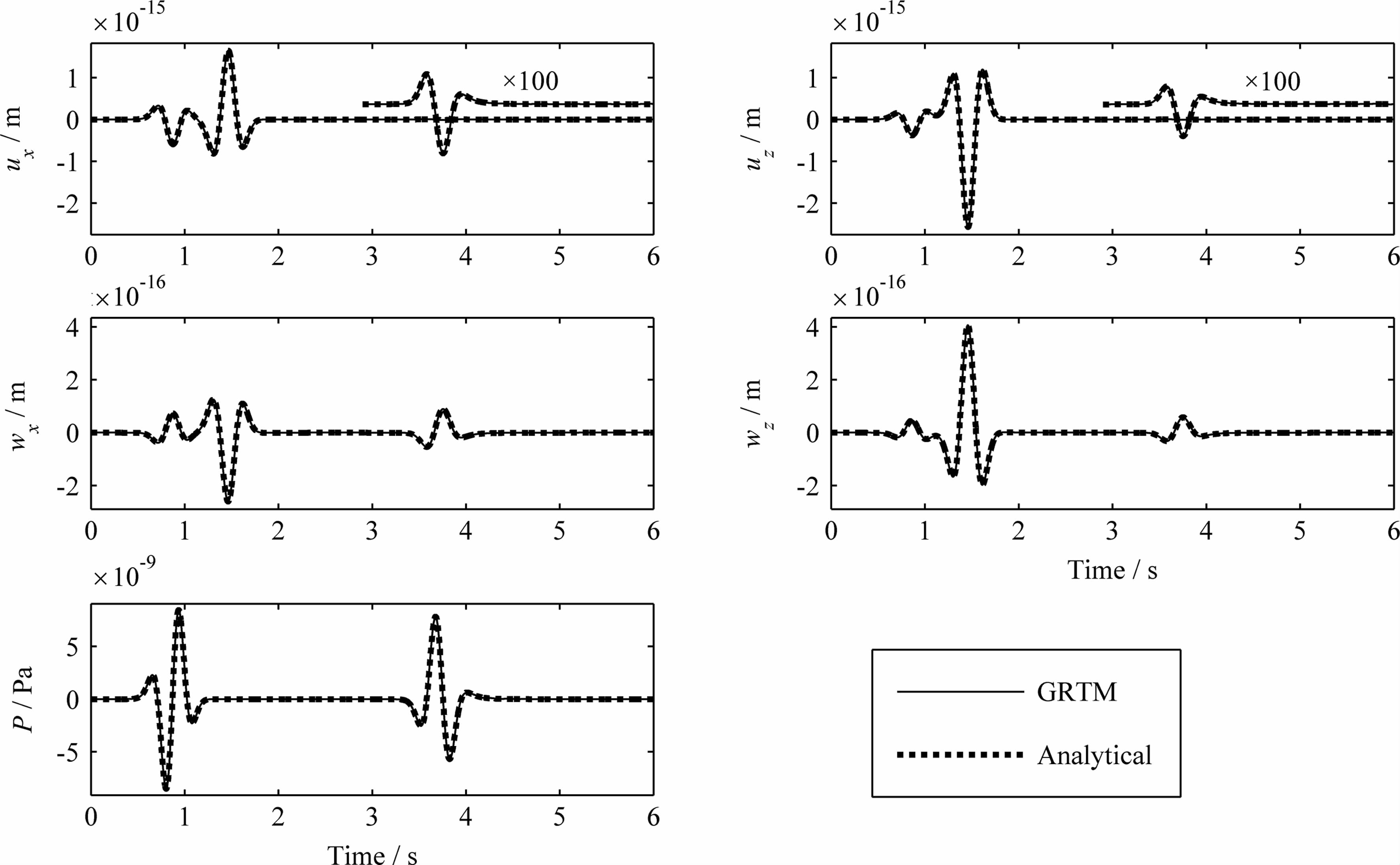图 1 单力点源解析解和LAC GRTM数值模拟结果的对比 Fig. 1 Comparison of the wave fields generated by the single force point source between the analytical solutions and the numerical solutions obtained by the LAC GRTM

现在我们将全空间模型中的单力点源替换为爆炸点源，其标量矩为M0=1.0×107 J，其他设置保持不变.仍然通过解析解和我们的方法(LAC GRTM)各自计算相应的固相位移 u 、渗流位移 w和孔隙流体压力P，结果如图 2所示.由于爆炸点源只产生纵波，所以我们只能看到快速纵波和慢速纵波，它们的到时和单力点源的情况一致，这是因为介质相同，波速不变.爆炸点源的对比结果也表明，解析解和我们的GRTM结果完全一致.

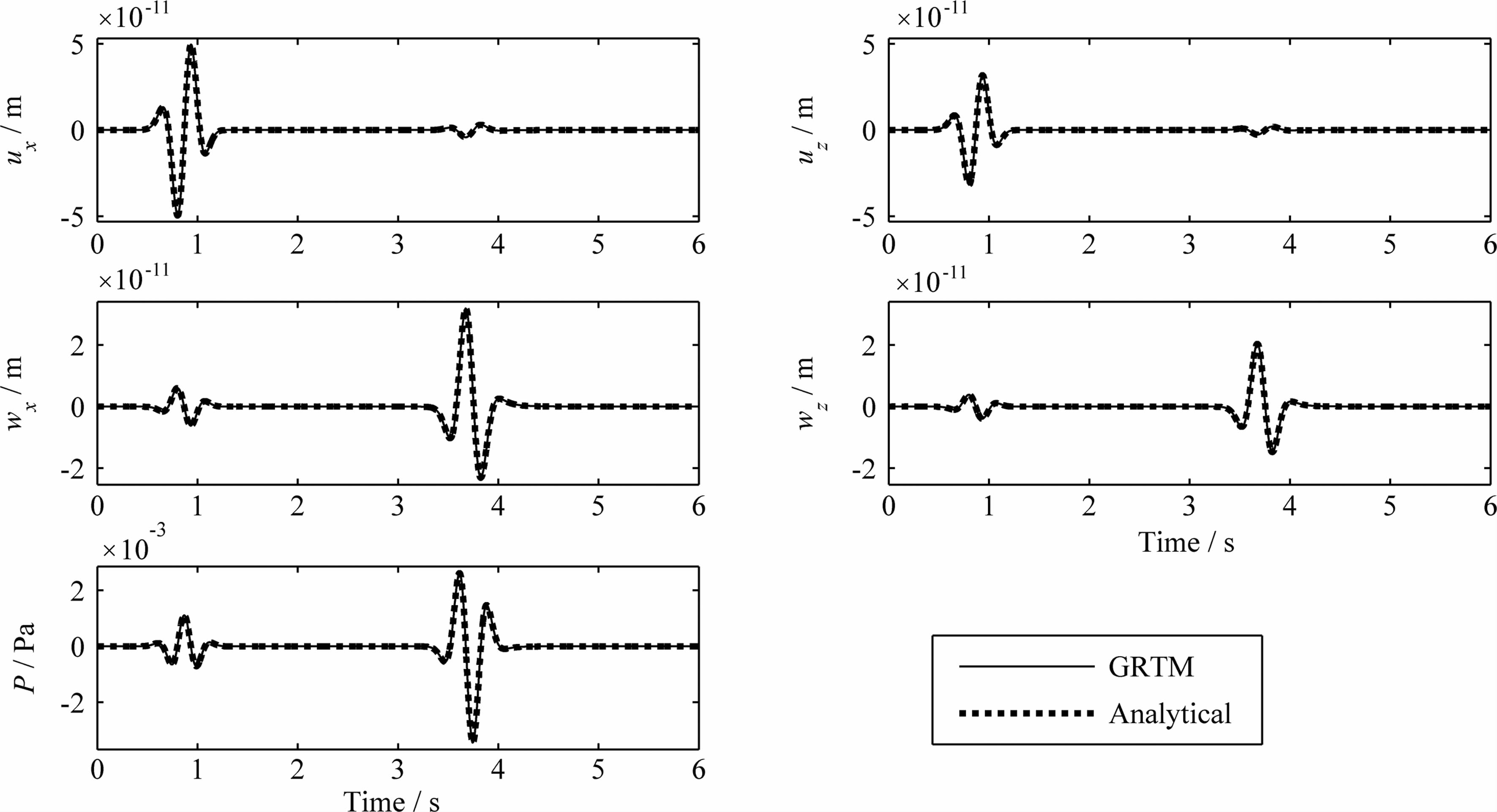图 2 爆炸点源解析解和LAC GRTM数值模拟结果的对比 Fig. 2 Comparison of the wave fields generated by the explosion point source between the analytical solutions and the numerical solutions obtained by the LAC GRTM

因此，无论是单力点源还是爆炸点源，我们的方法得到的结果均和解析解保持完全一致，计算得到的波型和到时也完全符合理论预期.

但是，应该指出，上述全空间模型中所用的介质l1具有非常高的达西渗透率，κ0=10-6 m2，它使得慢速纵波的速度变大，在2.5 Hz附近达到vps=789 m·s-1. 同时，关于流体流动的临界频率为ωJ/(2π)= φη/(2πα∞ρfκ0)=0.0265 Hz，在低于该频率的情况下，控制孔隙中流体流动的主要是黏滞性剪切力，而我们所用的震源时间函数为峰值频率2.5 Hz的Ricker子波，这时占主导的是高频情况，孔隙中流体的流动除了在固体-流体分界面处的一个黏性边界薄层之内是黏滞性剪切作用为主，在其余孔隙空间中是惯性作用占主导地位，所以高频情况下的衰减应该比低频情况小.然而，实际地球中孔隙介质的达西渗透率通常满足κ0<10-11 m2，例如，对于κ0=10-12 的情况，慢速纵波的波速在2.5 Hz附近为vps=11 m·s-1，慢速纵波的波长变小，所以传播相同空间距离后的衰减变大，而临界频率变为ωJ/(2π)=2.65×104 Hz，所以孔隙中的流体流动是低频情况下的黏性流动，衰减更快.以上两点原因使得在实际介质中很难观测到慢速纵波.在下文中，如无特殊说明，纵波(P波)均指快速纵波. 4 互易性检验

Green函数的空间互易性是一种很好的数值检验方法，可以用来检查我们所用的程序代码中可能存在的问题，比如，是否增加或者丢失了一些项，振幅和波形是否正确.

定义固相位移 u 1、渗流位移 w 1、应力张量 τ 1和孔隙流体压力P1是在力源 f 1作用下产生的物理场，而 u 2、 w 2、 τ 2和P2是力源 f 2作用下产生的场，则他们均满足孔隙介质的弹性波场控制方程组(参见前一篇文章(李娜等，2014)中的公式(1)—(4))，所以它们也满足等式

其中 n 是体积V表面S 的外法线.对于全空间介质中的有限源，波场在无穷远处为零，因此等式左边为零，而对于带自由表面的半空间介质，由于在自由表面处的应力为零(τ 1、P1、 τ 2和P2 均为零)，所以等式左边也为零，因此无论是对于全空间还是半空间都有

其中 V f 1和V f 2 为包含它们相应源的体积.考虑单力点源的情况，定义uij(x r，t; x s，t0)为t0时刻作用在介质中 x s位置的j方向单位单力点源作用下产生的t时刻 x r位置的固相位移沿i方向的分量，则根据上式可以得到

这就是固相位移场的空间互易性.下面我们将进行互易性检验.

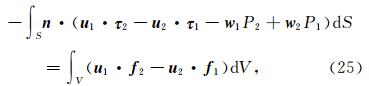
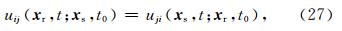
我们在这里采用了一个简单的两层半空间模型，上层由介质l2构成，厚度为150 m，下层是由介质l3构成的无限半空间，分别考虑了两种源和接收点的设置.如图 3所示，自由表面位于z=0 m，在第一种设置中(图 3a)，源位于(0 m，0 m，50 m)而接收点位于(300 m，225 m，250 m)，在第二种设置 中，源位于(0 m，0 m，250 m)而接收点位于(-300 m，-225 m，50 m).震源时间函数采用峰值频率为 50 Hz、无相位偏移的Ricker子波，力源的大小为1 N，分别考虑单力点源沿着x、y和z方向的情况.

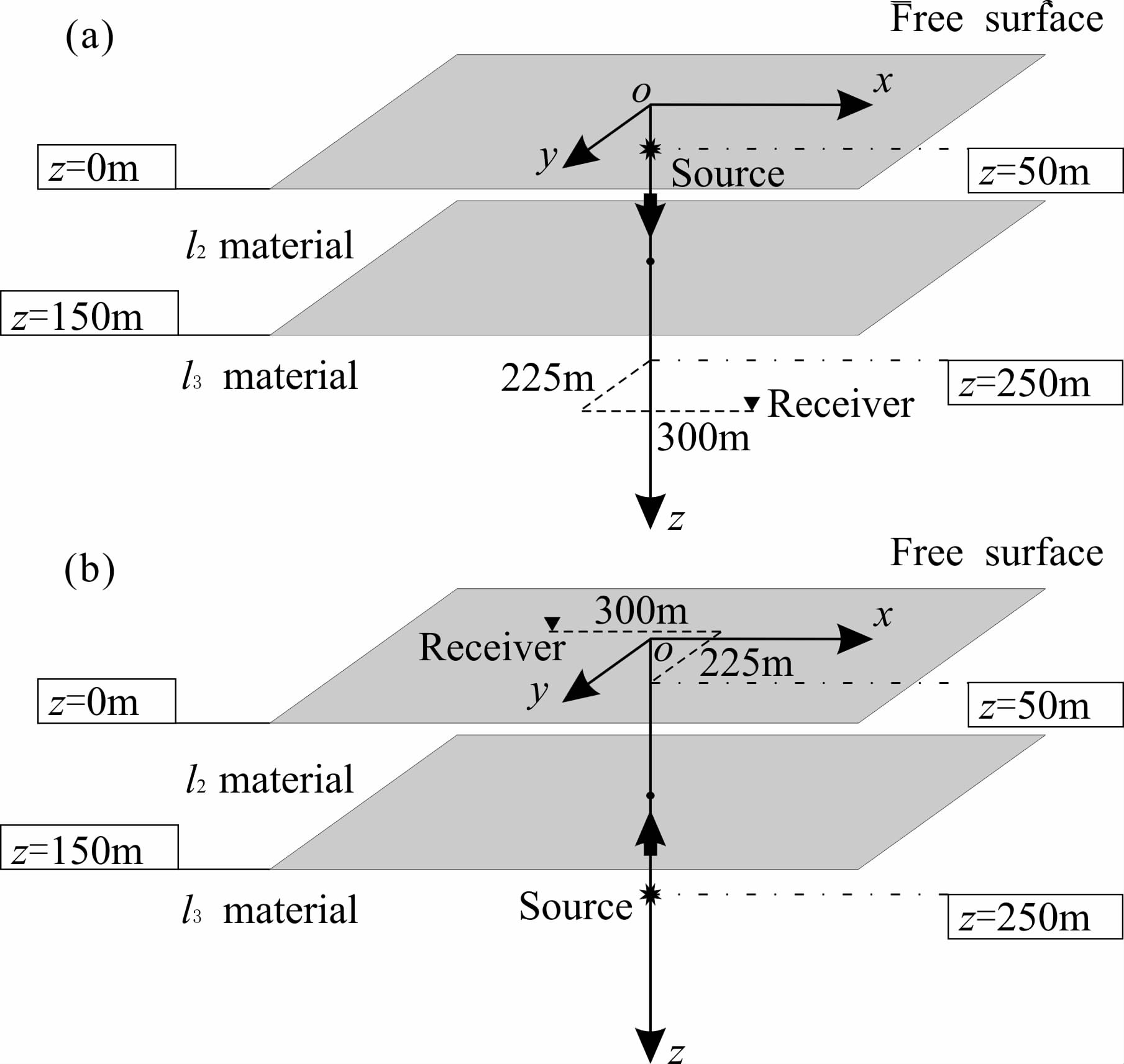图 3 互易性检验中所用的模型示意图 (a)接收点在源的下方;(b)接收点在源的上方. Fig. 3 Configuration of the model used for reciprocity validations (a)Receiver below the source(“down”)；(b)Receiver above the source(“up”).

图 4显示了9组空间互易性的对比情况.实线(“down”)表示了图 3a设置下不同方向的单力点源产生的固相位移场的各个分量，点线(“up”)则对应了图 3b设置下的结果.直达纵波和横波分别大约在0.12~0.15 s和0.25~0.28 s到达，由于自由表面和z=150 m处界面的存在，产生了各种不同的反射波和转换波.在9组对比中，均发现两种结果是完全一致的.因此，我们所用的程序通过了这种互易性检验.从另一个角度，也可以说我们用我们的基于半解析解的数值模拟方法验证了半空间层状孔隙介质中固相位移场的空间互易性.

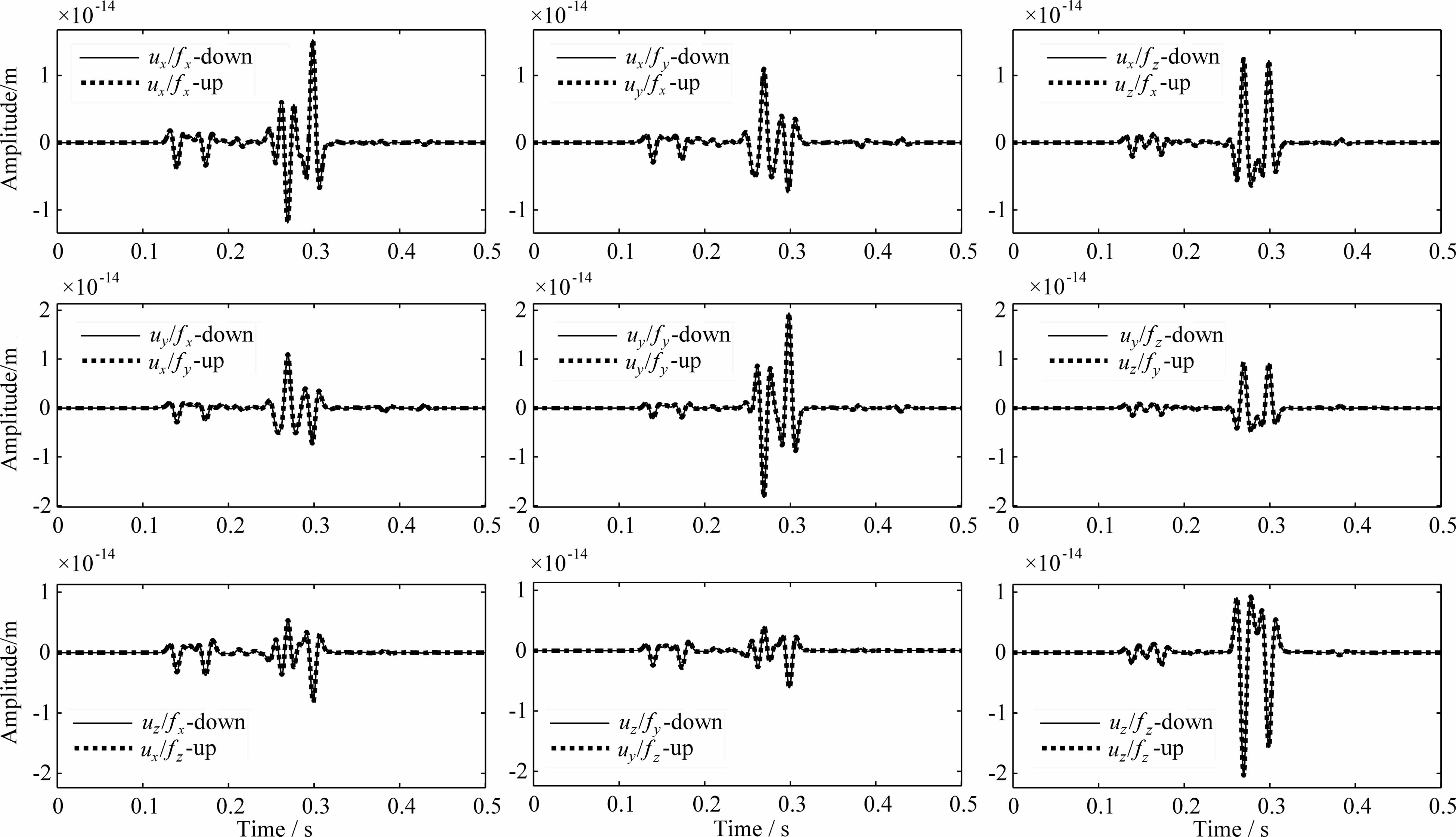图 4 固相位移场的互易性检验 Fig. 4 Reciprocity validations for solid displacement fields
5 数值模拟实验

我们将进行两个数值模拟实验，来分析和研究孔隙介质弹性波场的一些特征.其中一个是爆炸点源在界面上产生的反射波场对参数变化的敏感度分析，另一个是垂直地震剖面模型下的数值模拟. 5.1 敏感度分析

油气水储层的边界是一个介质物理性质发生变化的界面，会产生反射波，反射波场的特征与孔隙介质的物性参数密切相关.因此，反射波场对界面处参数变化的敏感度分析是非常有意义的工作，它可以为孔隙介质的实际数据分析和弹性波场反演问题提供指导和借鉴.在本节，我们将利用我们的理论数值模拟方法，考察爆炸点源激发的纵波在界面处产生的反射波场对介质参数变化的敏感度情况.

考虑一个两层的全空间模型，界面位于z=100 m处，爆炸点源位于界面上方(0 m，0 m，50 m)处，其释放的标量矩为M0=1.0×1013 J，所用的震源时间函数是峰值频率为200 Hz、无相位偏移的Ricker子波，接收点位于(200 m，0 m，0 m)的位置.上层介质固定为l4(砂岩)，我们让下层介质的其中一个参数变化而其余参数保持与上层介质相同，以此来分 析反射波场对该参数变化的敏感度情况.我们对所有的介质参数逐一开展分析，发现界面处参数变化的影响大体可以分为3种，图 5—7分别展示了这3种影响.

图 5展示了下层介质孔隙度φ的变化对波场的影响，黑色、蓝色、绿色和红色的线分别对应下层介质孔隙度为10%、15%、25%和30%的情况，并且做了不同的标记加以区分.该模型下一共存在3种波：直达P波、PP反射波和PSV反射波.为了使得直达P波和PP反射波在到时上能够分开，我们设置的爆炸点源到界面有一定的距离，因此反射波信号比直达波信号弱，为了能更清晰地展示结果，我们分别展示了直达P波、PP反射波和PSV反射波所产生 的信号.如图 5所示，首先到达的是直达P波，大约在0.062~0.075 s左右，显然，直达P波不会受到下层介质参数改变的影响.第二个到达的是PP反射波，大约在0.077~0.089 s左右，最后到达的则是PSV反射波，大约在0.112~0.123 s左右，PSV反射波当然不会产生孔隙流体压力.可以看出，无论是PP反射波还是PSV反射波，均受到孔隙度变化的影响，当变化幅度越大时，所产生的反射波场振幅也越大，此外，对比下层介质孔隙度变小(10%和15%)与变大(25%和30%)的情况，它们所产生的反射波场的振动方向完全相反.和孔隙度φ一样，固体密度ρs、流体密度ρf和固体骨架剪切模量G的变化都同时影响PP反射波和PSV反射波.

图 5 孔隙度对波场的影响.从左到右的三列分别是直达P波、PP反射波和PSV反射波 Fig. 5 Affection of the porosity to wave fields. The three columns(from left to right) show direct P wave，reflected PP wave， and reflected PSV wave，respectively

图 6展示了下层介质的固体骨架体积模量Kd变化对波场的影响，黑色、蓝色、绿色和红色的线分别对应Kd为1 GPa、3 GPa、7 GPa和9 GPa的情况.Aki和Richards(1980)关于反射系数的基本公式表明：当上下两层介质的密度和S波波速不变时，P波入射并不会产生SV波.这一结论也同样适用于孔隙介质，由于固体骨架体积模量Kd的变化只影响P波波速，介质密度和S波波速均不受影响，所以在界面上仅仅产生PP反射波.PP反射波的振幅随着上下两层介质固体骨架体积模量差异的增大而增大，对比Kd变小(1 GPa和3 GPa)与变大(7 GPa和9 GPa)的情况，它们所产生的PP反射波的振动方向完全相反.和固体骨架体积模量Kd一样，固体体积模量Ks和流体体积模量Kf的变化都仅仅产生PP反射波.

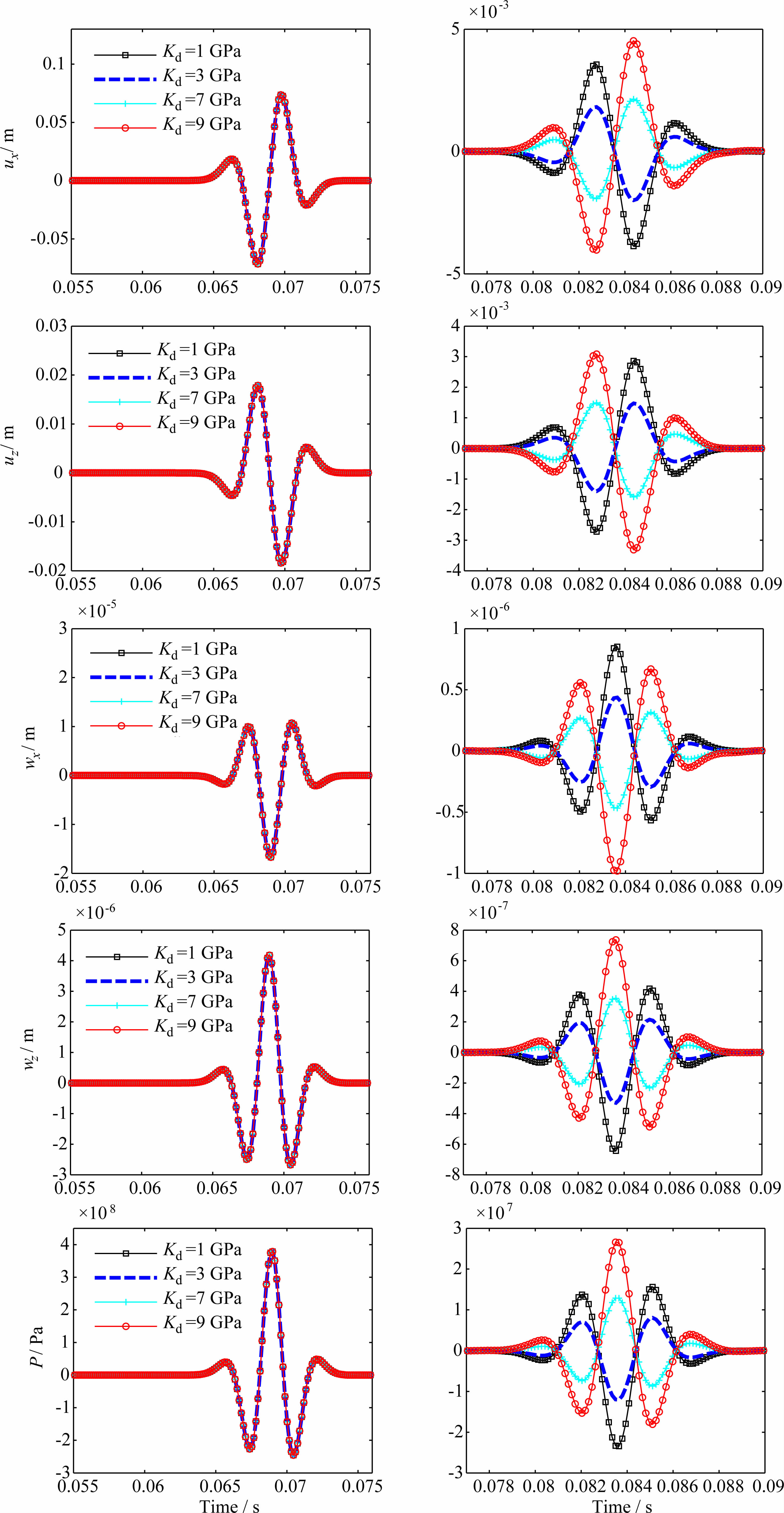图 6 固体骨架体积模量对波场的影响 左右两列分别是直达P波和PP反射波. Fig. 6 Affection of the solid frame bulk modulus to wave fields The left and right columns show direct P wave and reflected PP wave，respectively.

图 7展示了下层介质的达西渗透率κ0变化对波场的影响，黑色、蓝色、绿色和红色的线分别对应κ0为0.8×10-12 m2、0.9×10-12 m2、1.1×10-12 m2和1.2×10-12 m2的情况.可以看到，无论是PP反射波还是PSV反射波，其振幅均随着上下两层介质κ0差异的增大而增大，而κ0变大和变小时产生的PP和PSV反射波的振动方向完全相反.对比图 5、图 6和图 7，可以看到，κ0变化所产生的反射波场的振幅要比其余二者小4~6个数量级.所以，反射波场对κ0的敏感度要远远低于对φ和Kd等参数的敏感度，究其原因，是因为κ0的变化对弹性波场的影响很弱.图 8给出了达西渗透率κ0从1.0×10-6 m2变化到1.0×10-20 m2时对P波和S波速度的影响，可以看到，P波速度的变化小于1 m·s-1而S波速度的变化小于30 m·s-1.如果下层介质的达西渗透率从1.0×10-6 m2变化到1.0×10-20 m2，则相应地，其中κ0=1.0×10-6 m2时产生的反射波场振幅最大，但是即便如此，较图 5和图 6的结果而言，PP反射波仍然要小3个数量级，PSV反射波要小1个数量级.回顾孔隙介质的波场控制方程，不难发现，可以将(κ/η)整体视为一个参数，同时，(对于固定频率)动态渗透率κ和达西渗透率κ0成线性比例关系(Johnson et al., 1987)，所以也可以将(κ0/η)整体视为一个参数，那么我们很容易推断：下层介质κ0放大10倍与η缩小10倍所产生的反射波场是完全等同的，我们也通过我们的数值模拟方法证实了实际情况确实如此.因此，达西渗透率κ0和流体黏度η的变化均能产生PP反射波和PSV反射波，但是反射波场对这两个参数的敏感度要远远低于对φ和Kd等参数的敏感度.

图 7 达西渗透率对波场的影响 从左到右的三列分别是直达P波、PP反射波和PSV反射波，其中PP反射波的振幅远远小于PSV反射波的振幅. Fig. 7 Affection of the Darcy permeability to wave fields The three columns(from left to right)show direct P wave，reflected PP wave， and reflected PSV wave，respectively. The amplitude of reflected PP wave is far less than the amplitude of reflected PSV wave.

因此，若要反演地层渗透率或者是流体黏度，可以考虑一些其他对这两者具有更高敏感度的波场.例如，孔隙介质井中斯通利波就对渗透率具有高敏感度(Tang and Chen， 1996)，是反演地层渗透率的一种常用方法.而孔隙介质中由于固液界面上存在双电层结构，会产生动电效应，在不同性质的孔隙介 质的分界面上，垂直入射的地震波可以激发出以电磁波速度独立传播的转换电磁波，而这种界面转换电磁波恰恰是对于渗透率和黏度具有高敏感度的，因此，动电效应在油气水勘探方面也可能具有潜在 的应用价值(Pride，1994; Haartsen and Pride， 1997; Garambois and Dietrich， 2002; Ren et al., 2012).

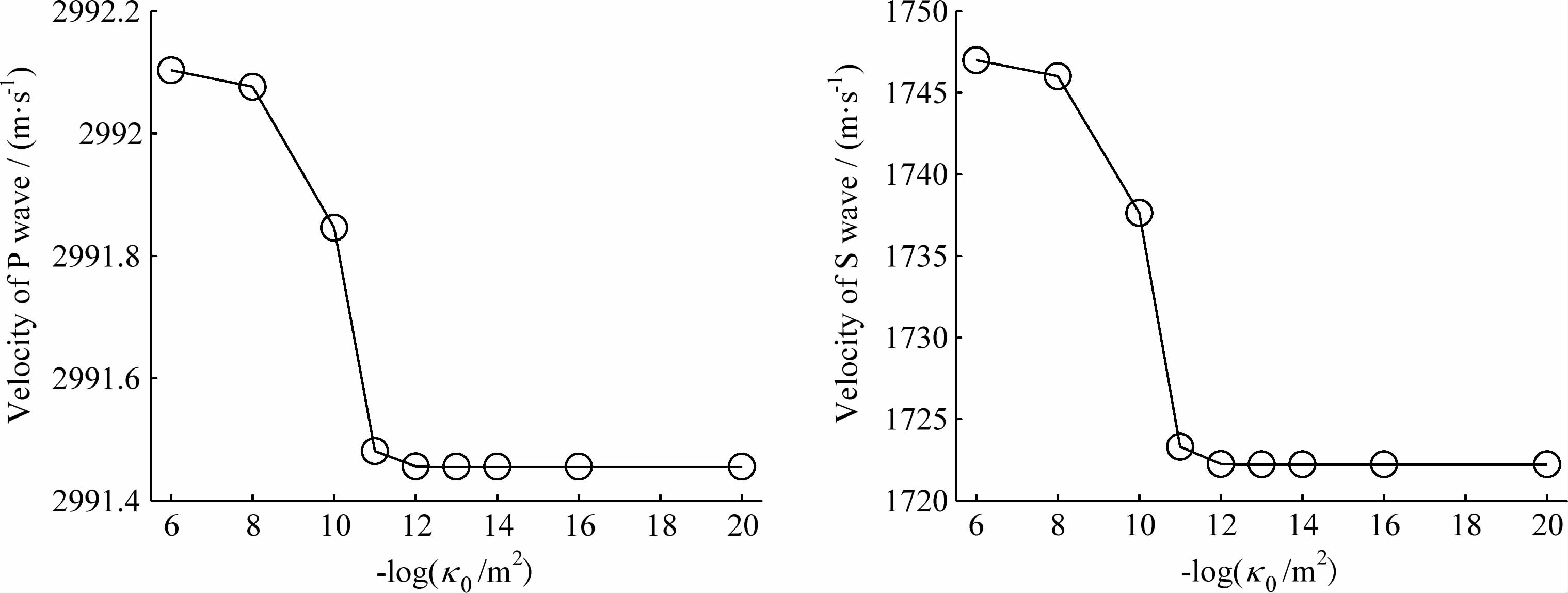图 8 达西渗透率κ0对P波和S波速度的影响 Fig. 8 Affection of the Darcy permeability to velocities of P wave and S wave
5.2 垂直地震剖面

垂直地震剖面(VSP)技术是石油勘探领域一项重要的地震观测方法，它可以将接收器放置在我们感兴趣的目标区域，因此利用VSP技术可以观测位于更深位置的目标区域.

我们考虑一个由三层介质构成的垂直地震剖面模型，以爆炸点源为坐标原点，在深度300~400 m范围内为l4(砂岩)介质，顶层和底层均由l5介质组成，共有30个接收点分布在一条垂线上，第一个接收点位于(50 m，0 m，255 m)处，后面每一个接收点依次加深10 m，所用的震源时间函数是峰值频率为150 Hz、无相位偏移的Ricker子波.数值计算得到的波场如图 9所示，第一行和第二行分别是固相位移场和渗流位移场的x分量，均可以清楚地看到顶层的直达P波以及在两个界面上产生的PP和PSV反射波或者是透射波，最后一行是流体孔隙压力，因此从中只能看到相应的P波.总体来说，无论是固相位移、渗流位移还是孔隙流体压力，均能很好地反映孔隙介质性质的变化.

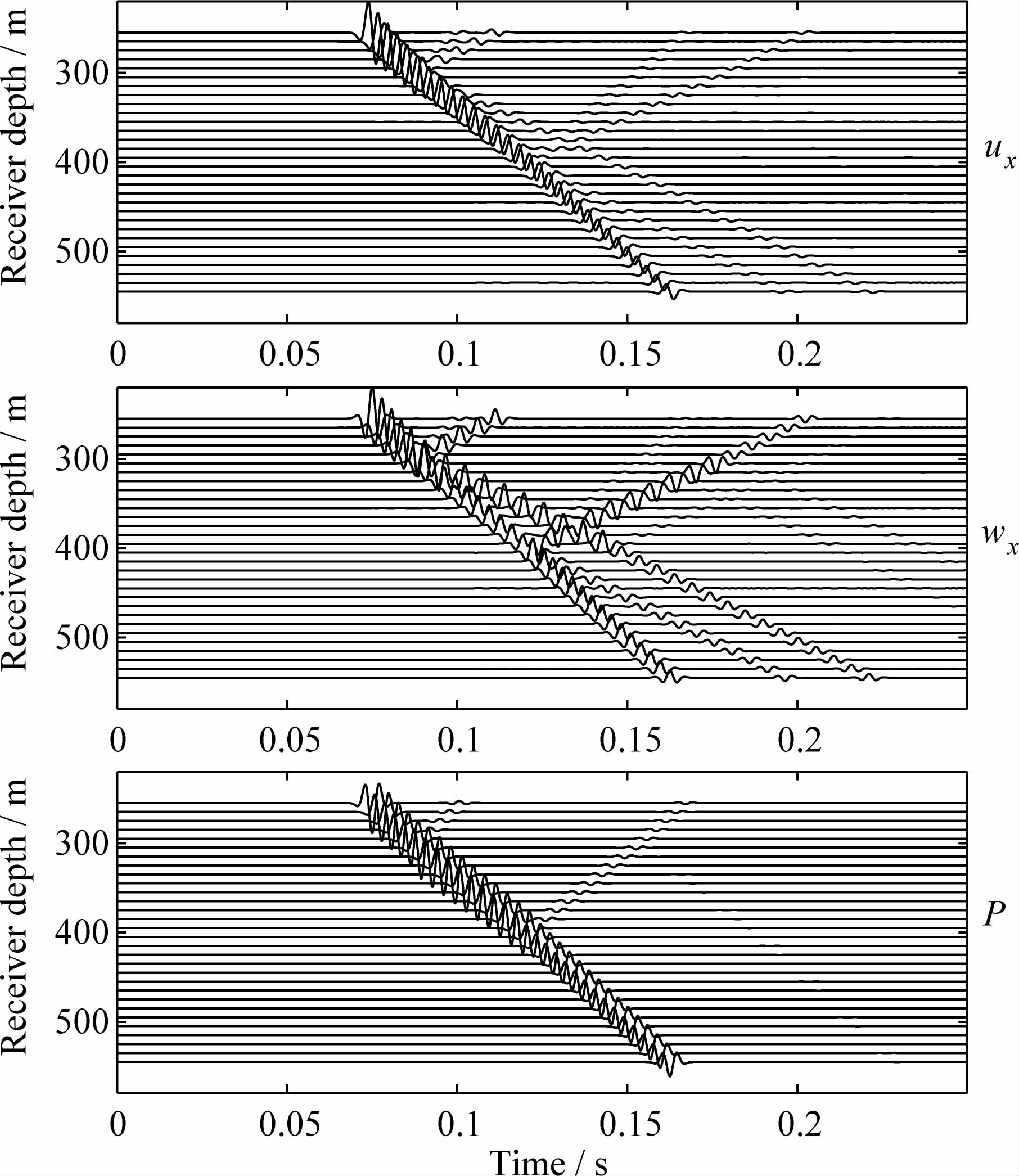图 9 三层模型(中间层为非动力协调介质)的数值模拟结果 Fig. 9 Numerical simulation results of the three-layer model with the intermediate layer unsatisfying the dynamic compatibility condition

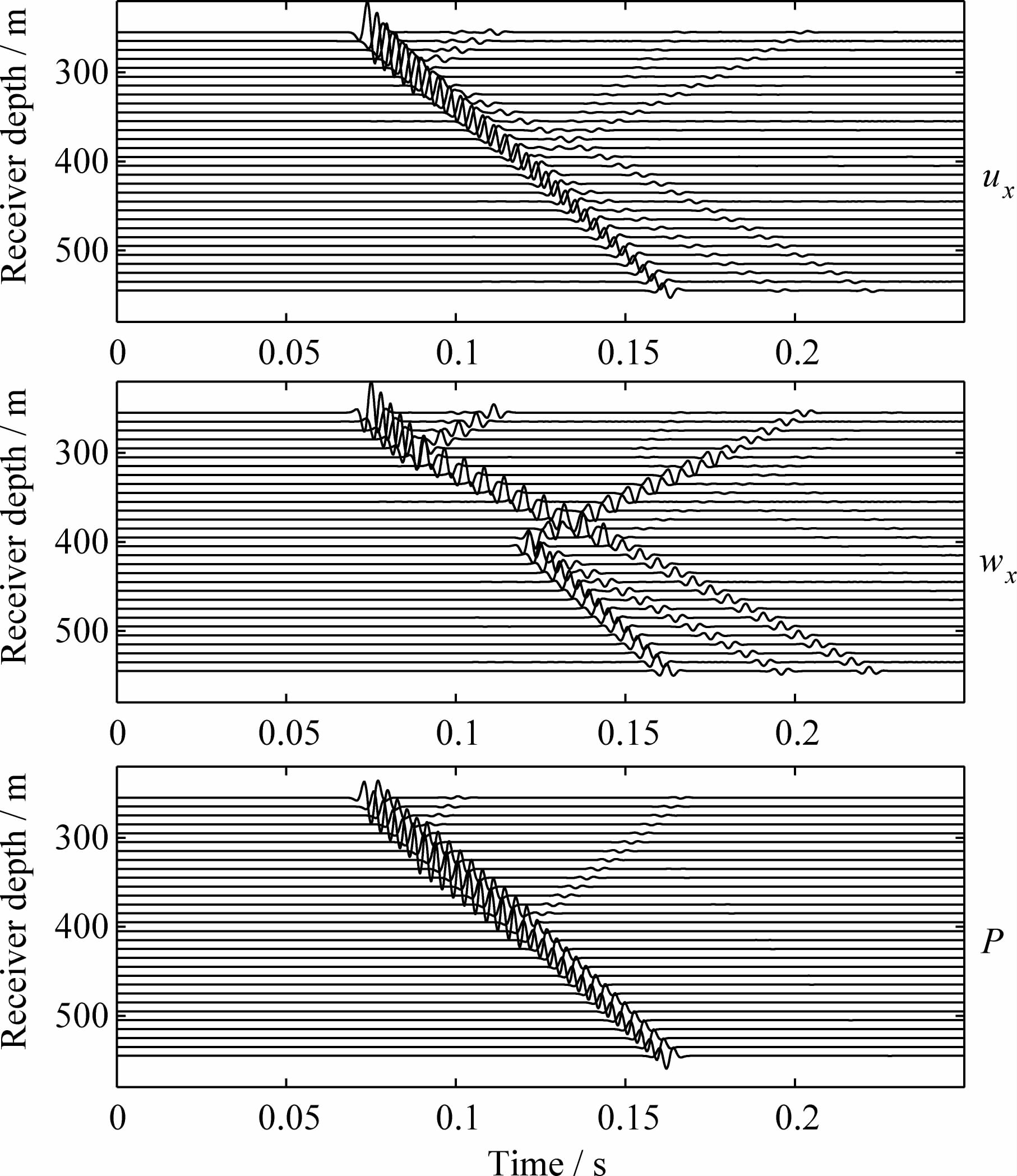
Biot(1956a)提出有可能存在一种特殊的动力协调(dynamic compatibility)的孔隙介质，在该介质中快速纵波不会产生渗流位移.胡恒山等(2002)基于对岩石骨架模量和孔隙度的研究，发现动力协调孔隙介质是可能实际存在的.动力协调的孔隙介质满足条件

此时快速纵波的慢度为(胡恒山等，2002)

将上式代入公式(17)可得

即渗流位移Green函数中关于快速纵波的振幅系数为0，这说明在满足动力协调条件的孔隙介质中，快速纵波产生的固相位移和流体位移不仅振幅相等，而且相位相同，固体和流体的运动完全一致，所以渗流位移为零.

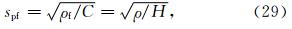
我们将中间层l4(砂岩)介质的孔隙度改为φ= 16.365328%，使其成为一种动力协调介质，重新计算弹性波场，结果如图 10所示，在满足动力协调条件的中间层中，伴随快速纵波的渗流位移全部消失，该数值结果和理论预期一致.由于动力协调介质是可能实际存在的，因此在研究孔隙介质时，有必要注意这一特征以及一些可能产生的相关现象，例如，孔隙介质中动电效应所产生的电磁场就与渗流位移密切相关，在动力协调介质中伴随快速纵波的同震电场也会完全消失(高永新和胡恒山，2009). 6 讨论和结论

基于我们在前一篇文章中得到的关于三维层状孔隙介质弹性波场(固相位移 u 、渗流位移 w和孔隙流体压力P)的积分形式的半解析解，我们通过离散波数法(Bouchon， 1979，1981)开展了数值模拟研究.通过数值模拟结果和解析解的对比，我们发现无论是对于单力点源还是爆炸点源，无论是在波型还是在到时方面，两者均完全一致.为了能在结果中展示慢速纵波，我们在全空间模型中采用了非常高的达西渗透率，而在真实的孔隙介质中，达西渗透率很低，慢速纵波速度非常小，通常是在几十米每秒这个数量级，波长很短，衰减很快，因此在实际情况中通常很难观测到慢速纵波.我们在一个两层半空间模型下开展数值模拟，发现固相位移Green函数的9组空间互易性结果均得到了满足.和解析解的对比检验以及固相位移Green函数的空间互易性检验，验证了我们的半解析解、数值模拟方法以及相应程序代码的正确性和可靠性，随后我们开展了敏感度分析和垂直地震剖面模型的数值模拟.

图 10 三层模型(中间层为动力协调介质)的数值模拟结果 Fig. 10 Numerical simulation results of the three-layer model with the intermediate layer satisfying the dynamic compatibility condition

我们关于爆炸点源在界面上产生的反射波场对界面处参数变化的敏感度分析表明：固体骨架体积模量Kd、固体体积模量Ks和流体体积模量Kf的变化仅产生PP反射波而不会激发PSV反射波，孔隙度φ、固体密度ρs、流体密度ρf、固体骨架剪切模量G、达西渗透率κ0和流体黏度η的变化同时影响PP反射波和PSV反射波；总体上来说，上下两层介质参数差异越大，所产生的反射波场振幅也越大，而下层介质参数增大和减小时产生的反射波场的振动方向刚好完全相反，因此，我们有可能能够利用反射波场来检测孔隙介质参数的变化；反射波场对达西渗透率κ0和流体黏度η的敏感度相对较低，因此可以考虑利用例如井中斯通利波(Tang and Chen， 1996)、动电效应(Pride，1994; Haartsen and Pride， 1997; Garambois and Dietrich， 2002; Ren et al., 2012)等的一些其他手段进行弥补.在垂直地震剖面模型的数值模拟中，我们发现无论是固相位移、渗流位移还是孔隙流体压力，均能很好地反映孔隙介质性质的变化.我们还考察了动力协调孔隙介质这一特殊情况，在其中不会产生伴随快速纵波(即我们通常所说的地震纵波)的渗流位移，这提示我们，如果要观测渗流位移或者是与其相关的物理场，例如，由动电效应所产生的同震电场，那我们布设观测点的时候应该尽量避开接近动力协调条件的地区，否者将无法记录到地震纵波产生的同震电场(高永新和胡恒山，2009).

我们发展的基于半解析解的数值模拟方法为三维层状孔隙介质弹性波场传播特征的研究提供了一种可供选择的有效工具和手段，它可以为有限差分和有限元等其他数值方法提供对比和检验.LAC广义反透射方法在合成理论地震图的研究中已经被证实具有稳定、高效且适用范围较广的优点(Luco and Apsel， 1983; Chen， 1993，2007; Martin and Thomson， 1997; Ge and Chen， 2008)，Chen(2007)、Ge和Chen(2008)利用LAC广义反透射方法开展了带不规则界面层状介质的数值模拟研究，同样地，我们在此提出的方法也可以推广到带不规则界面层状孔隙介质的情况.另一方面，为了能更好地与实际相吻合，国内外的专家学者发展了一些新的理论模型，Dvorkin和Nur(1993)用喷射流来描述局部流动效应，Pride和Berryman(2003a，2003b)以及Berryman(2006)发展了双重孔隙介质的理论和方法，Tang等(2012)发展了含孔隙和裂隙介质弹性波的统一理论，孔隙介质波动理论正在进一步地发展和被完善，而我们的方法也同样可以推广应用到新理论模型下的数值模拟研究中.

致谢 我们感谢三位审稿人认真仔细的审稿工作，他们提出的修改意见极具建设性且给予了极大的帮助.

参考文献
[1] Aki K, Richards P G. 1980. Quantitative Seismology, Theory and Methods. San Francisco CA: W. H. Freeman.
[2] Berryman J G. 2006. Effective medium theories for multicmponent poroelastic composites. J. Eng. Mech., 132(5): 529-531.
[3] Biot M A. 1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acoust. Soc. Am.  , 28(2): 168-178.
[4] Biot M A. 1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am.  , 28(2): 179-191.
[5] Biot M A. 1962. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys.  , 33(4): 1482-1498.
[6] Bouchon M. 1979. Discrete wave number representation of elastic wave fields in three-space dimensions. J. Geophys. Res.  , 84(B7): 3609-3614.
[7] Bouchon M. 1981. A simple method to calculate Green's functions for elastic layered media. Bull. Seismol. Soc. Am.  , 71(4): 959-971.
[8] Burridge R, Vargas C A. 1979. The fundamental solutions in dynamic poro-elasticity. Gerophys. J. R. Astr. Soc.  , 58(1): 61-90.
[9] Chen X F. 1993. A systematic and efficient method for computing seismic normal modes in layered half-space. Geophys. J. Int.  , 115(2): 391-409.
[10] Chen X F. 2007. Generation and propagation of seismic SH waves in multi-layered media with irregular interfaces.   Advances in Geophysics, 48: 191-264.
[11] Ding B Y, Fan L B, Wu J H. 1999. The Green function and wave field on two-phase saturated medium by concentrated force. ;Chinese J. Geophys.   (in Chinese), 42(6): 800-808.
[12] Ding B Y, Song X C, Yuan J H. 2009. The solution of Green function of fluid phase in two-phase saturated medium. Chinese J. Geophys. (in Chinese), 52(7): 1858-1866.
[13] Dvorkin J, Nur A. 1993. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms.   Geophysics, 58(4): 524-533.
[14] Gao Y X, Hu H S. 2009. Numerical simulation and analysis of seismoelectromagnetic wave fields excited by a point source in layered porous media. Chinese J. Geophys. (in Chinese), 52(8): 2093-2104.
[15] Garambois S, Dietrich M. 2002. Full waveform numerical simulations of seismoelectromagnetic wave conversions in fluid-saturated stratified porous media. J. Geophys. Res.  , 107(B7): ESE 5-1-ESE 5-18.
[16] Ge Z X, Chen X F. 2008. An efficient approach for simulating wave propagation with the boundary element method in multilayered media with irregular interfaces. Bull. Seism. Soc. Am.  , 98(6): 3007-3016.
[17] Haartsen M W, Pride S R. 1997. Electroseismic waves from point sources in layered media. J. Geophys. Res.  , 102(B11): 24745-24769.
[18] Hu H S, Wang K X, Liu J Q. 2002. Attenuation and dynamic compatibility of the fast compressional wave in porous medium. Chinese J. Computation Physics (in Chinese), 19(3): 203-207.
[19] Johnson D L, Koplik J, Dashen R. 1987. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J. Fluid Mech.  , 176(4): 379-402.
[20] Li N, Ren H X, Huang Q H, et al. 2014. An integral expression of elastic waves in 3D stratified porous media I: Theory. Chinese J. Geophys. (in Chinese),57(6): 1891-1899.
[21] Luco J E, Apsel R J. 1983. On the Green’s function for a layered half-space: Part I. Bull. Seism. Soc. Am.  , 73(4): 909-929.
[22] Martin B E, Thomson C J. 1997. Modelling surface waves in anisotropic structures II: Examples.   Physics of the Earth and Planetary Interiors, 103(3-4): 253-279.
[23] Norris A N. 1985. Radiation from a point source and scattering theory in a fluid saturated porous solid. J. Acoust. Soc. Amer.  , 77(6): 2012-2023.
[24] Pride S R. 1994. Governing equations for the coupled electromagnetic and acoustics of porous media. Phys. Rev. B.  , 50(21): 15678-15696.
[25] Pride S R, Haartsen M W. 1996. Electroseismic wave properties. J. Acoust. Soc. Am.  , 100(3): 1301-1315.
[26] Pride S R, Berryman J G. 2003a. Linear dynamics of double-porosity dual-permeability materials. I. Governing equations and acoustic attenuation. Phys. Rev.   E, 68(3): 036603.
[27] Pride S R, Berryman J G. 2003b. Linear dynamics of double-porosity dual-permeability materials. II. Fluid transport equations. Phys. Rev.   E, 68(3): 036604.
[28] Ren H X, Chen X F, Huang Q H. 2012. Numerical simulation of coseismic electromagnetic fields associated with seismic waves due to finite faulting in porous media. Geophys. J. Int.  , 188(3): 925-944.
[29] Tang X M, Chen C H. 1996. Fast inversion of formation permeability from stoneley wave logs using a simplified Biot-Rosenbaum model.   Geophysics, 61(3): 639-645.
[30] Tang X M, Chen X L, Xu X K. 2012. A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations.   Geophysics, 77(6): D245-D252.
[31] 丁伯阳, 樊良本, 吴建华. 1999. 两相饱和介质中的集中力点源位移场解与应用.   地球物理学报, 42(6): 800-808.
[32] 丁伯阳, 宋新初, 袁金华. 2009. 关于两相饱和介质中流相Green函数的解析解.   地球物理学报, 52(7): 1858-1866.
[33] 高永新, 胡恒山. 2009. 水平分层孔隙介质中点源激发的震电波场数值模拟及分析.   地球物理学报, 52(8): 2093-2104.
[34] 胡恒山, 王克协,刘家琦. 2002. 孔隙介质中快速纵波的衰减特征和动力协调现象.   计算物理, 19(3): 203-207.
[35] 李娜,任恒鑫,黄清华等. 2014. 三维层状孔隙介质中弹性波的一种积分表示 I: 理论.   地球物理学报,57(6): 1891-1899.