1 引言
近年来,随钻声波测井技术发展迅速,渐有替代常规的电缆声波测井的趋势(唐晓明和郑传汉,2004).关于随钻声波测井在均质地层的传播规律,国内外已进行了大量工作(Tang et al., 2002; 崔志文,2004; 苏远大等,2006; 王华等,2009).随钻声波测井在各向异性地层的模拟也取得了很大的进展(王瑞甲等,2012; 李希强等,2013).目前,随钻测井在非常规油气藏的勘探开发中应用也日益增大,已应用于页岩气的勘探开发(郝建飞等,2012).
在非常规油气勘探中,地层中发育的裂隙或裂缝会极大地影响弹性波的传播,为此,唐晓明(2011)提出一个描述含孔隙、裂隙地层的弹性波统一理论.Tang等(2012)进一步完善了该理论并将此应用于非常规的声波测井数据.陈雪莲和唐晓明(2012)将这一理论引入井孔声场中.模拟了不同裂隙参数下井孔中激发的模式波的频散曲线、衰减曲线、灵敏度及激发强度,并对多极子声源激发的全波 特征进行了分析.Chen等(2013)分析对比了孔裂隙地层电缆测井在井壁开孔与闭孔情况下的特征响应.
因此,研究随钻环境中的含孔隙、裂隙地层的声传播规律对非常规油气开发具有重要的意义.迄今为止,随钻环境下这方面的研究还未有报道.本文针对这一现状,模拟了随钻多极子波在低孔、低渗条件下裂隙发育地层的传播特征,并分析了声场在不同的孔隙流体下的响应.本文的工作为含孔隙、裂隙地层中的随钻声波测井数据解释和地层评价提供了理论依据.
2 随钻孔、裂隙介质井孔中的声场随钻声波测井时,钻铤占据了井中流体相当大的部分.声源则模拟为贴钻铤壁的环状多极子声源,源在钻铤及其内外的流体中,以及井外的地层中激发出沿井轴方向传播的声场.图 1给出了随钻声波测井模型的示意图.模型的界面有钻铤内流体与钻铤界面、钻铤与钻铤外流体界面、钻铤外流体界面与地层界面,三个界面据井眼中心轴距离分别为ra、rb、R.
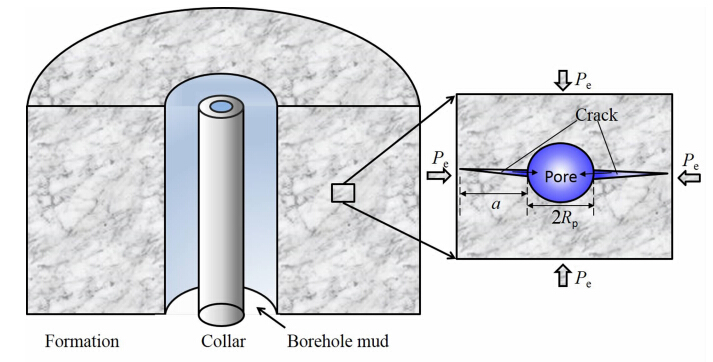 | 图 1 随钻声波测含孔隙、裂隙地层的物理模型Fig. 1 A pore-crack model for acoustic LWD |
2.1 钻铤内流体的声场
对于钻铤内的流体来讲,只有从外向内的入射波,而没有由内向外传播的波.采用柱坐标(r,θ,z),则钻铤内流体声场的位移势Φ′为
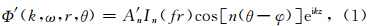
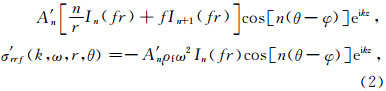
2.2 钻铤中的声场
钻铤中的纵波、SH横波、SV横波的位移势函数满足

考虑从内向外的出射波和由外向内的入射波,(3)式的解形式为
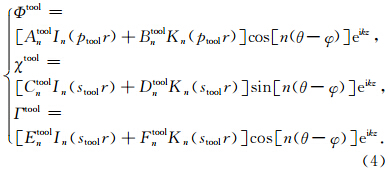
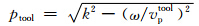 为钻铤纵波径向波数;
为钻铤纵波径向波数; 为钻铤横波径向波数;In和Kn分别为第一类和第二类n阶变形贝塞尔函数.Atooln(Btoon),Ctooln(Dtooln)和Etooln(Ftooln)分别是入射(出射)纵波,SH和SV横波的振幅系数.
为钻铤横波径向波数;In和Kn分别为第一类和第二类n阶变形贝塞尔函数.Atooln(Btoon),Ctooln(Dtooln)和Etooln(Ftooln)分别是入射(出射)纵波,SH和SV横波的振幅系数.求得位移应力表达式如下:
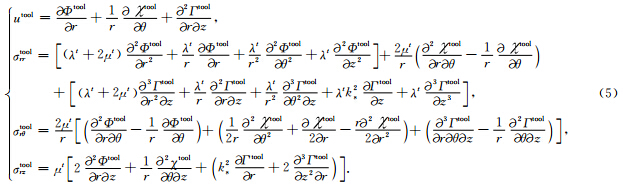
对于钻铤外的流体来讲,既有从外向内的入射波,也有由内向外传播的波,钻铤外流体的位移势Φ为
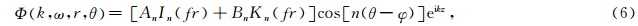
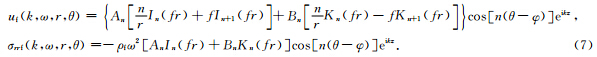
2.4 含孔隙、裂隙地层的弹性波动理论及声场
含孔隙、裂隙地层的应力位移的本构关系由下式给出(Tang et al., 2012):

 ,u是固体位移,w 是流体和固体的相对位移;eij是应变张量,且
,u是固体位移,w 是流体和固体的相对位移;eij是应变张量,且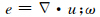 ;ω是角频率;α和β是由α=1-Kd/Ks和β=(α-)/Ks+/Kf分别给出的两个参数组合,其中φ为孔隙度,Ks和Kf分别是介质基质和孔隙流体的体积模量.函数S(ω)为描述裂隙和孔隙间的局部流动,即挤喷流效应.具体表达式如下:
;ω是角频率;α和β是由α=1-Kd/Ks和β=(α-)/Ks+/Kf分别给出的两个参数组合,其中φ为孔隙度,Ks和Kf分别是介质基质和孔隙流体的体积模量.函数S(ω)为描述裂隙和孔隙间的局部流动,即挤喷流效应.具体表达式如下:
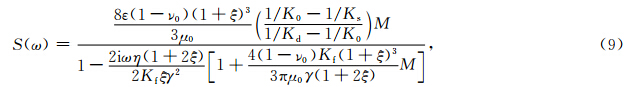
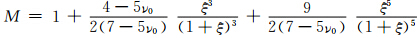 ;ξ为孔隙与裂隙的体积比,表达式为ξ=[3φ/(4πε)]1/3;η为孔隙流体黏度,ε是裂隙密度,γ是裂隙纵横比,μ0和ν0是没有挤喷流时背景介质的剪切模量和泊松比,这种情况下,μ和Kd可由Thomsen(1985)的Biot相恰理论计算得到.
;ξ为孔隙与裂隙的体积比,表达式为ξ=[3φ/(4πε)]1/3;η为孔隙流体黏度,ε是裂隙密度,γ是裂隙纵横比,μ0和ν0是没有挤喷流时背景介质的剪切模量和泊松比,这种情况下,μ和Kd可由Thomsen(1985)的Biot相恰理论计算得到.孔、裂隙介质中存在三种模式波,分别是快、慢纵波和横波,现引入这三种波的位移势,表示如下:
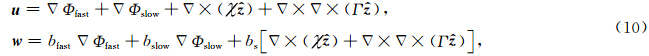
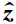 是沿井轴向的单位矢量.
是沿井轴向的单位矢量.对于井外的无限大孔、裂隙介质,由方程(8)到(10)可得到孔裂隙地层的应力和位移,其中(k,ω)域中的势函数表示如下(Chen et al., 2013):
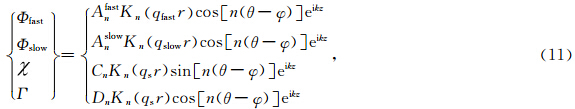

将方程(11)中的势函数表达为柱坐标下的形式,位移分量与孔隙压力和应力表示如下:
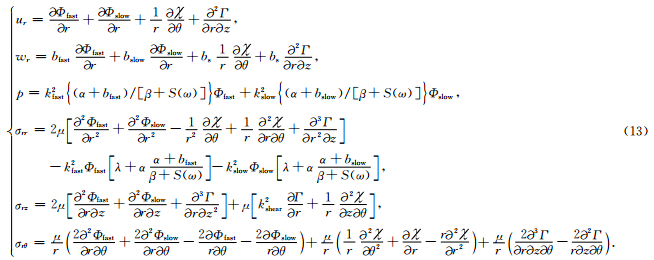
2.5 边界条件
以上理论给出了图 1所示模型各部分的声场,由界面处的边界条件衔接.计算声场时,在钻铤表面放置一环状多极子压力声源,以实现声场的激发.
2.5.1 钻铤内流体与钻铤界面: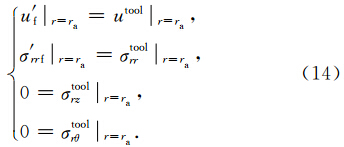
2.5.2 钻铤与钻铤外流体界面
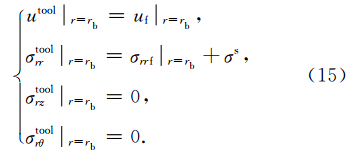

考虑井壁为开放孔隙的情况,即井中流体与孔隙中流体可以自由交换,此时井中压力与地层孔隙中的流体压力相等.这时井壁处的边界条件如下:
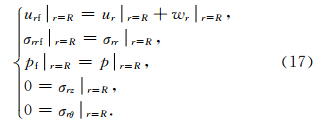
将(1)至(13)式中各部分声场的应力和位移用于(14)到(17)式的边界条件,得到以下矩阵方程:
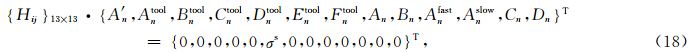
依照上述理论分析,我们对含孔隙、裂隙地层中的随钻多极子声波测井进行了数值模拟.表 1为模型的井内流体与钻铤的具体参数;地层为含孔隙、裂隙的无限大地层,本文模拟了不同的地层流体对声场的影响,表 2列出了两组孔裂隙流体参数.
| 表 1 井内流体与钻铤参数Table 1 Parameters of the fluid and the collar |
| 表 2 含孔隙、裂隙介质地层参数Table 2 Parameters of formation which contains pores and cracks |
本文主要针对模式波的频散曲线与衰减曲线进行探讨,模式波的频散特性主要由频散方程(18)决定,令式(18)矩阵的行列式为零,得出该频散方程:
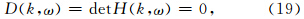
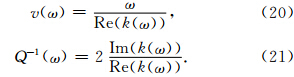
模式波的相速度与衰减对于某一模型参数q的灵敏度见下式(唐晓明和郑传汉,2004),其实质就是归一化后的相速度或衰减对该参数的偏微分.通过灵敏度分析可以探究不同频率条件下该参数对相速度或衰减的影响程度,有
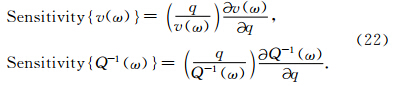
3.1 随钻单极子斯通利波
图 2是含水致密地层裂隙密度变化时,充液井孔中随钻单极子激发的钻铤外斯通利波的频散、衰减以及裂隙密度对相速度与衰减的灵敏度曲线.具体参数见表 1与表 2.当裂隙密度从0.00增大到0.25时,斯通利波相速度逐渐减小(图 2a),对应的衰减曲线逐渐增大(图 2b).斯通利波相速度对裂隙密度的灵敏度曲线随频率增大而减小(图 2c),说明致密地层的裂隙发育可以对斯通利波产生可观的影响.随着裂隙密度的增大,斯通利波的相速度与衰减对裂隙密度的灵敏度也会提高.
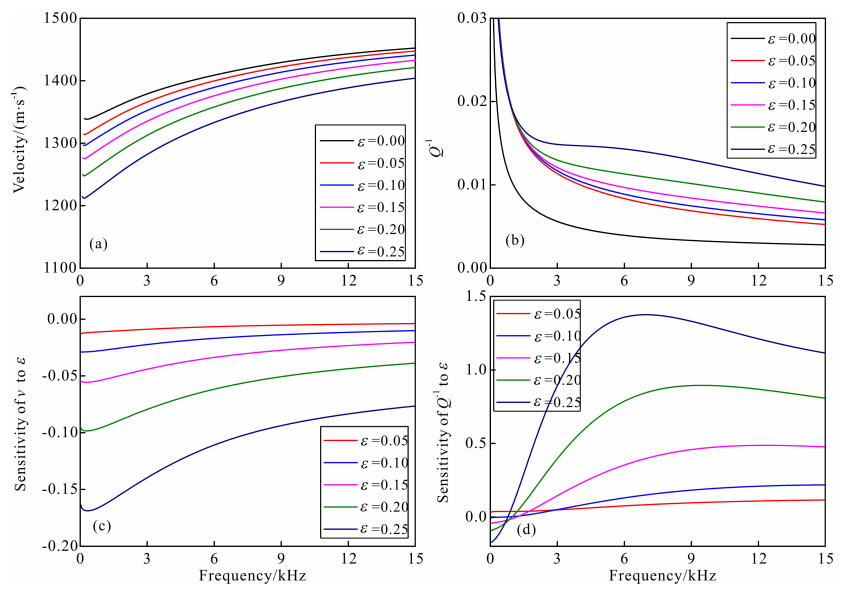 | 图 2 不同裂隙密度下的随钻单极子模拟(a)频散曲线;(b)衰减曲线;(c)速度灵敏度曲线;(d)衰减灵敏度曲线.Fig. 2 Simulation of LWD monopole for different crack density values(a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to ε;(d)Attenuation sensitivity to ε. |
孔裂隙理论所预示的流体灵敏度在地层的油气识别中有着重要的作用.为此,我们模拟了不同孔裂隙流体中含气饱和度下的变化规律.流体为水、气混合而成,混合后流体密度、模量和黏度的表达式为(Brie et al., 1995)
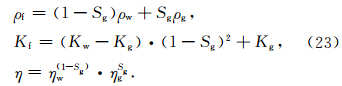
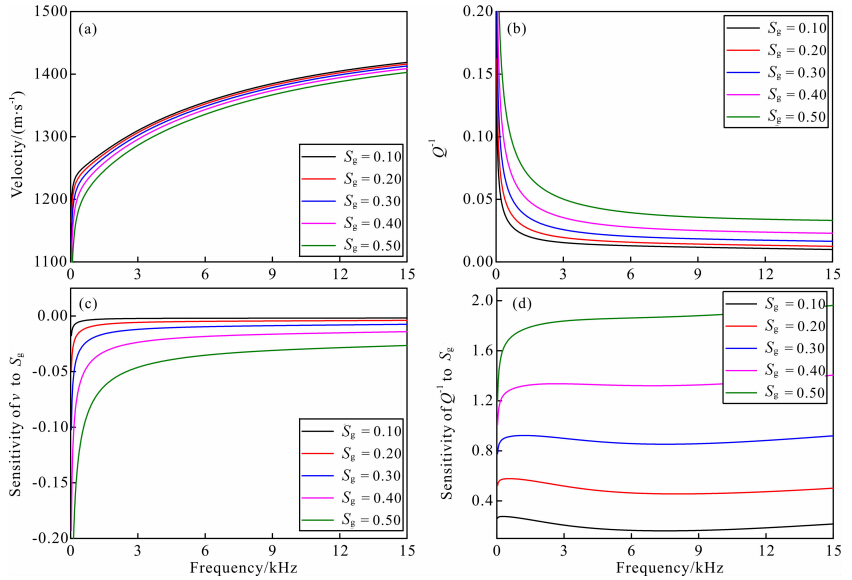 | 图 3 不同含气饱和度下的随钻单极子模拟(a)频散曲线;(b)衰减曲线;(c)速度灵敏度曲线;(d)衰减灵敏度曲线.Fig. 3 Simulation of LWD monopole for different gas saturations(a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to Sg;(d)Attenuation sensitivity to Sg. |
3.2 随钻偶极子模式波
式(18)中n=1对应的是偶极激发的情况,同样,我们模拟了随钻偶极子的响应特征.图 4是含水致密地层不同裂隙密度时随钻偶极子激发的弯曲波的频散、衰减以及灵敏度曲线.弯曲波相速度随裂隙密度的增加而减小(图 4a),与此相应的是衰减增加(图 4b).值得一提的是,低频处(3 kHz左右)随钻偶极的群速度有一极小值,群速度的极小值在波列中产生,称为“艾里相”(Airy Phase)的波包,且在此频段内的衰减极大值形成一个明显的脊峰.随着频率的增大,受井眼中钻铤的影响,速度的频散特性与电缆偶极相比变化较大.偶极子弯曲波速度对裂隙密度的灵敏度在艾里相频段剧烈减小,随着频率增大受钻铤的影响有所提高(图 4c).在常规的测井频段内,速度对裂隙密度的灵敏度恰好落在极小值区域,从这个角度上也说明了随钻偶极测井的缺点,即测井频段内的强烈频散以及对地层裂隙的低灵敏度.图 5表示不同的含气饱和度下充满液体井孔中偶极子弯曲波的特征响应.模拟表明,含气饱和度的增大会使得弯曲波速度减小,但变化不明显.衰减随着含气饱和度的增大而增加.
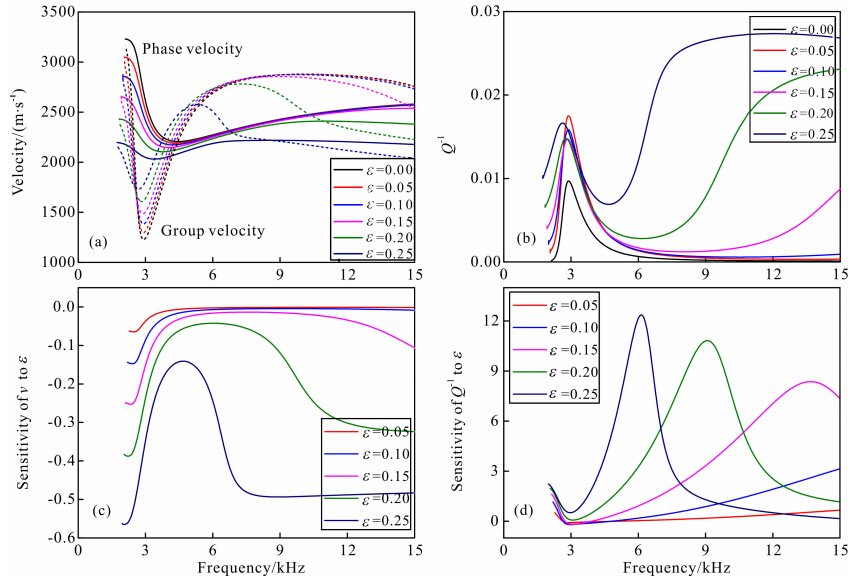 | 图 4 不同裂隙密度下的随钻偶极子模拟(a)频散曲线;(b)衰减曲线;(c)速度灵敏度曲线;(d)衰减灵敏度曲线.Fig. 4 Simulation of LWD dipole for different crack density values Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to ε;(d)Attenuation sensitivity to ε. |
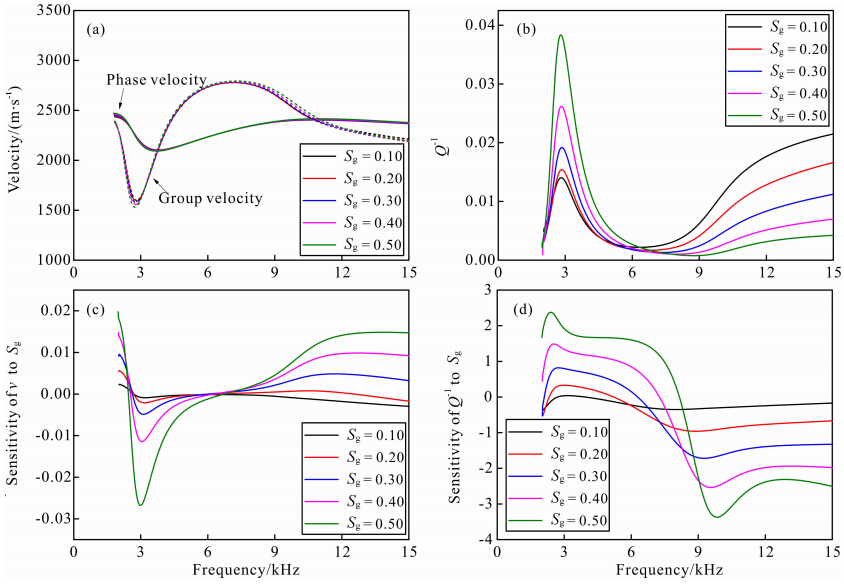 | 图 5 不同含气饱和度下的随钻偶极子模拟(a)频散曲线;(b)衰减曲线;(c)速度灵敏度曲线;(d)衰减灵敏度曲线.Fig. 5 Simulation of LWD dipole for different gas saturations(a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to Sg;(d)Attenuation sensitivity to Sg. |
3.3 随钻四极子模式波
式(18)中n=2对应的是四极激发的情况.鉴于四极子波已广泛应用于随钻横波测量(唐晓明和郑传汉,2004),对此情况的模拟尤为重要.图 6是含水致密地层不同裂隙密度时随钻四极子激发的螺旋波的频散、衰减、以及灵敏度曲线.裂隙密度的增大会使得四极子螺旋波相速度减小,而衰减增大.衰减曲线中的峰值区域对应着频散曲线的艾里相(图 6b)区域.随钻四极子波对不同裂隙密度和含气饱和度的变化特征与Chen等(2013)模拟的电缆偶极子变化规律很相似,说明了这类模式波(称为“低频相速度趋于横波波速”的横波型模式波)的一些共性.固定裂隙密度(ε=0.20),含气饱和度增大会使得四极子螺旋波相速度减小,衰减增大(图 7a、b).通过对含气饱和度灵敏的模拟,表明地层流体对衰减的影响很大.
 | 图 6 不同裂隙密度下的随钻四极子模拟(a)频散曲线;(b)衰减曲线;(c)速度灵敏度曲线;(d)衰减灵敏度曲线.Fig. 6 Simulation of LWD quadrupole for different crack density values(a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to ε;(d)Attenuation sensitivity to ε. |
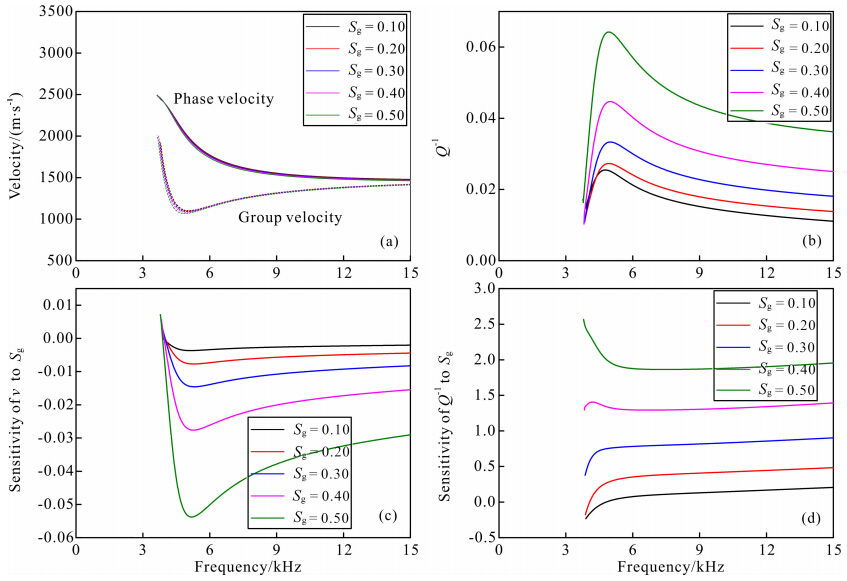 | 图 7 不同含气饱和度下的随钻四极子模拟(a)频散曲线;(b)衰减曲线;(c)速度灵敏度曲线;(d)衰减灵敏度曲线.Fig. 7 Simulation of LWD quadrupole for different gas saturation(a)Phase velocity dispersion curves;(b)Attenuation curves;(c)Velocity sensitivity to Sg;(d)Attenuation sensitivity to Sg. |
4 裂隙参数对随钻多极子波形的影响
随钻声波测井通常用单极子测量地层纵波和斯通利波,而用四极子测量横波信息(唐晓明和郑传汉,2004).为了研究随钻多极子声波在孔、裂隙地层中的传播特征,本文数值模拟了随钻单极子和四极子的波形.数值模拟所用地层及仪器参数由表 1、2中给出.
4.1 随钻单极子波形特征随钻单极子数值模拟时,源距为5 m.数值模拟采用高斯源加载于钻铤外壁,见文献(崔志文,2004),主频为9 kHz.图 8给出了不同裂隙密度下随钻单极子全波波形对比.黑线表示地层流体完全含水,红线表示地层百分百含气.在全波列中,有钻铤拉伸波、P波、S波和ST波模式,由于横波和斯通利波能量主导,我们将钻铤波和地层纵波幅度放大100倍来加以显示.由于地层很致密,地层纵波与钻铤波由于速度相近,叠加在一起,为了区分两者,在理论模拟时加大了钻铤波的衰减(Q=5),以此来模拟实际随钻声波仪器中隔声体的作用.为了方便对比,我们将裂隙密度为0和0.25影响下的波形起跳点连接起来.模拟表明,裂隙密度增大时,地层含气和含水情况下地层纵波、横波与斯通利波速度减小,幅度降低,钻铤波不受裂隙密度的影响.且斯通利波幅度减小,也就是说衰减会随裂隙密度增大而增大.红线与黑线对比可知,当地层流体性质发生变化,即地层含气时,流体的可压缩性变大,使得体积模量减小,孔、裂隙地层的纵波速度减小,在波形上表现为波至起跳点延迟,裂隙密度越大该现象越明显.流体性质的改变基本不影响横波速度,但对斯通利波产生巨大的衰减变化.以上模拟表明,地层含气时,纵横波速比会降低,斯通利波会严重衰减.相对比横波,地层纵波在地层含气时也会产生相当程度的衰减.可利用该特性判断地层是否含气.
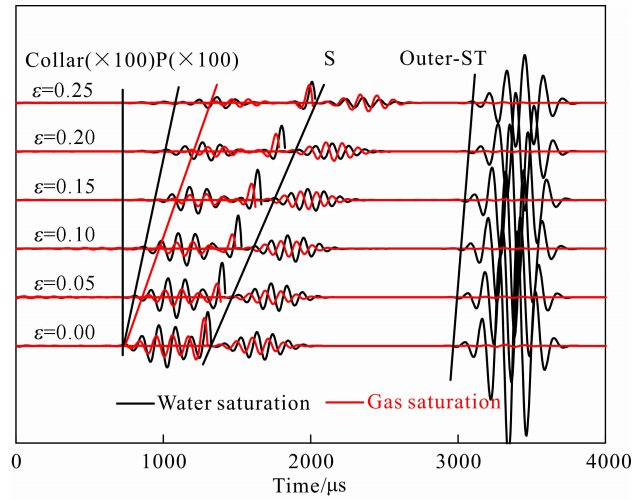 | 图 8 不同裂隙密度下随钻单极子波形模拟地层含水(黑线),地层含气(红线).Fig. 8 Simulation of LWD monopole waveform for different crack density values and saturation conditions for water(black) and gas(red) |
4.2 随钻四极子波形特征
图 9为孔裂隙地层随钻四极子声场模拟结果.源距为3 m,声源主频3 kHz.裂隙密度的增加会引起地层横波速度减小;对比地层含水和含气的模拟结果,黑线(水)与红线(气)起跳点一样,表明流体性质的变化不影响地层横波速度,这与随钻单极子模拟的结果吻合.值得注意的是,地层含气时,艾里相波的能量严重衰减,表明含气对具有艾里相的横波型导波衰减影响很大,图 7b与图 7d所对应的频域 模拟结果也证明了这一点.这与Chen等(2013)模拟的电缆偶极子波的变化规律很相似,可以将此现象作为声波测井中此类模式波的一个共性来识别油气.
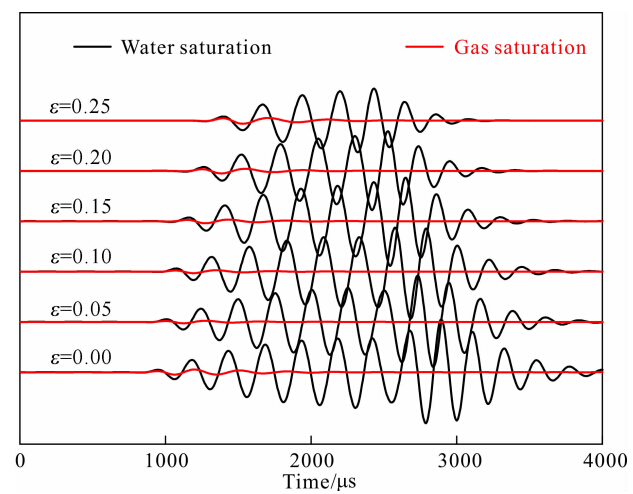 | 图 9 不同裂隙密度下随钻四极子波形模拟地层含水(黑线),地层含气(红线). Fig. 9 Simulation of LWD quadrupole waveform for different crack density values and saturation conditions for water(black) and gas(red) |
5 现场实例
在声波测井的解释中,通常利用纵波慢度与纵横波速度比的交汇图来识别地层流体.唐晓明(2011)对无限大地层含孔裂隙情况下的纵波慢度与纵横波速度比交汇图进行了详细的分析.
我们用一实测的随钻声波测井数据(仪器仅有单极采集模式)来验证本文的理论分析和模拟结果.图 10给出某快速地层的水平井的随钻声波数据.由于施工顺利,采集到了高质量的单极子阵列波形数据.图中第1道给出随钻单极子波形变密度显示.第2道给出了处理后的波形时差相关分析图.对单极子波形处理后得到地层的纵波(DTP)、横波(DTS)和斯通利波(DTST)时差曲线,在第3道画出.
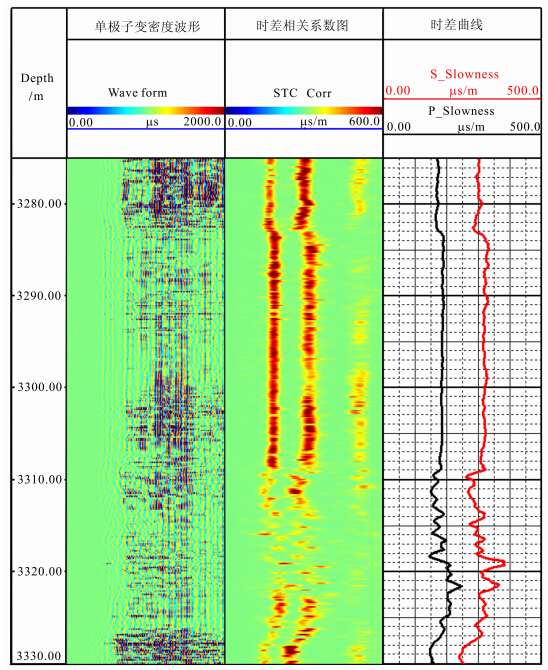 | 图 10 随钻孔裂隙地层现场实例Fig. 10 Field LWD data example |
图 11中绿点数据表示为井段3283~3309 m的时差数据,该井段是岩性一致的含气段,岩石中具有发育很好的裂隙,且裂隙密度变化不大,该井段斯通利波有明显衰减,与前述理论模拟(图 2,3)类似;用第3道中的时差数据做交汇图分析(见图 11),该井段的数据为图中绿点.含气饱和度不一导致该井段 纵横波速比变化.交汇图中橙点数据为3321~3324 m 的数据,该井段岩石含气饱和度高;其时差的剧烈变化反映了井段中裂隙密度(或发育度)的变化.
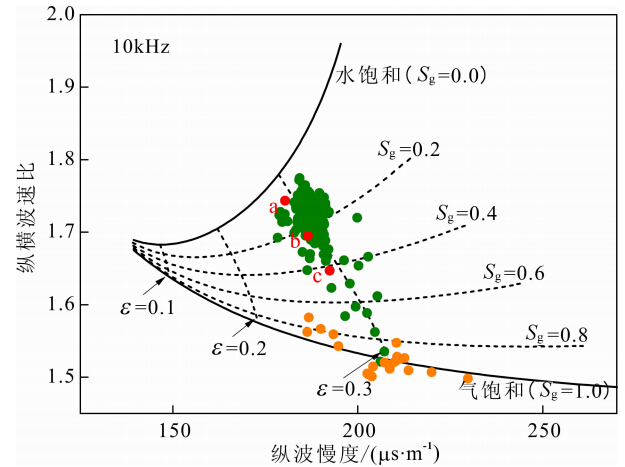 | 图 11 现场实例交汇图处理结果Fig. 11 A crossplot of VP/VS ratio versus compressional 11 slowness using a field LWD data |
作为一个例子,图 12给出含气饱和度不同时实际随钻单极子波形.我们从岩性一致的含气层段(3283~3309 m)找出三个点:a(3308.30 m)、b(3295.35 m)和c(3286.51 m).从交汇图可以看出,a、b、c三点的含气饱和度依次增大(图 11).在波形上体现的特征为纵波速度降低、幅度依次减小,而横波速度与幅度基本不变.众所周知,页岩的孔隙度一般在10%以下,按常规孔隙弹性波理论难以解释上述波形的变化特征.图 12的结果表明,当地层裂隙或裂缝发育程度高,含气饱和度变化时,在实际随钻波形中仍有明显的变化特征,与孔隙、裂隙介质弹性波理论相符.这些波形特征可以应用在页岩气的勘探和开发.
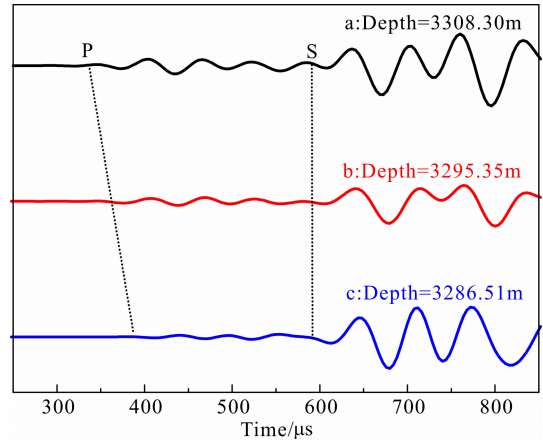 | 图 12 实际数据含气饱和度不同层段波形对比Fig. 12 Comparison of LWD monopole waveform data for different saturation conditions |
6 结论
本文通过对孔裂隙介质中随钻声波的频散、衰减以及波形的数值计算,对比分析了裂隙密度与含气饱和度对斯通利波、弯曲波、螺旋波以及接收到地层纵横波的影响,得到以下结论:
(1)在单极子随钻测井中,孔隙、裂隙并存的致密地层中的斯通利波速度对裂隙非常敏感,衰减对含气饱和度更加敏感;
(2)随钻偶极子低频或随钻四极子群速度极小值处对应着波列的“艾里相”,对应着衰减的峰值,在波形中显示为与艾里振相相关的能量大大落后于波的初至,含气影响导致振幅衰减很大,此现象可作为声波测井的一个标准来判断地层是否含气;
(3)地层中裂隙密度和含气饱和度的变化使测得的纵横波速产生可观的变化,可用于纵横波速比与纵波时差的交汇图分析,分析结果与理论预示一致.
致谢 感谢两位匿名审稿专家提出的宝贵意见和建设性建议,对本文的修改和提高很有助益.
附录
现给出(18)式矩阵H= 中的各个元素的表达式.为节省篇幅,我们采用以下符号来表示贝塞尔函数的组合:
中的各个元素的表达式.为节省篇幅,我们采用以下符号来表示贝塞尔函数的组合:
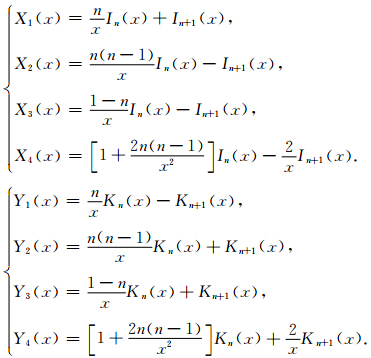
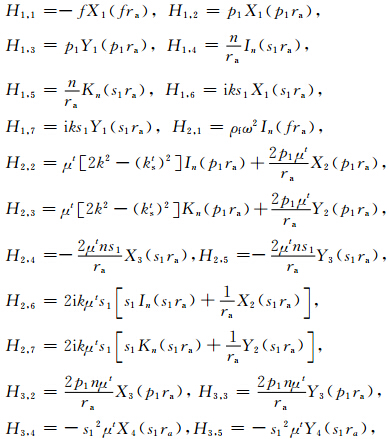

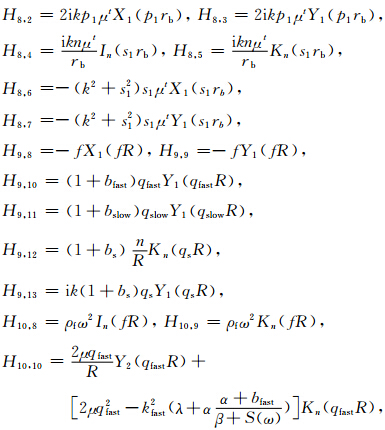
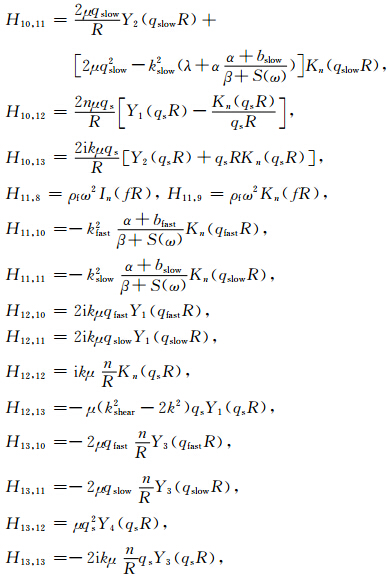
| [1] | Brie A, Pampuri F, Marsala A F, et al. 1995. Shear sonic interpretation in gas-bearing sands. SPE Annual Technical Conference and Exhibition, 701-710. |
| [2] | Chen X L, Tang X M. 2012. Numerical study on the characteristics of acoustic logging response in the fluid-filled borehole embedded in crack-porous medium. Chinese J. Geophysics. (in Chinese), 55(6): 2139-2140. |
| [3] | Chen X L, Tang X M, Qian Y P. 2013. Simulation of multipole acoustic logging in cracked porous formations. Geophysics, 79(1): D1-D10. |
| [4] | Cui Z W. 2004. Theoretical and numerical study of modified Biot's models, acous to electric well logging and acoustic logging while drilling excited by multipole acoustic source(in Chinese). Changchun: Jilin University. |
| [5] | Hao Jian-fei, Zhou Can-can, Li Xia, et al. 2012. Summary of shale gas evaluation applying geophysical logging. Progress in Geophysics, 27(4): 1624-1632. |
| [6] | Li X Q, Chen H, He X, et al. 2013. Analyses on mode waves of acoustic logging while drilling in transversely isotropic formations. Chinese J. Geophysics. (in Chinese), 56(9): 3212-3222. |
| [7] | Su Y D, Sun J M, Fan Y R, et al. 2006. On numerical study of the LWD multipole source propagation characteristics in slow formation. Well Logging Technology, 30(3): 205-207. |
| [8] | Tang X M. 2011. A unified theory for elastic wave propagation through porous media containing cracks-An extension of Biot's poroelastic wave theory. Sci China Earth Sci, 41(6):784-795. |
| [9] | Tang X M, Chen X L, Xu X K. 2012. A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations. Geophysics, 77(6): D245-D252. |
| [10] | Tang X M, Qian Y P, Chen X L. 2013. Laboratory study of elastic wave theory for a cracked porous medium using ultrasonic velocity data of rock samples. Chinese J. Geophysics. (in Chinese), 56(12): 4226-4233 |
| [11] | Tang X M, Wang T, Patterson D. 2002. Multipole acoustic logging-while-drilling. 72nd Annual International Meeting, SEG, Expanded Abstracts, 364-368. |
| [12] | Tang X M, Zheng C H. 2004. Quantitative Borehole Acoustic Methods (in Chinese). Beijing: Petroleum Industry Press: 20-39. |
| [13] | Thomsen L. 1985. Biot-consistent elastic moduli of porous rocks;low-frequency limit. Geophysics, 50(12): 2797-2807. |
| [14] | Wang R J, Qiao W X, Ju X D. 2012. Numerical study of formation anisotropy evaluation using cross dipole acoustic LWD. Chinese J. Geophysics. (in Chinese), 55(11): 3870-3882. |
| [15] | Wang H, Tao G, Wang B, et al. 2009. Wave field simulation and data acquisition scheme analysis for LWD acoustic tool. Chinese J. Geophysics. (in Chinese), 52(9): 2402-2409. |
| [16] | 陈雪莲, 唐晓明. 2012. 孔、裂隙并存地层中的声波测井理论及多极子声场特征. 地球物理学报, 55(6): 2139-2140. |
| [17] | 崔志文. 2004. 多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究[博士论文]. 长春: 吉林大学. |
| [18] | 郝建飞, 周灿灿, 李霞等. 2012. 页岩气地球物理测井评价综述. 地球物理学进展, 27(4): 1624-1632. |
| [19] | 李希强, 陈浩, 何晓等. 2013. 横向各向同性地层中随钻声波测井模式波分析. 地球物理学报, 56(9): 3212-3222. |
| [20] | 苏远大, 孙建孟, 范宜仁等. 2006. 基于软地层随钻多极子声源传播特性的数值研究. 测井技术, 30(3): 205-207. |
| [21] | 唐晓明. 2011. 含孔隙、裂隙介质弹性波动的统一理论-Biot理论的推广. 中国科学 地球科学, 41(6): 784-795. |
| [22] | 唐晓明, 钱玉萍, 陈雪莲. 2013. 孔隙、裂隙介质弹性波理论的实验研究. 地球物理学报, 56(12): 4226-4233, doi: 10.6038/cjg20131225. |
| [23] | 唐晓明, 郑传汉. 2004. 定量测井声学. 赵晓敏译. 北京: 石油工业出版社: 20-39. |
| [24] | 王瑞甲, 乔文孝, 鞠晓东. 2012. 利用随钻正交偶极子声波测井评价地层各向异性的数值研究. 地球物理学报, 55(11): 3870-3882. |
| [25] | 王华, 陶果, 王兵等. 2009. 多极子随钻声波测井波场模拟与采集模式分析. 地球物理学报, 52(9): 2402-2409. |
 2014, Vol. 57
2014, Vol. 57


