1 引言

通常情况下，油气和水的储层表现为孔隙介质，因此孔隙介质理论在地球物理勘探、地震工程和岩土动力学等领域有着广泛的应用.Biot的研究(Biot， 1956a，1956b，1962)建立了流体饱和孔隙介质中的弹性波传播理论，该理论指出，在孔隙介质中存在三种波，快速P波、慢速P波和S波，其中慢速P波的存在是孔隙介质特有的现象.Burridge and Keller(1981)从微观结构出发，导出了孔隙介质的运动学方程，当孔隙流体的无量纲黏度很小时，该方程与Biot理论完全一致.Plona(1980)用实验方法证实了孔隙介质中确实存在慢速P波.后人的研究(Levy，1979; Pride et al., 1992; Pride and Berryman， 1998)也为Biot理论提供了进一步的佐证，所以Biot理论现在被广泛地应用于孔隙介质弹性波场的研究.

孔隙介质中的弹性波场受孔隙度、渗透率、流体黏滞系数等参数的影响，因此研究波场的传播特征将有助于分析和提取这些信息.de Boer等(1993)仔细地分析了流体饱和孔隙介质的波场控制方程，用Laplace变换方法得到了时间域的一维解析解，并给出了加载源项分别为正弦函数、阶跃函数和脉冲函数的结果.Dominguez(1991)利用孔隙介质控制方程与热弹性控制方程在简谐点源作用下可比拟的特征，给出了频率域的二维基本解.Gupta等(2013)用一种解析的方法研究了刚性边界条件下各向异性的孔隙地层中Love波的传播特征，并讨论了孔隙度、各向异性、不均匀性和初始应力对相速度的影响.AI Rjoub(2013)研究了含黏性流体的半空间孔隙介质中P波入射所产生的表面应变、应力和能量分布的变化.丁伯阳等(1999，2009)基于Biot理论，给出了双相饱和介质中集中力点源作用下的Green函数解析解.申义庆和杨顶辉(2004)以兼顾了Biot流动和喷射流动的Biot-Squirt(BISQ)模型为基础，研究了弹性波在孔隙各向同性介质中的传播速度及与流体的Biot流动和喷射流动力学机制的关系，并给出了位移场的Green函数.唐晓明(2011)在Biot理论的基础上，具体分析了裂隙在弹性波动下的挤喷流效应，导出了一个描述孔隙、裂隙并存时的弹性波统一理论.国内外的专家学者开展了很多细致的研究工作，然而在实际应用中还存在一些问题，例如，实际地球岩石孔隙介质中弹性波波速的衰减和频散问题(张显文等，2010; Dvorkin and Nur， 1993; Tang et al., 2012)，所以进一步的研究工作有待展开.

正演的数值模拟是研究波场传播特征的有效工具和手段，可为实际应用提供重要的指导和借鉴，同时也是介质参数反演工作的基础.基于有限元和有限差分方法，很多工作开展了孔隙介质弹性波场的数值模拟研究(Masson et al., 2006; Guan et al., 2009; Zhang，1999; Carcione and Helle， 1999; Kang and Bolton， 1995; Panneton and Atalla， 1997; Rumpler et al., 2012).有限元和有限差分方法的优势在于可以处理复杂的介质模型，但是，它们需要的计算量也大，计算效率相对较低.而考虑到油气水储层常常呈现层状分布这一特征，本文在Biot理论的基础上，针对三维层状孔隙介质模型，利用在合成理论地震图的研究中已经被证实稳定、高效且适用范围较广的Luco-Apsel-Chen(LAC)广义反透射方法(Luco and Apsel， 1983; Chen， 1993，2007; Martin and Thomson， 1997; Ge and Chen， 2008; Ren et al., 2010，2012)，给出了弹性波场的一种积分形式的半解析解，基于该半解析解可以通过数值方法快速、准确地计算层状孔隙介质的理论波场，这给三维层状孔隙介质波场传播特征的理论数值模拟研究提供了一种新的途径和手段.

2 孔隙介质弹性波控制方程

根据Biot理论(Biot， 1956a，1956b，1962)，假定所有的波场都有e^-iωt的时间依赖关系，在均匀各向同性的流体饱和孔隙介质中，弹性波场的控制方程组可以表述如下：

其中，ω为圆频率，u和w 分别为固相位移和渗流位 移，τ 表示应力张量，P表示孔隙流体压力，f 表示作用在介质上的体力，I 表示单位矩阵，ρ=(1-φ)ρ_s+φρ_f表示介质平均密度，ρ_s和ρ_f分别代表介质的固相密度和孔隙流体密度，φ为孔隙度，η为流体黏度，κ为渗透率，G为固体骨架剪切模量，H、C和M为Biot定义的孔隙介质的弹性参数(Biot，1962)，它们与固相体积模量K_s、流体体积模量K_f以及排空流体后的固体骨架体积模量K_d存在如下的关系：

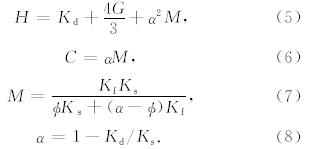
在频率足够高的情况下，孔隙介质的固体-流体边界存在黏性层，所以渗透率K与频率相关，是为动态渗透率.低频时，在黏滞性剪切力的作用下，孔隙中流体的流动剖面图在局部成抛物线形.高频时，除固体-流体分界面处的一个黏性边界薄层之外，惯性作用占主导地位，因此孔隙中流体的流动剖面图成塞子形状，而在黏性边界薄层之内仍然是剪切力占主导地位，这是因为在固体-流体分界面处的相对位移必然降为零.黏性边界薄层的厚度与频率的依赖关系为ω^-1/2，它随着频率的增加而减少.Johnson等(1987)通过一个复函数形式的表达式统一了低频和高频情况下的动态渗透率，其具体公式为

ω_J为临界频率，当频率达到该临界频率ω_J时，黏性边界薄层开始出现，其具体计算公式为

其中，κ₀为Darcy渗透率，α_∞为孔隙的弯曲度，n_J =φΛ²/(α_∞κ₀)是一个无量纲参数，Λ是加权孔隙体积和固相颗粒表面积的比值，对于砂岩，n_J可取为8，对于页岩，n_J远小于8.

3 层状模型下的通解

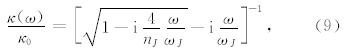
本文所考虑的是三维水平层状模型，共有N+1层.第j层的上下边界分别为平面z=z^(j-1)和z=z^(j)，底层为无限半空间，顶层可以是无限半空间，也可以是一个具有自由表面z=z⁽⁰⁾、厚度有限的层，源在第s层且该层不是无限半空间，即ss>1.我们将选用柱坐标系，z轴垂直于水平面，向下为其正方向.在本节，我们将用一套标量和矢量基函数对相关的物理量做展开，整理后得到基本的微分方程组，并给出该方程组的通解.

3.1 矢量和标量基函数

如公式(1)—(4)所示，描述孔隙介质弹性波传播的控制方程组中，既有标量场也有矢量场，我们将用一套标量和矢量基函数对相关的物理量做展开.

对于标量场，我们所用的基函数是柱坐标下的谐波函数

其中，m=0，±1，±2，…，J_m(kr)是m阶Bessel函数，则任意标量场例如B(r，θ，z)，可以做如下展开:

其中，b_m(k，z)是标量场B(r，θ，z)的展开系数，可以通过如下公式计算:

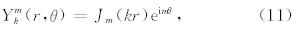
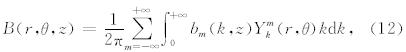
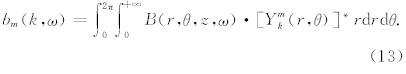
对于矢量场，我们使用如下的一套柱坐标矢量基函数:

其中 e _z表示z 方向的单位矢量，这是一套正交完备的基函数(Aki and Richards， 1980).因此，任意矢量场例如 A(r，θ，z)，可以做如下展开:

其中A_T，m，A_S，m和A_R，m是矢量场 A(r，θ，z)的展开系数.如果矢量场 A(r，θ，z)是已知的，则其展开系数可以通过如下公式计算:

其中，符号*表示复共轭，参数k在物理上对应波场的空间水平波数.

3.2 微分方程组

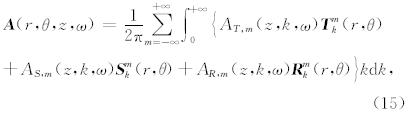
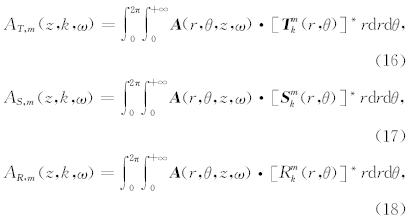
针对孔隙介质弹性波控制方程组，利用公式(12)对相应的标量物理场P做展开，利用公式(15)对相应的矢量物理场 u、w以及水平应力Q=τ · e _z 做展开，结合公式(14)所给出的矢量基函数的正交性(Aki and Richards， 1980)，整理后可以得到2套线性的微分方程组，分别对应SH波和PSV波.这2套方程组都可以写成如下形式:

其中j=1，2，…，N;δ_j，s是Kronecker delta函数，F(z)为源项.

矢量 y 对应SH波和PSV波的具体形式分别为

其中u_T，m、u_S，m和u_R，m为固相位移u的展开系数，w_R，m为渗流位移 w 的垂向分量的展开系数，Q_T，m、Q_S，m和Q_R，m为水平应力 Q = τ · e _z的展开系数，P_c为孔隙流体压力P的展开系数.将 y 写成由两个分向量组成的形式，即 y =[ y ₁ y ₂]^T，可以发现，不管是对于SH波还是PSV波，y ₁表示位移而 y ₂表示力.当所考虑的模型具有自由表面时，自由表面的应力为零，所以有

矩阵 A 包含了介质物性参数的信息.对于SH波，有

相关的参数为

从物理意义上来说，ρ_e是复数的有效渗流密度，由它控制孔隙介质中流体和固体的相对运动情况，而复数密度ρ_t与S波波速有关.

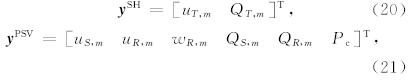
对于PSV波，6×6矩阵 A ^PSV可写成由4个3×3矩阵组成的形式:

其中，

相关的参数为

源项 F(z)对应SH波和PSV波的表达式分别为

由此可见，体力源 f 展开系数中的 f _T，m 这一项是激发产生SH波的真正原因，而PSV波由f_S，m和f_R，m这两项激发.将 F(z)写成由两个分向量组成的形式，即 F(z)=[ F ₁(z)F ₂(z)]^T，可以发现，不管是对于SH波还是PSV波，都有

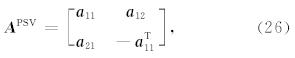
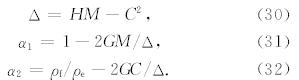
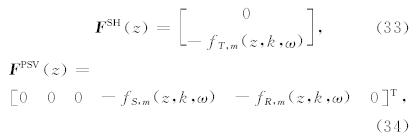
方程(19)中只包含了渗流位移 w 的垂向分量的展开系数w_R，m，而它的另外两个展开系数w_T，m和w_S，m 分别满足等式

因此，一旦我们得到了方程(19)的解，将u_T，m、u_S，m和P_c代入上述两个等式即可得到渗流位移 w 的另外两个展开系数的值.

3.3 通解

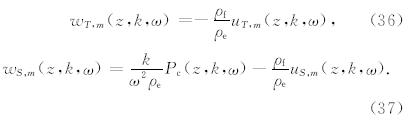
微分方程(19)的通解可以写成如下形式

其中，j=1，2，…，N+1.列向量 a ^(j)是我们将要求解的波场振幅，它由边界条件和介质的物理性质决定.矩阵 E ^(j)和对角矩阵 Λ ^(j)是关于矩阵 A ^(j) 的特征值分解:

其中γ_i是矩阵 A ^(j) 的特征值，它与波场的纵向波速相关，因为总是可能同时存在上行波与下行波，所以特征值总是成对出现的，即±γ_i.为了统一表述和便于理解其物理意义，我们定义Re(γ_i)>0，则公式(42)中的 Λ _d表示下行波，而公式(43)中的 Λ _u 表示上行波.

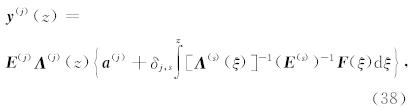
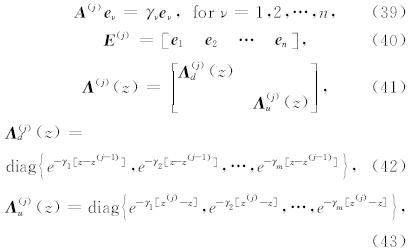
从数学上来说，2×2矩阵 A ^SH 的特征分解是比较容易的，而6×6矩阵 A ^PSV 的特征分解就比较复杂了.但是，当我们从物理意义的角度出发，通过分析不难发现，+iγ_i和-iγ_i实际上分别对应下行波和上行波的纵向波数，而特征向量对应相关展开系数的幅值之比，这无疑极大地简化了这里的特征分解问题.

对于2×2矩阵 A ^SH，有1对特征值±γ_s，对应S波，表达式为

其中s_s是S波的慢度(速度的倒数)，满足公式

在公式(42)和(43)中，令γ₁ =γ_s，则相应的特征向量矩阵为

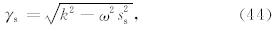
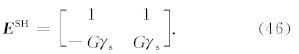
对于6×6矩阵 A ^PSV，有3对特征值±γ_s、±γ_pf和±γ_ps，分别对应S波、快速P波和慢速P波，γ_s满足公式(44)，γ_pf和γ_ps则满足

其中s_pf和s_ps分别是快速P波和慢速P波的慢度，满足公式

其中

在公式(42)和(43)中，令γ₁ =γ_s，γ₂=γ_pf，γ₃=γ_ps，则相应的特征向量矩阵为

其中，

3.4 通解的矩阵形式

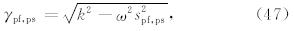
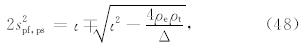
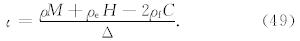
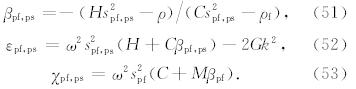
通解(38)写成矩阵的形式为

其中，下标d和下标u分别代表下行波和上行波所对应的项，E ₁₁、 E ₁₂、 E ₂₁和E ₂₂是矩阵 E 的子矩阵，对 于SH波它们就是单个元素，对于PSV波它们是3×3的矩阵.源项 b _d(z)和b _u(z)的表达式为

当j=1时，如果顶层是一个具有自由表面、厚度有限的层，公式(54)仍然成立，但是如果顶层是一个无限半空间，将不存在下行波，因此有

底层是无限半空间，不存在上行波，因此有

4 广义反透射方法

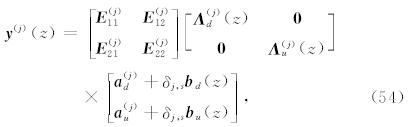
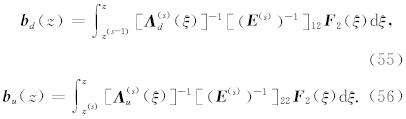
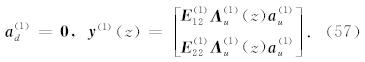
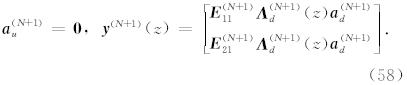
由公式(54)可知，只要我们确定了波场振幅 a _d和a _u，就可以确定 y ^(j)，得到相关波场函数的展开系 数.我们将采用LAC广义反透射方法(Luco and Apsel， 1983; Chen， 1993，2007; Martin and Thomson， 1997; Ge and Chen， 2008; Ren et al., 2010，2012)来计算波场振幅 a ^(j). 这一广义反透射方法最早由Luco and Apsel(1983)提出，Chen(1993，2007)进一步发展了该方法，因此Martin and Thomson(1997)将 其命名为Luco-Apsel-Chen(LAC)方法，并与Kennett(1983)方法进行了比较，证实LAC方法在计算效率和稳定性方面有优势.后来，Ge & Chen(2008)又提出了一种直接计算广义反透射系数的方法，进一步提高了该方法的计算效率.LAC广义反透射方法已经在合成理论地震图的研究中被证实是一种稳定、高效且适用范围较广的方法.

LAC广义反透射方法的核心思想，是将弹性波在界面上多次透射和反射的效果叠加，使其等效于在每个界面上只发生一次透射和反射的效果.对于源上方的界面，有广义的上行透射系数 T _u和反射系数 R _ud，相应的对于源下方的界面，有广义的下行透射系数 T _d和反射系数 R _du. 在下文中，我们将先给出LAC广义反透射系数的定义及其直接计算公式，然后我们将发现我们可以轻松地给出波场振幅 a _d和a _u 的计算公式.

4.1 LAC广义反透射系数的定义及其直接计算公式

对于源上方的界面z=z^(j)(其中j=1，2，…，s-1)，广义的上行透射系数 T _u和反射系数 R _ud 满足公式

在顶层，如果具有自由表面，则自由表面处的反射系数满足公式

当顶层为无限半空间时，因为没有下行波，所以有

对于源下方的界面z=z^(j)(其中j=s，s+1，…，N)，广义的下行透射系数 T _d和反射系数 R _du 满足公式

因为底层是无限半空间，不存在上行波，所以有

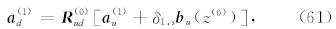
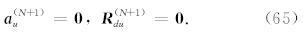
对于SH波而言，Λ _d、 Λ _u、 a _d、 a _u、 b _d(z)和b _u(z)实际上都是单个元素的矩阵，相应的广义反透射系数亦是如此；对于PSV波，Λ _d和Λ _u是3×3的矩阵，a _d、 a _u、 b _d(z)和b _u(z)是3×1的列向量，所以相应的广义反透射系数 T _u、 R _ud、 T _u和R _ud 都是3×3的矩阵.

由于固相位移、渗流位移的垂向分量、水平应力以及孔隙流体压力都是空间连续分布的，因此满足连续性边界条件，即

将广义反透射系数代入上式，整理可得，

其中，j=1，2，…，s-1，

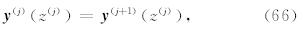
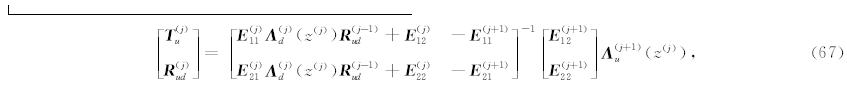
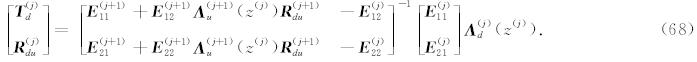
其中，j=s，s+1，…，N.

表达式(67)和(68)就是广义反透射系数的直接计算公式.很明显这是两组递推公式，我们需要知道 R ⁽⁰⁾_ud和R ^(N+1)_du的值，后者已经由公式(65)给出，前者在顶层是无限半空间时由公式(62)给出，而当顶层具有自由表面时，考虑到自由表面z=z⁽⁰⁾处应力为零，公式(22)成立，将式(61)代入可得

然后再通过两组递推公式，我们可以求得所有界面上的广义反透射系数.

4.2 确定波场振幅

一旦求得了广义反透射系数，我们就可以根据公式(59)、(60)、(63)和(64)很轻松地确定波场振幅 a _d和a _u，其具体公式如下：当j=1，2，…，s-1 时(即对于源上方的波场)，有

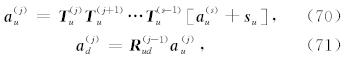
当j=s+1，s+2，…，N+1时(即对于源下方的波场)，有

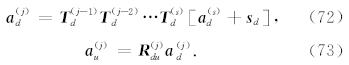
其中，

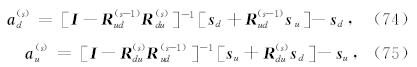
s _d= b _d(z^(s))，s _u= b _u(z^(s-1))，它们对应体力源 f 在 第s 层界面处直接产生的下行波场和上行波场的振幅.

5 半解析解

利用基函数对相关的物理场做展开之后，相应的公式都是频率波数域的，因此整理后即可得到固相位移 u 、渗流位移 w和孔隙流体压力P 在频率波数域的解(即其展开系数)：

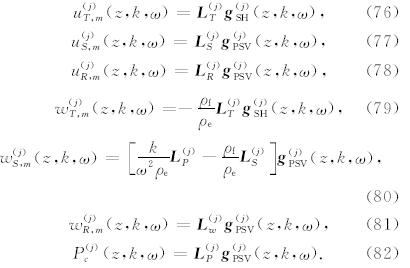
其中 L _T 是SH波对应的特征向量矩阵 E ^SH的第一行，L _S、 L _R、 L _w和L _P 分别是PSV波对应的特征向量矩阵 E ^PSV的第一行、第二行、第三行和第六行，如果 特征向量矩阵 E ^SH和E ^PSV分别取公式(46)和(50)的形式，则有

2×1列向量 g _SH和6×1列向量 g _PSV可以写成相同的形式：当z^(s-1)≤z≤z^(s)时，公式(76)—(82)中的上标j=s，有

当z＜z^(s-1)时，j＜s，有

当z＞z^(s)时，j＞s，有

其中，Λ _d(z，k，ω)和Λ _u(z，k，ω)满足公式(42)和(43)，a _d和a _u满足公式(74)和(75)，b _d(z，k，ω)和b _u(z，k，ω)满足公式(55)和(56)，s _d= b _d(z^(s))，s _u= b _u(z^(s-1))，广义反透射系数 T _u、 R _ud、 T _u和R _ud 由公式(67)和(68)给定，对应PSV波，它们是矩阵和向量，对应SH波，它们都是单个元素.

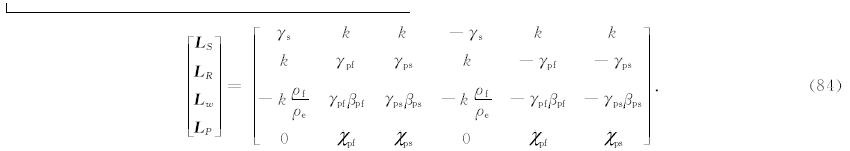
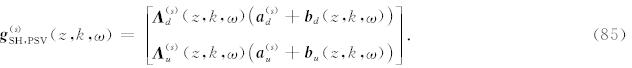
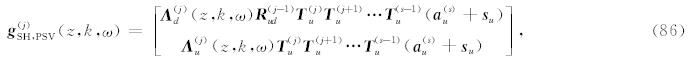
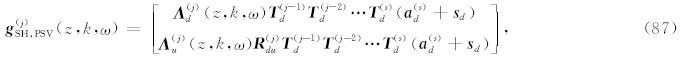
将公式(76)—(82)代入(15)和(12)，得到空间频率的解.固相位移 u 在柱坐标下的各个分量为

渗流位移 w 在柱坐标下的各个分量为

孔隙流体压力P为

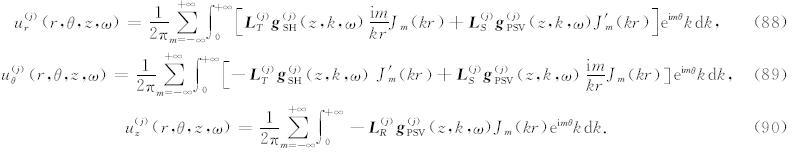
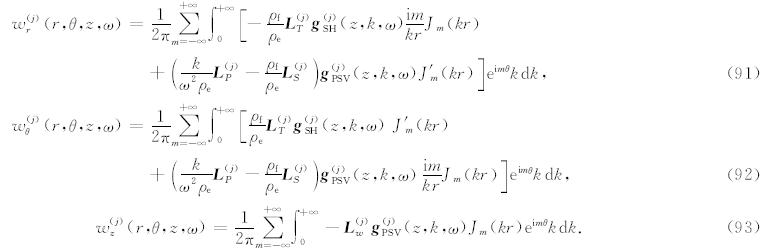
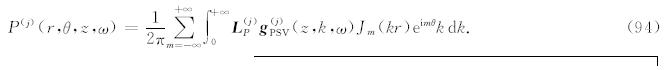
虽然从形式上来看，公式(88)—(94)都是m从-∞到∞的求和，但是，当我们取坐标系时，将源放置于z轴上，则对于单力点源和矩张量点源，实际上只需对|m|≤2进行求和即可，这是因为对于|m|＞2的情况，无论是单力点源还是矩张量点源，其展开系数均为零，所以源项 b _d(z)和b _u(z)为零，相应的波场展开系数也为零.

最后，进行从频率域到时间域的反Fourier变换，即可得到弹性波场在空间时间域的解.

6 结论

本文针对三维水平层状孔隙介质模型给出了固相位移 u 、渗流位移 w和孔隙流体压力P的积分形式的半解析解，它们是一组关于k 的积分公式.在过去的30多年中，如何快速有效地计算这类积分是地震学领域的一个经典问题.自然而然地，我们想到了数值积分方法，随着计算机性能的不断提高，这些积分表达式的数值计算也变得越来越快速准确和简单易行.通过对这些k积分的计算，我们可以得到层状孔隙介质中空间任意位置的理论波场，因此能够有效地分析波场的传播特征.

在下一篇文章中，我们将基于本文得到的半解析解进行数值模拟，验证我们理论公式的正确性，并且开展数值模拟实验，分析和讨论三维层状孔隙介质中弹性波场的一些传播特征.

致谢 我们感谢三位审稿人认真仔细的审稿工作，他们提出的修改意见极具建设性且给予了极大的帮助.