2. 武汉大学电子信息学院, 武汉 430072
2. College of Electronic Information, Wuhan University, Wuhan 430072, China
GRACE(Gravity Recovery And Climate Experiment)卫星是由美国国家航空航天局(NASA)和德国航空太空中心(DLR)联合研究和发射的“重力场重建与气候实验”卫星,主要科学目标是提供高精度和高空间分辨率的静态及时变地球重力场(Tapley et al., 2004).GRACE由两颗近圆形极轨卫星组成,在相同的轨道上前后跟飞,轨道倾角为89°,初始高度约500 km,卫星之间的距离约为180~220 km,于2002年3月17日发射升空,设计寿命为5年,实际已经运行了12年多,至今还在运行.
为了进行高精度重力场测算,GRACE星座装载有两星之间微波测距系统(KBR,K B and Ranging)和星载GPS双频接收机.微波测距数据中含有电离层的影响,电离层引起的载波相位超前所导致的测距误差需要消除;在消除电离层影响获取星间真实距离过程中,可提供电波传播路径上与积分电子密度有关的电离层修正量.本文介绍如何利用GRACE两颗卫星之间K波段载波相位测量和轨道数据,得到星间积分电子密度(TEC,Total Electron Content)和平均电子密度,并借助CHAMP 卫星的朗缪探针当地测量与GPS 掩星遥测得到的电子密度与等离子体垂直梯度标高(VSH,Vertical Scale Height)数据,消除所得平均电子密度固有的偏差.最后,通过与非相干散射雷达数据进行对比,以及从不同的时空变化角度,利用CHAMP当地测量数据,对所得多年的GRACE-A/B星间平均电子密度数据进行对比验证,证明其可靠性和可用价值. 2 GRACE星间微波测距系统简介
GRACE两颗卫星间的测距主要由星载精密微波测距系统(KBR)和双频GPS接收机来完成(Thomas,1999;Kim,2000),测距精度可达10微米.该系统是一个双向双频单程微波测距 系统,每颗卫星都装载有发射和接收K波段(24 GHz)和Ka波段(32 GHz)微波信号的喇叭形天线,两颗卫星上的天线互成镜像,接收对方发射的K/Ka波段双频微波信号,同时向另一颗卫星发射双频正弦型连续微波信号;有超稳振荡器(USO)提供高精度基准频率.为了区分相同频段的微波信号,其中一颗卫星相对另一颗卫星所发射的K/Ka波段信号的中 心频率都偏移0.5 MHz,即为24/32 GHz+0.5 MHz. 每个卫星接收到的信号经下变频混频后,通过GPS黑杰克(Blackjack)接收机的专用DSP通道反向旋转该变频信号相位,利用锁相环路跟踪和提取载波相位信息,以10 Hz的采样速率输出相位数据.图 1给出该系统的结构框图(Thomas,1999).
 |
图 1 GRACE卫星星间测距系统结构图(译自Thomas(1999)) Fig. 1 Block diagram for the K-B and Ranging system on-board GRACE(from Thomas,1999) |
每颗卫星接收到的K/Ka双频载波相位信号以及星载GPS信号发射到地面作进一步处理.图 2给出下传到地面的GRACE卫星KBR数据的处理流程框图(Thomas,1999).
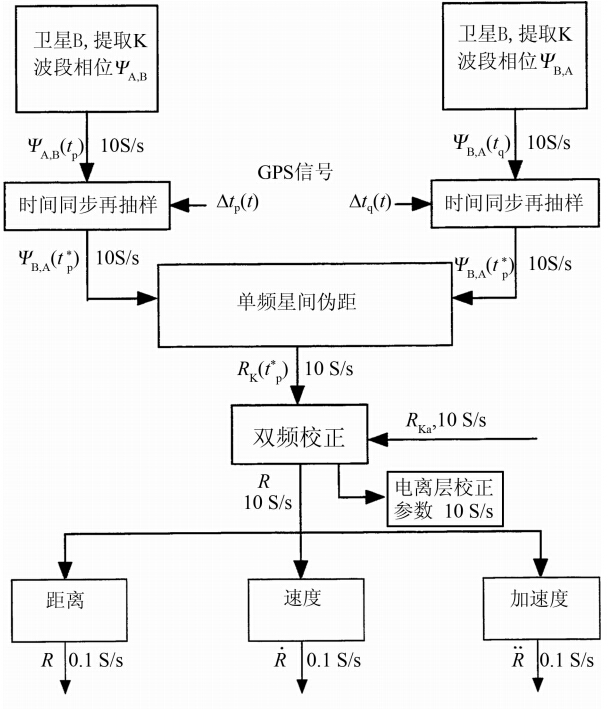 |
图 2 GRACE星间精密测距地面数据处理流程框图(译自Thomas(1999)) Fig. 2 Flow chart of the data processing system on the ground for precise ranging system of GRACE satellites (from Thomas,1999) |
如图 2所示,以K波段为例,卫星A和卫星B所接收并提取出的载波相位信号,分别利用GPS高精度时钟进行时间同步再抽样处理,然后将两卫星的同频段(相差0.5 MHz)两列微波信号相位相加,除以载波频率之和fKA+ fKB=(24 GHz+(24 GHz + 0.5 MHz)),乘以真空中光速c,便得到具有偏差的星间伪距,如公式(1)所示:
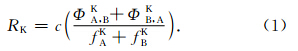
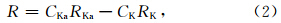
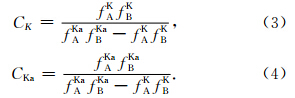
在消除电离层影响的同时可以得到含有电子密度信息的电离层校正参数,对于Ka频率,电离层校正参数如公式(5)所示:
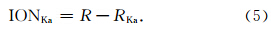
电离层校正参数在GRACE卫星的一级B类数据产品中提供(Case et al., 2002),第3节介绍由此校正参数得到星间平均电子密度的方法.
3 星间平均电子密度的获取 3.1 星间积分电子密度如第2节所介绍,在GRACE一级B类数据产品中,KBR1B提供了Ka波段上的电离层校正参数IONKa,由此可以计算两颗卫星之间水平电子总含量随时间的变化(星间TEC在依次相邻两时刻之差),如公式(6)所示(Case et al., 2002):
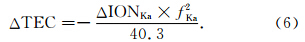
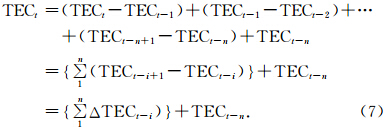
图 3给出了2003年1月份的前10天含有偏差的GRACE星间电子总含量.从图 3可以看出,所得到的GRACE星间电子总含量数据有比较频繁而剧烈的跳变,取值有正有负,最小与最大值相差近2×106TECU(即2×1022 el./m2),每段连续数据有各自不等的随机的整周模糊度偏差.纵观2002—2009年期间的数据,跳变出现的频率,有时一天会出现几次,有时连续几十天都没有;尽管相对而言比地面上接收GPS信号出现跳变的频率要低,但这种随意的跳变导致几乎提取不到有效的电离层参量信息.为了对长期大量数据进行处理,需要找到一种消除这种任意整周模糊度的有效方法.
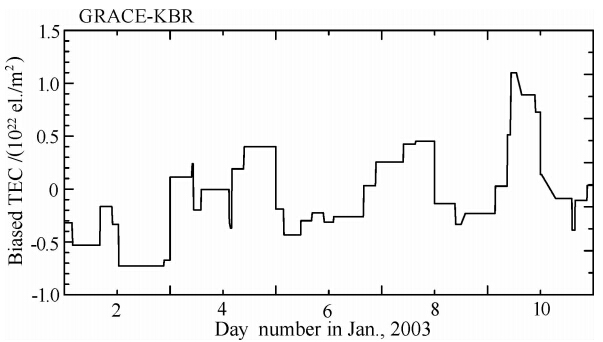 |
图 3 2003年1月1—10日含有整周模糊度等偏差的GRACE星间电子总含量 Fig. 3 Biased TEC containing integer cycle ambiguity between GRACE satellites on 1—10 Jan. 2003 |
如果微波测距得到的GRACE两颗卫星星间TEC在每个轨道上的极小值都小于一个整周相位所对应的TEC值,那么我们便可以将各连续测量段的TEC都加/减一个常数使每个连续段的最小值(它们含有任意大小的整周模糊度)都为零,这样处理后的数据将只具有小于一个整周模糊度的误差.
根据电离层电波传播理论,Ka和K波段双频差 分载波相位正比于星间电子总含量TEC,以f<sub>Ka=32 GHz=4×8 GHz和fK=24 GHz=3×8 GHz来计,一个整周相(π弧度)所对应的TEC大小为:
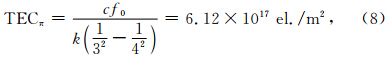
两颗卫星大多数时间都在顶部电离层飞行,GRACE轨道高度大于CHAMP卫星,通常情况下在大致相同的地方时与纬度处GRACE高度上的电子密度小于CHAMP.我们考察CHAMP卫星朗缪探针测量的电子密度沿每个轨道的极小值的分布特征,并藉此判断在GRACE高度上轨道电子密度极小值是否总小于上述估计的整周模糊度值3.06×1012 el./m3.
3.2.1 CHAMP轨道电子密度极小值的分布特征与GRACE卫星类似,CHAMP也是极轨卫星,轨道平面的倾角为87.3°,于2000年7月15日发射升空,轨道最初的高度为454 km,于2010年9月19日停止工作,共围绕地球飞行了58277圈.CHAMP和GRACE两星覆盖所有的地方时大约分别需要130天和160天.CHAMP卫星的朗缪探针主要提供电子密度和电子温度当地测量数据,电子密度测量范围为108~1012 el./m3,时间分辨率为15 s.在CHAMP飞行期间,提供了长达十年的可靠的电子密度测量数据.
通过对数据的观察发现,CHAMP卫星在一个轨道中电子密度的最小值一般出现在南北两半球的中纬槽区或极区,有时偶尔也会出现在夜晚赤道区.图 4给出2001和2009两年期间,CHAMP轨道电子密度极小值随Apex. 纬度的分布,这里只考虑了地理纬度高于±40°的情况.可以看出,南半球有两个极小值纬度带,一是中纬槽区,纬度约-60°(太阳 高年)至-65°(太阳低年),另一为极区极小值,纬度在-73°附近;而在北半球,除了中纬槽区电子密度极小值带,极区有两个电子密度极小值带,分别在70°和80°纬度附近(太阳高年)或75°和85°纬度附近(太阳低年).从图中可以看出,在太阳活动高年电子密度轨道极小值最大不超过1.0×1012 el./m3.为确切了解轨道极小值的取值情况,图 5给出2000— 2009年期间所有轨道电子密度极小值分布的直方图.
 |
图 4 CHAMP轨道电子密度极小值随磁纬的分布.(a)2001年;(b)2009年 Fig. 4 Distribution of orbital minimum electron density versus latitude from CHAMP observations during 2001(a) and 2009(b) |
由图 5可以清楚地看出,在CHAMP高度上,电子密度轨道极小值主要分布在109~1010 el./m3,极少超过1.0×1012 el./m3.我们可以推断,GRACE卫星轨道电子密度极小值几乎不可能超过1.0×1012 el./m3,此值对应GRACE星间电子总含量大约为200 km×1012 el./m3=2.0×1017 el./m2,相当于整周模糊度大小的0.3倍.
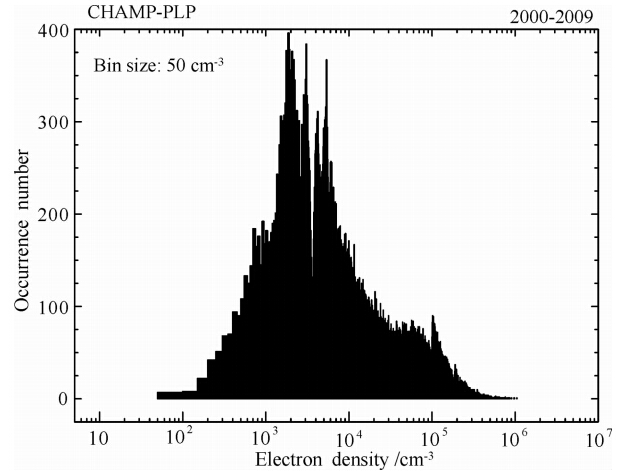 |
图 5 CHAMP轨道电子密度极小值的取值分布 Fig. 5 Occurrence rate histogram of the orbital minimum electron density from CHAMP |
根据3.2.1节的分析,我们采用轨道最小值零对齐法消除整周模糊度.对于每一段连续(可能包含多个轨道)的含有偏差的GRACE星间电子总含量TEC数据,先找到该段数据中的最小值,然后将该段连续的TEC数据减去这一最小值.通过这一方法,便可将多段不连续的含有偏差的电子总含量数据对齐至零附近.图 6给出用这种方法得到的2003年1月4日消除了整周模糊度的星间电子总含量.
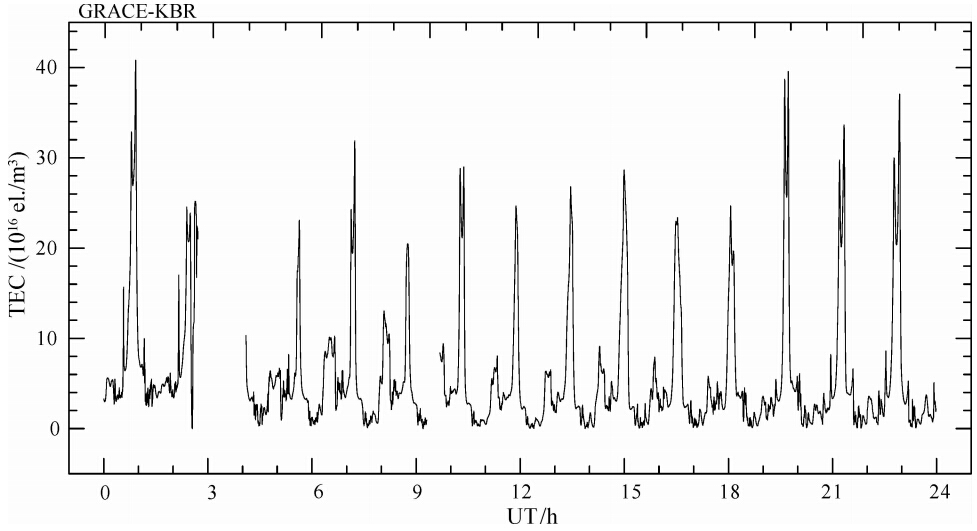 |
图 6 消除了整周模糊度后2003年1月4日星间电子总含量的变化 Fig. 6 Temporal variation of total electron content between the two satellites on 4 Jan. 2003 after integer cycle ambiguity eliminated |
根据3.2.1节所述的原理,这样处理后的数据不再含有大于一个整周的模糊度,但仍然含有由于未知初相、天线相位中心误差、以及零对齐处理引入的小误差等造成的偏差.
3.3 星间电子密度根据TEC的定义,若已知星间距离和星间电子总含量,可得到星间平均的电子密度:
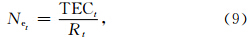
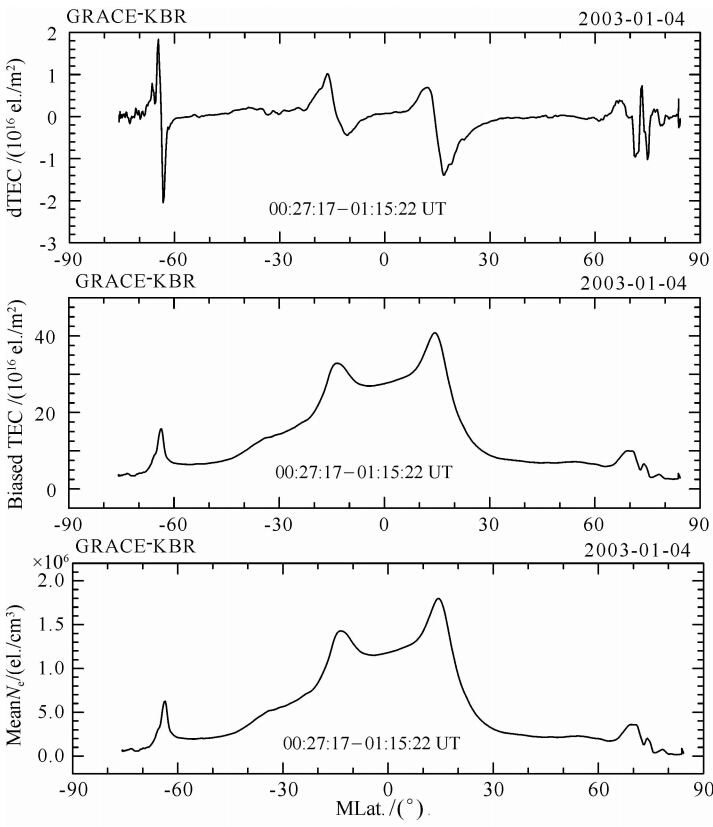 |
图 7 沿半个GRACE轨道计算得到的差分无偏星间ΔTEC(上),消除了整周模糊度的有偏星间TEC(中),以及相应的有偏星间平均电子密度(下) Fig. 7 Latitudinal variation of “Delta TEC” between GRACE-A and GRACE-B satellites computed along a half orbit(top),biased TEC with integer cycle ambiguity removed(middle) and corresponding biased mean Ne between the two satellites(bottom) |
下面介绍利用CHAMP/GPS掩星测量得到的顶部电离层的等离子体垂直梯度标高,由CHAMP轨道电子密度最小值,来估计GRACE高度电子密度极小,用以修正3.3节所述偏差的方法.
由于CHAMP和GRACE飞行轨道所处的地方 时(考虑升交点赤经)相重合的机会很少,在2002—2 009年期间只有4次,彼此相距在1小时之内的机会只在上述几个升交点赤经交会日的前后50天内,因此无法直接使用CHAMP卫星轨道电子密度最小值的个别观测值去修正GRACE轨道电子密度最小值,还考虑到在CHAMP卫星运行后期其高度有可能(虽然几率较小)会出现在F2峰附近或以下,以及在有扰动或F3层时电子密度高度剖面结构比较复杂的情况,我们利用轨道电子密度最小值的统计平均特性来进行修正.将CHAMP卫星在第i个轨道中观测到的电子密度最小值记为NeminCi,计算一年内所有卫星轨道中观测的电子密度的最小值的平均Nemin,称之为CHAMP卫星高度上的电子密度基值,如公式(9)所示: Nemin = 1 n ∑ n i=1 NeminCi,(10) 其中i为轨道序号,n为轨道数.将前述GRACE卫星连续数据段的最小值平移至零的电子密度数据,按照同样的方法可计算每一年内各个卫星轨道中观测的电子密度的最小值的平均,如公式(10)所示.值得注意的是,这里得到的GRACE卫星高度上的电子密度基值,Nemin bias,是有偏的.
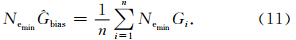
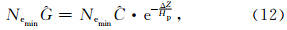
低轨道卫星LEO(如CHAMP等)对高轨道GPS卫星“升起/降落”期间信标信号的接收,称之为掩星(Occultation)接收;掩星接收事件期间,电波射线由高(或低)到低(或高)依次近似水平地穿过电离层,为获得电子密度高度剖面提供了一种新技术(Leitinger,1996). Stankov与Jakowski(2006a,2006b)曾利用2001年4月至2004年3月三年期间CHAMP卫星观测的GPS掩星数据,得到了顶部电离层等离子体垂直梯度标高,并分析了标高随季节、磁纬和地方时等因素变化的特征.他们的分析结果表明,在CHAMP/GRACE 卫星所在高度范围,等离子体垂直梯度标高随高度 的变化率比较小,处在比较稳定的状态,参看Stankov和Jakowski(2006b)的图 1,所以我们可以忽略卫星轨道高度变化对所采用标高值的影响,只取用大约 425 km高度的垂直梯度标高值.Stankov和Jakowski(2006b)的分析结果还表明,在扣除磁暴扰动情况下,由掩星数据得到的高纬区垂直梯度标高对太阳 活动性(以F10.7指数表征)的依赖较弱;在CHAMP/GRACE 卫星高度上,等离子体垂直梯度标高随季节、磁纬和地方时的不同而略有变化,变化范围为120~150 km,在磁纬±60°至±90°,该标高一般浮动在140 km上下.Liu等人(2007)利用1996—2002年半个太阳黑子周期的Arecibo非相干散射雷达的观测数据,分析得出低纬顶部电离层垂直梯度标高与太阳辐射指数P10.7近似呈线性关系,太阳活动水平越高,VSH越大.本文主要关心电子密度出现极小值的较高纬度,为了 简化,我们将公式(11)中的Hp取为常数值140 km.
利用这一垂直梯度标高值和CHAMP卫星高度上的基值,得到了GRACE卫星从2002年到2009年间每一年的电子密度基值,如图 8所示.将前面得到的GRACE卫星高度上的有偏电子密度基值Nemin bias与之进行比较,得到偏差修正值.图 8中的右下图给出消除偏差后的GRACE星间电子密度在一天中随时间的变化,左下图给出同一天CHAMP朗缪探针测量到的电子密度.
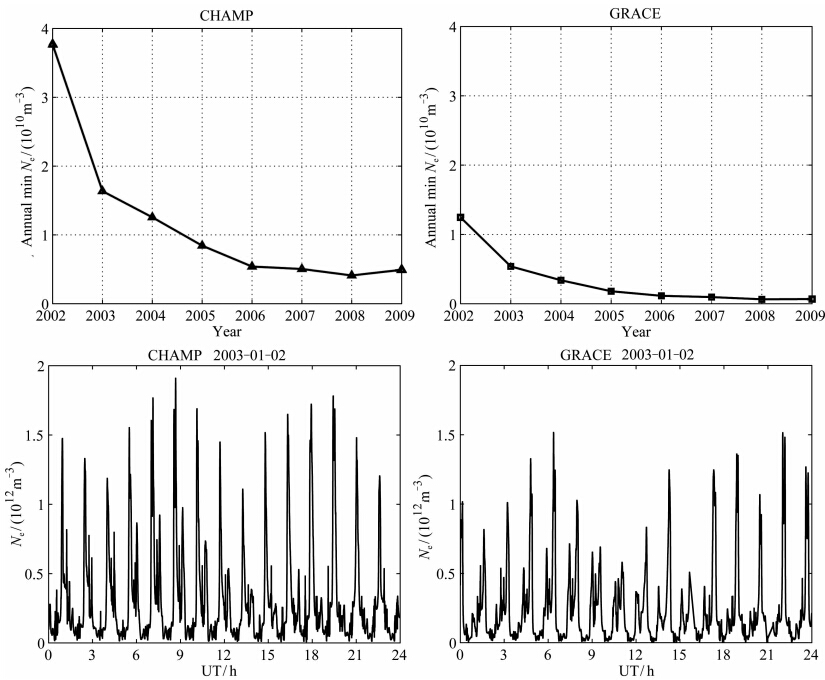 |
图 8 CHAMP高度上的电子密度基值(左上)与估计的GRACE高度上的电子密度基值(右上)逐年变化;在一天中CHAMP朗缪探针测量到的电子密度(左下)和消除偏差后的GRACE星间电子密度(右下) Fig. 8 Annual values of the minimum electron density from CHAMP every orbit(top left) and the derived annual values for GRACE(top right); Example of one day electron density observation from CHAMP(bottom left) and one day corrected electron density observation from GRACE(bottom right) |
为了验证本文得到的GRACE星间电子密度的可靠性,我们将消除偏差后GRACE星间电子密度 与Millstone Hill非相干散射雷达(地理纬度:42.62°,地理经度:288.51°)观测的电子密度数据作了对比. 我们选取了2002年4月—2009年1月期间,GRACE卫星过Millstone Hill上空,卫星和雷达同 时观测的电子密度数据,卫星的纬度限定在42.62°±1° 范围,经度限定在288.51°±5°.雷达所提供的时间分辨率为15 min,高度范围为100~548 km,高度间隔不等.对于每一次GRACE卫星过雷达上空,我们都选取了二者在时间上相隔最短,高度上距离最近的电子密度观测结果.
图 9给出了GRACE卫星和雷达同时观测的电子密度的对数的散点图以及卫星相对于雷达数据的相对偏差.从散点图 9a可以看出,二者之间具有很好的线性关系,相关系数达到0.97.从图 9b可以看出,本文所得到的GRACE星间电子密度在总体上要低于雷达观测结果,平均偏差为-7.28%,偏差的标准差为18.62%.
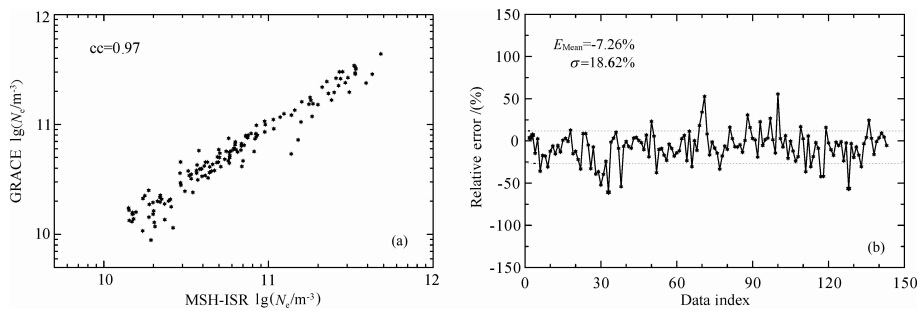 |
图 9 GRACE卫星星间电子密度和Millstone Hill非相干散射雷达观测结果的对比 (a)散点图;(b)GRACE星间电子密度对非相干散射雷达数据的偏差、偏差的平均值及标准差.灰色虚线之间的区域为正负一倍标准差内的区域. Fig. 9 Comparison between the corrected GRACE electron density data and incoherence scatter radar observations from Millstone Hill (a)Correlation coefficient;(b)The mean relative error and st and ard deviation. |
误差的来源有几个方面,首先我们采用了电子密度随高度指数衰减的近似,且使用了固定的等离子体垂直梯度标高,这将在由CHAMP卫星高度电子密度确定GRACE卫星高度上的电子密度基值时产生误差,特别是有较强扰动垂直梯度标高变大时会引起所计算的GRACE卫星高度上电子密度值偏小;第二,比较雷达与GRACE卫星电子密度数据时,数据点有一定的时间和空间位置差,引起二者电子密度值的偏差.但总的来说,这种大批量数据消除偏差的处理技术是可取的,所得到的长期大量的电子密度数据是基本可信的. 4.2 GRACE与CHAMP电子密度随经度和纬度全球分布的比较
为了进一步证明第3节中介绍的消除偏差后的GRACE卫星星间电子密度是可信的,我们对GRACE卫星与CHAMP卫星在近乎相同的地方时而高度不同的近圆极轨道上飞行的情况下,两颗卫星观测到的电子密度随经度和纬度的全球分布进行对比.在2005年4月6—10日期间,地磁活动水平较低,CHAMP和GRACE两颗卫星都飞行在 升/降交点地方时约为1230±0.5 LT和0030±0.5 LT的近圆极轨道上,两颗卫星飞行的平均高度分别约为360 km和470 km.图 10 给出了两颗卫星在这段时间内,向阳面(上图)和背阳面(下图)观测到的电子密度随地理经度和纬度的平均分布,图中白色的虚线代表磁倾角赤道.
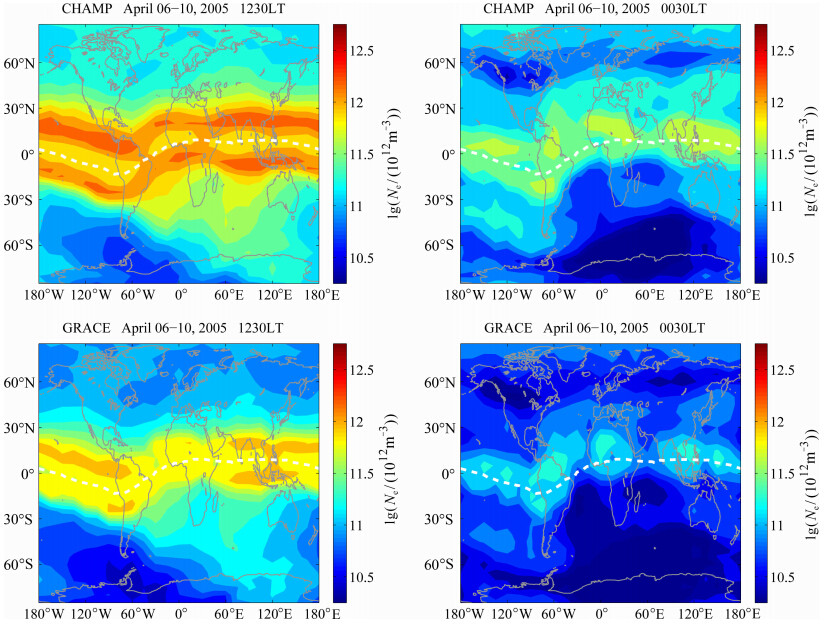 |
图 10 2005年4月6—10日CHAMP(左)和GRACE(右)两个卫星的轨道共面期间观测到的电子密度在向阳面(上)和背阳面(下)随地理经度和地理纬度的分布白色虚线为磁倾角赤道. Fig. 10 Global distribution of electron density versus geographic longitude and latitude observed from CHAMP(left) and GRACE(right)on dayside(top) and nightside(bottom)during their coplanar epoch on 6—10 April,2005 White dashed lines denote the magnetic dip equator. |
从图 10中可以看出,在1230 LT正午附近,在两颗卫星高度上观测到明显的赤道电离异常,电子密度关于磁磁道呈南北半球对称分布,赤道电离异常的峰区分别约为磁纬±17°和±13°.在两颗卫星高度上,电子密度的最小值均出现在南半球经度为90°W—0°的极区;同时在南半球地理纬度高于40°,地理经度为60°E—150°E的地方,电子密度要明显高于同一纬度的其他经度带.在0030 LT午夜附近,两颗卫星高度上均未观测到明显的赤道电离异常,电子密度仍然关于磁赤道在南北半球呈对称分布,磁赤道地区的电子密度要高于其他地区.赤道地区的电子密度随经度分布呈四波结构;在两颗卫星高度上,四波结构的电子密度波峰分别位于150°W、60°W、30°E和120°E.利用CHAMP卫星和修正后 的GRACE电子密度观测数据,Xiong等人(2013a),Xiong和Lühr(2013)对赤道电离异常随季节和地方时的变化,以及赤道地区电子密度随经度分布的四波结构进行了详细的分析.夜晚在北半球地理纬度约为60°的地方,两颗卫星同时观测到电子密度均小于周围的纬度,该电子密度的较小值可能和夜间电离层中纬槽有关(Xiong et al., 2013b).以上结果从某种角度显示了本文方法所得GRACE高度上电子密度数据的可信性. 5 结论
本文通过恰当处理GRACE-A/B两颗卫星K/Ka波段双频测距提供的电离层修正量和卫星轨道数据,计算得到了两颗卫星之间的平均电子密度;利用轨道电子密度极小值对应的星间电子总含量值远小于K/Ka波段相位测量的一个整周模糊度所对应的电子总含量这一特点,采用连续测量轨道电子密度极小值零对齐方法,消除了整周模糊度;并借助CHAMP卫星朗缪探针的电子密度当地测量和GPS掩星测量提供的电离层等离子体垂直梯度标高,大致消除了相位测量技术局限性所固有的未知偏差;从而得到长达十年之久的约500 km高度上 电离层电子密度数据.为了检验消除偏差后GRACE 星间电子密度数据的可靠性,对比了GRACE卫星观测的电子密度与卫星过Millstone Hill上空附近时,非相干散射雷达观测到的大致同时和相近位置的电子密度数据,对比结果显示GRACE卫星观测的电子密度相对于非相干散射雷达观测的电子密度的偏差平均为-7.26%,偏差的标准差为18.62%,证明了本文所得GRACE星间电子密度数据基本可信.为了进一步验证数据的可用价值,我们利用消除 偏差后的电子密度数据,对GRACE卫星与CHAMP 卫星在近乎相同的地方时而高度不同的近圆极轨道上飞行的情况下,两颗卫星观测到的电子密度随经度和纬度的全球分布进行了对比;对比分析表明,两颗卫星高度上电子密度的全球分布特征极为相似,所显示的电子密度大小的高度差异合理.从多种不同角度进行的对比检验,证明了本文方法得到的几乎连续10年的约500 km高度上全球电子密度数据基本可靠,为电离层气候学与天气学研究提供了宝贵资料.
应该指出,在修正测量偏差过程中,我们采用了电子密度随高度分布呈指数衰减的近似,且使用了固定的等离子体垂直梯度标高,这将会在利用CHAMP卫星高度电子密度和等离子垂直梯度标高来确定GRACE卫星高度上的电子密度基值的过程中产生误差,特别是对于存在较强扰动时,有可能垂直梯度标高增大(或减小)而导致计算所得到的GRACE卫星高度上电子密度值偏小(或偏大).在以后的工作中将进一步细致分析轨道电子密度基值以及垂直梯度标高随太阳活动水平、季节、地方时等变化的规律,以给出更为精准的修正.另一方面,本文利用非相干散射雷达数据来检验轨道极小值修正方法的效果,实际上也可以直接使用雷达观测数据来校准GRACE卫星星间有偏电子密度,这方面的工作及其与本文方法的比较将另文介绍.
致谢感谢德国地学研究中心提供CHAMP和GRACE卫星数据,感谢Hermann Luehr教授的帮助.本文所用的Millstone Hill 台站非相干散射雷 达数据,来自于MIT Haystack Observatory Madrigal 数据库; 感谢Dr. Shunrong Zhang(Millstone Hill)提供使用数据方面的协助;Millstone Hill 非相干散射雷达系由美国国家科学基金和MIT之间的合作项目所支持.
| [1] | Case K, Kruizinga G, Wu S. 2002. GRACE Level 1B Data Product User Handbook. JPL Publication D-22027. |
| [2] | Hargreaves J K. 1995. The Solar-Terrestrial Environment. Cambridge: Cambridge University Press. |
| [3] | Kim J. 2000. Simulation study of a low-low satellite-to-satellite tracking mission. Texas: Univ. of Texas at Austin. |
| [4] | Leitinger R. 1996. Tomography.// Kohl H, Ruester R, Schelegel K. Modern Ionospheric Science. ISBN3-9804862-1-4, Germany. |
| [5] | Liu L, Le H J, Wan W X, et al. 2007. An analysis of the scale heights in the lower topside ionosphere based on the Arecibo incoherent scatter radar measurements. J. Geophys. Res., 112(A6): A06307, doi: 10.1029/2007JA012250. |
| [6] | Stankov S M, Jakowski N. 2006a. Topside plasma scale height retrieved from radio occultation measurements. Adv. Space Res., 37(5): 958-962. |
| [7] | Stankov S M, Jakowski N. 2006b. Topside ionospheric scale height analysis and modelling based on radio occultation measurements. J. Atmos. Solar-Terr. Phys., 68(2): 134-162. |
| [8] | Tapley B D, Bettadpur S, Watkins M, et al. 2004. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett., 31(9): L09607, doi: 10.1029/2004GL019920. |
| [9] | Thomas J B. 1999. An Analysis of Gravity-Field Estimation Based on Inter-satellite Dual-1-Way Biased Ranging. JPL Publication, 98-15. |
| [10] | Xiong C, Lühr H. 2013. Nonmigrating tidal signatures in the magnitude and the inter-hemispheric asymmetry of the equatorial ionization anomaly. Ann. Geophys., 31(6): 1115-1130, doi:10.5194/angeo-31-1115-2013. |
| [11] | Xiong C, Lühr H, Ma S Y. 2013a. The magnitude and inter-hemispheric asymmetry of equatorial ionization anomaly-based on CHAMP and GRACE observations. J. Atmos. Solar-Terr. Phys., 105-106:160-169, doi: 10.1016/j.jastp.2013.09.010. |
| [12] | Xiong C, Lühr H, Ma S Y. 2013b. The subauroral electron density trough: Comparison between satellite observations and IRI-2007 model estimates. Adv. Space Res., 51(4): 536-544, doi: 10.1016/j.asr.2011.09.021. |
 2014, Vol. 57
2014, Vol. 57


