2. 中南大学地球科学与信息物理学院, 长沙 410083
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China
1 引言
电阻率层析成像(Electrical Resistivity Tomography,ERT)是地球物理学发展的前沿课题之一,该方法场源易于实现,野外实施简便,对现场无破坏作用,分辨率高(与普通电阻率法比较),勘探成本低(与地震波层析成像比较),穿透深度大(与电磁波层析成像比较),特别适合于浅层构造和工程探测等研究领域(卢元林等,1999).1987年Shima首次提出了“电阻率层析成像”(Resistivity Tomography)一词,并 提出了反演解释的方法(Shima and Sakayama, 1987). 此后各国学者从不同角度对这一问题从理论、实验到应用开展了研究,电阻率层析成像技术得到了快速的发展,探索有效的非线性反演方法,提高成像质量成为了ERT技术研究中新的热点.
由于ERT反演本质上是一个复杂的非线性问题,传统的线性反演将非线性问题在初始模型附近进行线性化,存在着容易陷入局部收敛、依赖初始模型选择、偏导数矩阵求解困难等问题(徐海浪和吴小平,2006).神经网络由于能够模拟人脑神经元的信息学习和处理,直接从样本数据中构造数学模型,近几年已广泛应用于电法勘探数据的解释和分析,其 应用范围既包含一维反演(Singh et al., 2013; Srinivas et al., 2012),也包含二三维反演(Neyamadpour et al., 2009; 徐海浪和吴小平,2006);既包含地表勘探数据的反演(El-Qady and Ushijima, 2001),也包含井-地勘探数据的反演(Ho,2009);既包含单一的神经网络方法反演(Neyamadpour et al., 2010),也包含神经网络与其他方法的联合反演(张凌云和刘鸿福,2011).以上研究工作大多基于BP神经网络(BPNN),为进一步深入研究神经网络的电阻率成像反演提供了坚实的理论和实践基础.虽然BP神经网络在求解电阻率反演问题时得到了广泛的应用,但是它也存在一些不足,具体表现在:(1)对初始权值敏感,易陷入局部极小;(2)训练易停滞于误差梯度曲面的平坦区,收敛缓慢甚至不能收敛;(3)隐层和隐节点数目难以确定,没有普遍适应的规律可循;(4)存在过拟合和过训练的问题.
RBF神经网络与BP神经网络相比,具有最佳逼近的特性,有效地改善了局部极小的问题,同时RBF神经网络拓扑结构紧凑,学习速度快,具有自组织和自适应的特征,正在越来越多的领域(齐玮等,2010; 赵海娟等,2008)被用来进行地球物理资料的分析与解释.由于以上文献中均使用Matlab自带的RBF函数进行建模,无法对RBF神经网络的不同学习算法进行分析和比较,具有一定的局限性.学习算法是影响RBF神经网络性能的最重要因素,本文根据ERT反演的非线性特征提出了一种基于 汉南-奎因信息准则(Hannan-Quinn Criterion,HQC)(Hannan and Quinn, 1979)的OLS学习算法(HQOLS),该算法通过计算并选择HQC的最小值来确定RBF网络结构,能够在训练精度和泛化性能之间取得较好的均衡,同时避免了传统OLS学习算法中的阈值参数设定,具有较强的实用性.通过分析和比较HQOLS算法与其他RBFNN学习算法对二维电阻 率层析成像反演结果的影响,建立了优化的RBFNN 电阻率层析成像反演模型.数值分析和模型仿真的结果表明,该方法学习速度和反演精度优于单隐层和双隐层的BP神经网络反演,成像质量优于传统最小二乘法反演. 2 RBF神经网络
RBF神经网络是一种前馈神经网络,其网络结构主要由输入层、单隐含层和输出层构成.RBF神经网络的基本思想是:用径向基作为隐单元的“基”构成隐藏层空间,隐含层对输入矢量进行变换,将低维的模式输入数据变换到高维空间中,使得在低维空间内的线性不可分问题在高维空间内线性可分(史峰等,2010).RBF神经网络的结构如图 1所示.
 | 图 1 三层RBF网络结构 Fig. 1 Three-layer structure of the RBF neural network |
图 1中RBF神经网络的结构为 n-h-m,其中 x =(x1,x2,…,xn) T 为网络的输入矢量,w∈ R h×m为输出权矩阵,b =(b1,b2,…,bm) T 为输出单元偏移,y =(y1,y2,…,ym) T 为网络输出,φ i(·)为第 i 个隐节点的激活函数,Σ 表示输出层神经元采用线性激活函数.RBF神经网络最显著的特征是隐节点的基函数采用距离函数,并使用径向基函数作为激活函数.若激活函数 φ i(·)采用高斯函数,则第 i 个隐节点的输出为:
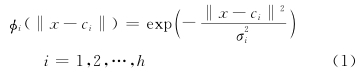
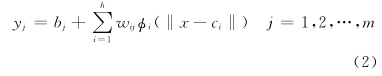
由RBF神经网络的结构可知,决定RBF神经网络性能的主要参数为隐层神经元的个数及中心,基函数宽度和输出权值.对于给定的训练样本,RBF神经网络主要通过学习算法来确定网络的结构和进行参数修正,因此选择合适的学习算法是设计RBF神经网络的重要前提. 3.1 正交最小二乘(OLS)学习算法
Chen等(1991,1992)提出的Orthogonal Least Squares(OLS)学习算法将RBF神经网络的中心选择归结为线性回归中回归子的选择问题,根据设定的阈值来确定回归子数,进而求解出网络权值.该算法能够有效地限制RBF神经网络的规模并避免随机选择中心带来的数值病态问题,其基本算法的求解过程如下:
将RBFNN看作以下线性回归模型:
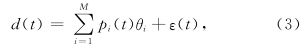


 为式(4)的最小二乘解,满足 P
为式(4)的最小二乘解,满足 P 是 d 在基向量张成空间上的投影.将回归矩阵 P 分解为:
是 d 在基向量张成空间上的投影.将回归矩阵 P 分解为:


 = H -1 W T d,其中
= H -1 W T d,其中  和
和 满足
满足
 ,其计算 A 的一列和正交化 P 的过程如下:
,其计算 A 的一列和正交化 P 的过程如下: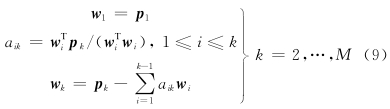

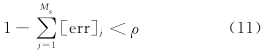
虽然OLS算法采用正交化的方法独立计算回归子对输出的贡献,对中心的选择简单有效,但是训练精度阈值ρ需人为设定,其值过大则无法保证训 练精度,过小则可能产生过拟合(Over-Fitting)问 题,需要反复验证,降低了算法效率.信息准则(Information Criterion)是衡量统计模型拟合优良性的一种标准,被广泛地应用于RBF模型性能的衡量和评价(Ghodsi and Schuurmans, 2003; Kokshenev and Padua Braga,2010; Zhou et al., 2011). 常见的信息准则包括赤池 信息准则(Akaike Information Criterion,AIC)(Akaike,1974),贝叶斯信息准则(Bayesian Information Criterion,BIC)(Schwarz,1978)和汉南-奎因信息准则(Hannan-Quinn Criterion,HQC),其中三者对模型复杂度的惩罚强度由弱到强为AIC<HQC<BIC(Tu and Xu, 2012).因此在RBF模型评估中,对于已知训练样本,AIC具有更好的训练精度,BIC具有更精简的模型结构,而HQC的拟合精度和泛化能力则更加均衡,更符合OLS算法在ERT反演中对模型评估的要求,所以本文采用HQC作为OLS算法的评估准则,其公式如下:
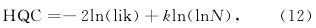
高斯模型下,公式(12)可改写为:

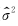 为样本的标准差,k 为输入的维数,N 为观测样本数量.
为样本的标准差,k 为输入的维数,N 为观测样本数量.由式(13)可以看到,在HQC中N ln(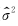 )项用来评价模型的拟合程度,k ln(ln N)项则是关于模型复杂度的惩罚项,用来防止过拟合问题.因此使用HQC评估OLS算法可以实现系统性能和模型复杂度之间的均衡,避免训练精度阈值的设定,使用HQOLS算法实现RBFNN反演的训练和测试过程如流程图 2所示.
)项用来评价模型的拟合程度,k ln(ln N)项则是关于模型复杂度的惩罚项,用来防止过拟合问题.因此使用HQC评估OLS算法可以实现系统性能和模型复杂度之间的均衡,避免训练精度阈值的设定,使用HQOLS算法实现RBFNN反演的训练和测试过程如流程图 2所示.
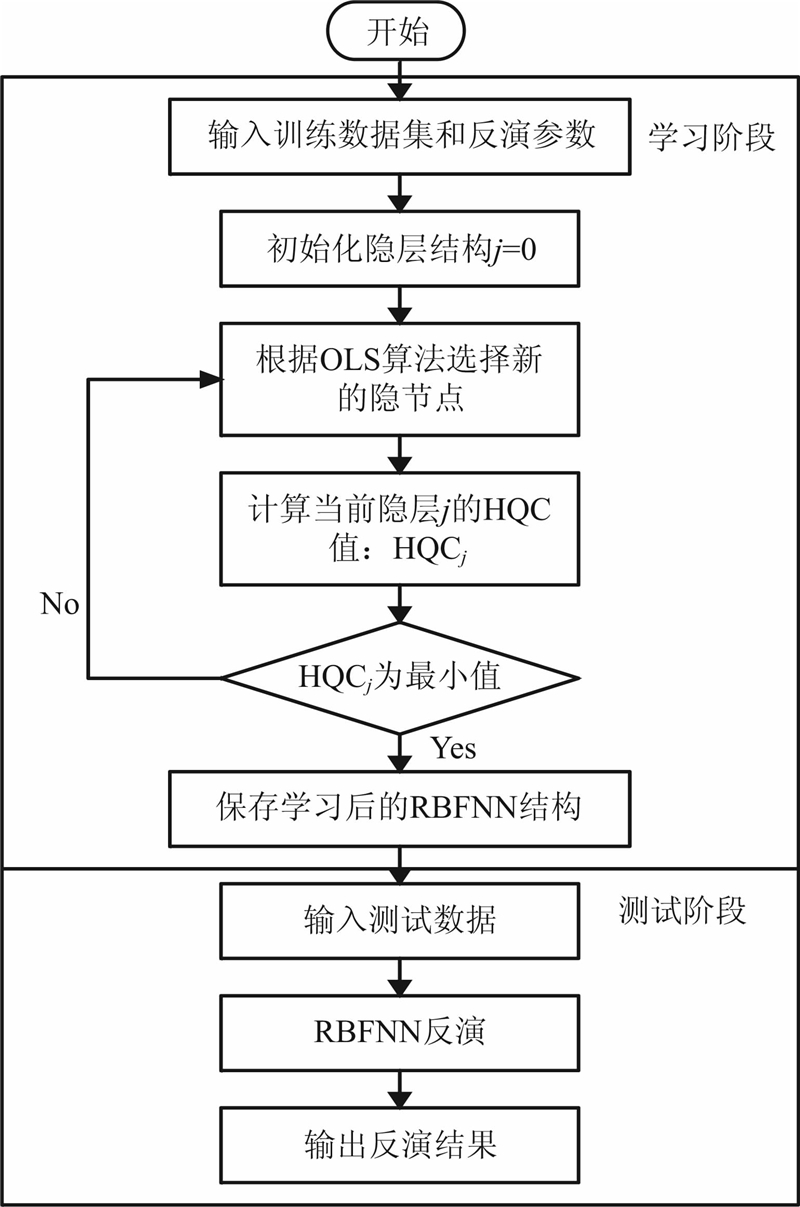 | 图 2 基于HQOLS算法的RBFNN反演流程图 Fig. 2 Flowchart for RBFNN inversion based on HQOLS algorithm |
其具体的实现步骤如下:
(1)使用有限单元法(RES2DMOD软件)产生训练与测试数据集,初始化RBFNN(归一化数据,设定扩展常数和初始化隐层结构等),使用训练数据集进行学习.
(2)根据OLS算法求解第 j 次选择回归子时的中心位置和权值,并计算当前网络的样本标准差:

(3)计算 j 个隐节点时的HQC值,其中用隐节点的个数作为评价模型复杂度的参数,计算公式如下:

(4)选择HQC最小值时的隐层结构,并以此结构构造RBFNN.
(5)输入测试数据集,使用构造好的RBFNN进行反演,输出并评估反演结果.
本文中通过采用HQOLS学习算法的RBFNN对采集的视电阻率样本数据进行训练,记录不同隐节点数目时的HQC值曲线如图 3,从图 3中可得到隐节点数目为132时的网络为HQOLS算法选择的 最优RBFNN,其HQC值为-1.7382×104,为HQC 曲线的最小值.
 | 图 3 HQC曲线 Fig. 3 HQC curve with different numbers of hidden layer nodes |
针对电阻率反演的神经网络建模,目前的文献中主要有两种方法,Neyamadpour等(2009)使用采集视电阻率的水平位置、垂直位置和视电阻率值为输入节点,对应位置的模型参数(真电阻率)值为输出节点,将每次测量的所有数据点设为一个数据集进行训练.其特点是神经网络的结构简单(输入节点数量为3,输出节点数量为1)、训练迅速,但是由于视电阻率和真电阻率一一对应,无法充分反映视电阻率是电场作用范围内地下电性不均匀体的综合反映这一本质特征;徐海浪(2006)考虑到上述缺点,将所有测量的视电阻率作为输入节点,所有模型参数作为输出节点,但输入输出节点数量巨大(输入节点990个,输出节点1062个),因此采用了3隐含层的BP神经网络,而且3隐含层的节点数分别为200、160、200.如此大规模的神经网络不仅建立需要通过大量的测试来确定隐含层的最优节点数、而且训练和测试需要更多的数据和时间.
对于RBF神经网络,以上两种建模方式均有不足:Neyamadpour采用的建模方法训练样本数过多,这将导致RBF神经网络的学习速度缓慢,网络结构臃肿,泛化能力差;徐海浪采用的建模方法由于输入输出节点数量过多,RBF神经网络的单隐含层结构无法保证较快的收敛,达到有效的训练精度.本文综合考虑以上两种建模方式的优缺点,采取以下建模方式:将采集并预处理后的视电阻率数据按分布区域分组,以每个分组数据为RBFNN的一个训练样本,同时允许不同样本在相邻处存在数据重叠,分组区域和样本重叠的大小视训练数据的实际规模而定.该建模方式既考虑了相邻视电阻率数据与真电阻率之间的相互影响,又控制了训练样本的输入输出节点规模,能够较好地配合RBF神经网络对二维电阻率层析资料进行反演.
为了验证不同学习算法对RBF神经网络反演能力的影响,本文采用温拿-斯伦贝格(Wenner-Schlumberger)装置进行测量,测量电极为37个,极距1 m,第一层可采集34个数据点,以下各层依次递减,共采集15层300个数据点.通过采用上述的建模方式,经过测试,本文中RBF神经网络输入节点数为45个,输出节点数为15个,每一次测量可获得16组数据.网络的训练数据通过改变不同异常体的位置、大小和形态来获得,图 4为部分用于训练的样本模型.
 | 图 4 用于训练的样本模型 Fig. 4 Sample models for RBFNN training |
其中训练样本应尽可能涵盖反演中异常体的形态和大小,测试样本应与反演目标较为接近,图 5为部分用于测试的样本模型.上述训练和测试的样本模型背景电阻率均为100 Ωm,异常体电阻率均为500 Ωm.
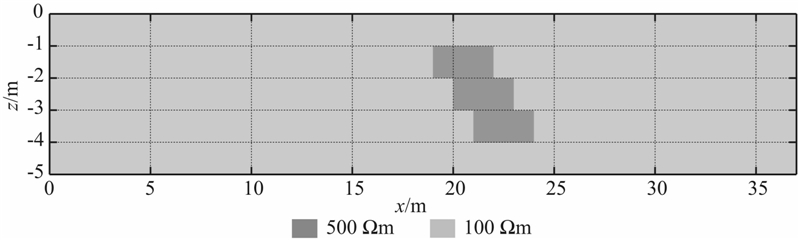 | 图 5 用于测试的样本模型 Fig. 5 Sample model for RBFNN test |
根据以上的原则,共获取40个训练样本,分为640组训练数据.同时提供10个测试样本,160组测试数据,测试数据均未参加网络训练.
RBF神经网络现有的学习算法分为离线学习和在线学习两类,其中离线学习方法主要适用于时不变模型,由于本文主要分析特定装置下的二维电阻率数据反演,因此使用离线学习方法来训练RBF神经网络.离线学习将RBFNN的训练过程在时间上分成几个独立的阶段:首先要收集训练样本,然后采用不同形式的聚类方法或其他方法从样本中确定RBF神经网络的结构并获取对网络性能有密切影响的各隐层单元“中心”,最后是校正网络输出层权 值.其主要的代表包含聚类算法(Moody and Darken, 1989)、 梯度算法(Rumelhart et al., 1988)和正交最小二乘算法(Chen et al., 1991).
分别使用以上三种算法和HQOLS算法对上述样本进行训练和测试,由于算法的实现方式不同,各算法所需设置的参数也有所不同,其中根据数据分组,四种算法的输入维数均为45,输出维数均为15;聚类方式和梯度方式隐节点经优选比较后设置为200,OLS算法的隐节点数目由目标误差自适应地决定;聚类算法的隐节点重叠系数设置为1;梯度算法的学习系数、训练次数和目标误差分别设置为:0.025、1000、0.01;OLS算法的隐节点扩展常数和目标误差分别设置为:0.6和0.01;HQOLS算法不需要设置目标误差,扩展常数设置为0.6.其具体的算法参数设置如表 1所示.
| | 表 1 不同学习算法的参数设置 Table 1 Parameters for different learning algorithms |
RBF神经网络通过四种学习算法的训练和测试,其隐层结构,均方误差(Mean Squared Error,MSE)的平均值和运行时间如表 2所示.从表 2中可以看出,在训练和测试误差方面,在40个给定的训练样本中OLS算法的训练误差最小,达到了训练的目标误差0.01,其主要的原因是OLS算法随着隐节点数目的增多,训练误差能够得到有效的抑制.事实上,进一步增加OLS算法的隐节点数目还将进一步减小训练误差,但此时网络可能会出现过拟合,泛化能力变差;聚类算法和HQOLS算法总体来说也能够达到较低的均方误差,其平均均方误差均低于0.02.在10个测试样本中HQOLS算法和聚类算法均显示出较强的泛化能力,其测试误差相当,均为0.048左右,同时HQOLS算法使用HQC准则限制了RBFNN的网络规模,其隐节点的选择更加合理;OLS算法也能够体现出较好的泛化能力,其平均均方误差低于0.1;梯度算法的训练和测试误差均比较大,学习效果和泛化能力不佳,这是由于梯度算法采用类似于BP神经网络的参数学习机制,但是其单隐层的网络结构过于简单且输出采用线性方式,无法较好地拟合训练样本的原因.在隐层结构和运行时间方面,聚类算法的效率最高,仅3.76 s就完成了运算;OLS算法运行至316隐节点时,需要29.64 s,但能够达到比聚类算法更低的训练均方误差;HQOLS算法由于需要计算HQC的最小值,所以需要比OLS算法更多的运行时间,但是其泛化性能优于OLS算法,同时HQOLS算法所获得的RBFNN结构最为精简;对于设定的目标误差,梯度算法一直无法达到,所以执行到了最大训练次数,所需时间最多,但性能最差.由于聚类算法需要反复测试来获得最优隐节点数目,而OLS算法则需要设定合适的训练精度阈值,综合考虑RBF神经网络的构造时间、训练精度和泛化能力,本文采用HQOLS算法作为RBF神经网络的学习算法,构造电阻率层析成像的非线性反演模型.
| | 表 2 不同学习算法的性能比较 Table 2 Comparisons of performances of different learning algorithms |
为了验证上述建模方式的反演性能,将RBFNN 与BPNN的反演结果进行比较,其训练和测试数据如4节所述,考虑到BP网络结构对其反演性能的影响,分别构造了单隐层(隐节点数为120)、双隐层(隐节点数为68~38)的BPNN,训练算法使用RPROP,训练次数为1000;RBFNN采用基于HQOLS的学习算法.在训练阶段三种结构的神经网络均能得到收敛,其中RBFNN的训练时间最短,也达到了最高的训练精度0.0156;双隐层BPNN也能够达到较好的训练效果,但训练时间较长;单隐层BPNN因为结构简单,训练时间较短,但是有相对较大的训练误差.三种结构的神经网络的测试和训练结果具体比较如表 3所示,可以看出采用HQOLS学习算法的RBFNN较单隐层和双隐层的BPNN具有更低的训练和测试均方误差值,通过与表 2中数据进行比较,采用聚类学习算法和OLS学习算法的RBFNN训练误差和测试误差也低于BPNN,且训练时间更短,验证了RBFNN在求解反演问题中的快速学习和避免局部极小值的能力;另一方面,采用HQOLS学习算法的RBFNN较采用RPROP算法的BPNN算法具有更优的决定系数值 R 2,表明其反演的结果与理论数据更加接近,误差波动小,具有较好的泛化性能和较高的稳定性.
为了进一步验证反演算法的可行性,在两个不 同的异常体模型下,使用采用HQOLS学习算法的RBFNN和最小二乘法(RES2DINV软件的反演结果)、BPNN进行了反演对比.
| | 表 3 不同神经网络的性能比较 Table 3 Comparisons of performance in different neural networks |
用于验证的模型1为一个不规则的高阻异常体.模型1的基本参数如下:采用温拿-斯伦贝格装置,每排含37个电极,15层电阻率数据,电极距为1.0 m,围岩电阻率为100 Ωm,高阻异常体电阻率为500 Ωm,顶部埋深为1 m.用该模型的正演视电阻率作为RBFNN网络的输入,对网络进行反演测试,网络输出的反演结果如图 6所示.
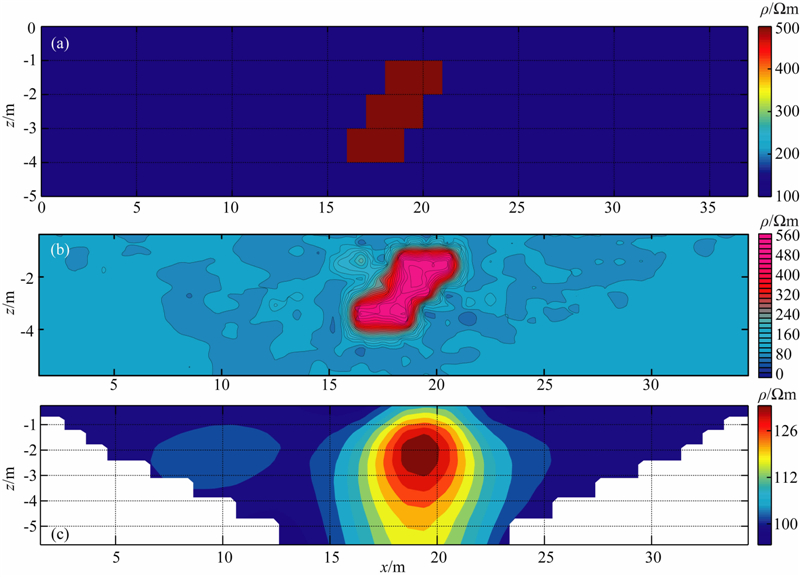 | 图 6 模型1的模型示意图及不同方法的反演结果 (a)模型1示意图;(b)HQOLS-RBFNN反演结果;(c)RES2DINV软件反演结果. Fig. 6Model 1 and inversion results by different methods (a)Model 1;(b)Inversion result of HQOLS-RBFNN;(c)Inversion result of RES2DINV. |
从反演的结果可以看出,最小二乘法和HQOLS-RBFNN 反演算法均能够较为准确地反映高阻异常体的位置和电阻率,但HQOLS-RBFNN反演算法的结果更加精确,异常体的形状和轮廓更加清晰,其结果优于最小二乘法的反演结果.从计算时间上来 看,HQOLS-RBFNN反演算法的反演时间为37.1 s(含训练学习时间35.4 s和反演测试时间1.7 s),最小二乘法的反演时间为2.4 s,仅从单个模型的反演时间而言,最小二乘法的反演速度更快;但是对于多个模型的反演来说,由于RBFNN训练好以后就可以直接反演,不需要重复训练,因此RBFNN也具有较高的反演效率.
用于验证的模型2为3个异常体的组合模型,用来检验RBFNN和BPNN反演结果之间的差异.模型2的基本参数如下:采用温拿-斯伦贝格装置,每排含37个电极,15层电阻率数据,电极距为1.0 m,围岩电阻率为100 Ωm,低阻异常体大小为1.5 m×3 m,电阻率为10 Ωm,其顶部埋深为1.5 m;高阻异常体1的大小为1.5 m×4 m,电阻率为1000 Ωm,其顶部埋深为1 m;高阻异常体2的大小为1.5 m×2 m,电阻率为500 Ωm,其顶部埋深为1 m.用该模型的正演视电阻率作为RBFNN网络的输入,对网络进行反演测试,网络输出的反演结果如图 7所示.
 | 图 7 模型2的模型示意图及不同方法的反演结果 (a)模型2示意图;(b)HQOLS-RBFNN反演结果;(c)双隐层BPNN反演结果;(d)单隐层BPNN反演结果. Fig. 7 Model 2 and inversion results by different methods (a)Model 2;(b)Inversion result of HQOLS-RBFNN;(c)Inversion result of double hidden-layers BPNN;(d)Inversion result of single-hidden layer BPNN. |
从反演结果来看,3种神经网络反演均能够较为准确地反演出异常体的存在和位置.相对而言,单隐层BPNN的反演结果在低阻异常体形态的重构 上存在着较大的失真,其高阻异常体2的电阻值也与模型存在着一定的差异;双隐层BPNN的反演结果较单隐层BPNN得到了改善,但低阻异常体的形态依然存在较大的失真;HQOLS-RBFNN反演算法的高低阻异常体的位置准确、形态与间隔清晰、电阻值与实际模型更加接近,其结果优于BPNN的反演结果,同时该结果也与前面数据仿真的结论相吻合,验证了算法的性能.通过对以上反演结果进行更深入的分析可知,本文采用的RBFNN和BPNN在学习方式上有着较大的区别,基于OLS算法的RBFNN是通过将典型样本映射成隐层结构来进行学习,而基于梯度法的BPNN是通过调整权值以将样本误差均匀分配至各个隐节点来进行学习.因此,当训练样本与测试模型接近时,RBFNN反演的精度更高,速度更快;反之当训练样本与测试模型差异较大时,BPNN反演的结果将相对更加准确. 6 结论
本文使用RBF神经网络来实现电阻率层析成像的非线性反演,比较了不同学习算法在RBFNN反演中的性能和效率.通过综合考虑神经网络的拟合能力和模型复杂度,提出了一种基于汉南-奎因信息准则的OLS学习算法,该算法不需要进行参数阈值的设定,能自适应选择RBFNN的网络结构,均衡了网络的训练精度和泛化能力,具有较好的反演性能.神经网络非线性反演建模的核心问题是设计神经网络的隐层结构和规划神经网络的训练样本,其中隐层结构与反演问题的复杂度相对应,训练样本与反演的异常体特征相对应.BPNN中,隐节点数的选择没有普适的方法,主要采用凑试法来确定;RBFNN中,OLS算法和本文的HQOLS算法均可较好地确定合适的隐节点数.训练样本的规划须尽可能涵盖可能的异常体特征,但又不能过多,以免造成神经网络结构的臃肿和训练效率的降低,本文采用的区域分组法将每个训练样本细分为多组训练数据,可以在训练样本的数量和反演速度中取得较好的均衡.
数据仿真和模型反演的结果表明:(1)合理的神经网络反演建模,能够使得训练出来的RBFNN基本准确地反映电阻率层析成像的输入输出关系,取得较好的反演效果;(2)不同学习算法对反演的结果有较大的影响,合理地选择RBF学习算法是构造RBFNN反演模型的关键;(3)不同的信息准则对于神经网络隐层结构的惩罚程度不一,在实际应用中应根据反演的具体需求和样本的数量来进行选择. 在本文的训练和测试条件下,HQOLS-RBFNN较BPNN的误差更小,效率更高;较传统的最小二乘反演成像更加清晰准确;(4)HQOLS学习算法的隐节点中心为训练样本的子集,基带宽为常数,如果和其他的算法相结合(例如:遗传算法,粒子群算法等)对中心和基带宽进行进一步优化可以获得更精确的反演结果.
当然,实际的地电模型非常的复杂,在针对实测数据进行反演时,RBFNN反演还存在以下一些问题:(1)当实际异常体的电阻率参数远大于(小于)训练样本中的异常体电阻率时,其误差会在反演结果中成倍的放大,造成电阻率值的解释错误;(2)当实际异常体的大小与训练样本中的异常体大小有较大差异时,反演结果中异常体的形态会有较大的失真;以上这些问题均是由于神经网络是基于对样本学习的反演方法造成的,在BPNN和RBFNN中均存在,一种可以采用的解决方法是先用最小二乘法进行反演,得到勘探区域中大致的异常体形态和电阻率值范围,再以此构造神经网络训练样本进行学习和反演以得到更加精确的反演结果.总之,RBFNN是一种新兴的ERT非线性反演技术,对于规模更大、参数更多的反演问题,RBFNN反演的理论研究和实际应用还需在以后的工作中不断完善.
| [1] | Akaike H. 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6): 716-723. |
| [2] | Chen S, Cowan C, Grant P. 1991. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Transactions on Neural Networks, 2(2): 302-309. |
| [3] | Chen S, Grant P, Cowan C. 1992. Orthogonal least-squares algorithm for training multioutput radial basis function networks. Radar and Signal Processing, IEE Proceedings F, 139(6): 378-384. |
| [4] | El-Qady G, Ushijima K. 2001. Inversion of DC resistivity data using neural networks. Geophysical Prospecting, 49(4): 417-430. |
| [5] | Ghodsi A, Schuurmans D. 2003. Automatic basis selection techniques for RBF networks. Neural Networks, 16(5-6): 809-816, doi: 10.1016/s0893-6080(03)00118-7. |
| [6] | Hannan E J, Quinn B G. 1979. The determination of the order of an autoregression. Journal of the Royal Statistical Society. Series B (Methodological), 41(2): 190-195. |
| [7] | Ho T L. 2009. 3-D inversion of borehole-to-surface electrical data using a back-propagation neural network. Journal of Applied Geophysics, 68(4): 489-499, doi: 10.1016/j.jappgeo.2008.06.002. |
| [8] | Kokshenev I, Padua Braga A. 2010. An efficient multi-objective learning algorithm for RBF neural network. Neurocomputing, 73(16-18): 2799-2808, doi:10.1016/j.neucom.2010.06.022. |
| [9] | Lu Y L, Wang X T, Wang R, et al. 1999. The simulated annealing method of electrical resistivity tomography. Chinese J. Geophys. (in Chinese), 42(S1): 225-233. |
| [10] | Moody J, Darken C J. 1989. Fast learning in networks of locally-tuned processing units. Neural Computation, 1(2): 281-294, doi: 10.1162/neco.1989.1.2.281. |
| [11] | Neyamadpour A, Wan Abdullah W A T, Taib S, et al. 2010. 3D inversion of DC data using artificial neural networks. Studia Geophysica et Geodaetica, 54(3): 465-485. |
| [12] | Neyamadpour A, Taib S, Wan Abdullah W A T. 2009. Using artificial neural networks to invert 2D DC resistivity imaging data for high resistivity contrast regions: A MATLAB application. Computers & Geosciences, 35(11): 2268-2274, doi: 10.1016/j.cageo.2009.04.004. |
| [13] | Qi W, Wang X F, Li X H, et al. 2010. A real time K-indices scaling method based on radial basis neural network. Chinese J. Geophys. (in Chinese), 53(1): 147-155. |
| [14] | Rumelhart D E, Hinton G E, Williams R J. 1988. Learning Representations by Back-Propagating Errors. Cambridge, MA, USA: MIT Press. |
| [15] | Schwarz G. 1978. Estimating the dimension of a model. The Annals of Statistics, 6(2): 461-464. |
| [16] | Shi F, Wang X C, Yu L, et al. 2010. Neural Network Case Study. Beijing: Beijing University of Aeronautics & Astronautics Press. |
| [17] | Shima H, Sakayama T. 1987. Resistivity tomography: An approach to 2-D resistivity inverse problems. SEG Technical Program Expanded Abstracts, 59-61, doi: 10.1190/1.1892038. |
| [18] | Singh U K, Tiwari R K, Singh S B. 2013. Neural network modeling and prediction of resistivity structures using VES Schlumberger data over a geothermal area. Computers & Geosciences, 52: 246-257, doi: 10.1016/j.cageo.2012.09.018. |
| [19] | Srinivas Y, Raj A S, Oliver D H, et al. 2012. A robust behavior of Feed Forward Back propagation algorithm of Artificial Neural Networks in the application of vertical electrical sounding data inversion. Geoscience Frontiers, 3(5): 729-736, doi: 10.1016/j.gsf.2012.02.003. |
| [20] | Tu S, Xu L. 2012. A theoretical investigation of several model selection criteria for dimensionality reduction. Pattern Recognition Letters, 33(9): 1117-1126, doi: 10.1016/j.patrec.2012.01.010. |
| [21] | Xu H L, Wu X P. 2006. 2D resistivity inversion using the neural network method. Chinese J. Geophys. (in Chinese), 49(2): 584-589. |
| [22] | Zhang L Y, Liu H F. 2011. The application of ABP method in high-density resistivity method inversion. Chinese J. Geophys. (in Chinese), 54(1): 227-233. |
| [23] | Zhao H J, Wang J L, Zong W G, et al. 2008. Prediction of the smoothed monthly mean sunspot numbers by means of radial basis function neural networks. Chinese J. Geophys. (in Chinese), 51(1): 31-35. |
| [24] | Zhou P, Li D H, Wu H, et al. 2011. The automatic model selection and variable kernel width for RBF neural networks. Neurocomputing, 74(17): 3628-3637, doi: 10.1016/j.neucom.2011.07.011. |
| [25] | 卢元林, 王兴泰, 王若等. 1999. 电阻率成像反演中的模拟退火方法. 地球物理学报, 42(S1): 225-233. |
| [26] | 齐玮, 王秀芳, 李夕海等. 2010. 一种基于径向基神经网络的地磁场 K 指数实时标定方法. 地球物理学报, 53(1): 147-155. |
| [27] | 史峰, 王小川, 郁磊等. 2010. MATLAB 神经网络30个案例分析. 北京: 北京航空航天大学出版社. |
| [28] | 徐海浪, 吴小平. 2006. 电阻率二维神经网络反演. 地球物理学报, 49(2): 584-589. |
| [29] | 张凌云, 刘鸿福. 2011. ABP 法在高密度电阻率法反演中的应用. 地球物理学报, 54(1): 227-233. |
| [30] | 赵海娟, 王家龙, 宗位国等. 2008. 用径向基函数神经网络方法预报太阳黑子数平滑月均值. 地球物理学报, 51(1): 31-35. |
 2014, Vol. 57
2014, Vol. 57


