2. 北京大学地球与空间科学学院, 北京 100871;
3. Rice大学地球科学系, 德克萨斯州, 休斯顿 77005-1892
2. School of Earth and Space Sciences, Peking University, Beijing 100871, China;
3. Department of Earth Science, Rice University, Houston, TX, 77005-1892, USA
探地雷达(Ground penetrating radar,GPR)是根据脉冲电磁波在地下不同介质之间的反射及绕射等波动规律,来探测地下结构和特性的重要浅部地球物理方法(曾昭发等,2010).GPR正演是计算地球物理学的一个重要分支,许多学者在此领域开展了大量研究:李展辉等(2009)将错格时域伪谱法应用于GPR模拟,解决了时域伪谱法的Gibbs现象;冯德山等(2007)应用时域多分辨算法开展GPR数值模拟,其每个波长仅采样2个点的精度可达到时 域有限差分法(Finite difference time domain,FDTD)每个波长采样10个点的精度;方宏远等(2012,2013)利用Hamilton 系统的辛分块龙格库塔方法开展了道路结构层雷达波传播特征研究;冯德山等(2013)将只需节点无需单元的无网格Galerkin算法应用于GPR正演,它具有前处理简单、解高次连续等优点;Lu等(2005)利用离散时域Galerkin进行色散介质中的GPR正演;沈飚(1994)应用有限单元法(FEM)进行了GPR简单模型正演;底青云与王妙月(1999)推导了含衰减项的GPR波有限元方程,实现了复杂形体的GPR波的FEM正演;冯德山等(2012)提出结合透射边界和Sarma边界的混合边界,改善了有限单元法GPR正演的边界反射.自Yee(1966)提出FDTD算法以来,FDTD算法在GPR正演中得到广泛应用:Giannopoulos(2005)编制了GPR正演软件“GprMax”,因为是免费软件,已得到许多用户青睐;Irving和Knight(2006)基于Matlab开发了GPR二维正演程序;李静等(2010)为了提高FDTD算法的模拟精度,采用高阶FDTD算法结合单轴各向异性理想匹配层(UPML)边界条件进行了GPR数值模拟;冯德山等(2010)应用基于UPML边界条件的交替方向隐式时域有限差分法(ADI-FDTD)进行GPR正演;田钢等(2011)将FDTD 算法应用于地面以上物体反射干扰特征GPR模拟和分析,为干扰压制研究提供理论依据;冯晅等(2011)通过水平正交双方向同时接收获取全极化信息,构建了基于FDTD算法的全极化GPR正演模拟方法,进而能更好地分析目标属性.这些研究指导了异常体的判读与GPR数据解释,考虑到雷达波在地下介质传播时,易产生波形畸变、能量衰减的频散现象.Bano(2004)、Cassidy and Millington(2009)、Teixeira(2008)等强调了GPR正演时频散特性的重要性;刘四新等(2007)开展了频散介质中二维FDTD法GPR数值模拟,对比了频散介质与非频散介质中GPR曲线的区别;方广有等(1996)开展了浅层地下目标电磁散射问题的FDTD数值模拟;Li等(2012)开展基于递归积分不分裂复频移PML的FDTD三维GPR正演,该边界条件对隐失波、低频波及近掠射波具有好的吸收效果.
由此可见,GPR正演算法种类繁多,各有特色,且经历了从不考虑介质频散向考虑频散的发展历程,在这些模拟方法中,FDTD具有概念清晰、编程简单等特点,成为GPR模拟中应用最广泛的方法.常规FDTD开展GPR模拟时,常采用一致网格剖分,为了保证计算精度、避免数值频散,当模型中存在局部物性参数变化剧烈小异常体时,需要采用统一的细网格剖分,精细的网格又要求小的时间步长;然而,除去这些局部区域,其他大部分区域波场变化都是平缓的,利用较粗的空间网格与大的时间步长就能进行正演.这样,在波场缓变区域存在时间与空间上过采样问题(黄超和董良国,2009a),造成计算机存储空间加大和计算效率降低.为了兼顾FDTD模拟效率与精度,避免过采样问题,Moczo(1989)首次提出网格连续变化的方法来减小计算量;Zivanovic等(1991)将变网格技术应用到电磁场Maxwell方程求解中,但仅限于空间一个方向,由于统一的小时间步长的存在,计算效率仍有待提高;Falk等(1998)提出一种长短时间步长比为2N倍的局部可变时间步长模拟方法;Tessmer(2000)对Falk的方法进行了改进,使长短时间步长的变化范围突破了2N的限制;黄超和董良国(2009b)提出一种可变网格与局部可变时间步长的高阶差分声波模拟方法,而后又将该算法引入到交错网格高阶差分弹性波模拟中;张慧和李振春(2011)基于时空双变网格算法的碳酸盐岩裂缝型储层正演模拟.这些双变步长FDTD算法解决了空间与时间维度上的过采样问题,但计算过程中时间步长算子作为一个全局变量,局部变化非常困难,给计算机编程增加了不少难度,同时也可能因时、空域的双插值带来稳定性问题.
本文继承了Wang et al.(2001),Ahmedy和Chen(2004),Diamanti和Giannopoulos(2009)等人FDTD 混合算法成果,提出基于Debye模型的复介电常数 开展 ADI-FDTD(Alternating-Direction-Implicit)亚网格技术的频散介质GPR正演,即在物性变化剧烈局部区域采用细网格剖分ADI-FDTD计算,其他的物性参数缓变区域采用粗网格常规FDTD计算,由于ADI-FDTD突破了CFL条件的约束,可选取与粗网格一致的大时间步长,计算中只需考虑空间不一致网格的插值连接问题,编程计算简便,从根本上降低内存占用及计算时间,在精确性与时效性之间取得满意的平衡.
2 频散介质混合ADI-FDTD亚网格技术原理及差分格式如图 1a所示,当模拟区域存在小的异常体时,常规FDTD算法采用固定的网格步长对整个模型区域进行精细的网格离散易导致物性参数缓变区空间与时间上的过采样.图 1b为局部亚网格的剖分方法,仅在异常体及其附近区域采用细网格剖分ADI-FDTD计算,其他区域采用粗网格剖分常规FDTD计算,因为ADI-FDTD可选取与粗网格中FDTD算法一致的大时间步长,计算中只需考虑空间不一致网格的插值连接问题,时间上完全不用考虑插值问题,编程计算较双变网格算法更为简便.
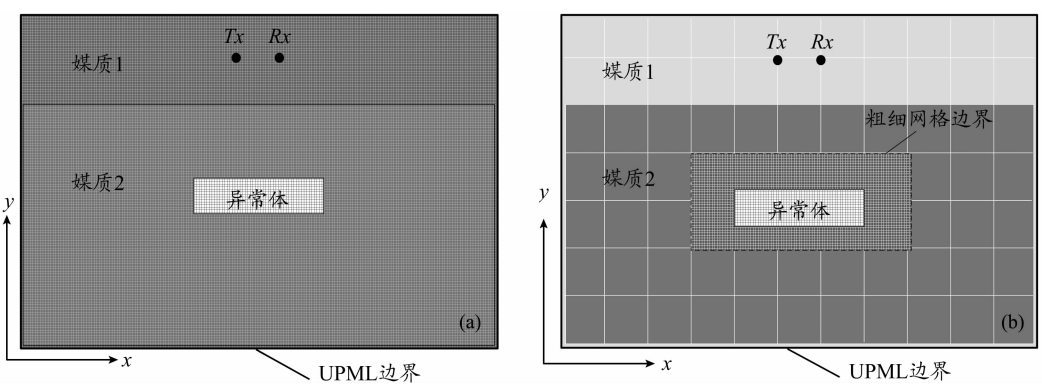 | 图 1 不同的网格剖分方式(a)精细网格剖分方式;(b)局部亚网格剖分(仅异常体及附近区域采用细网格).Fig. 1 Different grid splid methods |
由电磁波传播理论可知(Yee,1996),GPR遵循的Maxwell方程在二维情况下变为3个偏微分方程,其电磁分量仅为Ez、Hx、Hy三个,称之为TM波.在各向同性介质中D(t)=ε(r)E(t),介电常数ε(r)只是空间的函数,可直接将其代入Maxwell旋度方程的离散式.而在频散介质中介电常数是关于空间与频率的函数,频散介质中FDTD递推公式与各向同性介质中FDTD递推公式类似,仅仅是电磁 分量的推导稍显不同(Luebbers et al., 1990;Luebbers et al., 1991). 处理频散介质FDTD算法有许多种(刘少斌等,2010),包括递归卷积积分法、辅助方程法、Z变换法、位移算子法等.本文应用辅助差分法(葛德彪和闫玉波,2005)推导频散介质中的FDTD差分方程,无源情况下频散介质中Maxwell方程表示为
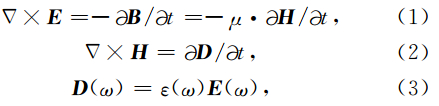
在粗网格区域,采用传统FDTD方法.运用Yee氏网格模型,把连续变量离散化,Δx、Δy为图 1b中粗网格区域的空间步长,Δt为差分时间步长,将每个节点进行编号,例如:nΔt时刻空间坐标位置(iΔx,jΔy)的电磁场值f(iΔx,jΔy,nΔt)按fn(i,j)方式对应起来.考虑到频散介质中,磁场分量的差分公式与非频散介质中是一致的,将(1)离散,并整理可得到磁场分量H x与 H y在t=nΔt时刻时间迭代FDTD公式:
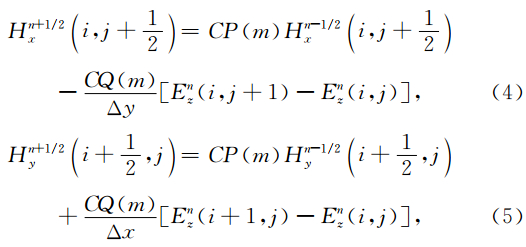
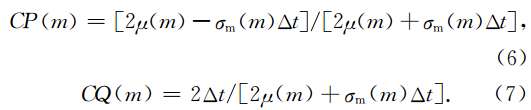
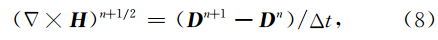

表达介质频散的模型主要有Lorentz(洛沦兹)模型、Drude(德鲁)模型、Debye(德拜)模型(刘少斌等,2010).下面根据Debye模型关系式,推导频散介质中的D和E的微分方程.可将有耗频散媒质的介电常数表示为
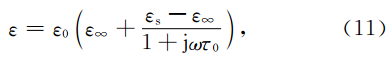
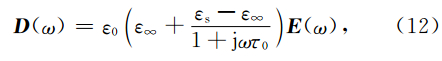
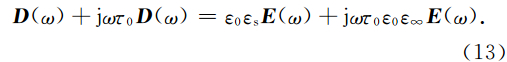
 /
/ t,将(13)式变成时域方程:
t,将(13)式变成时域方程:

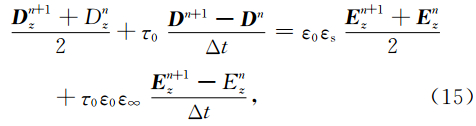
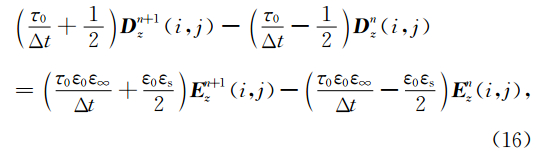

(1)根据常规的FDTD差分公式(4)—(5),由E计算H n+1/2的各个分量;
(2)根据(10)式由H计算Dn+1的各分量;
(3)根据(17)式由D计算En+1的各分量;
(4)回到步骤(1).
在异常体及其附近细网格剖分区域中,使用ADI-FDTD方法将传统的一个时间步分成两个子时间步,分别采用前向和后向差分,兼具隐式差分格式的无条件稳定性和显式差分格式计算相对简单的优点(Namiki,1999).ADI-FDTD方法中两个时间步的差分公式推导类似,以n→n+1/2步为例,n+1/2→n+1应用同样的方法导出.再分析Maxwell旋度方程(1)与(2),式中时间偏微分项仍采用中心差分格式,Δx′、Δy′为图 1b中细网格区域的空间步长,对x方向导数在子时间步的末时刻(n+1/2)Δt取隐式差分离散,对y方向导数在初时刻nΔt作显式差分离散,Hx分量在n和n+1/2时刻均取值,并定义:

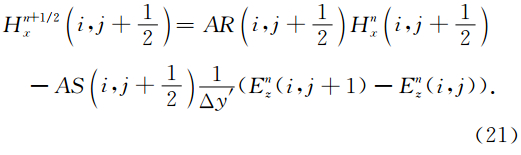
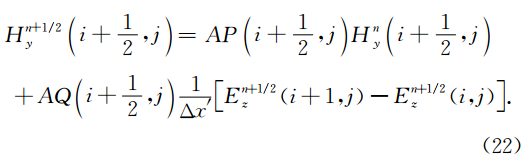
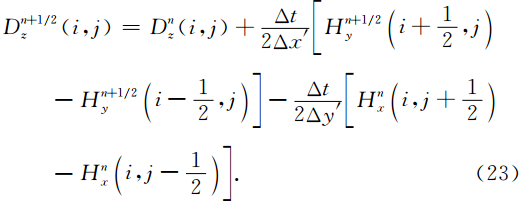



式(21)—(23)及(25)四个式子可用于子时间步n→n+1/2电磁场的时域推时计算,其中式(21)在计算n+1/2时刻场值时其右端只涉及n时刻场值,称为显式格式,但式(22)等式两边包含同时刻En+1/2z和Hn+1/2y场分量,式(23)等式两边包含同时刻Dn+1/2z和Hn+1/2y场分量,式(25)等式两边包含同时刻Dn+1/2z和En+1/2z场分量,不能构成显式时间推进计算,逻辑上讲时间步进是无法完成的,称为隐式格式.为此,将式(22)代入到式(23)中消除磁场分量Hn+1/2y的,再将得到的消除了Hn+1/2y的式(23)代入到式(25)消去Dn+1/2z,得:

多元方程组式(28)的系数矩阵可以改组成实三对角条带矩阵,结合吸收边界条件就可求解(郑奎松,2005).
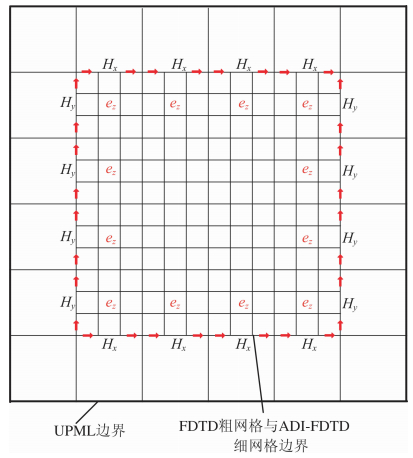
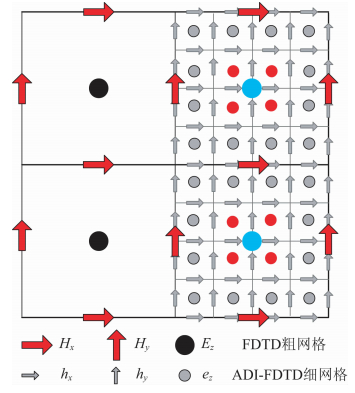
3 粗细网格场值交换格式如图 2所示,ADI-FDTD亚网格算法空间网格的布置与常规的FDTD算法是一致的,电场位于网格的中心垂直向里,磁场分别位于网格的边上,粗细网格比为3 ∶ 1,图 2中红色箭头表示粗网格磁场值、灰色小箭头表示需要插值计算的细网格磁场值,粗网格中应用FDTD算法,细网格中应用ADI-FDTD算法,进行电磁场时间步推进时,在大小网格的交界处,细网格的场值更新的部分数据在粗网格上是缺失的,这就需要用到插值技术,粗细网格之间过渡与衔接、场值的交换与更新是本算法的重要内容.
 | 图 2 ADI-FDTD亚网格技术粗细网格及场值分布示意图Fig. 2 The field distributing sketch map of coarse grid and fine grid on ADI-FDTD subgridding method |
粗细网格的场值交换格式有多种,可以采取粗细网格边界纯磁场交换格式、纯电场交换格式、电磁场结合交换格式(Diamanti,2008).此外,在选取场值交换时也有细微的区别,可以仅选取传递粗细网格边界上的磁场值,也可以选取粗细网格边界附近的一个粗网格上的电磁场值.本文采用电磁场结合的交换格式,其电磁场交换格式如图 3所示,图中粗网格FDTD计算出的磁场值H x、 H y置于每个网格边上的中间位置,传递进细网格hx、hy,红色的细箭头表示需要插值计算的磁场值,ADI-FDTD细网格计算完成以后,再将图 3中粗细网格边界向细网格内的0.5个粗网格处红色标记的电场值ez传回给FDTD粗网格E z,该算法的详细计算过程见流程图 4.根据Chevalier et al.(1997)与Diamanti(2008)的研究,应用亚网格算法进行电磁场计算中,粗细网格的比最好不超过11,为了避免电磁场的突然改变,物性介质分界面不要置于粗细网格的边界,而异常体的每边距离粗细网格的分界面最好有3个粗网格的距离.此外,计算过程中为了粗网格的FDTD与细网格的ADI-FDTD计算时间上的同步,将ADI-FDTD的时间步长设为粗网格FDTD时间步长的一半,这样在每计算一个FDTD时间步长,ADI-FDTD算法调用两次,两次加起来刚好与FDTD的一个时间步长相等,这样设置比将FDTD与ADI-FDTD采用同样的时间步长精度更高.
 | 图 3 粗细网格场值交换格式Fig. 3 The tranfer mode of field value between on coarse grid and fine grid |
 | 图 4 ADI-FDTD亚网格技术计算流程图Fig. 4 The flow chart of ADI-FDTD subgridding formulation computation |
分析图 2、3可知,设置粗细网格比为3 ∶ 1的奇数倍,可将粗网格的电磁场值直接赋予细网格的磁场值,方便粗细网格间的电磁场值的数据交换.当采用图 5所示的粗细网格比为4 ∶ 1的偶数倍时,则粗网格的磁场值并不在某一小格的边上,需要进行插值计算,而ADI-FDTD细网格计算完成以后,电场值ez传递回FDTD粗网格E z时(图中的绿色大圆点),需要周围的4个相邻的ez场值的平均,给计算带来了一定的不便,但理论上是可行的,因此,粗细网格比理论上可以为任意倍数.而图 3中的粗细网格界面处的磁场值(红色小箭头表示的),可以采用 简单的线性插值计算,如图 6所示,以y方向磁场为例:

本文仅需式(33)中2个插值公式即可.如果采用粗细网格边界1个粗网格内的场值交换方式,还需计算:
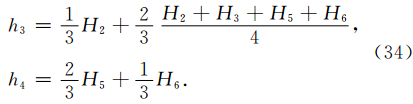
 | 图 5 粗细网格比为4倍时的网格及场值分布示意图Fig. 5 Sketch map of coarse grid to fine grid ratio equal to 4 |
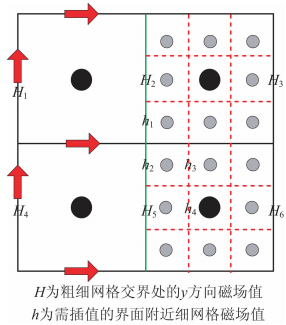 | 图 6 磁场线性插值计算示意图Fig. 6 Sketch map of line interpolation |
模型一如图 7所示,模型区域3.0 m×2.0 m,背景介质为混凝土,其介电常数6.0,电导率 0.0005 S·m-1,混凝土介质中有1个埋深0.5 m,大小0.4 m×0.1 m 薄矩状素填土缺陷,其介电常数10.0,电导率0.002 S·m-1,对角点坐标(1.3 m,0.6 m)、(1.7 m,0.5 m).正演中UPML边界设为8层粗网格,Ricker子波距边界为10层网格,主频900 MHz.为了说明ADI-FDTD亚网格技术的计算效率及精度,将该算法与均匀剖分的粗网格FDTD、细网格FDTD算法进行对比.计算环境为Intel(R)CoreTM i5 CPU,P8600@2.67 GHz,1.17 GHz+2.86 GB的内存物理地址扩展,Window XP操作系统的联想(IBM)X201笔记本.一致粗网格模拟步长Δx=Δy=0.009 m,粗网格数332×221,占用内存1.84 Mb,时间步长 Δt=2.123×10-11 s,时窗长度取12 ns,每隔0.05 m 采集一道雷达数据,计算50道雷达数据,共计花费时间1′24″.空间一致细网格模拟步长Δx′=Δy′=0.003 m,细网格数999×666,占用内存11.92 Mb,时间步长Δt′=0.826×10-11 s,时窗长度同样设为12 ns,模拟50道雷达数据,共计花费时间21′11″.应用异常体及其周围区域细网格剖分,其他区域采用粗网格剖分的ADI-FDTD亚网格技术计算,粗细网格比为3 ∶ 1,细网格区域大小设为0.81 m×0.42 m,细网格数270×140,其余区域设为粗网格,粗细网格时间步长统一取Δt=2.123×10-11,由于细网格区域的ADI-FDTD算法分2步进行,取它的时间步长为FDTD时间步长的一半,该算法占用内存2.38Mb,共计花费时间2′46″.3种算法的计算资源占用情况详见表 1.
 | 图 7 薄矩状异常体地电模型及亚网格剖分示意图Fig. 7 The sketch map of thin rectangle anomalous body model and subgridding splitting |
|
|
表 1 模型一3种算法计算资源占用详情Table 1 The occupation detail of calulate resource with three methods for model 1 |
图 8为3种方法模拟所得的单道雷达记录,图 8a中红色曲线代表粗网格方法,绿色的星号代表细网格方法,黑色曲线代表ADI-FDTD亚网格技术,图中可见,3种算法结果基本吻合,一致性比较好,只是在直达波的位置,粗网格的Ez负场值较另外两种方法稍大,8.2 ns与10.4 ns附近的正负波峰很好地对应了薄矩状异常体的上下界面;图 8b为截取图 8a中7~12 ns时刻放大后的雷达记录,图中黑色的曲线(ADI-FDTD亚网格技术)与绿色的曲线(细网格)吻合得更好,红色曲线(粗网格)与另外两条曲线稍有偏差.如果认为细网格与计算结果与解析解接近,说明ADI-FDTD亚网格技术在使用较 少内存、较短运行时间的前提下,计算结果具有较高的精度,在运算时间与计算精度方面达到了较好的平衡.
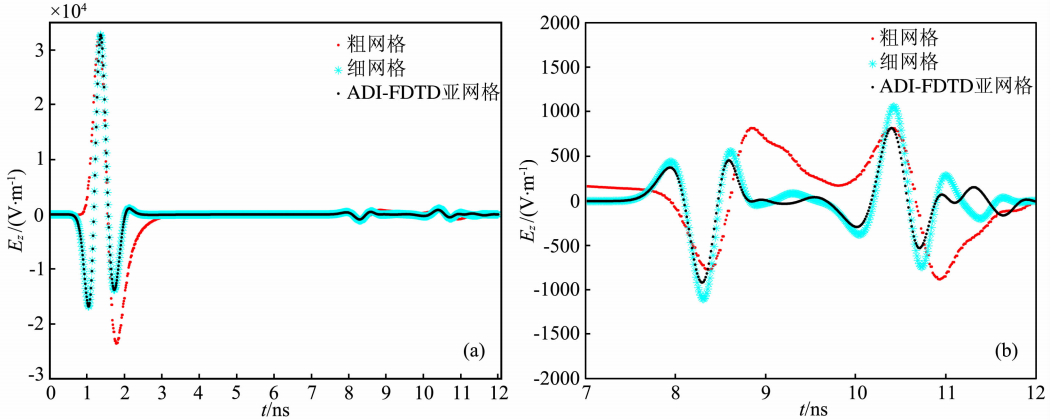 | 图 8 模型一3种方法计算的单道雷达数据(a)0~12 ns的雷达数据;(b)7~12 ns放大后的雷达数据.Fig. 8 The map of single track radar data of model one with three methods |
模型二设计为了对比频散介质与非频散介质的雷达波传播特征,如图 9所示,该模型为3.0 m×2.0 m的矩形区域,左边非均匀背景媒质的相对介电常数εr=6.0,电导率σ1=0.002 s·m-1,右边频 散媒质采用Debye模型表示,ε∞r=10.28,ε0r=19.0,电导率σ1=0.002 S·m-1,驰豫时间τ5 ns;在背景媒质中有3个异常体,其中2个圆形异常体具有相 同的半径r=0.1 m,左边圆形异常体为圆心在(1.2 m,0.5 m)处的金属介质,右边的圆形异常体其圆心在(1.8 m,0.5 m),相对介电常数εr=3.0,电导率σ1=0.0001 S·m-1.在2个圆形异常体的下方为矩形异常体,矩形异常体的长与宽均 为0.3 m,它距离左边界1.35 m,距离上边界0.85 m,圆形异常体的相对介电常数εr=6.0,电导率 σ1=0.005 S·m-1.Ricker子波主频为500 MHz,UPML边界与源的位置与上例一致.
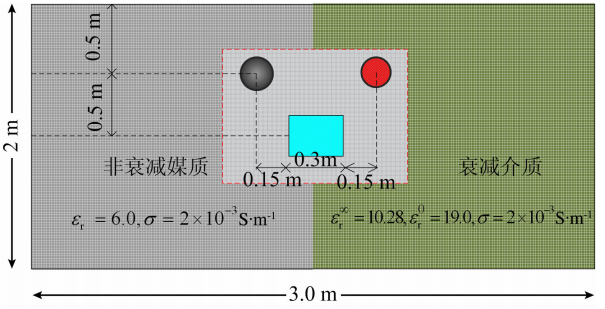 | 图 9 模型二示意图Fig. 9 The sketch map of model two |
一致粗网格空间步长Δx=Δy=0.015 m,占 用内存0.68 Mb,时间步长Δt=3.538×10-11 s,时窗长度取25 ns,采样间隔为0.015 m,与上例同等计算条件下计算190道雷达数据,共计花费时间 2′30″.细网格空间步长Δx′=Δy′=0.005 m,内存占用5.88 Mb,时间步长Δt′=1.1793×10-11 s,时窗长度取25 ns,采样间隔为0.015 m,计算190道雷达数据,共计花费时间45′36″.应用本文的基于亚网格技术的ADI-FDTD 算法,只在异常体及其周围区域采用细网格ADI-FDTD计算,其 他区域采用粗网格FDTD计算,粗细网格比为3 ∶ 1,细网格区域大小设为1.0 m×1.0 m,时间步长设为Δt=3.538×10-11,ADI-FDTD亚网格技术的算法占用内存为1.55 Mb,共计花费时间9′41″.模型二3种算法计算资源占用情况详见表 2.
|
|
表 2 模型二3种算法计算资源占用详情Table 2 The occupation detail of calulate resource with three methods for model 2 |
模型二的GPR正演剖面比较复杂,为了更好地理解正演图中的波形特征,采用在模型中分步加入异常体的方法,从简到繁,便于理解.图 10假定模拟 区域充填图 9中左边均匀非频散介质的情况,该均 匀介质雷达剖面图中因没有异常体的存在故不存在反射波,只有直达波与场源第二次到达时的波峰(简称场源二次波),该处显示的场源二次波及其后面的场源多次波是由于增益分段放大显示,与作者将数据写入GSSI软件显示方式有关;图 11为左右两边 存在不均匀非频散介质,左边介质与图 9中左边介 质一致,右边介质相对介电常数为19.0,电导率0.002 S·m-1.图中可见,由于介质分界面的存在,天线在左边介质时逐渐靠近界面时,分界面反射双程走时越来越短,最后靠近分界面,双程走时为零,故图中反射曲线为一条斜线,而当天线处于右边介质中时,雷达天线逐渐远离介质分界面,故分界面反射双程走时越来越长,由于天线两边介质雷达波传播速度的不同导致了两条强反射界面斜率的不一致,右边介质介电常数大,故传播速度小,导致斜率大.此外,介质分界面的二次反射波及场源的多次波峰图中也清晰可辨.
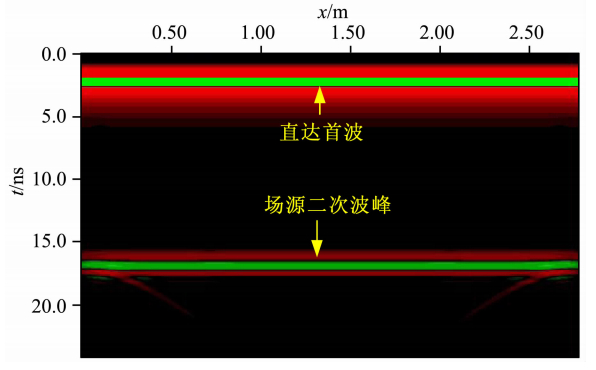 | 图 10 均匀介质常规FDTD计算的GPR扫描图Fig. 10 GPR map of homogeneous medium model |
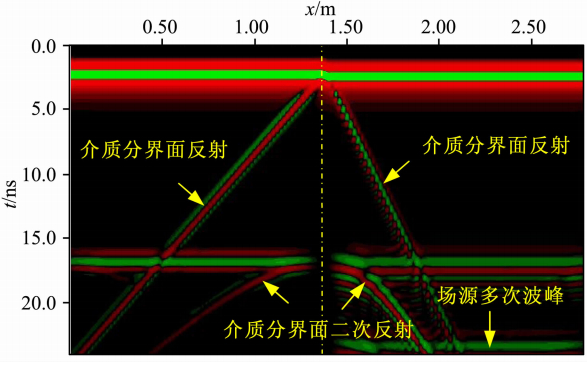 | 图 11 不均匀介质常规FDTD计算的GPR扫描图Fig. 11 GPR map of nonuniformity model |
图 12为去掉模型二中3个异常体所得的正演剖面图,由图 12中可见,由于右边频散媒质驰张时间及介电常数的差异,导致原本同一波形1与2,出现明显的错位,再利用该模型进行波场快照,将源与接收位置都置于模型中心,选取图 16中的7 ns与9 ns波场快照,分析可知,随着时间的推进,雷达波 以球面形式向外扩散能量以指数方式衰减,离场源中心越远则能量越弱,由于电磁波在左边介质传播得较右边更快,距离场源更远,能量应该更弱,但两幅图中Ez波场幅值与该结论明显相反,左边的波场幅值较右边的更大,显然这是由于右边频散介质对雷达波吸收较厉害,导致同时刻右边频散介质的波场能量较左边更弱.
 | 图 12 去掉模型二中异常体的不均匀介质GPR扫描图Fig. 12 GPR map of remove the anomalous bodies of model 2 |
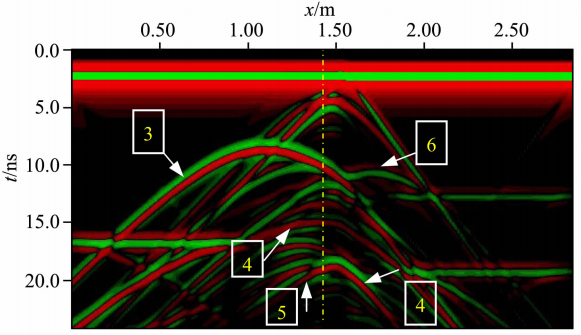 | 图 13 模型二一致细网格GPR扫描图Fig. 13 GPR map of model 2 with fine mesh |
图 13、14、15为分别运用一致细网格FDTD、一致粗网格FDTD及其ADI-FDTD亚网格技术对模型二模拟所得的GPR扫描图,图中波形3为左边圆形金属异常体上界面的反射波、6为右边圆形异常体的上界面,4与5分别为矩状异常体的上、下界面,3种算法对异常体都能有较好的反映,其中一致细网格算法的波场信息最为丰富,对细微结构反映最好,ADI-FDTD亚网格技术其次,粗网格算法在局部波形上甚至出现细微频散、不光滑现象,而ADI-FDTD亚网格方法尽管也出现了细微频散现象,但细节信息较一致粗网格FDTD算法更丰富、局部波形更光滑.综合考虑占用内存、模拟时间及数据精度,基于ADI-FDTD亚网格方法达到了一个较好的均衡.
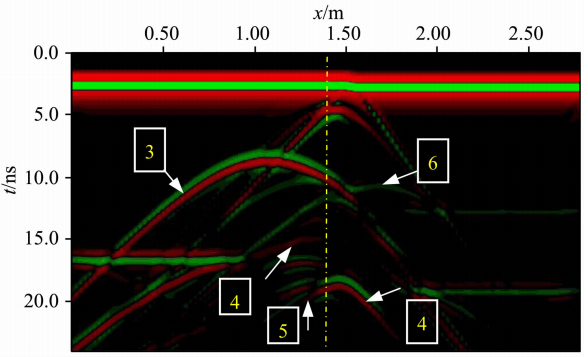 | 图 14 模型二一致粗网格GPR扫描图Fig. 14 GPR map of model 2 with coarse mesh |
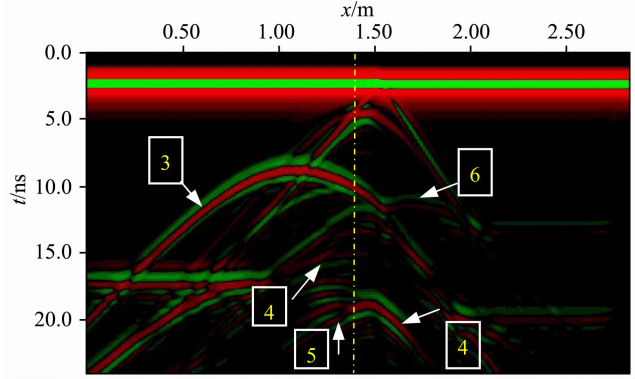 | 图 15 ADI-FDTD亚网格技术GPR扫描图Fig. 15 GPR map of model 2 with ADI-FDTD subgridding mesh |
为了能更直观地展示雷达波在地下媒质中的传播过程,将场源与接收点都置于模型中心,然后利用ADI-FDTD亚网格算法模拟模型2并绘制了图 17所示的5 ns、6 ns、7 ns、8 ns时的波场快照.图中颜色的强弱代表电场幅值的大小.图 17a中,GPR波在两边介质中以不同速度呈半圆形扩散,当遇到矩状异常体的4条边时,波形大部分能量继续向外传播,一部分能量被4条边反射回来;图 17b中,由于左右两边为不同介质,左边介质中雷达波传播较快,右边介质速度传播较慢,所以两边介质中圆的大小显然不一致,传播速度较快的左边介质,雷达波前传得更快、圆的半径更大,此时传播更快的左边介质中,波前刚好到达了圆形金属异常体的位置,并开始产生绕射波;图 17c中,GPR波继续向外扩散,速度较慢介质中雷达波前到达右边圆形异常体,刚开始产生绕射,而左边的圆形金属异常体、及其中间矩形异常体产生的绕射波与原波前以相反方向呈圆形扩散;图 17d中清晰可见GPR波波前到达的位置,由于介质两边雷达波传播速度的不一致,左边波前传播更快、左边圆形金属异常体绕射波产生的圆弧更大,而右边的异常体也产生了明显的绕射波,只是该绕射波产生的圆弧更小些.图中的各异常体反射波、绕射波清晰可辨.
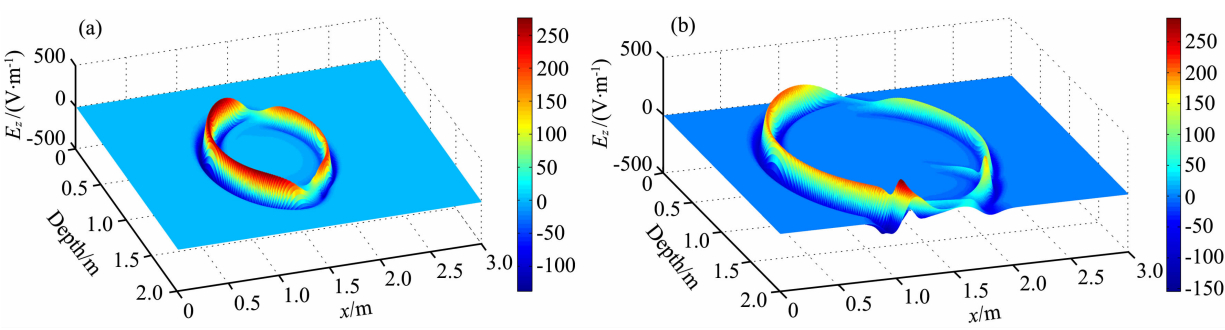 | 图 16 模型2去掉异常体不同时刻波场快照3D显示(a)7 ns波场快照;(b)9 ns波场快照.Fig. 16 The 3D display of wavefield snapshot in difference moment of model 2 by remove the anomalous bodies |
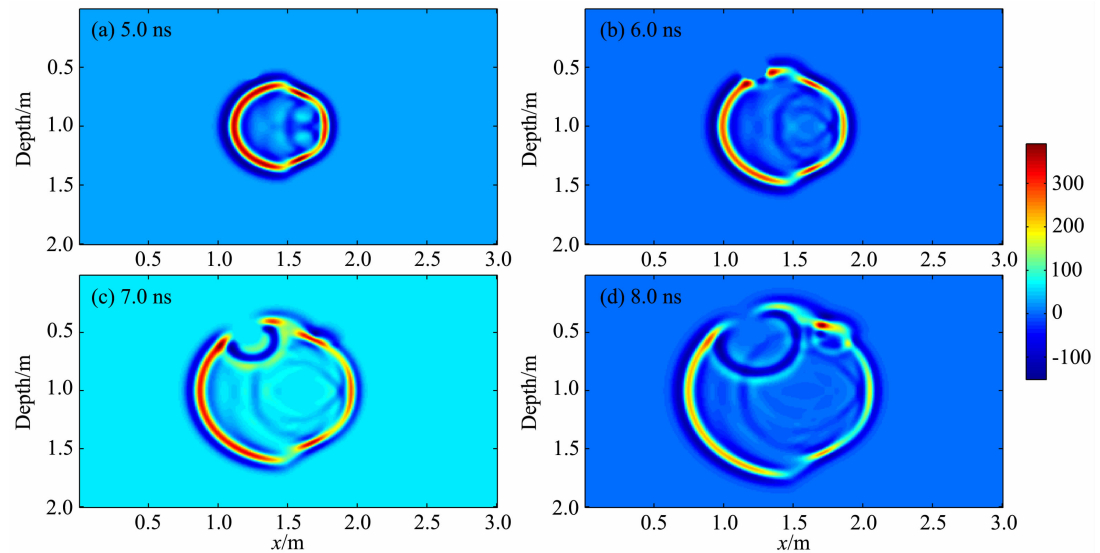 | 图 17 模型二不同时刻波场快照Fig. 17 The wavefield snapshot in difference moment of model 2 |
(1)提出了基于混合ADI-FDTD亚网格技术GPR正演算法,即在物性参数变化剧烈局部区域采用细网格剖分ADI-FDTD计算,其他的区域采用常规FDTD计算,因为ADI-FDTD突破了CFL条件的约束,可选取与粗网格一致的大时间步长,计算中只需考虑空间不一致网格的场值交换问题,时间步长一致完全不用考虑,编程计算较双变步长算法简便,有效地提高了计算效率.
(2)该混合ADI-FDTD亚网格技术能较好地适用于局部细微结构的模拟,在保证计算精度前提下有效减少内存占用,在精确性与时效性之间取得满意的平衡.该算法被用于频散介质及非频散介质的组合模型的正演计算中,雷达正演剖面图及波场快照结果都表明,考虑介质对雷达波的衰减的正演计算结果更符合雷达波实际地下的传播特征,能更有效指导工程资料的精确解释.
| [1] | Ahmed I, Chen Z Z.2004.A hybrid ADI-FDTD subgridding scheme for efficient electromagnetic computation. International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 17(3): 237-249. |
| [2] | Bano M.2004.Modelling of GPR waves for lossy media obeying a complex power law of frequency for dielectric permittivity. Geophysical Prospecting, 52(1): 11-26. |
| [3] | Cassidy N J, Millington T M.2009.The application of finite-difference time-domain modelling for the assessment of GPR in magnetically lossy materials. Journal of Applied Geophysics, 67(4): 296-308. |
| [4] | Chevalier M W, Luebbers R L, Cable V P.1997.FDTD local grid with material traverse. IEEE Transactions on Antennas and Propagation, 45(3): 411-421. |
| [5] | Di Q Y, Wang M Y.1999.2D finite element modeling for radar wave.Chinese J.Geophys. (in Chinese), 42(6): 818-825. |
| [6] | Diamanti N, Giannopoulos A.2009.Implementation of ADI-FDTD subgrids in ground penetrating radar FDTD models. Journal of Applied Geophysics, 67(4): 309-317. |
| [7] | Diamanti N.2008.An efficient Ground Penetrating Radar finite-Difference time-Domain Subgridding Scheme and Its Application to the Non-descructive Testing of Masonry arch Bridges. Edinburgh : The University of Edinburgh. |
| [8] | Falk J, Tessmer E, Gajewski D.1998.Efficient finite-difference modelling of seismic waves using locally adjustable time steps. Geophysical Prospecting, 46(6): 603-616. |
| [9] | Fang G Y, Zhang Z Z, Wang W B.1996.Numerical simulation of time-domain EM scattering by shallow subsurface objects. Journal of Electronics and Information Technology (in Chinese), 18(3): 276-282. |
| [10] | Fang H Y, Lin G.2012.Symplectic partitioned Runge-Kutta methods for two-dimensional numerical model of ground penetrating radar. Computers & Geosciences, 49: 323-329. |
| [11] | Fang H Y, Lin G.2013.Simulation of GPR wave propagation in complicated geoelectric model using symplectic method.Chinese J.Geophys.(in Chinese), 56(2): 653-659. |
| [12] | Feng D S, Chen C S, Dai Q W.2010.GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD.Chinese J.Geophys. (in Chinese), 53(10): 2484-2496. |
| [13] | Feng D S, Chen C S, Wang H H.2012.Finite element method GPR forward simulation based on mixed boundary condition.Chinese J.Geophys.(in Chinese), 55(11): 3774-3785. |
| [14] | Feng D S, Dai Q W, Weng J B.2007.Application of multi-resolution time domain method in three dimensions forward simulation of ground penetrating radar. Journal of Central South University: Science and Technology (in Chinese), 38(5): 975-980. |
| [15] | Feng D S, Wang H H, Dai Q W.2013.Forward simulation of Ground Penetrating Radar based on the element-free Galerkin method.Chinese J.Geophys.(in Chinese), 56(1): 298-308. |
| [16] | Feng X, Zou L L, Liu C, et al.2011.Forward modeling for full polarimetric ground penetrating radar.Chinese J.Geophys.(in Chinese), 54(2): 349-357. |
| [17] | Ge D B, Yan Y B.2005.Finite-Difference Time-Domain Method for Electromagetic Waves (2nd ed).(in Chinese).Xi'an: Xidian University Press. |
| [18] | Giannopoulos A.2005.Modelling ground penetrating radar by GprMax. Construction and Building Materials, 19(10): 755-762. |
| [19] | Huang C, Dong L G.2009.High-order finite-difference method in seismic wave simulation with variable grids and local time-steps.Chinese J.Geophys. (in Chinese), 52(1): 176-186. |
| [20] | Huang C, Dong L G.2009.Staggered-grid high-order finite-difference method in elastic wave simulation with variable grids and local time steps.Chinese J.Geophys. (in Chinese), 52(11): 2870-2878. |
| [21] | Irving J, Knight R.2006.Numerical modeling of ground-penetrating radar in 2-D using MATLAB. Computers & Geosciences, 32(9): 1247-1258. |
| [22] | Li J, Zeng Z F, Huang L, Liu F S.2012.GPR simulation based on complex frequency shifted recursive integration PML boundary of 3D high order FDTD. Computers & Geosciences, 49: 121-130. |
| [23] | Li J, Zeng Z F, Wu F S, et al.2010.Study of three dimension high-order FDTD simulation for GPR.Chinese J.Geophys (in Chinese), 53(4): 974-981. |
| [24] | Li Q W.2008.The Propagation of GPR Pulse in the Lossy, Dispersive, and Inhomogeneous Earth Medium (in Chinese).Chengdu: Chengdu University of Technology. |
| [25] | Li Z H, Huang Q H, Wang Y B.2009.A 3-D staggered grid PSTD method for borehole radar simulations in dispersive media.Chinese J.Geophys.(in Chinese), 52(7): 1915-1922. |
| [26] | Liu S B, Liu S, Hong W.2010.Dispersive medium FDTD method (in Chinese).Beijing: Science Press. |
| [27] | Liu S X, Zeng Z F.2007.Numerical simulation for Ground Penetrating Radar wave propagation in the dispersive medium.Chinese J.Geophys.(in Chinese), 50(1): 320-326. |
| [28] | Lu T, Cai W, Zhang P W.2005.Discontinuous galerkin time-domain method for GPR simulation in dispersive media. IEEE Transactions on Geoscience and Remote Sensing, 43(1): 72-80. |
| [29] | Luebbers R J, Hunsberger F P, Kunz K S, et al.1990.A frequency-dependent finite-difference time-domain formulation for dispersive materials.IEEE Trans.Electromagn.Compat. , 32(3): 222-227. |
| [30] | Luebbers R J, Hunsberger F P, Kunz K S.1991.A frequency-dependent finite-difference time-domain formulation for transient propagation in plasma.IEEE Trans. Antennas Propagat, 39(1): 29-34. |
| [31] | Moczo P.1989.Finite-difference technique for SH-waves in 2-D media using irregular grids-application to the seismic response problem. Geophysical Journal International, 99(2): 321-329. |
| [32] | Namiki T.1999.A new FDTD algorithm based on alternating-direction implicit method. IEEE Transactions on Microwave Theory and Techniques, 47(10): 2003-2007. |
| [33] | Shen B.1994.A study on wave eguation theory for ground——penetrating radar and forward mooelling. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 16(1): 29-33. |
| [34] | Teixeira F L.2008.Time-domain finite-difference and finite-element methods for Maxwell equations in complex media. IEEE Transactions on Antennas and Propagation, 56(8): 2150-2166. |
| [35] | Tessmer E.2000.Seismic finite-difference modeling with spatially varying time steps. Geophysics, 65(4): 1290-1293. |
| [36] | Tian G, Lin J X, Wang B B, et al.2011.Simulation and analysis reflections interference from above surface objects of ground penetrating radar.Chinese J.Geophys. (in Chinese), 54(10): 2639-2651. |
| [37] | Wang B Z, Wang Y J, Yu W H, et al.2001.A hybrid 2-D ADI-FDTD subgridding scheme for modeling on-chip interconnects. IEEE Transactions on Advanced Packaging, 24(4): 528-533. |
| [38] | Yee K S.1966.Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media. IEEE Transactions on Antennas and Propagation, 14(3): 302-307. |
| [39] | Zeng Z F, Liu S X, Feng X.2010.Theory and application of Ground Penetrating Radar (in Chinese).Beijing: Electronic Industry Press. |
| [40] | Zhang H, Li Z C.2011.Forward modeling of carbonate fracture reservoir based on time-space dual variable grid algorithm. Journal of China University of Petroleum: Edition of Natural Science (in Chinese), 35(3): 51-57. |
| [41] | Zheng K S.2005.Study of FDTD Parallel Computing and ADI-FDTD Method (in Chinese).Xi'an: Institute of Science, Xidian University. |
| [42] | Zivanovic S S, Yee K S, Mei K K.1991.A subgridding method for the time-domain finite-difference method to solve Maxwell's equations. IEEE Transactions on Microwave Theory and Techniques, 39(3): 471-479. |
| [42] | 底青云,王妙月。1999.雷达波有限元仿真模拟。 地球物理学报,42(6):818-825. |
| [42] | 方广有,张忠治,汪文秉。1996.浅层地下目标时域电磁散射问题的数值模拟。 电子与信息学报,18(3):276-282. |
| [43] | 方宏远, 林皋.2013.基于辛算法模拟探地雷达在复杂地电模型中的传播. 地球物理学报, 56(2): 653-659. |
| [44] | 冯德山, 陈承申, 戴前伟.2010.基于UPML边界条件的交替方向隐式有限差分法GPR全波场数值模拟. 地球物理学报, 53(10): 2484-2496. |
| [45] | 冯德山, 陈承申, 王洪华.2012.基于混合边界条件的有限单元法GPR正演模拟. 地球物理学报, 55(11): 3774-3785. |
| [46] | 冯德山, 戴前伟, 瓮晶波.2007.时域多分辨率法在探地雷达三维正演模拟中的应用. 中南大学学报: 自然科学版, 38(5): 975-980. |
| [47] | 冯德山, 王洪华, 戴前伟.2013.基于无单元Galerkin法探地雷达正演模拟. 地球物理学报, 56(1): 298-308. |
| [48] | 冯晅, 邹立龙, 刘财等.2011.全极化探地雷达正演模拟. 地球物理学报, 54(2): 349-357. |
| [49] | 葛德彪, 闫玉波.2005.电磁波时域有限差分方法(第二版).西安: 西安电子科技大学出版社. |
| [50] | 黄超, 董良国.2009a.可变网格与局部时间步长的高阶差分地震波数值模拟. 地球物理学报, 52(1): 176-186. |
| [51] | 黄超, 董良国.2009b.可变网格与局部时间步长的交错网格高阶差分弹性波模拟. 地球物理学报, 52(11): 2870-2878. |
| [52] | 李静, 曾昭发, 吴丰收等.2010.探地雷达三维高阶时域有限差分法模拟研究. 地球物理学报, 53(4): 974-981. |
| [53] | 李庆伟.2008.有耗色散地质介质中的GPR脉冲传播研究[博士论文]. 成都: 成都理工大学. |
| [54] | 李展辉, 黄清华, 王彦宾.2009.三维错格时域伪谱法在频散介质井中雷达模拟中的应用. 地球物理学报, 52(7): 1915-1922. |
| [55] | 刘少斌, 刘崧, 洪伟.2010.色散介质时域有限差分方法.北京: 科学出版社. |
| [56] | 刘四新, 曾昭发.2007.频散介质中地质雷达波传播的数值模拟. 地球物理学报, 50(1): 320-326. |
| [57] | 沈飚.1994.探地雷达波波动方程研究及其正演模拟. 物探化探计算技术, 16(1): 29-33. |
| [58] | 田钢, 林金鑫, 王帮兵等.2011.探地雷达地面以上物体反射干扰特征模拟和分析. 地球物理学报, 54(10): 2639-2651. |
| [59] | 曾昭发, 刘四新, 冯晅等.2010.探地雷达原理与应用.北京: 电子工业出版社. |
| [60] | 张慧, 李振春.2011.基于时空双变网格算法的碳酸盐岩裂缝型储层正演模拟. 中国石油大学学报: 自然科学版, 35(3): 51-57. |
| [61] | 郑奎松.2005.FDTD网络并行计算及ADI-FDTD方法研究[博士论文]. 西安: 西安电子科技大学理学院. |
 2014, Vol. 57
2014, Vol. 57


