地球物理学报  2014, Vol. 57 Issue (4): 1292-1299   PDF    
引用本文
李展辉, 黄清华. 2014. 复频率参数完全匹配层吸收边界在瞬变电磁法正演中的应用. 地球物理学报, 57(4): 1292-1299, doi: 10.6038/cjg20140426   
LI Zhan-Hui, HUANG Qing-Hua. 2014. Application of the complex frequency shifted perfectly matched layer absorbing boundary conditions in transient electromagnetic method modeling. Chinese J. Geophys. (in Chinese), 57(4): 1292-1299, doi: 10.6038/cjg20140426   
复频率参数完全匹配层吸收边界在瞬变电磁法正演中的应用
李展辉, 黄清华    
北京大学地球与空间科学学院地球物理学系, 北京 100871
投稿时间：2013-1-23; 最后修改时间：2014-3-11 .
基金项目：科技部国际合作项目（2010DFA21570），国家杰出青年基金项目（41025014）资助.
第一作者简介：李展辉，男，北京大学地球物理学系博士研究生，主要从事瞬变电磁法和探地雷达方面的数值模拟研究.E-mail：zhanhuipku04@163.com
通讯作者：黄清华，男，1967年生，北京大学教授，1990年毕业于中国科学技术大学，1999年获日本大阪大学博士学位.主要从事地震物理学、地球电磁学方面的教学和科研工作.E-mail：huangq@pku.edu.cn
摘要：本文将复频率参数完全匹配层（Complex Frequency Shifted Perfectly Matched Layer，CFS-PML）吸收边界应用到瞬变电磁法（Transient Electromagnetic，TEM）三维正演中，以替代传统的狄利克雷边界条件，使用时域有限差分法（Finite-difference time-domain，FDTD）进行空间离散和时间步进.本文给出了扩散场在CFS-PML内部的平面波解，分析了常规PML在TEM正演中失效的原因，并给出了CFS-PML在TEM正演中参数设置准则.最后分别使用全空间和半空间模型进行有效性检验.全空间检验结果表明，使用CFS-PML的解在我们正演的所有延迟时间内均与理论解吻合得非常好，而使用狄利克雷边界的解可与理论解偏离一个量级以上.半空间检验结果表明，CFS-PML亦明显优于狄利克雷边界，然而CFS-PML对空气中的场吸收甚微，相对误差依然会随着延迟时间缓慢增加，正演时需要根据误差容忍度设计适当的模型.
关键词： 瞬变电磁     三维正演     时域有限差分     吸收边界     CFS-PML    
Application of the complex frequency shifted perfectly matched layer absorbing boundary conditions in transient electromagnetic method modeling
LI Zhan-Hui, HUANG Qing-Hua    
Department of Geophysics, School of Earth and Space Sciences, Peking University, Beijing 100871, China
Abstract: Instead of the conventional Dirichlet boundary condition (DBC),the complex frequency shifted perfectly matched layer (CFS-PML) absorbing boundary condition was applied in transient electromagnetic (TEM) method modeling. A finite difference time domain (FDTD) method was used for space discretization and time stepping. We obtained the plane wave solutions inside the CFS-PML and pointed out the reason why the regular PML fails for TEM modeling. We also provided a criterion for the selection of the parameters of CFS-PML. These ideas were validated for both the whole space and the half space models. The results of a whole space model using CFS-PML showed excellent consistency with the analytical solutions, while those using DBC deviated more than one order of magnitude at the latest delay time. The results of a half space model also showed great superiority of CFS-PML compared to DBC. However, the lack of absorbing ability of CFS-PML in the air caused some errors which could increase with time slowly. Proper models should be designed according to the permitted error.
Key words: Transient electromagnetic     Three-dimensional forward modeling     Finite difference time domain (FDTD)     Absorbing boundary condition     CFS-PML    

1 引言

时域有限差分(Finite difference time domain，FDTD)是瞬变电磁法(Transient electromagnetic，TEM)正演常用方法之一.Goldman和Stoyer(1983)首次使用隐式FDTD模拟三维轴对称模型，随后Oristaglio和Hohmann(1984)使用修改的Du Fort-Frankel格式模拟了TEM二维模型，Wang和Hohmann(1993)在Du Fort-Frankel 格式的基础上发展了 一种TEM三维FDTD正演方法，为后续部分 学者借用(孙怀凤等，2013； 许洋铖等，2012； Commer and Newman， 2004；Endo and Noguchi， 2002).FDTD对TEM的三维正演是在有限模型空间内模 拟能扩散到更大区域的瞬变场，因而需要引入截 断边界条件.正演中通常采用狄利克雷边界条件(Dirichlet boundary condition，DBC)(Wang and Hohmann， 1993)，并设置边界足够远.DBC在扩散场未抵达或刚抵达边界时效果较好，但随着延迟时间的推移，反射场将对原扩散场产生较大的干扰.要消除这种干扰，则需要更大的模型，这将增加内存和计算量.因而一些学者开始研究其他的吸收边界来代替DBC，比如Mur吸收边界(秦臻和胡文宝，2004；姬金祖，2008；岳建华，2007)以及在其基础上修改而来的新吸收边界条件(杨海燕和岳建华，2009).但是他们并没有对吸收边界的效果作详细的讨论，也没有给出与理论解的对比.李墩柱(2010)将电磁波正演中应用最普遍的完全匹配层(Perfectly Matched Layer，PML)吸收边界(Berenger， 1994，1996；李展辉等，2009；Chew and Weedon， 1994)应用到TEM半空间模型正演中，然而文中模型的水平范围为[-3000m，3000m]，半空间电导率为0.01S·m-1，但是最长延迟时间仅为8ms，涡流电场形成的“烟圈”还远未到达边界，晚期吸收效果并不明确，在参数设置上也仅仅说明需要多次尝试.本文深入研究了PML在TEM正演中的吸收效果，并最终采用了其中的一种——复频率参 数完全匹配层(Complex Frequency Shifted Perfectly Matched Layer，CFS-PML)(Kuzuoglu and Mittra， 1996；Roden and Gedney， 2000；姜永金等，2004；Berenger，2012).首先通过推导扩散场在常规PML内部的平面波解的形式，指出了常规PML在TEM正演中失效的原因，然后给出了扩散场在CFS-PML内部的平面波解，研究了CFS-PML各项参数对吸收效果的影响，并给出了CFS-PML的参数选择方案.最后将CFS-PML应用到全空间和半空间模型中以验证CFS-PML的有效性.同时为了提高半空间模型的正演效率，本文采用了李展辉和黄清华(2011)提出的新方法，而全空间模型正演则采用普遍使用的Du Fort-Frankel格式.

2 理论推导 2.1 含PML的Maxwell频域方程组

频率域带PML的旋度方程可以表示为(Chew and Weedon， 1994)

其中

常规PML中(Chew and Weedon， 1994)，

CFS-PML中(Roden and Gedney， 2000)，

其中κu为网格延拓因子，由于本文采用非等距网格，κu可直接包含于网格中.因此在下文中所有的κu值都设置为1.令ε′=ε－jσ/ω，可得

2.2 常规PML和CFS-PML的吸收性质

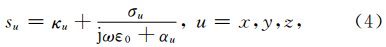
设式(5)的平面波解为

定义复波速

可得到频散方程

其中kx，ky，kz可表示为

对于常规PML，式(6)可写为

其中

而TEM的低频近似满足

那么复波速可以近似为

将式(13)代入到式(10)中，并且考虑在x方向吸收，设置(σx，σy，σz)=(σx，0，0)，可得

设

为PML的吸收系数，APML越小，代表吸收越强烈.从式(15)中可以看出，随着角频率ω的减小，APML也会随着减小，而当ω→0时，亦有APML→0.这意味着PML对低频场的吸收随着频率的降低而更为强烈，过强的吸收在数值计算中会引起大的异常(Berenger， 2000，1996).

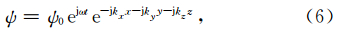
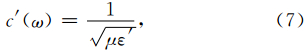
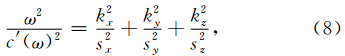
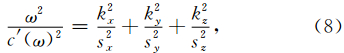
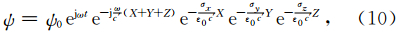
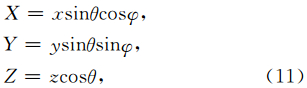
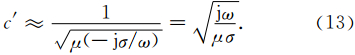
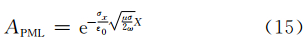
对于CFS-PML，经过类似的推导之后可以得到

从式(16)可以看出，αx的出现使得CFS-PML避免了在ω接近0时出现吸收非常强烈的现象.

设置CFS-PML的一个参考频率：

把式(17)代入式(16)，得

当f≥fαx时，式(18)近似为式(14)，CFS-PML退化成常规PML；当f≤fαx时，式(18)近似为

这仅仅是x方向的网格延拓.

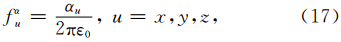
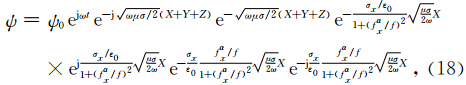
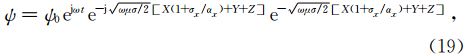
瞬变场的优势频率会随着时间逐渐变低.当优势频率足够低并进入PML内部时，PML会对这些优势频率产生过强的吸收进而使整个瞬变场产生异常.而CFS-PML能避免这种情况，但是σx/αx这个比例非常重要，从式(19)可以看出，对于f≤fαx频率部分只是一个网格延拓因子，如果过大同样 会引起数值异常.为此我们可以设置另一个参考频率：

fσx受到fαx的控制.式(18)可以进一步写成

2.3 含CFS-PML的Maxwell时域方程组

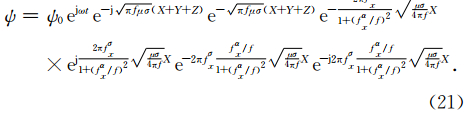
时域方程组可以用卷积的形式表达出来(Roden and Gedney， 2000)，以Ex为例：

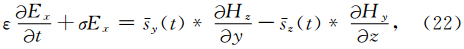
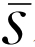其中y(t)和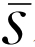z(t)分别是1/sy(ω)和1/sz(ω)的拉普拉斯逆变换：

其中δ(t)是狄拉克函数，ζu(t)可以表述如下：

其中u(t)为单位阶跃函数.那么最终式可以表示为

其中

其他分量可以类似地表达出来.

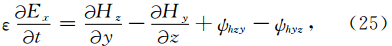
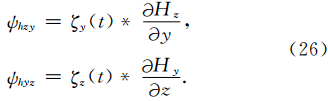
2.4 CFS-PML参数选取研究

设置CFS-PML层数为8层，由于fσx/fαx在f≤fαx 的低频段起到了网格延拓的作用，那么fσx/fαx不 应变化太快.类似一般PML的参数选取方式(Berenge，1994)，令fσx 从CFS-PML内边界从0开始以线性的形式增长：

其中L为PML的厚度.假设场沿x方向传播，X=x. 定义CFS-PML吸收系数为

式中

式(28)中存在两个可控参数：fαx和L.吸收系数A越小代表额外吸收越强烈.很明显，吸收系数A是CFS-PML厚度L的递减函数，L越大，吸收越强烈.下面将对参数fαx选取作具体的分析.

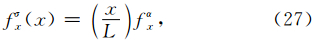
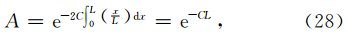
假设介质是均匀的，且电导率为σ=1×10－3S·m-1，场源到PML内边界的距离为L1=1400 m，PML厚度为L2=600 m，关注的最大时间为tmax=1 ms，那么抵达边界并穿过PML返回场内的最低频率为

CFS-PML仅需要对fmin以上的频率进行吸收.

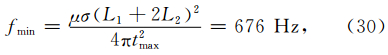
为比较CFS-PML在不同的fαx情况下对各频 段的吸收效果，分别选取fαx的值为500 Hz，1000 Hz，2000 Hz，4000 Hz，以及∞(此时CFS-PML对所有频率均为纯粹网格延拓)进行对比，结果如图 1所示.

图 1 不同参考频率fαx下CFS-PML对扩散场的额外吸收系数比较Fig. 1 The additional absorbing coefficient of CFS-PML under different reference frequencies

从图 1可以看出，吸收最强的点为f=fαx这一点.因此fαx的选取很重要.由于频率越高，自然衰减也越大，对CFS-PML的依赖性也就越小，因此fαx设置为fmin的4至几十倍均可，这个范围内CFS-PML虽然对远大于fαx的频率吸收很小，但是并不影响最终结果，同时保证了CFS-PML对低频段的吸收.图中虽然显示fαx=∞时吸收效果与其他fαx的吸收效果区别不是很大，尤其在低频段，但是纯粹的网格延拓还会导致部分频率因为网格变化太快而导致异常，本文的后续部分将会通过数值算例说明fαx=∞时的数值结果同样明显差于通过适当设置后的CFS-PML结果.

3 数值模拟结果及讨论

本文除巷道带异常体模型外，所有正演均采用相同的网格：网格数量为128×128×128，中央网格大小为Δxmin=Δymin=Δzmin=10 m，从中央到四周逐渐增加网格步长，最大处为Δxmax=10Δxmin，Δymax=10Δymin，Δzmax=7Δzmin.图 2描述了网格的主要特征.CFS-PML的层数为8层，已经包含在上述网格中.

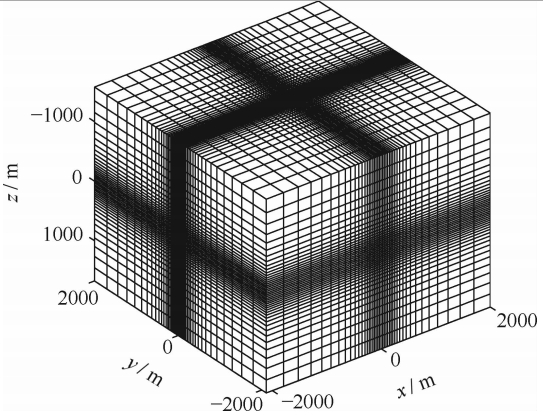图 2 瞬变电磁三维正演网格示意图Fig. 2 A sketch map of the mesh for TEM 3D forward modeling

3.1 均匀全空间

为了方便与理论解对比，我们采用了均匀全空 间模型.同时为了探讨CFS-PML对不同介质的适应 性，我们选取了两种不同的介质：σ=1×10－2S·m-1和σ=1×10－3S·m-1. 以水平正方形线框作为发射线框，线框边长L=70 m，垂直方向位于z=0处，水平方向位于x-y平面的正中央.采用脉冲形式的发射电流，最终比对垂直磁场Hz.

选择的测线为z=0和y=0平面的交线.我们定义在CFS-PML 与正常区域交接处Hz易号的时间 点为早期、晚期的分界点.首先对σ=1×10－2S·m-1 的三个早期时间点进行对比，根据牛之琏(2007)中 式(2-33)计算得到早晚期分界延迟时间约为4.5 ms，那么首先选取t=0.35 ms，1.23 ms和2.64 ms 三个时间点.图 3 为在上述三个时间点测线上分别使用CFS-PML、DBC得到的Hz值与理论值的对比.可以看出，在早期三者几乎一致.这是因为扩散场尚未或者刚刚抵达边界，边界条件的区别未能体现出来.因此在下文中，本文将着重扩散晚期的对比.

图 3 全空间σ=1×10－2S·m-1模型中，t=0.35 ms，1.23 ms和2.64 ms时使用CFS-PML吸收边界、DBC的Hz分量和理论解的对比 Fig. 3 The comparison among the Hz components obtained from CFS-PML，DBC， and the analytical solutions at the times of 0.35 ms，1.23 ms，and 2.64 ms of a whole space model with σ=1×10－2S·m-1

图 4为t=6.80 ms，12.50 ms，和20.00 ms时分别使用CFS-PML，DBC得到的Hz值和理论解的对比.可以看出t=6.8 ms时使用DBC的结果在边界处已经出现了较大的异常，随后这种异常开始扩散到场的中央，结果越来越偏离理论解.而使用CFS-PML吸收边界时，不管在中央还是在边界，Hz值依然和理论解符合得很好.CFS-PML的吸收作用在晚期非常显著.

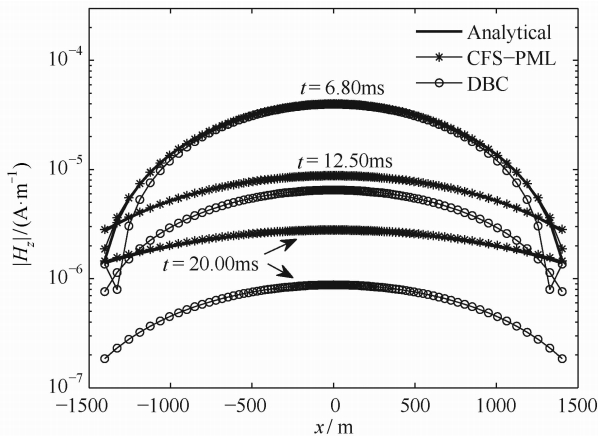图 4 全空间σ=1×10－2S·m-1模型中，t=6.80 ms，12.50 ms和20.00 ms时使用CFS-PML吸收边界条件、DBC的Hz分量和理论解的对比 Fig. 4 The comparison among the Hz components obtained from CFS-PML，DBC， and the analytical solutions at the times of 6.80 ms，12.50 ms， and 20.00 ms of a whole space model with σ=1×10－2S·m-1

图 5为σ=1×10－3S·m-1情况下不同时刻使用CFS-PML、DBC得到的Hz值和理论解之间的对 比，同时加入了CFS-PML中设置fαx=∞所得的结 果.σ=1×10－3S·m-1模型中场的扩散速度要明显 快于σ=1×10－2S·m-1的情况，但是两种情况下的场在一定的条件下具有相似性(王华军，2008).根据这种相似 性，t=2 ms时场的形态类似于σ=1×10-2 S·m-1 时t=20 ms情况下场的形态，因此本文将σ=1× 10－3S·m-1情况下最晚的一个时间点设定为t=2 ms.从图 5可以看出，在晚期CFS-PML的优势依然非常明显，而且经过适当设置后的CFS-PML也明显优于设置fαx=∞的CFS-PML.

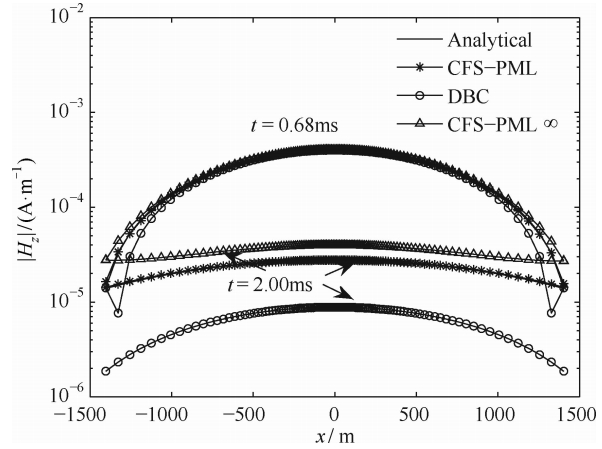图 5 全空间σ=1×10－3S·m-1模型中，t=0.680 ms和2.00 ms时使用CFS-PML吸收边界条件、DBC的Hz分量和理论解的对比，对比中还加入了在CFS-PML中设置fαx=∞所得的Hz分量Fig. 5 The comparison among the Hz components obtained from CFS-PML，DBC， and the analytical solutions at the times of 0.68 ms and 2.00 ms of a whole space model with σ=1×10－3S·m-1.The Hz component obtained from CFS-PML with fαx=∞ is also included for reference

为显示CFS-PML内部场的情况，我们将σ= 1×10－3S·m-1模型中2 ms时CFS-PML内外的场都描绘出来并与理论解进行对比，如图 6所示.可以看出，CFS-PML内部的场与理论解截然不同.CFS-PML内部出现了Hz 的正负变化，意味着涡流的存在，而理论解并没有Hz符号的变化.CFS-PML虽然不能将扩散场完全吸收，但是其在吸收的同时以某种方式将涡流限制在了CFS-PML内部，使得正常区域的扩散场不受影响.

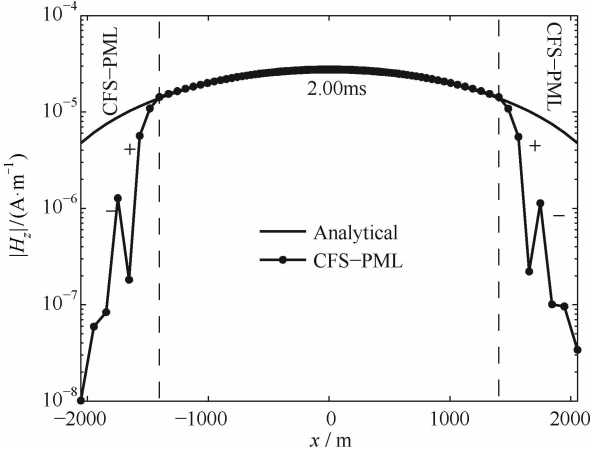图 6 全空间σ=1×10－3S·m-1模型CFS-PML内外Hz分量展示，并与理论解比较以体现CFS-PML内部场特征 Fig. 6 component in and out the CFS-PML of a whole space model with σ=1×10－3S·m-1 at 2 ms

3.2 均匀半空间

本文采用了李展辉和黄清华(2011)介绍的方法在半空间模型中引入空气层.由于空气层中波速远大于地下场的扩散速度，由式(10)可知，针对地下介质设计的CFS-PML在空气层中对波的吸收基本为零，因此在空气层中需要在CFS-PML介质内设置一定的电导率进行吸收.半空间模型中，地下介质的电导率设置为σ=1×10－2S·m-1，空气层中电导率设置为1×10-6S·m-1，并在靠近边界处逐渐增加.地空边界设置在z=0处，激励源的位置与形式均与全空间模型一致.

图 7显示了使用CFS-PML吸收边界、DBC所得到的Hz分量和理论解之间的对比.从图中可以看出，t=6.80 ms时使用DBC的Hz分量在两端已经偏离了理论解.随着时间的推移，误差越来越大，在20 ms时，误差已经在一个量级以上.而使用CFS-PML的Hz与理论解的吻合度大幅优于使用DBC的情况，但是也有一定的误差，而且这种误差也随时间的推移缓慢地增加.这可能是CFS-PML不能对空气层中的场产生有效的吸收造成的，越到 晚期越明显.图 8详细展示了线圈中心Hz相对误 差随时间变化.从图中可以看出，线圈中心相对误差 随着时间逐渐增加，在20 ms时误差达到了13%.实际应用中需要根据精度要求调整模型的大小以控制相对误差.

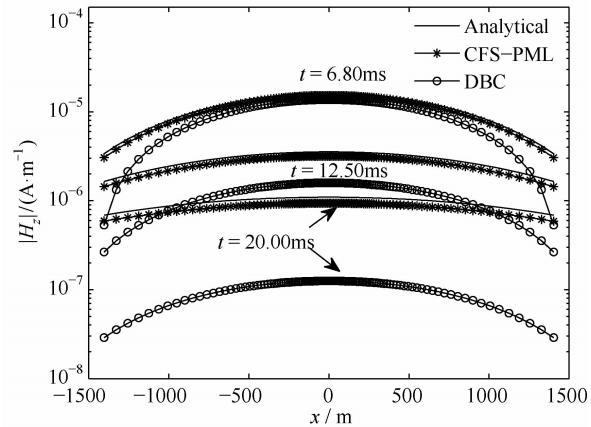图 7 半空间模型中，t=6.80 ms，12.50 ms和20.00 ms 时使用CFS-PML吸收边界条件、DBC的Hz分量和理论解的对比 Fig. 7 The comparisons among the Hz components obtained from CFS-PML，DBC， and the analytical solutions at the times of t=6.80 ms，12.50 ms， and 20.00 ms of a half space model

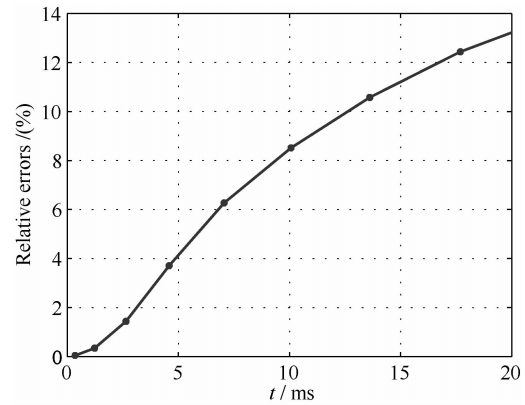图 8 回线中心Hz的相对误差随时间分布图 Fig. 8 The relative errors of Hz varying over time at the center of the rectangular loop

3.3 巷道模型

全空间瞬变电磁法典型的应用之一为煤矿巷道内地下水的探测(李宇等，2012； 于景邨等，2011；郭纯等，2006).模型如图 9所示.地下水所在的位置电导率较高，因此模型中设定围岩电导率为0.05 S·m-1，异常体电导率为0.5 S·m-1. 巷道内通常很狭小，因此发射线圈设定为3 m×3 m，并采用重叠回线的方式记录感应电压.由于该模型不存在理论解，为了获取类似理论解的参考解，我们将原网格x，y方向各增加60个网格，在z方向增加40个网格.总网格数量达到188×188×168，以保证在我们关心的时间窗内，边界反射场没有进入观测区域.考虑到模型尺寸问题，最大的延迟时间设置为0.6 ms，因为根据扩散深度公式(牛之琏，2007)

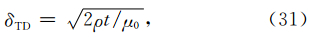
计算可得此时的扩散深度为124 m，已经超出了本模型范围.式(31)中ρ为电阻率，t为延迟时间.结果如图 10所示.从图中可以看出CFS-PML的结果与 参考解一直符合得很好，最终的相对误差不超过6%.
图 9 巷道内含异常体模型，模型关于y=0对称 Fig. 9 Underground roadway model with an anomalous body，which is symmetric about the y=0 plane

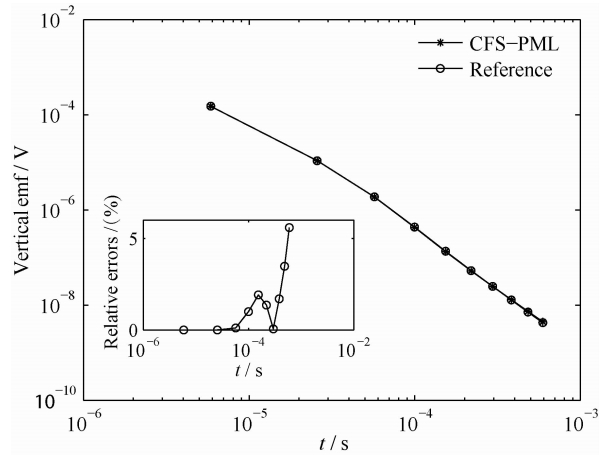图 10 巷道模型的重叠回线测量垂直感应电动势结果图，左下角的小图为相对于参考解的相对误差 Fig. 10 Vertical emf of the underground roadway model. The relative errors to the reference solution are shown in the embedded figure

4 结论

本文将CFS-PML应用到TEM三维FDTD正演中，通过适当地设置CFS-PML参数保证了数值计算的稳定性和良好的吸收效果.全空间和半空间数值结果表明CFS-PML在瞬变场早期与传统的狄利克雷边界条件的结果一致，晚期则明显优于狄利克雷边界条件的结果，并且能有效地节省计算时间和存储空间.但是针对地下扩散场设计的CFS-PML并不能有效地吸收空气中的电磁场，导致半空间模型结果到后期也产生一定的误差，并且随着时间缓慢的增长.实际应用中需要根据TEM正演的最大延迟时间以及对误差的容忍度适当调整模型的大小，以确保误差在要求之内.本文最后将CFS-PML应用到与实际情况贴近的巷道模型中，采用重叠回线测量感应电动势，并与参考解进行对比和误差分析，再一次证明了CFS-PML的有效性.

参考文献
[1] Bérenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics, 114(2): 185-200.
[2] Bérenger J P. 1996. Three-dimensional perfectly matched layer for the absorption of electromagnetic waves. Journal of Computational Physics, 127(2): 363-379.
[3] Bérenger J P. 1996. Perfectly matched layer for the FDTD solution of wave-structure interaction problems. IEEE Transactions on Antennas and Propagation, 44(1): 110-117.
[4] Bérenger J P. 2000. Numerical reflection of evanescent waves by PMLs: origin and interpretation in the FDTD case. Expected consequences to other finite methods. Int. J. Numer. Model, 13(2-3): 103-114.
[5] Bérenger J P. 2012. An optimized CFS-PML for wave-structure interaction problems. IEEE Transactions on Electromagnetic Compatibility, 54(2): 351-358.
[6] Chew W C, Weedon W H. 1994. A 3D perfectly matched medium from modified Maxwell's equations with stretched coordinates. Microwave and Optical Technology Letters, 7(13): 599-604.
[7] Commer M, Newman G. 2004. A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources. Geophysics, 69(5): 1192-1202.
[8] Endo M, Noguchi K. 2002. Three-dimensional modeling considering the topography for the case of the time-domain electromagnetic method. Amsterdam: Elsevier Science BV, 35: 85-107.
[9] Goldman M M, Stoyer C H. 1983. Finite-difference calculations of the transient field of an axially-symmetric earth for vertical magnetic dipole excitation. Geophysics, 48(7): 953-963.
[10] Guo C, Liu B Z, Bai D H. 2006. Prediction of water disasters ahead of tunneling in coal mine using continuous detection by UWTEM. Seismology and Geology (in Chinese), 28(3): 456-462.
[11] Ji J Z, Gao X, Liu Z H. 2008. Simplified format application of 2D two-rank Mur absorbing boundary condition. Journal of Shenyang Institute of Aeronautical Engineering (in Chinese), 25(2): 10-13.
[12] Jiang Y J, Mao J J, Cai S L. 2004. Implementation and analysis of the perfectly matched layer media with CFS for the PSTD method. Journal of Microwaves (in Chinese), 20(4): 36-39.
[13] Kuzuoglu M, Mittra R. 1996. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers. IEEE Microwave and Guided Wave Letters, 6(12): 447-449.
[14] Li D Z. 2010. Numerical Simulation of Transient Electromagnetic Fields (in Chinese) . Beijing: Peking University.
[15] Li Y, Tong B, Guo C F, et al. 2012. Study on application and denoising of mine full space transient electromagnetic method. Coal Engineering (in Chinese), (11): 29-31.
[16] Li Z H, Huang Q H, Wang Y B. 2009. A 3-D staggered grid PSTD method for borehole radar simulations in dispersive media. Chinese J. Geophys. (in Chinese), 52(7): 1915-1922.
[17] Li Z H, Huang Q H. 2011. A 3D curvilinear staggered-grid finite difference time-domain method with an impulse source for transient electromagnetic method. Chinese Geophysics (in Chinese), 240.
[18] Niu Z L. 2007. Principle of Time Domain Electromagnetic Method (in Chinese). Changsha: Central South University Press.
[19] Oristaglio M L, Hohmann G W. 1984. Diffusion of electromagnetic fields into a two-dimensional earth-a finite-difference approach. Geophysics, 49(7): 870-894.
[20] Qin Z, Hu W B. 2004. Modified Mur absorbing boundary conditions for lossy medium FDTD calculation. Journal of Jianghan Petroleum Institute (in Chinese), 26(2): 76-77.
[21] Roden J A, Gedney S D. 2000. Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media. Microwave and Optical Technology Letters, 27(5): 334-339.
[22] Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time. Chinese J. Geophys. (in Chinese), 56(3): 1049-1064.
[23] Wang H J. 2008. Time domain transient electromagnetism all time apparent resistivity translation algorithm. Chinese J. Geophys. (in Chinese), 51(6): 1936-1942.
[24] Wang T, Hohmann G W. 1993. A finite-difference, time-domain solution for 3-dimensional electromagnetic modeling. Geophysics, 58(6): 797-809.
[25] Xu Y C, Lin J, Li S Y, et al. 2012. Calculation of full-waveform airborne electromagnetic response with three-dimension finite-difference solution in time-domain. Chinese J. Geophys. (in Chinese), 55(6): 2105-2114.
[26] Yang H Y, Yue J H. 2009. Application of absorbing boundary condition in whole-space computation of transient electromagnetic response. Journal of China University of Mining & Technology (in Chinese), 38(2): 263-268.
[27] Yu J C, Liu Z Q, Liao J J, et al. 2011. Application of full space transient electromagnetic method to mine water prevention and control. Coal Science and Technology (in Chinese), 39(9): 110-113.
[28] Yue J H, Yang H Y, Hu B. 2007. 3D finite difference time domain numerical simulation for TEM in-mine. Progress in Geophysics (in Chinese), 22(6): 1904-1909.
[29] 郭纯, 刘白宙, 白登海. 2006. 地下全空间瞬变电磁技术在煤矿巷道掘进头的连续跟踪超前探测. 地震地质, 28(3): 456-462.
[30] 姬金祖, 高旭, 刘战合. 2008. 二维Mur二阶吸收边界条件简化格式的应用. 沈阳航空工业学院学报, 25(2): 10-13.
[31] 姜永金, 毛钧杰, 柴舜连. 2004. CFS-PML边界条件在PSTD算法中的实现与性能分析. 微波学报, 20(4): 36-39.
[32] 李墩柱. 2010. 地形起伏下的瞬变电磁场数值模拟[硕士论文]. 北京: 北京大学.
[33] 李宇, 童兵, 郭昌放等. 2012. 矿井全空间瞬变电磁法应用及其消噪研究. 煤炭工程, (11): 29-31.
[34] 李展辉, 黄清华, 王彦宾. 2009. 三维错格时域伪谱法在频散介质井中雷达模拟中的应用. 地球物理学报, 52(7): 1915-1922.
[35] 李展辉, 黄清华. 2011. 瞬变电磁正演之带激励源的三维曲线交错网格时域有限差分方法. 中国地球物理, 240.
[36] 牛之琏. 2007. 时间域电磁法原理. 长沙: 中南大学出版社.
[37] 秦臻, 胡文宝. 2004. 用于有耗介质FDTD计算的改进的Mur吸收边界条件. 江汉石油学院学报, 26(2): 76-77.
[38] 孙怀凤, 李貅, 李术才等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演. 地球物理学报, 56(3): 1049-1064.
[39] 王华军. 2008. 时间域瞬变电磁法全区视电阻率的平移算法. 地球物理学报, 51(6): 1936-1942.
[40] 许洋铖, 林君, 李肃义等. 2012. 全波形时间域航空电磁响应三维有限差分数值计算. 地球物理学报, 56(6): 2105-2114.
[41] 杨海燕, 岳建华. 2009. 吸收边界条件在全空间瞬变电磁计算中的应用. 中国矿业大学学报, 38(2): 263-268.
[42] 于景邨, 刘振庆, 廖俊杰等. 2011. 全空间瞬变电磁法在煤矿防治水中的应用. 煤炭科学技术, 39(9): 110-113.
[43] 岳建华, 杨海燕, 胡搏. 2007. 矿井瞬变电磁法三维时域有限差分数值模拟. 地球物理学进展, 22(6): 1904-1909.